1. Introduction
As a result of globalization, the distances that products travel from the producer to the final consumer have increased, so ensuring the constant flow of products in safe and quality environments have become a critical challenge from the point of view of logistics sustainability. In this sense, a tool that has been a valuable ally for proper planning of distribution networks is the vehicle routing problem (VRP), which belongs to the class of combinatorial optimization problems that have been studied extensively over the past several decades due to their multiple applications in everyday life [
1]. The VRP is focused on the proper and sustainable management of the elements that comprise the distribution system, a problem faced by thousands of companies and enterprises dedicated to the collection and/or delivery of goods in a distribution network.
Depending on each variant of the VRP, there can be different approaches to finding a solution, so the objectives and restrictions to be found in practice are very broad, offering the opportunity to apply different models and algorithms in the search for a solution that guarantees to secure the lowest cost possible based on the efficient use of the resources available in the distribution area. There are currently numerous research studies being carried out by different authors, in which they propose different solution algorithms of this problem [
2]. In the literature, the classic VRP model is characterized by the optimal design of routes, including the construction and selection of routes from a central depot to each customer and to which this vehicle must return upon completion of its distribution route. In this environment, it is necessary to fulfill different conditions or restrictions, such as visiting each customer only once to meet the demand (known), as well as respecting the different capacity restrictions on each type of vehicle if not heterogeneous, vehicle capacity, maximum distance covered, and working hours, with the main objective of finding the lowest cost when selecting distribution routes [
3]. The VRP has been the subject of research for many years due to the great scientific interest in its multiple applications to everyday problems, considered NP-complete problems, in which for it is not possible to find an optimal result in due time [
4].
Currently, many organizations focus their efforts on improving their different processes in order to be socially responsible, reduce costs, and increase profits. The area with the greatest interest in cost reduction in recent years has been logistics, especially in transport, which represents a direct impact upon the cost of the final product [
5]. It is essential to have a method that provides good management of the planning and programming of the different distribution and transport activities that aids in the suitable selection of the distribution route to each customer to minimize the costs associated with this process. To achieve this, it is necessary to use different tools, such as exact optimization, which employs mathematical models in the search of a solution that guarantees to attain the exact solution for small to midsize problems.
The aim of this research is to find a sufficiently robust and actionable solution to practical problems that seeks to streamline the different logistical processes of its distribution system via minimization of the costs associated with the system of transport to its main customers, considering that products are required in specific schedules (within time windows), vehicle capacities, and business hours. These must timely and quality solutions for the midsize instances operated by the company. To do this, a real case study is proposed to address the vehicle routing problem with hard time windows, i.e., each customer has a specific time window within which to be attended to meet demand. To achieve this, we propose a mathematical model based on mixed-integer linear programming, which contemplates the special case of the star distribution network, in which there are only direct routes between the distribution center and one of the customers for each vehicle trip.
2. Literature Review
Numerous works in the literature address the VRP, as well as multiple classifications, such as VRP with limited capacity, time windows, simultaneous deliveries and collections, and others.
A study into the distinct classifications of the VRP is presented in reference [
6], specifying the differences in the methods for modeling the objective functions of each variant of the problem, as well as the diverse restrictions. One of the most widely used variants in the VRP is the capacitated version of the problem. This variant considers that the destinations will be visited only once to deliver or collect products and its objective function is based on the minimization of the total distance covered by each of the vehicles. Another variant of this problem would be to consider simultaneous collections and deliveries for each customer, as well as restrictions on the product delivery or collection times for each customer.
The authors of reference [
7] propose that, due to the particular evolution of the VRP, it is necessary to include different aspects that were not previously considered, for example, multi-objective programming, since it is imperative to contemplate the need not only for reduction strategies but also for compliance with time windows and customer satisfaction. The aforementioned work also affirms that it is essential to find a balance between the environmental cost and the economic cost.
The research in reference [
8] describes, in general terms, the main characteristics of the VRP in use since its formulation in 1959, whose objective is to establish a set of routes to each geographically dispersed customer in one zone, complying with a series of limitations to minimize cost. In the past 10 years, great advances have been made regarding resolution techniques for large problems. It is also noted that the use of information technologies, such as global positioning systems, radio-frequency identification, and the use of high-capacity computerized information processing, favor the development of new techniques and models for obtaining efficient solutions in less time for large problems.
The use of heterogeneous vehicle fleets has given rise to the Heterogeneous Vehicle Routing Problem (HVRP) [
9], which aims to minimize the total distance covered on each route by each vehicle, satisfying each customer’s demand and including capacities in non-homogeneous vehicles and costs. It resolves the problem by applying a metaheuristic algorithm based on a taboo search, which works by accepting infeasible solutions with a penalty to give the search diversity, reaching quick and efficient solutions in comparison to the traditional method used by the company.
The work developed by the authors of reference [
10] presents the formulation of a mathematical model applied to the transport problem of two enterprises seeking to reduce operating costs in the logistics area, intending to improve their level of customer service and competitiveness.
In reference [
11], an exact programming model is proposed for programming deliveries from a central depot to each customer (meeting customer demand), looking to minimize the costs related to moving products throughout the distribution network. The results given by the algorithm show that for medium problems, quick, reliable, and valid solutions are obtained. Likewise, reference [
12] proposes the Fleet Size and Mix Vehicle Routing Problem with Time Windows (FSMVRPTW) for variations of the VRP and establishes that significant savings can be obtained by conjointly employing a knowledge base and computer-based and operations research tools.
Reference [
13] presents the VRP, considering multiple depots, classifying it as NP-hard. It presents a grouping technique (clustering) to generate initial solutions with a local search algorithm, an iterated location search (ILS) to obtain a quick solution that simultaneously seeks to establish the possible routes of a set of vehicles. The main objective is to determine the total distance covered by the vehicles in each route and to minimize that distance, considering the particular characteristics of the system in addition to the capacity of each depot and each vehicle. The performance of the proposed methodology is feasible and effective for resolving the problem in terms of the quality of the computational responses and the times obtained; a comparison was carried out with some testing instances in the literature.
In reference [
14], an alternative methodology was implemented to resolve the problem of flower collection and transportation, which used a model reflecting the stochastic behavior of the demand, where the solution method includes clusters for the collection points. This methodology required a model including the correct route design, the proper assignation of routes to trucks, and a regression model to obtain the equation of the total system cost. In reference [
15], the use of two heuristics is considered for resolving the vehicle routing problem, which considers a flexible demand in the mix of collection and delivery services, with restrictions on the maximum route duration, the main difference in the VRP with simultaneous collections and deliveries.
In reference [
16], two well-known strategies were implemented in delivery routes in urban areas—the first is the application of the capacitated VRP, and the second is the problem of loading plan optimization. This is based on the use of an approximation with a hybrid method of the two strategies and with the concept of robustness introduced into the route to guarantee a level of predefined service, according to vehicle performance.
In the work developed by the authors of reference [
12] for the case of large problems where computing time is of the essence when obtaining a solution, the use of Lagrangian relaxation is proposed to generate lower bounds [
17], which necessitates adding a penalty term to the objective function to avoid violating relaxed restrictions. When resolving the Lagrangian problem, a lower bound is returned for original optimal objective value minimization problems. Another technique can be applied later—for example, that of ant colony algorithms, simulated annealing, genetic algorithms, taboo search, and/or artificial neural networks—to seek a better solution to the problem [
18,
19].
The work presented in reference [
20] uses a discrete simulation to represent and analyze transport and distribution process performance in construction material mining enterprises. To this end, subjects such as construction materials, discrete simulation, transport, and distribution are covered. As a result of the article, the discrete simulation allows quantitatively analyzing transport and distribution performance, making it possible to measure the amounts mobilized, the efficiency of the process, and the use of resources.
A distribution network involves everything related to material delivery or collections; crucial elements to consider are the plant’s capacity, its distribution centers, and its transport fleet, to satisfy the demands of each customer in due time and manner. The efficient use of the logistical resources and the human capital are significant factors for meeting the objectives and challenges proposed in the logistics activities of an organization, with the result that the costs associated are minimal. The growing competition in today’s world stage, the introduction of new products with very short lifecycles, and growing customer demand have driven industrial organizations and enterprises to invest in improving their current logistics systems. The above added to the different changes in the systems of communication and technologies applied to transport systems (which aid and streamline movement) have contributed to the continuous development of logistics systems administration and management [
5].
Research into logistics is very varied and extensive, as can be observed in works such as reference [
21], in which the concept of logistics is managed from different perspectives, one of these being a business that establishes that suppliers must-have products to offer the customers, and that these must be provided in due time, manner, number, quality, undamaged, and at a minimal cost. Logistics addresses the flow of materials, of finished products, and the information associated with same (the flow of merchandise and the flow of information being developed in parallel), from the supplier to the customer, with the required quality, at the right place and right time, and a minimal cost. Logistics is that part of the process of the supply chain that plans, implements, and controls the flow and storage of products and services and related information, from the point of origin to the point of consumption, efficiently and at the lowest possible cost, to satisfy customer requirements [
22]. Logistics can also be called business logistics, emphasizing rapid customer response systems, distribution or delivery channel administration, industrial logistics, physical international distribution, supply chain administration, and currently, on a value network [
23]. Distribution channels allow marketing efforts to become a reality and are one of the main pillars in satisfying the end consumer [
24].
The objective consists of minimizing the total integrated transport cost by the sum of the costs of the trip, which includes the costs generated, whether due to arriving late or early to the customer, the cost of the fuel used to move from the central depot to each customer and vice versa, and meeting the demands of each customer while considering time windows, vehicle capacity, and distribution center restrictions, and duration of the workday.
In reference [
25], the importance of the transport and its impact on the company’s logistics distribution systems are weighted, so the proper use of the available logistical resources is at the center of most distribution route design problems. The cost associated with the transportation process represents between 10% and 20% of the total cost of the products [
26].
The work presented in reference [
27] establishes that land transport represents 75% of available transport utilized, making it the most widely used, followed by rail with 17%, maritime with 7%, and air with 1%. Among its main advantages are its door-to-door service, its flexibility due to a wide variety of adapted vehicles of all load types and volumes, and the speed and facility with which it can be coordinated with other means of transport. The main disadvantage is that it must be limited to the weight and volume of the load to be moved.
In many organizations, the planning of transport and distribution activities represents a serious decision-making problem. This situation has become increasingly important due to the contribution of distribution costs in the total product costs.
Many enterprises require a fleet of vehicles for the collection and/or delivery of products within a distribution network. The efficient programming and use of said fleet is the main problem in the majority of transport problems. Distribution area managers specifically ask themselves, how many, from which plant, and what capacity should the vehicles be to satisfy the demand of each customer at a minimal cost? This question is difficult to answer due to the substantial number of possible combinations among the mix of fleet and routes; this is at the heart of how the proposed model has been implemented in this work [
28].
There are currently two main variables that the business of cargo transport (VRP) focuses on. The first is the cost of fuel and the reduction in contaminant particle emissions into the environment. Therefore, cargo truck manufacturers have focused their attention over the last decade on technological development and innovation to achieve greater fuel consumption efficiency, seeking to gain a competitive advantage over rivals in the market that benefits the enterprise’s profitability. To increase truck carrying capacity, automotive equipment for more than 30 tons is being designed, with different interconnected equipment for greater load capacity and consolidation, thus maximizing the movement of goods in long hauls and reducing the transport cost [
29].
3. Methodology
The mathematical model proposed in reference [
28] was the foundation for the implementation of the practical problem addressed in this study. These works present an optimization model similar to the problem under study. Different modifications were made to adapt it to the problem addressed, which are based on the following:
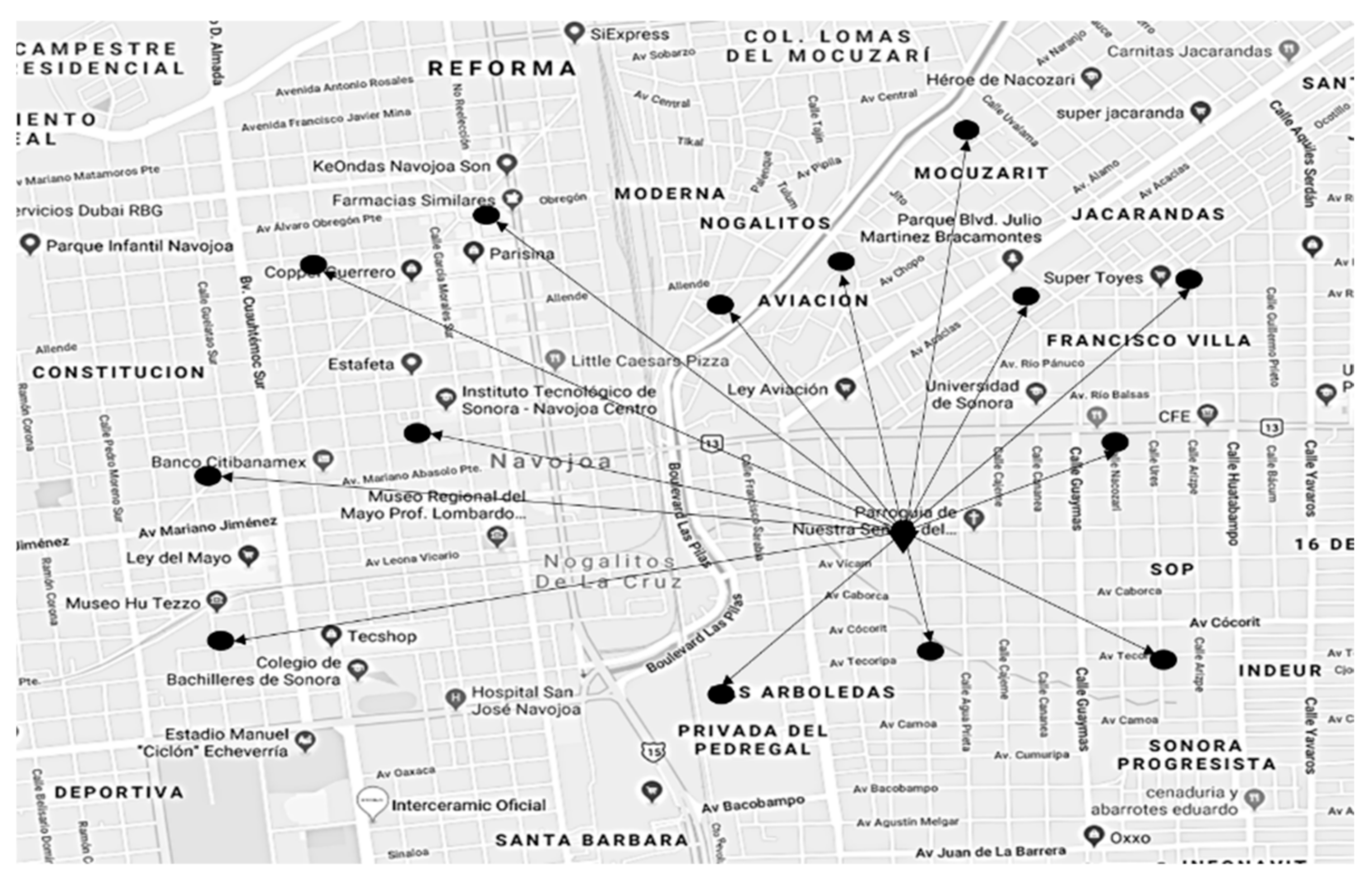
The transport network has a star configuration (
Figure 1), in which only one round trip per customer is allowed to meet the demand;
The time windows are closed, because unloading can only take place within an established timeframe, and the vehicle may not arrive either before or after the allocated time window, as this generates additional costs;
This problem is typical in those cases where the first and final destinations are the same point and not the customer;
The vehicles are assigned to a specific plant which forces you to return to this plant, that is to say a vehicle must start and finish its journey in the plant to which it is assigned.
One of the main differences between the model proposed in this real case study and the classic vehicle routing problems [
2] consists of the following: the assumption that, on one hand, the transport network has a star topology in those cases in which only direct routes are allowed, i.e., there can only be trips between the central depot and the customers, and, on the other hand, each customer can be visited several times (which can be by the same vehicle) in order to satisfy the demand.
Formulation of the model: sets, indices, and parameters used to characterize the model
Decision variables
Objective Function and Restrictions
The objective of the problem consists of determining a set of routes to be followed considering a fleet of heterogeneous vehicles that depart from one or more central depots or warehouses intending to satisfy the demand of various geographically dispersed customers, minimizing the total cost of product transport.
The resulting mathematical model in mixed-integer linear programming is presented below.
Equation (1) calculates the total transport cost, which includes the cost for visiting the customer, as well as the costs for deviations or non-compliance within the time windows for the different customers in the distribution network.
To ensure that for any trip, a vehicle is exactly in the plant (customer (0)) or visiting a customer, the following restriction is established (2):
An obligatory restriction in the majority of routing problems is that of meeting customer demand, which is established with Restriction (3), expressed by the following equation:
If a vehicle is used, the time-of-use conditions must be established as well as the departure time for each trip to be made. It is also established that a trip can only begin once vehicle k has returned to the depot after its previous trip. Restriction (4) is established for this purpose via the following expression:
This ensures that if on any trip
j, the customer is not visited (
) then there is no cost for arriving early, given that (
), otherwise, the time violation is calculated as standard, depending on Restriction (5) given by the following expression:
To estimate the cost of arriving after each customer’s closing time window, Restriction (6) is established, given by the following expression:
Here, M refers to a large positive integer to full fill . It must be clarified that in (5) and (6) only for , while only for , so for always .
Depending on the characteristics of the variables defined in the model, binary (0,1) and continuous variables are established. This situation is established through Restriction (7), given by the following expression:
4. Results
The present real case study addressed the vehicle routing problem with hard time windows, i.e., each customer has a specific time window within which to be attended to meet demand. To achieve this, a mathematical model based on mixed-integer linear programming was used, which contemplates the special case of the star distribution network, in which there are only direct routes between the distribution center and one of the customers for each vehicle trip.
An MIPL was obtained, represented by employing Expressions (1)–(7). The problem consists of the selection of transportation means (vehicles) within a distribution network composed of a single plant or distribution center, with vehicles of two distinct capacities and restrictions upon the windows of attention to each customer and the fulfillment of each customer’s demand. The solution must provide the number of vehicles necessary to meet the demand at a minimal cost or identify if the current fleet can face increasing customer demand.
In relation to the fulfillment of the time windows, although the model contemplates the option that the vehicle can reach the customer sooner or later by means of a penalty in the direct cost to the objective function, this situation is not presented for the practical case here addressed, since due to the nature of the VRP where it is sought to minimize total transportation costs, considering this penalty (which is very high) as an option that would result in an increase in the total cost of planning the route to follow.
The results obtained from the experimentation with the mathematical model applied are presented. An AMPL language was used for model implementation as well as CPLEX optimization software version 12.8 executed on a MacBook Pro with macOS High Sierra Version 10.13.4, with a 2.2 Ghz quad-core Intel Core i7 processor with 16 GB of RAM. The real case is performance in Navojoa Sonora, México. The model was used to resolve the practical problem of 22 customers, with a fleet of eight 48-ton capacity vehicles and two 20-ton capacity vehicles, with the demand and time windows known.
The intention is to obtain enough information to make the best decision that guarantees to reduce the costs associated with the distribution system; one important decision is the size and configuration of the fleet. It is important to consider that the results given by the model indicate that the current configuration is not suitable since there is the equipment of a greater capacity than is needed, as the trips normally made do not use 100% of the vehicle carrying capacity, leading to a deficit in the use of the equipment. The percentage of equipment use considering the demand is approximately 65%. Currently, 25 trips are made in total to meet customer demand, distributed as shown in
Table 1.
It can be seen that some of the vehicles make a greater number of trips than the rest, maintaining a standard deviation of 0.71 in the number of trips made, leading to the current discontent among equipment operators.
The total costs of distribution programming reported by the model ascend to 91,868 per operating day with the current vehicle fleet configuration. It is important to consider a more equitable distribution of each team’s trips to establish uniform workloads for each operator. Therefore,
Table 2 shows the trips carried made by each vehicle with the proposal for improvement in the number of pieces of equipment available, which was obtained by reducing the number of 40-ton capacity vehicles to be used from eight to two and increasing the number of 20-ton capacity vehicles from two to eight. Obtaining the same total transport cost with the difference in carrying capacity, which was increased to 78%. The standard deviation of the number of trips carried out by each vehicle was also improved to 0.52 of the total trips made.
Table 3 shows the trips made by each vehicle in a second proposal for improvements to the system, which consists of reducing to seven units in operation, considering a total of five 20-ton capacity units and two 40-ton capacity units. Although the total operating cost per day increases by 9980 per day, the equipment utilization rate of the total vehicle load capacity in improved to 87%.
5. Conclusions
It is of utmost importance to consider that the problem addressed considers atypical characteristics of a classic VRP, such as considering the star network and the fact that the same customer can be visited more than once to meet demand.
It was possible to satisfactorily resolve the real problem here addressed by applying a mathematical optimization model in addition to establishing two proposals for improvement to the fleet configuration, considering its size (amounts) and composition (capacities) suitable to the company’s available logistical resources.
First, the configuration maintains the same total number of vehicles but considers two 40-ton capacity vehicles and eight 20-ton capacity vehicles, resulting in the same total cost as the original but with a better workload distribution for the equipment operators and above all improving the equipment utilization rate without increasing the total distribution route programming cost.
Second, the reduction to seven units of the total number of vehicles available for use is recommended, considering two 40-ton capacity vehicles and five 20-ton capacity vehicles, where the total vehicle load utilization rate of 87% is considered the main contribution.
These two proposals for improvement are a significant contribution to the problem posed during the study and are considered of great value due to this being a real problem resolved through an exact method of mixed-integer linear programming for a case of 22 customers with capacity, demand, and time window restrictions.
This paper aims to contribute to the ONU sustainable development goal 12 to promote a responsibly consume of resource and energy efficiency, and sustainable use of the infrastructure.