Does Fertilizer Use Intensity Respond to the Urban-Rural Income Gap? Evidence from a Dynamic Panel-Data Analysis in China

1. Introduction

China’s agricultural productivity has experienced sustainable growth largely due to the application of chemical fertilizers since the late 1970s [1,2,3]. Over the period 1978–2017, the gross output value of agriculture in China has increased from 111.8 billion Chinese yuan to more than 5.8 trillion yuan with an average annual growth rate of 4.7 percent at the constant price [4]. In the context of a mild drop of sown area of grain crops, the total grain output in 2017 reached over 661.6 million tonnes, more than a twofold increase from 1978 [4]. Besides the institutional and technological changes, it has been well documented that the application of chemical fertilizers has contributed to the growth of agricultural productivity [3,5,6]. China has become the largest consumer of chemical fertilizers worldwide since 1981 [7,8]. According to official estimates, the total amount of chemical fertilizers in China’s agriculture has dramatically increased from 8.8 million tonnes in 1978 to 58.6 million tonnes in 2017 (Figure 1). Fertilizer use intensity has also increased from 58.9 kg per hectare (kg/ha) to 363.5 kg/ha in 2014, followed by a mild decrease to 352.3 kg/ha in 2017 (Figure 1).

However, the long-term and high dependency of farmers on chemical fertilizers results in the extensive overuse of chemical fertilizers, which severely threats the sustained development of agriculture in China [3,9]. In the economic sense, fertilizer overuse refers to that the actual level of fertilizer use exceeds its optimal level that maximizes agricultural profit [10]. Much literature has pointed out that farmers in China widely overuse chemical fertilizers to increase crop yield [3]. For example, the optimal amount of chemical fertilizers for maize production in China was approximately 249 kg/ha, while the actual amount of chemical fertilizers farmers used was 405 kg/ha [10]. A recent empirical analysis reveals that more than 80 percent of chemical fertilizers applied in rice production in China were overused [3]. In recent years, a growing body of literature documents the adverse effects of the overuse of chemical fertilizers, including agricultural non-point source pollution, greenhouse gas emission, water eutrophication, and soil salinization [11,12]. Hence, the sustained development of agriculture in China is facing grave challenges due to the overuse of chemical fertilizers.

While per capita rural income has increased by a large margin over the past four decades, the urban-rural income gap has also expanded. Due to the rural reform since the late 1970s, the urban-rural income ratio measured at the constant price shrank from 3.2 in 1978 to 1.9 in 1985 (Figure 2). In contrast, the continuous expansion of the urban-rural income gap since the late 1980s has caused social concerns [13]. In 2009, the urban-rural income ratio climbed to 3.1, which was the peak value over the past four decades (Figure 2). While the urban-rural income ratio has slightly fallen in recent years, it remained at 2.7 in 2017 (Figure 2). It has been repeatedly pointed out that the widening urban-rural income gap has been gravely challenging the sustained rural as well as overall economic development in China [14,15,16].

Both the urban-rural income gap and environmental degradation arising from excessive fertilizer use are detrimental to the sustainable development of agriculture and rural areas in China. In the context of deepening supply-side structural reform in agriculture and implementing the rural revitalization strategy, it is crucial to reduce fertilizer use to improve environmental quality and narrow the urban-rural income gap in China. Indeed, recent years have witnessed an increasing number of studies investigating the driving forces for fertilizer use as well as the effect of income inequality or gap on environmental degradation [3,10,17,18,19].

Note that the literature about the effect of income inequality on environmental degradation was extended from the so-called environmental Kuznets curve (EKC) hypothesis which describes a potential relationship between economic growth and the environment [20,21,22]. Many studies aimed to empirically examine the EKC hypothesis, but their conclusions are conflicting [21,22]. A group of empirical studies confirmed that an inverted U-shaped relationship exists between environmental degradation and per capita gross domestic product (GDP) or income. Using a cross-national panel dataset from the Global Environment Monitoring System, Seldon and Song concluded that per capita emission of suspended particulate materials, sulfur dioxide (SO₂), nitrogen oxide, and carbon monoxide showed a significant inverted U-shaped relationship with per capita GDP [23]. Jalil and Mahmud observed an inverted U-shaped relationship between per capita real GDP and CO₂ emission using a time series dataset of China from 1975 to 2005 [24]. Similarly, Riti et al. also supported the EKC hypothesis in China by applying different estimation techniques based on the annual time series data over the period 1970–2015 [25].

However, some studies questioned the validity of the EKC hypothesis. For example, using the data of 23 countries during the period 1974–1989, Kaufmann et al. found that the concentration of SO₂ falls as per capita GDP grows between 3000 to 12,500 United States dollars (USD), and then rises as per capita GDP rises beyond 12,500 USD [26]. Dinda et al. argued that per capita real GDP shows an explicitly negative and U-shaped relationship with the concentration of SO₂ and SPM, respectively, using the city-wise annual data for 33 countries during the three periods 1979–1982, 1983–1986, and 1987–1990 [27]. Recently, an empirical work conducted by Lin et al. re-examined the environment-income relationship in terms of CO₂ emission in five African countries, and denied the EKC hypothesis [28].

A considerable number of studies extended the EKC hypothesis to examine the relationship between income inequality and environmental degradation [18,19]. The pioneering work was conducted by Boyce who hypothesized that growing income inequality may increase the rate of environmental time preference of both the rich and poor, leading the two groups to take environmentally-damaging actions, and thus, the growing income inequality may induce environmental degradation by encouraging the rich to transfer the environmental costs to the poor [29]. Afterward, Torras and Boyce utilized the pooled ordinary least squares method to analyze the impact of inequality on air and water pollution but obtained contrasting results [30]. Using a cross-national dataset in terms of environmental degradation in 1985, Heerink et al. argued that higher inequality may reduce environmental degradation [31], which is contrary to the conclusion of Boyce [29]. Zhang and Zhao used the national and regional panel data from 1995 to 2010 in China to reveal that more equitable income distribution is useful for controlling CO₂ emissions [32]. Using a provincial panel dataset from 1995 to 2012 in China, Hao et al. argued that CO₂ emissions per capita increase as the income gap expands [33]. In the case of the United States, Jorgenson et al. showed that the state-level CO₂ emissions are positively associated with the income share of the top 10 percent based on the data over the period 1997–2012 [19]. Using a panel dataset of 158 countries from 1980 to 2008, Grunewald et al. argued that for low and middle-income countries, higher income inequality is associated with lower CO₂ emissions, while in upper-middle-income and high-income economies, higher income inequality increases per capita CO₂ emissions [18].

The previous studies have shed light on the relationship between environmental degradation and economic development. However, the conclusions are not consistent. Moreover, the relationship between the urban-rural income gap and environmental degradation, especially the environmental issues involving agriculture, attracts little attention. For example, little is known about the relationship between urban-rural income gap and fertilizer use, especially in China, the largest user of chemical fertilizers worldwide. Overall, the following three questions remain unanswered. First, does the relationship between fertilizer use and per capita rural income accord with the EKC hypothesis? Second, does fertilizer use respond to the change of the urban-rural income gap? Third, does there exist an interactive effect of per capita rural income and urban-rural income gap on fertilizer use? The motivation of this study is to answer the three questions in the case of China. For this purpose, a panel dataset covering 25 provincial-level administrative regions (hereafter referred to as “provinces”) over the period 1995–2017 was collected. The system Generalized Methods of Moments (GMM) was utilized to address the endogeneity issue of the dynamic panel-data model that describes the relationship between urban-rural income gap and fertilizer use intensity.

The novelty of this study to the literature is reflected in three aspects. First, this study enriches the literature regarding the EKC hypothesis by shedding light on the relationship between urban-rural income gap and fertilizer use intensity. Indeed, much literature attaches attention to the empirical studies on the EKC hypothesis for the impact of income inequality, rather than urban-rural income gap, on air and water pollutants, and deforestation [17,18,19,34,35,36]. However, little empirical evidence has been provided for the relationship between urban-rural income gap and agrochemical inputs in agricultural production, especially in the context of China. Second, note that the urban-rural income gap and excessive fertilizer use co-exist in many other developed and developing countries, and thus, the results of this study could have important implications for not only China but also for other countries regarding narrowing the urban-rural income gap and mitigating agricultural non-point source pollution by reducing fertilizer use. Third, the ordinary least squares method and the fixed-effects model were two widely used econometric techniques in the early previous studies, but these models ignore the endogeneity issue of income inequality [26,36]. In particular, the potential state dependence of environmental pollutants still remains neglected, though increasing attention has been attached to the endogeneity issue in recent years [28]. In this study, the adoption of the dynamic panel-data model and system GMM could capture the potential state dependence of fertilizer use, solve the potential endogeneity issue, and improve the estimation efficiency.

The remainder of this study is structured as follows. Section 2 constructs a theoretical framework to analyze the relationship between the urban-rural income gap and fertilizer use intensity, which provide a basis for the empirical analysis in this study. In Section 3, we first underline the path of empirical analysis, and then accordingly develop the econometric model. Meanwhile, the dependent and independent variables are defined, and the data source for the empirical analysis is described. The main results and robustness check are reported and discussed in Section 4. The final section concludes with some policy implications.

2. Theoretical Analysis

The previous literature has constructed some theoretical frameworks regarding the relationship between the income gap and environmental pollution [34]. However, the previous theoretical analysis is far from enough to reveal how fertilizer use intensity in agriculture would be associated with the urban-rural income gap. Hence, this study attempts to construct a theoretical framework to discuss the impact of the urban-rural income gap on fertilizer use intensity. The fundamental assumption in this study is that in the context of the urban-rural income gap, the relatively poorer rural households would endeavor to increase their income to narrow the income gap with urban households. The larger the urban-rural income gap is, the stronger the desire rural households have to increase their income.

Given the large urban-rural income gap, rural households could increase their income through agricultural productivity growth, in which fertilizer use plays a crucial role. The income components in China have experienced an impressive evolution since the reform and opening-up. Overall, while the percentage of non-agricultural income in per capita rural income ranged from 22.4 percent in 1995 to 40.9 percent in 2017, the percentage of business income remained at 37.4 percent in 2017 [4,37]. Note that agricultural business is the main source of rural households’ business income [38]. It illustrates that agricultural production still plays an important role in rural income growth [39]. When the urban-rural income gap becomes larger, rural households could increase fertilizer use to achieve high agricultural productivity to promote income growth [38,40].

The large urban-rural income gap could stimulate the rural labor force to seek for non-agricultural work in the urban areas for higher labor income, and thus, fertilizer use becomes a widely adopted measure to cover the shortage of agricultural labor force [41,42,43]. Since the early 1980s, the universal implementation of the household responsibility system has contributed to the rapid growth of agricultural productivity and correspondingly resulted in a large number of surplus rural labor force [42]. Over the past four decades, massive numbers of young rural laborers with relatively better health and education have been migrating to urban areas to pursue high non-agricultural income in the context of the large urban-rural income gap [44], which to some extent causes a shortage of the agricultural labor force [43,45]. To cover the shortage of the agricultural labor force, rural households would be much more likely to increase fertilizer use in agriculture [42].

In the context, it is reasonable to hypothesize that a larger urban-rural income gap would induce rural households to apply more fertilizers in agriculture.

3. Methods and Data

3.1. Econometric Model

In line with the theoretical analysis developed above, we conducted an empirical analysis as follows. While the theoretical analysis provided fundamental hypotheses to be validated, some other confounding factors of fertilizer use intensity were not included. To obtain the net impacts of per capita rural income and urban-rural income gap, an econometric model was developed based on the theoretical analysis to investigate the relationship between the urban-rural income gap and fertilizer use intensity. Hence, we first developed an initial panel-data model in which fertilizer use intensity was the dependent variable, and the linear and quadratic terms of per capita rural income, the urban-rural income gap, and other confounding factors were the independent variables. However, as previously argued, the application of chemical fertilizers and pesticides in agriculture might exhibit state dependence [38]. As a result, we extended the initial model by including a lag term of fertilizer use intensity as the second step. In the third step, an interaction term between per capita rural income and urban-rural income gap was further included to capture the interactive effect of these two variables on fertilizer use intensity. Taking these steps into account, the initial econometric model took the following form:

$$ln{F}_{it}={\alpha }_0+{\alpha }_{1}ln{y}_{it}+{\alpha }_2{\left(ln{y}_{it}\right)}^2+{\alpha }_3{G}_{it}+{\mathit{Z}}_{it}\mathit{\lambda }+\gamma T_t+v_i+u_{it}$$

(1)

where the subscript i and t refer to the i-th province and t-th year, respectively. The dependent variable lnF_it was fertilizer use intensity in its natural-logarithmic form. As for the independent variables, lny_it and (lny_it)² refer to the linear and quadratic terms of per capita rural income in their natural-logarithmic form, respectively. G_it, the variable of interest, denotes the urban-rural income gap. Z_it is a vector of control variables. In addition, T_t denotes the time trend term that describes technological progress, and v_i denotes the time-invariant effect. u_it is the independent identically distributed random error. α_j (j = 0, 1, 2, and 3), λ, and γ are coefficients to be estimated.

It was noted that the static panel-data model as described by Equation (1) ignores the state dependence of fertilizer use. Thus, a dynamic panel-data model including lnF_i,t−1 as the independent variable was developed as:

$$ln{F}_{it}={\alpha }_0+\phi ln{F}_{i,t-1}+{\alpha }_{1}ln{y}_{it}+{\alpha }_2{\left(ln{y}_{it}\right)}^2+{\alpha }_3{G}_{it}+{\mathit{Z}}_{it}\mathit{\lambda }+\gamma T_t+v_i+u_{it}.$$

(2)

Equation (2) does not take the potential interactive effect of per capita rural income and urban-rural income gap on fertilizer use intensity into account. To address this issue, we included the interaction term (lny_it × G_it) to test whether the relationship between urban-rural income gap and fertilizer use intensity depends on per capita rural income, as Equation (3):

$$ln{F}_{it}={\alpha }_0+\phi ln{F}_{i,t-1}+{\alpha }_{1}ln{y}_{it}+{\alpha }_2{\left(ln{y}_{it}\right)}^2+{\alpha }_3{G}_{it}+{\alpha }_{4}ln{y}_{it}\times G_{it}+{\mathit{Z}}_{it}\mathit{\lambda }+\gamma T_t+v_i+u_{it}.$$

(3)

However, the endogeneity issue emerged when Equations (2) and (3) were estimated using either the traditional fixed- or random-effects model, since lnF_i,t−1 may be correlated with the error term [46]. Firstly, some variables influencing fertilizer use intensity, rural income, and urban-rural income gap could have been omitted. Secondly, a reverse causality could have existed from fertilizer use intensity to rural income and the urban-rural income gap. To overcome the deficiency, the difference GMM was developed for the estimation of a dynamic panel-data model [47]. In detail, the difference GMM can remove the time-invariant unobserved effect with the help of the first-difference of the equation, and deal with the endogeneity by employing the lagged endogenous variables as the instrumental variables [48]. However, the lagged endogenous variables may lead to the weak instrument problem and further inefficient and biased estimation [49,50]. To address the weak instrument problem, the system GMM, a combination of the first-differencing and level equations, was developed [51,52]. Specifically, the difference of the lagged explained variable was used as the instrument for the lagged explained variable. There was evidence that the system GMM often performs better than the difference GMM, especially when the explained variable persists over time [53]. Thus, we used the system GMM to estimate Equations (2) and (3).

3.2. Variables

This study contained a vector of independent variables to control for the confounding impact. In addition to the dependent variable, the independent variables in this study included the lagged fertilizer use intensity, linear and quadratic terms of per capita rural income, the urban-rural income gap, interaction term of per capita rural income and the urban-rural income gap, percentage of non-agricultural income in per capita rural income, total sown area, percentage of the sown area in the total sown area by crop group, and the time trend term. The detailed definition of the dependent and independent variables was described as follows:

Fertilizer use intensity, the dependent variable, refers to the amount of chemical fertilizers used per hectare. It equals the total amount of chemical fertilizers divided by the total sown area for each province. To mitigate the potential heteroscedasticity, the natural-logarithmic form of fertilizer use intensity was adopted in the model.

Per capita rural income was an important independent variable. According to the EKC hypothesis, it was probable that the relationship between per capita rural income and fertilizer use intensity would be nonlinear, and thus, the quadratic term of per capita rural income was also included. It should be noted that the current value of per capita rural income was deflated with the rural consumer price indices. In the context, both per capita rural income and its quadratic term were measured at the 2017 constant price. Moreover, these income variables were also in their natural-logarithmic form.

The urban-rural income gap was the independent variable of interest in this study. The Theil index is widely used to measure the income gap or inequality in the literature [14]. Thus, we also used the Theil index to measure the urban-rural income gap in China. The calculation method for the Theil index (TL_it) is:

$$T{L}_{it}=\left(\frac{U{Y}_{it}}{Y_{it}}\right)\times \ln \left[\left(\frac{U{Y}_{it}}{Y_{it}}\right)÷\left(\frac{U{P}_{it}}{P_{it}}\right)\right]+\left(\frac{R{Y}_{it}}{Y_{it}}\right)\times \ln \left[\left(\frac{R{Y}_{it}}{Y_{it}}\right)÷\left(\frac{R{P}_{it}}{P_{it}}\right)\right]$$

(4)

where: Y_it is the sum of total urban and rural income; UY_it and RY_it refer to the total urban and rural income, respectively; P_it is the sum of the urban and rural population; and UP_it and RP_it refer to the urban and rural population, respectively. Similarly, the current value of per capita urban income was also deflated with the urban consumer price indices. Note that a higher Theil index implies a larger urban-rural income gap [14].

The percentage of non-agricultural income in per capita rural income was used to control for the impact of rural income components on fertilizer use intensity. Over the past decades, as argued, non-agricultural work has been playing an increasingly important role in rural income growth in China [4]. Logically, rural households depending more on non-agricultural income would attach less attention to agricultural production, because they earn their income mainly from non-agricultural work. Hence, it was assumed that rural households that depend more on non-agricultural work than the agricultural business might apply fewer fertilizers in agriculture.

The one-year lagged price indices of agricultural outputs were used to control for the market factor’s influence on fertilizer use intensity. It was reasonably assumed that rural households make decisions on fertilizer use based on what has happened to the price change of agricultural outputs [17]. In general, rural households might apply more fertilizers in agricultural production when the price of agricultural outputs grows faster. To avoid the potential endogeneity, we use the lagged rather than current price indices of agricultural outputs.

We include the total sown area in agriculture into the model. According to the previous studies, there might exist a scale effect of farm size on fertilizer use, and thus, there might exist a negative relationship between farm size and fertilizer use intensity [54]. In other words, a larger sown area in agriculture might reduce fertilizer use intensity, and vice versa.

In addition to the total sown area in agriculture, the percentages of the sown area for different crop types in the total sown area were also considered. It was apparent that the need for fertilizers in the production of different crops often greatly varies [55]. In this study, we divided crops into four types, namely grain, vegetable, oil, and other crops. Accordingly, the percentages of the sown area for vegetable, oil and other crops were included in the model, and that for grain crops was used as the control group.

In addition to the above variables, a time trend term was also included. As for panel data, a time trend term was often needed to control for the impact of technological progress on fertilizer use intensity [5]. In this study, the time trend term equaled the actual year minus 1995. In other words, the time trend term was zero for the year 1995, and 22 for the year 2017.

3.3. Data

Data used in this study come from multiple sources. In sum, this study employed balanced panel data covering 25 China’s provinces over the period 1995–2017. Provinces, namely Beijing, Shanghai, Tianjin, Chongqing, Hainan, and Tibet, were excluded due to the incompleteness and unavailability of data. Thus, we obtain a total sample of 575 observations. Since a dynamic panel data model was developed, the data covers the year 1994.

Overall, most of the data come from the National Data, an official website of the National Bureau of Statistics of China (http://data.stats.gov.cn/). Moreover, some are supplemented and adjusted using data from other sources. In sum, both per capita rural and urban income over the period 1994–2001 come from the China Compendium of Statistics (1949–2008). Data of total population come from the China Population and Employment Statistics Yearbook (2018), and data of the urban and rural population come from the China Compendium of Statistics (1949–2008), provincial-level statistical yearbooks over the period 1994–2004, and the National Data over the period 2005–2017. The rural consumer price indices of Guizhou in 1994, 1995, and 1997, as well as the net business income for all provinces over the period 1995–2001, and 2013–2017, come from the China Statistical Yearbook (1995–2002, and 2014–2018). Data of price indices of agricultural outputs were collected from the provincial-level statistical yearbooks for the year 1994 and 2001, the China Statistical Yearbook of Prices and Urban Household Income and Expenditure Survey (1996–2001) over the period 1995–2000, and the China Yearbook of Agricultural Price Survey (2004) for the year 2002.

Table 1. Descriptive statistics of the main variables.

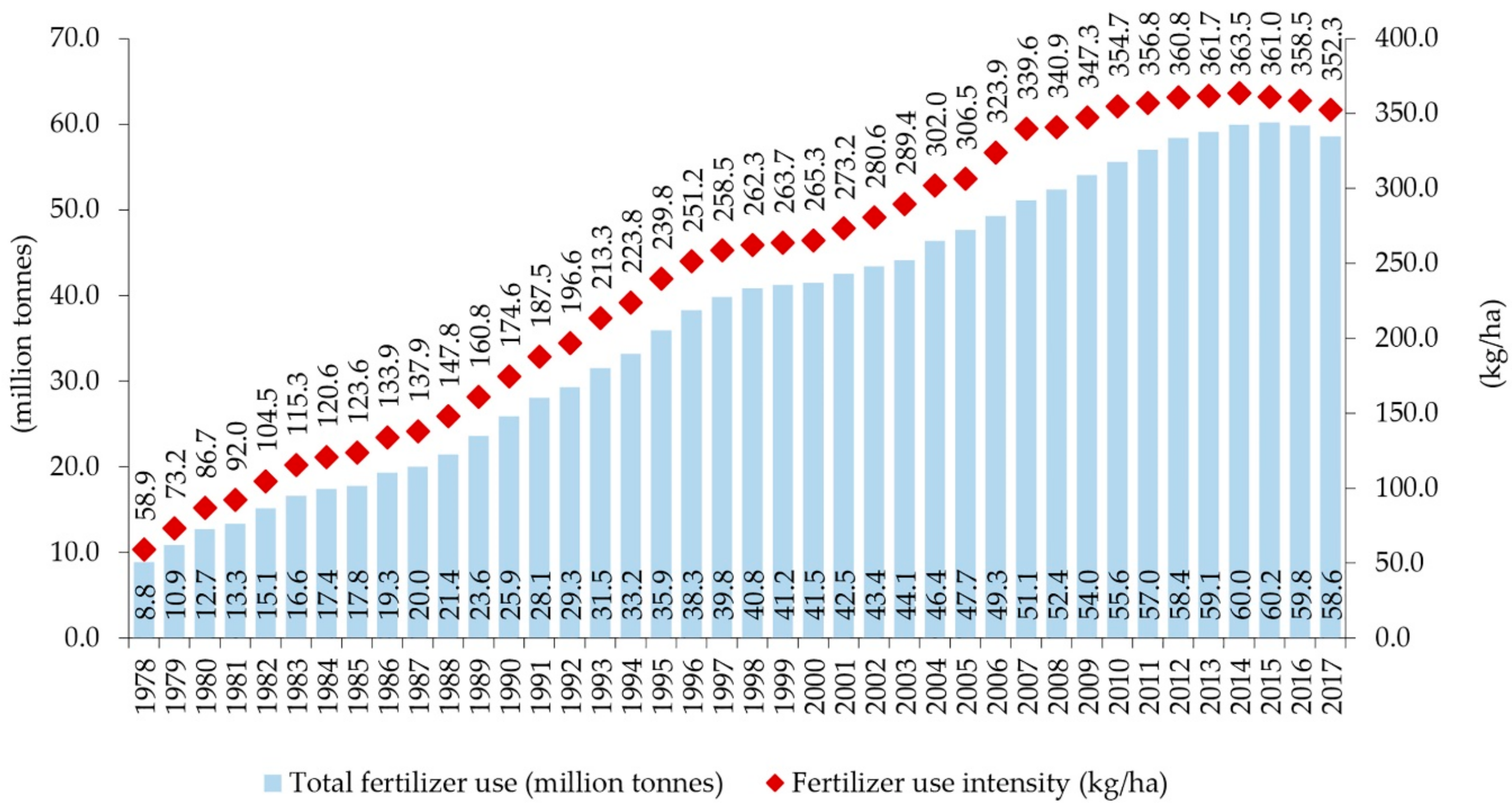
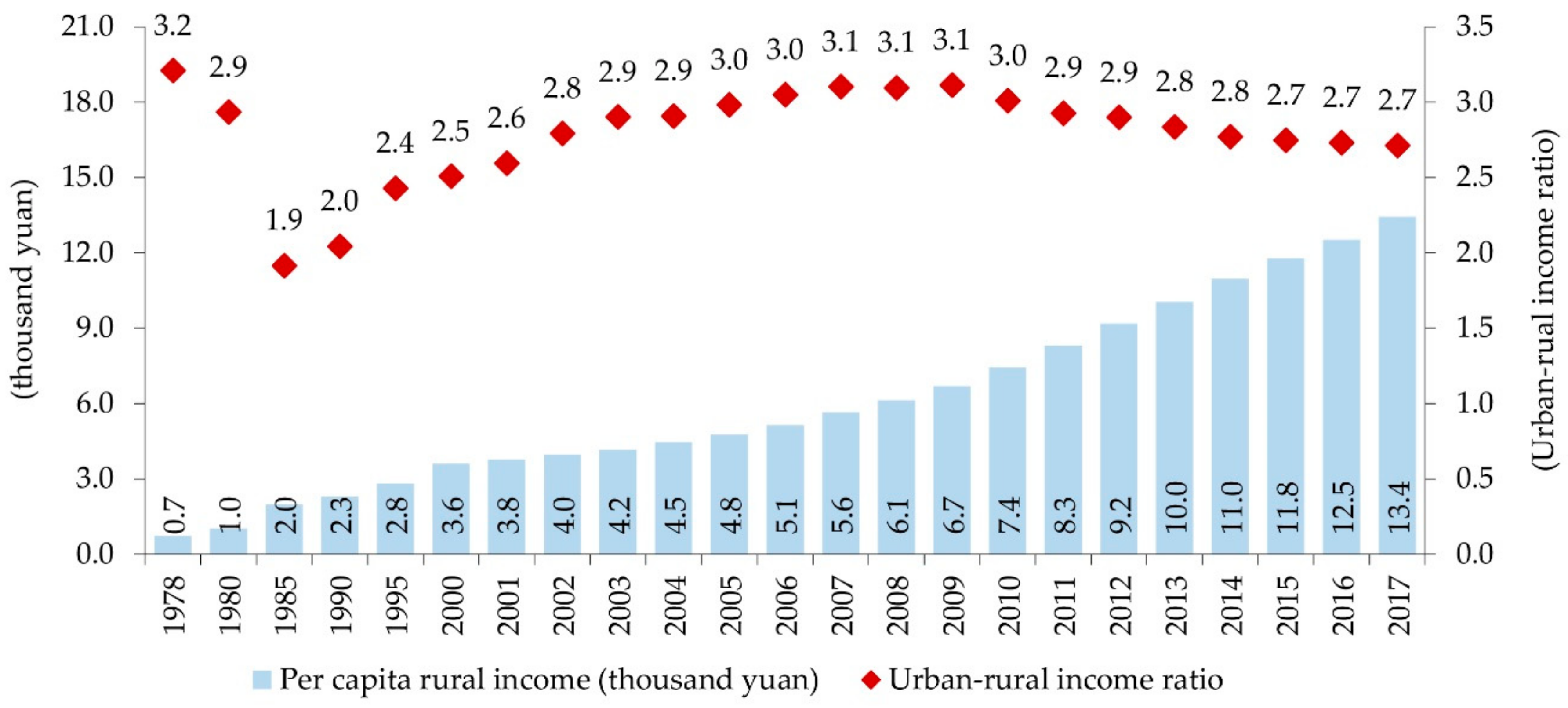
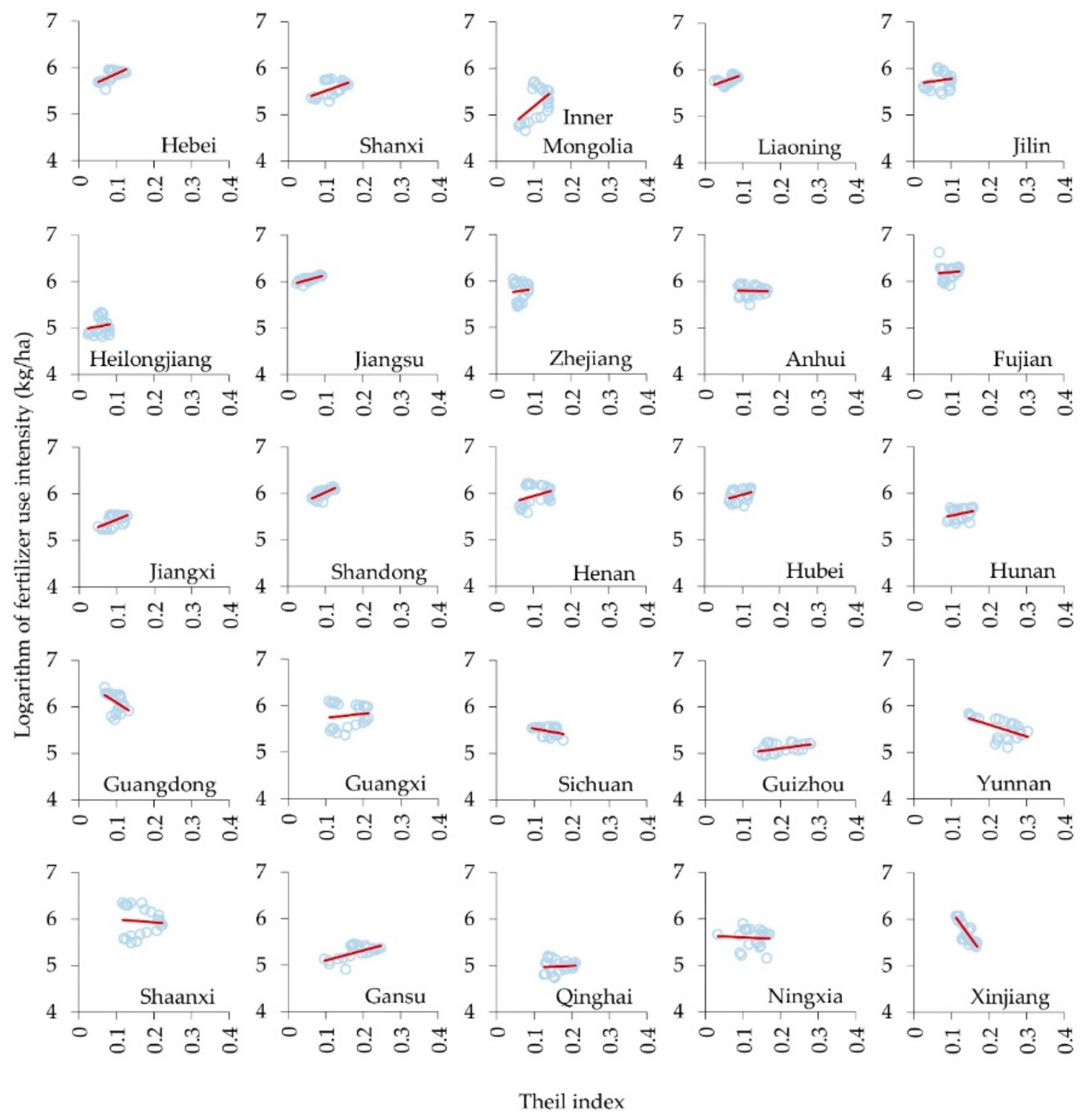
Variables	1995		2007		2017
	Mean	Standard Deviation	Mean	Standard Deviation	Mean	Standard Deviation
Fertilizer use intensity (kg/ha)	230.013	78.425	327.700	107.383	366.259	139.706
Per capita rural income (thousand yuan)	2.526	0.762	5.309	1.682	12.972	3.502
Theil index	0.115	0.050	0.151	0.057	0.094	0.032
% of non-agricultural income	24.624	8.453	43.517	10.758	59.944	9.168
One-year lagged price indices of agricultural outputs (%)	138.936	8.632	102.196	2.278	102.084	4.679
Total sown area (million ha)	5.743	2.916	5.929	3.316	6.447	3.720
% of the sown area of grain crops	73.199	8.818	67.238	12.899	67.627	14.908
% of the sown area of vegetable	6.090	3.434	11.607	6.988	13.351	9.099
% of the sown area of oil crops	9.198	5.251	7.753	5.656	8.366	5.920
% of the sown area of other crops	11.513	6.899	13.402	11.094	10.657	10.521

Note: Per capita rural income was measured at a 2017 constant price.

summarizes the descriptive statistics of the main variables in 1995, 2007, and 2017.

4. Results and Discussion

4.1. Urban-Rural Income Gap and Fertilizer Use Intensity

Figure 3 plots fertilizer use intensity in the natural-logarithmic form against the Theil index by province. In most of the provinces, an obviously positive relationship exists between fertilizer use intensity and the Theil index, which means that as the urban-rural income gap expands, there would be an increase in fertilizer use intensity. However, there are also several provinces in which the relationship between fertilizer use intensity and the Theil index was found to be negative, such as Guangdong, Sichuan, Yunnan, and Xinjiang (Figure 3). Nonetheless, it is more likely that the expansion of the urban-rural income gap would stimulate fertilizer use in agriculture in most of the provinces. Meanwhile, there is also a disparity of the positive relationship that was noted between fertilizer use intensity and the urban-rural income gap across provinces.

4.2. Main Results

Table 2. Impact of the Theil index on fertilizer use intensity.

Dependent Variable	Model I		Model II
	Coefficient	Standard Error	Coefficient	Standard Error
Ln(Fertilizer use intensity)	0.597 ***	0.148	0.630 ***	0.158
Ln(Per capita rural income)	0.746 ***	0.272	1.052 ***	0.350
[Ln(Per capita rural income)]2	−0.097 ***	0.037	−0.138 ***	0.050
Theil index	0.885 **	0.437	2.106 **	0.959
Ln(Per capita rural income) × Theil index			−1.029	0.697
% of non-agricultural income	−0.001	0.001	−0.002 *	0.001
One-year lagged price indices of agricultural outputs	0.001 ***	0.000	0.001 ***	0.000
Total sown area	−0.061 **	0.027	−0.084 ***	0.032
% of the sown area of vegetable	0.003	0.002	0.002	0.003
% of the sown area of oil crops	−0.002	0.002	−0.002	0.002
% of the sown area of other crops	−0.000	0.002	0.001	0.002
Trend	−0.019 **	0.009	−0.022 **	0.010
Constant	1.814 **	0.716	1.460 *	0.775
Sargan test	12.190		10.579
A-B test for AR (1)	−2.495 **		−2.470 **
A-B test for AR (2)	0.564		0.651
Observations	575		575
Provinces	25		25
Peak turning point (thousand yuan)	46.776		45.222

Note: The value of statistics is reported for Sargan and A-B tests. *, **, and *** denote the significance under 10, 5, and 1 percent, respectively.

reports the main estimation results. For ease of comparison, the estimation results for Model I (without the interactive effect), and Model II (with the interactive effect) are summarized. Several tests were conducted on the validity of the models. First, we conducted the Sargan test to examine whether the instrumental variables in the system GMM estimation are valid. As shown in Table 2, the statistics of the Sargan test are not statistically significant. We also conducted the Arellano-Bond (A-B) tests for the first-order auto-regression [AR (1)] and AR (2) to determine whether the first- and second-order autocorrelation of the error term exists. The statistics of the A-B test for AR (1) are significant at 5 percent, while those for AR (2) are not significant (Table 2), which means that significant autocorrelation of the error term does not exist. All these results demonstrate that the instrumental variables used in the system GMM estimation are valid.

The results illustrate that an inverted U-shaped relationship exists between fertilizer use intensity and per capita rural income, which is consistent with the EKC hypothesis. As shown in Table 2, the estimated coefficients of Ln(Per capita rural income) and [Ln(Per capita rural income)]² are significantly positive and negative, respectively. Theoretically, it seems to provide evidence that fertilizer use intensity would first increase, and then decrease with the growth of per capita rural income. Based on the first-order partially derivative, we calculated the peak turning point of per capita rural income at which fertilizer use intensity reaches the highest level with other factors held constant. The turning point can be calculated using the estimated coefficients of the linear (α₁) and quadratic terms (α₂) of per capita rural income. Specifically, the peak turning point equals the formula $\exp (\frac{-{\alpha }_1}{2\times {\alpha }_2})$. As for Model I and Model II, the peak turning point of per capita rural income is about 46,776 and 45,222 yuan, respectively (Table 2). Since per capita rural income in 2017 ranges from 8076 to 24,956 yuan across provinces, the results in this study demonstrate that fertilizer use intensity would further increase with the growth of per capita rural income across all the provinces.

More importantly, the expansion of the urban-rural income gap would result in an increase in fertilizer use intensity. The estimated coefficients of the Theil index are of great interest in this study. As shown in Table 2, the estimated coefficients of the Theil index are significant and positive, which indicates that fertilizer use intensity would increase as the urban-rural income gap expands. Our analysis here is based on the results of Model I. With other factors held constant, each 0.1 increase in the Theil index would result in an 8.85 percent (= 0.1 × 0.885 × 100 percent) increase in fertilizer use intensity (Table 2). Overall, the results provide firm evidence for the theoretical analysis in Section 2 and are consistent with the previous studies that assert the positive relationship between the income gap and environmental degradation [32,38]. In the context of reducing fertilizer use in agriculture, it is an urgent need for China to take firm steps to narrow the urban-rural income gap in the coming years.

However, the results in Table 2 show no significant interactive effect of per capita rural income and urban-rural income gap on fertilizer use intensity. As shown in Table 2, the estimated coefficient of the interaction term between Ln(Per capita rural income) and the Theil index is not statistically significant in Model II. This means that the positive impact of the urban-rural income gap on fertilizer use intensity would not be influenced by per capita rural income. It also means that the inverted U-shaped relationship between per capita rural income and fertilizer use intensity is not influenced by the urban-rural income gap.

In addition to per capita rural income and the urban-rural income gap, the price change of agricultural outputs could also influence fertilizer use intensity. As shown in Table 2, the estimated coefficients of one-year lagged price indices of agricultural outputs are significant and positive, implying that the faster growth of agricultural outputs price would stimulate rural households to apply more fertilizers in agricultural production. With other factors held constant, each 10-percentage-point increase in the lagged price indices of agricultural outputs would result in one percent (= 10 × 0.001 × 100 percent) increase in fertilizer use intensity (Table 2). Our results, here again, reveal that rural households’ fertilizer use could be partly regarded as a response to the benefit of agricultural production. In other words, rural households are regarded as rational entities, and thus, they would be inclined to apply more fertilizers in agricultural production when they have a higher profit expectation [56]. In this context, the growth of agricultural products price would induce them to use more fertilizers in agricultural production. The conclusions of many previous studies are consistent with the findings in the present study [3,56].

The results in Table 2 also show a significantly negative relationship between the total sown area and fertilizer use intensity. According to the results of Model I, each million-ha increase in the total sown area is significantly associated with a 6.1-percent increase in fertilizer use intensity, with other factors held constant (Table 2). As some previous studies argued, farm size might produce the scale effect of fertilizer use, implying that fertilizer use intensity would be likely to decrease as farm size becomes larger [54]. However, although our result supports the existence of scale effect of farm size on fertilizer use intensity, it should be viewed with caution. In China, most rural households are smallholders according to the definition given by the World Bank [57]. Lowder et al. showed that the average size of farms managed by rural households in China was merely 0.6 ha in 2010, falling from 0.67 ha in 2000 [58]. As previously argued, the relatively smaller farm size at the micro-level in China contributes to the overuse of fertilizers in agricultural production [59].

We also found that the coefficients of the time trend term are significant and negative (Table 2). This illustrates that with the development of fertilization technology, rural households apply fewer fertilizers in agricultural production. During the past four decades since 1978, China has been achieving great progress in agricultural technological innovation [6,60,61]. In terms of fertilizer use, not only fertilization techniques but also more types of efficient fertilizers have been developed, extended, and widely adopted in agricultural production [62]. As a result, a negative impact of technological progress on fertilizer use intensity is within our expectations.

4.3. Robustness Check

To check the robustness of regression results analyzed above, we adopted the urban-rural income ratio as an alternative to the Theil index to re-run Equations (2) and (3). Note that the urban-rural income ratio has also been widely adopted as a proxy of the urban-rural income gap in the existing literature [63,64].

Table 3. Impact of the urban-rural income ratio on fertilizer use intensity.

Dependent Variable	Model III		Model IV
	Coefficient	Standard Error	Coefficient	Standard Error
Ln(Fertilizer use intensity)	0.639 ***	0.137	0.666 ***	0.144
Ln(Per capita rural income)	0.668 ***	0.259	1.186 **	0.463
[Ln(Per capita rural income)]2	−0.093 **	0.036	−0.137 **	0.056
Urban-rural income ratio	0.062 *	0.036	0.186 **	0.090
Ln(Per capita rural income) × Urban-rural income ratio			−0.092	0.058
% of non-agricultural income	−0.001	0.001	−0.002 *	0.001
One-year lagged price indices of agricultural outputs	0.001 ***	0.000	0.001 ***	0.000
Total sown area	−0.058 **	0.027	−0.079 **	0.031
% of the sown area of vegetable	0.004 *	0.002	0.003	0.002
% of the sown area of oil crops	−0.002	0.002	−0.002	0.002
% of the sown area of other crops	0.000	0.002	−0.000	0.002
Trend	−0.016 *	0.009	−0.023 **	0.011
Constant	1.549 **	0.662	0.965	0.699
Sargan test	12.763		11.502
A-B test for AR (1)	−2.670 ***		−2.651 ***
A-B test for AR (2)	0.576		0.651
Observations	575		575
Provinces	25		25
Peak turning point (thousand yuan)	36.285		75.828

Note: The value of statistics is reported for Sargan and A-B tests. *, **, and *** denote the significance under 10, 5, and 1 percent, respectively.

reports the system GMM estimation results for the robustness check. It is apparent that the Sargan test and A-B tests for AR (1) and AR (2) jointly confirm that the instrumental variables in the system GMM estimation are valid, which is consistent with the results shown in Table 2. As expected, the sign and significance of the coefficients of all the independent variables are consistent with that shown in Table 2, which confirms the robustness.

Table 3 also shows that there is a significant and positive relationship between fertilizer use intensity and the urban-rural income ratio, which again confirms that the expansion of the urban-rural income gap would stimulate rural households to apply more fertilizers in agricultural production. The estimated coefficients of linear and quadratic terms of per capita rural income are significantly positive and negative, respectively, which means that there is an inverted U-shaped relationship between fertilizer use intensity and per capita rural income. The further calculation reveals that the peak turning point of per capita rural income here equals 36.285 and 75.828 yuan for Model III and IV, respectively (Table 3). Although the values of turning point differ from those in Table 2 to some extent, they are also much higher than the per capita rural income for all provinces in 2017.

5. Conclusions and Policy Implications

A large urban-rural income gap and excessive fertilizer use have challenged the sustainable development of agriculture and rural areas in China. In recent years, China’s government has been determined to narrow the urban-rural income gap and reduce fertilizer use. However, it was unclear whether there is a link between the urban-rural income gap and fertilizer use. This study aimed to investigate the relationship of the urban-rural income gap and fertilizer use intensity based on panel data covering 25 provinces in China over the period 1995–2017.

The estimation results of the system GMM show that the expansion of the urban-rural income gap would significantly increase fertilizer use intensity, which does not depend on per capita rural income. There is an inverted U-shaped relationship between per capita rural income and fertilizer use intensity, which supports the EKC hypothesis. However, the estimated peak turning point of per capita rural income is much higher than the actual level of all provinces in 2017, implying that fertilizer use intensity would further increase as per capita rural income grows in certain years. In addition, fertilizer use could also be regarded as a response to the change of agricultural products price and total sown area, and technological development.

The findings in this study have some significant implications for China as follows:

First, China’s government is expected to take practical measures to increase per capita rural income so as to narrow the urban-rural income gap. Our results demonstrate that narrowing the urban-rural income gap and reducing fertilizer use in China are compatible long-term aims. Although fertilizer use intensity would probably increase as per capita rural income grows over a certain period of time, it is better to consider these issues from a forward-looking perspective. In the short term, there would be a trade-off between the growth of per capita rural income and reduction of fertilizer use intensity, since the per capita rural income of all provinces remains at the left side of the inverted U-shaped curve. However, it is fundamental to stride across the peak turning point of per capita rural income to reduce fertilizer use intensity. More importantly, the narrowing urban-rural income gap would also significantly hinder the increase in and even promote the reduction of fertilizer use intensity.

Second, agricultural research and development (R&D) and extension should be encouraged to provide a firm foundation for reducing fertilizer use intensity. The findings in this study show that the estimated coefficient of time trend term used to measure agricultural technological progress is negative, implying that fertilizer use intensity would significantly decrease with the progress of agricultural technology. Hence, enhancing the R&D and extension of agricultural fertilization technology would be greatly conducive to the reduction of fertilizer use intensity. Some previous studies reveal that while agricultural R&D and extension have made a great contribution to agricultural production in China, some problems remain to be solved [65,66,67,68,69,70]. China’s government should deepen the reform of agricultural R&D and extension systems to meet the urgent need for the sustainable development of agriculture.

Third, it is reasonable to promote the conversion of cultivated land and appropriately scaled-up agricultural business. The findings in this study show that fertilizer use intensity would significantly decrease as the provincial-level total sown area expands. In fact, some previous studies also reveal that a negative relationship exists between farm size and fertilizer use intensity [54], which means that farm size has a scale effect on fertilizer use. Meanwhile, it should be noted that agricultural production in China has been being challenged by extensive rural-urban migration of the rural labor force, aging of the agricultural labor force, and small-scale farming systems. Hence, it is crucial for China to encourage and promote the conversion of cultivated land in a reasonable and orderly pattern and appropriately scaled-up agricultural business, which would further promote the reduction of fertilizer use intensity.

This study has several limitations. First, the study failed to examine the impact mechanism of the urban-rural income gap on fertilizer use intensity at the micro-level, which implies a great room for improvement in the future. Second, this study did not further investigate the impact of the urban-rural income gap on fertilizer use in the production of specific crops due to data availability. These two aspects are the research directions for further investigation about the relationship between the urban-rural income gap and fertilizer use intensity in agriculture.