Time Reliability of the Maritime Transportation Network for China’s Crude Oil Imports

Abstract

To evaluate the transportation time reliability of the maritime transportation network for China’s crude oil imports under node capacity variations resulting from extreme events, a framework incorporating bi-level programming and a Monte Carlo simulation is proposed in this paper. Under this framework, the imported crude oil volume from each source country is considered to be a decision variable, and may change in correspondence to node capacity variations. The evaluation results illustrate that when strait or canal nodes were subject to capacity variations, the network transportation time reliability was relatively low. Conversely, the transportation time reliability was relatively high when port nodes were under capacity variations. In addition, the Taiwan Strait, the Strait of Hormuz, and the Strait of Malacca were identified as vulnerable nodes according to the transportation time reliability results. These results can assist government decision-makers and tanker company strategic planners to better plan crude oil import and transportation strategies.

1. Introduction

According to the U.S. Energy Information Administration (EIA), China surpassed the United States in 2017 as the world’s largest crude oil importer, and more than 90% of the imported crude oil is carried by maritime transportation [1]. The transportation time reliability of maritime transportation will affect the timely supply of crude oil, which affects the smooth operation of the national economy.

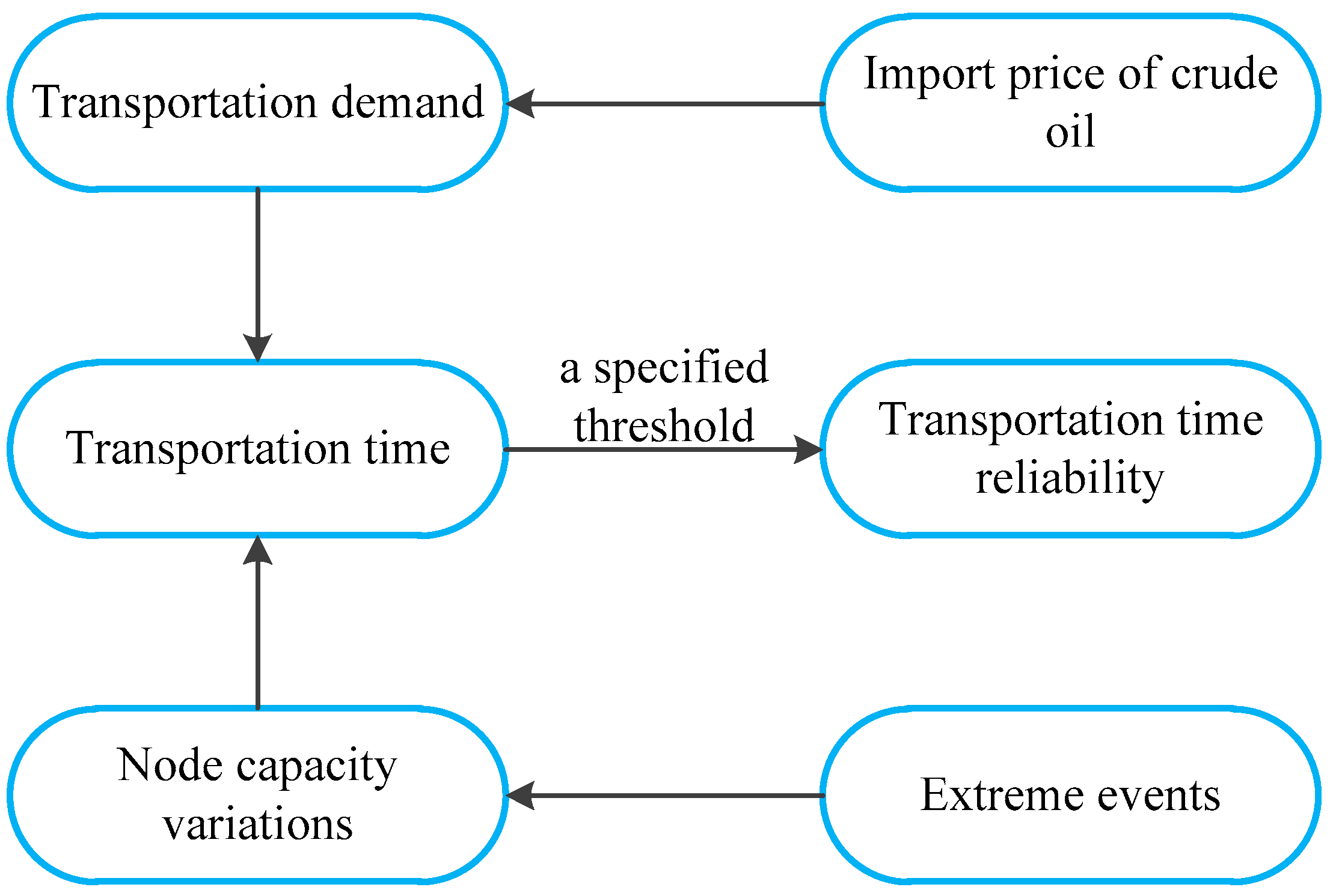
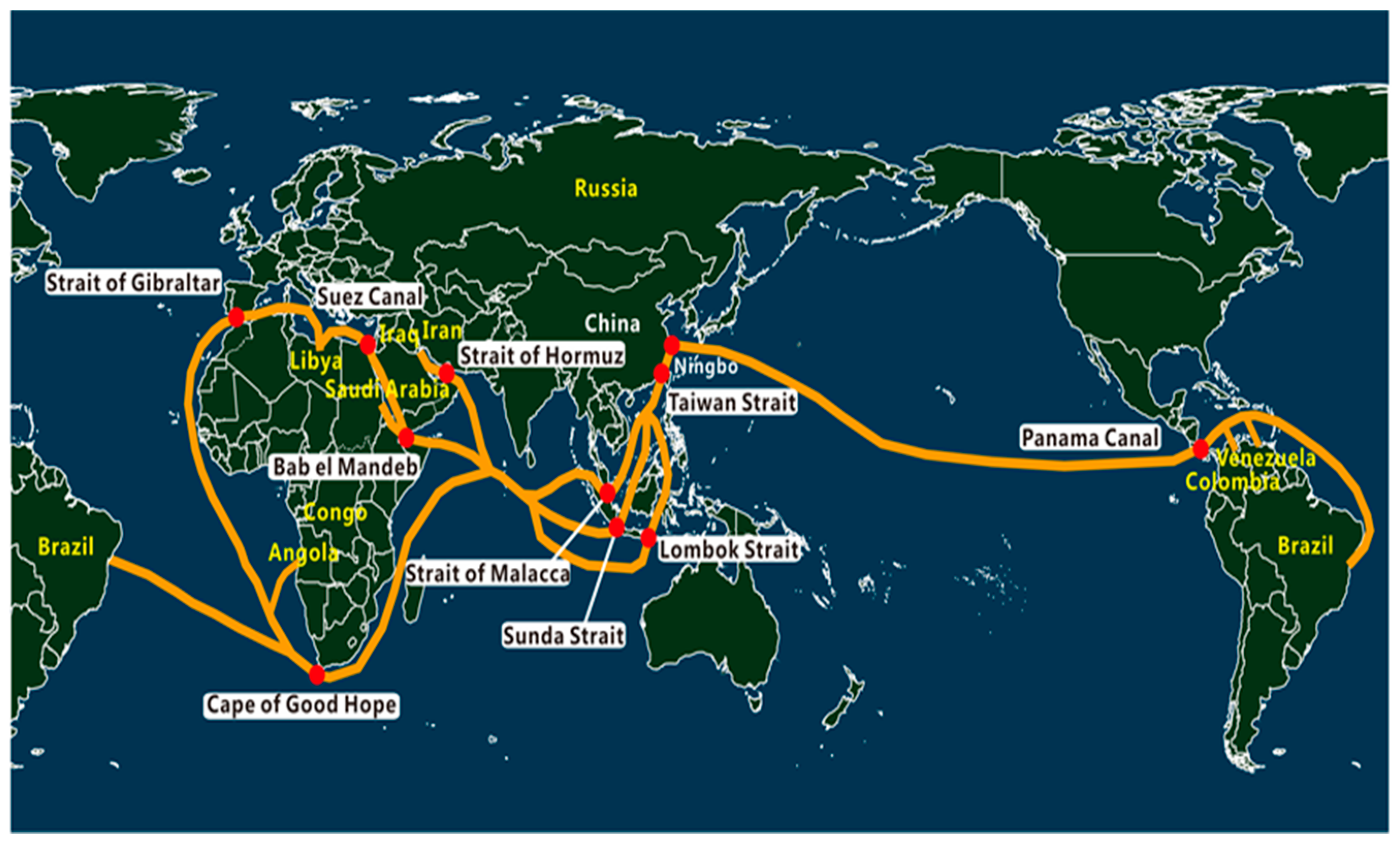
Transportation time reliability is defined as the probability that the transportation time under a degradable network is within a specified threshold [2]. Transportation time reliability is affected by node capacity variations and the transportation demand of each Origin-Destination (OD) pair, as shown in Figure 1. The maritime transportation network for China’s imported crude oil is composed of a set of port, strait, and canal nodes and a set of legs between nodes. The port nodes consist of major crude oil loading ports in the Middle East, Africa, and Latin America, as well as unloading ports in China. The strait or canal nodes include the Strait of Hormuz, the Strait of Malacca, the Sunda Strait, the Lombok Strait, the Strait of Gibraltar, the Bab el Mandeb, the Taiwan Strait, the Suez Canal, and the Panama Canal. The nodes stated above are vulnerable to regional geopolitics, military interventions from stakeholder countries, piracy, terrorism, war, and other extreme events. Thus, the transportation time reliability of imported crude oil may be affected.

Moreover, under node capacity variations, the transportation time reliability of imported crude oil in the maritime transportation network may also be affected by crude oil transportation demand. The crude oil transportation demand for each OD pair is reflected by the import volume from each source country, which is influenced by the import price of crude oil. The volume of imported crude oil from some source countries may be largely due to the low import price. However, in the case of a specific node capacity situation, the transportation time may be long due to the large volume of crude oil and poor operation capacity of nodes. The transportation time may exceed the threshold and result in an unsatisfactory transportation time reliability. In contrast, the import volume is small because of the high import price, and the transportation time may be within the threshold, which is reliable. To reduce the impact of capacity variations on the transportation time reliability, the import volume from each source country may change according to node capacities. For example, when the capacity of the Strait of Hormuz is under degeneration, the import volumes from source countries in the Middle East may be reduced. Consequently, how to quantify the impact of node capacity stochastic variations on the transportation time reliability of the maritime transportation network for China’s imported crude oil is a key issue, and it is of crucial importance to guarantee the supply of crude oil.

In this paper, bi-level programming and a Monte Carlo simulation are proposed to calculate the network transportation time as well as evaluate the transportation time reliability resulting from stochastic variations in node capacity, as shown in Figure 2. The volume of imported crude oil from each source country may change in correspondence to node capacity variations and is considered to be a decision variable. The upper problem of bi-level programming involves minimizing the import cost of crude oil and the monetary value of the transportation time. The imported crude oil volume from each source country to China is determined, which is the transportation demand for each OD pair. In the lower problem, Wardrop’s principle is proposed to obtain route choices and transportation time based on the transportation demand of the upper problem [3]. The transportation time is associated with the objective function value in the upper problem. The Monte Carlo simulation is used to simulate stochastic variations in the node capacities. As a result, the transportation time of each OD pair and the entire network under different node capacity conditions are indirectly obtained by solving the bi-level programming, and thus the transportation time reliability can be evaluated. The proposed problem is solved using genetic algorithms based on the Frank–Wolfe method [4]. Finally, a transportation time reliability evaluation application of the maritime transportation network for China’s imported crude oil is presented.

The main contributions of this paper are threefold. First, the transportation time reliability research, which is broadly concentrated on the road network, failed to consider the maritime transportation network [2,5,6,7]. In this paper, a preliminary attempt was made to evaluate the transportation time reliability of the maritime transportation network for imported crude oil under node capacity variations resulting from extreme events. Second, in previous studies regarding road network reliability evaluations under a degradable network, the transportation demand is considered to be a constant value or random variable [5,8,9]. In our study, considering that the imported crude oil volume from each source country may change in relation to the node capacity variations to reduce impacts on the transportation time reliability, the import volume was considered as a decision variable for evaluating the time reliability under stochastic variations in node capacity by employing a bi-level model. Third, a case study was conducted using real data regarding the maritime transportation network for China’s imported crude oil. The reliability evaluation results and identified vulnerable nodes, as well as the import volume of crude oil from each source country obtained according to the model, can assist government policy makers and tanker company strategic planners to better plan crude oil import and transportation strategies.

This paper is organized as follows. In Section 2, the relevant literature is reviewed. In Section 3, the transportation time reliability evaluation model is presented. In Section 4, a case study is illustrated. In Section 5, transportation time reliability results under each node’s capacity variations, possible explanations for varying transportation time reliability among nodes, and vulnerable nodes are discussed. Finally, major conclusions and policy implications are discussed in Section 6.

2. Literature Review

Transportation networks are affected by a number of uncertainties. In an attempt to characterize the performance of transportation networks, several reliability measures have been proposed in the literature. These reliability measures include connectivity reliability, travel time reliability, and capacity reliability. Connectivity reliability concerns the probability that specific OD pairs in a network remain connected when links are subject to complete failures [10]. The links are characterized by binary variables denoting two operating states: operating at full capacity or complete failure. Capacity constraints and travel time are not accounted for when measuring the connectivity reliability. As such, connectivity reliability is appropriate for modelling abnormal situations such as earthquakes. Another transportation network reliability measure is travel time reliability, which is related to the probability that a trip between a given OD pair can be successfully made within a given acceptable time threshold [11]. Capacity reliability was introduced by Chen et al. [12] as a performance measure to evaluate a degradable road network performance from the planner’s perspective. Capacity reliability is defined as the probability that the transportation network can accommodate a certain demand level at an acceptable service level, while also considering the route choice behaviour.

Among the reliability measures, travel time reliability is more important from the perspective of travellers and previously received the most focus. The main contents of this study are the travel time reliability of transportation networks under travel demand variations, link capacity variations, and changes in a traveller’s route choice behaviours.

As for the travel demand variations, Asakura and Kashiwadani [11] assumed a normal distribution of the OD travel demand and allocated traffic on the basis of Wardrop’s equilibrium principle (user equilibrium, UE). Then, a Monte Carlo simulation was proposed to estimate the travel time reliability. Bell et al. [13] used a sensitivity analysis to explore the influence of travel demand variations on travel time, which can overcome the problem of extensive calculations. Subsequently, Chen et al. [2] adopted a definition similar to the travel time reliability of Asakura [14] and considered the travel time reliability to be the probability that the travel time ratio is less than a certain threshold under degradable and normal networks. Departing from the single scalar performance index calculation philosophy as an overall network performance summary, Clark and Watling [5] developed a two-stage approach to acquire the travel time probability density function of transportation networks under the assumption that the travel demand is a random variable and follows a Poisson distribution. Zheng et al. [15] proposed a network travel time distribution model based on the Johnson curve system, and the network-level travel time reliability was investigated. Chen et al. [16], and Woodard et al. [17] used big data to calculate travel time reliability.

Regarding link capacity changes, Lo and Tung [18] supposed that the link capacity followed a uniform distribution and estimated the travel time reliability of OD pairs under the link capacity random degradation based on the probabilistic user equilibrium. Ng and Waller [8] presented a computationally efficient methodology based on the fast Fourier transform to numerically approximate the probability density function of the transportation network travel time under independent capacity variations. The work of these researchers can be treated as a complement to that of Clark and Watling [5]. Ng et al. [19] proposed a new method to evaluate travel time reliability, which is distribution free in the sense that the exact probability distributions are not needed to characterize the uncertainty. Bell [20], Bell and Cassir [21], Szeto et al. [6], and Szeto [7] also adopted a novel distribution free methodology. The proposed model is based on the game theory, which is used to assess the worst-case performance of transportation networks in terms of the travel time. Liu et al. [22] and Ahmad et al. [23] evaluated the impact of traffic incidents on travel time reliability.

A travellers’ route choice behaviour is dependent on the travel time estimation; however, this estimation cannot predict the changes in traffic conditions or link capacity degradation. Therefore, travellers will adjust their travel behaviours according to their risk attitudes and historical experience under uncertain conditions, which will consequently affect the performance of the transportation networks. Different route choice models and various network equilibrium models have been proposed to model this uncertainty [24,25,26,27,28,29,30,31,32,33,34].

In summary, travel time reliability studies mainly concern the road transportation network and travel demand is considered to be a constant value or random variable, which follows a specific distribution. The transportation time reliability evaluation of the maritime transportation network was not considered in previous studies, and only studies on performance evaluations of shipping routes and shipping companies exist [35,36,37]. In terms of the transportation time reliability evaluation of the maritime transportation network for imported crude oil, the imported crude oil volume from each source country affected by import price needs to be considered as a decision variable rather than a constant value or random variable. Therefore, in this paper, a bi-level model incorporating a Monte Carlo simulation is presented to assess the impacts of node capacity degradation on the transportation time reliability of the maritime transportation network for China’s imported crude oil.

3. Model for Transportation Time Reliability Evaluation

3.1. Problem Statement

Consider the graph G = (V, E) to be the maritime transportation network for China’s imported crude oil, which comprises a set of port, strait, and canal nodes denoted by V and a set of legs between nodes denoted by E. Regarding the network in Figure 3, the tankers depart from the ports of source countries, denoted by ①–③, and then the tankers traverse a sequence of straits and canals denoted by ④–⑩. The tankers eventually arrive at the destination ports in China, which are represented by ⑪. The transportation time between the origin and destination ports is composed of two parts: the transportation time at sea and the dwell time at the ports and transportation time through the straits or canals. In addition, the transportation time of the network is a weighted average of all OD pair transportation times, which is calculated by weighing the contribution of each OD pair according to its share of imported crude oil [2].

3.2. Model Formulation

To evaluate the transportation time reliability of the maritime transportation network for imported crude oil, the key issue is to calculate the transportation time for the imported crude oil. As shown in Figure 2, bi-level programming is proposed to calculate the transportation time for imported crude oil under specific node capacity situations. Moreover, a Monte Carlo simulation is used to simulate stochastic variations in node capacity, which in combination with bi-level programming, is used to evaluate the transportation time reliability. Before the model is formulated, the following assumptions are introduced.

(1)

The capacity of each node follows a uniform distribution defined by an upper bound (the node is under normal operation) and a lower bound (the worst-degraded capacity) [18,28]. In addition, we assume the lower bound to be a fraction of the capacity under normal operation, which is denoted by θ_a.

(2)

The crude oil flow on node a for other countries is a known constant, which is denoted by o_a.

(3)

Suppose the variables are a daily amount, which means that the annual demand of China’s imported crude oil is averaged daily, and the unit is 100,000 tons.

(4)

The speed of vessels on different maritime transportation routes is the same.

The notations are as follows:

R	R = (1,2,3,…r), set of origins for imported crude oil
S	S = (1,2,3,…s), set of destinations for imported crude oil
qrs	Transportation volume of crude oil for OD pair rs
pr	Import price of crude oil for country r
D	Daily demand for imported crude oil in China
Br	Largest possible import volume of crude oil from country r to China
φ	Time value of imported crude oil
xa	Crude oil flow on node a for China (a = 1,2,…,A)
oa	Crude oil flow on node a for other countries (a = 1,2,…,A)
Ca	Capacity of node a (a = 1,2,…,A)
θa	Fraction of the capacity under normal operation for node a
wa	Total flow volume of all cargo types on node a (100,000 tons)
x	Vector of flows across all nodes (a∈A)
ta	Time incurred on node a
ta0	Free-flow transportation time for node a
ta,a+1	Transportation time of legs connecting two adjacent nodes
Trs	Transportation time for OD pair rs
fkrs	Flow on path k of OD pair rs
δrsa,k	Indicator variable, which is equal to 1 if path k traverses node a, 0 otherwise
ηa	Proportion of crude oil flow to the total flow volume on node a
ka	Asymmetry factor that reflects the interaction among different cargo flows on node a
α, β	Parameters to be calibrated
Re	Transportation time reliability of the maritime transportation network for China’s imported crude oil
wrs	Weight of OD pair rs, which is calculated by its share of imported crude oil

On the basis of the above analysis and assumptions, the bi-level programming is established as follows.

Imported crude oil prices vary by countries, and crude oil transportation time will affect the productivity of the national economy due to crude oil inputs. Therefore, the objective of the upper model function is to minimize the import cost of crude oil and the monetary value of the transportation time from a national perspective.

The upper level model:

$$Min:{\displaystyle \sum _r{\displaystyle \sum _s{p}_r{q}_{rs}+\phi {\displaystyle \sum _a{t}_a(x_a)}}},$$

(1)

subject to

$${\displaystyle \sum _{\mathrm{r}\in R}{\displaystyle \sum _{s\in S}{q}_{rs}\ge D}},$$

(2)

$${\displaystyle \sum _{s\in S}{q}_{rs}\le B_r},\forall r,$$

(3)

$$p_r>0,\forall r.$$

(4)

${\displaystyle \sum _r{\displaystyle \sum _s{p}_r{q}_{rs}}}$ represents the total cost of the imported crude oil, and $\phi {\displaystyle \sum _a{t}_a(x_a)}$ represents the total monetary value of the transportation time.

Equation (2) denotes that the total volume of imported crude oil from various countries meets China’s oil demand. Equation (3) restricts the total import volume of crude oil from country r to less than its largest possible export capacity. Equation (4) is the sign restriction of the price of imported crude oil.

The lower level problem involves modelling the route choice behaviour under the user equilibrium principle from the perspective of the transportation company, on the basis of the transportation demand obtained from the upper level model. The transportation time acquired in the lower level model is associated with the objective value of the upper level model.

The lower level model:

$$Min:{\displaystyle \sum _a{\displaystyle {\int }_0^{x_a}{t}_a(w)dw}},$$

(5)

subject to

$${\displaystyle \sum _k{f}_k^{rs}}=q_{rs},\forall r,s,$$

(6)

$$x_a={\displaystyle \sum _r{\displaystyle \sum _s{\displaystyle \sum _k{f}_k^{rs}{\delta }_{a,k}^{rs},}}}\forall a,$$

(7)

$$f_k^{rs}\ge 0,\forall r,s,$$

(8)

$$t_a(x_a)=t_{a,a+1}+t_a^0\ast [1+{\alpha }_a{(\frac{x_a+o_a+k_a(w_a-x_a)}{C_a})}^{{\beta }_a}],$$

(9)

$$w_a=(x_a+o_a)/{\eta }_a.$$

(10)

Equation (5) is the objective function of the user equilibrium model, and Equation (6) denotes that the flow sums on each path connecting the OD pair rs are equal to the total amount of traffic for the OD pair. Equation (7) indicates the relationship between the node and path flows. Equation (8) is a non-negative constraint of the path flow. Equation (9) is the impedance function of nodes, and we assume that the time incurred on node a has a Bureau of Public Road (BPR) form, as the form can reflect the impact of congestion in a transportation system by involving the volume/capacity ratio [38]. Congestion phenomena can be observed on nodes due to degeneration of node capacity and a large volume of transportation demand. The transportation time for crude oil through node a is assumed to be affected by both tankers and other ships that share the same node a, whereas for port nodes, there is only crude oil flow, and thus, k_a = 0. Equation (10) is the expression for the total traffic volume of all cargo types on node a.

3.3. Solution Algorithm

As the bi-level programming problem is a non-deterministic polynomial (NP)-hard problem, there is no polynomial algorithm to solve the problem. In this paper, the genetic algorithm (GA) and Frank–Wolfe algorithm (FW) are employed to solve the proposed bi-level model, wherein FW is used to solve the lower model (user equilibrium model) and GA is used for the upper model [39].

The specific steps of the algorithm can be summarized as follows:

Step 1. Initialization. Set the required GA parameters such as population size M, iterations, crossover probability, and mutation probability. Determine the coding programme, where the real coding is for the upper model decision variables. The number of iterations is m = 0, which generates the initial population P_m.

Step 2. Conduct the fitness evaluation.

Step 2.1. Acquire q_rs in the upper model, which is the transportation demand for the OD pair rs.

Step 2.2. Solve the lower model using the FW algorithm to obtain x_a and the transportation time t_a.

Step 2.3. Calculate the fitness value for population m, and the upper level objective function $Min:{\displaystyle \sum _r{\displaystyle \sum _s{p}_r{q}_{rs}+\phi {\displaystyle \sum _a{t}_a(x_a)}}}$ is used as the fitness function.

Step 3. Conduct the crossover and mutation. Perform selection, crossover, and mutation operations to generate the new population P_m.

Step 4. Conduct the convergence check. According to the guidelines set by the termination criterion (such as whether the maximum number of iterations has been reached), stop if the termination criterion is satisfied and output the result, otherwise let m = m + 1 and return to Step 2.

3.4. Reliability Evaluation Procedure

The transportation time reliability evaluation procedure is as follows:

(1)

Set sample number n = 1 and parameter count = 0.

(2)

Generate the capacity value according to the distribution properties for a specified node, {x_an}, (a = 1,2,…,A), and the capacities for other nodes under normal conditions.

(3)

Perform the bi-level model with the node capacity and solve the model using the above algorithm.

(4)

Collect statistics such as the transportation time of each OD pair and calculate the network transportation time T_n.

$$T_n={\displaystyle \sum _r{\displaystyle \sum _s{T}^{rs}{w}_{rs}}}.$$

(11)

If T_n is within the specified threshold, then count = count + 1.

(5)

If sample number n is less than the required sample size N, the increment sample number is n = n + 1 and return to Step (2). Otherwise, go to Step (6).

(6)

Calculate the transportation time reliability of the network.

$$R_e=count/N.$$

(12)

(7)

Repeat Steps (1)–(6) above to calculate the transportation time reliability of the entire network under random capacity variations in each node.

4. Case Study

4.1. Problem Setting

Figure 4 shows the maritime transportation network for China’s imported crude oil. In this paper, the following source countries are chosen: Saudi Arabia, Iraq, Iran, United Arab Emirates, Kuwait, and Oman in the Middle East; Angola, Congo, Sudan, and Libya in Africa; and Venezuela, Colombia, and Brazil in Latin America.

The aim of this paper was to study the reliability of the transportation time from the source countries to China under node capacity variations due to extreme events. We did not consider the transit time of imported crude oil between domestic ports in China, and the selection of the unloading port will have no impact on the time reliability under the capacity variations in other nodes. Therefore, Ningbo port was selected in this paper as the only port to represent a domestic unloading port. In addition, the Ningbo port capacity will not be disturbed by extreme events and can satisfy the unloading demand in our study. The major ports of source countries were selected according to the world tanker ports map [40].

The ports, straits, and canals constitute the node set of the maritime transportation network for China’s imported crude oil, V = (v₁,v₂,…,v_n), and the cardinality of the node set is 33, where |V| = 33. We distributed the imported crude oil traffic over 13 OD pairs. The nodes in each OD pair, the transportation routes, the import price, and the largest possible import volume of crude oil from country r are shown in

Table 1. Maritime transportation network information for China’s imported crude oil.

Region	Sources	Major Ports	Crude Oil Transportation Routes	Price of Crude Oil (ton/$)	Br (100,000 tons)
Middle East	Saudi Arabia	Yanbu	Strait of Hormuz-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	393.2	2.0
		Ras Tanura
		Juaymah
	Iraq	Fao		375.2	2.0
		Al Basrah
	Iran	Kharg Island		382.9	2.0
		Bandar Mahshahr
	United Arab Emirates	Das Island		409.2	2.0
		Zirku
		Fujairah
	Kuwait	Mina Al Ahmadi		388.2	2.0
		Mina Saud
	Oman	Mina Al Fahal	Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	399.1	1.2
Africa	Angola	Cabinda	Cape of Good Hope-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	399.1	2.0
		Palanca
	Congo	Djeno Terminal		400.0	0.4
	Sudan	Port Sudan	Bab el Mandeb-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	406.4	0.2
	Libya	Es Sider	Suez Canal-Bab el Mandeb-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	423.0	0.6
		Ras Lanuf	Strait of Gibraltar-Cape of Good Hope-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo
Latin America	Venezuela	Puerto Jose	Panama Canal-Ningbo/Cape of Good Hope-Strait of Malacca/Sunda Strait/Lombok Strait-Taiwan Strait-Ningbo	301.7	2.0
		Puerto La Cruz
	Colombia	Barranquilla		360.3	1.4
	Brazil	Sao Sebastiao		397.4	2.0
		Gebig

.

The import price for each country was the average price of China’s imported crude oil in 2017, which was sourced from the International Trade Center. B_r is determined by the volume of crude oil production for each country and the recent export volume to China. According to the forecast of China’s crude oil imports, the total crude oil demand from the above countries is 800,000 tons per day. The parameter φ relates to the consumption of crude oil per gross domestic product (GDP). By referring to the China Statistical Yearbook, we set φ to be 1.4 $/h.

The parameter values of C_a for the impedance function of port nodes are from the port authority website. For strait and canal nodes, the values of C_a are represented by the volumes transported through the nodes and are from the U.S. Energy Information Administration. The parameter values of o_a are calculated according to the values of C_a and the import volume of China. In addition, the units for C_a and o_a are 100,000 tons/day. The values of η_a, k_a, α_a, and β_a are determined by referencing the study of Meng and Wang [38]. For port nodes, η_a = 1 and k_a = 0. For strait and canal nodes, η_a = 0.6 and k_a = 0.5. For all nodes, α_a = 2.5 and β_a = 2.

Table 2. Parameter values of t_a and t_a,a+1.

Region	Sources	Nodes	ta	ta,a+1
Middle East		Yanbu	22.73	149.13
		Ras Tanura	22.73	23.66
		Juaymah	22.73	24.12
	Saudi Arabia, Iraq, Iran, United Arab Emirates, Kuwait	Fao	25	33.74
		Al Basrah	95.24	32.29
		Kharg Island	10	27.04
		Bandar Mahshahr	125	3.07
		Das Island	16.67	13.98
		Zirku	43.25	15.13
		Fujairah	25	5.26
		Mina Al Ahmadi	50	32.92
		Mina Saud	56.67	31.63
		Strait of Hormuz	5.40	—
		Strait of Malacca	38.88	334.21
		Sunda Strait	5.40	380.91
		Lombok Strait	2.90	405.90
		Taiwan Strait	13.32	34.93
	Oman	Mina Al Fahal	11.11	—
		Strait of Malacca	38.88	323.61
		Sunda Strait	5.40	368.61
		Lombok Strait	2.90	393.60
		Taiwan Strait	13.32	34.93
Africa	Angola, Congo	Cabinda	25	119.69
		Palanca	45	113.14
		Djeno Terminal	125	121.98
		Strait of Malacca	38.88	492.01
		Sunda Strait	5.40	483.90
		Lombok Strait	2.90	556.62
		Taiwan Strait	13.32	34.93
	Sudan	Port Sudan	100	36.58
		Bab el Mandeb	1.80	—
		Strait of Malacca	38.88	360.32
		Sunda Strait	5.40	392
		Lombok Strait	2.90	476.18
		Taiwan Strait	13.32	34.93
	Libya	Es Sider	100	68.16/91.78
		Ras Lanuf	78.67	68.21/92.59
		Suez Canal	6.84	83.04
		Bab el Mandeb	1.80	—
		Strait of Gibraltar	2.09	340.43
		Strait of Malacca	38.88	360.32/492.01
		Sunda Strait	5.40	392/483.90
		Lombok Strait	2.90	476.18/556.62
		Taiwan Strait	13.32	34.93
Latin America	Venezuela, Colombia, Brazil	Puerto Jose	25	381.91/65.91
		Puerto La Cruz	33.67	381.69/66.57
		Barranquilla	125	422.52/24.87
		Sao Sebastiao	25	222.56/242.45
		Gebig	27.78	221.05/290.29
		Strait of Malacca	38.88	492.01
		Sunda Strait	5.40	483.90
		Lombok Strait	2.90	556.62
		Taiwan Strait	13.32	34.93
		Panama Canal	2.93	569.33

Note: The t_a for port nodes refers to the required loading time of 100,000 tons of crude oil. The unit for both t_a and t_a,a+1 is hours.

shows the parameter values for the free transportation time of each node according to the transportation routes to which the nodes belong. The free-flow transportation time t_a for port nodes are calculated using the port handling efficiency. In terms of strait or canal nodes, t_a values are calculated using the distance between the strait or canal entrance and exit as well as the tanker speeds. We assume the tanker speed is 15 kn. The parameter t_a,a+1 refers to the transportation time of the legs between two adjacent nodes. Selecting different nodes implies varied transportation distances between the connected legs and thus different transportation times. For example, for the transportation routes of the OD pair from Saudi Arabia to Ningbo, the t_a,a+1 of the Strait of Malacca is the sum of the transportation time from the Strait of Malacca to the Strait of Hormuz and from the Strait of Malacca to the Taiwan Strait. According to the transportation distances and speed of tankers, the parameter t_a,a+1 is calculated, as shown in Table 2.

When the capacity of each node is fixed at the upper bound of the uniform distribution (non-degraded capacity), the transportation time of each OD pair and entire maritime transportation network is obtained by applying the above model and algorithm. The results are shown in

Table 3. Transportation time for each OD pair and the network under a non-degraded capacity.

Region	Sources	Transportation Time	Import Volume	Transportation Time of the Network
Middle East	Saudi Arabia	736.5	2	814.4
	Iraq	876.2	2
	Iran	721.9	1.34
	United Arab Emirates	822.8	1.73
	Kuwait	760.5	0.33
	Oman	662.5	0.6
Africa	Angola	896.9	0.29
	Congo	999.2	0.4
	Sudan	648.67	0.2
	Libya	1078.7	0.22
Latin America	Venezuela	965.6	0.31
	Colombia	1083.2	0.39
	Brazil	839.7	0.23

Note: The unit of the crude oil import volume is 100,000 tons, and the transportation time unit is hours.

. The transportation time of the network under non-degraded capacity for each node is 814.4 h, which is approximately 34 days.

4.2. Transportation Time Reliability Results

In this paper, we set θ_a = 0, which is the lower bound of the capacity for each node. A Monte Carlo simulation was applied to generate random node capacities between the lower and upper bounds of the uniform distribution for each node, in order to illustrate the effects of extreme events on the node capacity. The estimated mean and standard deviation values resulting from 10,000 Monte Carlo simulations were close to those of the theoretical values. For example, the theoretical mean and standard deviation of the capacities for the Strait of Hormuz were found to be 11.5 and 6.64, respectively, whereas the estimated values were 11.49 and 6.62, respectively.

Recall that the transportation time reliability is the probability that the transportation time of the entire network is within a specified threshold when each node is subject to capacity variations. In this paper, we set the threshold to be 1.1 times the network transportation time under a non-degraded capacity. That is, when a node capacity is under stochastic variations, if the transportation time of the network does not exceed 1.1 times the normal transportation time (1.1 × 814.4 h), the network is considered to be reliable. Figure 5 shows the transportation time reliability of the maritime transportation network for China’s imported crude oil with respect to the perturbed capacities for each node.

5. Discussion

5.1. Transportation Time Reliability under Each Node’s Capacity Variations

As shown in Figure 5, when the port nodes were under capacity variations, the network transportation time reliability was relatively high, with an average reliability of 89.2%. This indicates that the maritime transportation network for China’s imported crude oil is relatively reliable, and the imported crude oil is more likely to be transported to China in a timely manner. The transportation time reliability of the network can reach 99% when some nodes are under random capacity variations, such as Kharg Island and Port Sudan. This was mainly because there are alternative ports and the imported volumes of the two ports are relatively small. The lowest transportation time reliability was more than 70% for Port Ras Tanura and Fao. The large import volume, long transportation time, and low capacity of the alternative ports for Ras Tanura resulted in a relatively low reliability. The large import volume and low capacity of the alternative port for Fao created a low time reliability.

On the other hand, the average transportation time reliability of the network was found to be 75.2%, when the strait or canal nodes were under capacity variations, and thus the timely transportation of imported crude oil cannot be guaranteed. For example, the transportation time reliability was found to be only 21.3% when the Taiwan Strait was subject to random capacity variations. For the Strait of Hormuz and the Strait of Malacca, the transportation time reliabilities were only 44.3% and 43.7%, respectively. For the Sunda Strait, the Lombok Strait, the Suez Canal, the Bab el Mandeb, the Panama Canal and the Strait of Gibraltar, the network transportation time reliabilities were all greater than 92%.

5.2. Causes of Transportation Time Reliability Variations

The results shown in Figure 5 demonstrate the large differences in transportation time reliability among the different nodes. Port nodes usually have alternative ports, and the crude oil flow volume in the port nodes is small relative to the entire network. When the capacity of a certain port node is under degradation, a small volume of crude oil may be affected or can be imported from other ports with similar functions. Therefore, the network is relatively reliable under port node capacity variations. For port nodes Ras Tanura and Fao, the import volumes were relatively large and the handling capacities of the alternative ports for Ras Tanura and Fao were relatively low. The above reasons make the network reliability relatively low under these two port capacity variations.

In terms of strait or canal nodes, the transportation time reliability was found to be relatively lower than that under port node capacity variations. This is because the crude oil flow volumes in the strait or canal nodes are larger than those of individual port nodes, and there are usually no alternative nodes. Even if there are alternative nodes, the transportation distance for a detour to the alternative nodes may increase, and then the transportation time is more likely to be longer. Moreover, according to Equation (10), the large volume of crude oil transferred to the alternative nodes may result in congestion of alternative nodes, and the transportation time through the alternative nodes may be long. The above situations may result in the total transportation time exceeding the specified threshold, and thus the network will not be reliable.

Regarding the Strait of Hormuz, the Strait of Malacca, and the Taiwan Strait, the transportation time reliability was low. The Strait of Hormuz is one of China’s most important chokepoints regarding oil transportation, as most of the imported crude oil from the Middle East is transported through the Strait of Hormuz. When the capacity of the Strait of Hormuz is under degeneration, the crude oil imported from the Middle East is more likely to be a backlog in the Strait of Hormuz. Even if we can transfer to other source countries in Africa and Latin America, the largest possible import volumes from the African countries of Congo (0.4), Sudan (0.2), and Libya (0.6) were found to be small, as shown in Table 1. In addition, the transportation time from countries in Africa and Latin America were nearly twice that from the Middle East, as shown in

Table 4. Comparison of transportation times from origin to destination.

Region	Sources	Crude Oil Transportation Routes	Transportation Time (Hours)
Middle East	Saudi Arabia	Strait of Hormuz-Strait of Malacca-Taiwan Strait-Ningbo	392.8
Africa	Congo	Cape of Good Hope-Strait of Malacca-Taiwan Strait-Ningbo	648.9
	Libya	Strait of Gibraltar-Cape of Good Hope-Strait of Malacca-Taiwan Strait-Ningbo/Suez Canal-Bab el Mandeb-Strait of Malacca-Taiwan Strait-Ningbo	958.5/538.7
Latin America	Brazil	Panama Canal-Ningbo/Cape of Good Hope-Strait of Malacca-Taiwan Strait-Ningbo	811.7/749.5

Note: The time in Table 4 refers to the sum of transportation times between two adjacent nodes from origin to destination, which does not include the time incurred in the nodes.

. Therefore, the transportation time of the entire network is more likely to be severely affected.

As for the Strait of Malacca, the imported crude oil from all three main source regions, the Middle East, Africa, and Latin America, is almost entirely transported through it. When the capacity of the Strait of Malacca is degraded, the large volume of crude oil may cause severe congestion in the strait. Although the Sunda Strait and the Lombok Strait are alternative nodes for the Strait of Malacca, transferring the oil to the Sunda Strait or the Lombok Strait will increase the transportation time. In addition, according to Equation (10), if the large volume of crude oil originally transported through the Strait of Malacca is transferred to the Sunda Strait or the Lombok Strait, the transportation time of the crude oil through the two straits will be long. The probability that the total transportation time exceeds the specified threshold may be high. Therefore, the transportation time reliability is low under the capacity variations in the Strait of Malacca. As for the Taiwan Strait, it is the closest node to the destination. In addition, most of the imported crude oil needs to be transported through the Taiwan Strait to the destination port in China. Consequently, when the Taiwan Strait is degraded, the network is more likely to be severely affected. Therefore, the transportation time reliability under the capacity variations in the Taiwan Strait was found as the worst, with a value of only 21.3%.

In terms of the Panama Canal and the Strait of Gibraltar, the import volumes of crude oil transported through these nodes are far smaller than those transported through the Strait of Hormuz or the Strait of Malacca. When the two nodes are degraded, we can transfer to the source countries in the Middle East, and the transportation time from the Middle East is shorter, as shown in Table 4. In addition, when the Panama Canal is degraded, the crude oil imported from Latin America previously transported through the Panama Canal can shift to transportation routes through the Strait of Malacca. Similarly, when the Strait of Gibraltar is degraded, the imported crude oil can shift to transportation routes through the Suez Canal and the Bab el Mandeb. Because the import volume of crude oil is small, congestion in the alternative nodes may not result. For the Suez Canal and the Bab el Mandeb, the two straits have a similar situation to that of the Panama Canal and the Strait of Gibraltar. The import volumes of crude oil transported through the two nodes are small. When the two nodes are degraded, we can also transfer to source countries in the Middle East. In addition, the imported crude oil can also shift to transportation routes through the Strait of Gibraltar. For the Sunda Strait and the Lombok Strait, the volumes transported through these two nodes are small, and the Strait of Malacca is a good alternative node to these two nodes. The Sunda Strait and the Lombok Strait can also act as a substitute for each other. In conclusion, the maritime transportation network is relatively reliable when the above four straits and two canals are under capacity variations.

5.3. Vulnerability Analysis

The vulnerable nodes in the maritime transportation network for China’s imported crude oil can be identified in terms of the transportation time reliability under random capacity variations in each node. The vulnerable nodes mainly include the Taiwan Strait, the Strait of Hormuz, and the Strait of Malacca because the transportation time reliabilities are lower and the imported crude oil cannot be transported in a timely manner when their capacities vary.

Military intervention from the United States and other countries may threaten the capacity of the Taiwan Strait, as the Taiwan Strait is the node closest to the destination, and the transportation routes of the 13 OD pairs all include the Taiwan Strait. The capacity variations in the Taiwan Strait are more likely to severely affect the transportation time reliability of the entire network, which is only 21.3% according to our evaluation results. Therefore, the transportation of imported crude oil will not be accomplished in a timely manner. This means the Taiwan Strait is the most vulnerable node in the maritime transportation network for China’s imported crude oil.

The Strait of Hormuz connects the Persian Gulf with the Gulf of Oman and the Arabian Sea. More than 70% of China’s imported crude oil is transported through the Strait of Hormuz. Recently, Saudi Arabia ended diplomatic relations with Iran, which increased instability in the gulf region. Countries with large amounts of maritime power want control of the Strait of Hormuz because of its strategic position. Occasionally, Iran declares a blockade of the Strait of Hormuz in response to western sanctions. The above factors will pose a threat to the capacity of the strait, and the transportation time reliability is 44.3% under capacity variations, which means timely transportation of imported crude oil is more likely to be threatened. Therefore, the Strait of Hormuz is another vulnerable node in the maritime transportation network for China’s imported crude oil.

The Strait of Malacca, which links the Indian Ocean and Pacific Ocean, is the shortest maritime transportation route between the Middle East and China. This strait is the main target of piracy and terrorism attacks. Interventions from stakeholder countries including Malaysia, Singapore, Indonesia, United States, Japan, India, and so on further complicate the safety situation of the Strait of Malacca. Consequently, these factors are more likely to result in capacity degeneration of the Strait of Malacca, and the transportation time reliability of the network was found to be only 43.7% when the capacity was degenerated, according to our model. The transportation of imported crude oil will be more likely to be delayed. Therefore, the Strait of Malacca is also a vulnerable node in the maritime transportation network for China’s imported crude oil.

6. Conclusions and Policy Implications

In this paper, a framework incorporating bi-level programming and a Monte Carlo simulation was proposed to evaluate the transportation time reliability of the maritime transportation network for China’s imported crude oil resulting from capacity variations in each node. The evaluation results illustrate that the transportation time reliability of the network is relatively low due to capacity variations in strait or canal nodes and is relatively high due to capacity variations in port nodes. In addition, a vulnerability analysis was also presented according to the reliability results. The Taiwan Strait, the Strait of Hormuz and the Strait of Malacca are relatively vulnerable in the maritime transportation network for China’s imported crude oil.

This paper can provide valuable policy implications for relevant policymakers and strategy planners, as discussed below.

First, under stochastic capacity variations in different nodes, the transportation time reliability is different, which leads to different strategies for the choice of crude oil source countries. For example, the volume of crude oil imported from Latin America is small, and the transportation time reliability of the entire network is relatively high when the port nodes in Latin America and the Panama Canal are under capacity variations. In addition, the largest possible import volume from Latin America is relatively large. Government policy makers may consider appropriately increasing the volume of crude oil imports from Latin America. Therefore, policy makers and tanker company strategic planners should focus on the operation situation of each node and plan appropriate crude oil import and transportation strategies.

Second, according to our model, the Strait of Malacca, the Strait of Hormuz and the Taiwan Strait were identified as vulnerable nodes, but these straits were also recognized as strategic nodes in the maritime transportation network of crude oil. To better perform the function of strategic nodes, the probability of some uncertain events causing capacity variations in the three nodes must be reduced. For example, measures such as improving relations with the countries to which the nodes belong, actively seeking cooperation with stakeholder countries and international organizations, and strengthening China’s maritime military forces should be considered by government policymakers to avoid blockade of the nodes and the occurrence of piracy and terrorism.

Third, the results also allow government policymakers to consider developing other transportation corridors for imported crude oil. Gwadar Port can be recognized as an important strategic node for imported crude oil transportation. Imported crude oil from the Middle East, Africa, and Latin America could be transported by sea to Gwadar Port and then via pipeline to China; thus, the two vulnerable nodes identified in this paper, which are the Strait of Malacca and Taiwan Strait, could be circumvented. Therefore, for Gwadar Port to better perform the function of a strategic node, improvement of the infrastructure at Gwadar Port and the construction of corresponding crude oil transportation pipelines, roads, and railways should be considered by government policymakers.

In the future, we could seek to improve upon the work presented in this paper in the following respects. First, we can attempt to collect historical incident data, and the distributions of node capacity can be calibrated using this data. However, it is difficult to collect all historical incident data. Second, we can attempt to establish a quantitative relationship between the uncertain factors and node capacity degeneration, and thus the node capacity values can be obtained according to uncertain factors without the requirement of node capacity distributions. However, this also requires historical incident data.