The Effects of Product Consistency and Consumer Resistance to Innovation on Green Product Diffusion in China
Abstract
:1. Introduction
- (1)
- Can the product consistency between the existing product offering and the new green product influence the diffusion of the green product?
- (2)
- Can consumers’ resistance to new innovation influence the diffusion of the green product?
2. Literature Review
3. Model Development
3.1. Basic Bass Model
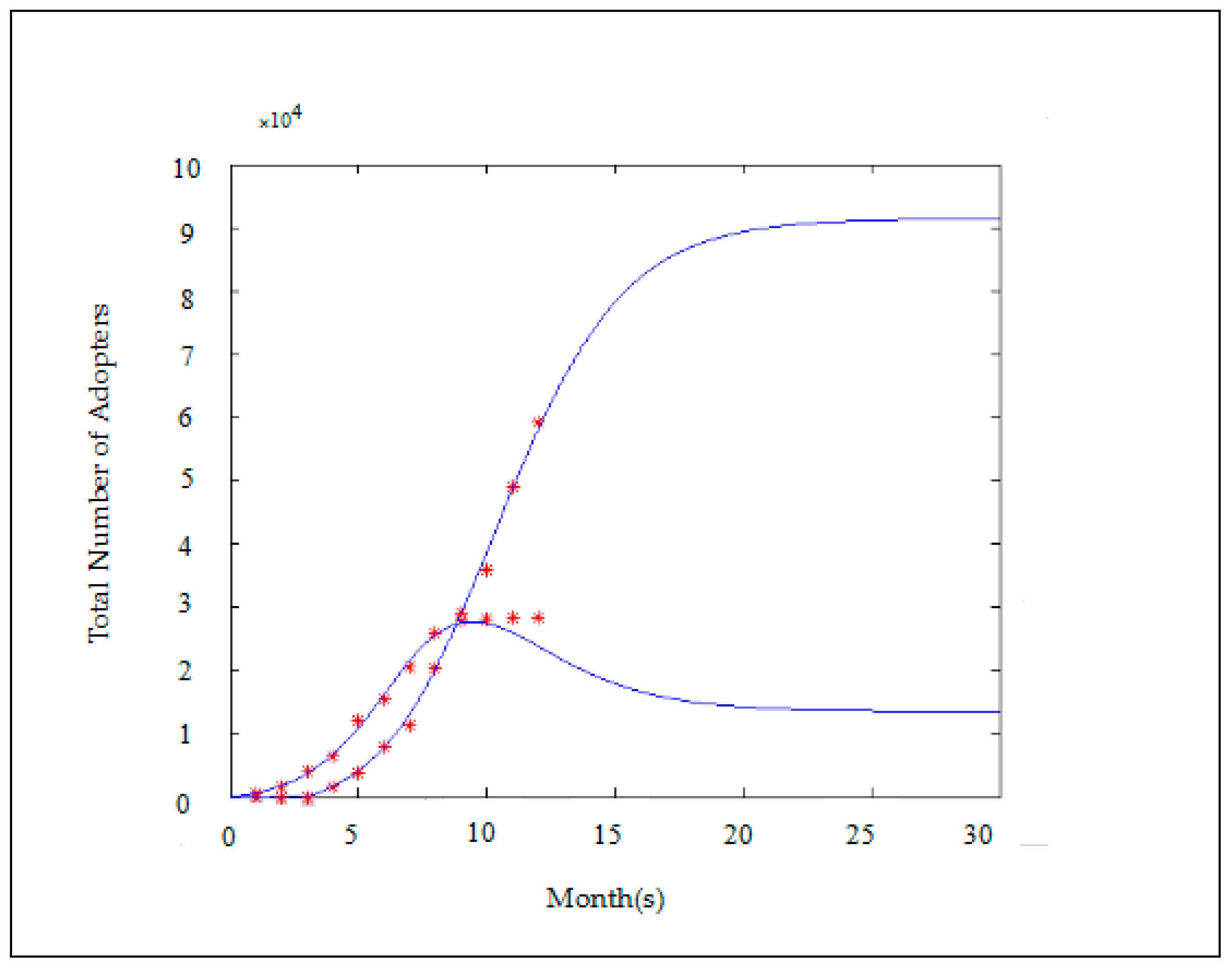
3.2. Classic Norton-Bass Model
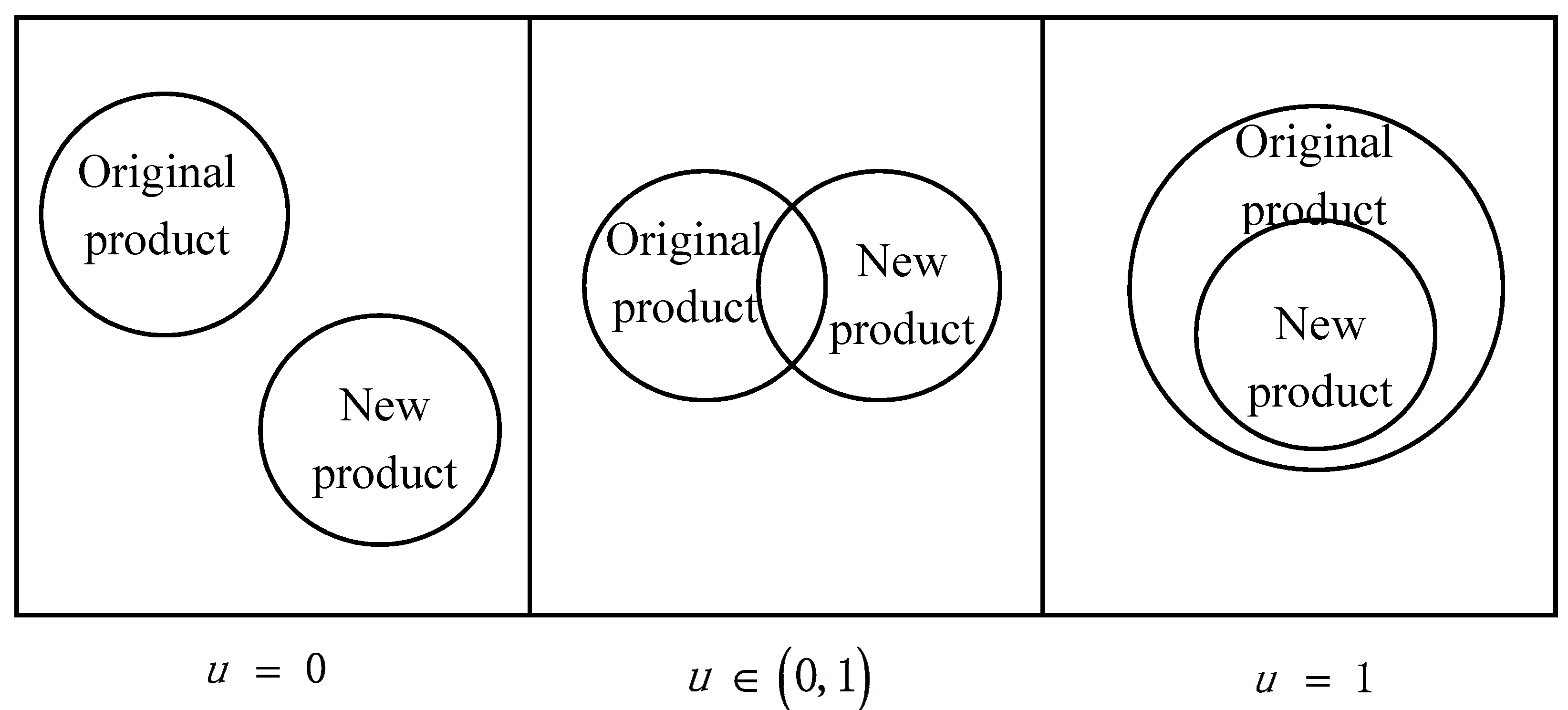
3.3. The Proposed New Model
- A company sells a product on the market, then, it will introduce a green product offering to the market after a certain time of period (t > t0).
- Because the new green product is not completely replacing the existing product offering, thus, different from the classic NB model, our model does not require the influences of innovation, imitation, and consumer resistance are persistent. Specifically, p1 at time t0 is set not always equal to p1′ at time t. Similarly, q1 at time t0 is not always equal to q1′ at time t; α1 is not always equal to α2.
4. Empirical Analyses
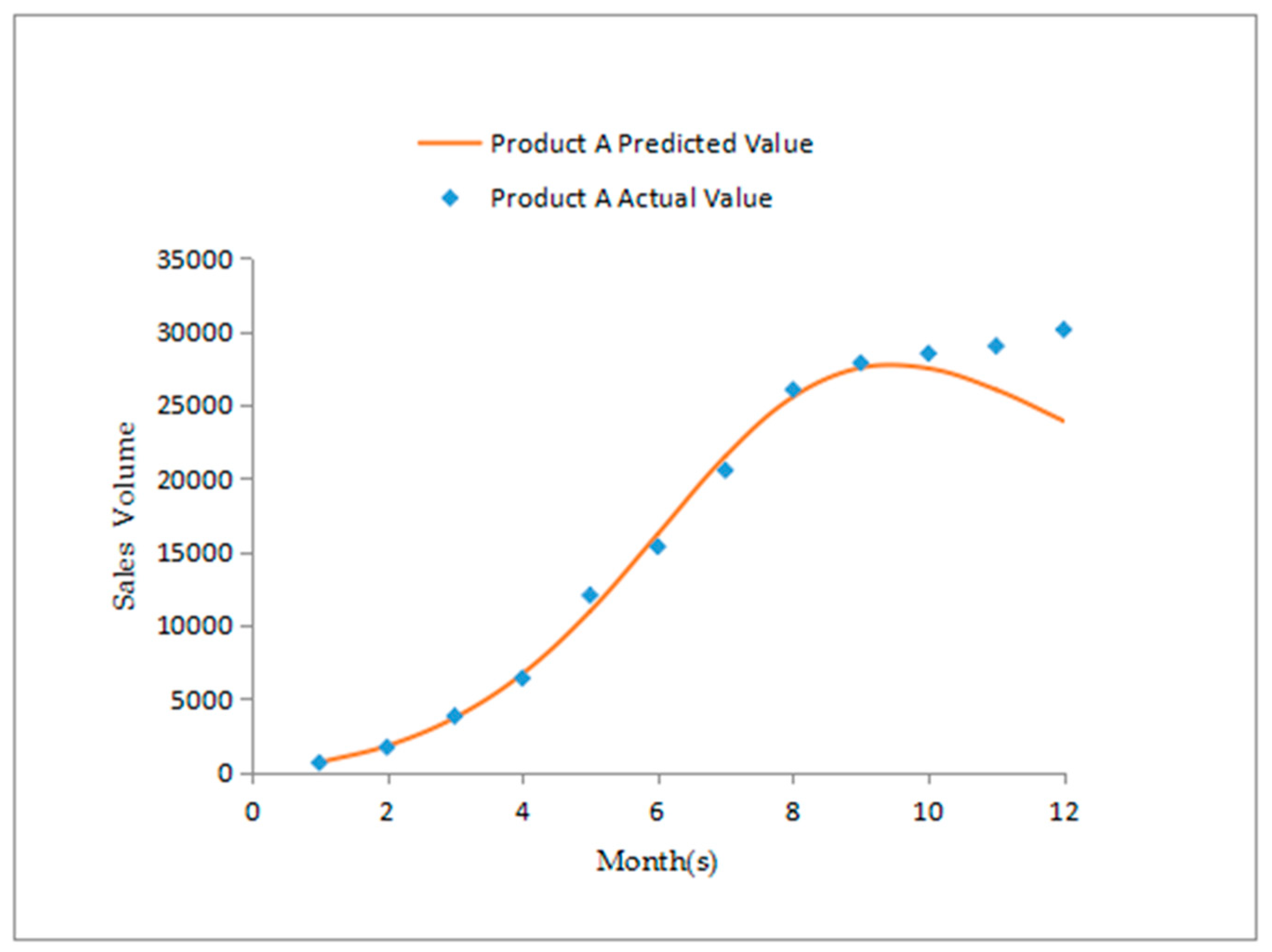
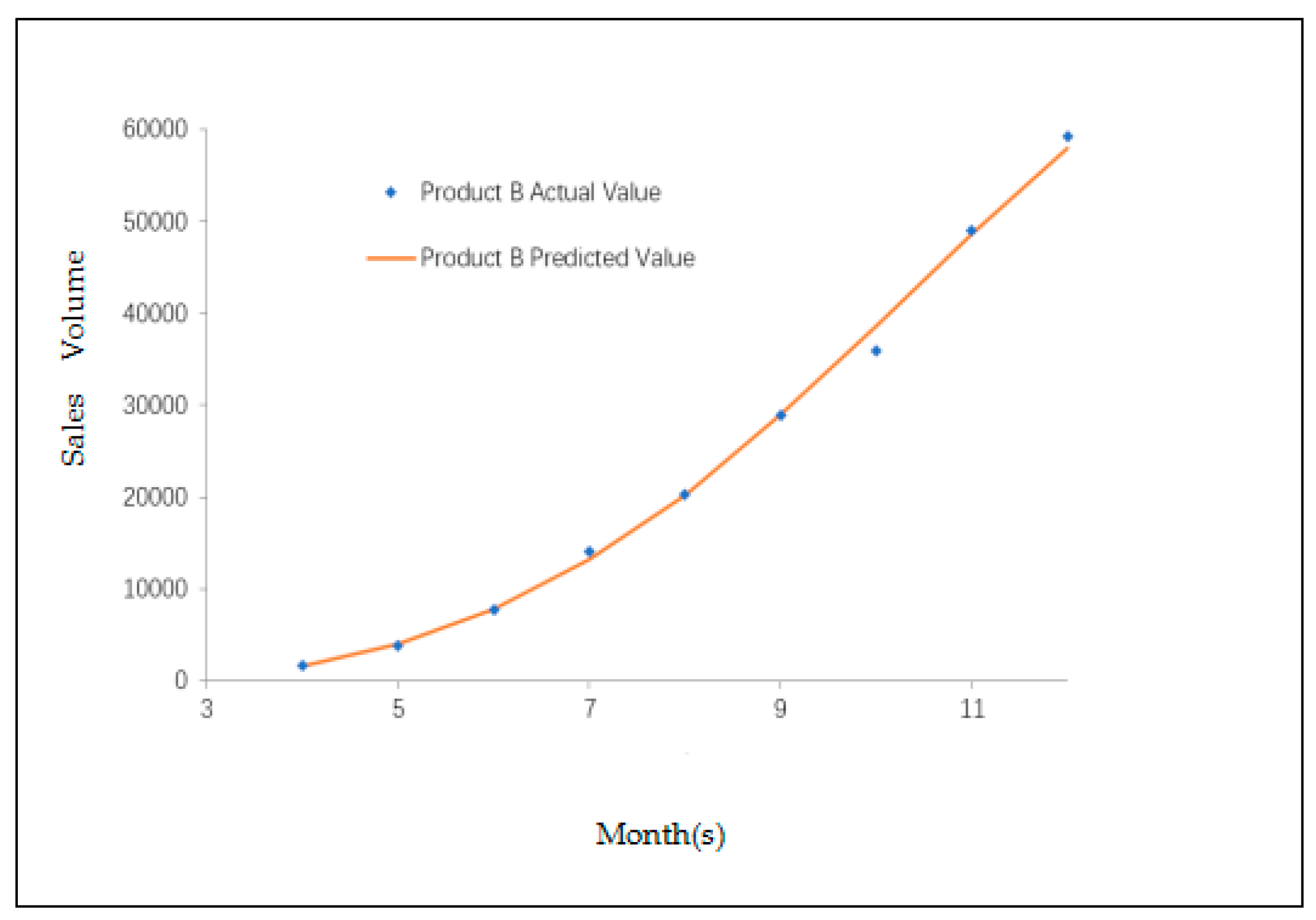
4.1. Study 1
4.2. Study 2
5. Discussions
6. Limitations and Future Research Directions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, C. Design for the environment: A quality-based model for green product development. Manag. Sci. 2001, 47, 250–263. [Google Scholar] [CrossRef]
- Pujari, D.; Wright, G.; Peattie, K. Green and competitive: Influences on environmental new product development performance. J. Bus. Res. 2003, 56, 657–671. [Google Scholar] [CrossRef]
- Baumann, H.; Boons, F.; Bragd, A. Mapping the green product development field: Engineering, policy and business perspectives. J. Clean. Prod. 2002, 10, 409–425. [Google Scholar] [CrossRef]
- Chang, C.H. The influence of corporate environmental ethics on competitive advantage: The mediation role of green innovation. J. Bus. Ethics 2011, 104, 361–370. [Google Scholar] [CrossRef]
- Chen, Y.S. The driver of green innovation and green image–green core competence. J. Bus. Ethics 2008, 81, 531–543. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lai, S.B.; Wen, C.T. The influence of green innovation performance on corporate advantage in Taiwan. J. Bus. Ethics 2006, 67, 331–339. [Google Scholar] [CrossRef]
- Krishnan, V.; Ramachandran, K. Integrated product architecture and pricing for managing sequential innovation. Manag. Sci. 2011, 57, 2040–2053. [Google Scholar] [CrossRef]
- King, W.R.; He, J. A meta-analysis of the technology acceptance model. Inf. Manag. 2006, 43, 740–755. [Google Scholar] [CrossRef]
- Venkatesh, V. Determinants of perceived ease of use: Integrating control, intrinsic motivation, and emotion into the technology acceptance model. Inf. Syst. Res. 2000, 11, 342–365. [Google Scholar] [CrossRef]
- Norton, J.A.; Bass, F.M. A diffusion theory model of adoption and substitution for successive generations of high-technology products. Manag. Sci. 1987, 33, 1069–1086. [Google Scholar] [CrossRef]
- Liu, R.; Gao, Z.; Yan, G.; Ma, H. Why should we protect the interests of “green food” certified product growers? Evidence from kiwifruit production in China. Sustainability 2018, 10, 4797. [Google Scholar] [CrossRef]
- Chang, T.; Chen, F.; Luan, H.; Chen, Y. Effect of green organizational identity, green shared vision, and organizational citizenship behavior for the environment on green product development performance. Sustainability 2019, 11, 617. [Google Scholar] [CrossRef]
- Bass, F.M. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Stummer, C.; Kiesling, E.; Günther, M.; Vetschera, R. Innovation diffusion of repeat purchase products in a competitive market: An agent-based simulation approach. Eur. J. Oper. Res. 2015, 245, 157–167. [Google Scholar] [CrossRef]
- Jiang, Z.; Jain, D.C. A generalized Norton–Bass model for multigeneration diffusion. Manag. Sci. 2012, 58, 1887–1897. [Google Scholar] [CrossRef]
- Janssen, M.A.; Jager, W. Stimulating diffusion of green products. J. Evol. Econ. 2002, 12, 283–306. [Google Scholar] [CrossRef]
- Olson, E. Green innovation value chain: A tool for evaluating the diffusion prospects of green products. J. Prod. Innov. Manag. 2013, 30, 782–793. [Google Scholar] [CrossRef]
- Bulte, C. New product diffusion acceleration: Measurement and analysis. Mark. Sci. 2000, 19, 366–380. [Google Scholar] [CrossRef]
- Mufidah, I.; Jiang, B.C.; Lin, S.C.; Chin, J.; Rachmaniati, Y.P.; Persada, S.F. Understanding the consumers’ behavior intention in using green ecolabel product through pro-environmental planned behavior model in developing and developed regions: Lessons learned from Taiwan and Indonesia. Sustainability 2018, 10, 1423. [Google Scholar] [CrossRef]
- Maccioni, L.; Borgianni, Y.; Basso, D. Value perception of green products: An exploratory study combining conscious answers and unconscious behavioral aspects. Sustainability 2019, 11, 1226. [Google Scholar] [CrossRef]
- Erkut, B. Product innovation and market shaping: Bridging the gap with cognitive evolutionary economics. Indraprastha J. Manag. 2016, 4, 3–24. [Google Scholar]
- Erkut, B. The emergence of the ERP software market between product innovation and market shaping. J. Open Innov. Technol. Mark. Complex. 2018, 4, 23. [Google Scholar]
- Myers, D.G. Social Psychology, 9th ed.; McGraw-Hill Companies: New York, NY, USA, 2012. [Google Scholar]
- Ram, S. Successful innovation using strategies to reduce consumer resistance: An empirical test. J. Prod. Innov. Manag. 1989, 6, 20–34. [Google Scholar] [CrossRef]
- Cherrier, H.; Black, I.R.; Lee, M. Intentional non-consumption for sustainability: Consumer resistance and/or anti-consumption? Eur. J. Mark. 2011, 45, 1757–1767. [Google Scholar] [CrossRef]
- Claudy, M.C.; Garcia, R.; O’Driscoll, A. Consumer resistance to innovation—A behavioral reasoning perspective. J. Acad. Mark. Sci. 2015, 43, 528–544. [Google Scholar]
- Aji, H.M.; Sutikno, B. The extended consequence of greenwashing: Perceived consumer skepticism. Int. J. Bus. Inf. 2015, 10, 433–468. [Google Scholar]
- Laufer, W.S. Social accountability and corporate greenwashing. J. Bus. Ethics 2003, 43, 253–261. [Google Scholar] [CrossRef]
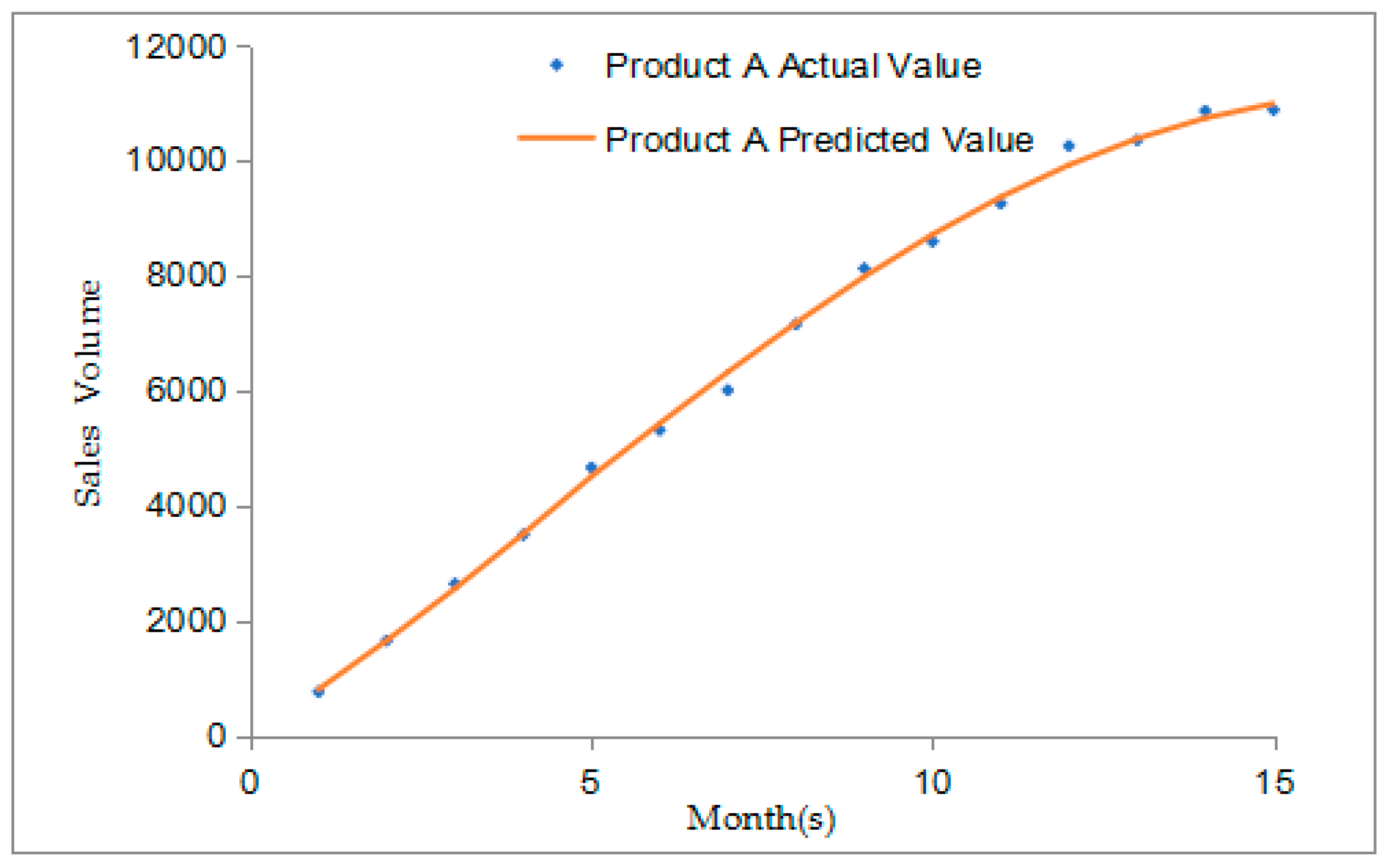
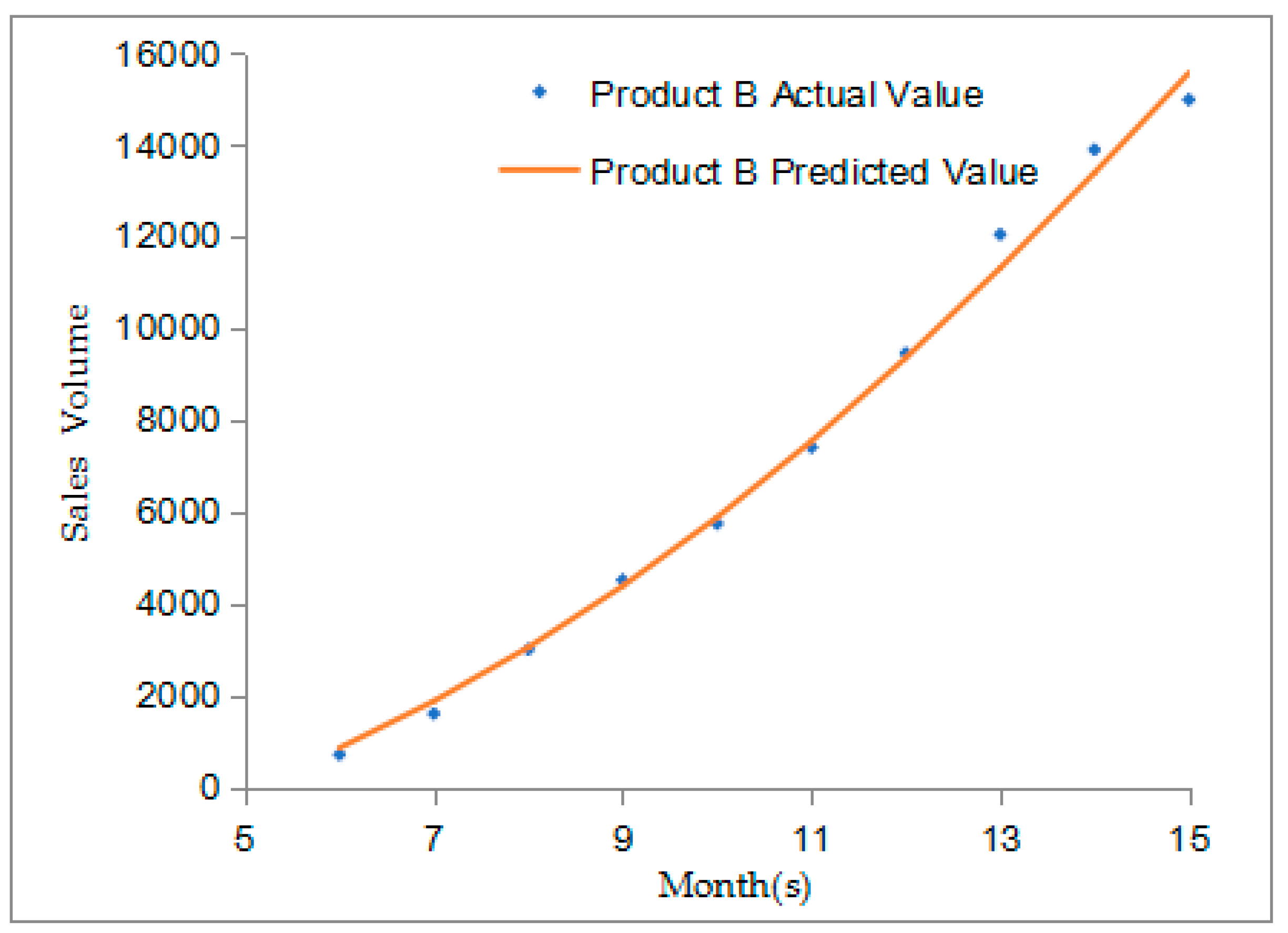
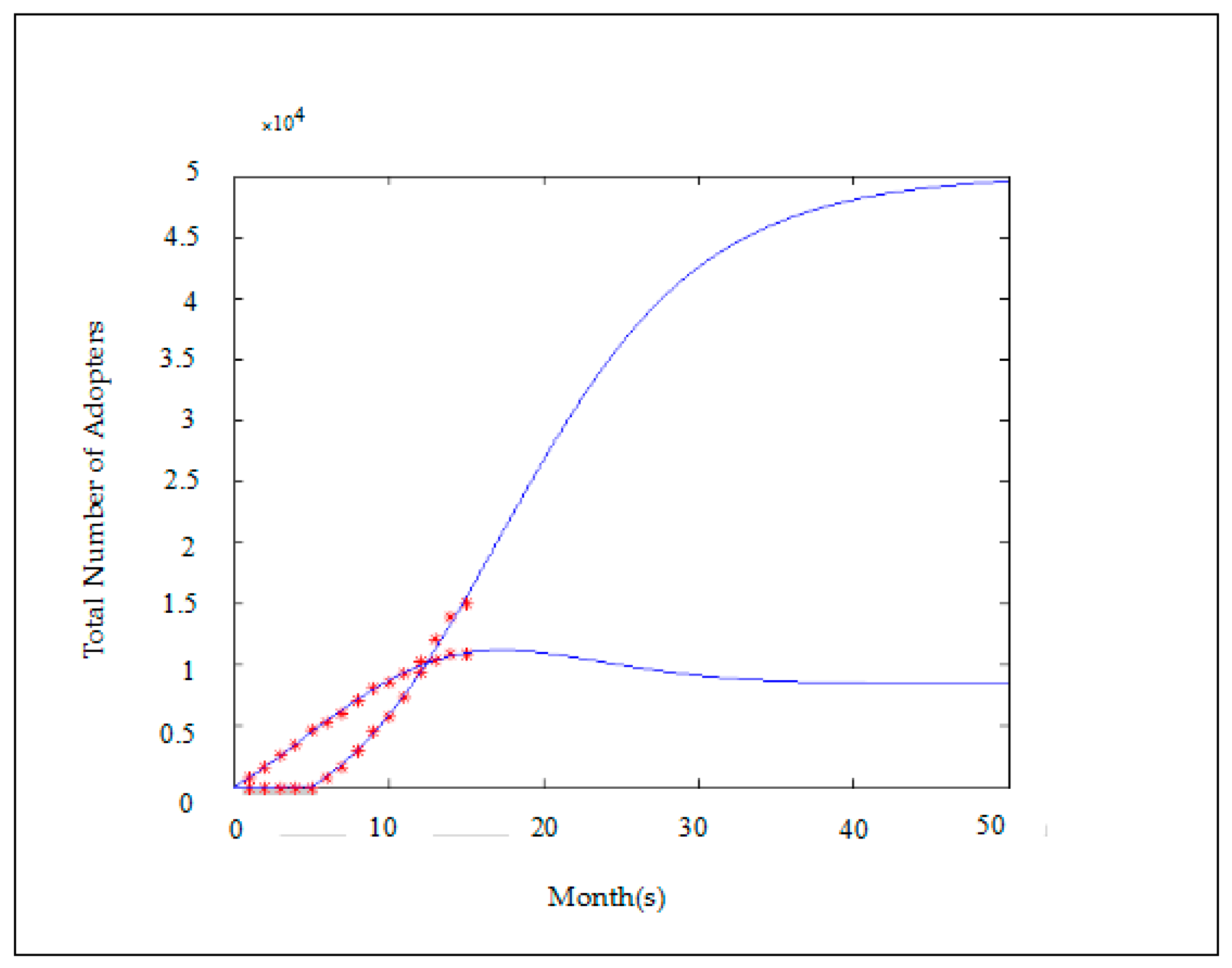
| Month | Error Rate | Month | Error Rate |
|---|---|---|---|
| 3.11% | 7 | 4.61% | |
| 2 | 4.86% | 8 | −1.88% |
| 3 | −3.03% | 9 | −1.19% |
| 4 | 4.44% | 10 | −3.59% |
| 5 | −9.08% | 11 | −10.27% |
| 6 | 5.54% | 12 | −20.68% |
| Month | Error Rate | Month | Error Rate |
|---|---|---|---|
| 1 | 7 | −6.70% | |
| 2 | 8 | −0.22% | |
| 3 | 9 | 0.14% | |
| 4 | −0.51% | 10 | 7.91% |
| 5 | 8.14% | 11 | −0.73% |
| 6 | 0.38% | 12 | −2.06% |
| Month | Error Rate | Month | Error Rate |
|---|---|---|---|
| 1 | 6.09% | 9 | −1.74% |
| 2 | 0.11% | 10 | 1.43% |
| 3 | −3.11% | 11 | 1.22% |
| 4 | 0.55% | 12 | −3.21% |
| 5 | −3.31% | 13 | 0.27% |
| 6 | 0.78% | 14 | −1.17% |
| 7 | 5.30% | 15 | 1.01% |
| 8 | 0.37% |
| Month | Error Rate | Month | Error Rate |
|---|---|---|---|
| 1 | 9 | −2.90% | |
| 2 | 10 | 2.35% | |
| 3 | 11 | 1.75% | |
| 4 | 12 | −1.04% | |
| 5 | 13 | −6.09% | |
| 6 | 19.59% | 14 | −3.61% |
| 7 | 16.77% | 15 | 3.88% |
| 8 | 1.59% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Zhang, T. The Effects of Product Consistency and Consumer Resistance to Innovation on Green Product Diffusion in China. Sustainability 2019, 11, 2702. https://doi.org/10.3390/su11092702
Chang Y, Zhang T. The Effects of Product Consistency and Consumer Resistance to Innovation on Green Product Diffusion in China. Sustainability. 2019; 11(9):2702. https://doi.org/10.3390/su11092702
Chicago/Turabian StyleChang, Yu, and Tao Zhang. 2019. "The Effects of Product Consistency and Consumer Resistance to Innovation on Green Product Diffusion in China" Sustainability 11, no. 9: 2702. https://doi.org/10.3390/su11092702
APA StyleChang, Y., & Zhang, T. (2019). The Effects of Product Consistency and Consumer Resistance to Innovation on Green Product Diffusion in China. Sustainability, 11(9), 2702. https://doi.org/10.3390/su11092702




