Assessing Land Fragmentation in Planning Sustainable Urban Renewal

Abstract

Planning of sustainable urban renewal is one of the key issues for city development. Particular emphasis is placed on the problem of the sustainable urban renewal of areas that are made up of a large number of private cadastral parcels that cause ownership fragmentation. Urban renewal is most often carried out to realize a large project where it is necessary to determine the optimal way of its realization. This paper proposes a methodology for assessing the index of fragmentation for the purpose of sustainable urban renewal planning. The methods used to solve the task are Simple Additive Weighting method (SAW) for ranking alternative solutions (i.e., cadastral parcels, spatial elements and areas of future construction), and the Fuzzy Analytic Hierarchy Process method (FAHP) for defining the criteria weights. In the process of defining the index of fragmentation model as well as the weighting determination, a group of experts was involved. The proposed model was tested on the field of the construction of the University of Split campus, for which implementation was planned in several periods. The obtained results show that the proposed methodology can provide support in analyzing the spatial–functional capacities of the existing land, and for decision making in optimizing the realization of urban projects.

1. Introduction

After the transition from communist to democratic political systems, through the privatization process, the urban space of many post-communist countries experienced significant changes mainly in terms of reduced public space. The unplanned development of urban and periurban areas as well as overpopulation not usually followed by the simultaneous development of urban infrastructure elements have led to the destruction of urban space that directly affects the quality of life of the city’s population as well as the quality of the city as a whole. Numerous public-type spaces are completely privatized, and a special problem is the area of illegal housing construction that is planned for social purposes. Absolute lack of control over this social trend in history, but also the absence of proper legislation, both in the past and at the present, have led to the emergence of new settlements that often do not meet the minimum conditions for a quality life. All of this is accompanied by an overly fragmented urban space, which is a significant problem for the sustainable development of the city. The most common definition of fragmentation in scientific literature is described as a situation where one area/unit is composed of a large number of parcels that are too small for their rational utilization [1,2,3,4]. King and Burton [5] and McPherson [6], along with the definition mentioned above, also describe fragmentation as a situation where one property is divided into more spatially separated land parcels. These given definitions refer to the fragmentation of agricultural land. Fragmentation of land is one of the major problems both in rural and urban areas, and is a significant obstacle to the sustainable development of the land. Given the existence of multiple types of fragmentation as well as the fact that their characteristics are often related to particular areas or countries, it is very difficult to define a fragmentation assessment procedure that would be globally applicable. Different parameters affect different types of fragmentation, and the definition of these parameters as well as the principle of determination is closely related to the spatial and legislative specificity of a particular area. By studying the available scientific and professional literature, the efforts made so far in defining the land fragmentation, especially its multifactorial form, mainly concern agricultural areas. Composting as a tool for suppressing land fragmentation is relatively easy to implement in rural areas because its purpose is to homogenize the spatial organization of land parcels of the same owner to achieve more productive agricultural production.

On the other hand, problems of fragmentation in urban environments due to the complexity both at the planning level and at the level of its implementation are still less represented as subjects of scientific and professional research. Also, the multidimensionality of the fragmentation definition of the urban area has been observed, which is usually related to different spatial fragmentation. Previous research has mainly focused on studying the impact of urbanization to protect ecosystems and urban landscapes. This type of fragmentation has dealt with: [7,8,9,10,11,12,13,14,15,16,17]. Wei and Zhang [18] have defined the fragmentation of urban land as a process by which land parcels are spatially dispersed in their allocation to create a severe barrier to optimum functional land. As the leading causes of land fragmentation, they indicate the fragmentation of construction land due to decentralized urban development, spatial heterogeneity of the parcels according to their use and highly developed transportation infrastructure.

Irwin and Bockstael [19] analyzed the fragmentation of land use over time based on six identified elements that separately defined the different dimensions of fragmentation. Guastella and Pareglio [20] conducted an empirical analysis of whether the morphological characteristics of a compact city are associated with the degree of urban fragmentation of land use, also relying on a discussion of the ecological and sociological consequences of morphological segments.

Donnelly and Evans [21] have developed a method for quantitatively describing land fragmentation by applying surface measurements of “parent” and “child” parcels and studying the change of land subdivision over a period of 70 years in Monroe County, Indiana.

Angel et al. [22] analyzed satellite images from 1990 to 2000 to estimate fragmentation of the urban area based on the open space area and the urban landscape versus the built-up area. Huang et al. [23] also analyzed satellite imagery to define parameters affecting the shape of an urban environment such as compactness, complexity, density, and regularity, while comparing world metropolises in said elements. You [24] analyzed satellite imagery from 1994 to 2013 to define the correlation of land fragmentation with economic transition in Shanghai, China.

The processes of urban sprawl, which can be described as growth by the creation of new low-density suburbs with detached or semi-detached housing and large commercial strips [25,26], inspired many authors to research the evolution of the territory and to diagnose its transformation from non-urban areas, such as agricultural ones, to urban areas. Sprawling cities, as the opposite of compact cities, are characterized by the empty spaces that indicate the inefficiencies in development and highlight the consequences of uncontrolled expansion [27], so the term of fragmentation was used as a measure of spatial discontinuity caused by uncontrolled expansion of the urban environment. This type of fragmentation has dealt with: [25,26,28,29,30,31,32]. Urban sprawl also has marked ecological and environmental impacts, such as the loss and fragmentation of farmland, biodiversity and natural habitat [33,34,35].

From the aforementioned studies it can be concluded that most of the current research on urban land fragmentation has implicated the fragmentation of land use, that is, the relationship between built-up areas of the city versus open space to define economic, sociological and/or ecological effects on land organization as well as the relationship between non-urban and urban areas, mostly in the periurban areas. None of the proposed indexes gives an overall image of the fragmentation of the urban space, taking into account the interrelationship of all relevant variables, and in particular, the image of fragmentation of urban area as an essential factor in the planning of urban renewal projects, the implementation of which is most common in phases. Also, no index of urban fragmentation was found that used multi-criteria methods for alternative rankings in combination with the Fuzzy Analytic Hierarchy Process method (FAHP) for the criteria weights definition.

Apart from the detailed definition of the urban fragmentation index, it is necessary to explain its usefulness for the realization of urban renewal projects. In the recent past efforts have been made to analyze the negative effects of the urban sprawl and to the use of preventive tools to control the “wild” construction process, but a major challenge remains in the improvement of already built urban areas. Considering the characteristics of urban construction, especially in the Mediterranean area, which relate to the narrow streets and the frequent absence of urban infrastructure elements and areas of public use, remediation of the resulting situation is only possible to the extent that the existing condition permits. Subsequent construction of the remaining elements must be adapted to the already built area, which only partially satisfies spatial infrastructure needs. On the other hand, the realization of a particular project may require a complete reorganization of a certain area. The current spatial distribution, most commonly caused with the illegal construction that is the result of the non-existence of a spatial planning strategy at the state and local level, does not often fit into the plans of the realization of most large public projects. These projects relate to the complete urban renewal of a particular area. In response to the requirements mentioned above, specifically related to the processes of the reorganization of urban and periurban areas, as well as complete urban renewal, and in order to improve the urban area in the world the urban land consolidation method has been recognized. In Croatian law, urban renewal is defined by terms “Urban Rehabilitation” and “Urban Transformation” [36], but the procedure of its implementation is not determined. Similarly, the new Physical Planning Act does not include the definition of urban land consolidation procedure, although there are requirements in the Spatial Development Strategy of the Republic of Croatia [37] for its adoption.

The encouragement for this research was primarily derived from the insufficiently effective acts of the urban consolidation method, as well as the urban renewal as its specific procedure, and has been further narrowed to the research of urban land fragmentation in order to optimize the realization of urban renewal for the purpose of implanting large public projects. The paper proposes a methodology for assessing the urban land fragmentation during the implementation of sustainable urban renewal to realize a large public project. Particular importance is attached to the issue of ownership within the area of construction, which, along with the financial segment, is the main limiting factor for the realization of the project. Spatial distribution of private parcels, their relationship and utility to the larger whole they belong to are the basis for defining the influential criteria for assessing the index of fragmentation. Given that large urban projects, which are planned on an already constructed area that was illegally built or that was not urbanized, often result in the complete urban renewal of a particular area, and as such require multiple planning levels. Accordingly, the index of fragmentation is developed for each of instance. Planning levels include the choice of location for the future project construction, planning of its realization for construction optimization and planning of urban renewal implementation to rank cadastral parcels (and their parts) for defining the stages of its implementation. The index of fragmentation is one of the essential spatial–functional criteria in each of these planning levels and therefore, a definition of a group of experts in the field of research should be included in its definition. All of these stages are described in detail in the theoretical and numerical sense hereafter.

2. Materials and Methods

In the beginning, it is essential to define the general term of the index of fragmentation. For the realization of any project that has a spatial element, it is very important to evaluate the pre-existing condition of the land. The land evaluation method depends precisely on the purpose of a particular project, i.e., on the definition of the necessary criteria that affect its realization. Based on those mentioned above, the general term of the index of fragmentation would be the evaluation of spatial elements in relation to the deviation from their ideal form. The ideal form of a spatial element depends on a specific task, and given that the subject of this paper is support for the sustainable urban renewal planning to realize large public projects, its ideal form is determined based on identified criteria that influence the progress of project implementation. Considering that the planning of the large public projects is a strategic process and encompasses multiple levels of planning, the index of fragmentation can be defined for each of them, as one of the criteria of the hierarchical goal structure in the decision-making process. One of these planning levels along with defining the hierarchical goal structure for the purpose of implementing the expropriation procedure for the private land parcels acquisition in the area of the campus project, University of Split is presented in the paper Kilić et al. [38]. The problem is primarily to identify all relevant criteria at all planning levels as well as their interrelationships, for their evaluation and relative comparison.

The architecture of an index of fragmentation model is defined by the diagram shown in Figure 1. Taking into account that the primary research point is the problem of land ownership within the area of the large public project, the set of alternatives refers to private land. At the beginning, it is necessary to define the ideal private cadastral parcel, the ideal spatial element (a set of cadastral parcels and its parts that make up a particular unit) and an ideal building area for the realization of the future project. Since the cadastral parcel is the smallest unit assigned the attribute of ownership, the research begins by defining its ideal form. It is necessary to identify which attributes should have an ideal private cadastral parcel and based on that define the criteria to evaluate and compare the defined alternatives.

To implement the steps mentioned above, a group of experts has been involved in the decision-making process. The term expert refers to a professional in a particular area who has the ability to solve new problem tasks based on the existing above-average and specific knowledge. The pre-existing condition of the project has been presented to the experts, altogether with an official urban plan which defines the distribution of future spatial elements within the area of the project implementation. The crucial component is to determine how the existing private cadastral parcels will be observed. If, on the one hand, it is already predefined the future use and purpose of spatial elements, it is clear that the main problem is belonging of private cadastral parcels to particular spatial elements. Likewise, the cadastral parcel rarely belongs to only one spatial element and already is, with different percentages of area, useful for the realization of multiple elements. According to the urban plan of the project area, spatial elements are divided into three basic categories: spatial units as areas of future objects in the project area, road infrastructure, and green areas.

Regarding the need to determine the affiliation of cadastral parcels to a particular spatial element, the road infrastructure and green areas are divided into logical units according to the connection in the sense of simultaneous construction. Cadastral parcels are divided into smaller parts that have been observed separately, and an index of fragmentation has been estimated for each part. A share of private cadastral parcel area or part of it in relation to the total (private) area of a given spatial element is only one of the criteria to be taken when assessing the index of fragmentation.

To implement a large public project, the index of fragmentation is defined for three levels of planning (Figure 2):

• Planning to select the location for the construction of a future project (Index of fragmentation for location selection),
• Planning the realization of future project construction (Index of fragmentation of spatial elements in the field of construction):
  • Spatial Unit Index of Fragmentation—IFSU,
  • Road Infrastructure Index of Fragmentation—IFRI,
  • Green Area Index of Fragmentation—IFGA,
• Planning of Urban Renewal (Parcel Index of Fragmentation—IFP).

Figure 2 shows defined criteria and users as decision-makers for three levels of planning (first level of planning—state/city, second level of planning—main project investor, third level of planning—main project investor and managers). As already mentioned above, research begins with defining criteria to evaluate cadastral parcels. With the first criterion, which is already explained in the text above and refers to the share of private cadastral parcel area in the total private area of a specific spatial element (spatial unit, element of road infrastructure, element of green area), the other three criteria relate to the number of other private cadastral parcels on a particular spatial element, the ownership fragmentation of the private cadastral parcel and the slope of the cadastral parcel. The reason for choosing these attributes as criteria for parcel comparison is the observation of a particular cadastral parcel in terms of its usefulness for the future realization of the spatial element. Although the impact of the criterion “slope of the cadastral parcel” is quite small and only affects the cost of construction works, it is necessary to include it in the definition of the ideal private cadastral parcel. Thus, the ideal private cadastral parcel would be the one which lies 100% in the total private area needed to form a particular spatial element, which has only one private owner and which has a 0° slope. Ownership fragmentation refers to the number of co-owners of a private cadastral parcel as the total number of people to negotiate for participation in the urban renewal process. The Parcel Index of Fragmentation ranges from 0 to 1, where an evaluation of 1 indicates a cadastral parcel that is not fragmented (the upper limit values of the evaluated cadastral parcel correspond to the values of the ideal cadastral parcel).

Table 1. Description and method for criteria assessment—IFP.

Criterion ID	Criterion Description	Spatial Element Example	Min/Max
C1	The share of cadastral parcel area or part of it in the total area of private cadastral parcels needed to form the spatial unit/element of road infrastructure/element of green surface. The assessment of this criterion is defined by percentage share (%).		max
C2	The number of other cadastral parcels on a given spatial unit/element of the road infrastructure/element of the green area.		min
C3	The number of co-owners of a particular cadastral parcel (ownership fragmentation of the cadastral parcel).		min
C4	Slope of the cadastral parcel. The assessment of this criterion is defined by the percentage (%) of the slope of the terrain.		min

shows the identification number of the criteria, their description, the explanatory drawing for every criterion and the assessment techniques, as well as the mathematical operator min/max. Three criteria have minimum optimal values, meaning that the best cadastral parcel is the one with the lowest values obtained by the evaluation techniques. One criterion has a maximum optimal value, which defines the highest value as the best variant solution. The explanatory drawings are given for one spatial unit (SU 11) which consists of nine private cadastral parcels, and their evaluation is presented according to the defined criteria. For the assessment of the index of fragmentation, it is necessary to normalize the criteria values that are carried out with linear normalization and specially created value functions based on the estimates of the experts involved in the decision-making process.

The second level refers to planning the realization of future project construction. As mentioned above, the analysis of the urban plan of construction area identified three essential spatial elements of use and purpose of the project area, and three different indexes of fragmentation were defined accordingly. The criteria defined for each spatial element are shown in

Table 2. Description and method for criteria assessment—IFRI, IFSU, IFGA.

Criterion ID	Criterion Description	Min/Max
Road Infrastructure Index of Fragmentation—IFRI
C1a (1), C2a (2), C3a (3), K1a (4), K2a (5), K3a (6), K4a (7), K5a (8), K6a (9), K7a (10), K8a (11)	Primary route network (1), Secondary route network (2), Other route networks (3), City road (4), Collector road (5), Access road (6), Other roads (7), Square (8), Main pedestrian street (9), Other pedestrian streets (10), Parking (11)
Nia (I = 1,…,15)	Parcel Index of Fragmentation (IFP)	max
Nja (j = 2, …,16)	A share of private land in relation to the total land of the road infrastructure element. The assessment of this criterion is defined by percentage share (%).	min
Spatial Unit Index of Fragmentation—IFSU
C1b	Number of cadastral parcels to be purchased to form an access road.	min
C2b	The area of the cadastral parcels to be purchased to form an access road. The assessment of this criterion is defined in meters square (m2).	min
C3b	Parcel Index of Fragmentation (IFP)	max
C4b	Share of private land in relation to the total land of the spatial unit. The assessment of this criterion is defined by percentage share (%).	min
Green Area Index of Fragmentation—IFGA
C1c	Parcel Index of Fragmentation (IFP)	max
C2c	Share of private land in relation to the total land of the green area element. The assessment of this criterion is defined by percentage share (%).	min

. To define the road infrastructure index of fragmentation, the roads are divided into primary (city and collector roads), secondary route networks (access roads, other roads and square) and other route networks (main and other pedestrian and parking areas). Similar to the Parcel Index of Fragmentation, this index has a range from 0 to 1, where the evaluation of 1 indicates a spatial element that is not fragmented (ideal spatial element). It is important to emphasize that one of the criteria at the second level refers to the Parcel Index of Fragmentation defined for the third level of planning and explained in the text above.

Table 2 also shows the identification number of the criteria, their description and the assessment techniques, as well the mathematical operator min/max. Road Infrastructure Index of Fragmentation and Green Area Index of Fragmentation are determined based on two criteria: (1) Parcel Index of Fragmentation which has a maximum optimal values and (2) Share of private land in relation to the total land which has a minimum optimal values. Spatial Unit Index of Fragmentation is defined with four criteria. Along with the two already defined for road infrastructure and green areas, this also includes the criteria relating to the possibility of building an access road which is the requirement for starting construction of buildings. Parcel Index of Fragmentation criterion has a maximum optimal values and the other three have minimum optimal values.

The index of fragmentation for the first level of planning is defined by five criteria, while the first criterion relating to Parcel Index of Fragmentation is divided into three additional subcriteria (ownership fragmentation, allocation fragmentation and slope of the cadastral parcels).

Table 3. Description and method for criteria assessment—Index of fragmentation for location selection.

Criterion ID	Criterion Description	Min/Max
C1d	Parcel Index of Fragmentation 2—IFP 2
C2d	Access to a registered road. Binary assessment: — Cadastral parcels having access to the registered road are assigned a rating of 1, — Cadastral parcels that do not have access to the registered road are assigned a rating of 0.	max
C3d	Dispersion of the private cadastral parcels in the project area (DoPP).	min
C4d	Share of private land in relation to the total land. The assessment of this criterion is defined by percentage share (%).	min
C5d	The number of private cadastral parcels in the project area.	min
K1d	The number of co-owners of a particular cadastral parcel (ownership fragmentation of the cadastral parcel).	min
K2d	Allocation fragmentation of the project area—share of construction land in relation to the total land. The assessment of this criterion is defined by percentage share (%).	max
K3d	Slope of a cadastral parcel. The assessment of this criterion is defined by the percentage (%) of the slope of the terrain.	min

shows the identification number of the criteria, their description, the assessment techniques and the mathematical operator min/max. It can also be noticed, although their name is equal, there is a difference in the definition of Parcel Index of Fragmentation at the first and third planning levels. Precisely, as stated above, the cause is specific objectives or needs at different levels of project planning that affect its definition. At the first level of planning, it is necessary to compare the areas of greater potential for the future project construction, so the cadastral parcels are observed as a group and their best combination is required. At the third level of planning, cadastral parcels are compared between themselves and their priority rank is determined in relation to which urban renewal of a particular area will be planned (large public projects of which implementation may take place over a longer period). From all of the above mentioned, it can be concluded that although the criteria for defining two (different) Parcel Index of Fragmentations partially overlap, they are not used for the same purpose or in the same calculation. A special emphasis is placed on the relation of the cadastral parcels; at the first level of planning the aggregate effect of the cadastral parcels is observed, while on the third level of planning their mutual comparison is performed. Along with the Parcel Index of Fragmentation, the other four criteria relate to access to registered road, dispersion of the private cadastral parcels in the project area, a share of private land in the total land and the number of private cadastral parcels in the project area. An ideal area for the construction of a future project would be construction land, which is not privately owned, having access to a registered road and with a slope of 0°. The criteria of access to a registered road and allocation fragmentation of the project area have ideal maximum values, and the other criteria have ideal minimum values.

The dispersion of the private cadastral parcels in the particular area is measured (DoPP) in meters, which is represented by the standard distance. The standard distance is a basic measure of spatial dispersion [39] which is the spatial equivalent of the standard deviation in the statistic (σ). It shows how cadastral parcels are concentrated or scattered around the spatial mean which is an important spatial statistical measure of central tendency (it indicates the average location of a set of points). The standard distance measures the degree to which cadastral parcels (precisely the centroids of parcels) are concentrated or dispersed around their geometric mean [1,39]. The mean center of the private cadastral parcels in the particular area can be calculated by the mean of the x coordinates and the y coordinates of the centroids of the private cadastral parcels. The location of the mean center of the private cadastral parcels in the project area is calculated according to the formula [1,39]:

$$\left(\overline{x_{hmc}},\overline{y_{hmc}}\right)=\left(\frac{{{\displaystyle \sum }}_{i=1}^n{x}_i}{n},\frac{{{\displaystyle \sum }}_{i=1}^n{y}_i}{n}\right)$$

(1)

where $\overline{x_{hmc}}$ and $\overline{y_{hmc}}$ are the coordinates of the mean center of the private cadastral parcels, $x_i$ and $y_i$ are the coordinates of each private cadastral parcel center (centroid coordinates) and n is a number of private cadastral parcels.

Finally, the dispersion of private parcels in the project area (DoPP) is obtained from the formula [1,39]:

$$DoPP=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-\overline{x_{hmc}}\right)}^2+{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y_{hmc}}\right)}^2}{n}}$$

(2)

In this paper, the index of fragmentation for the first level of planning is theoretically explained and its criteria are numerically defined, and can be used in future research as one of the criteria for selecting the most favorable location for the future project construction. Since the aim of the research is only to identify the criteria of an index of fragmentation at different levels of project planning, its comparison between the various possible locations of the future project has not been carried out.

After defining the criteria for the fragmentation assessment, the next two steps are performing simultaneously, referring to the evaluation of the cadastral parcels and its parts by defined criteria and defining the importance of the criteria (weight) using the Fuzzy AHP method. Weights are given by Saaty’s scale of relative importance based on the assessment of the experts involved in the decision-making process. In the end, by applying a Simple Additive Weighting method, the index of fragmentation is determined. It is important to emphasize that the priority ranking of the private cadastral parcels in the urban renewal planning process is implemented for whole cadastral parcels, so a unique index of fragmentation for each cadastral parcel needs to be provided. It was decided that the index of fragmentation would be obtained by the arithmetic mean of its values calculated for its particular parts.

The methods used to determine the index of fragmentation are the Fuzzy AHP method (FAHP) for defining weights and the Simple Additive Weighting Method (SAW) for alternatives ranking. The mathematical basis of the FAHP method is defined below [40,41,42,43,44,45,46].

Fuzzy AHP

Step 1—Calculation of Triangular Fuzzy Numbers (TFNs)

The experts included in the definition of the index of fragmentation model determined TFNs using AHP method (

Table 4. Membership function of linguistic scale.

Linguistic Scale of Importance	Fuzzy Triangular Scale (l, m, u)
Equally important	(1,1,2)
Weakly important	(1,2,3)
Moderate important	(2,3,4)
Moderate to strongly important	(3,4,5)
Essential or strongly important	(4,5,6)
Strongly to very strongly important	(5,6,7)
Very strongly important	(6,7,8)
Very strongly to extremely important	(7,8,9)
Extremely preferred	(8,9,9)

). The reason for choosing a Fuzzy AHP (FAHP) instead of the standard AHP method is to reduce the subjectivity and insecurity of the weight definition process. Instead of the crisp weight values, the triangular range of values is defined for each criteria weight. Table 6 defines the linguistic scale of importance and fuzzy triangular scale with lower (l), middle (m) and upper (u) values.

Step 2—Calculation of$\widetilde{G_i}$

Experts carried out a pair-wise comparison of the criteria in order to define their relative relation. The results of a pair-wise comparison are classified into the corresponding A matrix which consists of triangular fuzzy scale for every criteria relative relation. Compromise fuzzy weights for all experts are defined as a geometric mean of lower, middle and upper triangular values of criteria weight:

$${\tilde{G}}_i=\left(l_i, m_i, u_i\right)$$

(3)

$$l_i={\left(l_{i1}\otimes l_{i2}\otimes \dots \otimes l_{ik}\right)}^{1/k}; i=1,\dots , n;j=1, \dots , k$$

(4)

$$m_i={\left(m_{i1}\otimes m_{i2}\otimes \dots \otimes m_{ik}\right)}^{1/k};i=1,\dots , n;j=1, \dots , k$$

(5)

$$u_i={\left(u_{i1}\otimes u_{i2}\otimes \dots \otimes u_{ik}\right)}^{1/k}; i=1,\dots , n;j=1, \dots , k$$

(6)

where n is a number of criteria, and k is a number of experts.

Step 3—Calculation of$\widetilde{G_T}$and$\tilde{w}$

After the calculation of the compromise weights, the sum of lower, middle and upper geometric mean values of each criterion are obtained as follows:

$$\widetilde{G_T}=\left({\displaystyle \sum }_{i=1}^n{l}_i,{\displaystyle \sum }_{i=1}^n{m}_i, {\displaystyle \sum }_{i=1}^n{u}_i\right)$$

(7)

By dividing Equation (3) with (7), normalization of criteria weights is determined as is given below:

$$\begin{array}{ll}\tilde{w}=\frac{\widetilde{G_i}}{\widetilde{G_T}}& =\frac{\left(l_i, m_i, u_i\right)}{\left({{\displaystyle \sum }}_{i=1}^n{l}_i,{{\displaystyle \sum }}_{i=1}^n{m}_i, {{\displaystyle \sum }}_{i=1}^n{u}_i\right)}\\ & =\left[\frac{l_i}{{{\displaystyle \sum }}_{i=1}^n{u}_i},\frac{m_i}{{{\displaystyle \sum }}_{i=1}^n{m}_i},\frac{u_i}{{{\displaystyle \sum }}_{i=1}^n{l}_i}\right]\end{array}$$

(8)

Step 4—Calculation of$w{i}_{\alpha l}$

Any fuzzy set can be described by specifying its α-cuts. For each criterion, the factors corresponding to ten different α-cut values are defined based on which the lower and upper α values are calculated:

$$w{i}_{\alpha l}=\left(wi{l}_{\alpha l}, wi{u}_{\alpha l}\right);i=1,2,\dots , n;l=1, 2\dots , p.$$

(9)

where l is a number of α-cuts.

Step 5—Calculation of$W_{il}, W_{in}$

The final lower and upper α values for each criterion are obtained with the following formula:

$$W_{il}=\frac{{{\displaystyle \sum }}_{i=1}^L\alpha {\left(w_{il}\right)}_l}{{{\displaystyle \sum }}_{i=1}^L{\alpha }_l};i=1,2,\dots , n;l=1,2,\dots ,p$$

(10)

$$W_{iu}=\frac{{{\displaystyle \sum }}_{i=1}^L\alpha {\left(w_{iu}\right)}_l}{{{\displaystyle \sum }}_{i=1}^L{\alpha }_l};i=1,2,\dots , n;l=1,2,\dots ,p.$$

(11)

Step 6—Calculation of$W_{id}$

Defuzzified weight values are obtained by combining the lower and upper α values using the optimism index (λ):

$$w_{id}=\lambda ·w_{iu}+\left(1-\lambda \right)·w_{il}; \lambda \in \left[0,1\right]; i=1,2,\dots ,n;l=1,2,\dots ,p$$

(12)

Step 7—Calculation of$W_{in}$

Defuzzified weight values are normalized as follows:

$$W_{in}=\frac{W_{id}}{{{\displaystyle \sum }}_{i=1}^n{W}_{id}}; i=1,2,\dots ,n$$

(13)

3. Results

3.1. Preliminary Analysis of the Study Area

The validation of the index of fragmentation model was carried out in the area of the campus project, University of Split in the city of Split, Republic of Croatia (Figure 3).

The basis for spatial analysis was the overlap of the existing land subdivision defined by the official data of the cadaster and urban plan of the campus project. These documents defined the facilities within the campus (most relevant for this study were spatial units that related to faculty buildings and other objects in function of the University, the road infrastructure and the green area) and the boundaries and conditions of their future construction. The urban plan represented a new land subdivision of the project area in such a way that new cadastral parcels represented construction parcels in accordance with spatial planning documentation and rules that apply to the area of project realization. The research included subprojects relating to spatial units, road infrastructure and green areas whose realization had not been implemented nor has the way of implementing them been planned. Accordingly, property ownership, along with the financial segment, was the fundamental limiting factor for planning the realization of subprojects within the campus area, which was primarily related to private owners who are residents in the defined area. The distribution of private cadastral parcels, their relation to the entities to which they belong as well as land allocation affiliation defined by the urban plan were key spatial elements that affected the progress of project realization. Figure 4 shows the research area bordered by the urban plan boundary, with a special emphasis on cadastral parcel ownership. The numbers within the figure indicate spatial units as areas of existing and future facilities in the project area of the campus.

By preliminary spatial analysis and discussion with the experts involved in the research, the key spatial elements in the project area were defined. Apart from defining the steps of the index of fragmentation model, the same experts were involved in the process of defining the weights of criteria for the index of fragmentation assessment.

The definition of spatial elements was of great importance for selecting the most optimal method for the index of fragmentation determination. The research began with the identification of all cadastral parcels (or its parts) belonging to the area of research and then their spatial affiliation to a particular spatial element. Subsequently, the elements of road infrastructure and green areas were divided into a number of logical units according to the connection in the sense of simultaneous construction (

Table 5. Spatial elements and their logical units.

Spatial Element	Total Number of Logical Units	Number of Logical Units on the Private Land
Spatial unit	19	11
Element of the road infrastructure	47	28
Element of the green area	7	3

). In accordance with these divisions, the identification tag of each logical unit was specified. The identification tag defined a spatial element that contained a certain number of cadastral parcels and its parts.

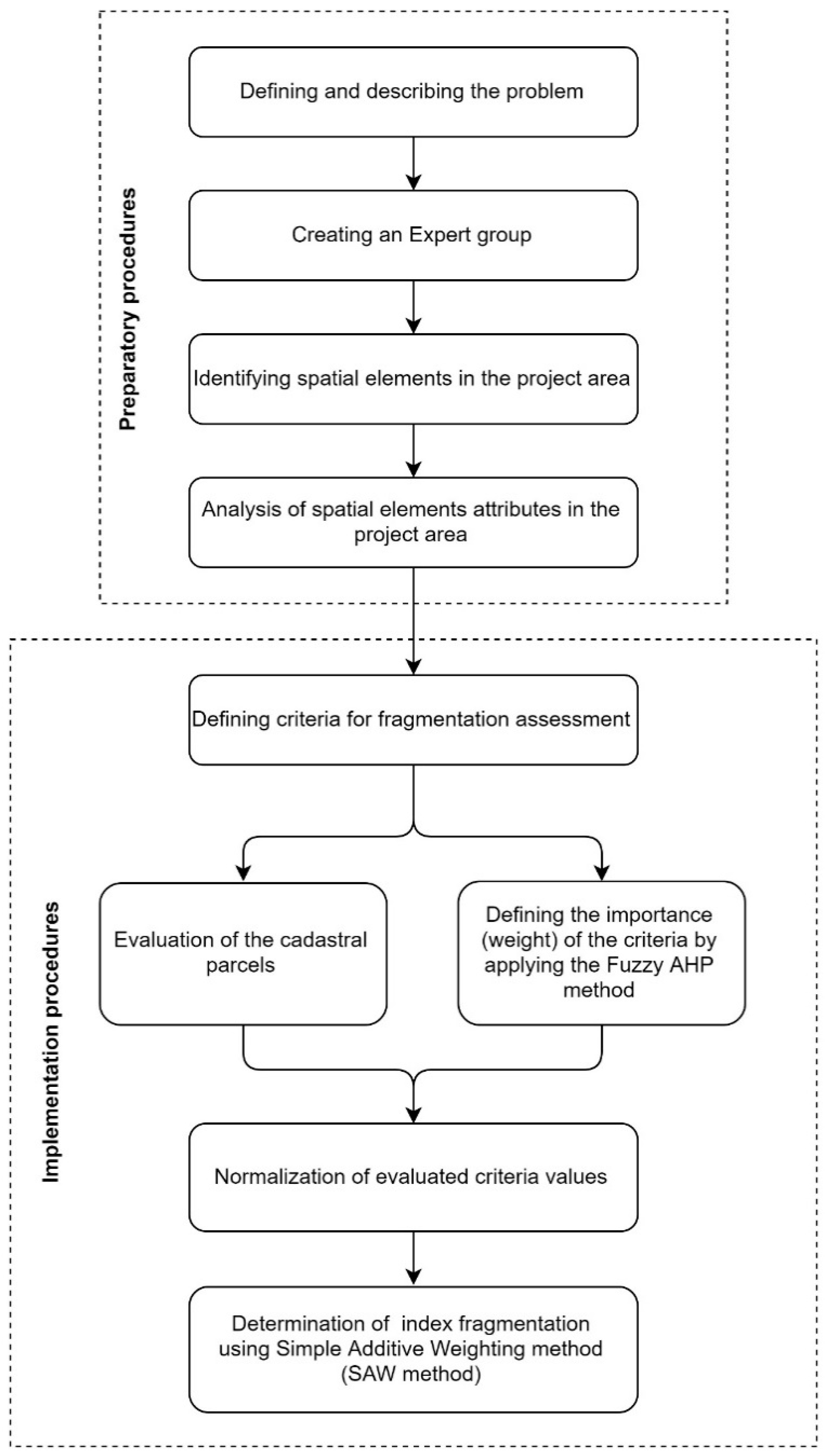
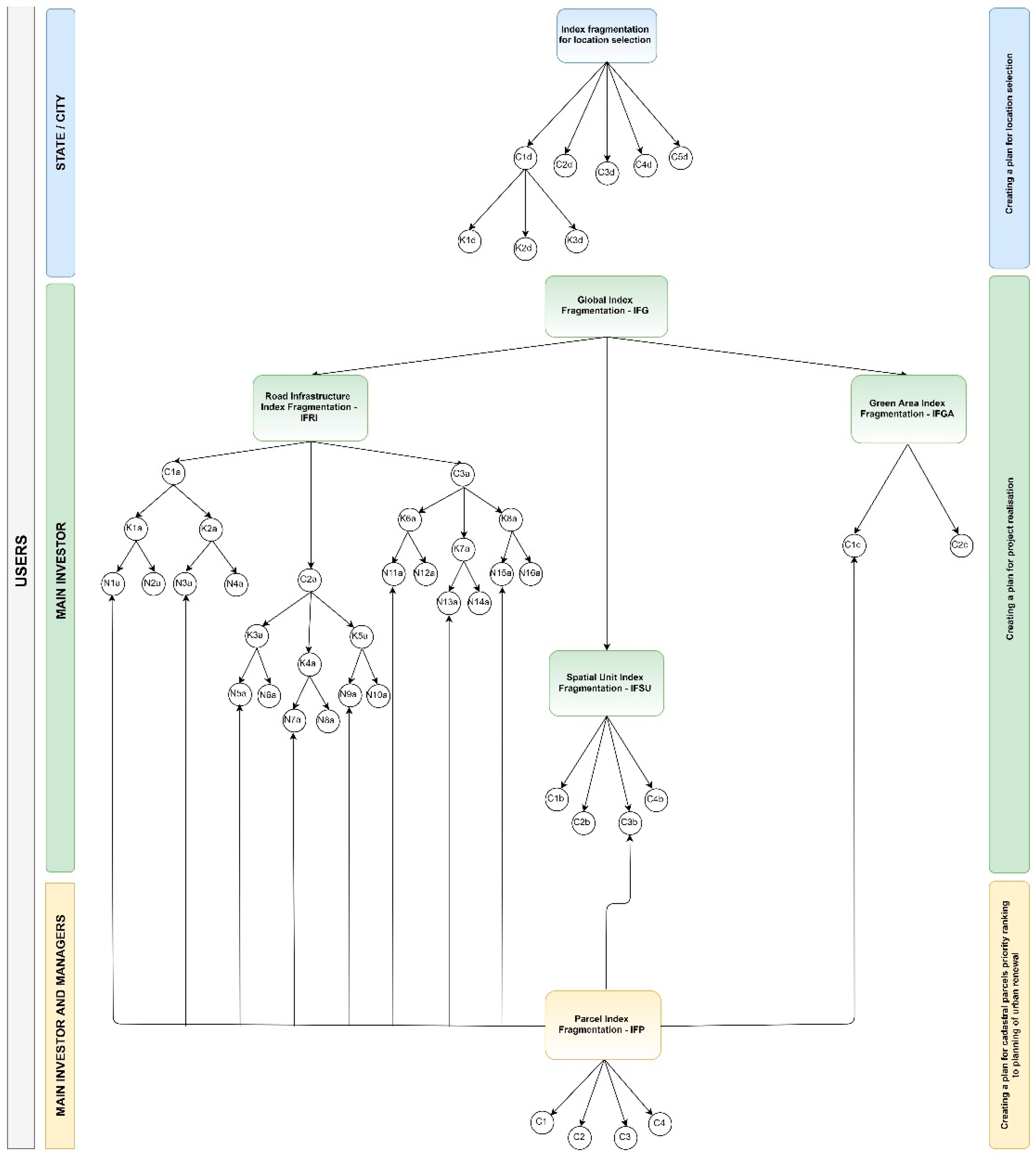
3.2. Index of Fragmentation Assessment

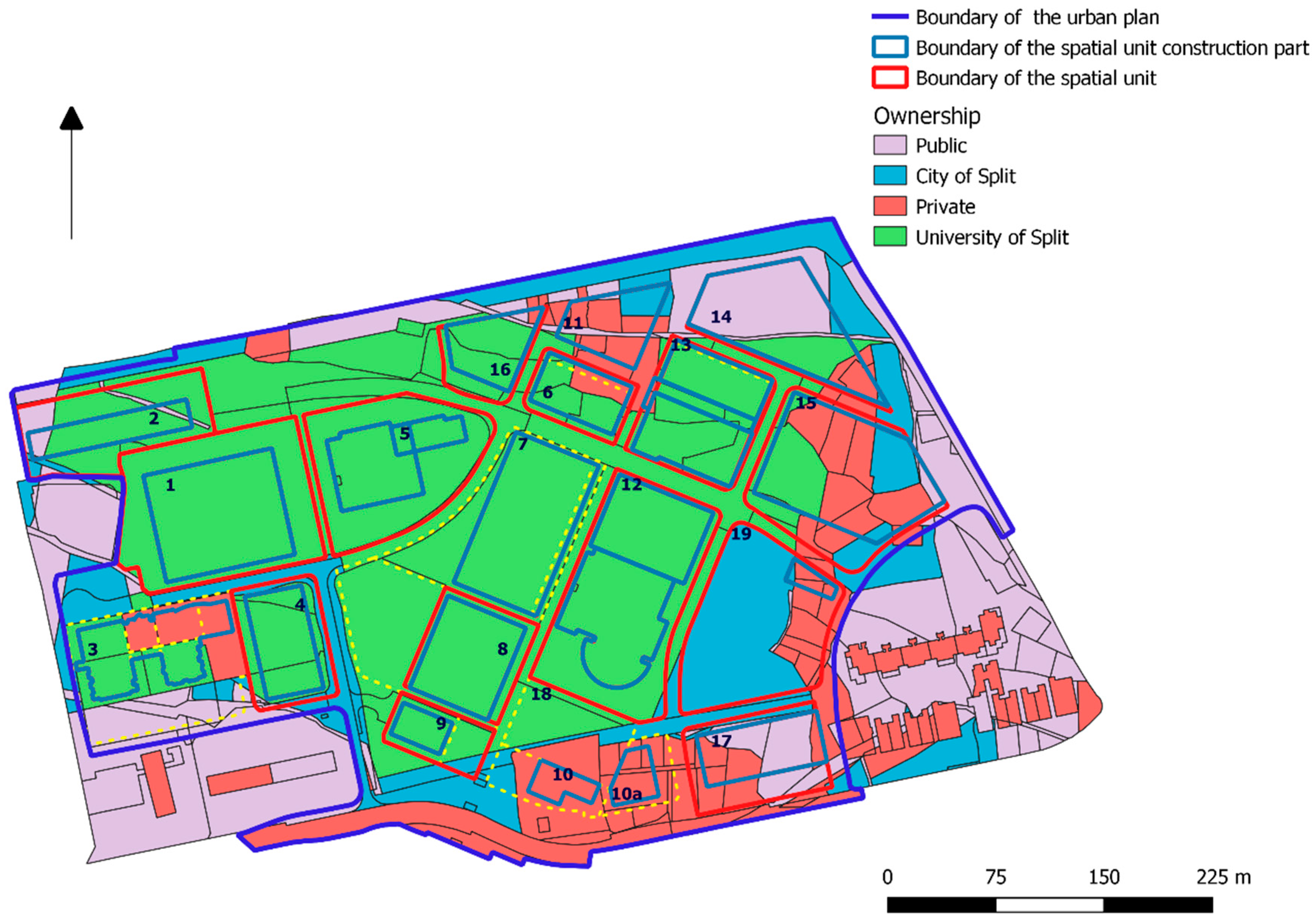
After the identification of the spatial elements and their logical units, all private cadastral parcels in the campus area were identified and a set of 62 parcels was established based on which validation of the index of fragmentation model was performed. By analyzing the cadastral parcels attributes, a basis for defining the ideal parcel and evaluation criteria for determining the index of fragmentation was established. Four criteria were identified for Parcel Index of Fragmentation. Two defined the relationship of a particular cadastral parcel to other cadastral parcels belonging to the same spatial element (C1 and C2), while two were related to the internal fragmentation of cadastral parcel (C3 and C4). Ownership fragmentation referred to the number of co-owners of each cadastral parcel as the total number of people to negotiate for participation in the urban renewal process. This criterion could be elaborated in more detail taking into account along with the number of owners also their ownership condition that can be defined as co-ownership, joint ownership and tenant ownership. Each of those mentioned above could be assigned a weight of importance, but given that the owners of all the cadastral parcels on the campus area are in the co-ownership, the simpler version was used. The next step was the evaluation of private cadastral parcels by each criterion. The GIS tools were used for alternatives assessment by all defined criteria. Based on these values the decision matrix was formed where each row gave an estimate of one cadastral parcel through all criteria, and each column gave an evaluation of all cadastral parcels by one criterion.

Table 6. Part of decision matrix for Parcel Index of Fragmentation assessment.

Number of Cadastral Parcel	Identification Tag	C1	C2	C3	C4
part of 6505/1	OP3	56,59	1	2	0,00
part of 6505/1	OP7	42,86	1	2	0,00
part of 6505/1	SC21	4,29	1	2	0,00
part of 6505/2	OP3	43,41	1	2	0,00
part of 6505/2	OP7	57,14	1	2	0,00
part of 6505/2	SC21	95,71	1	2	0,00
6541/1	SU15	5,21	11	6	11,19
part of 6545	SU19	15,18	9	6	1,37
part of 6545	OP23	10,35	6	6	1,37
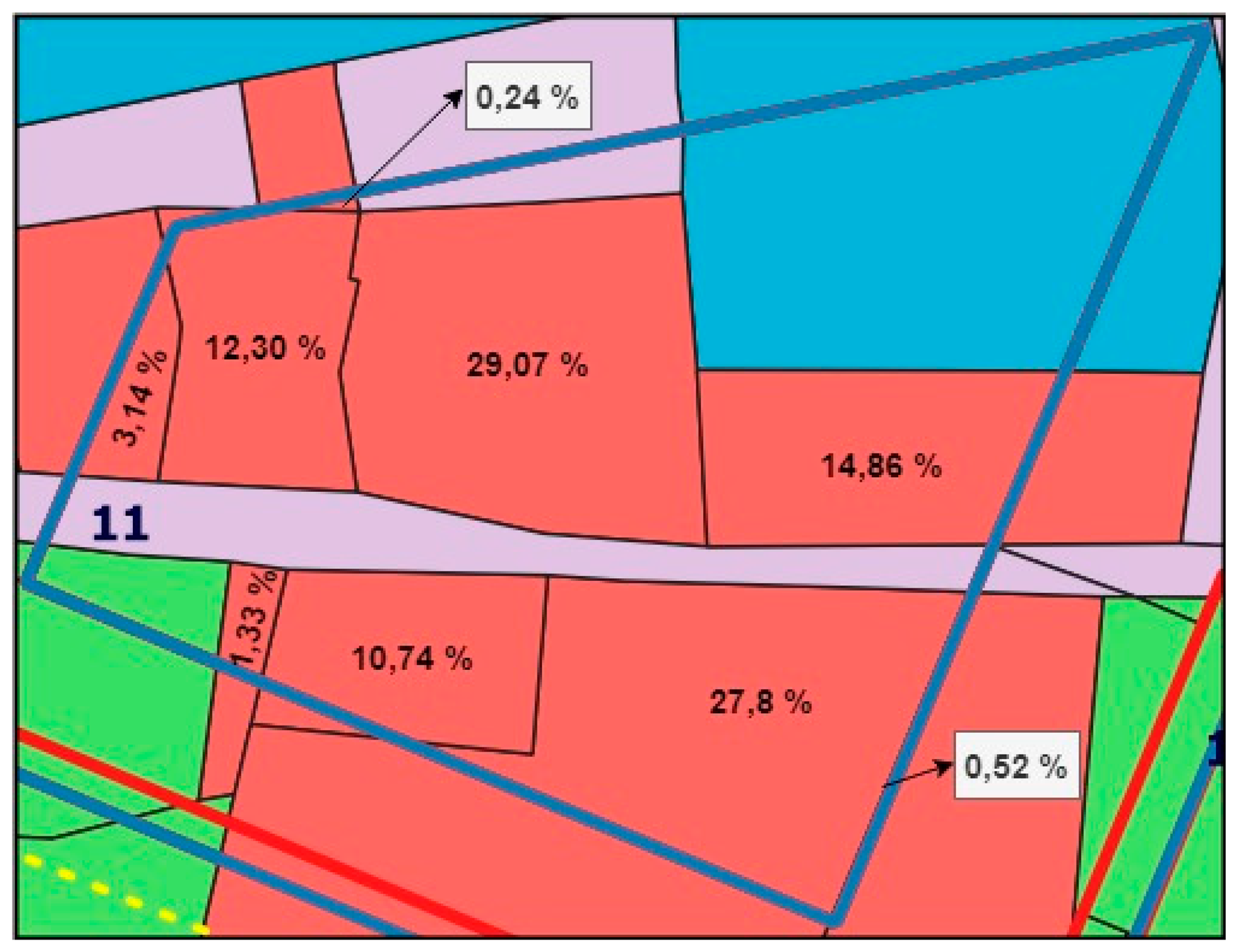
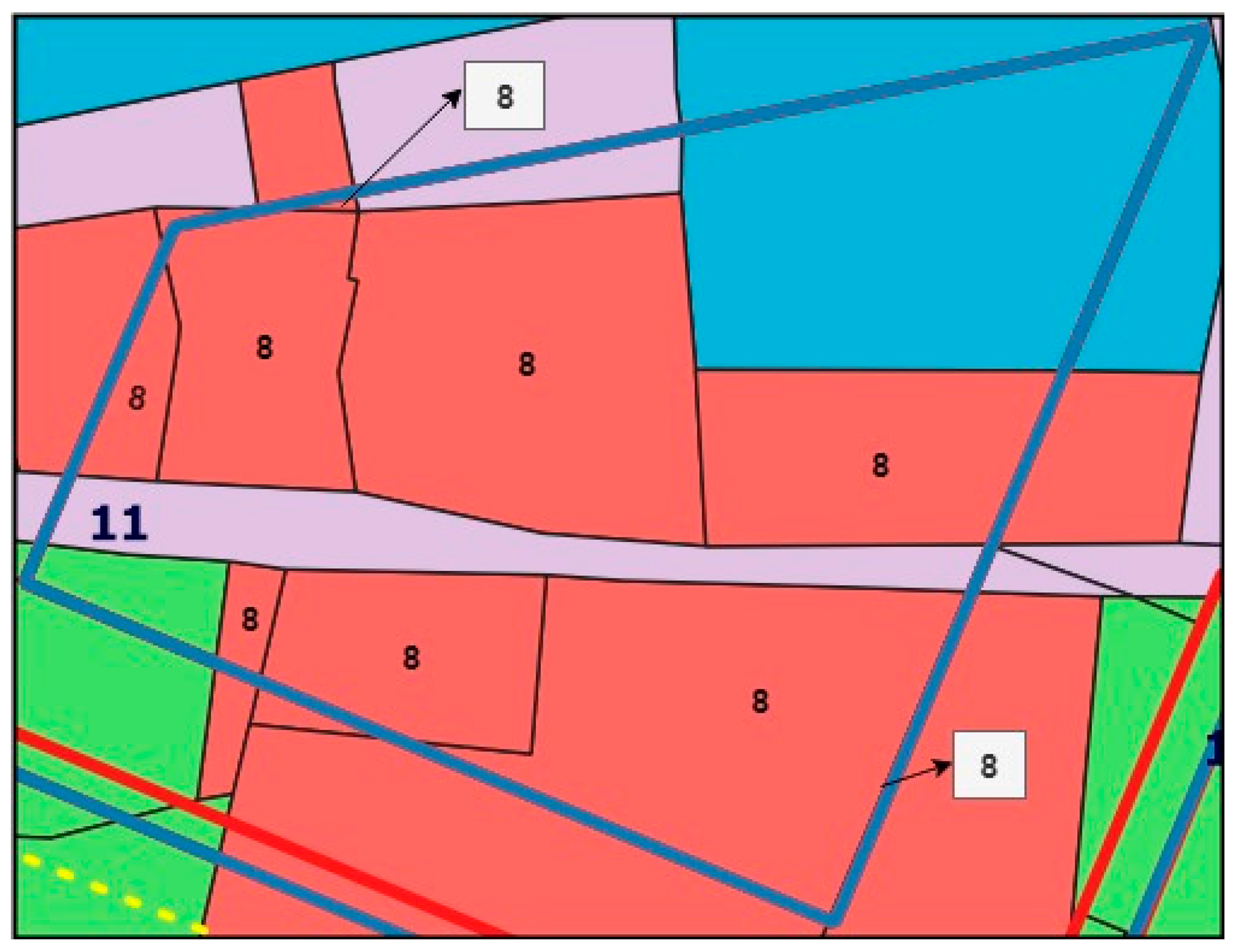
part of 6545	PC11	27,40	4	6	1,37

shows part of the decision matrix with the values of evaluated cadastral parcels and its parts in the campus area. The first column shows the number of cadastral parcels or its parts, while the second column refers to the identification tag of the logical unit to which a particular cadastral parcel or its part belongs. For the sake of transparency, the decision matrix is shown for 10 of 62 cadastral parcels or its parts.

As already mentioned, the weights were defined by the Fuzzy AHP method according to the Saaty’s scale of relative importance. Five experts from the Faculty of Civil Engineering, Architecture and Geodesy, University of Split and the Faculty of Geodesy, University of Zagreb were involved in the research process.

Table 7. Criteria weights obtained by five experts.

	C1			C2			C3			C4
	l	m	u	l	m	u	l	m	u	l	m	u
C1	1	1	2	0.5	0.33	0.25	0.33	0.25	0.2	0.2	0.17	0.14
C2	2	3	4	1	1	2	1	0.5	0.33	0.33	0.25	0.2
C3	3	4	5	1	2	3	1	1	2	0.5	0.33	0.25
C4	5	6	7	3	4	5	2	3	4	1	1	2

shows fuzzy compromise weights of five experts which are defined by Equations (4)–(6) as a geometric mean of lower, middle and upper triangular value of criteria weight.

Normalization of criteria weights was derived by Equation (7). After that geometric mean of each column was derived to obtain final lower, middle and upper weights of each criterion. In

Table 8. Triangular normalized and final criteria weights.

Normalized Criteria Weights
2.8925	2.9130	4.6807	1.4463	0.9710	0.5851	0.9642	0.7282	0.4681	0.5785	0.4855	0.3343
2.3403	3.8337	4.4267	1.1702	1.2779	2.2134	1.1702	0.6389	0.3689	0.3901	0.3195	0.2213
1.8128	3.1302	4.5180	0.6043	1.5651	2.7108	0.6043	0.7825	1.8072	0.3021	0.2608	0.2259
1.2223	2.0598	2.9910	0.7334	1.3732	2.1364	0.4889	1.0299	1.7091	0.2445	0.3433	0.8546
Final Criteria Weights
1.9680	2.9130	4.0906	0.9306	1.2779	1.6549	0.7598	0.7825	0.8546	0.3593	0.3433	0.3457

triangular normalized and final criteria weights are given.

The final lower and upper α values for each criterion calculated by Equation (9) are given in

Table 9. Final fuzzy criteria weights.

C1		C2		C3		C3
Wl	Wu	Wl	Wu	Wl	Wu	Wl	Wu
2.6295	3.2663	1.1737	1.3910	0.7757	0.8042	0.3481	0.3440

.

Defuzzified weight values were obtained by combining the lower and upper α values using the optimism index and their normalized values are given in

Table 10. Defuzzified criteria weights.

Criterion ID	Defuzzified Criteria Weights
C1	0.5725
C2	0.2401
C3	0.1320
C4	0.0554

.

In order to combine and compare the defined criteria, it was necessary to perform the normalization of the input data, i.e., to resume their values in the range from 0 to 1. Sometimes the relation between the original data and their normalized values are much more complex and cannot be described with a linear function. For this reason, the normalization of certain criteria is carried out by applying value functions that, apart from factual information, are also related to the experiential judgments of experts involved in its definition. Creating value functions is a very important and complex task because their values directly affect the accuracy of later accounting [1]. Value functions are the result of a specially designed interview conducted between decision-makers and experts involved in the decision-making process. There are several different methods of defining value functions, and for this research the direct value rating method [47] was chosen. Below is explained the linear normalization of the slope criteria and the normalization of the number of co-owners criterion using the value function in the form of the fourth order polynomial function.

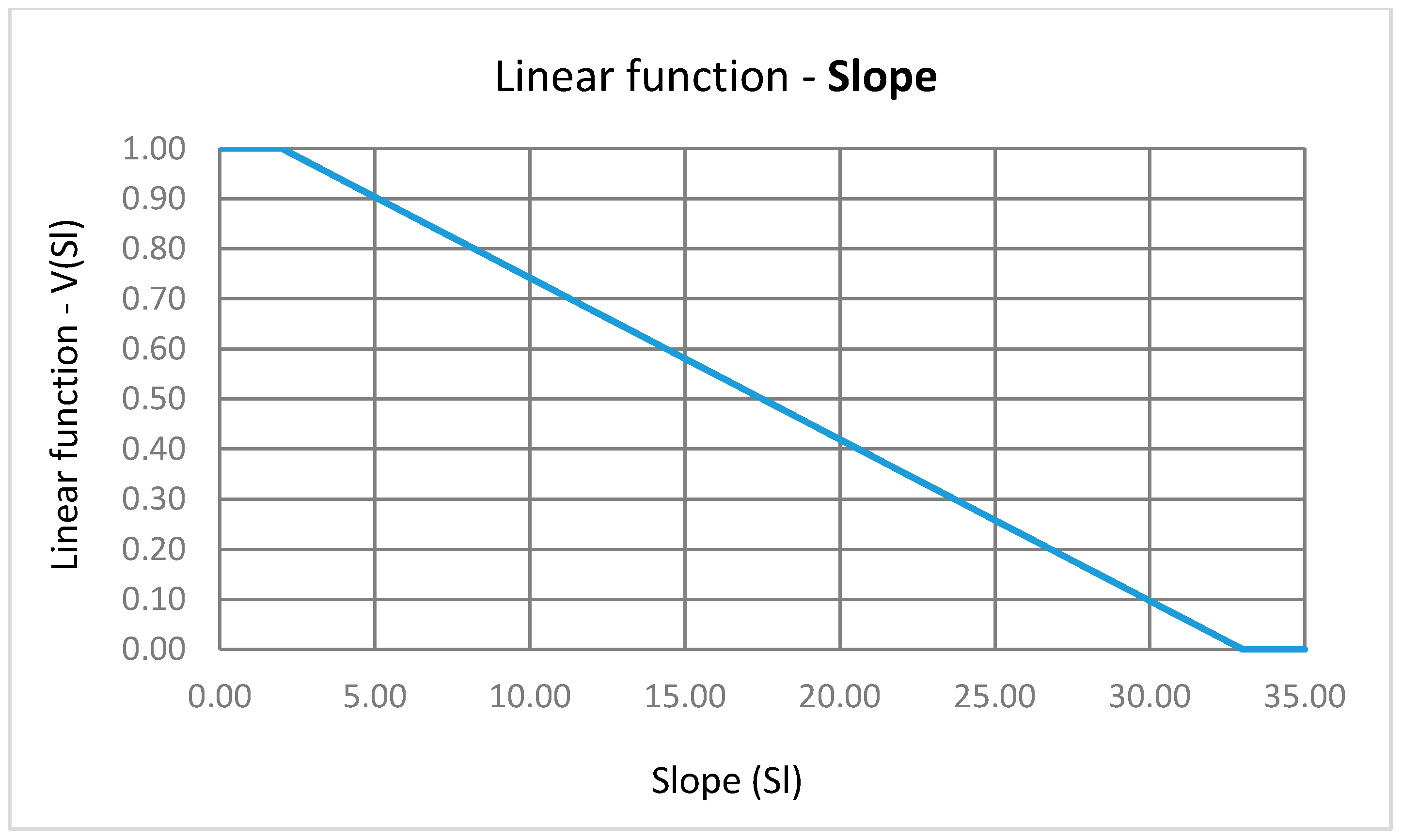
The value of the “Slope” criterion is defined by the linear transformation of the cadastral parcels’ slope expressed in degrees in the range from 0 to 1. In accordance with the ordinance of standards for the determination of particularly valuable land for cultivation (P1) and the valuable agricultural land (P2) [48], value 1 was assigned to those cadastral parcels having a slope from 0° to 2°, while value 0 was assigned to the cadastral parcels which have a slope of 33° and above. The linear function for slope normalization was defined by the expression ($S{l}_j$ is slope of the cadastral parcel j, ${Sl}_j^{\prime }$ is normalized slope value of the cadastral parcel j, and $V\left(Sl\right)$ is an expression for linear function):

$$\begin{array}{c}V\left(Sl\right)=-0.0323·S{l}_j+1.0645\\ S{l}_j\le 2\to S{l}_j^{\prime }=1\\ S{l}_j\ge 33\to N_j^{\prime }=0\end{array}$$

(14)

Figure 5 is a graphical representation of a linear function for slope criterion.

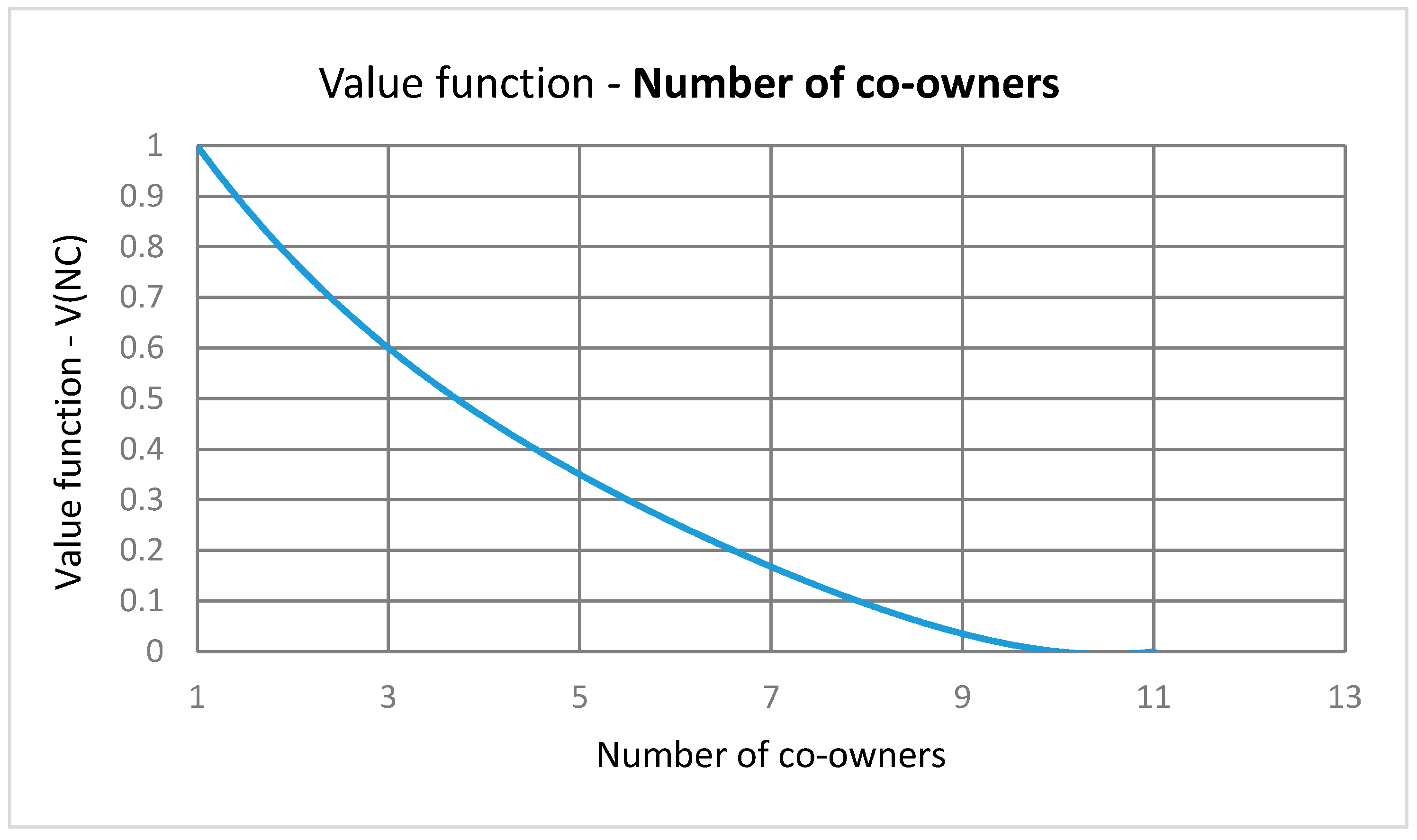
The value of the “Number of co-owners” criterion was defined by the fourth order polynomial function expressed in the range from 0 to 1. Value 1 was assigned to those cadastral parcels having only one private owner, while value 0 was assigned to the cadastral parcels which had 10 or more co-owners. The value function for the number of co-owners normalization was defined by the expression ($N{C}_j$ is number of the cadastral parcel j co-owners, $N{C}_j^{\prime }$ is a normalized number of co-owners values of the cadastral parcel j, and $V\left(NC\right)$ is an expression for the fourth order polynomial function):

$$\begin{array}{c}V\left(NC\right)=0.0002·N{C}_j{}^4-0.0044·N{C}_j{}^3+0.0487·N{C}_j{}^2-0.3442·N{C}_j+1.2997\\ N{C}_j=1\to N{C}_j{}^{\prime }=1\\ N{C}_j\ge 10\to N{C}_j{}^{\prime }=0\end{array}$$

(15)

Figure 6 presents the number of a co-owners value function.

Table 11. Part of decision matrix with normalized criteria assessment and FAHP weights.

Number of Cadastral Parcel	Identification Tag	C1	C2	C3	C4	V
Defuzzified weights		0.5725	0.2401	0.1320	0.0554
part of 6505/1	OP3	0.5659	0.9091	0.7741	1.0000	0.6998
part of 6505/1	OP7	0.4286	0.9091	0.7741	1.0000	0.6212
part of 6505/1	SC21	0.0429	0.9091	0.7741	1.0000	0.4004
part of 6505/2	OP3	0.4341	0.9091	0.7741	1.0000	0.6244
part of 6505/2	OP7	0.5714	0.9091	0.7741	1.0000	0.7030
part of 6505/2	SC21	0.9571	0.9091	0.7741	1.0000	0.9238
6541/1	SU15	0.0521	0.0000	0.2965	0.7031	0.1079
part of 6545	SU19	0.1518	0.1818	0.2965	1.0000	0.2251
part of 6545	OP23	0.1035	0.4545	0.2965	1.0000	0.2629
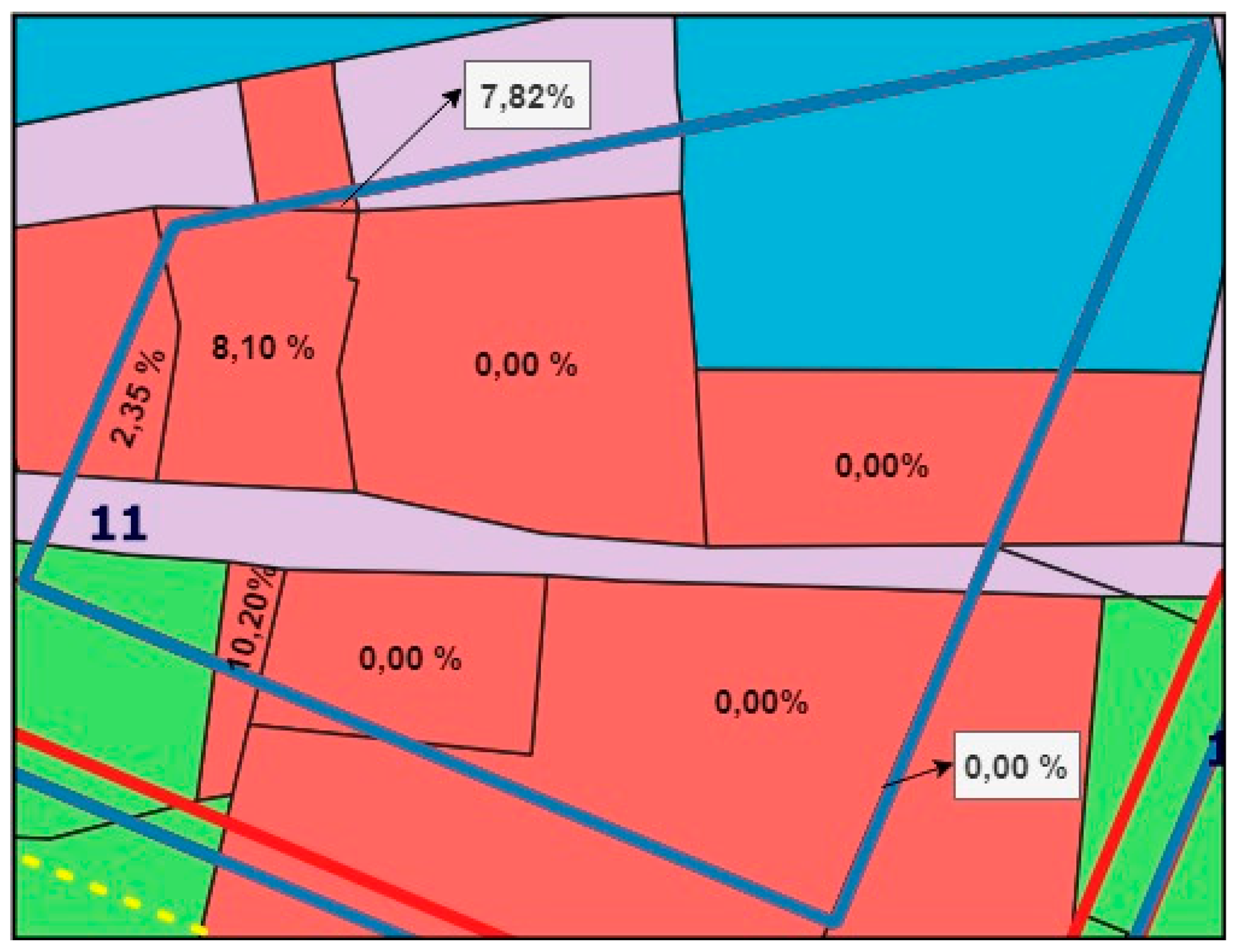
part of 6545	PC11	0.2740	0.6364	0.2965	1.0000	0.4042

presents the normalized values of the cadastral parcels evaluated by the defined criteria and the normalized values of their defuzzified weights. By using the SAW method, the final values of the index of fragmentation are given for all 62 cadastral parcels as well as for its parts. The final result of each alternative was obtained as a sum of the product of the normalized criteria values and normalized values of criteria weights:

$$IF\left(A_i\right)={\displaystyle \sum }_{j=1}^k{w}_j{x}_{ij}$$

(16)

For the sake of transparency, the decision matrix is shown for 10 of 62 cadastral parcels or its parts.

Since the priority ranking of the private cadastral parcels in the urban renewal planning process was implemented for whole cadastral parcels their final values were, in respect to the expert decision, determined by arithmetic mean:

$$I{F}_{XY\left(mean\right)}=\frac{I{F}_{XY\left(1\right)}+I{F}_{XY\left(2\right)}+\dots +I{F}_{XY\left(n\right)}}{n}$$

(17)

Table 12. Parcel Index of Fragmentation.

Number of Cadastral Parcel	IFP Medium	Number of Cadastral Parcel	IFP Medium
6505/1	0.5738	6565/1	0.3235
6505/2	0.7504	6565/2	0.4436
6541/1	0.1079	6565/3	0.2784
6545	0.2974	6565/4	0.3458
6541/2	0.2642	6565/5	0.3850
6523	0.4184	6565/6	0.3565
6536/2	0.5994	6565/7	0.4107
6535/1	0.1217	6537/1	0.1666
6535/2	0.1123	6633/1	0.3786
6535/3	0.1078	6633/2	0.3660
6566/2	0.6637	6542/1	0.3604
6550	0.2528	6542/2	0.4286
6543	0.3386	6551/3	0.1967
6551/1	0.4036	6551/2	0.2913
6516	0.4081	6538/2	0.2583
6520	0.4193	6565/8	0.2950
6598/14	0.8563	6565/9	0.2849
6598/15	0.3313	6565/10	0.2747
6528/1	0.3132	6565/11	0.3886
6528/2	0.2155	6565/12	0.2982
6528/3	0.4162	6565/13	0.1969
6528/4	0.7079	6536/1	0.6029
6528/5	0.4118	6519	0.3817
6528/6	0.9011	6518	0.5478
6528/7	0.7690	6515/2	0.3254
6528/8	0.3009	6515/3	0.6834
6513/1	0.2160	6565/14	0.2229
6513/2	0.3580	6552/2	0.6086
6538/1	0.2285	6566/3	0.3875
6539/1	0.3945	6552/3	0.2472
6539/2	0.5250	13662/2	0.2279

shows the final index of fragmentation values for 62 cadastral parcels. The index of fragmentation values of the private cadastral parcels at the campus area ranged from IF (6535/3) = 0.1078 as a minimum value (indicating the most fragmented cadastral parcel) to IF (6528/6) = 0.9011 as a maximum value (indicating the least fragmented cadastral parcel). More than half, precisely 49 out of 62 cadastral parcels had index of fragmentation (IF) values less than 0.5. That made up 79% of the total number of cadastral parcels, so it can be considered that the campus area is an extremely fragmented area for the purpose of urban renewal. The obtained index of fragmentation values were used in the later calculation for the final ranking of the private cadastral parcels in the process of urban renewal planning.

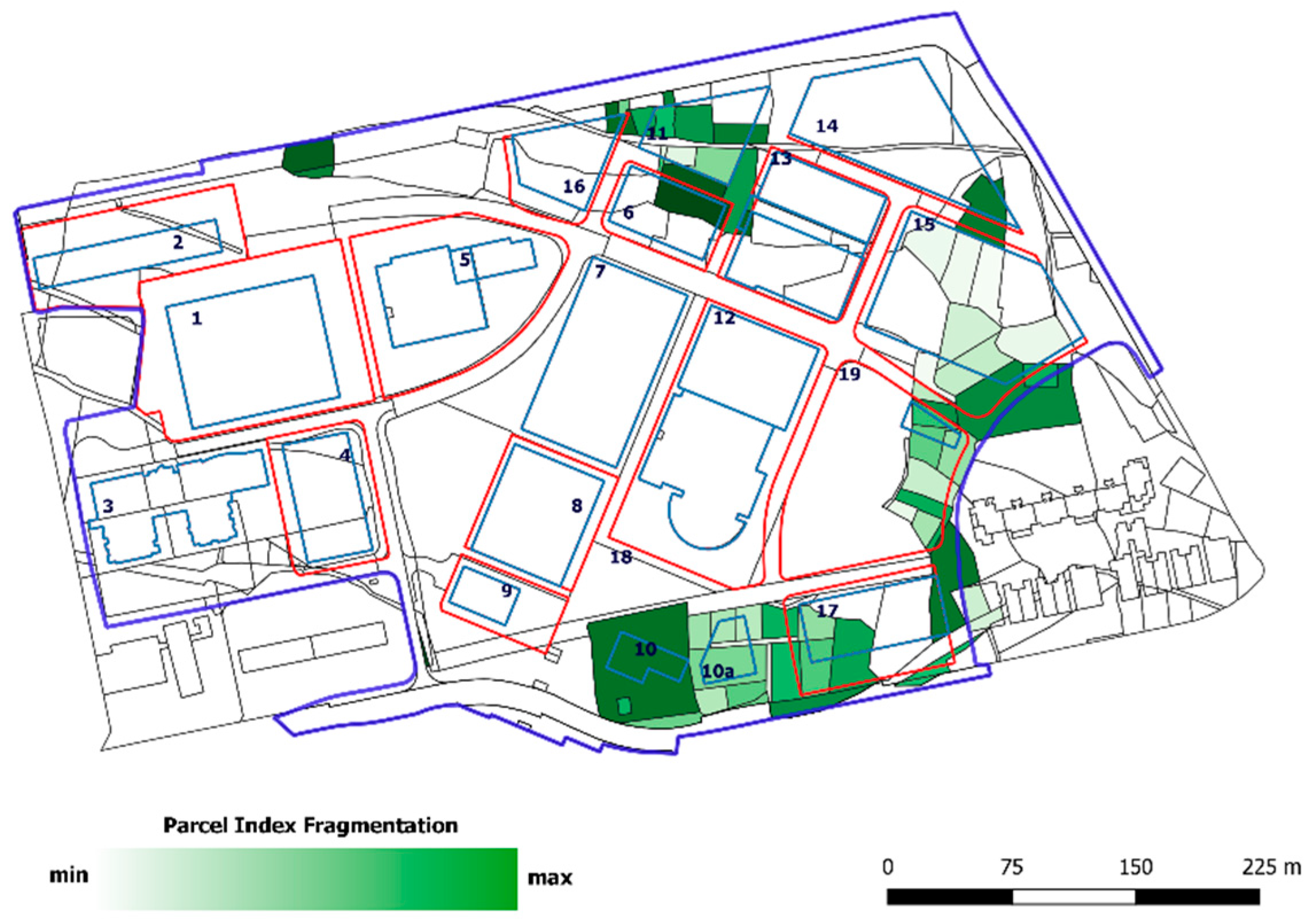
Figure 7 shows the distribution of private cadastral parcels along with their index of fragmentation in the campus area. Light green tones show private cadastral parcels with a higher degrees of fragmentation, while dark green tones depict private cadastral parcels that are best rated by defined criteria (with the smallest degrees of fragmentation).

Parcel Index of Fragmentation was one of the elements to define an index of fragmentation of basic spatial elements (spatial units, elements of road infrastructure and elements of green areas) which refer to the second level planning of the future project construction realization.

Road Infrastructure Index of Fragmentation was determined by two criteria, and its final estimate is obtained by the arithmetic mean:

$$I{F}_{XY\left(mean\right)}=\frac{I{F}_{XY\left(1\right)}+I{F}_{XY\left(2\right)}}{2}$$

(18)

After calculating the Parcel Index of Fragmentation, the Road Infrastructure Index of Fragmentation, Spatial Unit Index of Fragmentation and Green Area Index of Fragmentation can now be calculated on the second level of planning the large public project.

Table 13. Road Infrastructure Index of Fragmentation—IFRI.

Logical Unit	IFRI	Logical Unit	IFRI
CR22	0.6363	OP5	0.8071
CR21	0.7896	OP7	0.7909
AR8	0.4991	OP8	0.9213
AR11	0.3722	OP9	0.5096
AR13	0.7321	OP10	0.7505
AR7	0.5337	OP11	0.8066
AR9	0.6973	OP16	0.4445
OR10	0.6373	OP17	0.3576
OR12	0.7649	OP18	0.6801
PA14	0.3405	OP19	0.4715
PA15	0.2289	OP20	0.4770
MP24	0.6510	OP21	0.8216
OP3	0.7812	OP22	0.4345
OP4	0.6342	OP23	0.2744

presents the Road Infrastructure Index of Fragmentation values for 28 elements of road infrastructure which contained private cadastral parcels or its parts. The index of fragmentation values of road infrastructure elements at the campus area range from IF (PA15) = 0.2289 as a minimum value (indicating the most fragmented element of road infrastructure) to IF (OP8) = 0.9213 as a maximum value (indicating the least fragmented element of road infrastructure). Most of the elements, precisely 18 of 28 had index of fragmentation values greater than 0.5. That made up 64% of the total number of elements, so it can be concluded that road infrastructure elements do not show a high level of fragmentation for the project realization planning.

Similarly to Road Infrastructure Index of Fragmentation, Green Area Index of Fragmentation is determined by two criteria, and its final estimate is obtained by the arithmetic mean.

Table 14. Green Area Index of Fragmentation—IFGA.

Logical Unit	IFGA
GA3	0.8032
GA5	0.3628
GA7	0.8474

presents Green Area Index of Fragmentation for three elements. Two of three IFGA have relatively high values which means that green areas show a low level of fragmentation for the project realization planning.

As before mentioned, Spatial Unit Index of Fragmentation was defined with four criteria and its final assessment was obtained by the arithmetic mean:

$$I{F}_{XY\left(mean\right)}=\frac{I{F}_{XY\left(1\right)}+I{F}_{XY\left(2\right)}+I{F}_{XY\left(3\right)}+I{F}_{XY\left(4\right)}}{4}$$

(19)

In

Table 15. Spatial Unit Index of fragmentation—IFSU.

Spatial Unit	IFSU	Spatial Unit	IFSU
SU6	0.9079	SU15	0.2979
SU10	0.7009	SU16	0.8865
SU10a	0.5450	SU17	0.7065
SU11	0.6543	SU18	0.7709
SU13	0.8845	SU19	0.2663
SU14	0.8950

the final values of Spatial Unit Index of Fragmentation are given. The table shows IFSU for 11 future objects in the campus area. Considering that a total number of objects in the campus was 19, it can be concluded that most of the areas of future object construction have a problem with ownership issues. The table presents the Spatial Unit Index of Fragmentation for 11 future objects. The index of fragmentation values ranged from IF (SU19) = 0.2663 to IF (SU6) = 0.9079 and the vast majority, nine of eleven, have the very high index of fragmentation values. This result, similarly to IFRA and IFGA does not show a high level of fragmentation for the project realization planning.

For the first level of planning in order to select the most favorable location for the future project construction, the criteria for comparing the alternative solutions were numerically defined and given in

Table 16. Criteria assessment of index of fragmentation for location selection.

C1d	C2d	C3d	C4d	C5d
0.2074	1 (4)	161.6569	0.1391	62

. As is stated above, for this level of planning the identified criteria are just numerically defined while their total assessment, i.e., the index of fragmentation for location selection, can be obtained when compared with other potential alternative solutions. Since the location of the campus project is already known in advance, and to truly use a realistic example for validation of this model, the possibility and the need to use the index of fragmentation as a spatial functional criterion was identified in selecting the most favorable location for the construction of the future project. For comparison, criteria values should be normalized using linear standardization or specially designed value functions based on the opinion of the experts involved in the decision-making process.

The results obtained show applicability in the context of decision-making in the process of planning a large public project. As one of the criteria in the goal tree to support the realization of a large public project, they cover an important spatial–functional segment that quantifies the condition of an existing situation in the context of use for the construction of future spatial elements. In this case, the priority rank of the spatial elements was defined by the assessment of the index of fragmentation. The realization of a large public project, such as a campus of the University of Split, involves several project phases of realization, from selecting the location of a future project, making a plan of project realization and making a plan for implementing urban renewal as a specific urban land consolidation process. For each of the above-mentioned phases, spatial functionality of the study areas, i.e., spatial elements defined by the urban plan is analyzed and it is expressed through their deviation from the ideal area of construction, the ideal spatial element and the ideal cadastral parcel. It is important to emphasize that the index of fragmentation supports the project planning process, but when elaborating the final plan it is necessary also to analyze in detail all the technical, social, economic, ecological and other spatial–functional effects on the future project implementation, the overall impact of which will give insight in order to support the decision-making of the stakeholders involved in the planning process.

4. Discussion

This paper proposes a unique methodology for assessing the index of fragmentation for use in sustainable urban renewal planning. For the first time, a multifactor urban index of fragmentation was presented with its detailed definition for all project planning levels. The application of a Simple Additive Weighting method (SAW) as well as the choice of Fuzzy AHP methods to determine the relative importance of the weight of criteria has been shown by a highly practical combination for assessment of the index of fragmentation. The SAW makes it easy and quick to calculate, while Fuzzy AHP allows the inclusion of experts in the weight definition process that is considered the most sensitive part of this methodology.

The difference between the proposed index of fragmentation and those found in scientific and professional literature is that the existing fragmentation indexes of urban areas are usually based on only land use analysis by studying the spatial heterogeneity that is most often a result of unplanned construction and insufficient concerns about the sustainable development of the urban environment. They most commonly are of a single-factor character, and a cumulative characterization of multiple criteria with their varying importance in the literature has not been found in the literature. The methodology proposed in this paper provides an improvement over the existing definition of the index of fragmentation, defining its multifactor form. The proposed index of fragmentation is defined in relation to the analysis of the existing land condition, with the aim of optimizing the construction of a large public project. The ideal spatial elements have been defined, and the index of fragmentation assessment is given in relation to the deviation of the existing elements from their ideal form. In the model design, as well as defining the relation between the criteria based on which the index of fragmentation is assessed, a group of experts is included. The experts that have been included in the planning process are eminent specialists from the field of research who have contributed to solving the new problems based on their specific experience in solving tasks related to the sustainable spatial planning. Given that there was a difference between expert assessments but also in order to reduce the uncertainty of defining the weights, a Fuzzy AHP method was used which provided the final weights of criteria based on the evaluation of the five experts involved in the decision-making process.

By selecting the criteria for defining the index of fragmentation of private land parcels, a wider spatial image was obtained that on the one hand depicted the relationship of a particular cadastral parcels or its part to the whole or the spatial element to which it belonged, while on the other side it showed the internal fragmentation of a particular cadastral parcel or its part. It is especially important to clarify this sort of criteria. It is clear that a broader image in determining the index of fragmentation yielded more land parcel attributes, but the defined index of fragmentation would not necessarily better represent the problem of each project that has a spatial element. Thus, criteria such as shape of cadastral parcel need to be taken into account when evaluating existing parcels, but to define what is needed for the realization of a particular project, it is very important to select those criteria that directly or indirectly have an impact on the dynamics of realization, from those whose influence in that segment is negligible.

As already mentioned above, the index of fragmentation is one of the identified spatial–functional criteria to be taken into account when planning the realization of a large public project. Further research is concerned with the integration of the index of fragmentation into the context of the hierarchy goal tree with which the main goal, the sub-goals and the criteria for comparing alternative solutions are defined. It is necessary to identify the project implementation phases and to elaborate in detail the flow chart of their implementation. Likewise, the cadastral parcels need to be evaluated except for the purpose of assessing the index of fragmentation and in order to assess their existing status for the purposes of the private landowners’ allocation by calculating their bonitet values. By implementing a complete urban renewal of a given area, the existing land status is evaluated with a view to the fair allocation of private owners to newly created real estates. In further research, a model of allocation will be developed, which will be balanced between the preference of private owners, the real estate valuation as well as the valuation of the property’s bonitet value for the purpose of implementing a fair allocation and gaining public confidence in the fairness of the urban renewal procedure.

The most important contribution of the proposed model is providing support to the decision makers when optimizing the process of a large public project implementation that is realized in more than one period of time. It is particularly important to emphasize that the proposed methodology is adaptable and allows the modification of the goal tree as well as the relative importance (weights) of criteria when defining a unique urban index of fragmentation to solve a new problematic task related to the urban area.