Selecting Socially Responsible Portfolios: A Fuzzy Multicriteria Approach

Abstract

We propose a multi-objective approach for portfolio selection, which allows investors to consider not only return and downside risk criteria but also to include environmental, social and governance (ESG) scores in the investment decision-making process. Owing to the uncertain environment of portfolio selection, the return and ESG score of each asset are considered as independent L-R power fuzzy variables. To make the model more realistic, we take budget, floor ceiling and cardinality constraints into account. In order to select the optimal portfolio along the efficient frontier, we apply the Sortino ratio in a credibilistic environment. The subsequent empirical application uses a data set from Bloomberg’s ESG Data in combination with US Dow Jones Industrial Average data. The experimental results show that the proposed model offers promising results for socially responsible investors seeking ethical and sustainability goals beyond the return-risk trade-off and its ability to beat the benchmark.

1. Introduction

Multiple criteria decision making is a method which pursues making choices in the presence of multiple criteria, goals or objectives [1]. It has been applied in several areas [2,3,4] and in investment decisions are not an exception [5,6,7,8].

In the last decades, financial, social and environmental crises have led to considerable growth of social responsibility (SR) consciousness in society and amongst investors [9,10,11]. Socially responsible investment (SRI), also known as ethical, green, impact, responsible or sustainable investing, is defined as an investment decision-making process that considers not only financial performance but also environmental, social and governance (ESG) criteria [12,13]. In other words, socially responsible investors (SRIs) consider non-financial criteria (e.g., social responsibility performance) in their investment decisions in addition to conventional criteria such as return, risk or liquidity [14,15].

Nowadays, the main investment instrument of SRIs are socially responsible mutual funds [16]. The first modern SR mutual fund, the Pax World Fund, was created in 1971 in the United States and appealed to investors objecting to the Vietnam War [17]. Since then, the SRI industry has expanded by drawing attention of academics and professionals in various cultural contexts and industries around the world [18,19,20,21,22,23,24,25,26,27].

Over the last decades, several studies have focused on comparing financial performances between SR funds (or SR indexes) and non-SR funds (or non-SR indexes). The main conclusions of these studies can be summarized as follows: (i) the financial performance of SR funds/indexes is larger than that of non-SR funds/indexes [28,29,30,31,32]; (ii) the financial performance of SR funds/indexes is lower than that of non-SR funds/indexes [33,34,35,36,37]; and (iii) there are no statistical differences in financial performance between both forms of funds/indexes [38,39,40,41,42]. Noted that the results of above studies are inconclusive and even somewhat contradictories. This discrepancy is mainly due to the methodological choices made by researchers in the different studies [43]. Furthermore, it could reflect the complex relationship between SRI and financial performance, which is based on both company corporate social responsibility (CSR) performance and market characteristics (e.g., portfolio management and influence of investors).

Another strand of SRI literature is concerned with analysing the relationship between CSR activity and firm financial performance. McWilliams and Siegel [44] for example, argue that there is an ideal level of CSR which can be determined by manager via cost-benefit analysis and that there is a neutral relationship between CSR and financial performance. Goss and Roberts [45] find that firms with SR concerns pay higher financing rates than firms that are more responsible, due to lenders are more sensitive to CSR concerns in the absence of security. Ghoul et al. [45] suggest that firms with better CSR scores exhibit cheaper equity financing and hence, have higher valuation and lower risk. Attig et al. [46] found that credit rating agencies tend to award relatively high ratings to firms with good social performance, as CSR performance conveys important non-financial information that is likely to be used in the evaluation of a firm’s creditworthiness. Finally, Cheng et al. [47] argue that CSR strategies reduce agency costs and informational asymmetry, which lead to firms have a better access to finance.

The portfolio selection problem is frequently approached by an application of quantitative methods. The aim is to select an optimal portfolio that maximises investors’ goals with regards to several criteria such as return and risk. Markowitz [48] established the first mathematical formulation of this problem and proposed the relationship between the mean and the variance of the assets as selection criteria. A rich literature seeks to include non-financial criteria for integrating ESG concerns into the portfolio selection problem. Hallerbach et al. [49], for example, proposed a framework for managing an SR portfolio based on firm-level SR data. Steuer et al. [50] extended the classical risk-return approach to add further objectives such as liquidity, dividends, portfolio size, social responsibility and so forth. Bilbao-Terol et al. [51] proposed a fuzzy decision making process for selecting portfolios that take financial, social, environmental and ethical criteria into account. Utz et al. [52] seek to maximise the portfolio’s ESG as the third criterion and to apply the proposed model to SR mutual funds. Calvo et al. [53] propose a model for selecting portfolios taking a fuzzy secondary non-financial goal into account. Finally, Li et al. [54] studied the ESG portfolio return and risk based on the list of the “100 Best CSR companies in the world” published by the Reputation Institute.

However, all of the aforementioned studies of SR portfolio selection focus on funds instead on individual assets. The literature reviewed so far indicates that there are only a few studies of SR portfolios optimisation models that are based on individual assets [55,56,57]. In fact, for investors and portfolio managers it is important that these kinds of studies exist that help them pick the most reliable approach to make SR portfolio investment-related decisions. Due to the above consideration, this paper extends current knowledge by employing the Bloomberg ESG Disclosure Score in order to measure the level of social responsibility of each asset. To our knowledge, this approach is one of the first uses of Bloomberg’s ESG score in an academic study on SR portfolio investment.

There are currently numerous specialised rating institutions, which rate and analyse the environmental, social and governance-related business practices of companies throughout the world. Some of the most important ESG rating scores include the Bloomberg ESG Disclosure Score, the Thomson Reuters ESG Score, the MSCI ESG Score and the Vigeo-Eiris ESG Score. In practice, each rating agency has its own measurement methodologies and uses its own social performance criteria, which are beset by uncertainty, vagueness and/or imprecision [9]. As a result researchers have applied the fuzzy set theory [58] to characterise the fuzziness associated with SR portfolio [53,59,60].

In order to gauge a fuzzy event, Zadeh [58] proposed a non-self-dual possibility measure. However, since the self-dual property is intuitive and important both in theory and practice, Liu and Liu [61] developed a self-dual credibility measure. Different researchers have used credibility distributions to approximate the uncertainty on returns [62,63,64,65,66,67,68]. Nevertheless, to the best of our knowledge, there is no SR portfolio selection model using a credibility-based approach to deal with fuzzy events. Hence, this paper seeks to make a contribution to the SR portfolio selection model approach by assuming that both the return and ESG performance of each asset are an L-R power fuzzy variable whose moments are assessed employing their credibility distributions.

Most previous studies use the variance to measure portfolio risk despite its undesirable properties such as the lack of coherence [48]. However, in real-life decisions investors are more sensitive to downside losses than upside gains but variance does not reflect investors’ concern about underperformance [69]. In order to solve this limitation, several downside risk measures have been proposed. The mean-absolute semi-deviation (MASD) is a popular downside risk measure originally introduced by Speranza [70] and it is used in mean-absolute semi-deviation portfolio selection models. MASD was introduced as a downside risk measure in stochastic environments. However, it has only been used in a single study in a credibilistic context [64].

Modern portfolio theory assumes that investors are rational and always try to minimize risk while striving for the highest return possible [48]. Nowadays, the so-called Sortino ratio introduced by Sortino and Van Der Meer [71] is a well-known measure to evaluate portfolio performance. It is a modification of the Sharpe ratio, using downside measure rather than dispersion measure as the measure of risk. Therefore, to select the optimal portfolio along the efficient frontier, this paper defines for the first time the credibilistic Sortino ratio as the ratio between the credibilistic risk premium and the credibilistic mean-absolute semi-deviation.

On the basis of the SRI literature review, the aim and contribution of this paper is two-fold: First, we present a multi-objective approach for the portfolio selection model, which allows investors to consider not only return and downside risk criteria but also ESG performance as part of the investment decision-making process. The return and the ESG score of each asset are quantified by the credibilistic mean values of return and the ESG score, respectively; the downside risk is determined by the credibilistic mean-absolute semi-deviation of return. The return and the ESG score are considered as L-R power fuzzy numbers. In order to make this model more applicable to reality, we consider budget, floor-ceiling and cardinality constraints. To solve the constrained portfolio optimisation problem, we apply the Non-dominated Sorting Genetic Algorithm II (NSGA-II). Second, we present a real-world empirical application using a data set from Bloomberg’s ESG Data in combination with US Dow Jones Industrial Average data for the period from February 2014 to December 2017.

The experimental results show that the proposed model offers promising results for socially responsible investors seeking ethical and sustainability goals beyond the return-risk trade-off and its ability to beat the benchmark.

Furthermore, in Section 2, the fundamental concepts relevant to the proposed study are introduced. Thereafter, Section 3 describes the mean-downside risk-socially responsibility model. The solution methodology to solve the above model is presented in Section 4, followed by an empirical study in Section 5, which illustrates the usefulness of the proposed model. The paper closes with the key conclusions.

2. L-R Fuzzy Numbers and Credibility Theory

This section briefly presents the key definitions of fuzzy set theory essential for the subsequent sections.

2.1. L-R Power Fuzzy Numbers

The reference functions ${\mathrm{L}}_{\mathsf{\pi }}(.)$, ${\mathrm{R}}_{\mathsf{\rho }}(.)$: [0, 1]→[0, 1] of a L-R fuzzy number are strictly decreasing and upper semi continuous functions such that [72]:

$${\mathrm{L}}_{\mathsf{\pi }}\left(\mathrm{x}\right),{\mathrm{R}}_{\mathsf{\rho }}\left(\mathrm{x}\right)=\{\begin{array}{ll}0\hfill & \mathrm{If}\mathrm{x}=1\hfill \\ 1\hfill & \mathrm{If}\mathrm{x}=0\hfill \end{array}$$

The membership function of L-R fuzzy number $\tilde{\mathrm{A}}$ [i.e. $\tilde{\mathrm{A}}={\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)}_{{\mathrm{L}}_{\mathsf{\pi }}{\mathrm{R}}_{\mathsf{\rho }}}$] has the following form:

$${\mathsf{\mu }}_{\tilde{\mathrm{A}}}(\mathrm{x})=\{\begin{array}{ll}{\mathrm{L}}_{\mathsf{\pi }}(\frac{\mathrm{b}-\mathrm{x}}{\mathrm{b}-\mathrm{a}}),& \mathrm{If}\mathrm{a}\le \mathrm{x}<\mathrm{b}\\ 1,& \mathrm{If}\mathrm{b}\le \mathrm{x}\le \mathrm{c}\\ {\mathrm{R}}_{\mathsf{\rho }}(\frac{\mathrm{x}-\mathrm{c}}{\mathrm{d}-\mathrm{c}}),& \mathrm{If}\mathrm{c}<\mathrm{x}\le \mathrm{d}\\ 0,& \mathrm{Otherwise},\end{array}$$

where (b−a) and (d−c) represent the left and right spreads of $\tilde{\mathrm{A}}$, respectively. Following Jalota et al. [67], this research considers the reference functions of the power family of positive parameters $\mathsf{\pi }$ and $\mathsf{\rho }$, where ${\mathrm{L}}_{\mathsf{\pi }}\left(\mathrm{x}\right){=1-\mathrm{x}}^{\mathsf{\pi }}$ and ${\mathrm{R}}_{\mathsf{\rho }}\left(\mathrm{x}\right){=1-\mathrm{x}}^{\mathsf{\rho }}$, respectively. All over this study, L-R power fuzzy numbers will be defined as $\tilde{\mathrm{A}}={\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)}_{\mathsf{\pi },\mathsf{\rho }}$.

2.2. Credibility Theory

The credibility theory was founded by Liu [73] in 2004 and refined by Liu [74] in 2007. It has been fairly well applied to the study of the behaviour of fuzzy phenomena.

• Definition 1.Credibility measure [61]. Let ξ be a fuzzy variable with membership function µ and x a real number. The credibility measure of a fuzzy event, characterised by ξ ≤ x, is defined by Equation (1).

  $$\mathrm{Cr}\left\{\mathsf{\xi }\le \mathrm{x}\right\}=\frac{1}{2}\left(\underset{\mathrm{y}\le \mathrm{x}}{\sup }\mathsf{\mu }\left(\mathrm{y}\right)+1-\underset{\mathrm{y}>\mathrm{x}}{\sup }\mathsf{\mu }\left(\mathrm{y}\right)\right),\forall \mathrm{x}\in \mathrm{R}$$

  (1)

  The credibility measure of L-R power fuzzy numbers is expressed as:

  $$\mathrm{Cr}\{\mathsf{\xi }\le \mathrm{x}\}=\{\begin{array}{ll}0,& \mathrm{If}\mathrm{x}\le \mathrm{a}\\ \frac{1}{2}\left(1-{\left(\frac{\mathrm{b}-\mathrm{x}}{\mathrm{b}-\mathrm{a}}\right)}^{\mathsf{\pi }}\right),& \mathrm{If}\mathrm{a}<\mathrm{x}<\mathrm{b}\\ \frac{1}{2},& \mathrm{If}\mathrm{b}\le \mathrm{x}\le \mathrm{c}\\ \frac{1}{2}\left(1+{\left(\frac{\mathrm{x}-\mathrm{c}}{\mathrm{d}-\mathrm{c}}\right)}^{\mathsf{\rho }}\right),& \mathrm{If}\mathrm{c}<\mathrm{x}<\mathrm{d}\\ 1,& \mathrm{If}\mathrm{d}\le \mathrm{x}\end{array}\mathrm{Cr}\{\mathsf{\xi }>\mathrm{x}\}=\{\begin{array}{ll}1,& \mathrm{If}\mathrm{x}\le \mathrm{a}\\ \frac{1}{2}\left(1+{\left(\frac{\mathrm{b}-\mathrm{x}}{\mathrm{b}-\mathrm{a}}\right)}^{\mathsf{\pi }}\right),& \mathrm{If}\mathrm{a}<\mathrm{x}<\mathrm{b}\\ \frac{1}{2},& \mathrm{If}\mathrm{b}\le \mathrm{x}\le \mathrm{c}\\ \frac{1}{2}\left(1-{\left(\frac{\mathrm{x}-\mathrm{c}}{\mathrm{d}-\mathrm{c}}\right)}^{\mathsf{\rho }}\right),& \mathrm{If}\mathrm{c}<\mathrm{x}<\mathrm{d}\\ 0,& \mathrm{If}\mathrm{d}\le \mathrm{x}\end{array}$$
• Definition 2.Expected value [61]. Let ξ be a fuzzy variable. Then the expected value of ξ is defined by Equation (2) provided that at least one of the two integrals is finite.

  $$\mathrm{E}\left(\mathsf{\xi }\right)={{\displaystyle \int }}_0^{+\infty }\mathrm{Cr}\left\{\mathsf{\xi }\ge \mathrm{x}\right\}\mathrm{dx}-{{\displaystyle \int }}_{-\infty }^0\mathrm{Cr}\left\{\mathsf{\xi }\le \mathrm{x}\right\}\mathrm{dx}$$

  (2)

  The crisp equivalent expression for the credibilistic expected value of an L-R power fuzzy number is formulated by Equation (3) [67].

  $$\mathrm{E}\left(\mathsf{\xi }\right)=\frac{1}{2}\left[\mathrm{b}+\mathrm{c}+\frac{\mathsf{\rho }(\mathrm{d}-\mathrm{c})}{\mathsf{\rho }+1}-\frac{\mathsf{\pi }(\mathrm{b}-\mathrm{a})}{\mathsf{\pi }+1}\right]$$

  (3)
• Definition 3.Mean-absolute semi-deviation [64]. Let ξ be a fuzzy variable with finite expected value $\mathrm{e}$ = $\mathrm{E}\left[\mathsf{\xi }\right]$. Its below-mean absolute semi-deviation is defined by Equation (4).

  $$\mathrm{MASD}\left[\mathsf{\xi }\right]=\mathrm{E}[{({\left[\mathsf{\xi }-\mathrm{e}\right]}^{-})}^2]$$

  (4)

  where,

  $${\left[\mathsf{\xi }-\mathrm{e}\right]}^{-}=\{\begin{array}{ll}\mathsf{\xi }-\mathrm{e},\hfill & \mathrm{S}\mathsf{í}\mathsf{\xi }\le \mathrm{e}\hfill \\ 0,\hfill & \mathrm{S}\mathsf{í}\mathsf{\xi }>\mathrm{e}\hfill \end{array}$$

  Finally, following Vercher and Bermúdez [64], the crisp equivalent expression for the credibility-measure-based MASD of an L-R power fuzzy number is expressed as:

  $$\mathrm{MASD}[\mathsf{\xi }]=\{\begin{array}{ll}\frac{1}{2}(\mathrm{e}-\mathrm{a})-\frac{1}{2}\frac{\mathrm{b}-\mathrm{a}}{\mathsf{\pi }+1}\left(1-{\left(\frac{\mathrm{b}-\mathrm{e}}{\mathrm{b}-\mathrm{a}}\right)}^{\mathsf{\pi }+1}\right)& \mathrm{Si}\mathrm{a}\le \mathrm{e}\le \mathrm{b}\\ \frac{1}{2}(\frac{1}{2}\left(\mathrm{c}-\mathrm{b}+(\mathrm{b}-\mathrm{a})\frac{\mathsf{\pi }}{\mathsf{\pi }+1}+(\mathrm{d}-\mathrm{c})\frac{\mathsf{\rho }}{\mathsf{\rho }+1})\right)& \mathrm{Si}\mathrm{b}\le \mathrm{e}\le \mathrm{c}\\ \frac{1}{2}(\mathrm{d}-\mathrm{e})-\frac{1}{2}\frac{\mathrm{d}-\mathrm{c}}{\mathsf{\rho }+1}\left(1-{\left(\frac{\mathrm{e}-\mathrm{c}}{\mathrm{d}-\mathrm{c}}\right)}^{\mathsf{\rho }+1}\right)& \mathrm{Si}\mathrm{c}\le \mathrm{e}\le \mathrm{d}\end{array}$$

  (5)

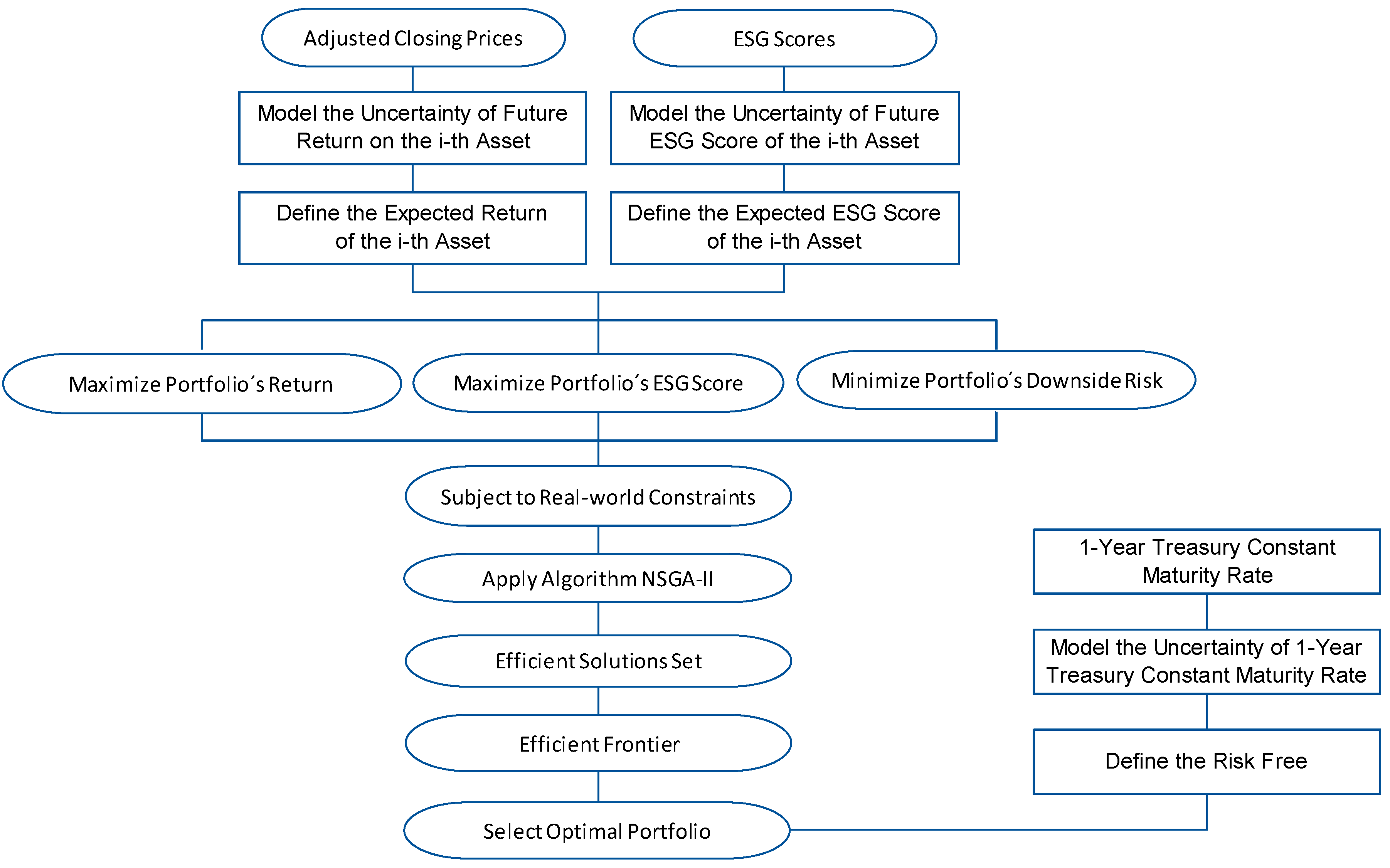
3. The Mean-Downside Risk-Socially Responsible Portfolio Selection Model

This section formulates the mathematical model of the socially responsible portfolio investment. The portfolio selection model considers three criteria: risk, return and social responsibility (RRS). The parameters and variables used in this study to formulate this model are:

• ${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{i}}}$: L-R fuzzy return of the i-th asset, that is, ${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{i}}}=\left({\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}\right){\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}},{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}$,
• ${\mathsf{\xi }}_{{\mathrm{ESG}}_{\mathrm{i}}}$: L-R fuzzy ESG score of the i-th, that is, ${\mathsf{\xi }}_{{\mathrm{ESG}}_{\mathrm{i}}}=({\mathrm{a}}_{{\mathrm{ESG}}_{\mathrm{i}}}{,\mathrm{b}}_{{\mathrm{ESG}}_{\mathrm{i}}}{,\mathrm{c}}_{{\mathrm{ESG}}_{\mathrm{i}}},{\mathrm{d}}_{{\mathrm{ESG}}_{\mathrm{i}}}{)}_{{\mathsf{\pi }}_{{\mathrm{ESG}}_{\mathrm{i}}},{\mathsf{\rho }}_{{\mathrm{ESG}}_{\mathrm{i}}}}$,
• ${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{p}}}:$ L-R fuzzy return of the portfolio, that is, ${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{p}}}=({\mathrm{a}}_{{\mathrm{r}}_{\mathrm{p}}},{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{p}}},{\mathrm{c}}_{{\mathrm{r}}_{\mathrm{p}}},{\mathrm{d}}_{{\mathrm{r}}_{\mathrm{p}}}{)}_{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{p}}},{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{p}}}}$,
• $\mathrm{e}:$ expected return of the portfolio,
• ${\mathrm{u}}_{\mathrm{i}}$: upper bound of the proportion invested in the i-th asset,
• ${\mathrm{l}}_{\mathrm{i}}$: lower bound of the proportion invested in the i-th asset,
• k: the number of assets held in the portfolio,
• ${\mathsf{\omega }}_{\mathrm{i}}$: the proportion of wealth invested in the i-th asset,
• ${\mathrm{y}}_{\mathrm{i}}$: a binary variable indicating whether the i-th asset is contained in the portfolio. It takes value 1, if the i-th asset is included in the portfolio, otherwise it takes value 0.

3.1. Objective Functions

3.1.1. Return

Stock returns are beset with ambiguity and vagueness. For the above reasons, this research assumes that an investor allocates his/her total wealth among n US risky assets which offer L-R fuzzy returns. Following Vercher and Bermúdez [64,75,76] we build the membership function of the L-R fuzzy return by using the empirical percentiles of their historical returns. Concretely, the support and core of ${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{i}}}=({\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}{,\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}{)}_{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}},{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}}$ are represented by intervals [${\mathrm{q}}_3{,\mathrm{q}}_{97}$] and [${\mathrm{q}}_{45}{,\mathrm{q}}_{55}$], respectively. The shape parameters are obtained in such a way that the fuzzy and empirical quartiles coincide, that is, ${\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}=\frac{\mathrm{Ln}0.5}{\mathrm{lns}}$, where $\mathrm{s}=\frac{{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}-25\mathrm{th}\mathrm{percentile}}{{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}{-\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}}$ and ${\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}=\frac{\mathrm{Ln}0.5}{\mathrm{lnh}}$, where $\mathrm{h}=\frac{{75\mathrm{th}\mathrm{percentile}-\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}{-\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}}$. Then, the maximisation of the expected return of the portfolio can be expressed as:

$${\mathrm{Max}\mathrm{R}}_{\mathrm{p}}{=\mathrm{F}}_1\left({\mathsf{\omega }}_{\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left[\left[\frac{1}{2}\left[{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}{+\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}+\frac{\left({\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}{-\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}\right){\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}+1}-\frac{\left({\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}{-\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}\right){\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}+1}\right]\right]{\mathsf{\omega }}_{\mathrm{i}}\right]$$

(6)

3.1.2. ESG score

In recent years, portfolio managers are incorporating ESG criteria during portfolio creation. In this study, the ESG score of each asset is defined by the Bloomberg ESG Disclosure Score. Bloomberg provides insight on ESG data for over 9500 companies across over 83 countries. This is collected from company’s public filings such as CSR reports, annual reports and websites and a proprietary Bloomberg survey that requests corporate data directly. The ESG score measures the SR performance of a company on a scale from 0 to 100, with 100 being the best-rated ESG score possible and 0 being lowest ESG score possible. In this work, we divide Bloomberg ESG scores by 100, resulting in ESG scores, which vary within a range from 0 to 1.

As already mentioned, social performance criteria used to measure social responsibility of companies are by their very nature ambiguous, uncertain and imprecise. Therefore, this research assumes that the ESG score of each asset is a L-R fuzzy number. The parameters of the L-R power fuzzy numbers are obtained from the empirical percentiles of the historical ESG score data, as previously explained. Then, the maximisation of the expected ESG score of the portfolio can be expressed as:

$${\mathrm{Max}\mathrm{ESG}}_{\mathrm{p}}{=\mathrm{F}}_2\left({\mathsf{\omega }}_{\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left[\left[\frac{1}{2}\left[{\mathrm{b}}_{{\mathrm{ESG}}_{\mathrm{i}}}{+\mathrm{c}}_{{\mathrm{ESG}}_{\mathrm{i}}}+\frac{\left({\mathrm{d}}_{{\mathrm{ESG}}_{\mathrm{i}}}{-\mathrm{c}}_{{\mathrm{ESG}}_{\mathrm{i}}}\right){\mathsf{\rho }}_{{\mathrm{ESG}}_{\mathrm{i}}}}{{\mathsf{\rho }}_{{\mathrm{ESG}}_{\mathrm{i}}}+1}-\frac{\left({\mathrm{b}}_{{\mathrm{ESG}}_{\mathrm{i}}}{-\mathrm{a}}_{{\mathrm{ESG}}_{\mathrm{i}}}\right){\mathsf{\pi }}_{{\mathrm{ESG}}_{\mathrm{i}}}}{{\mathsf{\pi }}_{{\mathrm{ESG}}_{\mathrm{i}}}+1}\right]\right]{\mathsf{\omega }}_{\mathrm{i}}\right]$$

(7)

3.1.3. Risk

Mean-absolute semi-deviation of returns is a more appropriate risk measure than variance of returns, since it is focuses exclusively on adverse deviations. By taking the above into account, portfolio risk is calculated using expected value based MASD measure. Therefore, the minimisation of MASD of the portfolio can be expressed as:

$${\mathrm{Min}\mathrm{MASD}}_{\mathbf{P}}={\mathrm{F}}_3\left({\mathsf{\omega }}_{\mathrm{i}}\right)=\{\begin{array}{ll}\frac{1}{2}\left({\mathrm{e}-\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}\right)-\frac{1}{2}\frac{{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}+1}\left(1-{\left(\frac{{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}-\mathrm{e}}{{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}}\right)}^{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}+\mathrm{+1}}\right)& {\mathrm{Si}\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}\le \mathrm{e}\le {\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}\\ \frac{1}{2}(\frac{1}{2}\left({\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}+\left({\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{a}}_{{\mathrm{r}}_{\mathrm{i}}}\right)\frac{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\pi }}_{{\mathrm{r}}_{\mathrm{i}}}+1}+({\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}-c_{{\mathrm{r}}_{\mathrm{i}}})\frac{{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}+1}\right))& {\mathrm{Si}\mathrm{b}}_{{\mathrm{r}}_{\mathrm{i}}}\le \mathrm{e}\le {\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}\\ \frac{1}{2}\left({\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}-\mathrm{e}\right)-\frac{1}{2}\frac{{\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}+1}\left(1-{\left(\frac{\mathrm{e}-{\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}}{{\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}-{\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}}\right)}^{{\mathsf{\rho }}_{{\mathrm{r}}_{\mathrm{i}}}+1}\right)& {\mathrm{Si}\mathrm{c}}_{{\mathrm{r}}_{\mathrm{i}}}\le \mathrm{e}\le {\mathrm{d}}_{{\mathrm{r}}_{\mathrm{i}}}\end{array}$$

(8)

3.2. Real-World Constraints

Portfolio managers incorporate different types of restrictions, which consider investor preferences and market conditions. Based on the above statement, our proposed model includes the following five real-world constraints:

(i)

Capital budget constraint on the assets is defined as

$${\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\omega }}_{\mathrm{i}}=1$$

(9)

(ii)

Maximum number of assets held in the portfolio is defined as

$$\begin{gathered} {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{y}}_{\mathrm{i}}=\mathrm{k}, \\ {\mathrm{y}}_{\mathrm{i}}\in \left\{0,1\right\},\hspace{1em}\mathrm{i}=1,2,\dots ,\mathrm{n} \end{gathered}$$

(10)

(iii)

Maximal proportion of the capital that can be invested in a single asset is defined as

$${\mathsf{\omega }}_{\mathrm{i}}\le {\mathrm{u}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}},\hspace{1em}\mathrm{i}=1,2,\dots ,\mathrm{n}$$

(11)

(iv)

Minimal proportion of the capital that can be invested in a single asset is defined as

$${\mathsf{\omega }}_{\mathrm{i}}\ge {\mathrm{l}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}},\hspace{1em}\mathrm{i}=1,2,\dots ,\mathrm{n}$$

(12)

(v)

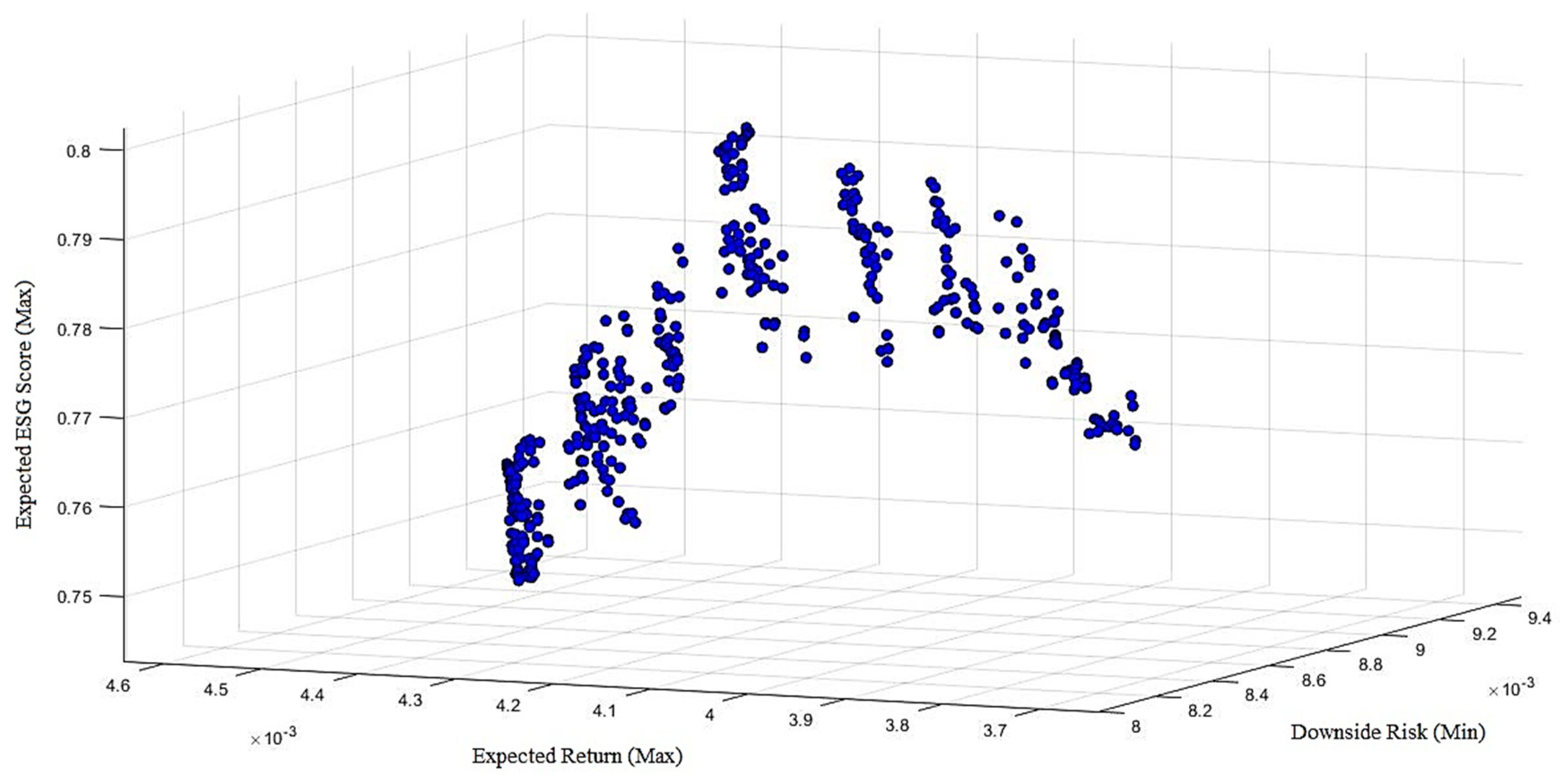
No short selling of assets is defined as

$${\mathsf{\omega }}_{\mathrm{i}}\ge 0,\hspace{1em}\mathrm{i}=1,2,\dots ,\mathrm{n}$$

(13)

On the basis of the aforementioned assumptions, the RRS portfolio selection model is formulated as:

$${\mathrm{Max}\mathrm{R}}_p{=\mathrm{F}}_1\left({\mathsf{\omega }}_{\mathrm{i}}\right)\hspace{1em}{\mathrm{Max}\mathrm{ESG}}_p{=\mathrm{F}}_2\left({\mathsf{\omega }}_{\mathrm{i}}\right)\hspace{1em}{\mathrm{Min}\mathrm{MASD}}_p{=\mathrm{F}}_1\left({\mathsf{\omega }}_{\mathrm{i}}\right)$$

$$\mathrm{Subject}\mathrm{to}\{\begin{array}{ll}{\displaystyle {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}}{\mathsf{\omega }}_{\mathrm{i}}=1,\hfill & \mathrm{i}=1,2,\dots ,\mathrm{n}\hfill \\ {\displaystyle {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}}{\mathrm{y}}_{\mathrm{i}}=\mathrm{k}\hfill & \\ {\mathrm{y}}_{\mathrm{i}}\in \left\{0,1\right\},\hfill & \mathrm{i}=1,2,\dots ,\mathrm{n}\hfill \\ {\mathsf{\omega }}_{\mathrm{i}}\le {\mathrm{u}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}},\hfill & \mathrm{i}=1,2,\dots ,\mathrm{n}\hfill \\ {\mathsf{\omega }}_{\mathrm{i}}\ge {\mathrm{l}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}},\hfill & \mathrm{i}=1,2,\dots ,\mathrm{n}\hfill \\ {\mathsf{\omega }}_{\mathrm{i}}\ge 0,\hfill & \mathrm{i}=1,2,\dots ,\mathrm{n}\hfill \end{array}$$

Here, an admissible portfolio ${\mathrm{P}}^{\mathrm{e}}$ is said to be Pareto-efficient if there is no other admissible portfolio ${\mathrm{P}}^{\mathrm{o}}$ such that ${\mathrm{P}}_{{\mathrm{F}}_{{1(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{o}}\ge {\mathrm{P}}_{{\mathrm{F}}_{{1(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{e}}$, ${\mathrm{P}}_{{\mathrm{F}}_{{2(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{o}}\ge {\mathrm{P}}_{{\mathrm{F}}_{{2(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{e}},$ ${\mathrm{P}}_{{\mathrm{F}}_{{3(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{o}}\le {\mathrm{P}}_{{\mathrm{F}}_{{3(\mathsf{\omega }}_{\mathrm{i}})}}^{\mathrm{e}}$, and, with at least one strict inequality [76]. The efficient solutions set is the Pareto optimal set in the decision space and each of their three objective function values constitute the Pareto optimal frontier in the criterion space. The solutions of the Pareto optimal frontier are non-dominated.

4. Solution Methodology

Incorporating real-world constraints into the portfolio optimisation problem converts it into a constrained portfolio optimisation problem (CPOP) that is NP-hard. In order to overcome this drawback, various multi-objective evolutionary algorithms (MOEAs) have been proposed in the literature. Among them, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) is the most commonly used MOEA for solving CPOPs [77]. In this study, we propose a methodology based on the algorithm NSGA-II introduced by Deb [78] in 2001. The main objective of this algorithm is to find a set of solutions ordered by fronts under the concept of Pareto dominance. Procedural steps of algorithm NSGA-II are those described by Deb et al. [79] in 2002.

The experimental parameter configuration for testing this algorithm is: population size (400), distribution index for crossover (10); probability of crossover (0.9); distribution index for mutation (50); probability of mutation (0.01); and the maximum number of generations (500). Figure 1 shows the overall structure of the MDRSR modelling approach.

5. Experimental Results

In this section, we illustrate the usefulness of the MDRSR model with a real-world empirical study using a data set from Bloomberg’s ESG Data in combination with data from companies included in the Dow Jones Industrial Average (DJIA). The data corresponds to weekly closing adjusted prices and ESG scores, observed in t = 203 periods from 10 February 2014 until 25 December 2017. In this study, we only consider 29 companies (n = 29), as one company was not included in the Bloomberg ESG Disclosure Score throughout the period under consideration.

The asset returns sample (r_it) is obtained as ${\mathrm{r}}_{\mathrm{it}}=\left({\mathrm{p}}_{\mathrm{it}}{-\mathrm{p}}_{\mathrm{it}-1}\right)/\left({\mathrm{p}}_{\mathrm{it}-1}\right)$, i = 1, 2, …, 29; t = 1, 2, …, 203, where p_it is the closing price of the i-th asset on Friday of week t. Then, the membership function of the L-R fuzzy return (${\mathsf{\xi }}_{{\mathrm{r}}_{\mathrm{i}}})$ and the L-R fuzzy ESG score ${(\mathsf{\xi }}_{{\mathrm{ESG}}_{\mathrm{i}}})$ are obtained from the sample percentiles of their historical returns and ESG score, respectively, as explained in Section 3.

In order to analyse the performance of our procedure, this study assumes as diversification parameters: l_i= 0.05 and u_i= 0.3 for every i = 1, 2,…, 29. Following Gupta et al. [80], it is not recommended to have either very few or a very large number of assets in the portfolio so as to achieve diversification. Overall, portfolio diversification by investors lies in the narrow range of 3–10 assets. Furthermore, Skolpadungket et al. [81] state that by limiting the number of assets included in the portfolio, transaction costs are reduced significantly due to the reduction of brokerage fees and taxes. By following the above recommendations, this paper considers setting k = 10 assets for an admissible portfolio.

Figure 2 shows a three-dimensional representation of the approximated Pareto front (or efficient front) generated by NSGA-II for the RRS model. The set of points represents the set of non-dominated (or efficient) portfolios for which none of the three objectives (i.e., return, downside risk or ESG score) can be improved without sacrificing any others. As can be observed, NSGA-II provides efficient portfolios, which are widely distributed along the efficient front.

The influence of the inclusion of the ESG score criterion into the Markowitz base model is examined in Figure 2: non-dominated portfolios with the highest expected return and downside risk achieved the lowest expected ESG score. Furthermore, non-dominated portfolios with the highest expected ESG score obtain both a medium expected return and downside risk. As previously mentioned, the table reveals that there is no portfolio that dominates all others in terms of achieving both a high-expected return and ESG score and low risk simultaneously.

In addition, we applied the Spearman’s rank partial correlation to analyse the relationship between the three selected criteria (i.e., return, ESG score and downside risk). Thanks to this measure, we can check the coherence of the relationship between return and downside risk, removing the influence of the ESG score on both variables. It was not possible to identify the relationship of both variables with the ESG score. As shown in

Table 1. Spearman’s rank partial correlation matrix.

	Return	Risk	ESG Score
Return	1.000
Risk	0.957 **	1.000
ESG score	−0.614 **	0.449 **	1.000

Note: ** Correlation is significant at the 0.01 level.

, there is a positive correlation between return and downside risk, which means that more profitable portfolios are riskier. The relationship between ESG Scores and downside risk could be accounted for by the fact that stocks of companies with a high ESG scores are traded more often than firms with low ESG scores and hence are subject to more volatility, hence increasing their risk. Finally, the relationship between ESG Scores and return suggest that stocks of companies with high ESG scores are not as profitable as their peers with low ESG scores.

This paper has proposed a fuzzy multi-objective approach that optimises the expected return, the expected ESG score and the downside risk of a given portfolio, taking budget, floor-ceiling and cardinality constraints into consideration. Each portfolio on the efficient frontier (Figure 2) offers the maximum possible expected return and expected ESG score for a given level of downside risk. However, investors and portfolio managers want to select the optimal portfolio along the efficient frontier that meets their preferences and expectations.

Modern portfolio theory assumes that investors are rational and always try to minimise risk while striving for the highest return possible [48]. The so-called Sortino ratio introduced by Sortino and Van Der Meer [71] in 1991 is a well-known measure to evaluate portfolio performance. It is a modification of the Sharpe ratio [82], using a downside measure rather than a dispersion measure to quantify risk. To select the optimal portfolio along the efficient frontier, we will define the credibilistic Sortino ratio as the ratio between the credibilistic risk premium and the credibilistic mean-absolute semi-deviation.

According to Sharpe [82], an optimal portfolio is one that seeks to maximise expected risk-adjusted returns. In order to select the SR optimal portfolio, we maximise the credibilistic Sortino ratio; it gauges the risk-adjusted return of an asset or portfolio in a downside risk framework. The Sortino ratio is expressed as:

$$\mathrm{Sortino}\mathrm{ratio}=\frac{\mathrm{E}\left({\mathsf{\xi }}_{\mathrm{P}}\right)-\mathrm{E}\left({\mathsf{\xi }}_{\mathrm{Rf}}\right)}{{\mathrm{MASD}(\mathsf{\xi }}_{\mathrm{p}})}$$

(14)

where, $\mathrm{E}\left({\mathsf{\xi }}_{\mathrm{p}}\right)$ is the expected fuzzy return of the portfolio, ${\mathrm{MASD}(\mathsf{\xi }}_{\mathrm{p}})$ is the fuzzy downside risk of the portfolio and $\mathrm{E}\left({\mathsf{\xi }}_{\mathrm{Rf}}\right)$ is the target or required rate of return (i.e., US 1-Year Treasury Constant Maturity Rate).

Finally, we compare the performance of the SR optimal portfolio selected using the proposed Sortino ratio with a similar investment alternative in the financial markets.

Table 2. ETF Dow Jones versus social responsibility (SR) optimal portfolio selected.

	VaR	Return	ESG Score
SPDR Dow Jones ETF (DIA)	0.0157	0.0426	0.6381
SR Optimal Portfolio	0.0182	0.1433	0.7110

compares the SR optimal portfolio with its benchmark, the SPDR Dow Jones Industrial Average ETF (DIA), which replicates the performance of DJIA Index, during the period from January 2018 to December 2018. Note that the selected SR portfolio beats the benchmark regarding return, value at risk and ESG score by an average of 1.007, 729 y 25 bps, respectively. On the basis of the above knowledge, it can be concluded that the applied model in this research offers promising results for SR-investors seeking ethical and sustainability goals beyond the return-risk trade-off.

6. Conclusions

This paper contributes to the SRI literature by proposing a novel fuzzy multi-objective approach that optimises the expected return, the expected ESG score and the downside risk of a given portfolio, subject to real-world constraints such as budget, floor-ceiling and cardinality. Owing to the uncertain environment of portfolio selection, we considered the return and the ESG score of each as L-R power fuzzy numbers, where all their parameters were obtained from the sample percentiles of the historical data set of the returns and ESG score, respectively. Furthermore, in order to quantify the return and ESG score of the portfolio we used the credibilistic mean and to quantify the downside risk of the portfolio we used credibilistic mean-absolute semi-deviation. A real-world empirical study was presented using a data set from Bloomberg’s ESG Data in combination with Dow Jones Industrial Average (DJIA). Additionally, by maximising the expected risk-adjusted returns (via credibilistic Sortino ratio), we selected the SR optimal portfolio and evaluated its performance in relation to another similar investment alternative in financial markets. The results of the numerical experiment establish that the proposed model offers promising results for socially responsible investors seeking ethical and sustainability goals beyond the return-risk trade-off.

Our proposed approach has several advantages over previous work on SR portfolio selection as we use, for the first time: i) the credibilistic fuzzy framework to deal with uncertainty, vagueness and imprecision environment of the SR portfolio selection; ii) the credibilistic mean-absolute semi-deviation of returns to gauge the portfolio risk; iii) the Bloomberg ESG Disclosure Score to measure the level of social responsibility of each asset; iv) the credibilistic Sortino ratio as the ratio between the credibilistic risk premium and the credibilistic mean-absolute semi-deviation to select the optimal portfolio along efficient frontier.

Finally, there are several future research possibilities for overcoming the limitations of our study. First, this study considers a specific period of time of 47 months. However, stock prices are sensitive to news to changes in macroeconomic and financial conditions. Therefore, a future interesting research would be to consider a wider time window in order to observe and identify stock market behaviour (i.e., bear and bull markets). On the other hand, this research uses a data set from Bloomberg’s ESG Data in combination with US Dow Jones Industrial Average. Nevertheless, a future research objective would be to consider other ESG rating scores, such as the Thomson Reuters ESG Score, the MSCI ESG Score and the Vigeo-Eiris ESG Score, and compare their results with the proposed model. Additionally, this study considers the below-mean absolute semi-deviation as a measure of portfolio risk. However, in the literature has been proposed other coherent risk measures such as expected shortfall, conditional value at risk and lower partial moment. Therefore, it would be interesting to consider some of these risk measures in order to quantify portfolio risk. Moreover, in this research, we consider five real-world constraints. Nevertheless, it is still far from reflecting the real-world trading scenarios. Thus, a future research opportunity would be to extend the proposed model and incorporate other realistic constraints, such as transaction costs, class, trading and turnover and so forth.