Dispatching High-Speed Rail Trains via Utilizing the Reverse Direction Track: Adaptive Rescheduling Strategies and Application

Abstract

This paper studies the train rescheduling problem on high-speed railway corridor in the situation where contingencies occur and lead to sudden deceleration of some trains. First, we develop an adaptive rescheduling strategy (AR-S) which allows normal trains to use reverse direction track to overtake front decelerating trains based on delay comparison under different path choices. Second, the traditional rescheduling strategy (TR-S) which does not allow any trains to switch tracks is mentioned as a sharp contrast to AR-S. Furthermore, a performance evaluation criterion is designed to evaluate the effectiveness of the train rescheduling approaches. Finally, numerical experiments carried out on Beijing-Tianjin intercity high-speed railway show that AR-S can reduce the total delay of trains up to 24% in comparison with TR-S.

1. Introduction

1.1. Motivation

At present, the total length of the high-speed railways (HSR) in China is more than 20,000 km, accounting for two-thirds of the total length of the world’s high-speed railways [1,2]. Furthermore, it is estimated that, by 2025, the total length of China’s HSR will reach 38,000 km, and by 2030, all provincial capitals (excluding Lhasa) will be connected by HSR [3]. Ensuring punctuality of trains traveling on such large-scale rail networks as well as fully utilizing railway infrastructure is significant to promote its sustainable development. Therefore, train scheduling/rescheduling problems become critical topics in the operation of railway systems [4].

In this paper, we focus on the train rescheduling problem. When two consecutive trains travel on corridor and the front train decelerates due to contingencies, it is necessary for the following train to reduce speed for avoiding the rear-end collision. The contingencies happen occasionally and the reasons are various. For example, if the communication of train and ground equipment is interrupted, the focus train is forced to reduce speed below 160 km/h less than half of the maximal speed 350 km/h; if someone smokes on a train, the train will slow down or emergency stop in sections. The data show that the daily average delay time of Guangzhou South Railway Station is 105 min during 24 March 2015 to 10 November 2016, and the number of delayed trains with over 10 min delay accounts for 22% in all delayed trains [5]. That is the phenomenon normal trains are delayed by decelerating trains. Especially on highly congested railway lines, more trains could be delayed and more total train delay could be caused [6], resulting in the decrease of passenger satisfaction with railway services and the increase of operation costs of railway industry [7]. To handle the problem mentioned above, this paper proposes an adaptive rescheduling strategy to reschedule normal trains to overtake front decelerating trains by utilizing reverse direction tracks.

1.2. Literature Review

In literature, train scheduling involves works at tactical level, which is to generate a nominal timetable in advance through comprehensive consideration on passenger demands and rail resource constraints and safety constraints [8,9,10,11]. To obtain the optimal/near-optimal solutions in the process of train scheduling, mathematical models are formulated and then solved by heuristic methods. For instance, Cacchiani et al. [12] proposed a Lagrangian heuristic based on an integer linear programming formulation, aiming to introduce as many extra freight trains as possible in railway transportation while keeping the disposition timetable conflict-free and as close as possible to the nominal one. To obtain an efficient train timetable in congested lines, Cacchiani et al. [13] developed an iterative heuristic algorithm that can produce solutions in short computing time. Similarly, to introduce extra passenger trains in highly congested lines thus meet the increasing passenger demand, Jiang et al. [14] extended the heuristic method proposed in Cacchiani et al. [12] and obtained an improved heuristic method, where trains are able to stop at additional stations or even skip a few stations and the dwelling time of some trains at some stations can be prolonged. Interestingly, energy conservation is also taken into account in some literatures concerning train scheduling. For instance, Yang et al. [15] formulated an integer programming model to improve the utilization of regenerative energy (i.e., electrical energy converted from kinetic energy during the train braking process). A genetic algorithm with binary encoding was further applied to obtain the energy-efficient schedule. Yang et al. [16] enhanced the utilization rate of regenerative energy by altering the dwell times of current timetable slightly in urban rail systems. Moreover, the period time and number of trains remain unchanged for practical concern. To reduce both travel time and energy consumption in urban rail systems, Yang et al. [17] formulated an integer programming model with two objectives to jointly optimize train schedule and speed profile. Moreover, an adaptive genetic algorithm was designed to obtain the optimal solution. Yang et al. [18] presented a survey on energy-efficient train operation for urban rail systems, concluding that jointly optimizing train schedule and train speed profile would be a future trend for achieving a better energy and time saving performance in railway transportation. It is worthwhile pointing out that for further study about train scheduling, we can refer to literature [19,20,21,22]. For example, Cacchiani and Toth [19] presented the main works concerning the train scheduling problem in its robust and nominal versions, and Caimi et al. [22] surveyed the combinatorial optimization models and practical applications for train scheduling problem.

Train rescheduling involves works at operational level and its main purpose is to keep the timetable as close as possible to the nominal one in emergency situations. Cacchiani et al. [23] presented an overview of recovery models and algorithms for real-time railway disruption and disturbance management. Zhan et al. [24] focused on rescheduling trains on macroscopic railway networks in a highly disrupted situation, then a mixed integer programming model was proposed to generate disposition timetables. Samà et al. [25] modeled the real-time train routing selection problem as an integer linear programming formulation which was solved by an ant colony optimization algorithm. In order to handle the rescheduling problem on metro lines, Gao et al. [26] proposed an optimization model which was heuristically decomposed into a set of mixed-integer linear programming sub-problems. An iterative algorithm based on the decomposition was further proposed to solve the model. On the basis of reinforcement learning (i.e., Q-learning), a train rescheduling method was introduced in Šemrov et al. [27], where five components of the Q-learning principles (i.e., environment and its states, learning agent and its actions, and the reward function) were further discussed. Aiming at defining a set of actions which are essential to ensure operation security in rail systems, Bettinelli et al. [28] proposed a parallel algorithm on the basis of an iterated greedy scheduling of trains on a time-space network. To reschedule trains on urban railway lines after small faults, a real-time train rescheduling strategy was developed by Gao et al. [29], where the integration of dynamic feedback of fault handling was considered in the proposed strategy. Binder et al. [30] introduced an integer linear programming model for rescheduling trains with multi-objectives on a disrupted railway network, where operational costs, passenger inconvenience, and deviation from the nominal timetable are three different objectives to minimize. Yang et al. [31] interested in rescheduling metro trains with energy-efficient approach, where an integer programing model was formulated and an allocation algorithm was designed to obtain the optimal schedule that can reduce net energy consumption under the premise of ensuring train punctuality. For further information about train rescheduling problem, we can refer to literature [32,33,34,35,36,37].

In order to reschedule trains under contingencies thus enhance the efficiency of railway operation, this paper proposes a rescheduling strategy that allows normal trains to adaptively select routes for punctually. The positions for trains’ switching tracks are not limited to stations. The crossovers in sections can also be utilized, which increases the flexibility of the proposed strategy. The utilization of reverse direction track was also considered by literature [38,39,40], but these works did not consider the train rescheduling process, and the track-switching positions are limited to stations. Different from these works, this paper considers the utilization of reverse direction track under contingencies. Moreover, trains can switch tracks not only in stations, but also in sections between stations using nodes. In this paper, nodes are the crossovers in sections between stations. We also described the deficiency of the currently applied strategy in Chinese HSR operations, and concluded that adaptively adjusting routes for trains can be a key step to efficiently use railway infrastructures and improve train punctuality. The main contributions of this paper are as follows:

(1)

Two train delay models for calculating train delays on double-track railway lines are rigorously formulated. Specifically, different train path choices lead to different train delay models. In this paper, the considered train path choices are: (a) the normal trains travel behind decelerating trains on dedicated tracks; (b) the normal trains overtake front decelerating trains by utilizing the reverse direction track if corresponding conditions are satisfied. Furthermore, we develop an adaptive rescheduling strategy which is based on the analysis of train delays under different path choices.

(2)

A performance evaluation criterion is specifically designed to evaluate the effectiveness of train rescheduling approaches.

(3)

Numerical experiments are carried out on a real-life HSR line, i.e., Beijing-Tianjin intercity high-speed railway, and result shows that the proposed rescheduling approach is superior to the traditional rescheduling approach.

To clarify the contributions of our research, the detailed features of some closely related studies are listed in

Table 1. The detailed features of closely related studies.

Publication	Type of Problem	Position for Switching Tracks	Safety Constraints	Adaptively Selecting Routes
Mu and Dessouky [38]	scheduling	Stations	Not consider	Not consider
Xu et al. [39]	scheduling	Stations	Consider	Consider with local optimum
Xu et al. [40]	scheduling	Stations	Consider	Not consider
This paper	rescheduling	Stations & Nodes	Consider	Consider with local optimum

.

The rest of this paper is arranged as follows. Section 2 depicts the considered problem. In Section 3, we first analyze in detail the safety constraints that must be met during train operation process. Then, analysis on train delays under different path choices is given, based on which an adaptive rescheduling strategy is developed. Section 4 demonstrates the effectiveness and efficiency of the proposed strategy by numerical experiments on the real-life Beijing-Tianjin HSR. Finally, we make a conclusion in Section 5.

2. Problem Description

We consider the train rescheduling problem on double-track railway lines, where tracks are bi-directional so that they can be occupied by trains traveling in both directions. Figure 1 presents the infrastructures on a Chinese high-speed railway corridor, where nodes are the crossovers in sections between stations. Different from the train stations, nodes are only for trains’ switching tracks and cannot be the dwelling position for any trains for safety concern. As shown in Figure 1, nodes are denoted by capitalized English letters. Further, node A and node B are two consecutive nodes and the segment between them is called as segment AB, the name of other segments can be deduced by analogy. In Figure 1, the direction from right to left is defined as inbound direction, whereas the direction from left to right is outbound direction. Moreover, the trains traveling toward inbound/outbound direction are termed as inbound/outbound trains and the tracks they use are termed as inbound/outbound tracks.

For the traditional rescheduling strategy, inbound tracks are dedicated to inbound trains, whereas outbound tracks are dedicated to outbound trains. The interested problem is that, when a train traveling on corridor decelerates suddenly due to contingencies, its following normal train needs to decelerate for the purpose of avoiding rear-end collision, thus suffering undesirable delay. To reduce the time delay of normal train, we consider to reroute the normal train to travel on reverse direction track in the next segment so as to overtake front decelerating train. Figure 2 illustrates the specific process of a normal train overtaking its front decelerating train by using reverse direction track, where inbound train i is a decelerating train that encounters contingencies on segment BC. As time goes on, inbound train i + 1 passes train i by traveling on reverse direction track in segment BC, which may reduce the time delay of train i + 1. It is worth remarking that from the practical point of view, in order to avoid excessive stress on switches, there is a process of deceleration and acceleration before and after a train switching tracks. However, the additional delay time caused by switching tracks is much less than the delay caused by train conflicts in real-word train operations, thus the acc/deceleration process is ignored, for it is not the focus of our study, although it is easy to take this part into account.

To describe the interested problem concisely, we assume that decelerating train i starts to decelerate at time t, and let $D_{i,BC}$ be the time delay of decelerating train i on segment BC caused solely by contingencies. $T_{k,B}$ is the planned traveling time for train k from time t to its arrival time at node B, and the meaning of $T_{i,B}$ and $T_{i+1,B}$ can be easily deduced by analogy.

For example, in Figure 2a, the original planed speed for train i, train i + 1 and train k is 300 km/h (i.e., 5 km/min), we assume that train i decelerates to 90 km/h (i.e., 1.5 km/min) at time t. The distances from train k, i and i + 1 to node B at time t are L_k, L_i and L_i+1, respectively. We set the operation information as L_k = 80 km, L_i = 30 km, L_i+1 = 60 km, then we have T_i,B = 30/5 = 6 min, T_i+1,B = 60/5 = 12 min, T_k,B = 80/5 = 16 min, D_i,BC = 30/1.5 − T_i,B = 14 min. As time goes on, if train i + 1 travels behind train i, without considering time headway, it is easy to deduce that the delay time of train i + 1 is 6 + 14 − 12 = 8 min. But if train i + 1 is rescheduled to travel on reverse direction track in segment BC, we will find that there is no conflicts between any two trains, thus normal trains will not be delayed. The corresponding ideal timetables are shown in Figure 3. However, by further analysis we realize that it is not always the optimal solution to let normal trains travel on reverse direction track. For instance, if we set the operation information as L_k = 15 km, L_i = 30 km and L_i+1 = 60 km at time t, we have T_i,B = 30/5 = 6 min, T_i+1,B = 60/5 = 12 min, T_k,B = 15/5 = 3 min, D_i,BC = 30/1.5 − T_i,B = 14 min. Considering the following two rescheduling strategies: (a) train i + 1 travels behind train i on inbound tracks; (b) train i + 1 travels on reverse direction track in segment BC. We can deduce that the total train delay for (a) is 6 + 14 − 12 = 8 min (for train i + 1) while that for (b) is 12 − 3 = 9 min (for train k), which means rescheduling train i + 1 to travel on dedicated track is a better option. By further analysis, we can conclude that whether rescheduling normal trains to travel on reverse direction track is an optimal solution depends on practical operation data. Therefore, how to determine the routes of normal trains based on practical operation information so as to minimize the total train delay is one of the central problem this paper focuses on. One possible solution for that problem is that we determine the route of normal trains based on the comparison of the total train delay under different path choices, and the route that is finally decided to use will lead to the minimum total train delay.

3. Formulation of Adaptive Rescheduling Strategy

To deal with the train rescheduling problem presented in Section 2, in this section an adaptive rescheduling strategy is proposed. For the feasibility of the proposed strategy, we first consider the safety constraints that must be met in the real-life train operation process. It is worth mentioning that energy efficiency is also a key aspect of train operation [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. But in Chinese high-speed train rescheduling process, safety and punctuality of trains directly relate to service quality, which is prior to energy efficiency in railway managers’ perspective. Consequently, we choose to minimize the total train delay in this paper.

To understand and describe the problem conveniently, some decision variables and parameters are listed in

Table 2. Some subscripts and parameters.

Symbol Definition		Symbol Definition
I	Set of inbound trains	O	Set of outbound trains
R	Set of trains using reverse direction tracks	i, i + 1, k	Index of train
$d_{k,B}$	Departure time for train k from node B	H	Departure interval between two consecutive trains
t	The time point when corresponding trains begin to decelerate because of contingencies	T	Minimal interval between two consecutive trains traveling in same direction
$T_{k,B}$	Planned traveling time for train k from time t to its arrival time at node B	$D_{i,BC}$	Time delay of train i caused solely by contingencies in segment BC
$H_{i+1,i}^{aa}$	Minimal headway between train i + 1 and train i reaching the same node. i ∈ 6I, i + 1 ∈ I and i + 1 ∈ R	$H_{i+1,k}^{da}$	Minimal headway between train i + 1 leaving and train k reaching the same node. K ∈ O, i + 1 ∈ I and i + 1 ∈ R

. Besides, some assumptions are made below first.

(A1)

All the trains travel on double-track railway corridors where each track is bi-directional so that it can be occupied by trains traveling in both directions.

(A2)

The communication capacity of the railway systems is guaranteed for a train switching tracks.

(A3)

In comparison with the length of each railway segment, lengths of trains and nodes are extremely short. Thus, for simplicity, trains and nodes are regarded as particle points.

(A4)

The decelerating trains in contingencies travel at a constant speed below normal speed.

3.1. Safety Constraints

The premise for the implementation of any train rescheduling strategy is that the strategy fully considers and satisfies the safety constraints in practical train operation, thus operation safety can be ensured. In this paper, the considered safety constraints (C1–C3) are shown in Figure 4.

• C1. As shown in Figure 4a, to avoid the risk of collision between inbound train i + 1 and outbound train k and in consideration of the responding time of the corresponding equipment (i.e., switches at node B), the time interval between train i + 1 and train k arriving at node B should be no less than a fixed value, i.e., $H_{i+1,k}^{da}$.
• C2. As shown in Figure 4b, similar to (C1), the time interval between train i + 1 and train i arriving at node B should be no less than $H_{i+1,i}^{aa}$.
• C3. As shown in Figure 4c, the time headway between two consecutive trains traveling in same direction should be no less than T.

3.2. Analysis of Train Delays under Different Path Choices

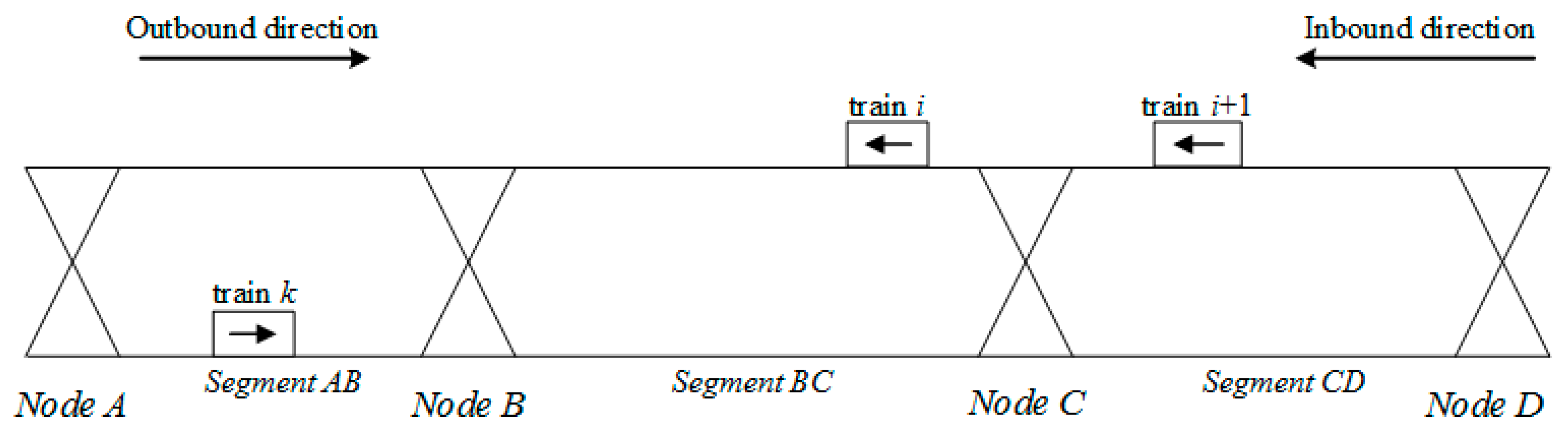
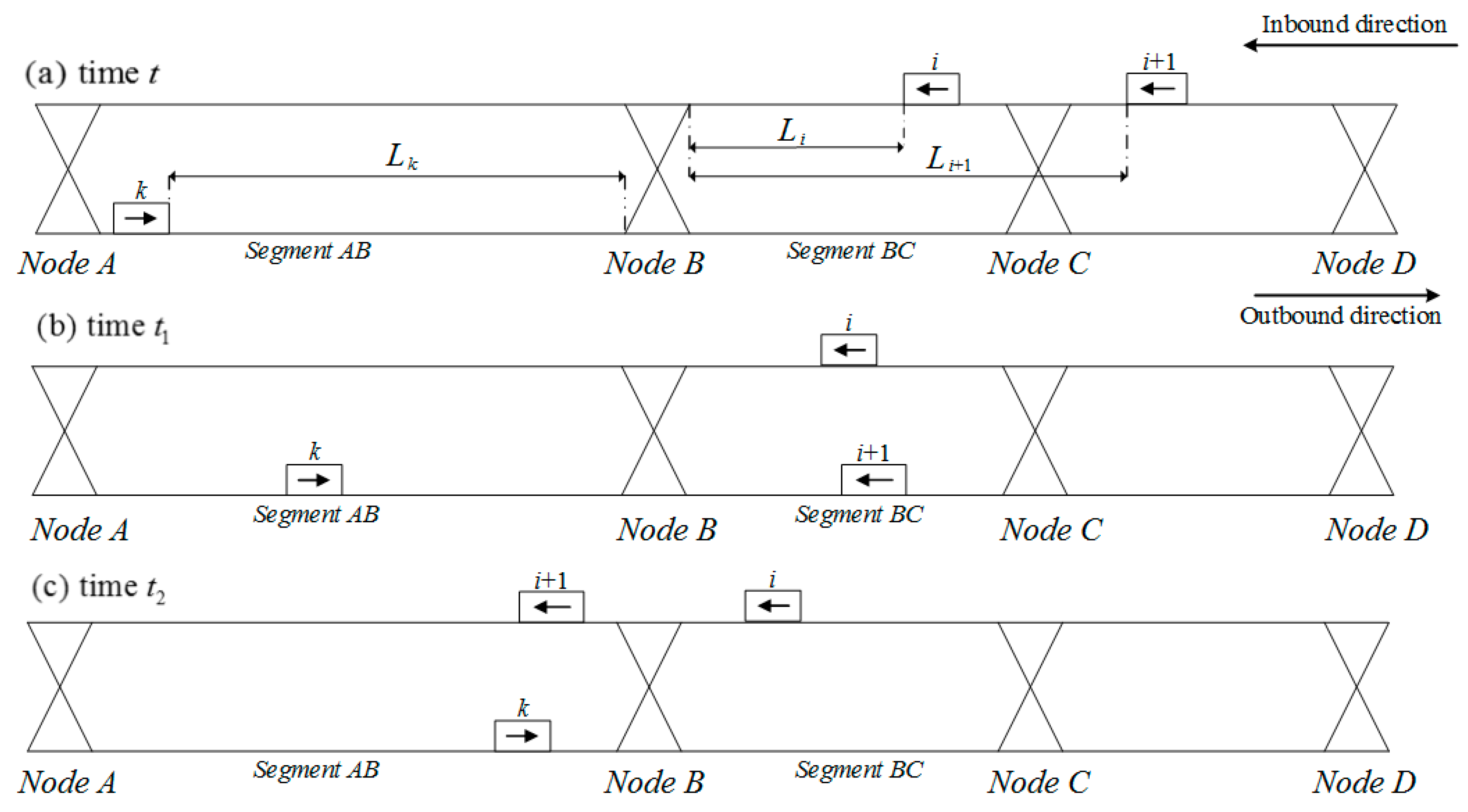
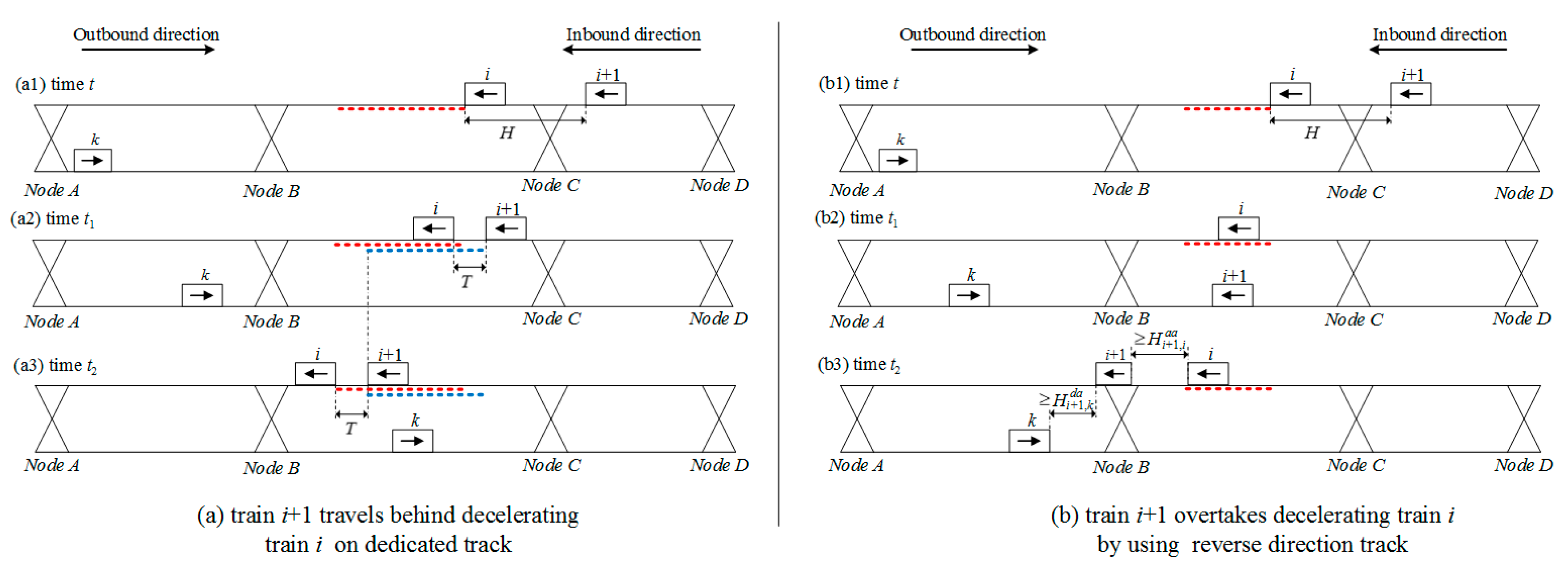
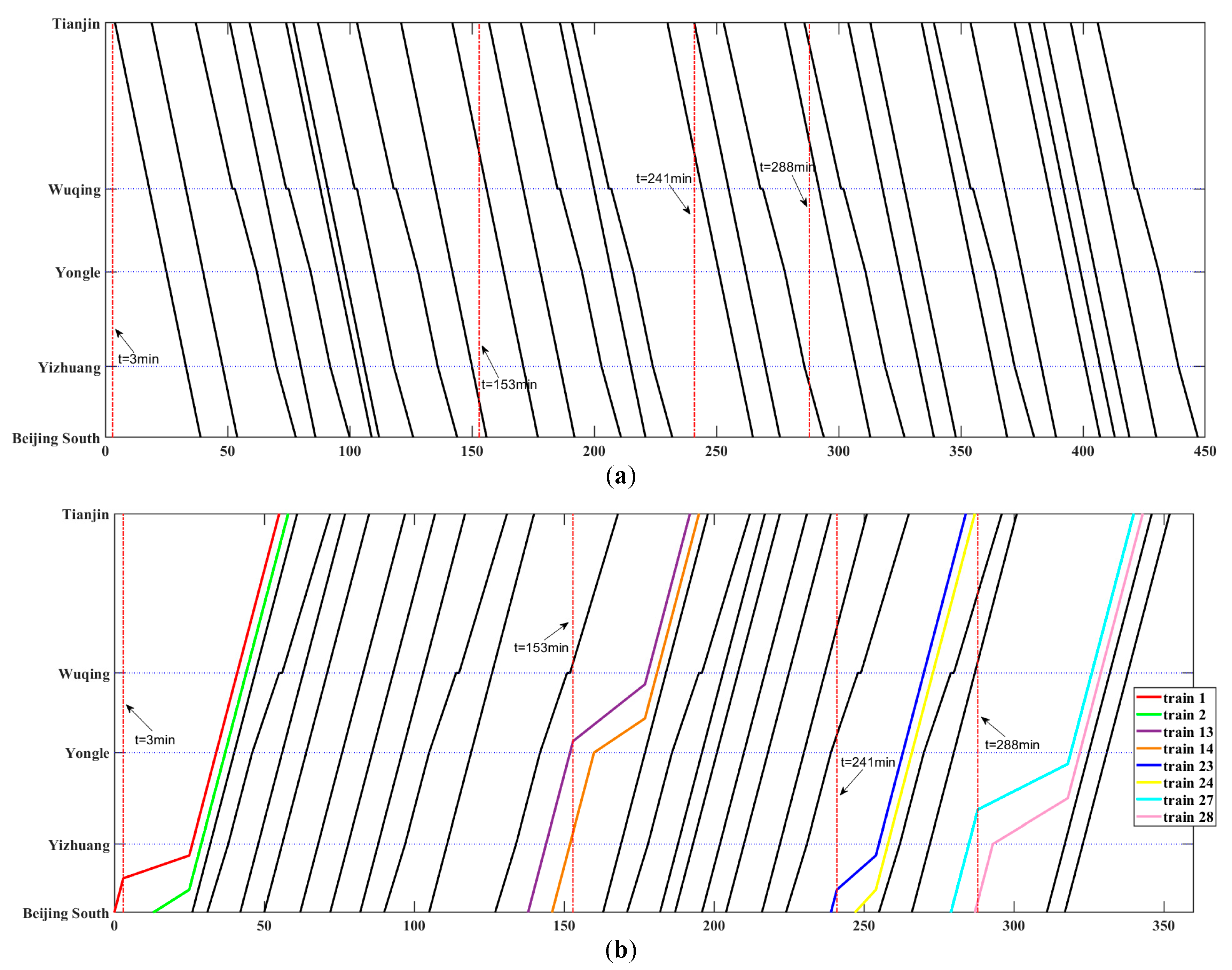
Based on the analysis of safety constraints, we further analyze the calculations for train delays under different path choices. As show in Figure 5(a1,b1), at time t, inbound train i encounters a contingency and begins to slow down to a constant speed that below normal speed on the inbound track in segment BC, and the track where train i decelerates is highlighted with dash line in red color in Figure 5. Meanwhile, the rest of trains (i.e., train k and train i + 1) travel normally on their dedicated tracks. At time t, neither train i + 1 nor train k has passed node B or node C. Moreover, the outbound track in segment BC is not occupied by any other trains. As time goes on, if inbound train i + 1 chooses to travel on dedicated track in segment BC, case 1 showed in Figure 5a will be obtained; otherwise, we will obtain case 2 showed in Figure 5b, where train i + 1 uses the reverse direction track to overtake decelerating train i in segment BC.

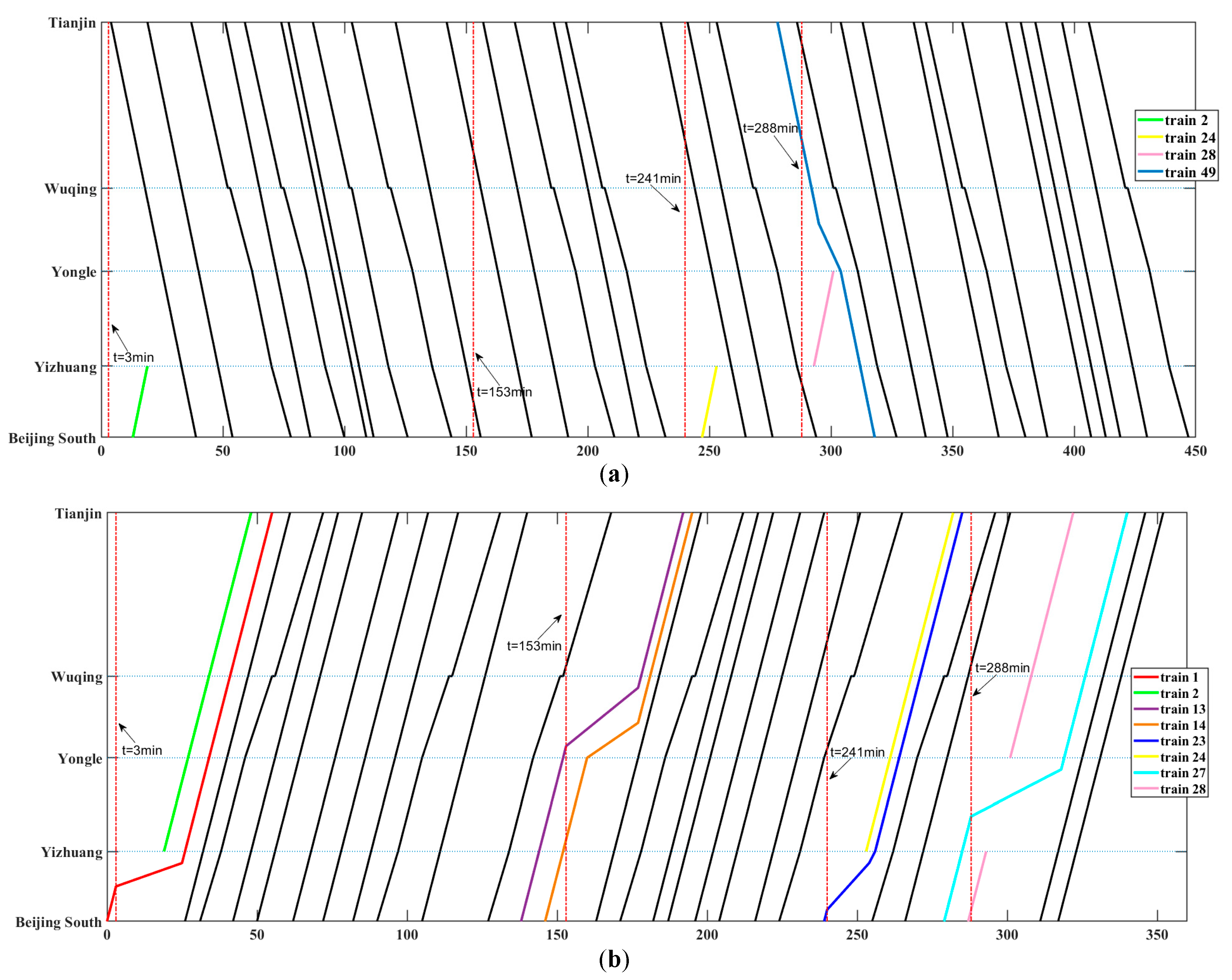
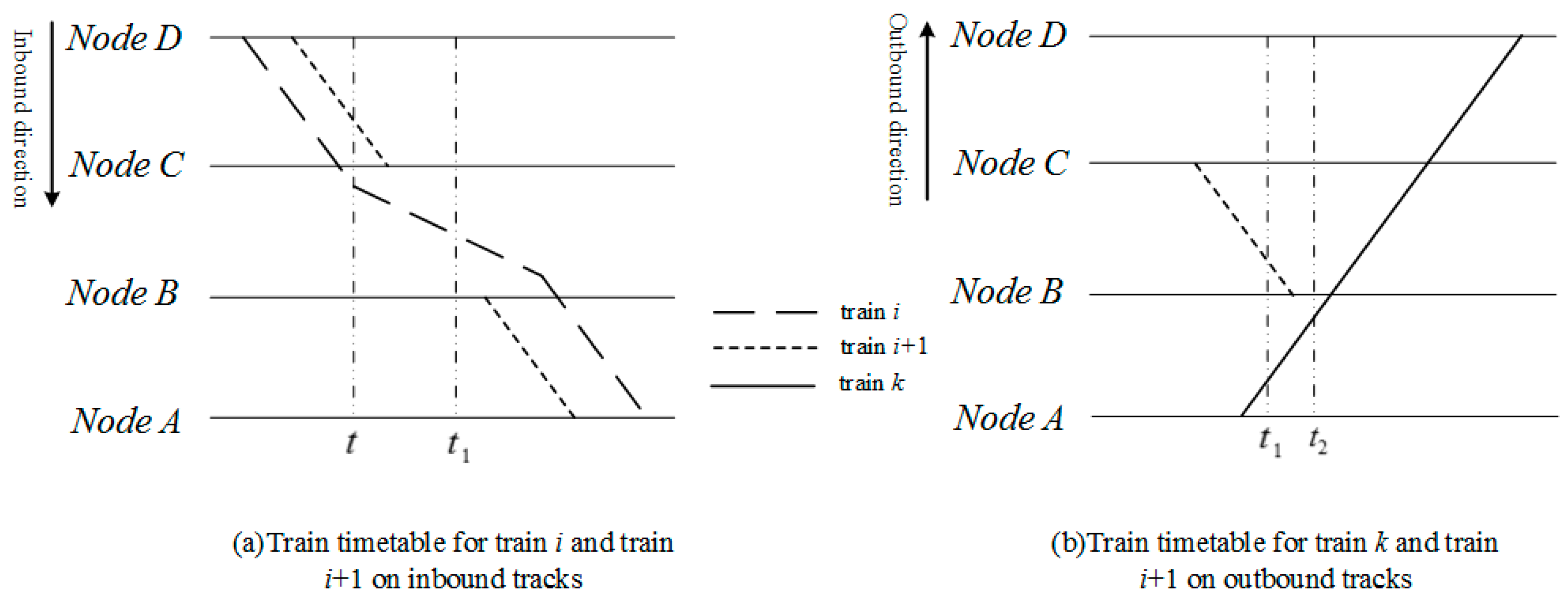
In case 1, in order to meet C3, train i + 1 may need to reduce its speed if train i is delayed greatly by contingencies. The dash line in blue color in Figure 5a highlights the track where train i + 1 is delayed by train i. In case 2, to satisfy C1 and C2, train k and train i may be delayed by train i + 1. Figure 6, Figure 7 and Figure 8 respectively illustrate the possible delay of each train in case 1 and case 2, where corresponding timetables are also presented. The dash lines in the timetables presented in Figure 6, Figure 7 and Figure 8 denote the ideal trajectory of trains. In this paper, a train is called in the state of obstacle-travel situation when it has to decelerate due to potential train conflicts; otherwise, a train in free-travel situation is such a train that travels without potential conflicts with any other trains. Here, let $Z_k^o$ and $Z_k^f$ be the time duration $d_{k,B}-t$ for train k in obstacle-travel situation and free-travel situation, respectively. Then, if train i + 1 conflicts with train k, train k’s delay $Z_{k,i+1}$ caused by train i + 1 equals to $Z_k^o-Z_k^f$. The same calculation also goes for train i and train i + 1.

Actually, the train delay in this paper can be categorized into two types: one is the train delay caused solely by contingencies (e.g., equipment failure, bad weather, etc.) and cannot be avoided or reduced by any rescheduling strategies, which is termed as fixed train delay (e.g., $D_{i,BC}$); the second train delay is cause by operational conflicts between trains, which is termed as conflict train delay. Specifically, under same conditions, different rescheduling strategies may lead to different conflict train delay. Further, we can evaluate the effectiveness of the rescheduling strategies according to the total conflict train delay. The less total conflict train delay is, the more effective rescheduling strategy can be. The following discussions present the detailed analysis on conflict train delay.

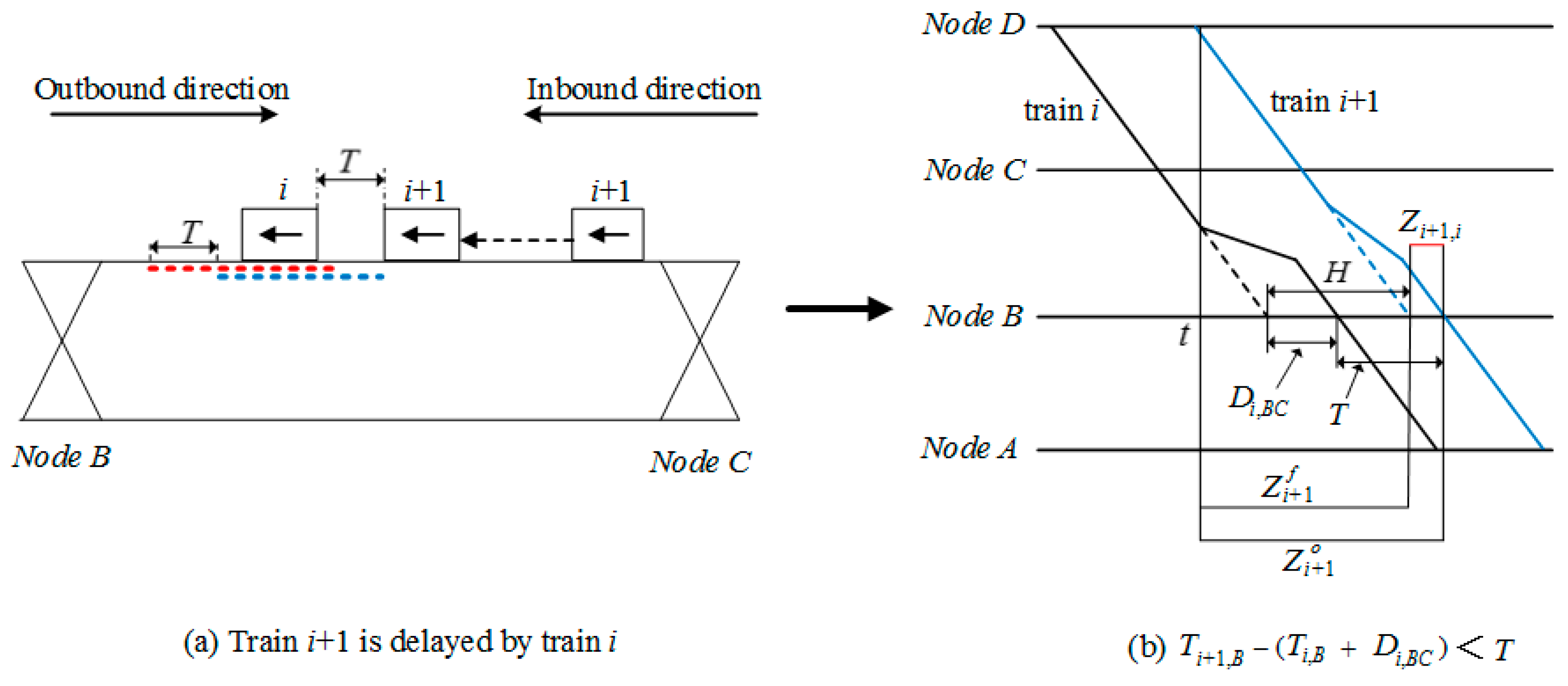
3.2.1. Case 1 Normal Train Traveling on the Dedicated Track

The possible delay that train i + 1 may encounter when tracing behind train i on dedicated track is illustrated in Figure 6. In fact, if $T_{i+1,B}-(T_{i,B}+D_{i,BC})\ge T$, train i + 1 is able to travel on dedicated track without decelerating, meanwhile safety constraint C3 can always be satisfied because of the relatively large departure interval between train i + 1 and train i. Train i’s sudden decelerating does not affect the normal operation of any other trains, thus train i + 1’s switching track is unnecessary.

However, if $T_{i+1,B}-(T_{i,B}+D_{i,BC})<T$, train i + 1 have to decelerate in consideration of C3, then we have

$$\begin{array}{l}{Z}_{i+1}^o=T_{i,B}+D_{i,BC}+T\\ Z_{i+1}^f=T_{i+1,B}\end{array}$$

(1)

Accordingly, the conflict train delay of train i + 1 can be calculated by

$$Z_{i+1,i}=T_{i,B}+D_{i,BC}+T-T_{i+1,B}$$

(2)

Moreover, the operation of train i will not be affected by any other trains if train i + 1 travels on dedicated track, thus we have $Z_{i,i+1}=0$. Obviously, no outbound trains will be delayed since the outbound track in segment BC will not be utilized by any inbound trains in case 1.

Finally, the total conflict train delay here equals to that of train i + 1, which can be calculated by

$$Z(i,i+1)=\{\begin{array}{ll}{T}_{i,B}+D_{i,BC}+T-T_{i+1,B}& \mathrm{otherwise}\\ 0& T_{i+1,B}-(T_{i,B}+D_{i,BC})\ge T\end{array}$$

(3)

3.2.2. Case 2 Normal Train Traveling on Reverse Direction Track

If we reschedule inbound normal train i + 1 to travel on reverse direction track in segment BC, there are two kinds of potential conflicts between train i + 1 and other trains, leading to different delays. One is the head-on conflicts between train i + 1 and the outbound trains (i.e., train k); the second is the rear-end conflicts between train i + 1 and the inbound trains (i.e., train i).

To analyze these two types of conflicts in detail, we divide case 2 into two subcases, namely subcase 2.1 and subcase 2.2, which will be discussed respectively below.

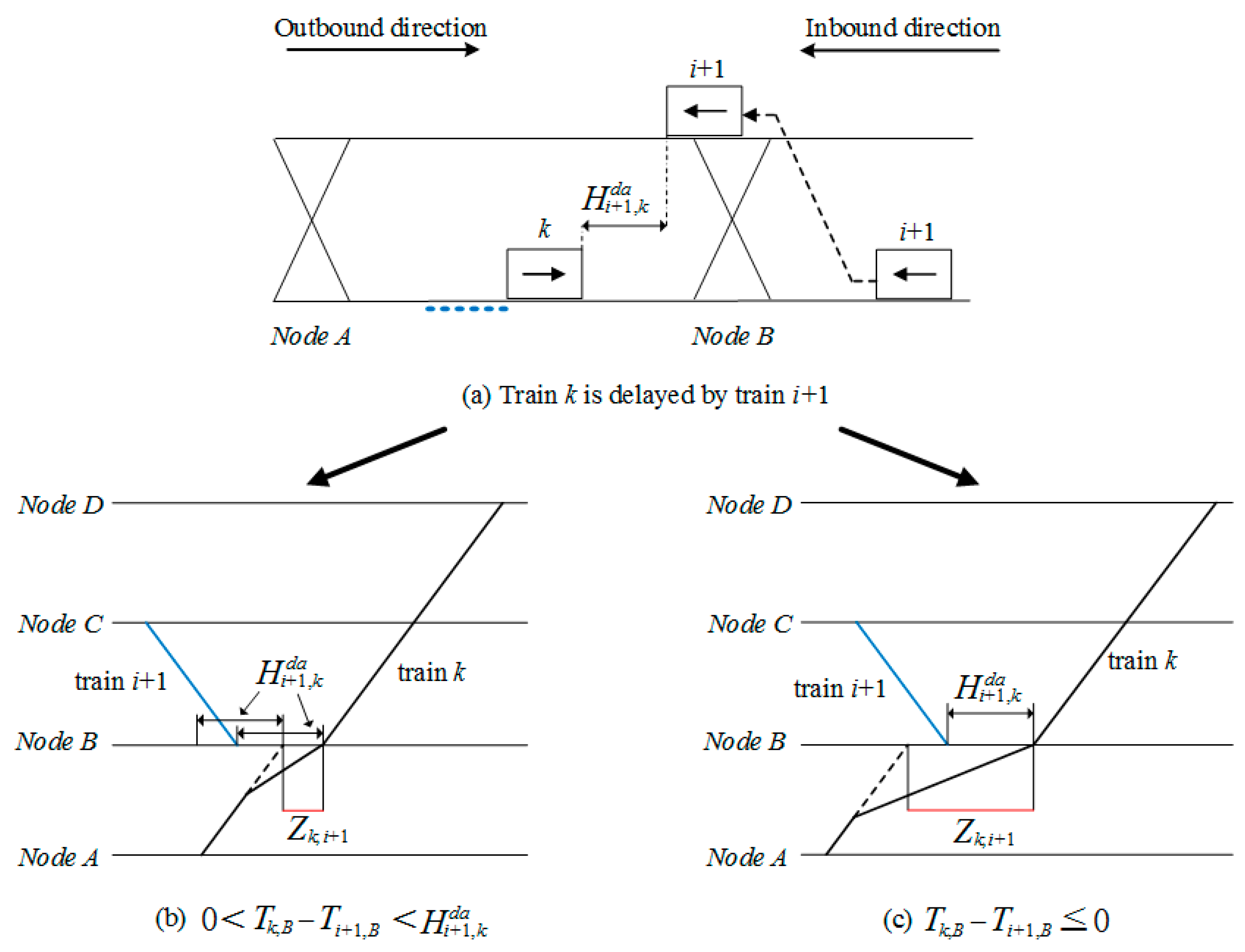
(1) Subcase 2.1 Delay analysis of train i + 1 and train k

In the condition that $T_{k,B}-T_{i+1,B}\ge H_{i+1,k}^{da}$, train i + 1’s arrival time at node B is earlier than train k and the time interval is longer than time headway $H_{i+1,k}^{da}$, which means C1 can always be satisfied while train k traveling with normal speed on dedicated track.

However, if $0<T_{k,B}-T_{i+1,B}<H_{i+1,k}^{da}$, timetable shown in Figure 7b will be obtained, in this situation train k’s arrival time is later than train i + 1 but the time interval is shorter than $H_{i+1,k}^{da}$, train k still needs to decelerate before reaching node B. If $T_{k,B}-T_{i+1,B}\le 0$, timetable shown in Figure 7c will be obtained, in which the planned arrival time for train i + 1 at node B is later than train k. Therefore, in the condition that $T_{k,B}-T_{i+1,B}<H_{i+1,k}^{da}$, train k needs to reduce its speed in segment AB because of C1, and the dash line in blue color in Figure 7a highlights the track where train k travels below normal speed. Moreover, in both Figure 7b,c, we have $Z_k^o=T_{i+1,B}+H_{i+1,k}^{da}$ and $Z_k^f=T_{k,B}$. Then, the conflict train delay of train k caused by train i + 1, in the condition that $T_{k,B}-T_{i+1,B}<H_{i+1,k}^{da}$, can be calculated by

$$Z_{k,i+1}=Z_k^o-Z_k^f=T_{i+1,B}+H_{i+1,k}^{da}-T_{k,B}$$

(4)

Then, according the above-mentioned analysis in this subsection, the delay time of outbound train k in case 2 can be calculated by

$$Z_{k,i+1}=\{\begin{array}{ll}0& T_{k,B}-T_{i+1,B}\ge H_{i+1,k}^{da}\\ T_{i+1,B}+H_{i+1,k}^{da}-T_{k,B}& \mathrm{otherwise}\end{array}$$

(5)

Obviously, there is no delay for train i + 1 in this subcase, i.e., $Z_{i+1,k}=0$.

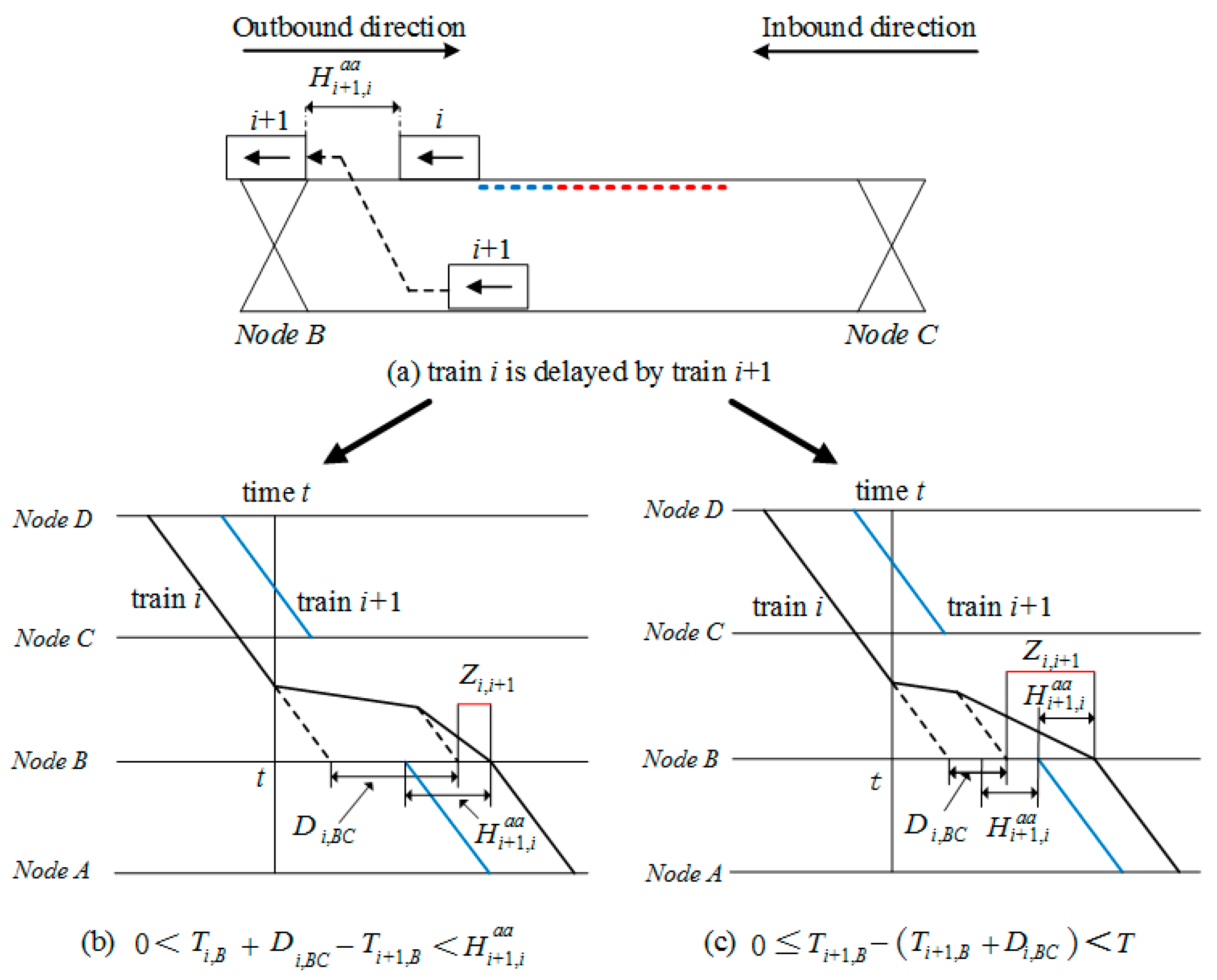
(2) Subcase 2.2 Delay analysis of train i + 1 and train i

According to the discussion in Section 3.2.1, the condition that $T_{i+1,B}-(T_{i,B}+D_{i,BC})<T$ is true when train i + 1 is rescheduled to travel on the reverse direction track. Specifically, we will consider to reschedule train i + 1 to travel on reverse direction track only in the condition that train i + 1 will experience time delay on dedicated track. Moreover, safety constraint C2 should be taken into account when train i + 1 travels on reverse direction track.

For detailed analysis, we divide the condition that $T_{i+1,B}-(T_{i,B}+D_{i,BC})<T$ into three scenarios, namely $T_{i,B}+D_{i,BC}-T_{i+1,B}\ge H_{i+1,i}^{aa}$ and $0<T_{i,B}+D_{i,BC}-T_{i+1,B}<H_{i+1,i}^{aa}$ and $0\le T_{i+1,B}-(T_{i,B}+D_{i,BC})<T$, and each scenario will be discussed respectively. First, in the condition that $T_{i,B}+D_{i,BC}-T_{i+1,B}\ge H_{i+1,i}^{aa}$, the arrival time of train i + 1 at node B is earlier than train i and the time difference is no less than $H_{i+1,i}^{aa}$, thus, there is no conflict between train i + 1 and train i in case 2, then we have $Z_{i,i+1}=0$.

However, if $0<T_{i,B}+D_{i,BC}-T_{i+1,B}<H_{i+1,i}^{aa}$ or $0\le T_{i+1,B}-(T_{i,B}+D_{i,BC})<T$ is true, train i + 1 will conflict with train i because of C2, which leads to conflict train delay of train i. In Figure 8a, the dash line in blue color highlights the track where train i is delayed by train i + 1 and the dash line in red color highlights the part of track where train i decelerates due to contingencies. Both in Figure 8b,c, we have

$$\begin{array}{l}{Z}_i^f=T_{i,B}+D_{i,BC}\\ Z_i^o=T_{i+1,B}+H_{i+1,i}^{aa}\end{array}$$

(6)

Then, conflict train delay of train i caused by train i + 1 can be calculated by

$$Z_{i,i+1}=Z_i^o-Z_i^f=T_{i+1,B}+H_{i+1,i}^{aa}-(T_{i,B}+D_{i,BC})$$

(7)

Based on the aforementioned analysis, the conflict train delay of train i in case 2 can be calculated by

$$Z_{i,i+1}=\{\begin{array}{ll}0& T_{i,B}+D_{i,BC}-T_{i+1,B}\ge H_{i+1,i}^{aa}\\ T_{i+1,B}+H_{i+1,i}^{aa}-(T_{i,B}+D_{i,BC})& \mathrm{otherwise}\end{array}$$

(8)

For train i + 1, no conflict train delay will be obtained in case 2, i.e., $Z_{i+1,i}=0$.

In conclusion, the total conflict train delay of train i, i + 1 and k in the case that train i + 1 chooses to travel on the reverse direction track can be calculated by

$$Z(i,i+1,k)=Z_{k,i+1}+Z_{i,i+1}$$

(9)

where $Z_{k,i+1}$ and $Z_{i,i+1}$ can be calculated by Equations (5) and (8), respectively.

3.3. Adaptive Rescheduling Strategy

Based on the aforementioned analysis in Section 3.1 and Section 3.2, we propose an adaptive rescheduling strategy in this section. Without loss of generality, we assume that the trains experiencing contingencies travel at a constant speed that below normal speed. All the decelerating trains travel on dedicated tracks and all the normal trains can keep their current running state. The first train starts at time t₀ = 0. For more details, we can see the following rules designed for the proposed strategy.

● Rules for rescheduling trains

Train i + 1 is a normal train and its front train i is a decelerating train that starts to decelerate at time t. We set up the following three conditions: (a) there is a node between train i and train i + 1 at time t; (b) the reverse direction track for train i + 1 in its next segment is not occupied by any other trains; (c) the risk of rear-end collision does exist if train i + 1 travels behind train i at normal speed on dedicated tracks. At time t, if any one of the conditions (a) and (b) and (c) is not satisfied, we will reschedule train i + 1 to travel on dedicated track; otherwise, if condition (a) and (b) and (c) are all met, train i + 1’s track choice is decided by the delay comparison between aforementioned case 1 and case 2: if the conflict train delay in case 1 is greater than case 2, train i + 1 uses reverse direction track to overtake train i in its next segment; otherwise, train i + 1 travels on dedicated track.

We here develop the path-selecting algorithm to clarify the proposed strategy (Algorithm 1). Parameter Ψ and Θ are used to record the numbers of trains which satisfy judgement conditions. Respectively, n and N denote the index of train and the total number of trains.

Algorithm 1. Path-selecting Algorithm

Step 1. (Initialization) Inbound train i decelerates at time t in segment BC because of contingencies, Ψ = Θ = 0, n = 1, i + 1 = k = 0 and Z(i,i + 1) = Z(i,i + 1,k) = 0. Step 2. If n ≤ N, go to step 3; otherwise go to step 4 Step 3. Update Ψ, Θ, Z(i,i + 1) and Z(i,i + 1,k) according to the information of train n as follows. (a) If train n is an inbound train following train i, and there is a node between train n and train i at time t and the condition that $T_{n,B}-(T_{i,B}+D_{i,BC})<T$ is true, update Θ = Θ + 1, record this train’s ID as i + 1 = n, and calculate the total conflict train delay Z(i,i + 1) of train i and train i + 1 according to Equation (3); (b) If train n is an outbound train and travels on outbound track in segment BC, update Ψ = Ψ + 1, then go to step 4; (c) If train n is an outbound train and has not reached node B at time t, moreover train k is the head train to pass node B, record train n’s ID as k = n, and calculate the total conflict train delay Z(i,i + 1,k) of train i, i + 1 and k according to Equation (9); (d) Otherwise, Θ = Θ, Ψ = Ψ. Then, n = n + 1. If n = i, update n = n + 1. Lastly, go to step 2. Step 4. If Θ > 0, Ψ = 0 and Z(i,i + 1) > Z(i,i + 1,k), train i + 1 will be rescheduled to travel on reverse direction track; otherwise, train i + 1 travels on its dedicated track.

3.4. Performance Evaluation Criteria for Rescheduling Strategies

To accurately evaluate the efficiency of the train rescheduling strategy, this paper introduces a performance evaluation criterion, termed as suppression rate of conflicts. Moreover, a universal but effective performance evaluation criterion, i.e., total train delay, is also applied in this paper.

(1) The suppression rate of conflicts, designed by this paper.

$$\eta =\frac{{\displaystyle \sum _i^{}{Z}_{i,total}^o}}{{\displaystyle \sum _i^{}{D}_{i,total}}}$$

(10)

where $D_{i,total}$ and $Z_{i,total}^o$, respectively, denote the total fixed train delay and the total conflict train delay of train i from the starting station to the terminal station.

In fact, the application of different rescheduling strategies under the same contingencies may lead to different total conflict train delay, while total fixed train delay remains unchanged. Therefore, the strategy with minimum total conflict train delay tends to be the optimal one among all the strategies applied.

Obviously, the less value of η is, the more efficient the corresponding strategy can be.

(2) The total delay for all trains.

$$J_1={\displaystyle \sum _i(a_{i,Des}^o-a_{i,Des}^f)}$$

(11)

where $a_{i,Des}^o$ and $a_{i,Des}^f$, respectively, denote the arrival time for train i at its terminal station in obstacle-travel situation and free-travel situation.

4. Case Studies

In this section, numerical experiments on the Beijing-Tianjin intercity high-speed railway are carried out to demonstrate the effectiveness of the proposed strategy. In real-word Chinese HSR operations, the TR-S approach is widely used by dispatchers for it is simple. Adaptively selecting trains’ path is however ignored, thus we choose the TR-S approach as the comparison of the AR-S approach in this paper. In practice, the Beijing-Tianjin HSR is a double-track railway line where each track is bi-directional. Trains on this line have the same speed grade, the maximal velocity for each train is 350 km/h. Figure 9 presents the sketch map of Beijing-Tianjin HSR with the planned traveling time for a normal train in each segment. In practical operations, most high-speed trains on Beijing-Tianjin HSR do not dwell at any intermediate stations, while the other few trains only dwell at Wuqing for 1 min. All trains can switch tracks at each station. According to the real-life operation data, we can set some parameters of the numerical experiments to $H_{i+1,i}^{aa}=H_{i+1,k}^{da}=T=3 \min$.

4.1. Case Study 1

In this experiment, we use aforementioned two rescheduling approaches, i.e., TR-S approach and AR-S approach, to reschedule the first thirty inbound trains and thirty outbound trains on Beijing-Tianjin HSR. Let train i (i = 1, 2, 3, …, 30) be the thirty outbound trains (Beijing → Tianjin) and train k (k = 31, 32, 33, …, 60) be the thirty inbound trains (Tianjin → Beijing). The first train is train 1 and its departure time at starting station is $t_0=0 \min$.

As the approaches mentioned in this paper are specifically applied in the situation where some trains traveling on segment decelerate due to contingencies, therefore, in our numerical experiment, we need to randomly select some trains as decelerating train and make some assumptions reasonably.

Table 3. Assumptions for decelerating trains.

Decelerating Trains	Dsegment	Dmoment	Fixed Train Delay
train 1	Beijing-Yizhuang	3 min	20 min
train 13	Yongle-Wuqing	153 min	19 min
train 23	Beijing-Yizhuang	241 min	10 min
train 27	Yizhuang-Yongle	288 min	26 min

lists the decelerating trains and the corresponding assumptions, where D_moment and D_segment indicate the time when the decelerating train starts to decelerate and the segment where contingencies occur.

Figure 10 and Figure 11, respectively, present the train timetables rescheduled by TR-S approach and AR-S approach under the same conditions. As shown in Figure 10, because of the inflexibility of TR-S approach that allows no train to switch tracks, all the normal trains behind decelerating train 1, 13, 23 and 27 are delayed. Moreover, in Figure 10, we find that shorter departure interval between a decelerating train and its following normal train tends to cause longer conflict train delay in practical train operation.

As shown in Figure 11, outbound trains 2, 24 and 28 choose to use reverse direction track to overtake front decelerating trains. Train 2 successfully avoids conflicts with any other trains. Though the utilization of the reverse direction track of trains 24 and 28 conflicts with trains 23 and 49, which delays train 23 and train 49 by 1 min and 5 min, more total train delay is reduced by AR-S approach compared with TR-S approach. Moreover, train 14 is rescheduled to travel on dedicated track by AR-S approach because the utilization of reverse direction track for train 14 would not reduce the total train delay. Consequently, letting train 14 to travel on dedicated tracks is a better option for it can avoid the operation of switching tracks.

For more detailed comparison of the performance of TR-S approach and AR-S approach, some evaluation criteria values associated with these two approaches are listed in

Table 4. Results and related comparisons for two train rescheduling approaches.

Train Rescheduling Approach/ε	TR-S	AR-S	ε (%)
η	0.667	0.267	60%
J1 (min)	125	95	24%

, where relative error ε ($\epsilon =(V_{AR-P}-V_{TD-P})/V_{TD-P}$) is also given.

From Table 4, we can see that all the performance evaluation criteria of AR-S approach are superior to those of TR-S approach. Especially the suppression rate of conflicts (i.e., η), compared with TR-S approach, the AR-S approach reduces η by 60%. This is because AD-S allows normal trains to overtake front decelerating trains by using reverse direction tracks, which increases the flexibility of the rescheduling strategy.

Moreover, the AR-S approach can reduce the total train delay by 24% in comparison to TR-S approach. In practice, the reduction of total train delay not only improves customer satisfaction with rail services, but also reduces energy consumption in railway operations.

4.2. Case Study 2

In case study 2, all trains that departure from initial station between 10:00 a.m. and 12:00 p.m. are considered. Different from case study 1, more trains are involved, i.e., 58 inbound trains and 60 outbound trains, moreover, the average departure interval is shorter and the total fixed train delay are assumed to be longer. Assumptions for decelerating trains are listed in

Table 5. Assumptions for decelerating trains.

Decelerating Trains	Direction	Dsegment	Dmoment	Fixed Train Delay
C2041	Outbound	Beijing-Yizhuang	313 min	15 min
C2069	Outbound	Beijing-Yizhuang	585 min	20 min
C2085	Outbound	Yongle-Wuqing	774 min	20 min
C2046	Inbound	Wuqing-Yongle	451 min	15 min
C2100	Inbound	Wuqing-Yongle	970 min	24 min

.

As show in Figure 12a, train C2100 decelerates in Wuqing-Yongle segment due to contingencies, causing time delays of the following two trains, i.e., C2102 and C2580. However, in Figure 13a, C2102 is rescheduled to travel on reverse direction track in Wuqing-Yongle segment, which enables C2580 to maintain normal running status because of the relatively large departure interval between C2100 and C2580.

As show in Figure 12b train C2043, C2227 and C2087 are all delayed by front decelerating trains. As presented in Figure 13b, C2043 and C2227 are rescheduled to travel on reverse direction track, which causes time delays of inbound train C2218 and C2588 (see Figure 13a). Train C2087 does not switch tracks according to AR-S approach.

Experimental results in

Table 6. Results and related comparisons for two train rescheduling approaches.

Train Rescheduling Approach/ε	TR-S	AR-S	ε (%)
η	0.691	0.287	58.5%
J1 (min)	159	121	24%

illustrates that AR-S approach can reduce conflict train delay more efficiently in comparison with TR-S approach.

5. Conclusions

In order to reduce the total train delays in the situation some trains suffer sudden deceleration due to contingencies, this paper proposed an adaptive rescheduling approach, denoted by AR-S approach. First, we analyzed the safety constraints that must be met in practical HSR systems. Second, we discussed the total conflict train delays under different path choices. Third, an adaptive rescheduling strategy which allows normal trains to switch tracks to overtake front decelerating trains was developed. A performance evaluation criterion was specifically designed to evaluate train rescheduling approaches. The traditional rescheduling approach, denoted by TR-S approach, which allows no train to switch track was also introduced as a sharp contrast to AR-S approach.

It is known that the reverse direction track is forbidden for any trains due to safety issues in most of current real-world high-speed railways (HSR) systems. With the continuous improvement of railway information system [43], both the safety and reliability of train operation have been improved. For example, the routing plan is much flexible because of the wide application of centralized-train-control (CTC) equipment to HSR systems. The developed AR-S strategy is tested by numerical simulations based on real-world train timetable on Beijing-Tianjin HSR line, which shows a good performance and hopefully be programmed into the CTC equipment in future HSR systems.

This paper only considered the train rescheduling problem among homogeneous trains, thus the developed AR-S strategy is not suitable for the practical operation with heterogeneous trains (e.g., some Europe railway systems). Train priority was also neglected in this paper, which is, however, an involved factor in practical train rescheduling process. Therefore, train priority can be considered in the future research. Moreover, rail freight is an important part of railway transportation, and is important to sustainable traffic [44]. As described in Zunder et al. [45], the utilization of electric traction for freight trains endows a massive advantage, by virtue of the ability to use power generated from clean energy. As freight trains are much slower in comparison with high-speed trains, the developed AR-S strategy can be applied to rescheduling freight trains more efficiently when the line condition is allowable.

Finally, if a normal train is rescheduled to travel on a reverse direction track while the focus track is in maintenance task, traveling time on this track will be prolonged for safety concern, which inspires us that the future research can put emphasis on further analyzing train delays under different circumstances so as to further enhance the feasibility of the proposed approach.