Learning Curve Analysis of Wind Power and Photovoltaics Technology in US: Cost Reduction and the Importance of Research, Development and Demonstration
Abstract
1. Introduction
2. Literature Review
2.1. Learning-Curve and Variable Selection
2.2. Studies on the Learning Curve of US Wind Power and Photovoltaics
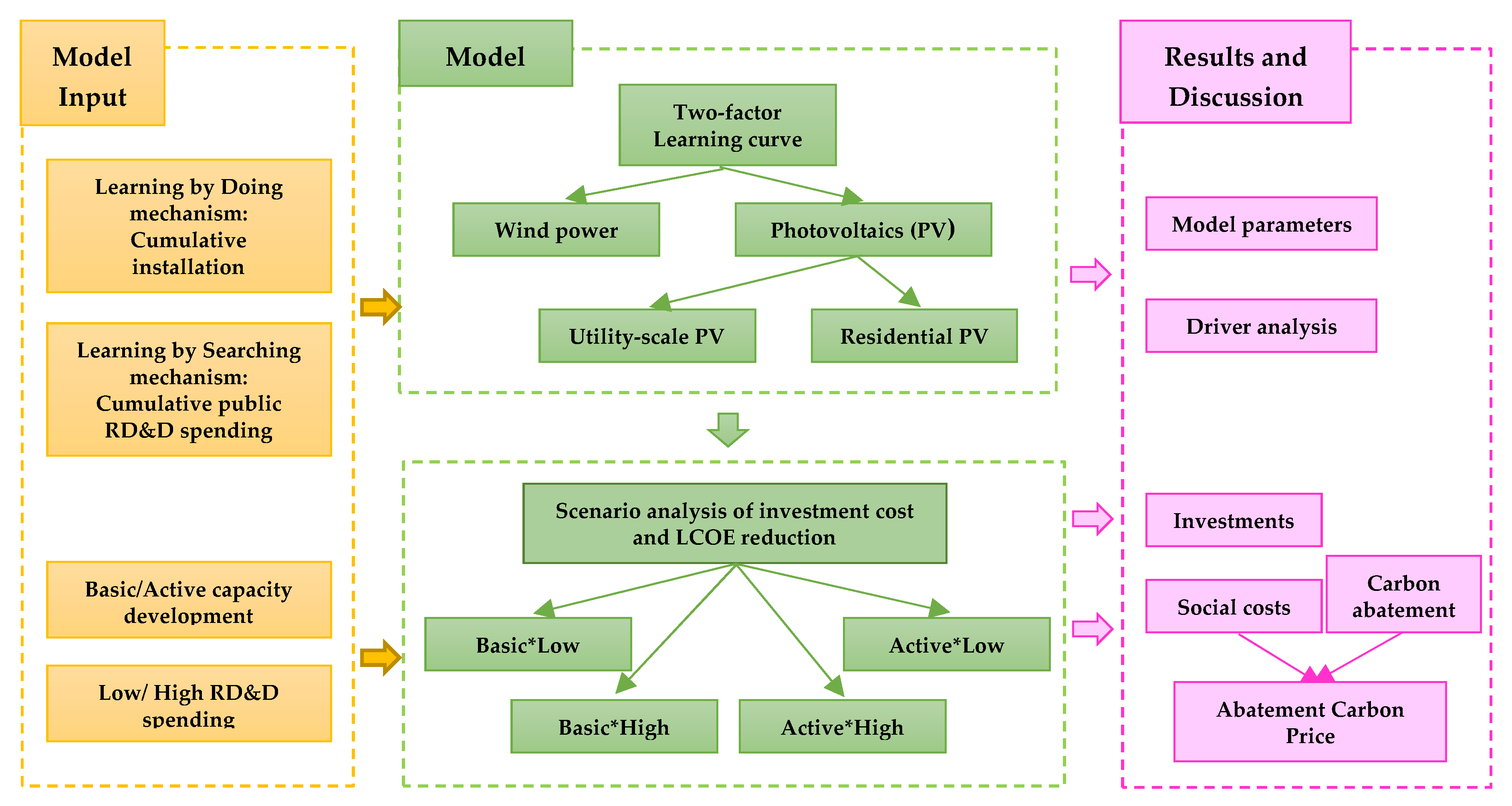
3. Methods
3.1. Learning-Curve and Variable Selection
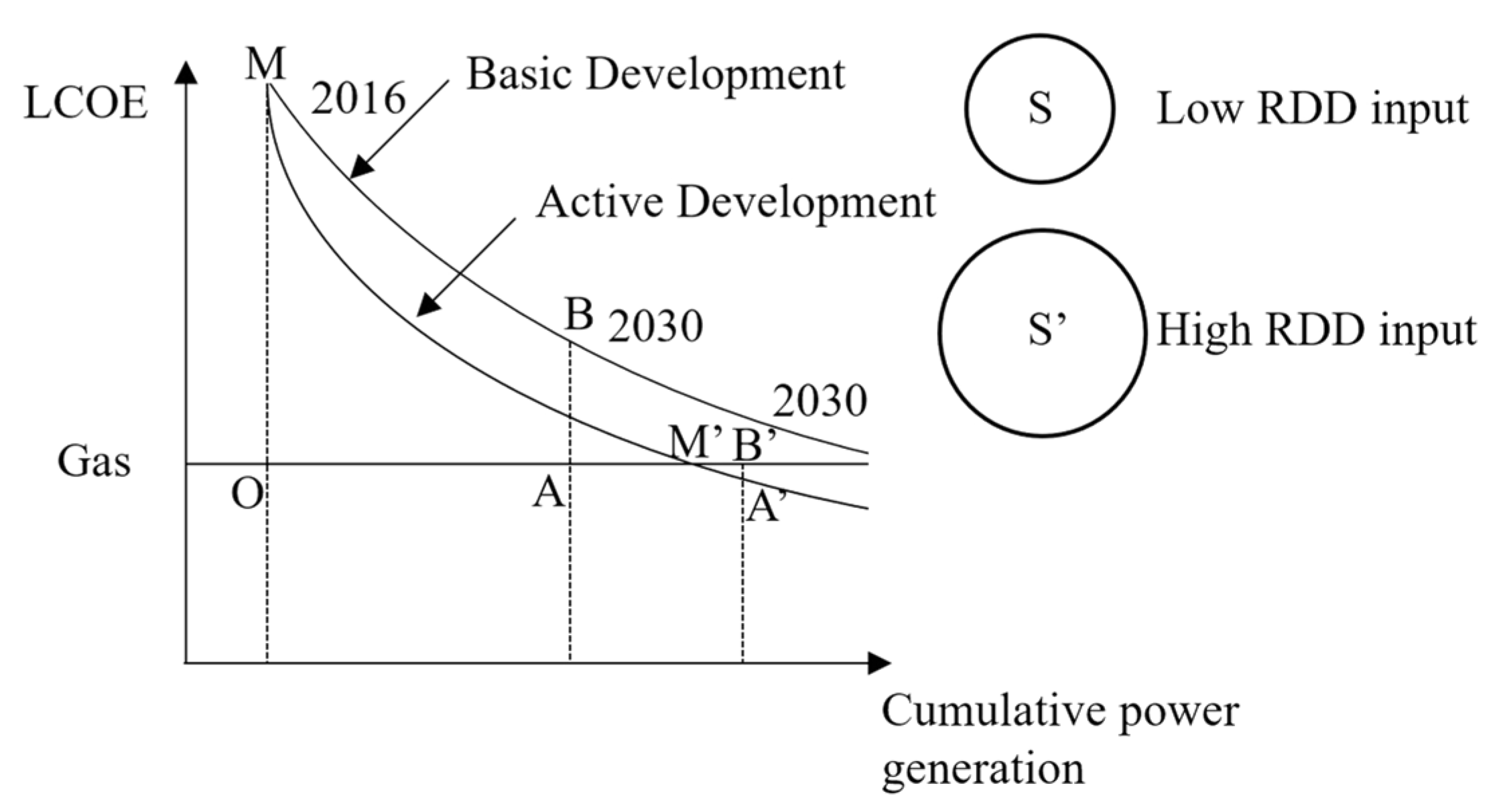
3.2. Scenario Settings
3.3. Levelized Cost of Energy
3.4. Social Costs and Carbon Abatement
4. Results and Discussion
4.1. Learning-Curve Evaluation of Cost Reduction
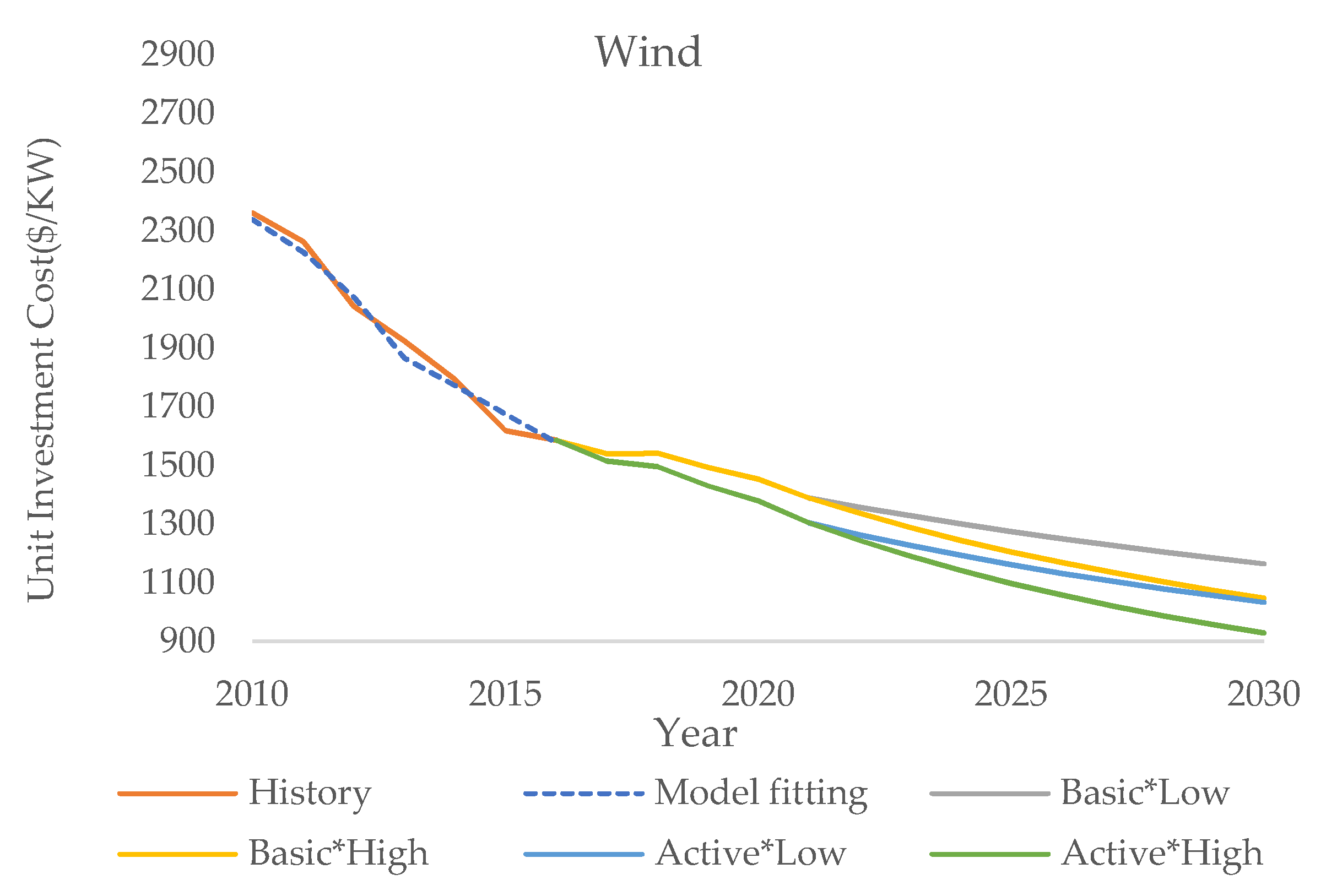
4.1.1. Wind Power
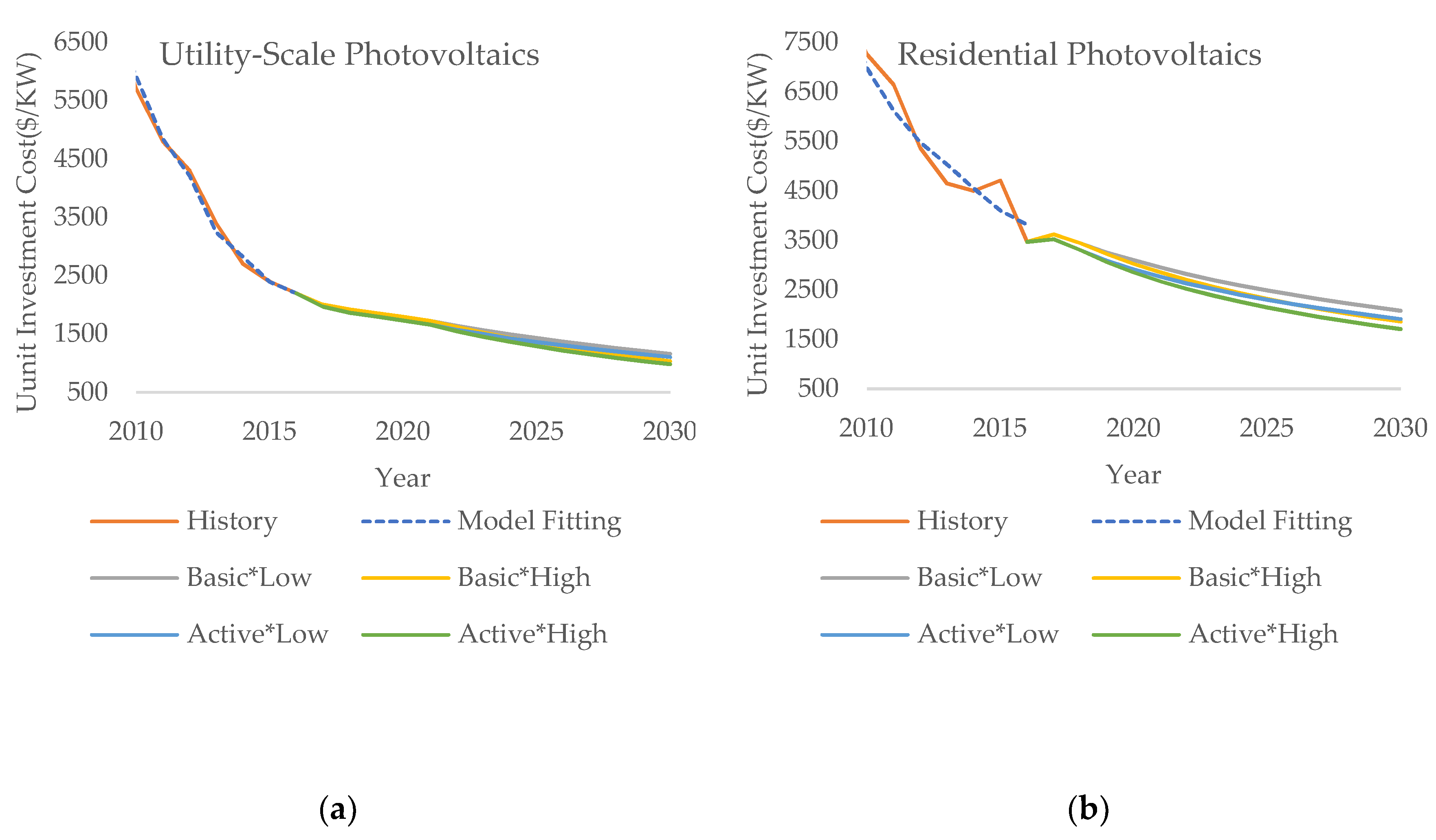
4.1.2. Photovoltaics
4.2. Driver Analysis of Cost Reduction
4.3. Investment-Scale Analysis
4.4. Social Costs and Carbon Abatement
5. Conclusions and Policy Implications
Author Contributions
Funding
Conflicts of Interest
References
- British Petroleum (BP). Statistical Review of World Energy 2018; BP: London, UK, 2018. [Google Scholar]
- National Development and Reform Commission (NDRC) of China. China’s 13th Five-Year Energy Plan; NDRC: Beijing, China, 2016.
- Energy: New Target of 32% from Renewables by 2030 Agreed by MEPs and Ministers. Available online: http://www.europarl.europa.eu/news/en/press-room/20180614IPR05810/energy-new-target-of-32-from-renewables-by-2030-agreed-by-meps-and-ministers (accessed on 18 March 2019).
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. Future Trajectories of Renewable Energy Consumption in the European Union. Resources 2018, 7, 10. [Google Scholar] [CrossRef]
- Mehedintu, A.; Sterpu, M.; Soava, G. Estimation and Forecasts for the Share of Renewable Energy Consumption in Final Energy Consumption by 2020 in the European Union. Sustainability 2018, 10, 1515. [Google Scholar] [CrossRef]
- Falconea, P.M.; Lopolitob, A.; Sica, E. The networking dynamics of the Italian biofuel industry in time of crisis: Finding an effective instrument mix for fostering a sustainable energy transition. Energy Policy 2018, 112, 334–348. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Finance and Investment Database. Available online: http://www.irena.org/financeinvestment (accessed on 10 January 2019).
- International Renewable Energy Agency (IRENA). Renewable Electricity Capacity and Generation Statistics Query Tool. Available online: http://resourceirena.irena.org/gateway/dashboard/?topic=4&subTopic=54 (accessed on 10 January 2019).
- Anadon, L.D.; Gallagher, K.S.; Holdren, J.P. Rescue US energy innovation. Nat. Energy 2017, 2, 760. [Google Scholar] [CrossRef][Green Version]
- Obama Rejects Keystone XL Pipeline. Available online: https://edition.cnn.com/2015/11/06/politics/keystone-xl-pipeline-decision-rejection-kerry/index.html (accessed on 18 March 2019).
- International Energy Agency (IEA). RD&D Database. Available online: http://wds.iea.org/wds/ReportFolders/ReportFolders.aspx?CS_referer=&CS_ChosenLang=en (accessed on 10 January 2019).
- International Energy Agency (IEA). Countries-Key Indicators Database. Available online: https://www.iea.org/statistics/?country=USA&year=2016&category=Key%20indicators&indicator=TPESbySource&mode=chart&categoryBrowse=false&dataTable=INDICATORS&showDataTable=true (accessed on 10 January 2019).
- Department of Energy (DOE). Department of Energy FY 2018 Congressional Budget Request; DOE: Washington, DC, USA, 2017.
- Christiansson, L. Diffusion and Learning Curves of Renewable Energy Technologies; IIASA Working Paper; IIASA: Laxenburg, Austria, 1995; p. WP-95-126. [Google Scholar]
- Loiter, J.M.; Norbergbohm, V. Technology policy and renewable energy: Public roles in the development of new energy technologies. Energy Policy 1999, 27, 85–97. [Google Scholar] [CrossRef]
- Mackay, R.M.; Probert, S.D. Likely market-penetrations of renewable-energy technologies. Appl. Energy 1998, 59, 1–38. [Google Scholar] [CrossRef]
- Cody, G.D.; Tiedje, T. A learning curve approach to projecting cost and performance for photovoltaic technologies. AIP Conf. Proc. 1997, 404, 45. [Google Scholar] [CrossRef]
- Wene, C.-O. Experience Curves for Energy Technology Policy; OECD/IEA: Paris, France, 2000. [Google Scholar]
- Bolinger, M.; Wiser, R. Understanding wind turbine price trends in the US over the past decade. Energy Policy 2012, 42, 628–641. [Google Scholar] [CrossRef]
- Kobos, P.H.; Erickson, J.D.; Drennen, T.E. Technological learning and renewable energy costs: Implications for US renewable energy policy. Energy Policy 2006, 34, 1645–1658. [Google Scholar] [CrossRef]
- Rubin, E.S.; Azevedo, I.M.L.; Jaramillo, P.; Yehb, S. A review of learning rates for electricity supply technologies. Energy Policy 2015, 86, 198–218. [Google Scholar] [CrossRef]
- Wright, T.P. Factors Affecting the Cost of Airplane. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Boston Consulting Group (BCG). Perspectives on Experience; BCG: Boston, MA, USA, 1968. [Google Scholar]
- Niu, Y.L.; Huang, R.B.; Chang, H.B. The change of energy technology cost based on learning curve. J. Ind. Eng. Eng. Manag. 2013, 27, 74–80. [Google Scholar] [CrossRef]
- Papineau, M. An economic perspective on experience curves and dynamic economies in renewable energy technologies. Energy Policy 2006, 34, 422–432. [Google Scholar] [CrossRef]
- Jamasb, T. Technical Change Theory and Learning Curves: Patterns of Progress in Electricity Generation Technologies. Energy J. 2007, 28, 51–71. [Google Scholar] [CrossRef]
- Yelle, L.E. The Learning Curve: Historical Review and Comprehensive Survey. Decis. Sci. 2010, 10, 302–328. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, J.; Wang, J. Learning of Power Technologies in China: Staged Dynamic Two-Factor Modeling. Sustainability 2017, 9, 861. [Google Scholar] [CrossRef]
- Wei, M.; Smith, S.J.; Sohn, M.D. Non-constant learning rates in retrospective experience curve analyses and their correlation to deployment programs. Energy Policy 2017, 107, 356–369. [Google Scholar] [CrossRef]
- Zeng, M.; Lu, W.; Duan, J.H.; Li, N. Study on the cost of solar photovoltaic power generation using double-factors learning curve model. Mod. Electr. Power 2012, 29, 72–76. [Google Scholar] [CrossRef]
- Huo, M.L. Transnational research on the driving mechanism of photovoltaic power generation cost reduction. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. [Google Scholar]
- Song, D.; He, Y. Study on Cost of Wind Power Generation Based on Double-factors Learning Curve. Northeast Electr. Power Technol. 2017, 9, 1. [Google Scholar] [CrossRef]
- Li, P.Y.; Sun, S. Analysis of cost of the Photovoltaic Industry in Northwest China based on Learning Curve. Energy Conserv. Technol. 2017, 35, 469–474. [Google Scholar] [CrossRef]
- Zhu, Y.C.; Lin, L.; Xu, J.J.; Zhao, D.M. Analysis of wind power cost based on learning curve. Power Demand Side Manag. 2012, 14, 11–13. [Google Scholar] [CrossRef]
- Hong, S.; Chung, Y.; Woo, C. Scenario analysis for estimating the learning rate of photovoltaic power generation based on learning curve theory in South Korea. Energy 2015, 79, 80–89. [Google Scholar] [CrossRef]
- Arrow, K.J. The Economic Implications of Learning by Doing. Rev. Econ. Stud. 1962, 29, 155–173. [Google Scholar] [CrossRef]
- Li, G.; Rajagopalan, S. A learning curve model with knowledge depreciation. Eur. J. Oper. Res. 1998, 105, 143–154. [Google Scholar] [CrossRef]
- Barreto, L.; Kypreos, S. Endogenizing R and D and market experience in the “bottom-up” energy-systems ERIS model. Technovation 2004, 24, 615–629. [Google Scholar] [CrossRef]
- Miketa, A.; Schrattenholzer, L. Experiments with a methodology to model the role of R and D expenditures in energy technology learning processes; first results. Energy Policy 2004, 32, 1679–1692. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2017; IRENA: Abu Dhabi, UAE, 2018. [Google Scholar]
- Ibenholt, K. Explaining learning curves for wind power. Energy Policy 2002, 30, 1181–1189. [Google Scholar] [CrossRef]
- Trappey, A.J.C.; Trappey, C.V.; Liu, P.H.Y.; Lin, L.C.; Ou, J.J.R. A hierarchical cost learning model for developing wind energy infrastructures. Int. J. Prod. Econ. 2013, 146, 386–391. [Google Scholar] [CrossRef]
- S. 3234—93rd Congress: Solar Energy Research Act. Available online: https://www.govtrack.us/congress/bills/93/s3234 (accessed on 18 March 2019).
- The International Energy Agency (IEA). IEA Guide to Reporting Energy RD&D Budget/Expenditure Statistics; IEA: Paris, France, 2011. [Google Scholar]
- Lawrence Berkeley National Laboratory. 2016 Wind Technologies Market Report; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2017.
- Barbose, G.; Darghouth, N.; Millstein, D. Tracking the Sun 10: The Installed Price of Residential and Non-Residential Photovoltaic Systems in the United States; DOE: Washington, DC, USA, 2017.
- US Energy Information Administration (EIA). Annual Energy Outlook 2018; EIA: Washington, DC, USA, 2018.
- National Renewable Energy Laboratory (NREL). Enabling the SMART Wind Power Plant of the Future through Science-Based Innovation; NREL: Denver, CO, USA, 2017.
- International Renewable Energy Agency (IRENA). Summer of Solar. Available online: https://www.irena.org/-/media/Images/IRENA/Infographics/irena_summer-of-solar_27731007612_o.jpg (accessed on 10 March 2019).
- Ueckerdt, F.; Hirth, L.; Luderer, G.; Edenhofer, O. System LCOE: What are the costs of variable renewables? Energy 2013, 63, 61–75. [Google Scholar] [CrossRef]
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2013, 15, 4470–4482. [Google Scholar] [CrossRef]
- Hernández-Moro, J.; Martínez-Duart, J.M. Analytical model for solar PV and CSP electricity costs: Present LCOE values and their future evolution. Renew. Sustain. Energy Rev. 2013, 20, 119–132. [Google Scholar] [CrossRef]
- Office of Indian Energy. Levelized Cost of Energy (LCOE); DOE: Washington, DC, USA, 2015.
- US Energy Information Administration (EIA). Electric Power Monthly with Data for November 2018; EIA: Washington, DC, USA, 2019.
- National Renewable Energy Laboratory (NREL). 2018 Annual Technology Baseline (ATB); NREL: Denver, CO, USA, 2018.
- Wiser, R.H.; Bolinger, M. 2016 Wind Technologies Market Report; DOE: Washington, DC, USA, 2017.
- Lazard. Lazard Levelized Cost of Energy Version 11.0; Lazard: New York, NY, USA, 2017. [Google Scholar]
- Jonathan, L.R. U.S. Carbon Dioxide Emissions in the Electricity Sector Factors, Trends, and Projections; Congressional Research Service (CRS): Washington, DC, USA, 2019.
- Wind Energy Technologies Office. Wind Vision: A New Era for Wind Power in the United States; DOE: Washington, DC, USA, 2015.
- Advanced Energy Initiative. Available online: https://georgewbush-whitehouse.archives.gov/stateoftheunion/2006/energy/index.html (accessed on 18 March 2019).
- SunShot 2030. Available online: https://www.energy.gov/eere/solar/sunshot-2030 (accessed on 18 March 2019).
- The Regional Greenhouse Gas Initiative (RGGI). Allowance Prices and Volumes Database. Available online: https://www.rggi.org/Auctions/Auction-Results/Prices-Volumes (accessed on 10 March 2019).
- California Carbon Dashboard. Available online: http://calcarbondash.org/ (accessed on 10 March 2019).
- Sutter, K.R.; Morehouse, E.; Sullivan, K.; Sean, D. CALIFORNIA: An. Emissions Trading Case Study; Environmental Defense Fund (EDF): Sacramento, CA, USA; Climate Challenges Market Solutions (LETA): Toronto, ON, Canada, 2018. [Google Scholar]
- Mazzucato, M. From Market. Fixing to Market-Creating: A New Framework for Economic Policy; Science Policy Research Unit (SPRU): Falmer, UK, 2015. [Google Scholar]
- Falconea, P.M.; Moroneb, P.; Sica, E. Greening of the financial system and fuelling a sustainability transition A discursive approach to assess landscape pressures on the Italian financial system. Technol. Forecast. Soc. 2018, 127, 23–37. [Google Scholar] [CrossRef]
| Model | Learning Mechanism | Equation | Explanatory Variables |
|---|---|---|---|
| One-Factor | Learning-by-doing | Cumulative production | |
| Two-Factor | Learning-by-doing Learning-by-searching | Cumulative production, knowledge stock | |
| Three-Factor | Learning-by-doing Learning-by-searching Learning-by-using | Cumulative production, knowledge stock, average scale |
| Wind Power | PV | |
|---|---|---|
| Cost | Unit investment cost | Unit investment cost |
| Source | Lawrence Berkeley national laboratory report [45] | Tracking the Sun report [46] |
| Cumulative production | Cumulative installed capacity | Cumulative installed capacity |
| Source | IRENA renewable-energy database [8] | |
| Knowledge stock | Cumulative wind-power public RD&D spending | Cumulative photovoltaic (PV) public RD&D spending |
| Source | International Energy Agency (IEA) RD&D database [11] | |
| Wind | Utility Photovoltaic | Residential Photovoltaic | ||
|---|---|---|---|---|
| Production Experience | Learning-by-doing elasticity | −0.278 | −0.101 | −0.166 |
| Learning-by-doing ratio (LDR) | 17.53% | 6.78% | 10.86% | |
| p-value | 0.009 | 0.005 | 0.100 | |
| Knowledge stock | Learning-by-searching elasticity | −0.670 | −2.012 | −1.544 |
| Learning-by-searching ratio (LSR) | 37.13% | 75.21% | 65.70% | |
| p-value | 0.009 | 0.001 | 0.038 | |
| Time lag (g) | 4 | 4 | 1 | |
| Depreciation factor (ρ) | 0.025 | 0.000 | 0.000 | |
| Adj. R2 | 0.974 | 0.993 | 0.949 | |
| DW | 2.442 | 2.462 | 2.279 | |
| VIF | 4.079 | 6.946 | 8.734 | |
| Constant | 15.388 | 25.768 | 22.879 | |
| $Billion | Basic*Low | Basic*High | Active*Low | Active*High |
|---|---|---|---|---|
| Wind | 64.1 | 61.7 | 146.5 | 141.2 |
| Utility-Scale Photovoltaic | 132.0 | 127.4 | 231.2 | 223.1 |
| Residential Photovoltaic | 63.8 | 60.8 | 110.8 | 105.6 |
| Wind | Utility Photovoltaic | Residential Photovoltaic | ||
|---|---|---|---|---|
| Social Costs ($million) | Basic*Low | 437 | 36,614 | 37,282 |
| Basic*High | −63 | 35,270 | 35,835 | |
| Active*Low | −6754 | 59,335 | 64,239 | |
| Active*High | −8315 | 56,731 | 63,372 | |
| Carbon Abatement (million t) | Basic | 567 | 726 | 146 |
| Active | 1394 | 1,324 | 271 | |
| Abatement Carbon Price ($/t) | Basic*Low | 0.77 | 50.45 | 255.09 |
| Basic*High | −0.11 | 48.6 | 245.19 | |
| Active*Low | −4.84 | 44.82 | 237.06 | |
| Active*High | −5.96 | 42.85 | 233.86 |
| Wind | Utility-Scale Photovoltaic | Residential Photovoltaic | ||
|---|---|---|---|---|
| Reference | −2.54 | 46.68 | 242.80 | |
| Cumulative Capacity | −10% | −0.98 | 47.87 | 244.57 |
| +10% | −3.82 | 45.61 | 240.88 | |
| Depreciable Life | 15 years | 9.52 | 67.35 | 291.20 |
| 25 years | −9.19 | 35.28 | 216.10 | |
| Capacity Factor | −10% | 8.37 | 64.18 | 280.89 |
| 10% | −11.24 | 32.74 | 211.63 | |
| Operating and Maintenance (O&M) Costs | −10% | −4.30 | 45.44 | 239.91 |
| 10% | −0.77 | 47.92 | 245.68 | |
| Gas-fired plant Levelized Cost of Energy (LCOE) | −10% | 7.41 | 56.74 | 252.80 |
| 10% | −12.49 | 36.61 | 232.80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Gu, A. Learning Curve Analysis of Wind Power and Photovoltaics Technology in US: Cost Reduction and the Importance of Research, Development and Demonstration. Sustainability 2019, 11, 2310. https://doi.org/10.3390/su11082310
Zhou Y, Gu A. Learning Curve Analysis of Wind Power and Photovoltaics Technology in US: Cost Reduction and the Importance of Research, Development and Demonstration. Sustainability. 2019; 11(8):2310. https://doi.org/10.3390/su11082310
Chicago/Turabian StyleZhou, Yi, and Alun Gu. 2019. "Learning Curve Analysis of Wind Power and Photovoltaics Technology in US: Cost Reduction and the Importance of Research, Development and Demonstration" Sustainability 11, no. 8: 2310. https://doi.org/10.3390/su11082310
APA StyleZhou, Y., & Gu, A. (2019). Learning Curve Analysis of Wind Power and Photovoltaics Technology in US: Cost Reduction and the Importance of Research, Development and Demonstration. Sustainability, 11(8), 2310. https://doi.org/10.3390/su11082310




