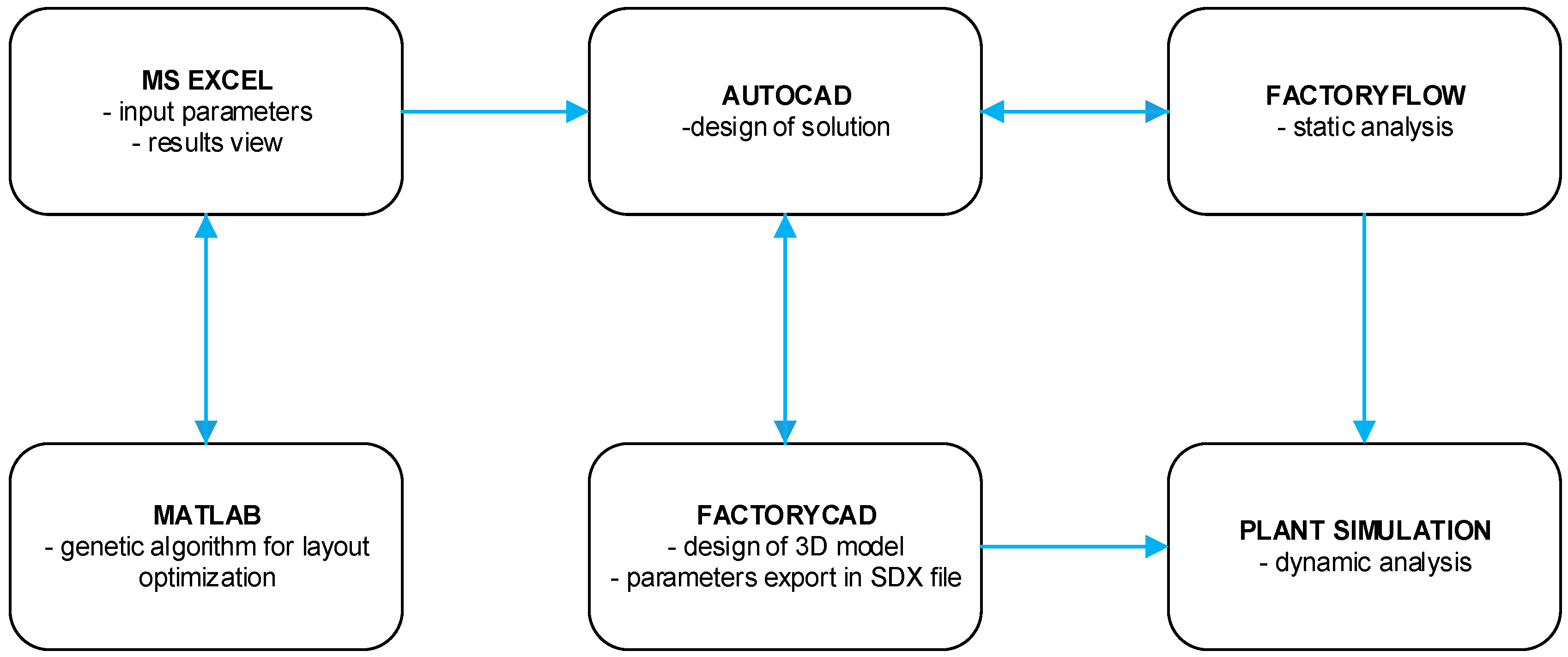
3.2.2. Genetic Algorithm for Layout Optimization and Its Basic Parameter Setting
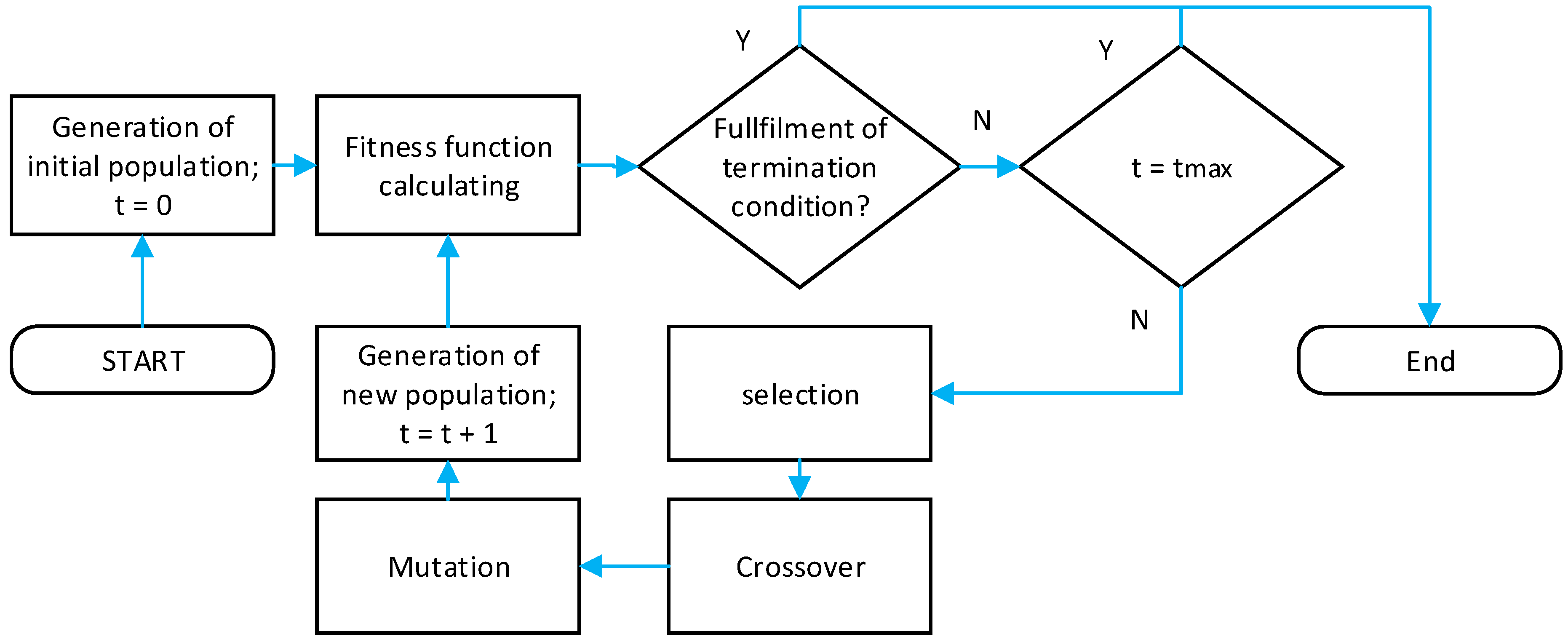
After specification of all input data, our own optimization of space arrangement follows with the help of a genetic algorithm. The basic parts of the GA core as shown in
Figure 5 will be explained in the following text.
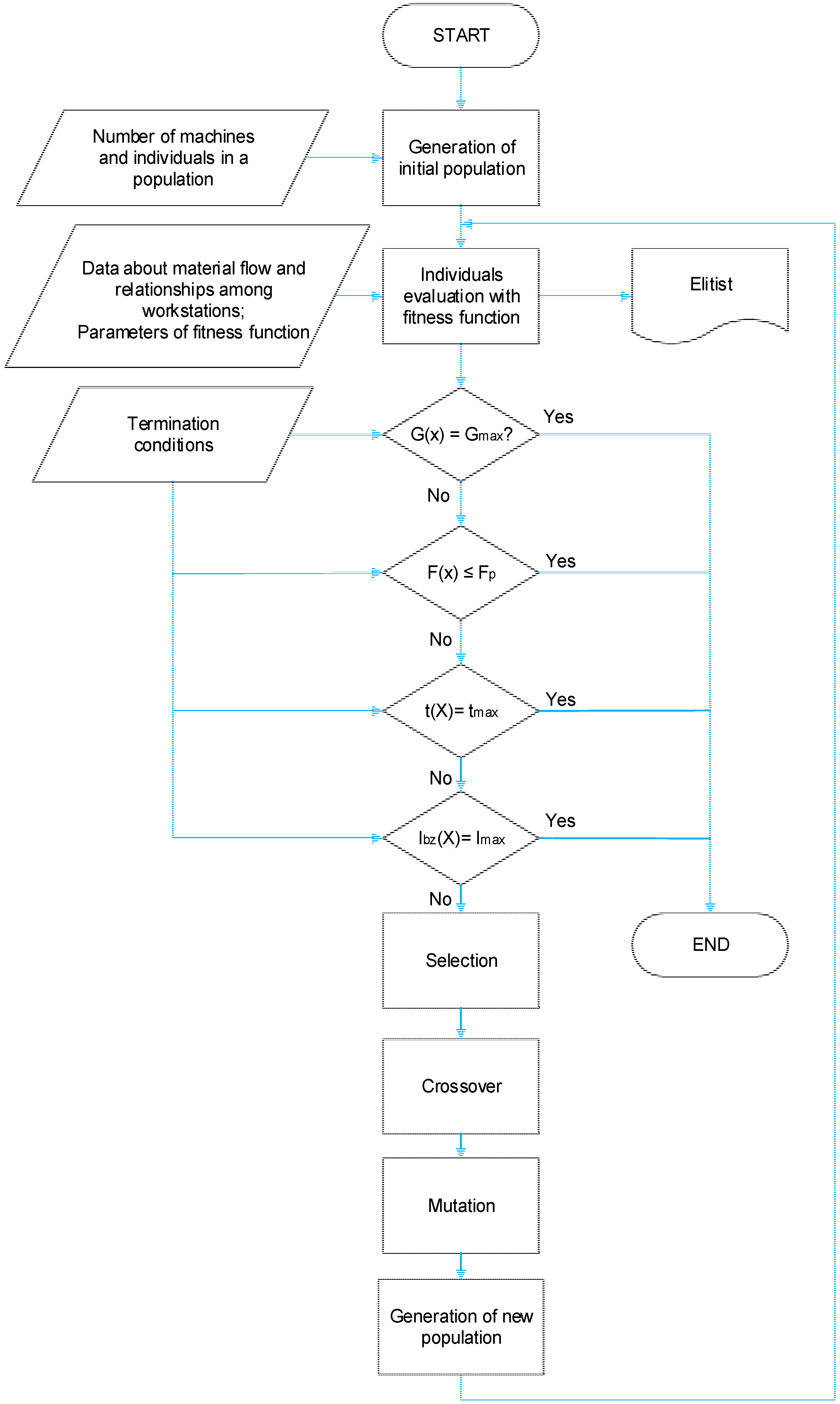
1. Generation of an initial population
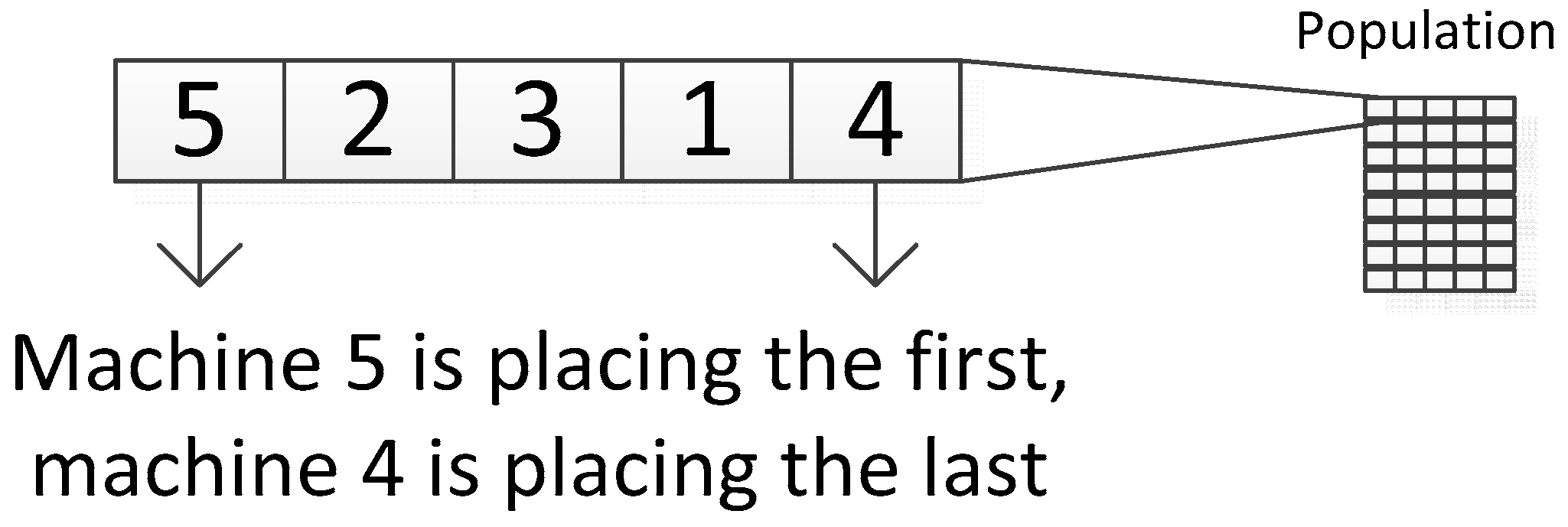
The first step is to create a population that represents a group of solutions which will be further developed. In this solution, an individual is created by genes in the quantity that is equivalent to the value of placed machines. These can have a value of 1 up to n, where n is equal to the number of deployed machines. A sequence of individual genes corresponds with a sequence of where machines will be placed in the proposal. Next, there is one gene in each individual reserved for a pattern definition by which workplaces will be included in the proposal as it shows
Figure 6.
The total matrix dimension corresponding to a population in one generation [
20] is, therefore, the number of individuals in a generation * (number of placed machines + 1).
2. Individual evaluation of fitness function
After having created a population, it is necessary to evaluate a fitness function. The resulting fitness function was designed as a sum of two components with verified weight. Verification was done according to the intensity of material flow and distance (fID) and according to relations and distance (fV).
Equation (1)—Evaluation according to the intensity and distance [
19]:
where n = number of placed machines; D = right-angle distance between workplaces
; I = intensity between workplaces i and j.
See note: Right angle distance was chosen for the distance evaluation of a closer real state rather than straightforward distance.
Equations (2) and (3)—Evaluation according to relations and distance [
21]:
where n = number of placed machines; D = right angle distance between workplaces i–j
; V = evaluation coefficient of a relation between workplaces i and j (A,E,I,O,U,X).
Equation (4)—Final fitness function value is set as:
where α = ratio coefficient of partial fitness functions (α ∈<0;1>)
Various restrictions are checked in layout construction and the algorithm itself:
Verification if each object is not mutually overlapping;
Verification of placed objects in a defined space (dimensions of a production hall);
Verification of the production hall height restriction;
Verification of a production hall’s height restriction;
Verification of restrictions regarding transport street arrangement in the production hall;
Verification of restrictions regarding the definition of the selected object’s fixed position in a production hall.
After evaluating all individuals by a fitness function, the best solution is identified and saved in a given generation—an elite individual with his or her reached value and the average value of the fitness population. This data could be displayed during algorithm operation after each generation, to track solution progress. After completion, it is also possible to display a progress graph of average and elite fitness values.
3. Decision-making blocks
In this step, it is necessary to compare specific conditions for algorithm termination in four decision-making blocks. The first condition is to reach the maximum number of generation (iteration) Gmax. The second condition is to reach or exceed the highest permissible fitness value fp. The third condition is to reach maximum solution time tmax. The last condition is to exceed set iteration number (Imax) without improving a reached solution.
The last condition was integrated into the proposal to prevent extensive calculation time if the required or unachievable fitness function value fp is not set and fitness function value is not improving. Therefore, there is an assumption, that the extreme has been found in a group of solutions.
When meeting any out of four stated conditions, the genetic algorithm is completed.
4. Selection
In case none of the finishing criteria was fulfilled, the algorithm continues by selection, in other words, by selecting individuals who will crossbreed and eventually mutate between each other. For such a solution, the roulette rule was selected. Probability selection was proportional to an individual’s achieved suitability. This form was chosen based on a better possibility to search a complex set of solutions when later combining parents and their evaluation as well as their calculation speed [
3].
To prevent early convergence, suitability of individuals was integrated into the algorithm via the help of sigma scaling. The average expected number of generated offsprings with sigma scaling is p
(i,g) from an individual
i in generation
g given as Equation (5):
where
f(i,g) = fitness i of an individual in generation g;
f(g) = average population fitness in generation
g;
kš = coefficient for sigma scaling;
σ(g) = determinant population deviation in generation
g.
For a sigma scaling coefficient ks = 1, an individual rated by the suitability of its standard deviation being closer to a required extreme as the average population suitability will on average produce two offsprings for a new population. The higher the value ks, the lower the selective pressure.
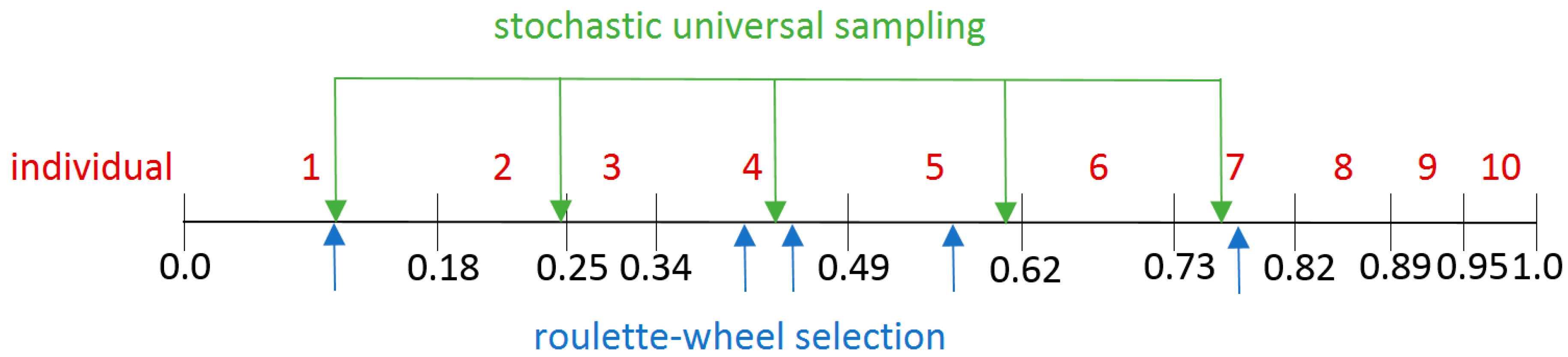
After remapping, it is possible to select a choice of parents (
Figure 7) either by the classical roulette mechanism (generation of random numbers) or by stochastic universal sampling (they are generated uniformly spread indicators that will choose parents in one iteration).
After selecting, pairing follows, where Parent 1 and Parent 2 will be randomly selected from chosen individuals. These should make Offspring 1 and 2.
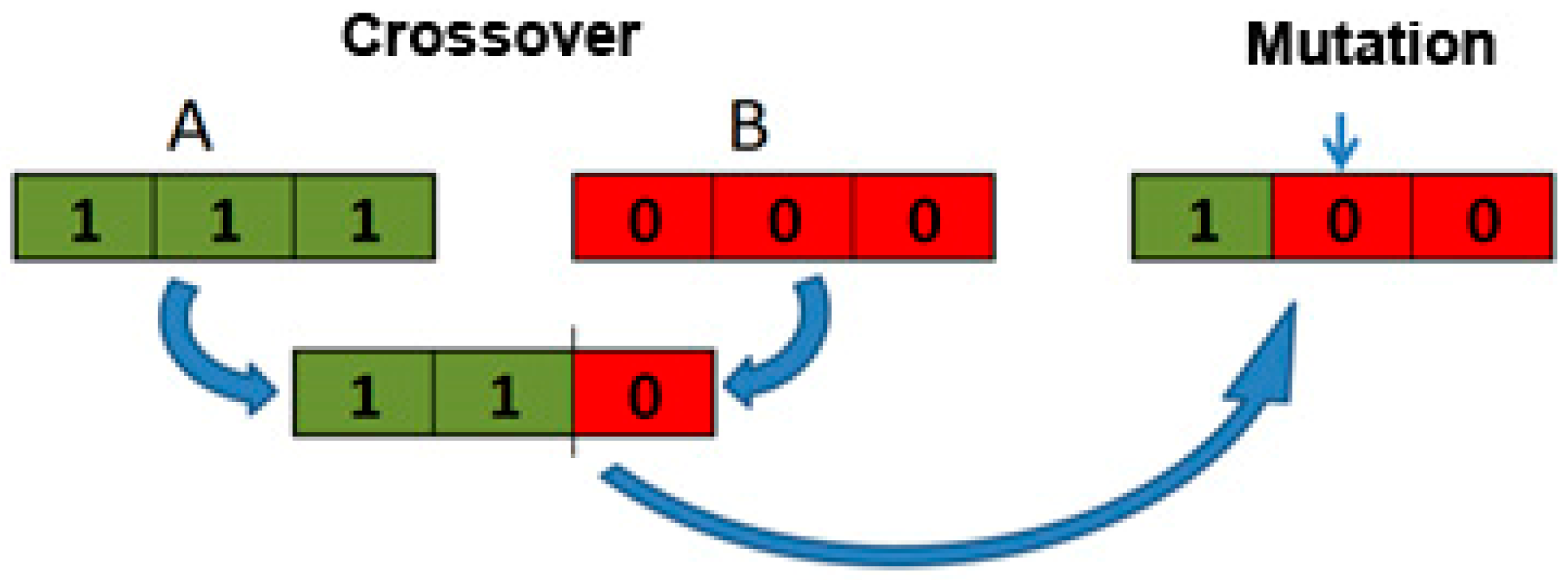
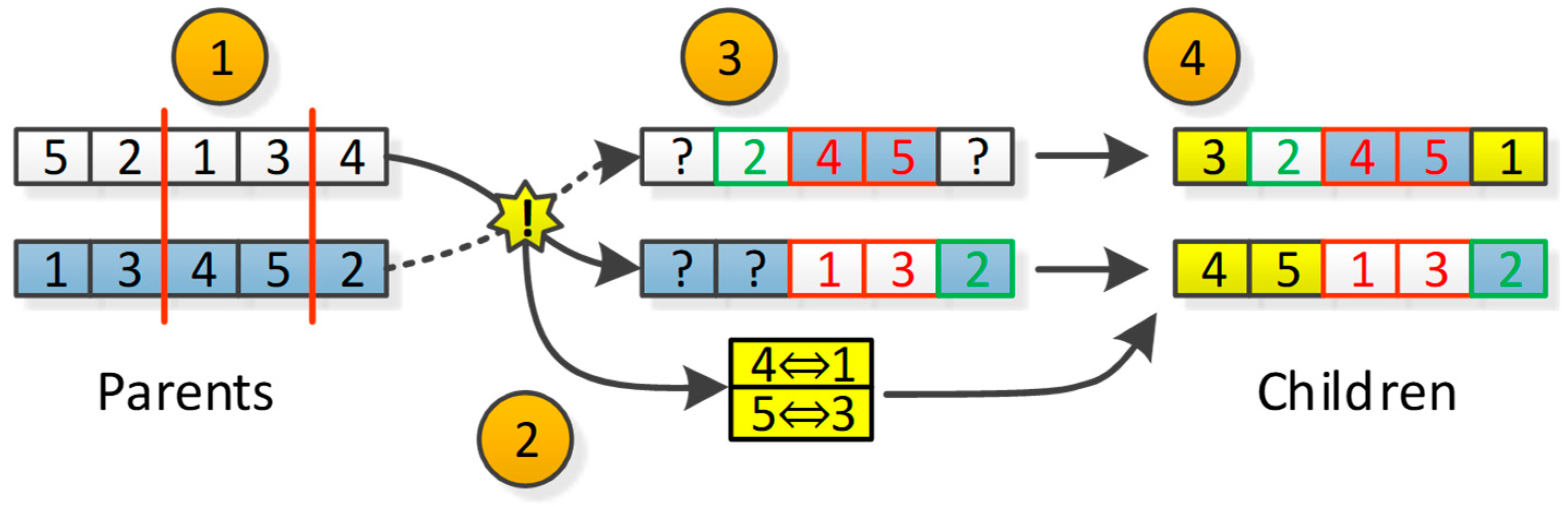
5. Crossover
To prevent a duplicate of identical machines in crossover or omission of the same machines from the genetic chain, a mechanism of partially matched crossover was designed. This type of crossover has within its procedure implemented measures. This guarantee that each coded solution will have its machine only once [
21].
A procedure of partially matched crossover (
Figure 8) is as follows:
Generation of two random points delimiting genes, parents will mutually exchange.
Pairing of gene values that have been exchanged.
Adding parent values to genes where conflicts do not occur.
Use of paired values for conflict genes.
It is also necessary to set the crossover’s probability and to determine an optimal value range of probability. A series of experiments were carried out. There were two case studies, and the only changed parameter was the probability of crossover. [
22] Mutation was switched off and the finishing criterion was set to reach 200 generations. The fitness function and generation value were reached through closely observed parameters. In Experiment 1, 20 machines were placed into a layout, and in Experiment 2, 28 machines were placed. Results of experiments can be seen in
Table 1 and
Table 2.
The optimal crossover probability was set in the range from 75% to 95%, based on a series of experiments. The probability of 100% was not taken into consideration because it was possible for the small part of the previous population to survive.
6. Mutation
After the crossover, mutation follows. The heuristic insert mutation was adopted to better ensure population diversity and individual qualities after mutation as well as satisfy the process constraints. [
18] However, in this type of solution encoding, traditional mutation or in other words value change of a random gene, is out of the question. This would automatically require remedial measures to eliminate duplication or not classified machines. That is why mutation via the help of inversion or exchange was selected in
Figure 9. Due to inversion of a rather big intervention into solution, the probability was divided for exchange or inversion in 80:20 ratio.
Furthermore, it was necessary to set the probability in mutation and the majority of resources state range, depending on the type of problem, from 0.1% to 5%. However, in applications for object arrangement, some resources state probability values of up to 20% [
23]. Due to this, the optimal probability ratio of mutation for this specific problem was selected similarly as in crossover. The set of experiments for the same initial conditions (Experiment 1—20 machines, Experiment 2—28 machines) as was the case for selecting optimal crossover probability values were carried out. However, the difference was the mutation probability, which was substituted. In the experiments, crossover probability was set to a constant value of 0.85. The results of the experiments are stated in
Table 3 and
Table 4.
The results of experiments state that with low probability mutation, functioning converges later as it is mainly dependent on randomly generated initial population and crossbreeding in all iterations. Only a small number of individuals is modified by mutation operators. With increasing mutation probability, race converges on average earlier with a higher quality solution, although it is accompanied by a higher generation dispersion of a found solution. This is caused by mutation randomness. The optimal value probability range of mutation was set between 0.05 and 0.15. As we want to avoid the algorithm going into a random search, we do not recommend higher probabilities of initial settings.
One of the conditions of algorithm functioning termination is crossing the fixed number of iterations (Imax) without improving the reached solution. In case the extreme has been achieved, it is advised to verify if it is only a local extreme. To verify this, the variable mutation was implemented in the algorithm. This variable mutation increases the probability of its application with an increasing number of interactions, without any improvement. In the basic setting—when functioning finishes after 100 interactions without any improvement, after 70 iterations (Ibz = 70), there is a mutation probability increased to 1.5 multiple of the original value. After 80 iterations it is 1.875 multiple of the original value, and eventually, after 90 iterations, it is totally 2.34 multiple of the original value. If there is a different setting for the number of iterations without any improvement, Imax is the variable probability of mutation proportionally recalculated.
7. Making of a new generation
Following the genetic operator activity, parents are replaced by offsprings. In case elitism is used in suitability evaluation and the best possible solution has been saved, this individual replaces one of the offsprings with the worst suitability.
After this step, the algorithm goes back to evaluating new individuals through the help of the fitness function. Furthermore, the algorithm keeps repeating in cycles until one of the finishing conditions is fulfilled in
Figure 6.
8. Genetic algorithm finishing
In decision-making blocks, each genetic algorithm cycle checks whether one of the finishing conditions has not been fulfilled: achieving the maximum number of generations (iterations); achieving or exceeding the highest permissible fitness value; achieving the maximum solution time; exceeding the set number of iterations without improvement.
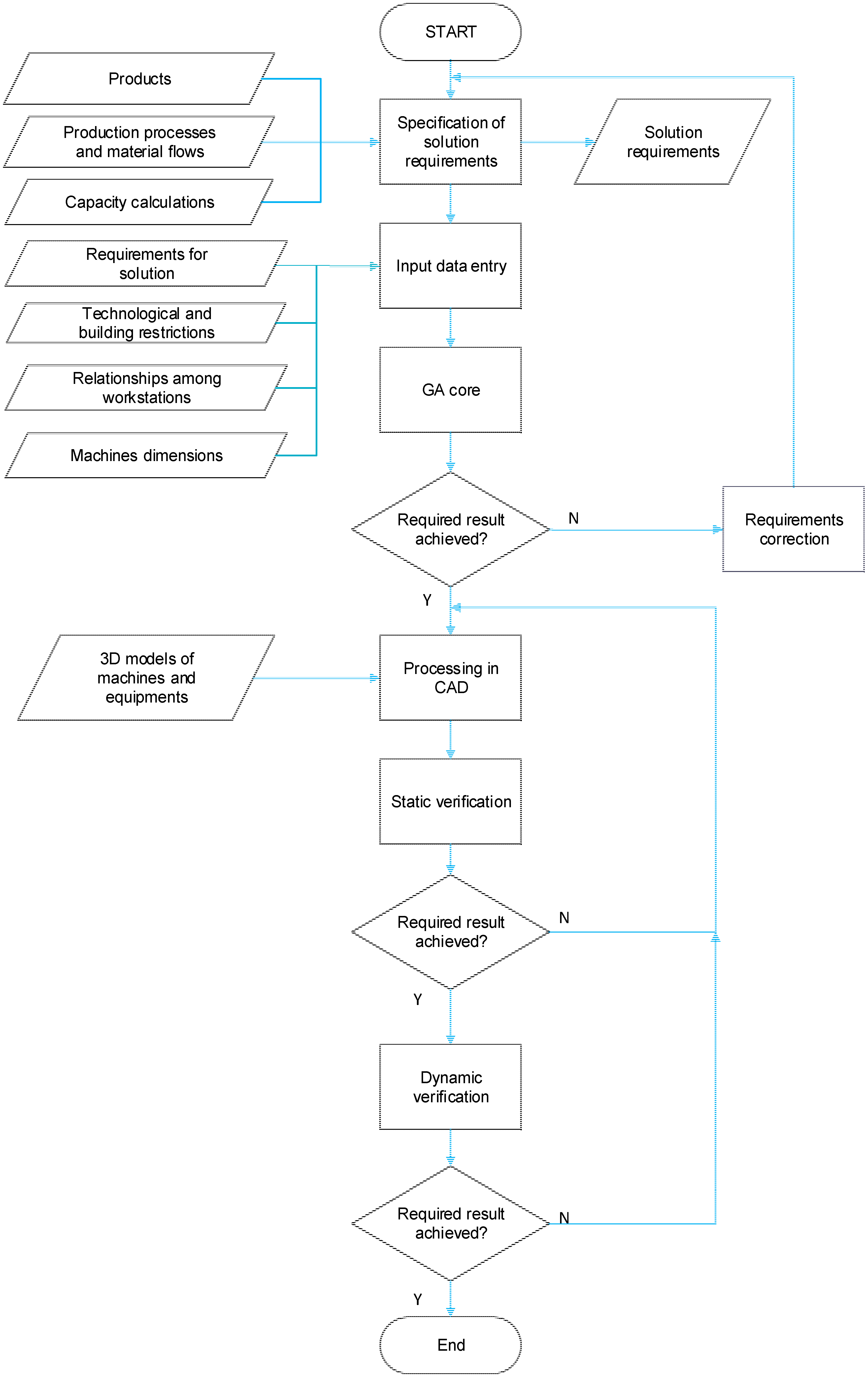
If some of the finishing conditions were fulfilled, the activity of a genetic algorithm will finish. After completion of its activities, there are generated outputs in the user interface (
Figure 10): block layout; achieved fitness value and information in which iteration it was achieved; graph showing the progress of average and elite fitness population values.
In the final phase, the user will decide whether the solution proposed by the genetic algorithm fulfilled all its requirements. If not, it is necessary to closely specify requirements and repeat the generation of an optimal layout. If requirements were fulfilled, the methodology continues by the result of processing in a CAD system.
3.2.3. Experimental Verification of Genetic Algorithm and Result Compared with the Use of Classical Heuristic
To check the functionality of the proposed GALP algorithm (Genetic Algorithm Layout Planner) a series of experiments were carried out. These results were then compared with optimization results with the help of heuristic according to Murat (sequence–pair approach). Heuristic according to Murat has been selected because it is believed the heuristic approach is implemented in Factory PLAN/OPT module, which is a part of Factory Design and Optimization package from Siemens Tecnomatix. The final PLAN/OPT and genetic GALP algorithm proposals were subsequently compared in FactoryFLOW software.
A common characteristic for both algorithms is the block layout output. Both algorithms require a finishing requirement and total time of algorithm functioning. For more complex result comparison, experiments were carried out for 1.5, 10, and 20 min.
Our own experiments were carried out for two types of inputs. Our own experiments were carried out for two types of inputs. In Case 1 a simple manufacturing system that represents a small manufacturing system was generated. This system contains three product families (each of the family has minimum of eight process steps) and 24 workplaces. The number of workplaces was determined based on the planned annual production volume of product families. In Case 2 a complex manufacturing system with nine product families and 60 workplaces. This system represents a large manufacturing system in practice. Of course, there are also much larger manufacturing systems in practice, howe;ver, these systems can be segmented into smaller, mutually independent production groups, based on the classification of the manufactured products.
Evaluation of the application results of the classic heuristics and the GALP algorithm was made on the calculation basis of three basic material flow parameters, which are automatically calculated by Tecnomatix FactoryFLOW software. The first parameter is distance. This parameter determines the total amount of distance traveled in the production layout when considering the right-hand distances and the total number of journeys between different twin of workstations. The second parameter is the cost. This parameter determines the total transport costs on the basis of total distance traveled, the type of transport equipment, and the fixed and variable rates of transport costs. The third parameter, time, specifies total shipment time based on the known distance traveled, the type of transport equipment, defined transport cycle structure (i.e., load–drive-unload) and the time parameters of the transport cycle (i.e., load time, unload time, transportation speed).
Case 1 results are shown in
Table 5,
Table 6 and
Table 7. The graphical expression of comparison results shown (
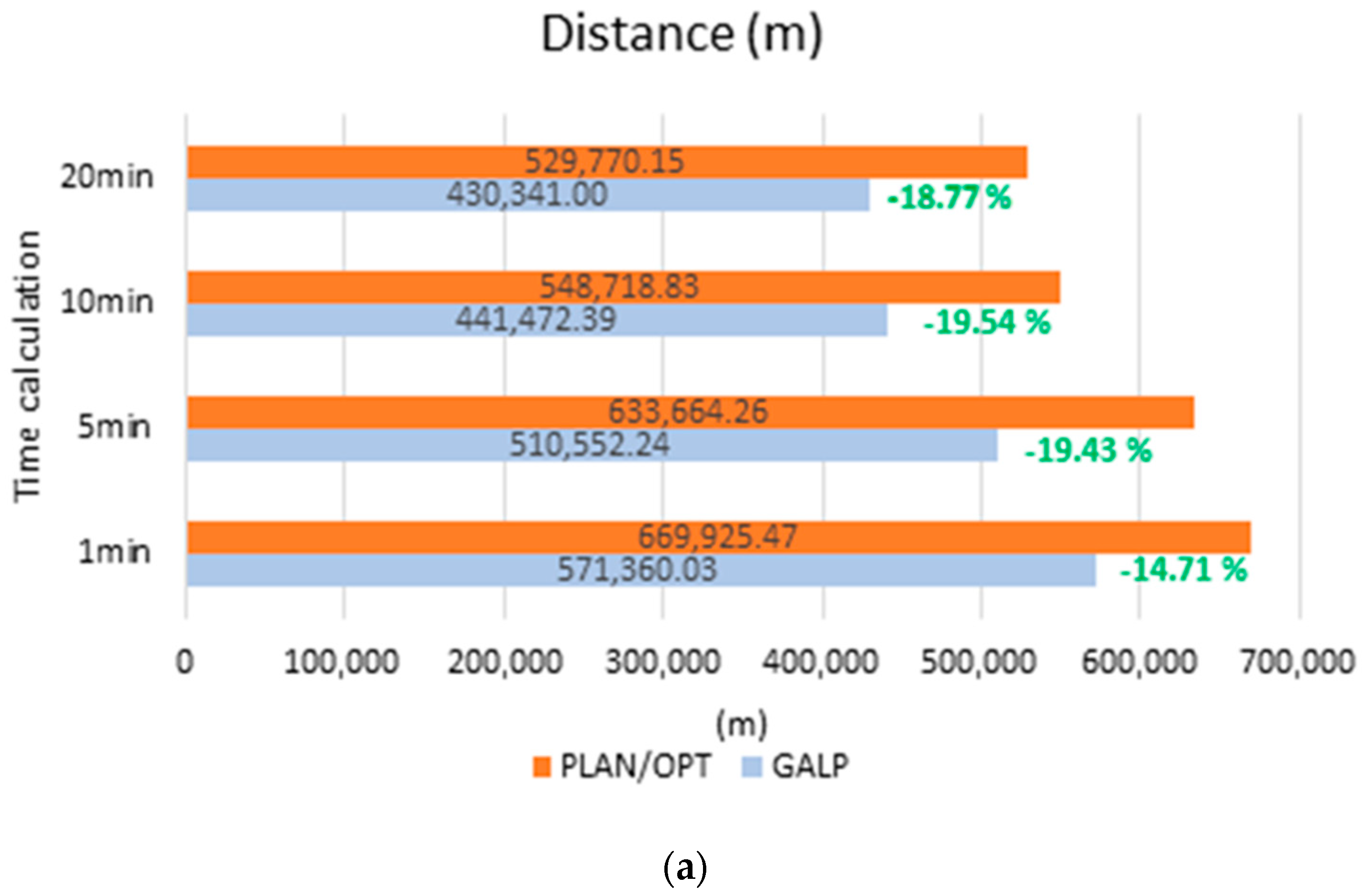
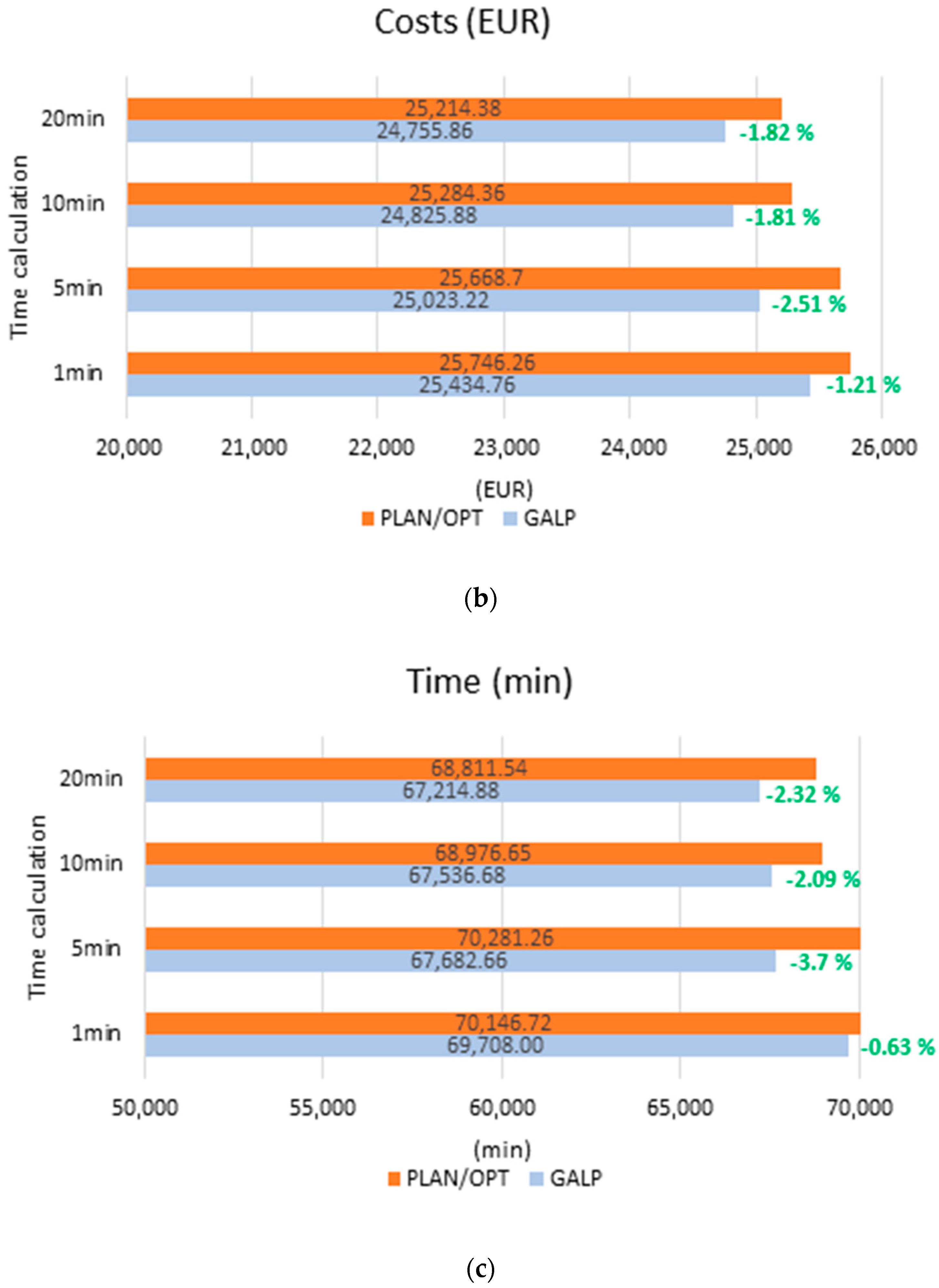
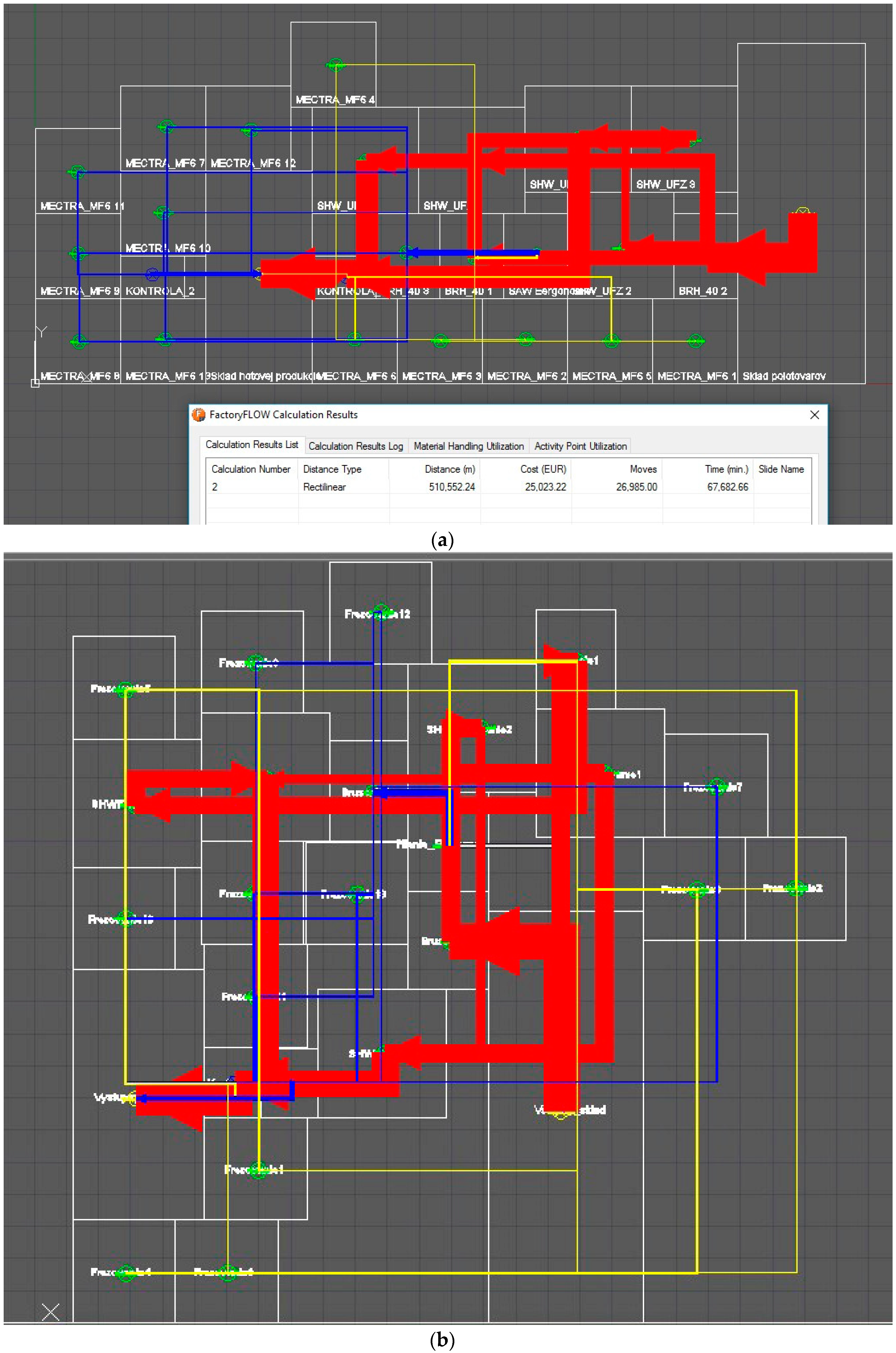
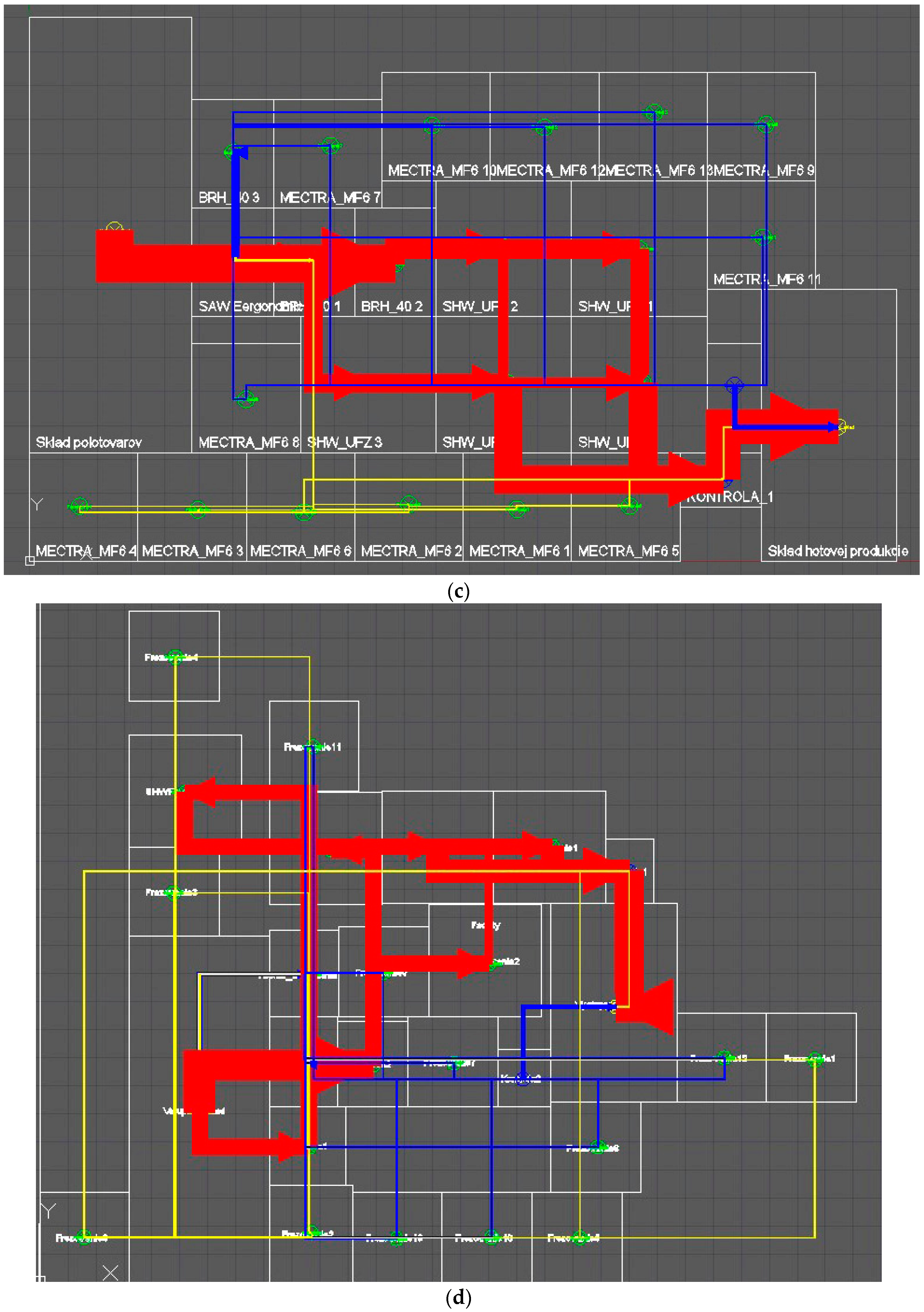
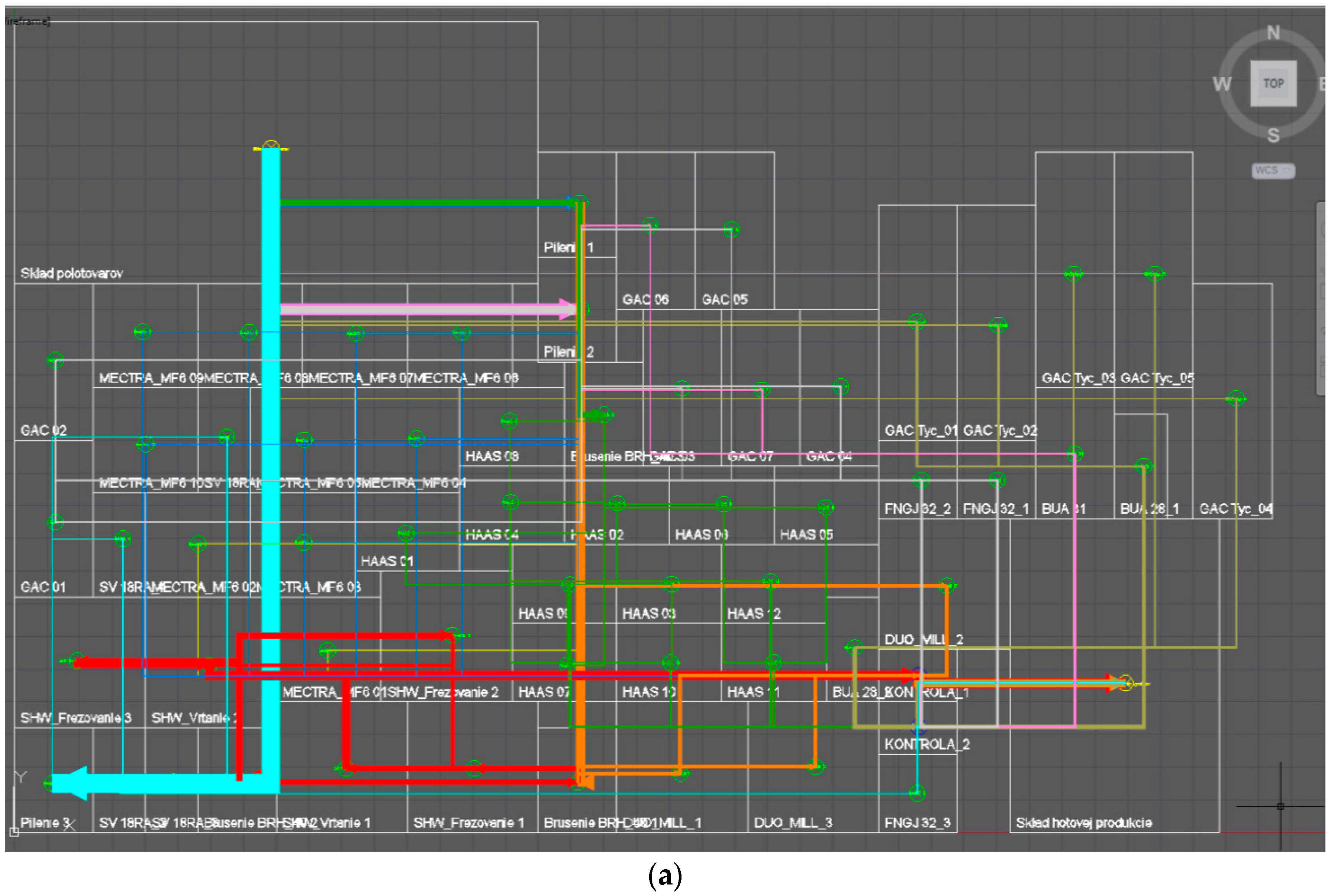
Figure 11). These experimental results indicate that GALP achieved better results in all cases than the PLAN/OPT algorithm, which, due to unknown reasons, did not keep workplace dimensions in some cases (
Figure 12). Case 1 results show that the difference between the classic heuristics (PLAN/OPT) and the GALP algorithm also depends on the calculation time and, hence, on the total number of iterations used by the algorithm. For the shortest calculation time of 1 min, the differences between results at 1.21% (distance and cost savings) and 0.63% (time savings) are in favor of the proposed GALP algorithm. At the longest calculation time (20 min), savings increased to 1.82% (distance and cost savings) and 2.32% (time savings). GALP has also proposed solutions preferring singular direction of material flow with minimum crossing or backward material flow. Due to comparing both algorithms, no restrictions have been imposed on workplace arrangement. However, the GALP algorithm enables basic restriction definition in the layout (production hall dimensions, the height of spaces, material component arrangement, fixed installations or transport corridors in the layout).
The graphical expression of comparison results (
Figure 11) shows that the proposed GALP algorithm achieved better results than classical heuristics PLAN/OPT. The results support the decision of the choice of a genetic algorithm as a tool for disposition layout planning and, thus, its applicability in industry.
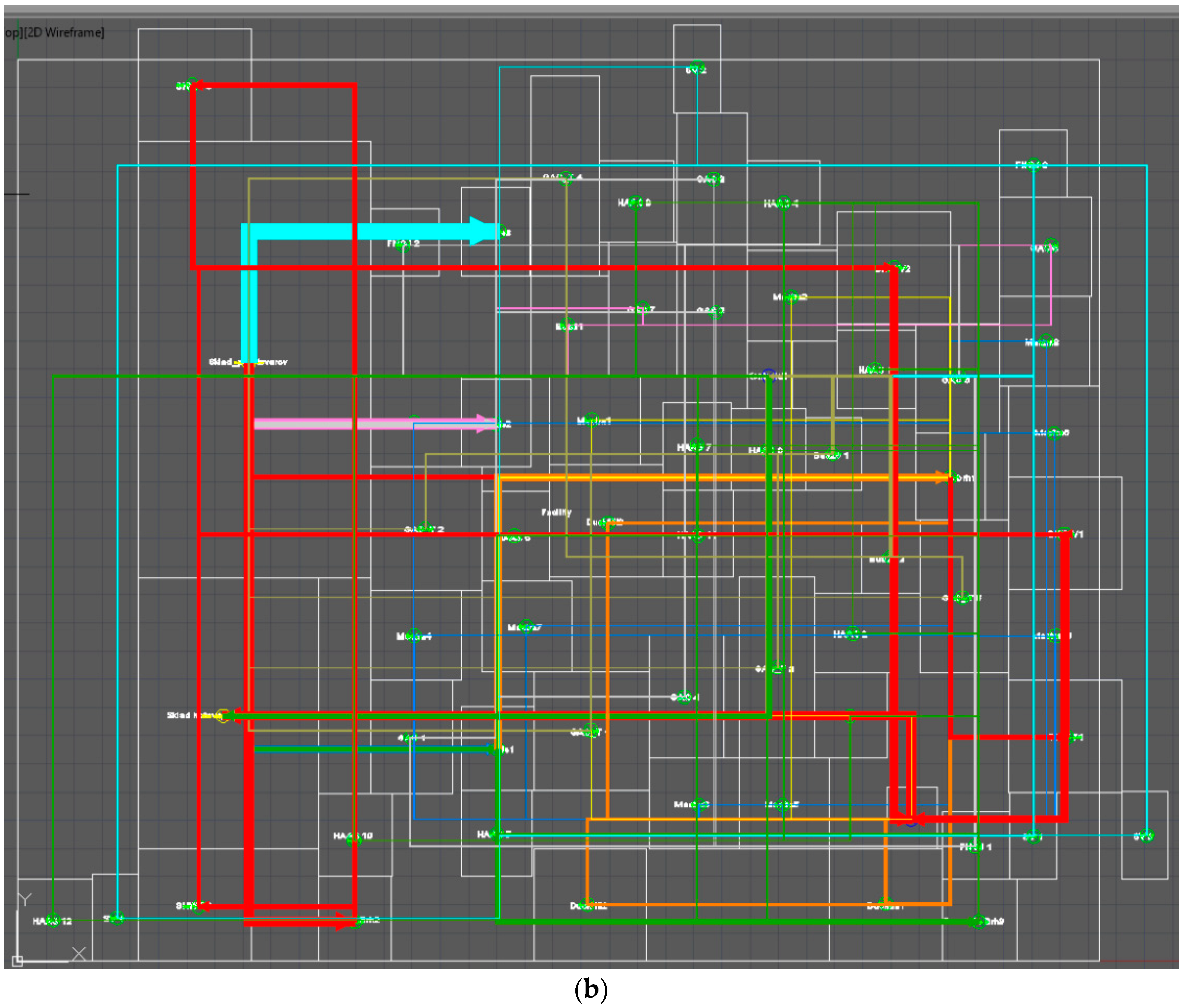
Experiment results were also consequently verified taking into account the complex solution of a manufacturing system (Case 2) and solution time was set to 5.5 h (solution time 1000 task generations in GALP). Advantages of the genetic algorithm became evident in a more extensive problem. Final material flow is directed with a minimum crossing. However, in case of the PLAN/OPT algorithm, there is a crossing, where material flow keeps coming back, and there is not any technology island creation in the manufacturing system. The genetic algorithm proposed layout with a greatly lower value of transportation performance (38.18%) than the heuristic algorithm in a PLAN/OPT module. Experiment result comparison is stated in
Table 8. Final block layouts are shown in
Figure 13 below.