Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes
Abstract
1. Introduction
2. Materials and Methods
2.1. Site and Climate of Experimental Field
2.2. Experimental Treatments
2.3. Data Measurement and Collection
2.4. Model Calibration and Validation Process
3. Results and Discussion
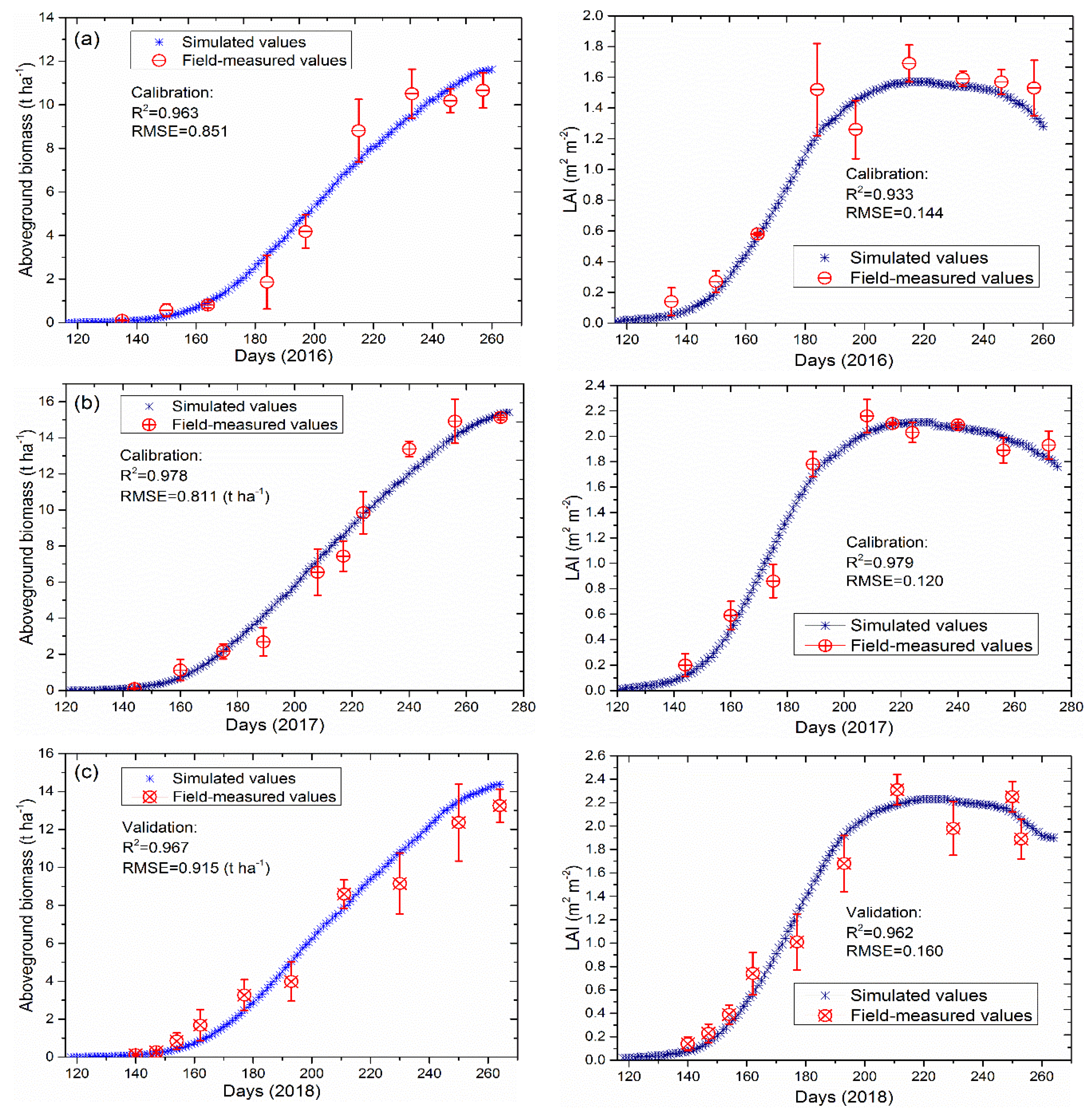
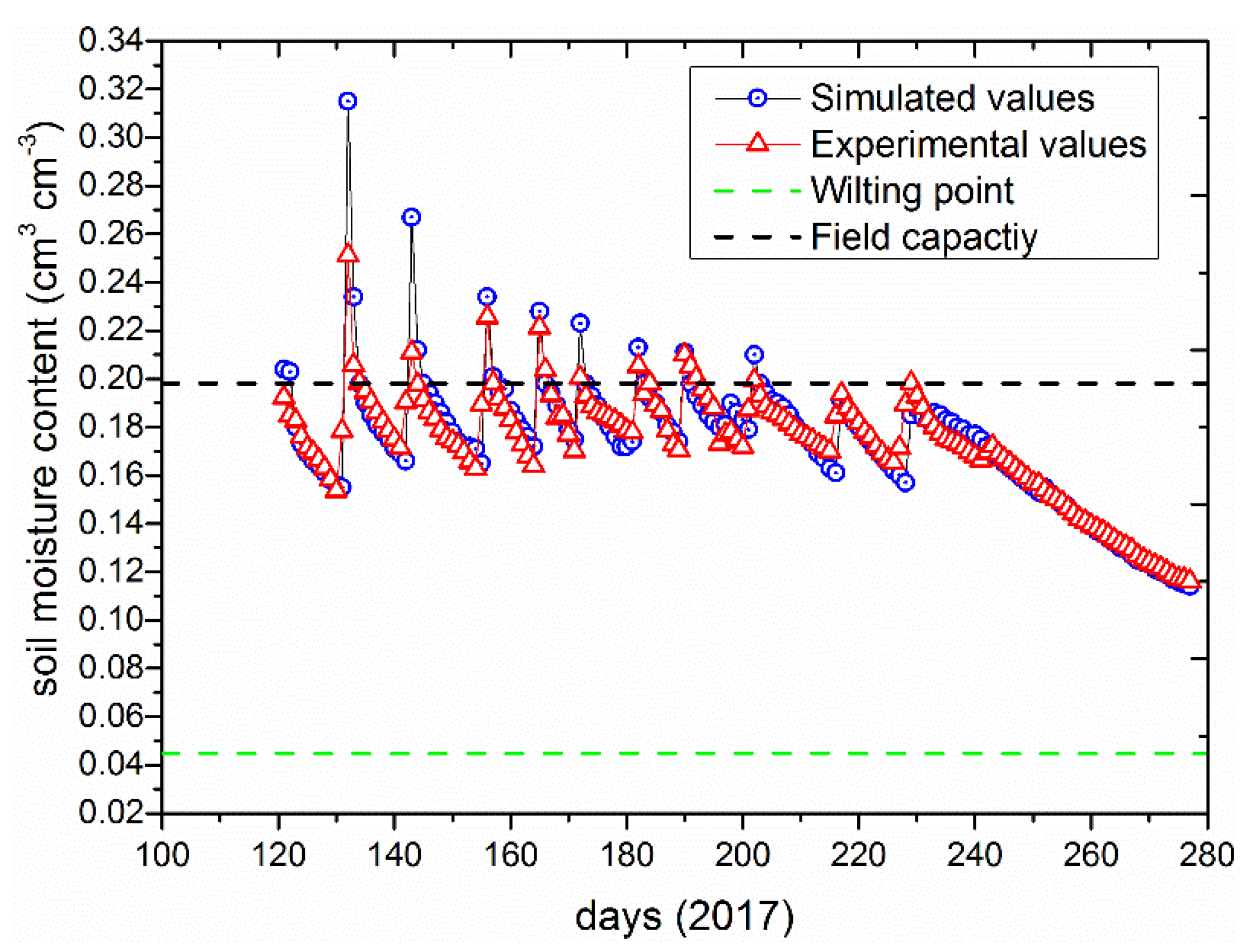
3.1. Model Calibration and Validation under Full Irrigation
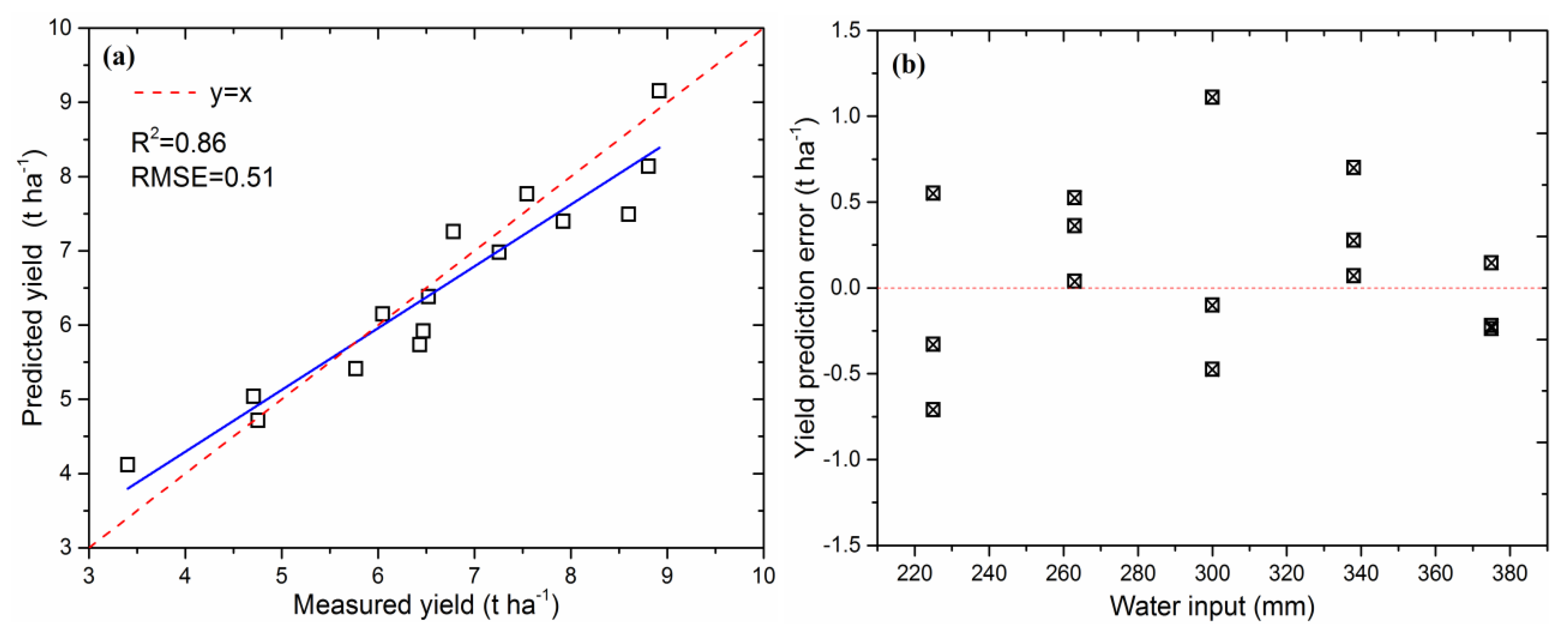
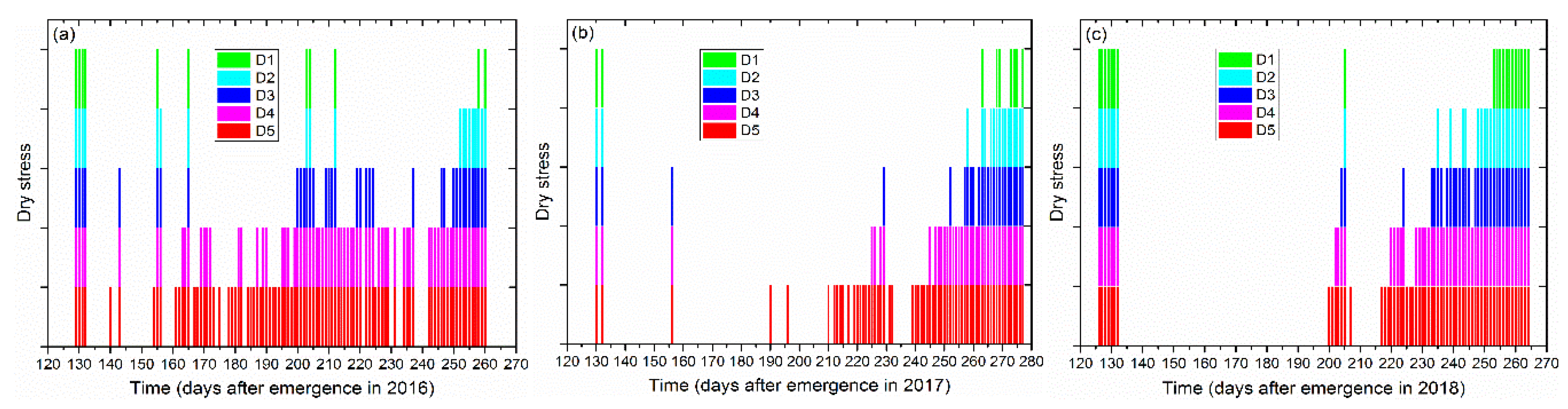
3.2. Model Evaluation under Different Irrigation Regimes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, J.W.; Fan, L.P.; Ding, S.D.; Ding, X.L. Nutritional composition of five cultivars of chinese jujube. Food Chem. 2007, 103, 454–460. [Google Scholar] [CrossRef]
- Zhu, K.Y.; Tsim, K.W.K.; Chen, J.; Lam, C.T.W.; Li, Z.; Maiwulanjiang, M.; Lau, D.T.W.; Zhan, J.Y.X.; Choi, R.C.Y.; Zhang, W.L.; et al. Chemical and Biological Assessment of Ziziphus jujuba Fruits from China: Different Geographical Sources and Developmental Stages. J. Agric. Food Chem. 2013, 61, 7315–7324. [Google Scholar]
- Ewert, F.; Rötter, R.P.; Bindi, M.; Webber, H.; Trnka, M.; Kersebaum, K.C.; Olesen, J.E.; van Ittersum, M.K.; Janssen, S.; Rivington, M.; et al. Crop modelling for integrated assessment of risk to food production from climate change. Environ. Model. Softw. 2015, 72, 287–303. [Google Scholar] [CrossRef]
- Supit, I.; van Diepen, C.A.; De Wit, A.J.W.; Wolf, J.; Kabat, P.; Baruth, B.; Ludwig, F. Assessing climate change effects on European crop yields using the Crop Growth Monitoring System and a weather generator. Agric. For. Meteorol. 2012, 164, 96–111. [Google Scholar] [CrossRef]
- Van Walsum, P.E.V.; Supit, I. Influence of ecohydrologic feedbacks from simulated crop growth on integrated regional hydrologic simulations under climate scenarios. Hydrol. Earth Syst. Sci. 2012, 16, 1577–1593. [Google Scholar] [CrossRef]
- Kroes, J.G.; Supit, I. Impact analysis of drought, water excess and salinity on grass production in The Netherlands using historical and future climate data. Agric. Ecosyst. Environ. 2011, 144, 370–381. [Google Scholar] [CrossRef]
- Supit, I.; van Diepen, C.A.; de Wit, A.J.W.; Kabat, P.; Baruth, B.; Ludwig, F. Recent changes in the climatic yield potential of various crops in Europe. Agric. Syst. 2010, 103, 683–694. [Google Scholar] [CrossRef]
- Alexandrov, V.A.; Eitzinger, J.J. The Potential Effect of Climate Change and Elevated Air Carbon Dioxide on Agricultural Crop Production in Central and Southeastern Europe. J. Crop Improv. 2005, 13, 291–331. [Google Scholar] [CrossRef]
- Palosuo, T.; Kersebaum, K.C.; Angulo, C.; Hlavinka, P.; Moriondo, M.; Olesen, J.E.; Patil, R.H.; Ruget, F.; Rumbaur, C.; Takáč, J.; et al. Simulation of winter wheat yield and its variability in different climates of Europe: A comparison of eight crop growth models. Eur. J. Agron. 2011, 35, 103–114. [Google Scholar] [CrossRef]
- De Wit, A.; Baruth, B.; Boogaard, H.; Van Diepen, K.; Van Kraalingen, D.; Micale, F.; Te Roller, J.; Supit, I.; Van Den Wijngaart, R. Using ERA-INTERIM for regional crop yield forecasting in Europe. Clim. Res. 2010, 44, 41–53. [Google Scholar] [CrossRef]
- De Wit, A.J.W.; van Diepen, C.A. Crop growth modelling and crop yield forecasting using satellite-derived meteorological inputs. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 414–425. [Google Scholar] [CrossRef]
- Dobermann, A.; Dawe, D.; Roetter, R.P.; Cassman, K.G. Reversal of rice yield decline in a long-term continuous cropping experiment. Agron. J. 2000, 92, 633–643. [Google Scholar] [CrossRef]
- Bussay, A.; van der Velde, M.; Fumagalli, D.; Seguini, L. Improving operational maize yield forecasting in Hungary. Agric. Syst. 2015, 141, 94–106. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rötter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827–832. [Google Scholar] [CrossRef]
- Todorovic, M.; Albrizio, R.; Zivotic, L.; Abi Saab, M.T.; Stöckle, C.; Steduto, P. Assessment of aquacrop, cropsyst, and WOFOST models in the simulation of sunfl ower growth under different water regimes. Agron. J. 2009, 101, 509–521. [Google Scholar] [CrossRef]
- Confalonieri, R.; Acutis, M.; Bellocchi, G.; Donatelli, M. Multi-metric evaluation of the models WARM, CropSyst, and WOFOST for rice. Ecol. Modell. 2009, 220, 1395–1410. [Google Scholar] [CrossRef]
- De Wit, A.; Boogaard, H.; Fumagalli, D.; Janssen, S.; Knapen, R.; van Kraalingen, D.; Supit, I.; van der Wijngaart, R.; van Diepen, K. 25 years of the WOFOST cropping systems model. Agric. Syst. 2019, 168, 154–167. [Google Scholar] [CrossRef]
- Van Diepen, C.A.; Wolf, J.; van Keulen, H.; Rappoldt, C. WOFOST: A simulation model of crop production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Proc. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.R.; Gassman, P.W.; Baffaut, C.; Izaurralde, R.C.; Jeong, J.; Kiniry, J.R. EPIC and APEX: Model Use, Calibration, and Validation. Trans. Asabe. 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model STICS. Proc. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.V.; Diepen, C.A. Van Theory of SWAP version 2.0. Softw. Man. 1997, 153. [Google Scholar]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. Aquacrop-The FAO crop model to simulate yield response to water: II. main algorithms and software description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Proc. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Abedinpour, M.; Sarangi, A.; Rajput, T.B.S.; Singh, M.; Pathak, H.; Ahmad, T. Performance evaluation of AquaCrop model for maize crop in a semi-arid environment. Agric. Water Manag. 2012, 110, 55–66. [Google Scholar] [CrossRef]
- Aggarwal, P.K.; Banerjee, B.; Daryaei, M.G.; Bhatia, A.; Bala, A.; Rani, S.; Chander, S.; Pathak, H.; Kalra, N. InfoCrop: A dynamic simulation model for the assessment of crop yields, losses due to pests, and environmental impact of agro-ecosystems in tropical environments. II. Performance of the model. Agric. Syst. 2006, 89, 47–67. [Google Scholar] [CrossRef]
- Bregaglio, S.; Frasso, N.; Pagani, V.; Stella, T.; Francone, C.; Cappelli, G.; Acutis, M.; Balaghi, R.; Ouabbou, H.; Paleari, L.; et al. New multi-model approach gives good estimations of wheat yield under semi-arid climate in Morocco. Agron. Sustain. Dev. 2014, 35, 157–167. [Google Scholar] [CrossRef]
- Chen, C.; Wang, E.; Yu, Q. Modelling the effects of climate variability and water management on crop water productivity and water balance in the North China Plain. Agric. Water Manag. 2010, 97, 1175–1184. [Google Scholar] [CrossRef]
- Eweys, O.A.; Elwan, A.A.; Borham, T.I. Integrating WOFOST and Noah LSM for modeling maize production and soil moisture with sensitivity analysis, in the east of The Netherlands. F. Crop. Res. 2017, 210, 147–161. [Google Scholar] [CrossRef]
- García-Vila, M.; Fereres, E. Combining the simulation crop model AquaCrop with an economic model for the optimization of irrigation management at farm level. Eur. J. Agron. 2012, 36, 21–31. [Google Scholar] [CrossRef]
- Geerts, S.; Raes, D.; Garcia, M. Using AquaCrop to derive deficit irrigation schedules. Agric. Water Manag. 2010, 98, 213–216. [Google Scholar] [CrossRef]
- Kroes, J.G. Modeling water management strategies using the SWAP/WOFOST model. In Proceedings of the Climate Variability, Modeling Tools and Agricultural Decision-Making. In Proceedings of the AGRIDEMA Workshop, Valladolid, Spain, 28–29 June 2007; pp. 127–136. [Google Scholar]
- McNider, R.T.; Handyside, C.; Doty, K.; Ellenburg, W.L.; Cruise, J.F.; Christy, J.R.; Moss, D.; Sharda, V.; Hoogenboom, G.; Caldwell, P. An integrated crop and hydrologic modeling system to estimate hydrologic impacts of crop irrigation demands. Environ. Model. Softw. 2015, 72, 341–355. [Google Scholar] [CrossRef]
- Zhou, J.; Cheng, G.; Li, X.; Hu, B.X.; Wang, G. Numerical Modeling of Wheat Irrigation using Coupled HYDRUS and WOFOST Models. Soil Sci. Soc. Am. J. 2012, 76, 648. [Google Scholar] [CrossRef]
- Qin, W.; Heinen, M.; Assinck, F.B.T.; Oenema, O. Exploring optimal fertigation strategies for orange production, using soil-crop modelling. Agric. Ecosyst. Environ. 2016, 223, 31–40. [Google Scholar] [CrossRef]
- Ismail, S.M.; El-Abedin, T.K.Z.; El-Ansary, D.O.; El-Al, A.A. Modification of FAO Crop Model to Simulate Yield Response to Water for Peach Trees. Irrig. Drainage. 2015, 32, 145–172. [Google Scholar]
- Rallo, G.; Agnese, C.; Minacapilli, M.; Provenzano, G. Assessing AQUACROP water atress function to evaluate the transpiration reductions of olive mature tree. Ital. J. Agrometeorol. 2012, 1, 21–28. [Google Scholar]
- Marsal, J.; Stöckle, C.O. Use of CropSyst as a decision support system for scheduling regulated deficit irrigation in a pear orchard. Irrig. Sci. 2012, 30, 139–147. [Google Scholar] [CrossRef]
- Eitzinger, J.; Trnka, M.; Hösch, J.; Žalud, Z.; Dubrovský, M. Comparison of CERES, WOFOST and SWAP models in simulating soil water content during growing season under different soil conditions. Ecol. Modell. 2004, 171, 223–246. [Google Scholar] [CrossRef]
- Abi Saab, M.T.; Todorovic, M.; Albrizio, R. Comparing aquaCrop and cropSyst models in simulating barley growth and yield under different water and nitrogen regimes: Does calibration year influence the performance of crop growth models? Agric. Water Manag. 2015, 147, 21–33. [Google Scholar] [CrossRef]
- Todorovic, M. An excel-Based tool Forreal-Time irrigation management at field scale. In Proceedings of the International Symposium on Water and Land Management for Sustainable Irrigated Agriculture, Adana, Turkey, 4−8 April 2006. [Google Scholar]
- De Wit, A.; Wolf, J. Calibration of WOFOST Crop Growth Simulation Model for Use within CGMS; Plant Production Systems Group, Wageningen University: Wageningen, Holland, 2010; pp. 1–38. [Google Scholar]
- Ceglar, A.; van der Wijngaart, R.; de Wit, A.; Lecerf, R.; Boogaard, H.; Seguini, L.; van den Berg, M.; Toreti, A.; Zampieri, M.; Fumagalli, D.; et al. Improving WOFOST model to simulate winter wheat phenology in Europe: Evaluation and effects on yield. Agric. Syst. 2019, 168, 168–180. [Google Scholar] [CrossRef]
- Joint Research Centre (European Commission). An Agricultural Information System System Description of the Wofost 6. 0 Crop Simulation Model Implemented in Cgms Volume 1: Theory and Algorithms; European Commission: Luxembourg, 1994. [Google Scholar]
- Kroes, J.G.; Van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Jacobs, C.M.J. SWAP Version 4.0: Theory Descripition and User Manual; Wageningen UR-Wageningen Environmental Research: Wageningen, Holland, 2017. [Google Scholar]
- Rallo, G.; Agnese, C.; Minacapilli, M.; Provenzano, G. Comparison of SWAP and FAO Agro-Hydrological Models to Schedule Irrigation of Wine Grapes. J. Irrig. Drain. Eng. 2011, 138, 581–591. [Google Scholar] [CrossRef]

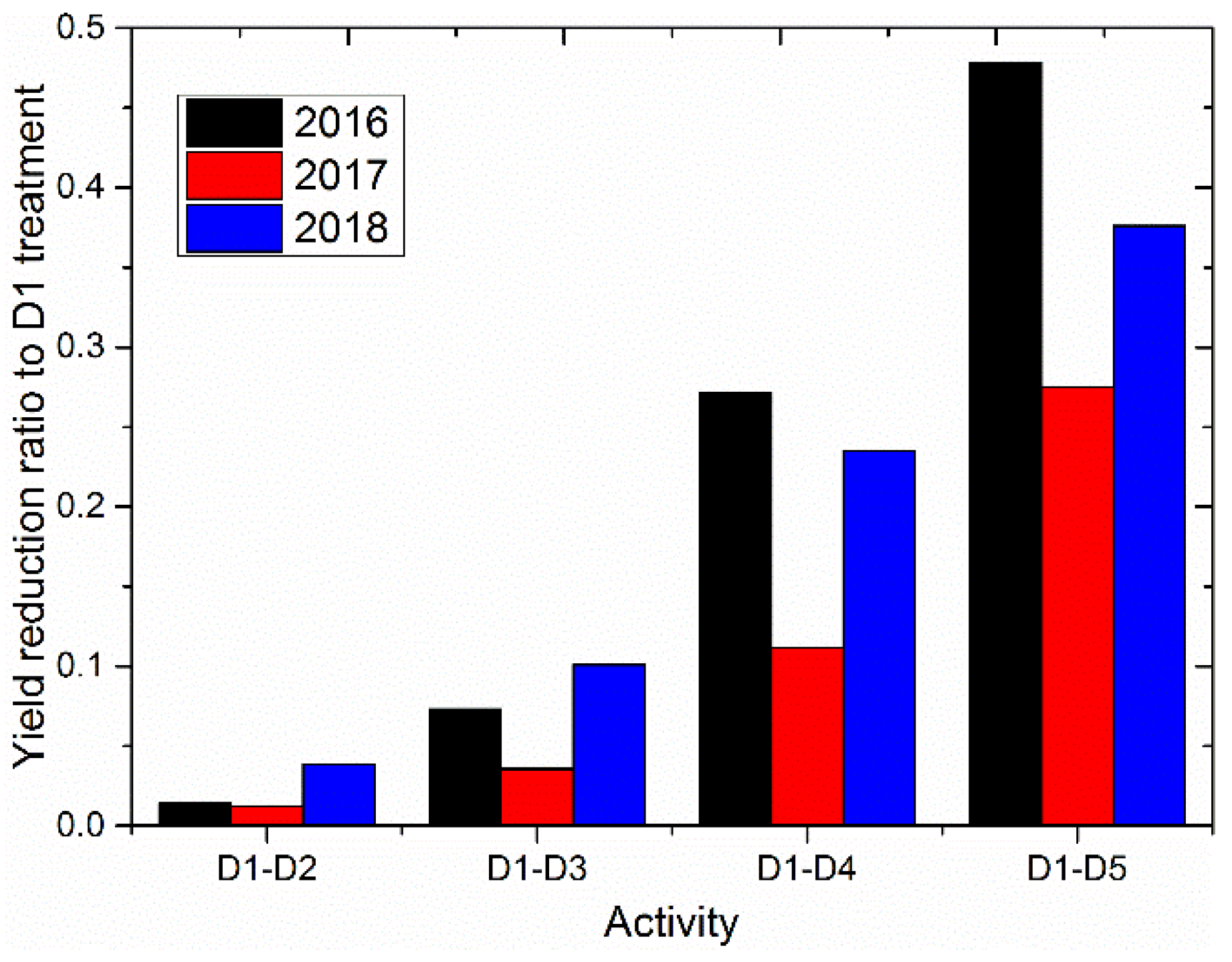
| Year | Yield for Different Irrigation Degree (t ha−1) | ||||||
|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | Average | SD | |
| 2016 | 6.380 | 5.733 | 6.149 | 4.716 | 4.115 | 6.380 | 0.866 |
| 2017 | 9.155 | 8.738 | 7.490 | 7.398 | 5.918 | 9.155 | 1.140 |
| 2018 | 7.767 | 6.981 | 7.259 | 5.409 | 5.039 | 7.767 | 1.071 |
| Parameter | Description | Value | Units | Source |
|---|---|---|---|---|
| *Emergence | ||||
| TBASEM | lower threshold temperature emergence | 10 | °C | e |
| TEFFMX | max effective temperature emergence | 30 | °C | e |
| TSUMEM | temperature sum from sowing to emergence | 230 | °C | m-c |
| *Phenology parameter | ||||
| TSUM1 | temperature sum from emergence to anthesis | 967 | °C d−1 | m-c |
| TSUM2 | temperature sum from anthesis to maturity | 960 | °C d−1 | m-c |
| DTSMTB0 | daily increase in temperature sum as a function of average at = 0 °C | 0.00 | °C d−1 | e |
| DTSMTB100 | daily increase in temperature sum as a function of average at = 10 °C | 0 | °C d−1 | e |
| DTSMTB355 | daily increase in temperature sum as a function of average at = 35.5 °C | 25.5 | °C d−1 | e |
| DTSMTB400 | daily increase in temperature sum as a function of average at = 40 °C | 25.5 | °C d−1 | e |
| *Initial parameters | ||||
| TDWI | Redefine initial total emergence dry weight | 15.1/17.2/19.4 | kg ha−1 | m |
| LAIEM | leaf area index at emergence | 0.0007 | ha ha−1 | d |
| RGRLAI | maximum relative increase in LAI | 0.05 | ha ha−1 d−1 | d |
| *Green area | ||||
| SLATB000 | specific leaf area when DVS = 0 | 0.00165 | ha kg−1 | m-c |
| SLATB55 | specific leaf area when DVS = 0.55 | 0.0013 | ha kg−1 | m-c |
| SLATB100 | specific leaf area when DVS = 1 | 0.0013 | ha kg−1 | m-c |
| SLATB200 | specific leaf area when DVS = 2 | 0.0014 | ha kg−1 | m-c |
| SPAN | life span of leaves growing at 35 degrees Celsius | 60 | [d] | e |
| TBASE | lower threshold temp. for ageing of leaves | 10 | °C | e |
| *CO2 assimilation | ||||
| KDIFTB00 | extinction coefficient for diffuse visible light at DVS = 0 | 0.8 | \ | m-c |
| KDIFTB200 | extinction coefficient for diffuse visible light at DVS = 2 | 0.8 | \ | m-c |
| EFFTB19.5 | light-use efficiency single leaf at average temp. = Celsius | 0.495 | kg ha−1 hr−1 J−1 m2 s | m-c |
| EFFTB355 | light-use efficiency single leaf at average temp. = Celsius | 0.495 | kg ha−1 hr−1 J−1 m2 s | m-c |
| AMAXTB00 | maximum leaf CO2 assimilation. Rate at DVS = 0 | 39.0 | kg ha−1 hr−1 | m-c |
| AMAXTB170 | maximum leaf CO2 assimilation. Rate at DVS = 1.7 | 39.0 | kg ha−1 hr−1 | m-c |
| AMAXTB200 | maximum leaf CO2 assimilation. Rate at DVS = 2 | 20.0 | kg ha−1 hr−1 | m-c |
| TMPFTB10 | reduction factor of AMAX at 10 °C | 0 | \ | d |
| TMPFTB195 | reduction factor of AMAX at 19.5 °C | 1 | \ | d |
| TMPFTB355 | reduction factor of AMAX at 35.5 °C | 1 | \ | d |
| *Conversion of assimilates into biomass | ||||
| CVL | efficiency of conversion into leaves | 0.732 | kg kg−1 | m-c |
| CVO | efficiency of conversion into storage organs | 0.780 | kg kg−1 | m-c |
| CVR | efficiency of conversion into roots | 0.690 | kg kg−1 | m-c |
| CVS | efficiency of conversion into stems | 0.751 | kg kg−1 | m-c |
| * maintenance respiration | ||||
| Q10 | Relative increase in respiration rate per 10 °C temperature increase | 2 | kg CH2O kg−1 d−1 | d |
| RML | Relative maintenance respiration rate of leaves | 0.03 | kg CH2O kg−1 d−1 | d |
| RMO | Relative maintenance respiration rate of storage organs | 0.01 | kg CH2O kg−1 d−1 | d-c |
| RMR | Relative maintenance respiration rate of roots | 0.01 | kg CH2O kg−1 d−1 | d |
| RMS | Relative maintenance respiration rate of stems | 0.015 | kg CH2O kg−1 d−1 | d-c |
| *Dartitioning parameters | ||||
| FRTB00 | fraction of above-ground dry matter to roots at DVS = 0 | 0.3 | kg kg−1 | m-c |
| FRTB154 | fraction of above-ground dry matter to roots at DVS = 1.54 | 0.0 | kg kg−1 | m-c |
| FLTB00 | fraction of above-ground dry matter to leaves at DVS = 0 | 0.67 | kg kg−1 | m-c |
| FLTB012 | fraction of above-ground dry matter to leaves at DVS = 0.12 | 0.31 | kg kg−1 | m-c |
| FLTB022 | fraction of above-ground dry matter to leaves at DVS = 0.22 | 0.41 | kg kg−1 | m-c |
| FLTB032 | fraction of above-ground dry matter to leaves at DVS = 0.32 | 0.55 | kg kg−1 | m-c |
| FLTB051 | fraction of above-ground dry matter to leaves at DVS = 0.51 | 0.4 | kg kg−1 | m-c |
| FLTB097 | fraction of above-ground dry matter to leaves at DVS = 0.97 | 0.15 | kg kg−1 | m-c |
| FLTB100 | fraction of above-ground dry matter to leaves at DVS = 1.00 | 0.1 | kg kg−1 | m-c |
| FLTB145 | fraction of above-ground dry matter to leaves at DVS = 1.45 | 0 | kg kg−1 | m-c |
| FLTB200 | fraction of above-ground dry matter to leaves at DVS = 2.00 | 0 | kg kg−1 | m-c |
| FSTB00 | fraction of above-ground dry matter to stems at DVS = 0 | 0.33 | kg kg−1 | m-c |
| FSTB012 | fraction of above-ground dry matter to stems at DVS = 0.12 | 0.69 | kg kg−1 | m-c |
| FSTB022 | fraction of above-ground dry matter to stems at DVS = 0.22 | 0.59 | kg kg−1 | m-c |
| FSTB032 | fraction of above-ground dry matter to stems at DVS = 0.32 | 0.45 | kg kg−1 | m-c |
| FSTB051 | fraction of above-ground dry matter to stems at DVS = 0.51 | 0.6 | kg kg−1 | m-c |
| FSTB097 | fraction of above-ground dry matter to stems at DVS = 0.97 | 0.85 | kg kg−1 | m-c |
| FSTB100 | fraction of above-ground dry matter to stems at DVS = 1.00 | 0.43 | kg kg−1 | m-c |
| FSTB145 | fraction of above-ground dry matter to stems at DVS = 1.45 | 0.2 | kg kg−1 | m-c |
| FSTB200 | fraction of above-ground dry matter to stems at DVS = 2.00 | 0 | kg kg−1 | m-c |
| FOTB00 | fraction of above-ground dry matter to storage organs at DVS = 0 | 0 | kg kg−1 | m-c |
| FOTB012 | fraction of above-ground dry matter to storage organs at DVS = 0.12 | 0 | kg kg−1 | m-c |
| FOTB022 | fraction of above-ground dry matter to storage organs at DVS = 0.22 | 0 | kg kg−1 | m-c |
| FOTB032 | fraction of above-ground dry matter to storage organs at DVS = 0.32 | 0 | kg kg−1 | m-c |
| FOTB051 | fraction of above-ground dry matter to storage organs at DVS = 0.51 | 0 | kg kg−1 | m-c |
| FOTB097 | fraction of above-ground dry matter to storage organs at DVS = 0.97 | 0 | kg kg−1 | m-c |
| FOTB100 | fraction of above-ground dry matter to storage organs at DVS = 1.00 | 0.47 | kg kg−1 | m-c |
| FOTB145 | fraction of above-ground dry matter to storage organs at DVS = 1.45 | 0.8 | kg kg−1 | m-c |
| FOTB164 | fraction of above-ground dry matter to storage organs at DVS = 1.64 | 1.0 | kg kg−1 | m-c |
| FOTB200 | fraction of above-ground dry matter to storage organs at DVS = 2.00 | 1 | kg kg−1 | m-c |
| *Death rates | ||||
| RDRSTB00 | Relative death rate of stems at DVS = 0 | 0 | \ | e |
| RDRSTB200 | Relative death rate of stems at DVS = 2.0 | 0 | \ | e |
| Water use and soil parameters | ||||
| CFET | correction factor transpiration rate | 1.02 | - | d-c |
| DEPNR | correction factor for crop water stress sensitivity | 1.5 | - | c |
| RDI | initial rooting depth | 10 | cm | d |
| RRI | maximum daily increase in rooting depth | 1.2 | cm d−1 | e |
| RDMCR | maximum rooting depth | 120 | cm | m |
| SMW | soil moisture content at wilting point | 0.0449 | cm3 cm−3 | e |
| SMFCF | soil moisture content at field capacity | 0.198 | cm3 cm−3 | m-c |
| SM0 | soil moisture content at saturation | 0.39 | cm3 cm−3 | m |
| CRAIRC | critical soil air content for aeration | 0.075 | cm3 cm−3 | d |
| Phase | AT (°C) | AI (MJ m−2 d−1)) | TP (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | 2016 | 2017 | 2018 | 2016 | 2017 | 2018 | |
| Beginning-Emergence | 16.4 | 15.7 | 15.5 | 12.4 | 15.1 | 11.8 | 1 | 6 | 1 |
| Emergence-flowering | 23.9 | 23.9 | 23.1 | 19.8 | 22.3 | 20.3 | 19 | 15 | 46 |
| Flowering-maturity | 23.2 | 21.8 | 23.2 | 18.1 | 17.8 | 18.6 | 76 | 61 | 26 |
| Whole season | 23.6 | 22.9 | 23.1 | 18.9 | 20.1 | 19.5 | 97 | 83 | 73 |
| Phase | End Day | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2016 Calibration | 2017 Calibration | 2018 Validation | |||||||
| Ob | Si | Diff | Ob | Si | Dif | Ob | Si | Diff | |
| Beginning–Emergence | 117 | 116 | −1 | 121 | 121 | 0 | 120 | 118 | −2 |
| Emergence–flowering | 187 | 186 | −1 | 190 | 192 | +2 | 196 | 193 | −3 |
| Flowering–maturity | 260 | 260 | 0 | 271 | 275 | +4 | 267 | 264 | −3 |
| Whole season | 143 | 144 | +1 | 150 | 154 | +4 | 147 | 146 | −1 |
| Year | R2 | RMSE(t ha−) | MAE(t ha−) | MBE(t ha−) |
|---|---|---|---|---|
| 2016 | 0.93 | 0.41 | 0.34 | −0.02 |
| 2017 | 0.80 | 0.62 | 0.62 | −0.52 |
| 2018 | 0.90 | 0.31 | 0.33 | +0.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, T.; Zhang, N.; Chen, Y.; Mercatoris, B. Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes. Sustainability 2019, 11, 1466. https://doi.org/10.3390/su11051466
Bai T, Zhang N, Chen Y, Mercatoris B. Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes. Sustainability. 2019; 11(5):1466. https://doi.org/10.3390/su11051466
Chicago/Turabian StyleBai, Tiecheng, Nannan Zhang, Youqi Chen, and Benoit Mercatoris. 2019. "Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes" Sustainability 11, no. 5: 1466. https://doi.org/10.3390/su11051466
APA StyleBai, T., Zhang, N., Chen, Y., & Mercatoris, B. (2019). Assessing the Performance of the WOFOST Model in Simulating Jujube Fruit Tree Growth under Different Irrigation Regimes. Sustainability, 11(5), 1466. https://doi.org/10.3390/su11051466






