Quantitative Multi-Hazard Risk Assessment of Crop Loss in the Yangtze River Delta Region of China
Abstract
1. Introduction
2. Study Area and Data
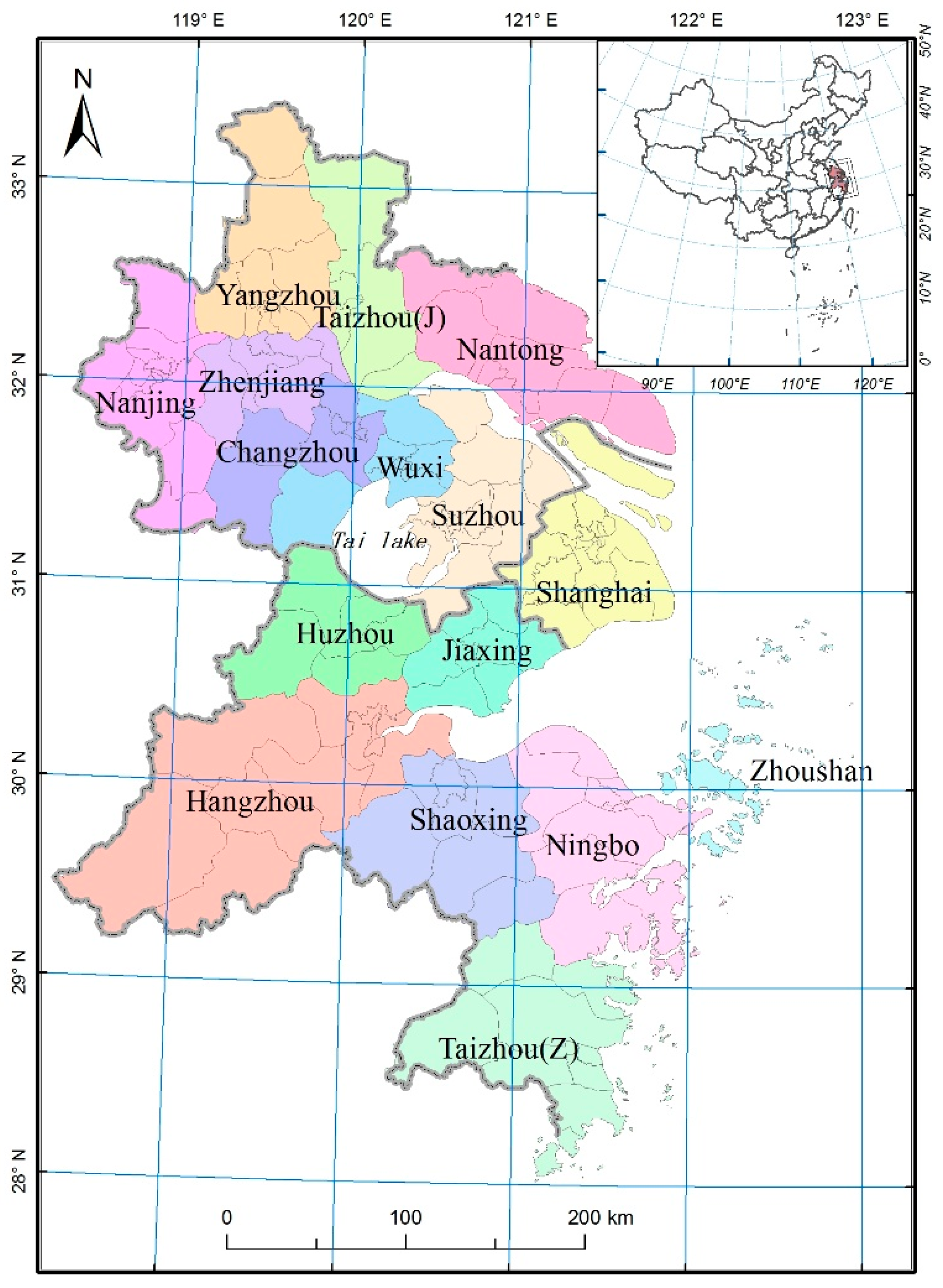
2.1. Study Area
2.2. Data and Preprocessing
3. Method
3.1. Fitting the Joint Distribution Based on a Copula
3.2. Fitting the Vulnerability Surface
3.3. Calculating the Multi-Hazard Risk
4. Results
4.1. Joint Return Period for Rain and Wind
4.1.1. Parameter Fitting Result of the Copula Function
4.1.2. Joint Hazard Analysis
4.1.3. Multi-Hazard Return Period
4.2. Vulnerability Analysis
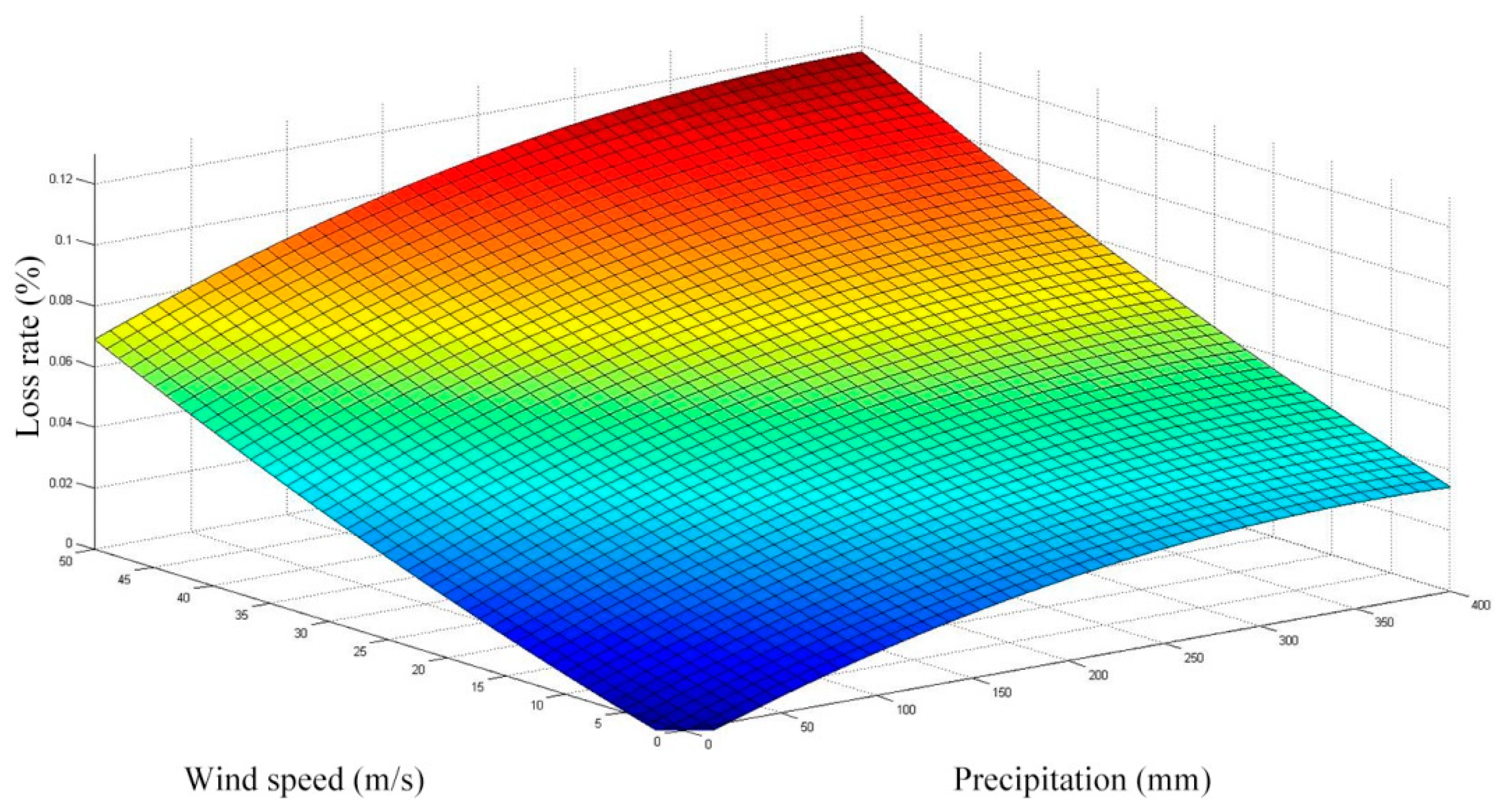
4.2.1. Vulnerability Surface
4.2.2. Integrated Vulnerability Model
4.3. Risk Assessment Results
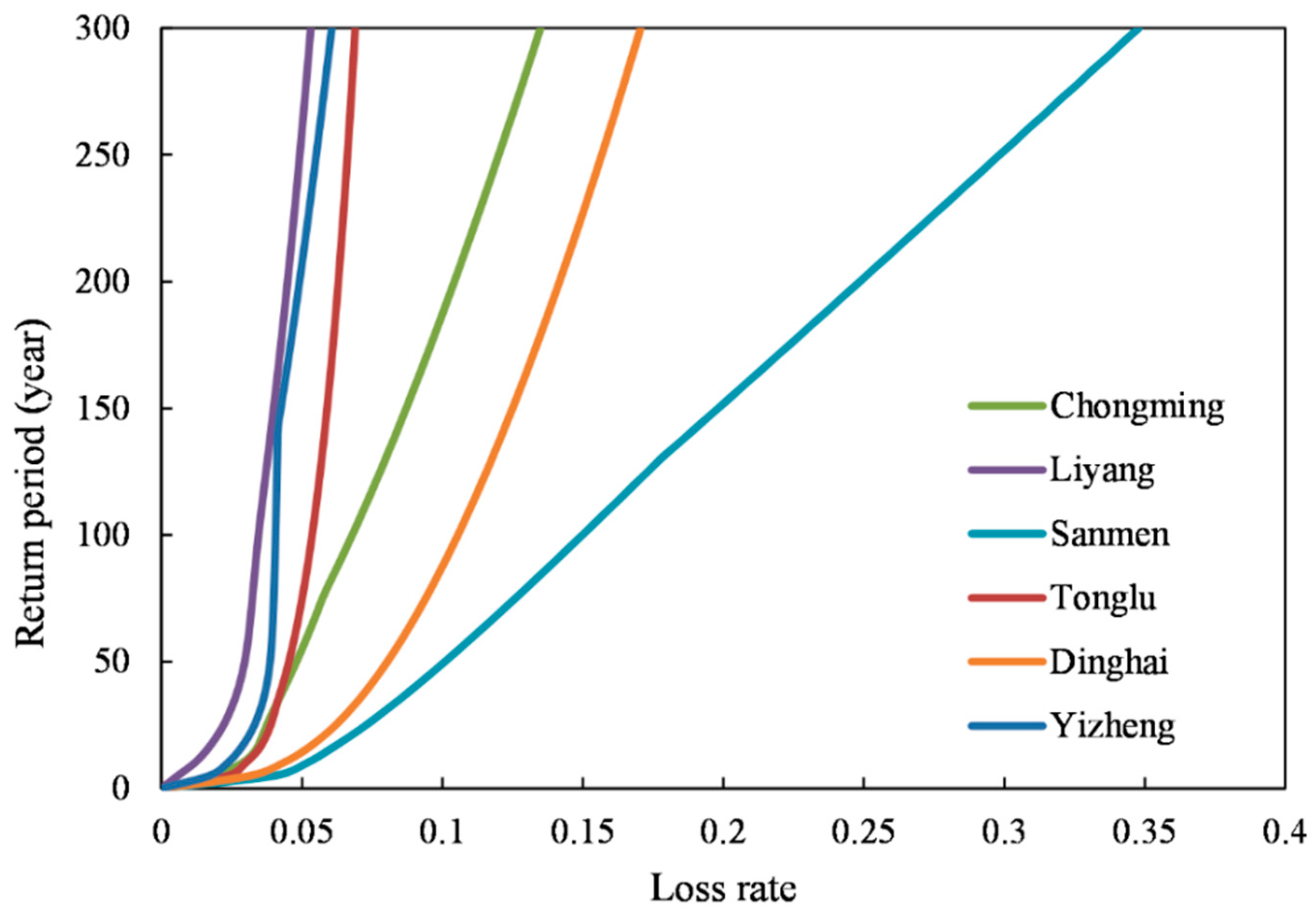
4.3.1. Loss–Return Period Curves
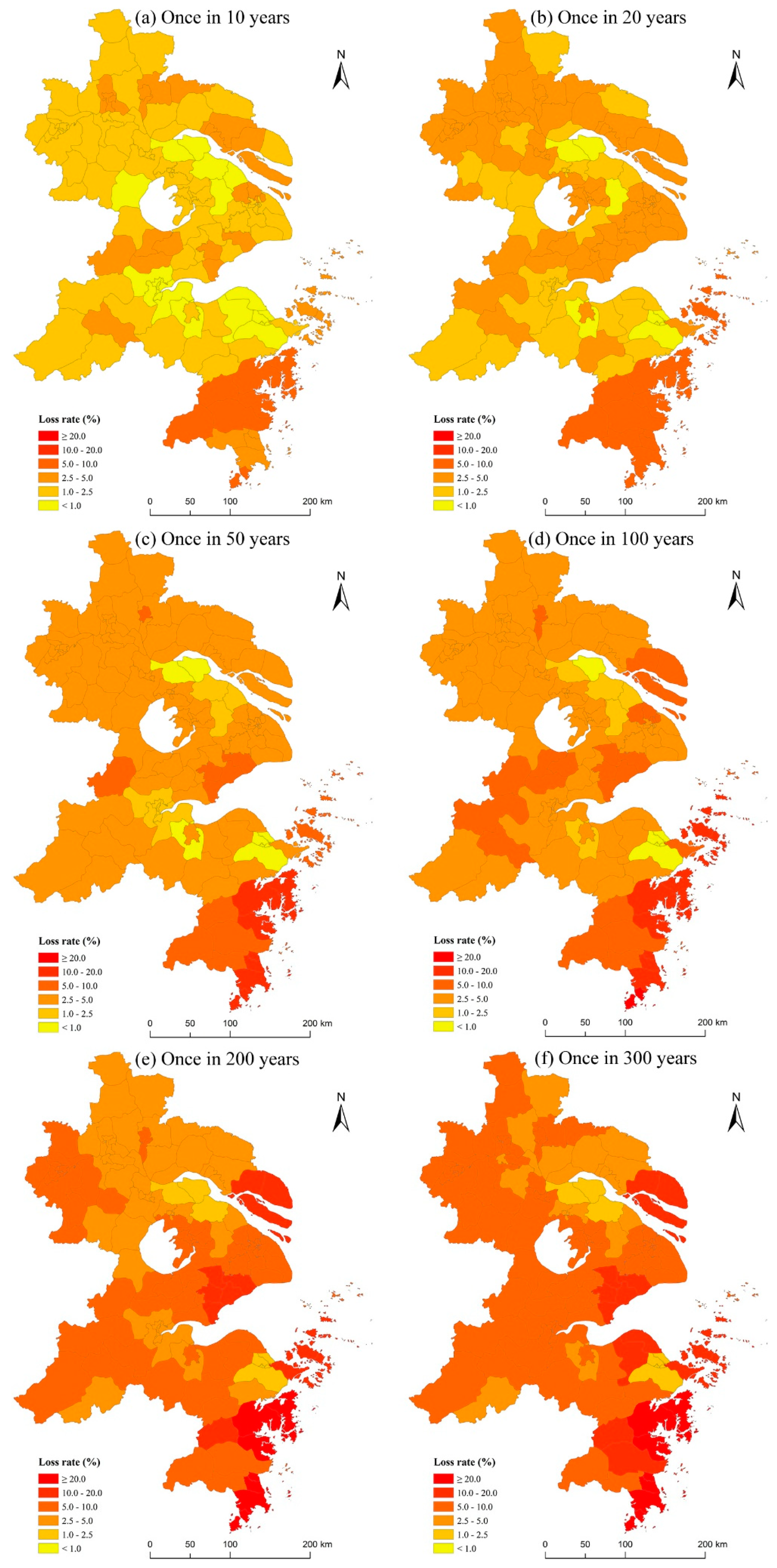
4.3.2. Crop Loss Rate under Different Return Periods
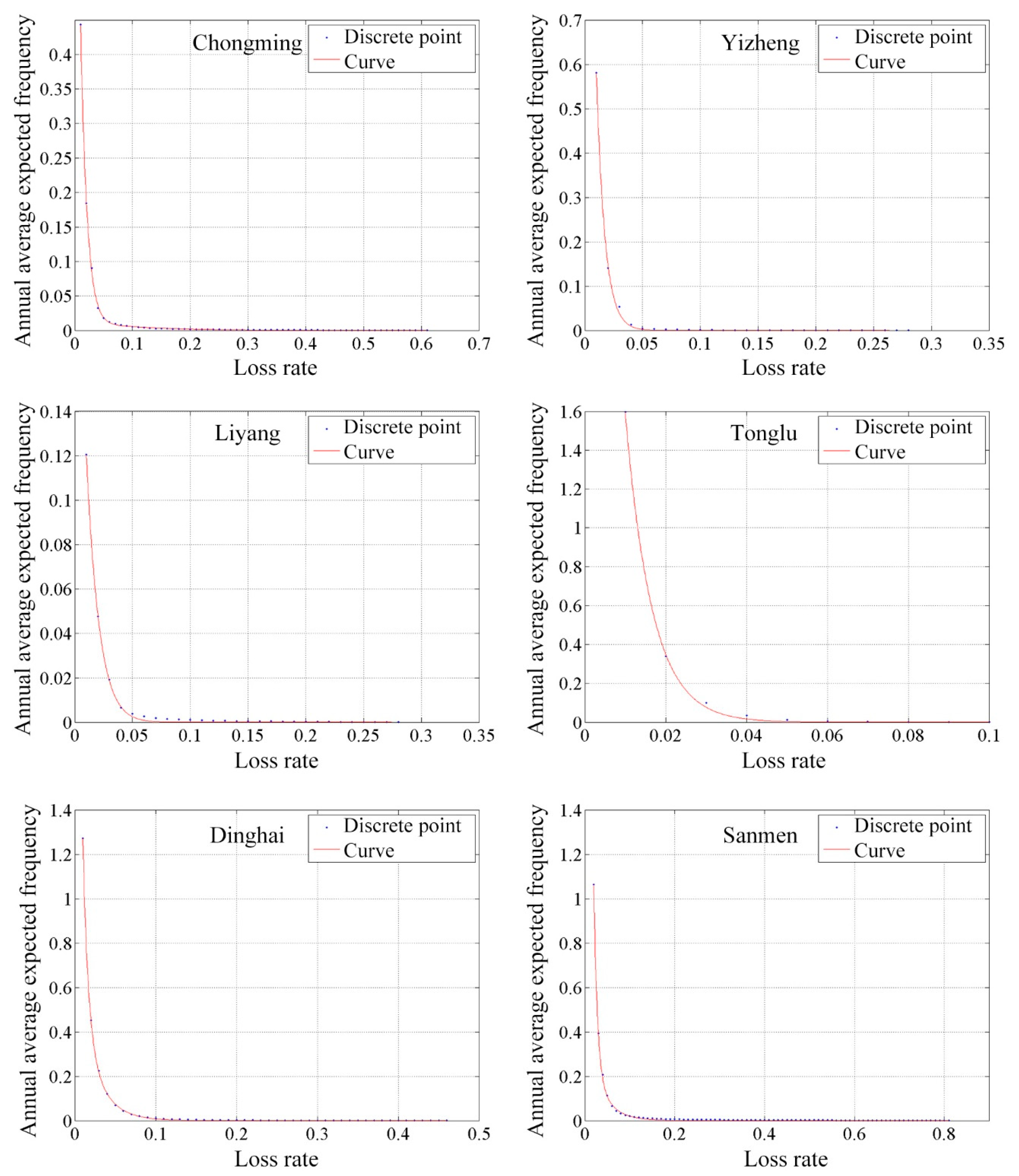
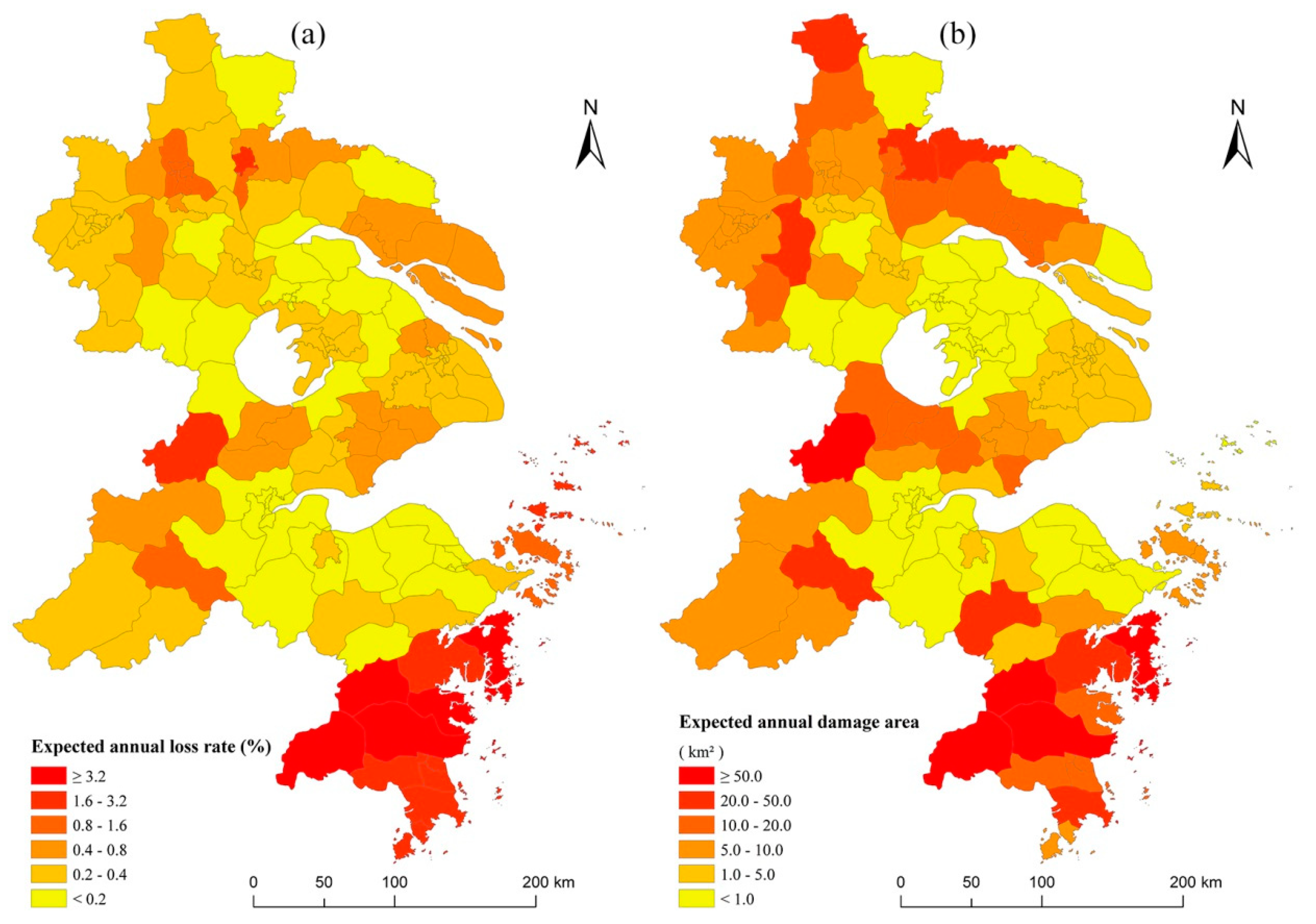
4.3.3. Annual Average Frequency of Losses and the Annual Average Expected Losses
5. Conclusion and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Transforming Our Word: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Gill, J.C.; Malamud, B.D. Reviewing and visualizing the interactions of natural hazards. Rev. Geophys. 2014, 52, 680–722. [Google Scholar] [CrossRef]
- Pelling, M.; Maskrey, A.; Ruiz, P.; Hall, L. Reducing Disaster Risk: A Challenge for Development; UNDP, United Nations Development Programme: New York, NY, USA, 2004; pp. 113–115. ISBN 92-1-126160-0. [Google Scholar]
- Dilley, M.; Chen, R.S.; Deichmann, U.; Lerner-Lam, A.L.; Arnold, M.; Agwe, J.; Buys, P.; Kjekstad, O.; Lyon, B.; Yetman, G. Natural Disaster Hotspots: A Global Risk Analysis; The World Bank: Washington, DC, USA, 2005; pp. 1–132. ISBN 0-8213-5930-4. [Google Scholar]
- UNU-EHS (United Nations University Institute for Environment and Human Security). World Risk Report; Bündnis Entwicklung Hilft: Berlin, Germany, 2013; ISBN 978-3-9814495-3-2. [Google Scholar]
- Schmidt-Thomé, P. The Spatial Effects and Management of Natural and Technological Hazards in Europe—ESPON 1.3.1; European Spatial Planning Observation Network Monitoring Committee: Luxembourg, 2006; pp. 1–197. ISBN 951-690-918-3. Available online: https://www.espon.eu/sites/default/files/attachments/fr-1.3.1_revised-full.pdf (accessed on 25 December 2018).
- JRC (European Commission Joint Research Centre). Index for Risk Management—INFORM; Publications Office of the European Union: Luxembourg, 2015. [Google Scholar]
- Shi, P.; Yang, X.; Liu, F.; Li, M.; Pan, H.; Yang, W.; Fang, J.; Sun, S.; Tan, C.; Yang, H.; et al. Mapping Multi-hazard Risk of the World. In World Atlas of Natural Disaster Risk; Shi, P., Kasperson, R., Eds.; Springer: Heidelberg/Berlin, Germany, 2015; ISBN 978-3-662-45430-5. [Google Scholar]
- Shi, P.; Yang, X.; Fang, J.; Wang, J.; Xu, W.; Han, G. Mapping and ranking global mortality, affected population and GDP loss risks for multiple climatic hazards. J. Geogr. Sci. 2016, 26, 878–888. [Google Scholar] [CrossRef]
- Shi, P.; Yang, X.; Xu, W.; Wang, J. Mapping Global Mortality and Affected Population Risks for Multiple Natural Hazards. Int. J. Disaster Risk Sci. 2016, 7, 54–62. [Google Scholar] [CrossRef]
- UNISDR (United Nations International Strategy for Disaster Reduction). From Shared Risk to Shared Value: The Business Case for Disaster Risk Reduction; Global Assessment Report; Disaster Risk Reduction (GAR): Geneva, Switzerland, 2013; ISBN 978-92-1-132038-1. [Google Scholar]
- UNISDR (United Nations International Strategy for Disaster Reduction). Making Development Sustainable: The Future of Disaster Risk Management; Global Assessment Report; Disaster Risk Reduction (GAR): Geneva, Switzerland, 2015; ISBN 978-92-1-132042-8. [Google Scholar]
- UNISDR (United Nations International Strategy for Disaster Reduction). The GAR Atlas: Unveiling Global Disaster Risk; Disaster Risk Reduction (GAR): Geneva, Switzerland, 2017. [Google Scholar]
- Xu, W.; Tian, Y.; Zhang, Y.; Zheng, J.; Fang, W.; Lv, H.; Yang, X.; Wang, R.; Zhao, T.; Shi, P. Integrated Risk Governance: Natural Hazards and Risk Assessment in the Yangtze River Delta Region; Science Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Xu, W.; Zhuo, L.; Zheng, J.; Ge, Y.; Gu, Z.; Tian, Y. Assessment of the Casualty Risk of Multiple Meteorological Hazards in China. Int. J. Environ. Res. Public Health 2016, 13, 222. [Google Scholar] [CrossRef] [PubMed]
- Kappes, M.S.; Keiler, M.; von Elverfeldt, K.; Glade, T. Challenges of analyzing multi-hazard risk: A review. Nat. Hazards 2012, 64, 1925–1958. [Google Scholar] [CrossRef]
- Ordaz, M. A simple probabilistic model to combine losses arising from the simultaneous occurrence of several hazards. Nat. Hazards 2015, 76, 389–396. [Google Scholar] [CrossRef]
- Bernal, G.A.; Salgado-Ga´lvez, M.A.; Zuloaga, D.; Tristancho, J.; Gonza´lez, D.; Cardona, O. Integration of Probabilistic and Multi-Hazard Risk Assessment Within Urban Development Planning and Emergency Preparedness and Response: Application to Manizales, Colombia. Int. J. Disaster Risk. Sci. 2017, 8, 270–283. [Google Scholar] [CrossRef]
- Liu, B.; Siu, Y.L.; Mitchell, G.; Xu, W. Exceedance probability of multiple natural hazards: Risk assessment in China’s Yangtze River Delta. Nat. Hazards 2013, 69, 2039–2055. [Google Scholar] [CrossRef]
- Ming, X.; Xu, W.; Li, Y.; Du, J.; Liu, B.; Shi, P. Quantitative multi-hazard risk assessment with vulnerability surface and hazard joint return period. Stoch. Environ. Res. Risk Assess. 2015, 29, 35–44. [Google Scholar] [CrossRef]
- Li, N.; Liu, X.; Xie, W.; Wu, J.; Zhang, P. The return period analysis of natural disasters with statistical modeling of bivariate joint probability distribution. Risk Anal. 2013, 33, 134–145. [Google Scholar] [CrossRef] [PubMed]
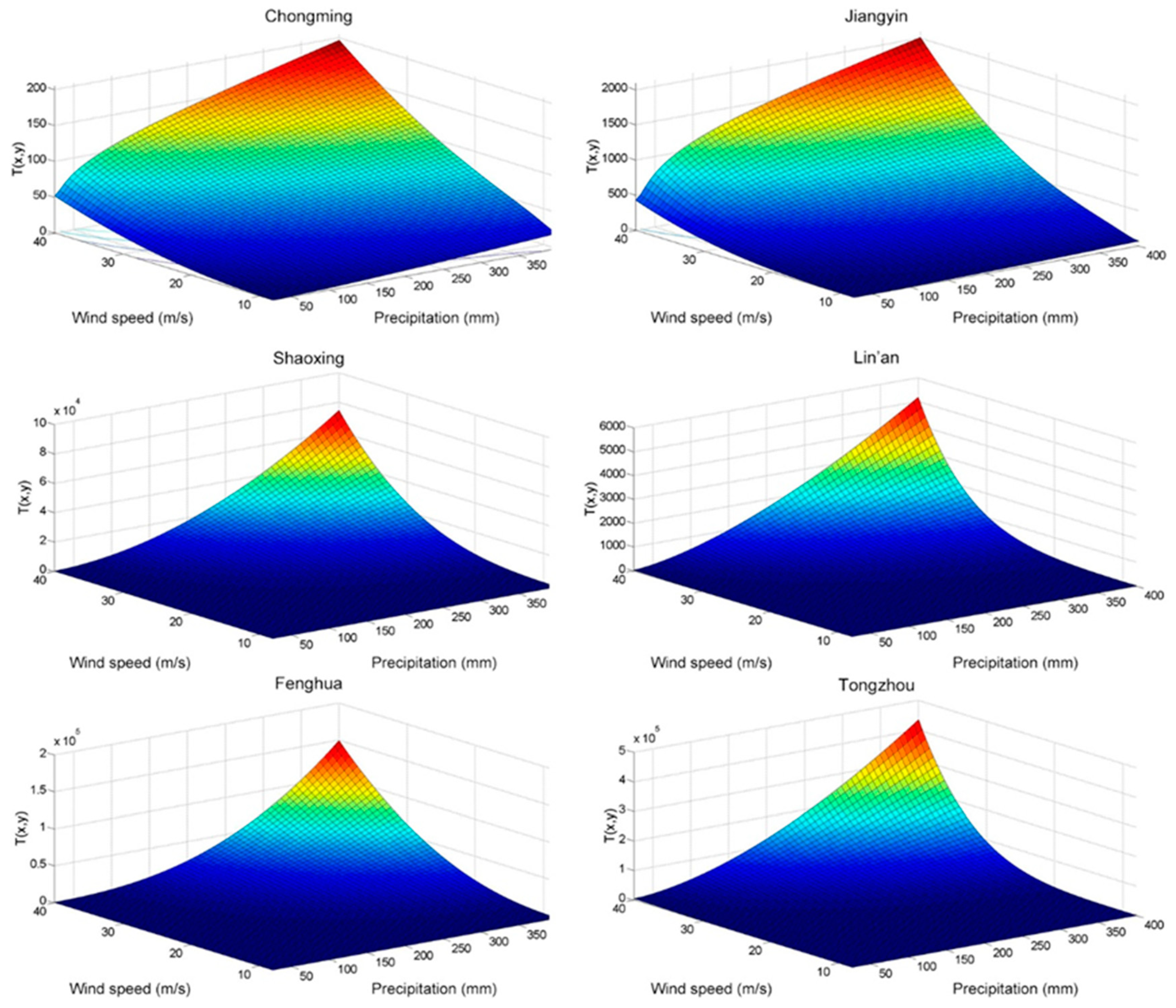
| Parameter | Chongming | Jiangyin | Shaoxing | Lin’an | Fenghua | Tongzhou | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | ||
| 0.77 | 0.47 | 0.66 | 0.36 | 0.51 | 0.31 | 0.65 | 0.13 | 0.38 | 0.42 | 0.58 | 0.21 | ||
| 8.80 | 1.23 | 8.93 | 1.03 | 7.79 | 1.53 | 8.49 | 3.21 | 11.44 | 0.93 | 11.58 | 1.08 | ||
| 32.76 | 9.34 | 33.67 | 9.23 | 32.62 | 9.86 | 32.70 | 11.94 | 37.13 | 9.07 | 36.34 | 9.35 | ||
| Copula | Type | Gumbel | Gumbel | Frank | Frank | Clayton | Clayton | ||||||
| θ | 1.1496 | 1.0807 | -0.3269 | 0.5267 | 0.3587 | 0.5330 | |||||||
| Parameter | A0 | A1 | A2 | A3 | A4 | A5 |
|---|---|---|---|---|---|---|
| Estimated value (10−6) | −5188.03 | 222.86 | 1077.19 | −0.31 | 0.46 | 8.12 |
| Variable | Estimated Value | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Constant | 0.03225403 | 0.01386430 | 2.32640975 | 0.02155579 |
| Land area (X1) | −0.00000005 | 0.00000526 | −0.01034332 | 0.99176335 |
| Crop planting area (X2) | −0.00020566 | 0.00005626 | −3.65557475 | 0.00037223 |
| Average elevation (X3) | −0.00005530 | 0.00002225 | −2.48517400 | 0.01422862 |
| Total population (X4) | 0.00003522 | 0.00014548 | 0.24208981 | 0.80909502 |
| GDP (X5) | −0.00000049 | 0.00000036 | −1.35049321 | 0.17922225 |
| GDP per capita (X6) | 0.00001312 | 0.00004715 | 0.27832100 | 0.78121158 |
| Total rural machinery power (X7) | 0.00000001 | 0.00000002 | 0.46568557 | 0.64222586 |
| Machinery power per square kilometer (X8) | −0.00002247 | 0.00001741 | −1.29055754 | 0.19916546 |
| Variable | Estimated Value | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Constant | 0.02471651 | 0.00763312 | 3.23806313 | 0.00151713 |
| Crop planting area (X1) | −0.00014351 | 0.00004606 | −3.11597140 | 0.00224336 |
| Average elevation (X2) | −0.00003605 | 0.00001543 | −2.33726150 | 0.02090731 |
| GDP per capita (X3) | −0.00000043 | 0.00000016 | −2.76799742 | 0.00643898 |
| County | Return Period (Year) | |||||
|---|---|---|---|---|---|---|
| 10 | 20 | 50 | 100 | 150 | 200 | |
| Chongming | 0.0286 | 0.0357 | 0.0481 | 0.0679 | 0.0871 | 0.1042 |
| Liyang | 0.0118 | 0.0194 | 0.0296 | 0.0345 | 0.0399 | 0.0449 |
| Yizheng | 0.0235 | 0.0307 | 0.0387 | 0.0406 | 0.0425 | 0.0491 |
| Tonglu | 0.0299 | 0.0370 | 0.0454 | 0.0536 | 0.0589 | 0.0630 |
| Dinghai | 0.0432 | 0.0570 | 0.0804 | 0.1055 | 0.1250 | 0.1417 |
| Sanmen | 0.0517 | 0.0664 | 0.1009 | 0.1498 | 0.1981 | 0.2486 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Ming, X.; Ma, Y.; Zhang, X.; Shi, P.; Zhuo, L.; Lu, B. Quantitative Multi-Hazard Risk Assessment of Crop Loss in the Yangtze River Delta Region of China. Sustainability 2019, 11, 922. https://doi.org/10.3390/su11030922
Xu W, Ming X, Ma Y, Zhang X, Shi P, Zhuo L, Lu B. Quantitative Multi-Hazard Risk Assessment of Crop Loss in the Yangtze River Delta Region of China. Sustainability. 2019; 11(3):922. https://doi.org/10.3390/su11030922
Chicago/Turabian StyleXu, Wei, Xiaodong Ming, Yunjia Ma, Xinhang Zhang, Peijun Shi, Li Zhuo, and Bingqiang Lu. 2019. "Quantitative Multi-Hazard Risk Assessment of Crop Loss in the Yangtze River Delta Region of China" Sustainability 11, no. 3: 922. https://doi.org/10.3390/su11030922
APA StyleXu, W., Ming, X., Ma, Y., Zhang, X., Shi, P., Zhuo, L., & Lu, B. (2019). Quantitative Multi-Hazard Risk Assessment of Crop Loss in the Yangtze River Delta Region of China. Sustainability, 11(3), 922. https://doi.org/10.3390/su11030922





