Abstract
Pinus arizonica is a widely distributed tree species growing in temperate forests of Northwest Mexico where it is utilized through different regeneration harvest methods. Yet, management models based on estimations of its productive potential are sorely lacking. In this study, a procedure to create a productive map using site index (SI) equations and Geographic Information Systems (GIS) was developed. A SI model for P. arizonica was created for the study area and used to classify a group of randomly sampled plots on three productivity categories (High, Medium, and Low) for management purposes. Climatic, topographic and edaphic variables were determined on the sampled plots. Then, a statistically-based analysis was performed to identify the climatic, topographic and edaphic variables significantly influencing the productivity levels. Based on the values of these significant variables, a map of productive potential was elaborated for the whole study area. Sites with the highest productivity were those with slopes ≤12°, soil depths ≥0.46 m, minimum and maximum mean annual temperatures of 5 °C and 18 °C respectively, and precipitation ≥900 mm. This methodology could be considered for similar species/conditions where productivity models do not exist or to update old models rendered obsolete by climate change.
1. Introduction
Forest ecosystems play an important role in biodiversity conservation and the provision of ecosystem services, such as timber production and carbon sequestration []. These ecosystems play an important role in the economies of worldwide rural communities [,]. The need to provide forest products to a growing world population despite major obstacles such as climate change, desertification, environmental pollution, and loss of biodiversity is a major challenge for forest managers []. Forest ecosystems have experienced strong degradation due to deforestation, changes in land use and land cover, fires, climate variability and fragmentation [,,,]. Forests in northern Mexico are used extensively for timber extraction but have experienced disturbance by changes in land use by agricultural and pastoral activities, resulting in productivity changes as well as habitat modification for many species of fauna and flora [].
Forest productivity estimations are necessary for both effective forest management decisions and the assessment of site conditions for ecological studies [,]. This knowledge greatly improves the ability to manage forest resources at a specific site, which in turn will help in making cost-effective decisions on the use of silvicultural soil []. Site productivity can be defined in many ways, depending on the objectives of resource managers []. From a forest management perspective, productivity is generally defined as the ability of a site to produce wood volume []. Assessing forest productivity is essential to understand sustainability in forest management because timber extraction should be based on the capacity for recovery of a forest area [].
Commonly, forest monitoring has been carried out by traditional methods, which include extensive field sampling []. However, these methods are highly costly and time-consuming, especially in inaccessible locations [,]. Productivity assessments have traditionally been performed by determining the quality of the forest stands based on the site index (SI) approach []. For more than 100 years, the SI has been implemented as the world’s most widely used forest productivity measure. The SI based decision making serves as the baseline for land use management, forestry investment analysis, and growth and yield predictions [,]. The SI models are generally developed to describe the response of a defined variable, commonly the height of dominant trees [,], with respect to the quality of several edaphic, topographic, climatic and biotic variables [].
For example, Ercanli et al. [] developed a multiple linear regression model in Turkey for Picea orientalis with field sampling data and topographic, soil nutrients and climatic factors. The model explained 77% of the variation between factors and field data. In Ireland, Farrely et al. [] generated a series of models to predict the SI of Picea sitchensis using climate variables and soil chemical factors as predictor variables. Bueis et al. [] developed a discriminant model for estimating SI for Pinus yvestris L. in northern Spain using soil, climatic, and physiographic parameters. Sharma et al. [] also developed a set of multiple linear regressions with different combinations of sites and climatic factors for Picea abies and Pinus silvestris. These studies agree that soil, topographic and climatic variables have the greatest influence on tree height and thus in SI modeling. In addition, studies have highlighted the feasibility of using accessible and low cost tools such as digital elevation models, lidar, or spectral images, to classify forest SI with high accuracy [,,].
The use of SI curves based on height analysis is a preferred estimation of productivity because of the strong relationship between height and age of dominant trees [], i.e., the age of healthy trees can serve as a predictor for the height of the trees. This and other plant-based analysis are called phytocentric methods while the geocentric methods are based on site properties such as climate, topography and soil []. It has been also stated that the productivity analysis should neither be constrained to the use of tree structural variables nor to the use of biophysical variables exclusively []. In many cases the use of both phytocentric and geocentric methods could be highly useful. Other procedures to estimate SI involve the use of some relationships such as the ratio of height/diameter as an inverse measure of productivity [] or the use of non-parametric random forest models to estimate SI as a function of climatic variables []. In many cases, the SI cannot be measured directly and must be estimated from other site characteristics related to climate, topography, and soil []. However, the use of geographic variability is essential to account for local plant growth responses.
The increasing availability of spatially explicit data created by digital mapping using the geographic information system (GIS) allows the development of models with a spatial context for forest management that promise high regional accuracy. The combination of this spatial information with field data provides valuable information on the relationships between site condition and environmental variables []. For this reason, the joint GIS use of the SI is an attractive alternative in forest management [,]. The main benefit of the GIS is the capacity to model environmental problems, including large volumes of spatial data that link processes occurring across space and time []. Prediction models are applied to field data and as a result only provide point estimates of site productivity. The application of geostatistical techniques to layers of point data allows to pass from a point representation to a continuous one, as well as the obtaining of the uncertainty measure of the sites not sampled []. Several studies have been developed to create useful maps for forest management [,,,]. However, attempts to map geospatial attributes to measure forest productivity have been limited []. To bridge the gap between geospatial information, the relationship with forest productivity and reduce fieldwork, SI and GIS as a set of spatial variables such as climate, soil, and topography, allow the development of maps, which could be effective tools for managing complex ecosystems [,,]. Recent approaches to bridge the gap between geospatial information and its relationship to SI have been employed by Waring et al., (2014) [], where they used a forest growth model based on 3-PG (Physiological Principles Predicting Growth) processes using satellite estimates of the Maximum Foliar Area Index contrasting it with the site’s growth potential for Pseudotsuga menziesii and thus visualizing its variation in the western region of North America. Brandl et al., (2014) [] used national forest inventory information from the state of Bavaria, Germany, together with maps derived from the digital elevation model, temperature and precipitation maps, soil maps, to spatially predict the productivity of the SI, using the Generalized Additive Model. Mestre et al., (2017) [] used geospatial slope and exposure variables together from a productivity index map constructed using a multi-Gaussian Kriging method in a geographic information system, where they evaluated high, intermediate, and low productivity levels.
Despite the development of allometric equations and fitting models for SI [], the incorporation of geospatial variables influencing tree growth and the use of GIS tools have been poorly studied and applied to forests management in Mexico. This is particularly the case of the temperate forests of Northwest Mexico, where Pinus arizonica Engelm is a species distributed on a wide range of soil and topographic conditions []. The need for current forest productivity estimations, not only in Mexico but worldwide, arises also because of contemporary climate change, as forest growth estimations based on decades-old equations may not reflect current tree growth rates [].
Pinus arizonica is a key species of great ecological, economic, and social importance in the Sierra Madre Occidental, which includes the states of Chihuahua and Durango, Mexico [,]. Yet, little information exists on its productivity related to the spatial environmental variability and thus timber utilization cannot have a sustainability target. Here, we attempted to analyze the validity and usefulness of growth curves linked to GIS techniques to generate an easy-to-use geographic model to predict tree productivity. The objectives of this study were (1) to develop a SI model for P. arizonica under the conditions of southern Chihuahua, Mexico, considering the height and age of dominant trees, and (2) to create a spatial model to display the landscape productivity for this species as a function of topographic, climatic and edaphic variables on a scale relevant to regional forest management. We used the Schumacher model as basis for our SI analysis and the obtained productivity classes were assigned according to the conditions of physical variables in the field to obtain useful predictor maps. The results could be used by forest managers and planners to better understand forest productivity and to implement decisions based on sustainable forest management plans. Likewise, geospatial information could be useful for territorial ecological ordering considering the spatial distribution of forest productivity.
2. Materials and Methods
2.1. Study Area
This study was conducted in the area of Guadalupe y Calvo, Chihuahua, which is part of the Sierra Madre Occidental, in Northwest Mexico (Figure 1). This area was chosen because P. arizonica is a key species naturally and amply distributed in these forest ecosystems. The altitude of the study area ranges from 1600 m to 3020 m, with an average slope of 33% (Table 1). The most common soil types are regosols and lithosols with an average A-horizon depth of 33 cm, about 23% of rockiness, and an average mulch depth of 2 cm. The predominant climate is temperate sub-humid with an annual precipitation between 576 mm to 1248 mm, mainly occurring as rainfall in the summer, and with occasional snowfall occurring from December to February. In this region, the main productive activities are timber harvesting, cattle ranching, rainfed agriculture, and mining. The forests of this region are of great economic importance and, particularly, P. arizonica is one of the most exploited species due to its timber quality [].
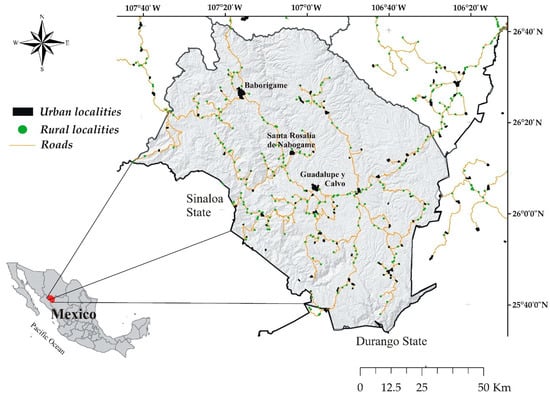
Figure 1.
Location of the study area in the Guadalupe y Calvo municipality, Chihuahua, Mexico.

Table 1.
Summary of site and forest characteristics of the P. arizonica sampled plots of the study.
2.2. Methodological Outline and Data
To create a spatial model of productivity we used physical variables of soil, topography and climate. The general methodological outline to elaborate such spatial model appears in Figure 2. The information was obtained from pure and mature stands of P. arizonica distributed over different aspects. We selected 42 P. arizonica dominant trees (tallest trees of the stands) from different conditions of slope, soil depth and aspect in the study area. Then, we carried out a stem analysis following the methodology proposed by the British Columbia Forest Productivity Council []. Each tree was harvested to subsequently perform cross-sectional cuts at 0.30 m, 1.30 m (diameter at breast height or DBH) and every 2 m until the stem reached 10 cm in diameter. The length of the remaining tip was recorded. Following guidelines, we counted the number of annual rings, measured diameters of the stem transverse cross sections, and estimated the height of the tree at different ages. This information integrated the database of height-age data pairs to perform the SI analysis.
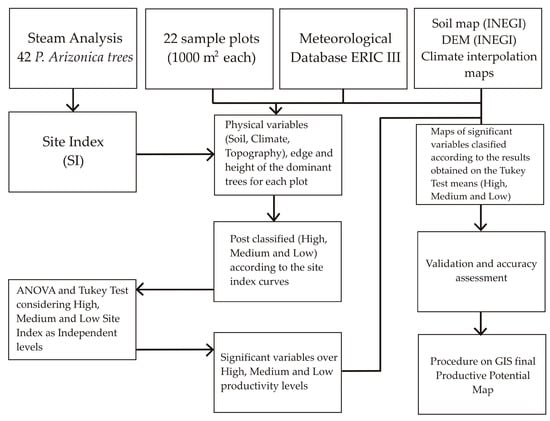
Figure 2.
Framework used to develop the productivity potential map of P. arizonica based on a site index model. ERIC: Extractor Rápido de Información Climatológica (source of climatic information from Mexico), DEM: digital elevation model. INEGI: Instituto Nacional de Geografía e Informática (National Institute of Geography and Informatics) (Mexico). ANOVA: Analysis of Variance.
To identify the influence of the physical variables over the forest productivity 220 circular plots of 1000 m2 each with the presence of P. arizonica were located and sampled by using a 5 km systematic design. Every site was georeferenced using a Garmin Etrex Global Positioning System (GPS) and then the height and the age of the two dominant trees were registered for each plot. The height was measured with a Suunto clinometer, whereas the age was determined by counting the trees annual rings through samples extracted with a Pressler drill. At the center of each sampling plot we recorded slope and aspect and located a 1 m2 sub-plot to determine percent bare soil area, pedregosity, and litter depth. Also, a soil pit was dug adjacent to the subplot to determine soil depth. We also included in the database climate variables such as the means of minimum and maximum annual temperatures and annual precipitation from a time series of 64 years (1940–2004). Climate data were obtained from ERIC III, a historical weather information depository provided by the Mexican Meteorological Service (Mexican Institute of Water Technology) [] (https://www.imta.gob.mx/productos/software/eric-iii-version-3-2-extractor-rapido-de-informacion-climatolo-detail). The selected climate data corresponded to weather stations placed around and within the study area.
2.3. Site Index Model
In this study, the Schumacher model (Equation (1)) (see Palahi et al. [] for details) was evaluated.
where H is the dominant height (m); E is the age (years); and β0 and β1 are empirical parameters of the model. Our analysis considered a tree base age of 80 years. This model was tested using the guide curve (GC) methodology []. To evaluate the results of the model we considered the value of the root mean square error (RMSE), the value of R2, and the distribution of residuals.
2.4. Analysis
The analysis to determine the best-fitted model was performed through the NLIN procedure and the DUD method by using the Statistical Analysis System version 10.1 (SAS Inc® Cary, NC, USA). The Shapiro–Wilk test was conducted to verify compliance with the assumptions of regression. Additionally, the relative and cumulative residual frequencies were obtained. These frequencies resemble a straight line with respect to the probability of normal distribution and the corresponding percentages resemble a Gauss-bell curve [].
We used the predicted height according to the model using the guide curve method, and then a group of anamorphic site index curves were fitted. Tree growth was stratified in three quality classes (25 m = High, 21 m = Medium and 12 m = Low). The curves showing the growth trend were constructed by holding the shape parameters of the chosen model constant and varying the asymptote parameter as necessary to achieve the required dominant height when the tree age equaled base age, which was 80 years in this study. This approach has been used in previous studies [].
The three height classes generated with the Schumacher model were used to assign the quality level of productivity to each of the 220 plots according to the height-age data of their dominant trees. Then, we performed analyses of variance (ANOVA) to determine if each of the physical variables recorded from the plots significantly influence the productivity level (High, Medium, and Low). A comparison of means with the Tukey test (α = 0.1) was also performed to determine differences of such variables among productivity levels.
In a following step, a spatial layer for each of the physical variables significantly influencing the productivity level was created with the software ArcGIS 10.2 []. The layer of topography (slope) was elaborated from a Digital Elevation Model (DEM) 1:50,000 []. The layer of soil depth was taken from a soil digital map of the state of Chihuahua, Mexico. The climatic layers (precipitation and temperatures) were created by interpolating the data of climate variables obtained from ERIC III. Interpolation was based on the Inverse Distance Weighting method [], employing the Geostatistical Wizard available in the software ArcGIS 10.2 []. The cell size used for all the layers was of 25 m.
For each layer, their values were categorized in three levels of productivity; High (3), Medium (2), or Low (1), according to the results from the Tukey tests. Then, the mean value of each level was assigned to the pixels based on their corresponding category. Once categorized, the layers were summarized (slope + soil depth + mean minimum temperature + mean maximum temperature + precipitation). As a result, a map was created, which was then reclassified in three equal intervals (High, Medium, and Low) to create the productive potential map.
To validate this new map model, age and height of the trees were taken from a random sample of 190 sites within the study area. The effectiveness of the productive potential map was assessed with the KAPPA Index, which is denoted by Equation (2) []
where: KAPPA = Kappa index, k = number of matrix files, xii = observation number of row i and column i (along the diagonal), xi+ and x+i = Total marginal for row i and column i, respectively, and N = total number of observations. To characterize the level of agreement suggested by the KAPPA index, we used the qualitative descriptors pointed out by Monserud and Leemans []. These authors classified the effectiveness as poor (0–0.4), fair (0.4–0.55), good (0.55–0.7), very good (0.7–0.85), and excellent (0.85–1.0).
3. Results
Descriptive statistics of the diameter at breast height (DBH) and height at different ages of the dominant trees used to fit the SI model are shown in Table 2. We considered records of every ten years. Such records were gotten from a stem analysis performed by following the methodology proposed by the British Columbia Forest Productivity Council []. The maximum height registered from the trees was 25.6 m at an age of 90 years, with diameters of 33.1 ± 6.1 cm, which may indicate the existence of high variability in the productivity of the study area. This may be an effect of the high topographic and soil variability of the sites where the trees grew. This response could be observed in young (10–30 years), as well as in full mature trees (50–90 years).

Table 2.
Descriptive statistics of the sampled trees.
The Schumacher model [] showed an adequate fit to the stem analysis data (Table 3). Although we initially found positive autocorrelation in the residuals, estimated with the Durbin–Watson statistic (DW = 0.33), the autocorrelation was corrected (DW = 1.4) by applying two delays in the residuals using a CAR (2) shape structure []. The quality of the SI model adjustment for P. arizonica was then in compliance with the assumptions of normality of the regression sample errors, since the SW test was acceptable with W normal = 0.99. In addition, no trend was observed on the variance of the residual distribution, thus discarding heteroscedasticity.

Table 3.
Statistical fit for the Schumacher model, parameters values and their significance.
The resulting equation used to classify the SI on the study area was H = 25.21029e−31.7766 E−1. By using this equation, the guide curve was estimated considering a base age of 80 years. Upon defining the base age and the trend of the guide curve, the SI was established at 25 m, 21 m, and 12 m for High, Medium, and Low levels of productivity, respectively. This fitted model produced the height curves shown in Figure 3. These curves were plotted together with the observed data. The shape of the curves is very close to the shape of the observed data with realistic asymptotes and growth patterns. This allowed us to assign the levels of productivity to the group of plots sampled on the field.
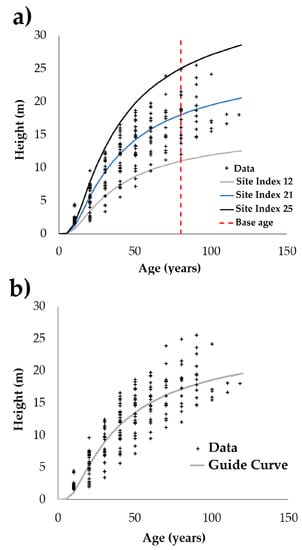
Figure 3.
Graphical representation of the Site Index for P. arizonica Engelm fitted by using the Schumacher model (a) and the guide curve method (b).
The ANOVA results showed statistical differences among productivity levels for slope, precipitation, minimum and maximum temperature, and soil depth. As previously stated, autocorrelation was not a limiting factor for our result analysis. The values associated to the highest productivity level of P. arizonica through the selected model were 12° of slope, 46 cm of soil depth, 901 mm of precipitation, as well as 5 °C and 18 °C of minimum and maximum mean annual temperature, respectively (Table 4).

Table 4.
Mean values of physical variables in areas with different productivity levels of P. arizonica in the area of Guadalupe y Calvo, Chihuahua, Mexico.
Following the methodology, the map of productivity was created, and an estimation of the surface for each productivity class was made. The sites with High productivity in the area occupied by the temperate forest corresponded to 6.5% (43,112 ha), whereas the sites with Medium and Low productivity corresponded to 60.4% (402,887 ha), and 33.1% (220,679 ha) of the study area, respectively (Figure 4). The rest of the surface (26%) (236,480 ha) is considered as non-forest area and corresponded to deciduous forest with an elevation lower than 1800 m, where the presence of P. arizonica was not detected. The accuracy of the spatial model was assessed by comparing values from the map with records of productivity measured on the field. The estimated value for KAPPA Index was 0.79 ± 0.08, resulting in a very good agreement.
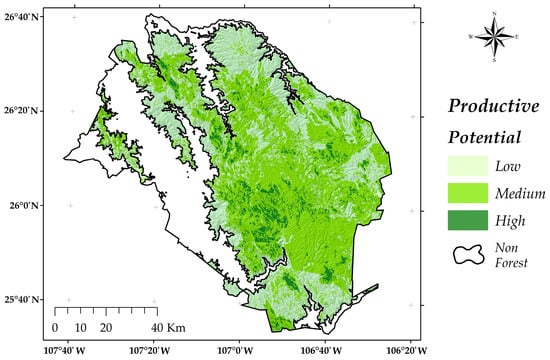
Figure 4.
Spatial model of productivity of Pinus arizonica in the area of Guadalupe y Calvo, Chihuahua, Mexico.
4. Discussion
Estimating the distribution of the productive potential through traditional sampling is a costly and time-consuming activity []. In this study we show a parsimonious methodology that allows mapping the spatial distribution of the productive potential of P. arizonica which has been carried out in other countries such as Germany [], Spain [], and Finland []. Forest productivity estimations are essential to achieve a sustainable forest management []. The most utilized indirect method worldwide is modeling height of dominant trees []. This is generally performed with data pairs of age-height from stem analysis of trees growing in permanent monitoring plots []. The use of data from stem analysis has been extensively documented []. Thus, we used stem analysis data to fit the P. arizonica SI model. Our study constitutes a methodological proposal for mapping and documenting the SI in the northwestern region of the state of Chihuahua, using field information and GIS. Because of the high adjustment value that we obtained, our ability to map local information (weather stations) and available spatial information (digital elevation model, soil map), the proposed approach confirms the successful use of GIS, field data sets, and overlapping of layers. This offers the possibility for land managers to obtain and generate accurate information at the scales of their interest and with information from their inventories.
Our results showed an adequate growth prediction for all tree ages, which ratifies the effectiveness of this procedure in our study area. Since acceptable statistical and graphical results were obtained with the Schumacher model in this study, testing more equations was considered not necessary. Due to the close relationship between tree height and tree age that we found for P. arizonica (R2 = 0.93) our results are comparable to SI models obtained for a hybrid Larix x eurolepis in Sweden (R2 = 0.99) [], P. silvestris in Spain (R2 > 0.92) [], and other pine species in Mexico (R2 > 0.96) []. The statistical analysis clearly showed that the SI is adequate to measure forest productivity as indicated by the study carried out by Günlü et al. [] in an unmanaged forest where analyze the relationship between direct and indirect methods using the Chi-square test. The test indicated a statistically significant relationship between the SI determined by the indirect method is satellite imagery.
Even though high levels of agreement between the real and predicted values can be achieved with the SI models, they still present some limitations. Such limitations include that these models are developed and are effective for monospecific and even age stands. In addition, for the development of these models it is supposed that the quality of the stand is calculated from the information of the specific points in which the sampled trees are located; however, it does not include the variability of the physical or biological variables all over the stand [] and geographical location between ecoregions [].
Moreover, thinning or hard grading tend to modify the height of the trees growing in the stand, which also modifies the dominant height causing over or sub estimations on the trend of the trees growth. In these cases, the use of soil-site relationships is more suitable for estimating site quality []. With these limitations in mind our modeling results had adequate agreement with our ground-truth comparisons []. The visual interpretation of the SI and the map of productive potential revealed an expected agreement with the topographic variations and the distribution of the SI, found in the study area. The High SI level appeared near urban–rural areas, indicating the presence of management in the forests, while the Low productive potential SI appear in the most remote areas, where the forests are possibly unmanaged, affecting the quality of the SI [].
Our results highlight the importance of relating SI models with direct methods through the use of biophysical variables to generate continuous models that are acceptable and easy to understand. We integrated a procedure combining both direct and indirect methods to generate spatial maps of productivity. We accomplished that by classifying the biophysical variables influencing the height of dominant trees. Our findings showed that slope, precipitation, minimum and maximum temperature, as well as soil depth are the five variables with the highest relationship with the SI model of P. arizonica. The spatial distribution of the SI was consistent with the gradient of temperature and precipitation in the municipality. Therefore, an increase in SI productivity is probably the result of increased precipitation and low temperatures which is documented by Reich et al. [] and Peters et al. []. The approach of this study shows that field work together with digital maps of slope, precipitation, minimum and maximum temperature, as well as soil depth provide a representative sample of the relationship between average forest productivity across the SI and the variability of biophysical conditions as reported by Waring et al. [] at least on a regional scale [].
That allowed elaborating a productivity map with a good accuracy. Productivity maps as developed with our procedure can be a useful and handy tool for forest managers as the maps show spatial patterns easy to visualize. Besides, maps created by these procedures could allow to estimate forest productivity even in areas where no forest inventories exist [].
The values associated to the highest productivity level of P. arizonica, through the selected model were 12° of slope, 46 cm of soil depth, and 5 °C and 18 °C of minimum and maximum annual temperature, respectively. Our results agree with other findings obtained for forest areas of Mexico, where productivity is commonly affected by slope, aspect and soil depth []. In agreement with this, it has been reported that soil variables may explain about 55% of the variation in forest productivity []. Other studies have found influence by other more specific variables such as soil pH and organic matter []. This is due to the scale of work we use, which is a regional scale []. If more detailed investigations are conducted, probably some other micro variable could be found influencing the growth of the trees. Yet, when trying to incorporate micro variables on mapping procedures, map generation could be prohibitively expensive and time consuming [].
Multiple regression techniques and multivariate analysis have also been effective in the evaluation of forest productivity when employing direct methods because they allow inferring on the influence of complex variables over the variability of the productivity phenomenon []. Some examples of these are studies developed for Picea in forest of Turkey [], which reported R2 values of 0.77 when variables of soil, climate and topography were included in the analysis. Moreover, another study carried out also in Turkey compared three methods for the estimation of productivity: (1) indirect model of dominant height with guide curve, (2) direct, using soil samples, and (3) using satellite images. Differences among the methods were non-significant and the authors recommended the use of direct methods, especially in degraded and open land areas [].
Our findings confirm the importance of using direct or combined methods to evaluate productivity of dry forest, such as the forest in northern Mexico. The use of maps of productivity could also offer reliable and easy to apply tools for the local forest managers. Additionally, the maps of productivity, which were created by using the influence of biophysical variables over species growth, could also allow to spatially classifying the productivity of lands without presence of trees. That could be useful for multiple purposes such as the establishment of forest plantations with the studied species [,]. However, the establishment of monitoring plots could be valuable to evaluate the productive variability of the species with a greater precision, also considering some factors such as the genetic variability [] or the influence of forest, agricultural or livestock exploitation activities. Overall, we agree with Rodhouse et al. [] that biogeographic modeling is a parsimonious approach to connect land management decisions with spatial monitoring.
Based on our results, we recommend the use of variables such as slope, temperature, and soil depth to perform cartographic studies and to estimate the productivity of these types of ecosystems in similar parts of Mexico and the world. The use of outdated growth forest models may be risky considering that global modification of climate is altering current vegetation growth patterns []. We expect our results and models to provide sorely needed tools that can be adopted for forest management in other regions of Mexico as part of the national strategy to increase forest productivity and production (Estrategia Nacional de Manejo Forestal Sustentable para el Incremento de la Producción y Productividad—ENAIPROS).
5. Conclusions and Recommendations
The combination of phytometric (SI models) and geocentric analysis provides a powerful tool for forest productivity. The use of variables such as slope, temperature, and soil depth to perform cartographic studies aimed at estimating forest productivity in temperate, mountainous, sub-humid areas was supported by our results. Based on the values of these significant variables, a map of productive potential was elaborated for the whole study area. Sites with the highest productivity have slopes ≤12° with soil depths ≥0.46 m, with minimum and maximum mean annual temperatures of 5 °C and 18 °C respectively, and precipitation ≥900 mm (α ≤ 0.1).
We recommend to generate growth forests models where they do not exist and to update old models following the methodology we proposed here. The use of outdated growth forest models involves the risk of assuming growth patterns that do exist any longer because of environmental changes imposed by climate change. We expect our results and models to provide sorely needed tools that can be adopted for forest management in Mexico.
Additionally, these results could be used to identify sites for the potential establishment of permanent monitoring plots to learn more about the dynamics of forest growth. For further research, we recommend to carry out more detailed studies about the influence of variables such as genetic diversity, forest exploitation or anthropogenic activities like agriculture and livestock, on the productive variability of forest species.
Author Contributions
M.M.-S., A.P.-A. and G.V.-Q. conceived and designed the research; J.A.P.-A., C.R.M.-N. and F.V.-G., processed the data, analyzed it and elaborated the first draft; R.M.-G. substantially contributed to the editions and final revision of the present manuscript.
Funding
This work was supported by the Comisión Nacional Forestal of Mexico (Grant number. C0310027) and the Consejo Nacional de Ciencia y Tecnología (CONACYT). CONACYT provided a postdoctoral fellowship to the first author at Oregon State University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weiskittel, A.R.; Crookston, N.L.; Radtke, P.J. Linking climate, gross primary productivity, and site index across forests of the western United States. Can. J. For. Res. 2011, 41, 1710–1721. [Google Scholar] [CrossRef]
- Babulo, B.; Muys, B.; Nega, F.; Tollens, E.; Nyssen, J.; Deckers, J.; Mathijs, E. The economic contribution of forest resource use to rural livelihoods in Tigray, Northern Ethiopia. For. Policy. Econ. 2009, 11, 109–117. [Google Scholar] [CrossRef]
- Youn, Y.C. Use of forest resources, traditional forest-related knowledge and livelihood of forest dependent communities: Cases in South Korea. For. Ecol. Manag. 2009, 257, 2027–2034. [Google Scholar] [CrossRef]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manag. 2006, 225, 378–390. [Google Scholar] [CrossRef]
- Mas, J.F.; Velázquez, A.; Díaz-Gallegos, J.R.; Mayorga-Saucedo, R.; Alcántara, C.; Bocco, G.; Castro, R.; Fernandez, T.; Pérez-Vega, A. Assessing land use/cover changes: A nationwide multidate spatial database for Mexico. Int. J. Appl. Earth. Obs. 2004, 5, 249–261. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidi, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Taubert, F.; Fischer, R.; Groeneveld, J.; Lehmann, S.; Müller, M.S.; Rödig, E.; Wiegand, T.; Huth, A. Global patterns of tropical forest fragmentation. Nature 2018, 554, 519–522. [Google Scholar] [CrossRef]
- Návar, J. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. For. Ecol. Manag. 2009, 257, 427–434. [Google Scholar] [CrossRef]
- Altun, L.; Başkent, E.Z.; Bakkaloğlu, M.; Günlü, A.; Kadioğullari, A.İ. Comparing methods for determining forest sites: A case study in Gümüşhane-Karanlıkdere forest. Eur. J. For. Res. 2008, 127, 395. [Google Scholar] [CrossRef]
- Kodani, E.; Tarumi, A.; Awaya, Y. Estimating Forest Productivity of Manmade Coniferous Forest Stands Using Low Density Lidar. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 628–630. [Google Scholar]
- Ercanli, I.; Gunlu, A.; Altun, L.; Zeki Baskent, E. Relationship between site index of oriental spruce [Picea orientalis (L.) Link] and ecological variables in Maçka, Turkey. Scand. J. For. Res. 2008, 23, 319–329. [Google Scholar] [CrossRef]
- Mohamed, A.; Reich, R.M.; Khosla, R.; Aguirre-Bravo, C.; Briseño, M.M. Influence of climatic conditions, topography and soil attributes on the spatial distribution of site productivity index of the species rich forests of Jalisco, Mexico. J. For. R. 2014, 25, 87–95. [Google Scholar] [CrossRef]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; Waveland Press: Long Grove, IL, USA, 2015; pp. 211–229. ISBN 1-4786-2908-8. [Google Scholar]
- Richardson, B.; Skinner, M.F.; West, G. The role of forest productivity in defining the sustainability of plantation forests in New Zealand. For. Ecol. Manag. 1999, 122, 125–137. [Google Scholar] [CrossRef]
- Fox, D.M.; Maselli, F.; Carrega, P. Using SPOT images and field sampling to map burn severity and vegetation factors affecting post forest fire erosion risk. Catena 2008, 75, 326–335. [Google Scholar] [CrossRef]
- Runkle, J.R. Guidelines and Sample Protocol for Sampling Forest Gaps; Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1992; p. 283. [Google Scholar]
- Vásconez, N.L.; Sevilla, H.C. Uso De Los Sensores Remotos En Mediciones Forestales. Eur. Sci. J. 2018, 14. [Google Scholar] [CrossRef]
- Stearns-Smith, S. Making sense of site index estimates in British Columbia: A quick look at the big picture. J. Ecosyst. Manag. 2001, 1, 1–4. [Google Scholar]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Carmean, W.H. Forest site quality evaluation in the United States. Adv. Agron. 1975, 27, 207–269. [Google Scholar] [CrossRef]
- Shen, C.; Lei, X.; Liu, H.; Wang, L.; Liang, W. Potential impacts of regional climate change on site productivity of Larix olgensis plantations in northeast China. iForest 2015, 8, 642. [Google Scholar] [CrossRef]
- Farrelly, N.; Dhubhain, A.N.; Nieuwenhuis, M. Site index of Sitka spruce (Picea sitchensis) in relation to different measures of site quality in Ireland. Can. J. For. Res. 2011, 41, 265–278. [Google Scholar] [CrossRef]
- Bueis, T.; Bravo, F.; Pando, V.; Turrión, M.B. Relationship between environmental parameters and Pinus sylvestris L. site index in forest plantations in northern Spain acidic plateau. iForest 2016, 9, 394. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway. Scand. J. For. Res. 2012, 27, 619–636. [Google Scholar] [CrossRef]
- Socha, J.; Pierzchalski, M.; Balazy, R.; Ciesielski, M. Modelling top height growth and site index using repeated laser scanning data. For. Ecol. Manag. 2017, 406, 307–317. [Google Scholar] [CrossRef]
- Clutter, J.L.; Fortson, J.C.; Peinar, L.V.; Bailey, R.L. Timber Management: A quantitative Approach, 1st ed.; Wiley: New York, NY, USA, 1983; pp. 1–333. ISBN 978-0894647475. [Google Scholar]
- Meyer, H.A. A mathematical expression for height curves. J. For. 1940, 38, 415–420. [Google Scholar]
- Crookston, N.L.; Rehfeldt, G.E.; Dixon, G.E.; Weiskittel, A.R. Addressing climate change in the forest vegetation simulator to assess impacts on landscape forest dynamics. For. Ecol. Manag. 2010, 260, 1198–1211. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Muys, B. Evaluation of modelling techniques for forest site productivity prediction in contrasting ecoregions using stochastic multicriteria acceptability analysis (SMAA). Ann. For. Sci. 2011, 26, 929–937. [Google Scholar] [CrossRef]
- Brandl, S.; Falk, W.; Klemmt, H.J.; Stricker, G.; Bender, A.; Rötzer, T.; Pretzsch, H. Possibilities and limitations of spatially explicit site index modelling for spruce based on National Forest Inventory data and digital maps of soil and climate in Bavaria (SE Germany). Forests 2014, 5, 2626–2646. [Google Scholar] [CrossRef]
- González, J.G.Á.; González, A.D.R.; Soalleiro, R.R.; Anta, M.B. Ecoregional site index models for Pinus pinaster in Galicia (northwestern Spain). Ann. For. Sci. 2005, 62, 115–127. [Google Scholar] [CrossRef]
- Mestre, S.; Alegria, C.; Albuquerque, M.T.D.; Goovaerts, P. Developing an index for forest productivity mapping-A case study for maritime pine production regulation in Portugal. Rev. Árvore 2017, 41. [Google Scholar] [CrossRef]
- Goodchild, M.; Haining, R.; Wise, S. Integrating GIS and spatial data analysis: Problems and possibilities. Int. J. Geogr. Inf. Syst. 1992, 6, 407–423. [Google Scholar] [CrossRef]
- Pelissari, A.L.; Caldeira, S.F.; Figueiredo Filho, A.; Amaral, M.S. Propostas de mapeamentos da capacidade produtiva de sítios florestais por meio de análises geoestatísticas. Sci. For. 2015, 43, 601–608. [Google Scholar]
- Ollinger, S.V.; Aber, J.D.; Federer, A. Estimating regional forest productivity and walter yield using an ecosystem model linked to a GIS. Landsc. Ecol. 1998, 13, 323–334. [Google Scholar] [CrossRef]
- Payn, T.W.; Hill, R.B.; HÖck, BK.; Skinner, M.F.; Thorn, A.J.; Rijkse, W.C. Potential for the use of GIS and spatial analysis techniques as tools for monitoring changes in forest productivity and nutrition, a New Zealand example. For. Ecol. Manag. 1999, 122, 187–196. [Google Scholar] [CrossRef]
- Korkalainen, T.; Laurén, A. Using phytogeomorphology, cartography and GIS to explain forest site productivity expressed as tree height in southern and central Finland. Geomorphology 2006, 74, 271–284. [Google Scholar] [CrossRef]
- Minowa, Y.; Suzuki, N.; Tanaka, K. Estimation of site indices with an artificial neural network (in Japanese with English abstract). Jpn. J. For. Plan. 2005, 39, 23–38. [Google Scholar]
- Waring, R.H.; Coops, N.C.; Mathys, A.; Hilker, T.; Latta, G. Process-based modeling to assess the effects of recent climatic variation on site productivity and forest function across Western North America. Forests 2014, 5, 518–534. [Google Scholar] [CrossRef]
- Tang, D.; Bian, F. Forest Site Evaluation Based on GIS and Kriging. In Proceedings of the First International Conference on Information Science and Engineering, Nanjing, Jiangsu, China, 26–28 December 2009. [Google Scholar]
- Wulder, M.; White, J.; Fournier, R.; Luther, J.; Magnussen, S. Spatially explicit large area biomass estimation: Three approaches using forest inventory and remotely sensed imagery in a GIS. Sensors 2008, 8, 529–560. [Google Scholar] [CrossRef]
- Corral-Rivas, J.J.; Alvarez-Gonzalez, J.G.; Ruız-Gonzalez, A.D.; Von-Gadow, K. Compatible height and site index models for five pine species in El Salto, Durango (Mexico). For. Ecol. Manag. 2004, 201, 145–160. [Google Scholar] [CrossRef]
- Alanis Morales, H.; Navar, J.; Dominguez, P.A. The effect of prescribed burning on surface runoff in a pine forest stand of Chihuahua, Mexico. For. Ecol. Manag. 2000, 137, 199–207. [Google Scholar] [CrossRef]
- Tarango, J.A.; Valdez, R.; Zwank, P.J.; Cardenas, M. Mexican spotted owl characteristics in Southwestern Chihuahua, Mexico. Southwest. Nat. 1997, 42, 132–136. [Google Scholar]
- Crecente-Campo, F.; Corral-Rivas, J.J.; Vargas-Larreta, B.; Wehenkel, C. Can random components explain differences in the height–diameter relationship in mixed uneven-aged stands? Ann. For. Sci. 2014, 71, 51–70. [Google Scholar] [CrossRef]
- Chávez Rodriguez, N. Estudio Regional Forestal. Asociación Regional de Silvicultores De Guadalupe y Calvo, A.C. Unidad De Manejo Forestal No. 0808 Guadalupe Y Calvo, Chihuahua. Available online: http://www.conafor.gob.mx:8080/documentos/docs/9/1147ERF_UMAFOR0808.pdf (accessed on 20 December 2016).
- British Columbia Forest Productivity Council (BCFPC). Minimum Standards and Stem Analysis Procedures for Site Index Research. Forest Productivity Council; BCFPC: Victoria, BC, Canada, 1998; pp. 1–13. [Google Scholar]
- Instituto Mexicano de Tecnología del Agua (IMTA). Banco de datos histórico nacional del Servicio Meteorológico Nacional. Base de datos digital; Instituto Mexicano de Tecnología del Agua: Mexico City, Mexico, 2006. [Google Scholar]
- Palahí, M.; Tome, M.; Pukkala, T.; Trasobares, A.; Montero, G. Site index model for Pinus sylvestris in northeast Spain. For. Ecol. Manag. 2004, 187, 35–47. [Google Scholar] [CrossRef]
- SAS Institute Help and Documentation, version 9.1.3; SAS Institute Inc.: Cary, NC, USA, 2006.
- Onyekwelu, J.C. Site index curves for site quality assessment of nauclea diderrichii monoculture plantations in Omo Forest Reserve, Nigeria. J. Trop. For. Sci. 2005, 17, 532–542. [Google Scholar]
- ArcGIS Desktop: 10.2. Environmental Systems Research Institute (ESRI) Home Page. Available online: www.esri.com (accessed on 26 September 2017).
- Instituto Nacional de Estadística, Geografía e Informática (INEGI). Continúo de elevaciones mexicano 3.0. Available online: http://www.inegi.org.mx/geo/contenidos/datosrelieve/continental/Descarga.aspx (accessed on 8 December 2016).
- Burrough, P.A.; McDonnell, R. Principles of Geographical Information Systems, 2nd ed.; Oxford University Press: Oxford, UK, 1998; pp. 1–356. ISBN 9780198233664. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Monserud, R.A.; Leemans, R. Comparing global vegetation maps with the Kappa statistic. Ecol. Model. 1992, 62, 275–293. [Google Scholar] [CrossRef]
- Zimmerman, D.L.; Nunez-Anton, V. Parametric modelling of growth curve data: An overview. Test 2001, 10, 1–73. [Google Scholar] [CrossRef]
- Seynave, I.; Gégout, J.C.; Hervé, J.C.; Dhôte, J.F.; Drapier, J.; Bruno, É.; Dumé, G. Picea abies site index prediction by environmental factors and understorey vegetation: A two-scale approach based on survey databases. Can. J. For. Res. 2005, 35, 1669–1678. [Google Scholar] [CrossRef]
- Bolte, A.; Ammer, C.; Löf, M.; Madsen, P.; Nabuurs, G.J.; Schall, P.; Spathelf, P.; Rock, J. Adaptive forest management in central Europe: Climate change impacts, strategies and integrative concept. Scand. J. For. Res. 2009, 24, 473–482. [Google Scholar] [CrossRef]
- Curt, T.; Bouchaud, M.; Agrech, G. Predicting site index of Douglas-fir plantations from ecological variables in the Massif Central area of France. For. Ecol. Manag. 2001, 149, 61–74. [Google Scholar] [CrossRef]
- Solberg, S.; Dobbertin, M.; Reinds, G.J.; Lange, H.; Andreassen, K.; Fernandez, P.G.; Hildingsson, A.; de Vries, W. Analyses of the impact of changes in atmospheric deposition and climate on forest growth in European monitoring plots: A stand growth approach. For. Ecol. Manag. 2009, 258, 1735–1750. [Google Scholar] [CrossRef]
- Johansson, T. Site index curves for young hybrid larch growing on former farmland in Sweden. Forests 2012, 3, 723–735. [Google Scholar] [CrossRef]
- Günlü, A.; Baskent, E.Z.; Kadiogullari, A.İ.; Ercanli, İ. Classifying oriental beech (Fagus orientalis Lipsky.) forest sites using direct, indirect and remote sensing methods: A case study from Turkey. Sensors 2008, 8, 2526–2540. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.P.; Matney, T.G.; Land, S.B., Jr.; Belli, K.L.; Duzan, H.W., Jr. Incorporating genetic parameters into a loblolly pine growth-and-yield model. Can. J. For. Res. 2006, 36, 1959–1967. [Google Scholar] [CrossRef]
- Vicca, S.; Luyssaert, S.; Penuelas, J.; Campioli, M.; Chapin, F.S., III; Ciais, P.; Heinemeyer, A.; Högberg, P.; Kutsch, W.L.; Law, B.E.; et al. Fertile forests produce biomass more efficiently. Ecol. Lett. 2012, 15, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Reich, R.M.; Bonham, C.D.; Aguirre-Bravo, C.; Chazaro-Basañeza, M. Patterns of tree species richness in Jalisco, Mexico: Relation to topography, climate and forest structure. Plant Ecol. 2010, 210, 67–84. [Google Scholar] [CrossRef]
- Peters, E.B.; Wythers, K.R.; Bradford, J.B.; Reich, P.B. Influence of disturbance on temperate forest productivity. Ecosystems 2013, 16, 95–110. [Google Scholar] [CrossRef]
- Coops, N.C.; Waring, R.H.; Hilker, T. Prediction of soil properties using a process-based forest growth model to match satellite-derived estimates of leaf area index. Remote Sens. Environ. 2012, 126, 160–173. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Mapping site index and age by linking a time series of canopy height models with growth curves. For. Ecol. Manag. 2009, 257, 951–959. [Google Scholar] [CrossRef]
- Gómez-Tagle, R.A. Levantamiento de suelos del Campo Experimental Forestal Barranca de Cupatitzio y sus relaciones con la vegetación de confieras. Master’s Thesis, Universidad Nacional Autonoma de Mexico, México City, Mexico, 1985. [Google Scholar]
- Fontes, L.; Tomé, M.; Thompson, F.; Yeomansi, A.; Sales, L.J.; Savilli, P. Modelling the Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) site index from site factors in Portugal. Forestry 2003, 76, 491–507. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Muys, B.; Van Orshoven, J. Effects of scale and scaling in predictive modelling of forest site productivity. Environ. Modell. Softw. 2012, 31, 19–27. [Google Scholar] [CrossRef]
- Mitsuda, Y.; Ito, S.; Sakamoto, S. Predicting the site index of sugi plantations from GIS-derived environmental factors in Miyazaki Prefecture. J. For. R. 2007, 12, 177–186. [Google Scholar] [CrossRef]
- Johnsen, K.; Samuelson, L.; Teskey, R.; McNulty, S.; Fox, T. Process models as tools in forestry research and management. For. Sci. 2001, 47, 2–8. [Google Scholar]
- Rodhouse, T.J.; Irvine, K.M.; Sheley, R.L.; Smith, B.S.; Hoh, S.; Esposito, D.M.; Mata-Gonzalez, R. Predicting foundation bunchgrass species abundances: Model-assisted decision-making in protected-area sagebrush steppe. Ecosphere 2014, 5, 1–16. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).