The Pelagic Habitat of Swordfish (Xiphias gladius) in the Changing Environment of the North Indian Ocean
Abstract
1. Introduction
2. Materials and Methods
2.1. Environmental Variables
2.2. Swordfish Fish Catch Data
2.3. Statistical Models for Spatial Predictions of Catch Rate
3. Results
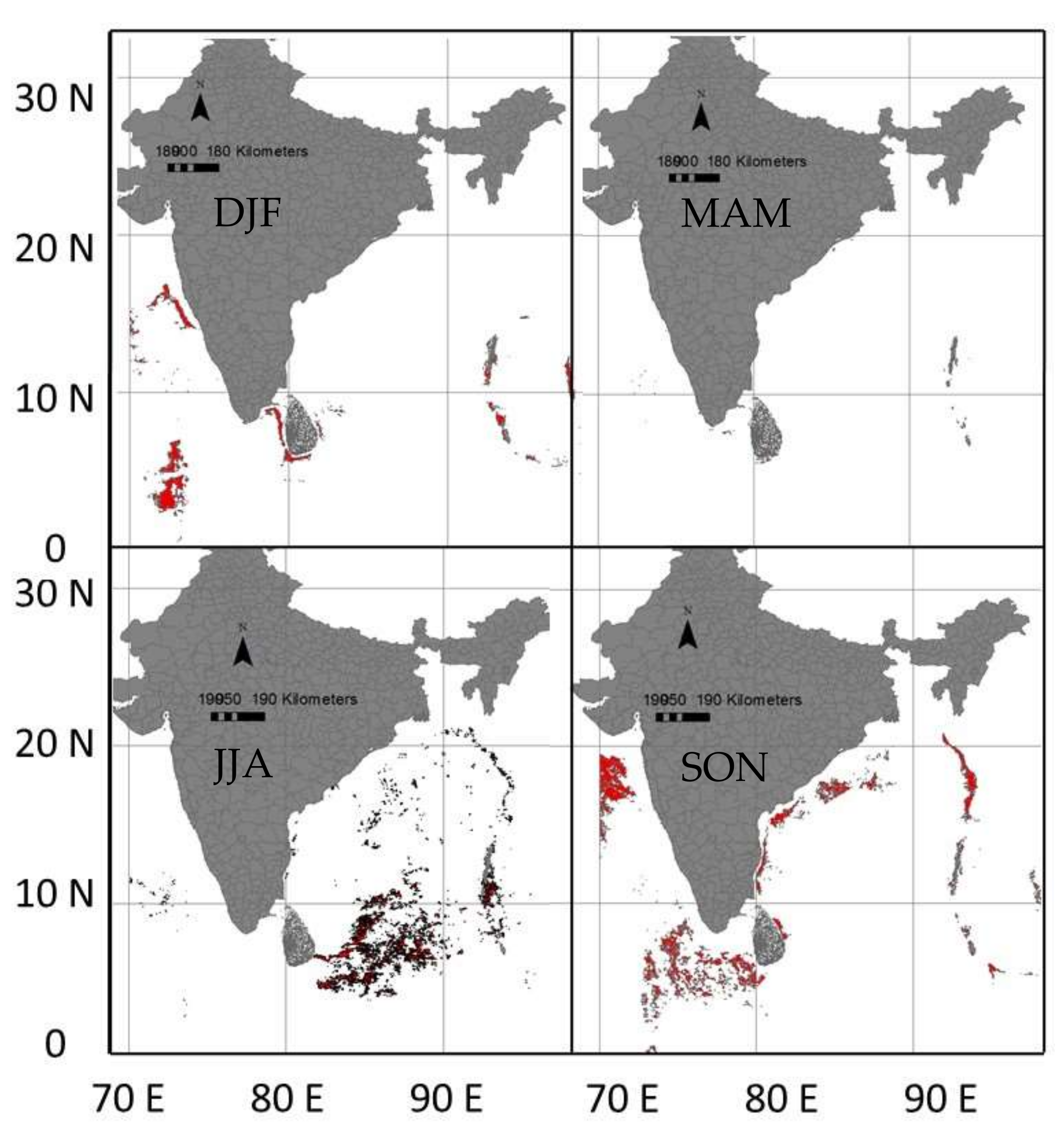
3.1. The Swordfish Catch Distribution in North Indian Ocean
3.2. Identification of Influencing Variables for Swordfish Catches Distribution with BRT Model
3.3. GAM Selection and the Influencing Variables on Swordfish Distribution
3.4. Inter-Annual and Seasonal Variability of the Environmental Variables
3.5. Predicted Spatial Distribution of Swordfish in the Indian Ocean
4. Discussion
4.1. Overview
4.2. Inter-Annual and Seasonal Changes in Environmental Variables and CPUE
4.3. Environmental Variations Affecting the Swordfish Catch
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Food and Agriculture Organization of the United Nations. FAO Fisheries & Aquaculture—Species Fact Sheets—Xiphias gladius (Linnaeus, 1758). Fisheries and Aquaculture Department, 2011. Available online: http://www.fao.org/fishery/species/2503/en (accessed on 27 May 2019).
- Potier, M.; Marsac, F.; Cherel, Y.; Lucas, V.; Sabati, R.; Maury, O. Forage fauna in the diet of three large pelagic fishes (lancetfish, swordfish and yellowfin tuna) in the western equatorial Indian Ocean. Fish. Res. 2007, 83, 60–72. [Google Scholar] [CrossRef]
- Poisson, F.; Fauvel, C. Reproductive dynamics of swordfish (Xiphias gladius) in the southwestern Indian Ocean (Reunion Island). Part 1: Oocyte development, sexual maturity and spawning. Aquat. Living Resour. 2009, 22, 45–58. [Google Scholar] [CrossRef]
- Mejuto, J.; García-Cortés, B.; Ramos-Cartelle, A. Iotc 2006-wpb-11 an Overview of Research Activities on Swordfish (Xiphias Gladius) and the by-Catch Species, Caught by the Spanish Longline Fleet in the Indian Ocean; Report No. 2006; IOTC 2006-WPB-11; IOTC: Victoria, Seychelles; pp. 1–23.
- IOTC–WPEB07 2011: Report of the Seventh Session of the IOTC Working Party on Ecosystems and Bycatch; IOTC: Lankanfinolhu, North Malé Atoll, Republic of Maldives, 2011.
- Das, P. Indian Deep Sea Fisheries—Its Prospects, Issues and Challenges. J. Aquacult. Marine Biol. 2017, 5. [Google Scholar] [CrossRef]
- Roxy, M.K.; Ritika, K.; Terray, P.; Masson, S. The Curious Case of Indian Ocean Warming. J. Clim. 2014, 27, 8501–8509. [Google Scholar] [CrossRef]
- Anoop, T.R.; Kumar, V.S.; Shanas, P.R.; Johnson, G. Surface Wave Climatology and Its Variability in the North Indian Ocean Based on ERA-Interim Reanalysis. J. Atmos. Ocean. Technol. 2015, 32, 1372–1385. [Google Scholar] [CrossRef]
- Fritz, H.M.; Blount, C.; Albusaidi, F.B.; Al-Harthy, A.H.M. Cyclone Gonu storm surge in the Gulf of Oman. In Indian Ocean. Tropical Cyclones and Climate Change; Springer: Dordrecht, The Netherlands, 2010; pp. 255–263. [Google Scholar]
- Sumesh, K.G.; Ramesh Kumar, M.R. Tropical cyclones over north Indian Ocean during El-Niño Modoki years. Nat. Hazards 2013, 68, 1057–1074. [Google Scholar] [CrossRef]
- Fogarty, H.E.; Burrows, M.T.; Pecl, G.T.; Robinson, L.M.; Poloczanska, E.S. Are fish outside their usual ranges early indicators of climate-driven range shifts? Glob. Chang. Biol. 2017, 23, 2047–2057. [Google Scholar] [CrossRef]
- Hays, G.; Richardson, A.; Robinson, C. Climate change and marine plankton. Trends Ecol. Evol. 2005, 20, 337–344. [Google Scholar] [CrossRef]
- Lauria, V.; Attrill, M.J.; Pinnegar, J.K.; Brown, A.; Edwards, M.; Votier, S.C. Influence of climate change and trophic coupling across four trophic levels in the Celtic Sea. PLoS ONE 2012, 7, e47408. [Google Scholar] [CrossRef]
- Bornatowski, H.; Angelini, R.; Coll, M.P.; Barreto, R.R.P.; Amorim, A.F. Ecological role and historical trends of large pelagic predators in a subtropical marine ecosystem of the South Atlantic. Rev. Fish Biol. Fish. 2017, 28, 241–259. [Google Scholar] [CrossRef]
- Chang, Y.J.; Sun, C.L.; Chen, Y.; Yeh, S.Z.; DiNardo, G.; Su, N.J. Modelling the impacts of environmental variation on the habitat suitability of swordfish, Xiphias gladius, in the equatorial Atlantic Ocean. ICES J. Mar. Sci. 2013, 70, 1000–1012. [Google Scholar] [CrossRef]
- Lan, K.W.; Lee, M.A.; Wang, S.P.; Chen, Z.Y. Environmental variations on swordfish (Xiphias gladius) catch rates in the Indian Ocean. Fish. Res. 2014, 166, 67–79. [Google Scholar] [CrossRef]
- Irby, I.D.; Friedrichs, M.A.M.; Da, F.; Hinson, K.E. The competing impacts of climate change and nutrient reductions on dissolved oxygen in Chesapeake Bay. Biogeosciences 2018, 15, 2649–2668. [Google Scholar] [CrossRef]
- Jensen, T.G. Arabian Sea and Bay of Bengal exchange of salt and tracers in an ocean model. Geophys. Res. Lett. 2001, 28, 3967–3970. [Google Scholar] [CrossRef]
- Kay, S.; Caesar, J.; Janes, T. Marine Dynamics and Productivity in the Bay of Bengal. In Ecosystem Services for Well-Being in Deltas; Springer International Publishing: Cham, Switzerland, 2018; pp. 263–275. [Google Scholar]
- De’ath, G. Boosted trees for ecological modeling and prediction. Ecology 2015, 88, 243–251. Available online: http://www.jstor.org/stable/27651085 (accessed on 1 January 2007). [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Gu, H.; Wang, J.; Ma, L.; Shang, Z.; Zhang, Q. Insights into the BRT (Boosted Regression Trees) Method in the Study of the Climate-Growth Relationship of Masson Pine in Subtropical China. Forests 2019, 10, 228. [Google Scholar] [CrossRef]
- Lampa, E.; Lind, L.; Lind, P.M.; Bornefalk-Hermansson, A. The identification of complex interactions in epidemiology and toxicology: A simulation study of boosted regression trees. Environ. Health 2014, 13, 57. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapmom and Hall: London, UK, 1990. [Google Scholar]
- Wood, S.N. On confidence intervals for generalized additive models based on penalized regression splines. Aust. N. Z. J. Stat. 2006, 48, 445–464. [Google Scholar] [CrossRef]
- Su, N.J.; Sun, C.L.; Punt, A.E.; Yeh, S.Z.; DiNardo, G. Modelling the impacts of environmental variation on the distribution of blue marlin, Makaira nigricans, in the Pacific Ocean. ICES J. Mar. Sci. 2011, 68, 1072–1080. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, D.F.; Ghert, M.; Simpson, A.H.R.W. Interpreting regression models in clinical outcome studies. Bone Jt. Res. 2015, 4, 152–153. [Google Scholar] [CrossRef] [PubMed]
- Golub, G.H.; von Matt, U. Generalized Cross-Validation for Large-Scale Problems. J. Comput. Graph. Stat. 1997, 6, 1. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Khouloud, T.; Hedia, B.; Nissaf, B.A.; Marc, S.; Dhafer, M.; Kouni, C.M. Comparative Performance Analysis for Generalized Additive and Generalized Linear Modeling in Epidemiology Methods of Evaluation for Modeling Disease Incidence. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 418–423. [Google Scholar]
- Adeniyi, M.O. Characteristics of total solar radiation in an urban tropical environment. Int. J. Phys. Sci. 2012, 7, 5154–5161. [Google Scholar] [CrossRef]
- Brown, B.E.; Dunne, R.; Ambasari, I.; Le Tissier, M.D.A.; Satapoomin, U. Seasonal fluctuations in environmental factors and variations in symbiotic algae and chlorophyll pigments in four Indo-Pacific coral species. Mar. Ecol. Prog. Ser. 1999, 191, 53–69. Available online: https://www.semanticscholar.org/paper/Seasonal-fluctuations-in-environmental-factors-and-Brown-Dunne/68ef180657a754b4589fc60f3caf420cd1111000 (accessed on 3 May 2019). [CrossRef]
- Kumar, G.S.; Prakash, S.; Ravichandran, M.; Narayana, A.C. Trends and relationship between chlorophyll-a and sea surface temperature in the central equatorial Indian Ocean. Remote. Sens. Lett. 2016, 7, 1093–1101. [Google Scholar] [CrossRef]
- FAO Fisheries & Aquaculture—Fishery Statistical Collections—Global Capture Production. Global Capture Production, 2019. Available online: http://www.fao.org/fishery/statistics/global-capture-production/en (accessed on 29 May 2019).
- IOTC. Data and Statistics|IOTC. Data and Statistics 2019. Available online: https://www.iotc.org/data-and-statistics (accessed on 29 May 2019).
- De Vos, A.; Pattiaratchi, C.B.; Wijeratne, E.M.S. Surface circulation and upwelling patterns around Sri Lanka. Biogeosciences 2014, 11, 5909–5930. [Google Scholar] [CrossRef]
- Vinayachandran, P.N.; Yamagata, T. Monsoon Response of the Sea around Sri Lanka: Generation of Thermal Domesand Anticyclonic Vortices. J. Phys. Oceanogr. 1998, 28, 1946–1960. [Google Scholar] [CrossRef]
- Yan, D.; Kai, L.; Wei, Z.; Wei-Dong, Y. The Kelvin Wave Processes in the Equatorial Indian Ocean during the 2006–2008 IOD Events. Atmos. Ocean. Sci. Lett. 2015, 5, 324–328. [Google Scholar] [CrossRef][Green Version]
- Dietrich, G.B.Z.Z. The Biology of the Indian Ocean, 1st ed.; Gerlach, S.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Tang, D.; Kawamura, H.; Luis, A.J. Short-term variability of phytoplankton blooms associated with a cold eddy in the northwestern Arabian Sea. Remote Sens. Environ. 2002, 81, 82–89. [Google Scholar] [CrossRef]
- Cheung, W.W.L.; Dunne, J.; Sarmiento, J.L.; Pauly, D. Integrating ecophysiology and plankton dynamics into projected maximum fisheries catch potential under climate change in the Northeast Atlantic. ICES J. Mar. Sci. 2011, 68, 1008–1018. [Google Scholar] [CrossRef]
- Bœufa, G.; Payan, P. How should salinity in uence sh growth? Comp. Biochem. Physiol. Part 2001, 130, 411–423. [Google Scholar]
- Fuentes, J.; Eddy, F.B. Drinking in Atlantic salmon presmolts and smolts in response to growth hormone and salinity. Comp. Biochem. Physiol. Physiol. 1997, 117, 487–491. [Google Scholar] [CrossRef]
- Perrott, M.N.; Grierson, C.E.; Hazon, N.; Balment, R.J. Drinking behaviour in sea water and fresh water teleosts, the role of the renin-angiotensin system. Fish Physiol. Biochem. 1992, 10, 161–168. [Google Scholar] [CrossRef]
- Machado, P.B.; Gordo, L.S.; Figueiredo, I. Skate and ray species composition in mainland Portugal from the commercial landings. Aquat. Living Resour. 2004, 234, 231–234. [Google Scholar] [CrossRef]
- D’Addezio, J.M.; Subrahmanyam, B.; Nyadjro, E.S.; Murty, V.S.N. Seasonal Variability of Salinity and Salt Transport in the Northern Indian Ocean. J. Phys. Oceanogr. 2015, 45, 1947–1966. [Google Scholar] [CrossRef]
- Seo, H.; Xie, S.P.; Murtugudde, R.; Jochum, M.; Miller, A.J. Seasonal Effects of Indian Ocean Freshwater Forcing in a Regional Coupled Model. J. Clim. 2009, 22, 6577–6596. [Google Scholar] [CrossRef]
- Mateo, I.; Hanselman, D. A Comparison of Statistical Methods to Standardize Catch-Per-Unit-Effort of the Alaska Longline Sablefish Fishery; NOAA Technical Memorandum NMFS-AFSC-269; National Technical Information Service, U.S. Department of Commerce: Springfield, VA, USA, February 2014; pp. 1–71.
- Sengupta, D.; Ravichandran, M. Oscillations of Bay of Bengal sea surface temperature during the 1998 summer monsoon. Geophys. Res. Lett. 2001, 28, 2033–2036. [Google Scholar] [CrossRef]
- Yu, L.; McPhaden, M.J. Ocean Preconditioning of Cyclone Nargis in the Bay of Bengal: Interaction between Rossby Waves, Surface Fresh Waters, and Sea Surface Temperatures. J. Phys. Oceanogr. 2011, 41, 1741–1755. [Google Scholar] [CrossRef]
- Kaimuddin, A.H. Climate Change Impacts on Fish Species Distribution. Approach Using GIS, Models and Climate Evolution Scenario. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, June 2016. [Google Scholar]
- Taning, X.Y. On the breeding areas of the swordfish (Xiphias). Papers Mar. Biol. Oceanogr. 1955, 3, 438–450. [Google Scholar]
- Mejuto, J.; García-Cortés, B. Reproductive activity of swordfish Xiphias gladius, in the Atlantic Ocean inferred on the basis of macroscopic indicators. Rev. Biol. Mar. Oceanogr. 2014, 49, 427–447. [Google Scholar] [CrossRef]
- Jereb, P.; Roper, C.F.E. Cephalopods of the World: An Annotated and Illustrated Catalogue of Cephalopod Species Known to Date; Food and Agriculture Organization of the United Nations: Rome, Italy, 2005. [Google Scholar]
- Swordfish Retention Limit Adjustment|NOAA Fisheries. NOAA Fisheries is Adjusting the Swordfish General Commercial Permit Retention Limits in the Northwest Atlantic, Gulf of Mexico, and U.S. Caribbean Regions. 2017. Available online: https://www.fisheries.noaa.gov/bulletin/swordfish-retention-limit-adjustment (accessed on 14 November 2019).

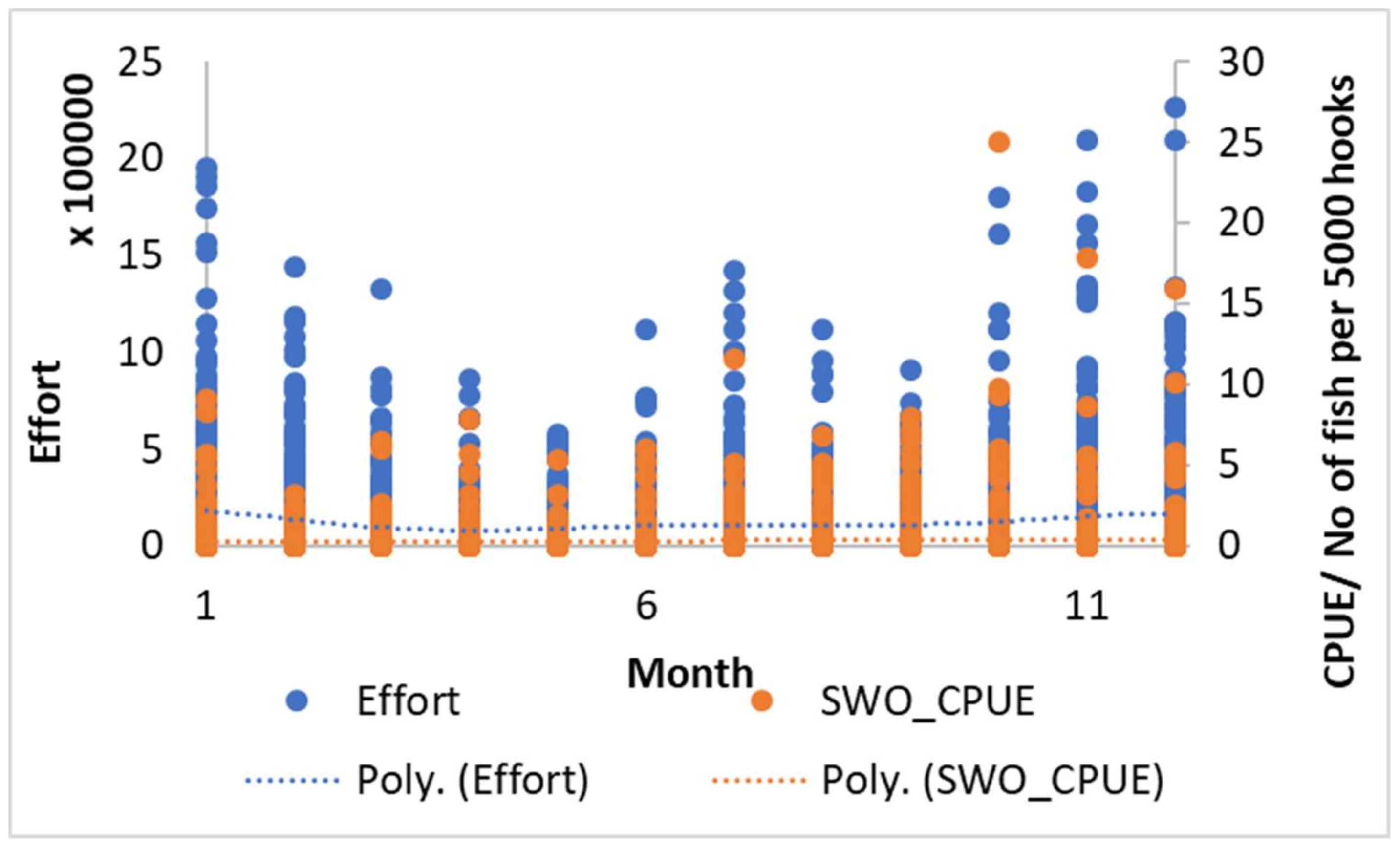
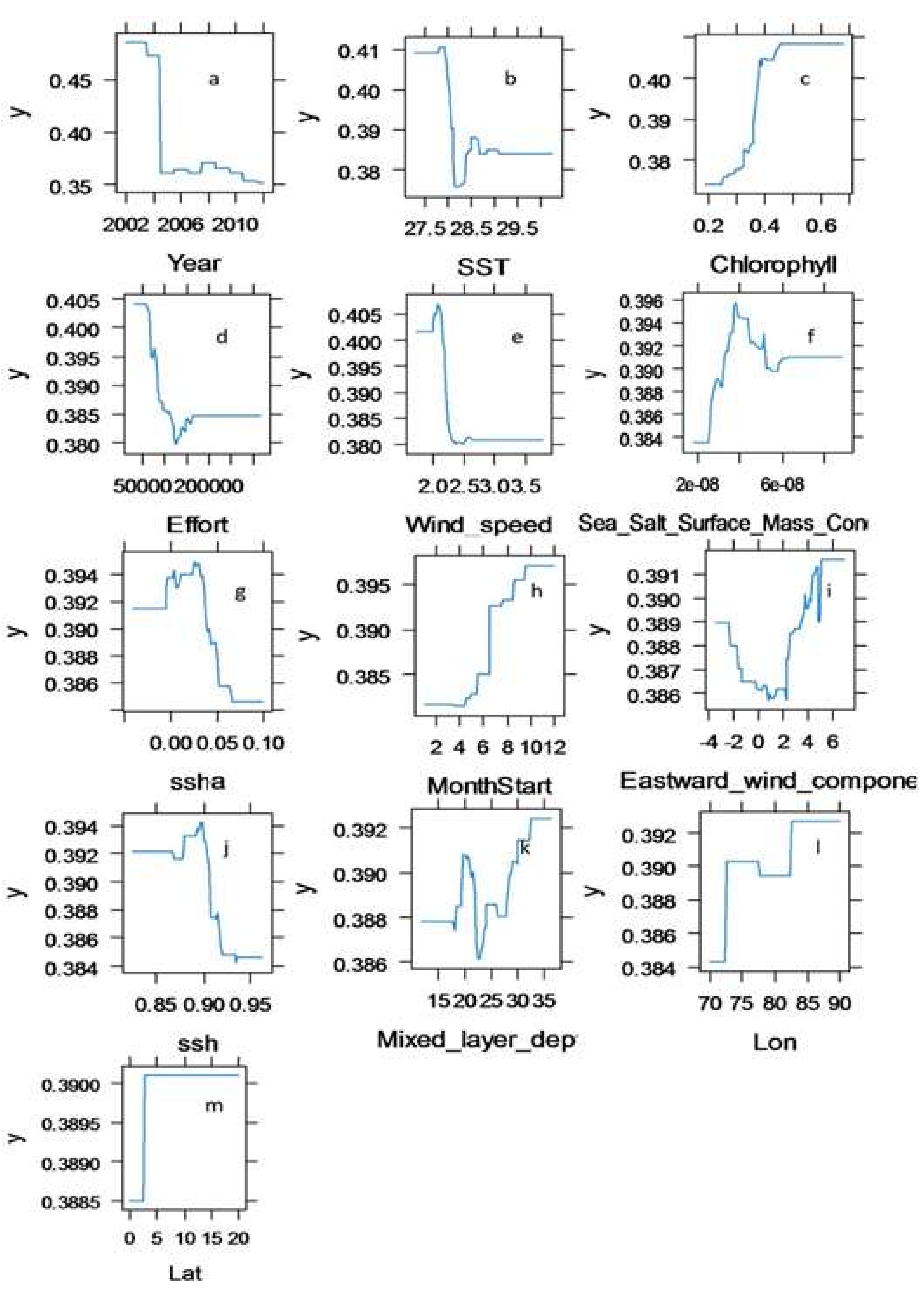
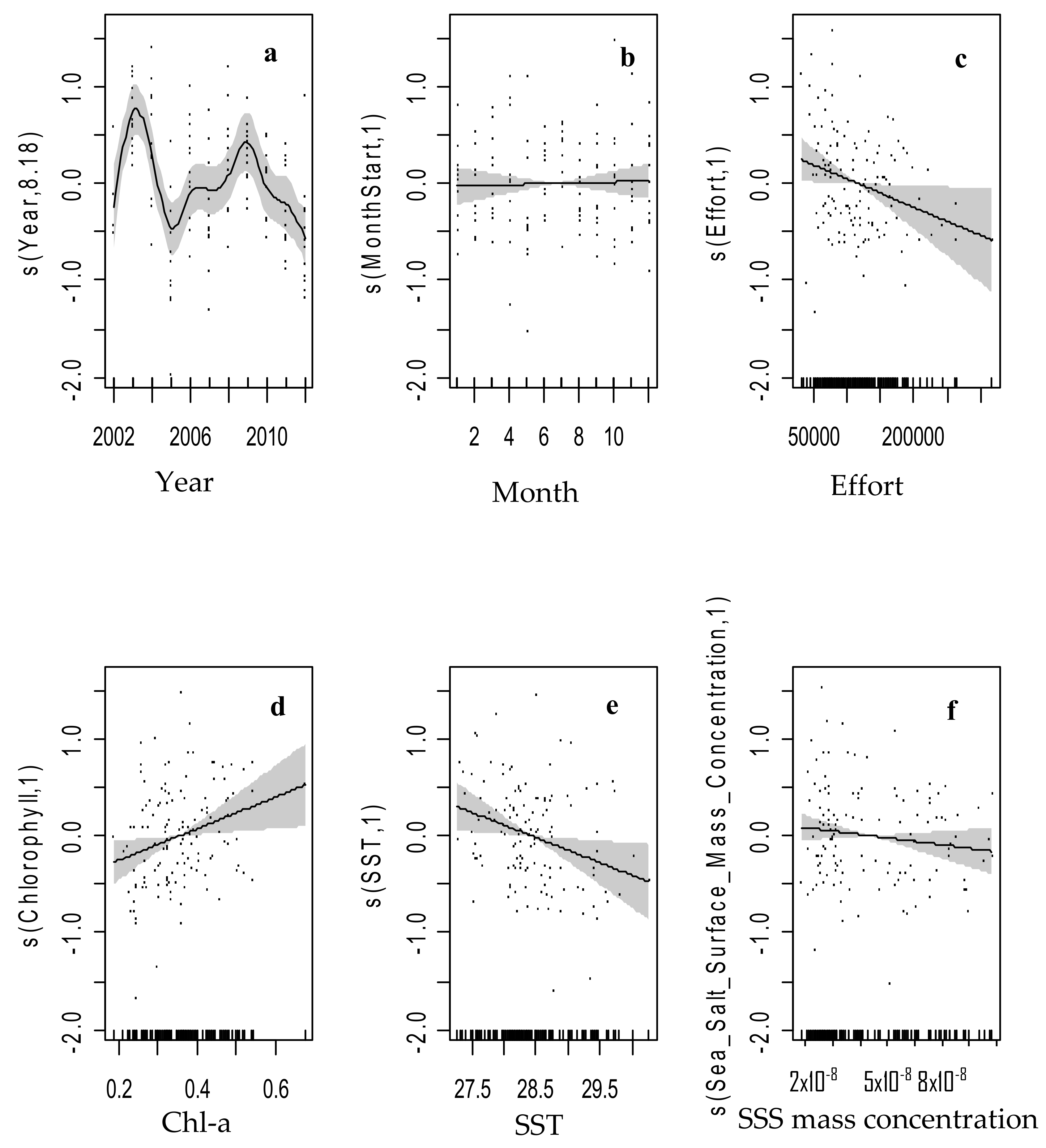
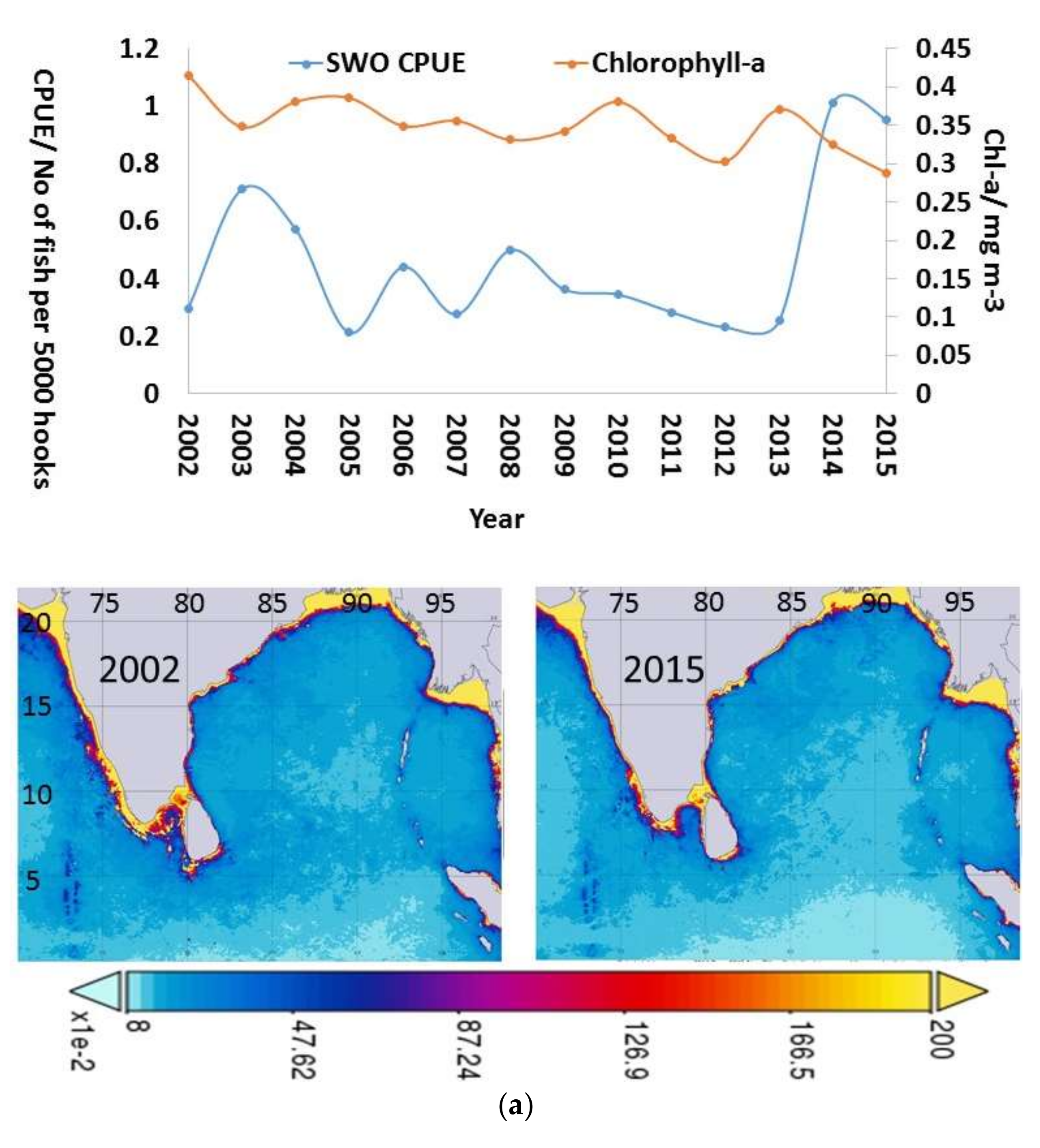
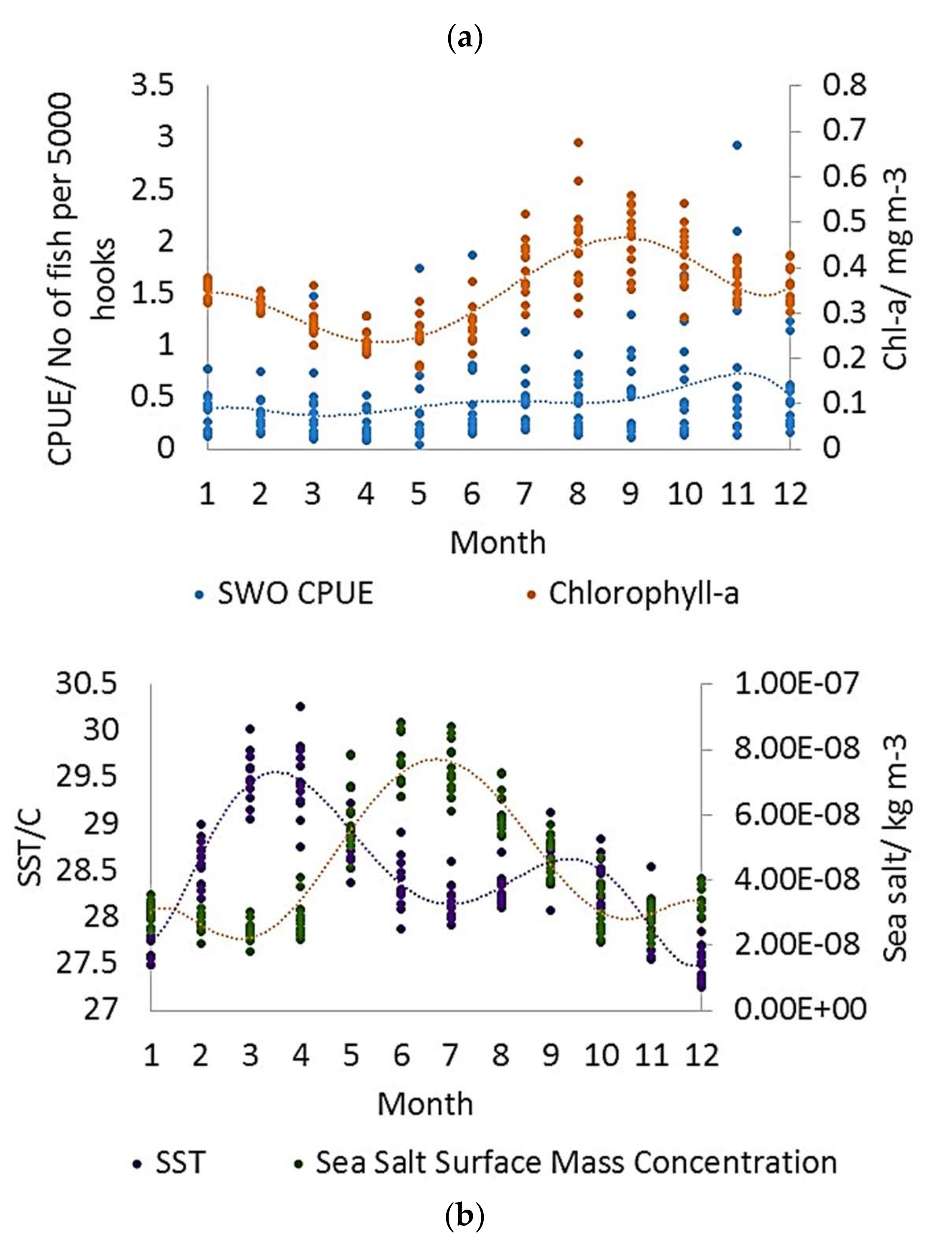
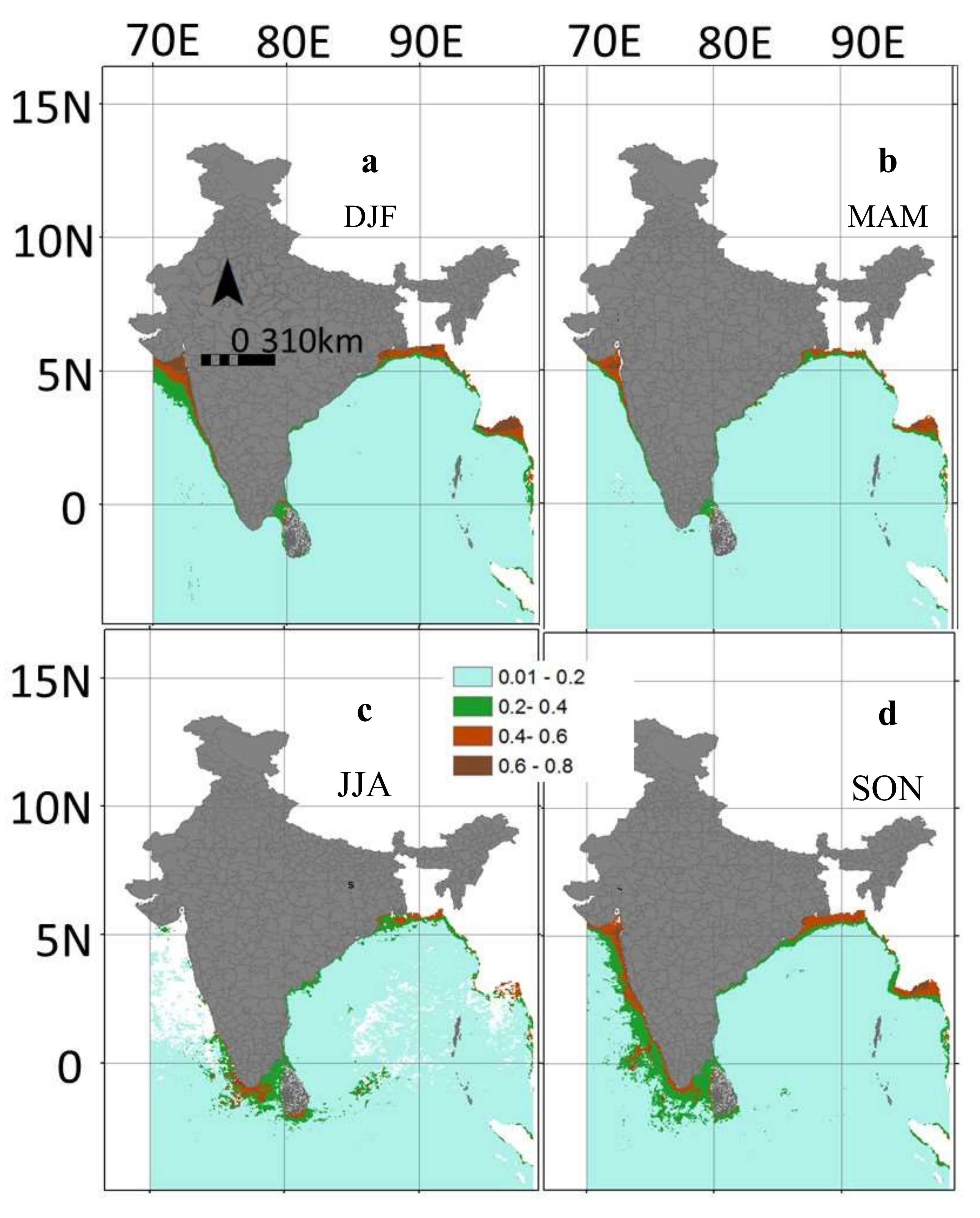
| Variable | Relative Influence (%) |
|---|---|
| Year | 38.16 |
| Sea surface temperature (SST) | 10.89 |
| Chlorophyll-a | 10.28 |
| Effort | 9.02 |
| Wind speed | 7.47 |
| Sea Salt Surface Mass Concentration | 4.99 |
| Sea surface height anomaly (SSHA) | 3.81 |
| Month | 3.43 |
| Eastward wind component | 3.28 |
| Sea surface height (SSH) | 3.18 |
| Mixed layer depth | 3.08 |
| Longitude | 2.00 |
| Latitude | 0.41 |
| edf | Ref.df | F | p-Value | R-sq. Adjusted | Deviance Explained | GCV | AIC | |||
|---|---|---|---|---|---|---|---|---|---|---|
| s(Year) | 8.18 | 8.82 | 6.369 | 3.45 × 10−7 | *** | 0.33 | 40..30% | 0.31996 | 214.26 | Model 1 |
| s(Month) | 1 | 1 | 0.075 | 0.7847 | ||||||
| s(Effort) | 1 | 1 | 4.773 | 0.031 | * | |||||
| s(Chl-a) | 1 | 1 | 5.992 | 0.0159 | * | |||||
| s(SST) | 1 | 1 | 5.897 | 0.0167 | * | |||||
| s(Sea Salt) | 1 | 1 | 1.733 | 0.1907 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elepathage, T.S.M.; Tang, D.; Oey, L. The Pelagic Habitat of Swordfish (Xiphias gladius) in the Changing Environment of the North Indian Ocean. Sustainability 2019, 11, 7070. https://doi.org/10.3390/su11247070
Elepathage TSM, Tang D, Oey L. The Pelagic Habitat of Swordfish (Xiphias gladius) in the Changing Environment of the North Indian Ocean. Sustainability. 2019; 11(24):7070. https://doi.org/10.3390/su11247070
Chicago/Turabian StyleElepathage, Thushani Suleka Madhubhashini, Danling Tang, and Leo Oey. 2019. "The Pelagic Habitat of Swordfish (Xiphias gladius) in the Changing Environment of the North Indian Ocean" Sustainability 11, no. 24: 7070. https://doi.org/10.3390/su11247070
APA StyleElepathage, T. S. M., Tang, D., & Oey, L. (2019). The Pelagic Habitat of Swordfish (Xiphias gladius) in the Changing Environment of the North Indian Ocean. Sustainability, 11(24), 7070. https://doi.org/10.3390/su11247070





