Abstract
With the rapid development of plug-in electric vehicles (PEVs), the charging of a number of PEVs has already brought huge impact and burden to the power grid, particularly at the medium and low voltage distribution networks. This presents a big challenge for further mass roll-out of electric vehicles. To assess the impact of charging of substantial number of electric vehicles on the grid, a model of 30000 PEVs integrated with unit commitment (UCEV) was investigated in this study. The unit commitment was a large-scale, mixed-integer, nonlinear, NP-Hard (non-deterministic polynomial) optimization problem, while the integration of PEVs further increased the complexity of the model. In this paper, a global best inspired negatively correlated search (GBNCS) method which extends the evolutionary logic of negatively correlated search is proposed to tackle the UCEV problem. In the proposed algorithm, a rounding transfer function in GBNCS, is deployed to convert real-valued variables into binary ones; further, the global best information is combined in the population to improve the efficiency of the algorithm. Numerical results confirmed that the proposed GBNCS can achieve good performance in both a basic IEEE 10 unit commitment problem and the UCEV problem. It was also shown that, among four charging modes, the off-peak charging mode and EPRI (Electric Power Research Institute) charging mode are more economical in PEV charging.
1. Introduction
Industry revolutions and urbanization have led to a number of intractable environmental and resource problems, such as global warming, due to extensive consumption of fossil fuels [1]. According to a research by the U.S. Energy Information Administration (EIA) in 2014, carbon emission is the single most important factor for the global warming and the transportation sector accounts for more than 1/3 of the total greenhouse gas emissions [2]. Therefore, to reduce the carbon emissions from the transportation sector is an important part of the global effort to curb global warming. To achieve this goal, many governments have introduced a wide range of policies to promote the development of electric vehicles.
Generally speaking, electric vehicles can be grouped into three categories: battery electric vehicles (BEVs), hybrid electric vehicles (HEVs), and plug-in electric vehicles (PEVs). Due to the technical limitations of fuel cells and the huge costs in the production and storage of hydrogen, the fuel cell electric vehicles are still not suitable for large-scale applications, while HEVs have already been widely used. In recent years, the advances in the battery technology and power control [3] have further improved the efficiency of HEVs. But they still use fossil fuels. With the maturity of battery technology, lithium batteries, nickel metal hydride batteries, and lead-acid batteries have been widely used in electric vehicles [4,5,6], and the PEV has become the most popular EV type. Both the research and practice have confirmed the great potentials of PEVs in energy conservation and emission reduction [7,8].
However, the rapid growth of the electric vehicle market has introduced new problems and challenges. The charging of a massive number of electric vehicles is likely to have a huge impact and burden to the power grid, which is another problem that needs to be addressed [9,10]. Further, questions such as how to save the operational costs while integrating the charging of EVs and how to cope with stochastic charging behavior of different EV owners should be answered. In [11], Zhou et al. presented a probability model of EV charging load in the distribution network. In [12], the EV charging model was studied from the demand side, and the charging demand data was collected from a real application in Korea and the load control strategy was employed to develop a smart charging technique suitable for practical applications. In this paper, in order to investigate the effect of EV charging, the charging of EVs is combined with the unit commitment problem. The charging demand is formulated as an unpredictable load to the power system which needs to be addressed for power secure operation at the lowest cost.
The unit commitment problem (UC) is a large-scale, mixed-integer, nonlinear, NP-Hard (non-deterministic polynomial) optimization problem. The aim of unit commitment is to minimize the generation costs by reasonably scheduling the on/off status and output power of generations under various system constraints. Conventional methods such as dynamic programming [13] and lagrangian relaxation [14] are able to quickly solve low dimension UC problems. But these two methods both have poor performance and may not guarantee to find the optimum solutions in large-scale UC problems [15]. In the last few decades, various methods, including artificial neural networks [16], Tabu search [17], simulated annealing [18], branch and cut (BC) [19], Benders decomposition (BD) [20], and intelligent meta-heuristic algorithms, such as particle swarm optimization [21] and a genetic algorithm [15], have been applied to solve the UC problem. However, the complexity of the UC problem is significantly increased due to the introduction of new participants such as electrical vehicles.
To handle the increased complexity, Saber proposed an intelligent unit commitment model with vehicle-to-grid (V2G) and applied binary particle swarm optimization to find a balance in reducing both fuel costs and emissions [22]. But the paper does not consider the stochastic charging scenario and uncertainties associated with charging and discharging. To investigate the impact of EV charging in different situations, Foley proposed two charging modes; namely, peak charging mode and off-peak charging mode [23]. Ma et al. further combined Foley’s EV charging mode witha multi-objective, dynamic, economic, emission load dispatch problem [24]. In Liu’s research, a stochastic unit commitment model with plug-in electric was combined with wind power [25]. Mohammadi designed a solar-powered EV which reduces the use of fossil cells and can be combined into the research of optimization problems in power systems such as UC [26]. Yang et al. further proposed a framework to comprehensive study the unit commitment problem integrating various renewable generations and PEVs [27]. Further, bidirectional power charging control strategy is also an important research direction which can help reduce the burden to the power grid [28,29]. In this paper, four charging modes, including the peak charging mode, the off-peak charging mode, the Electric Power Research Institute (EPRI) charging mode, and a stochastic charging mode are combined with the UC problem to thoroughly investigate the effect of EV charging on the power system.
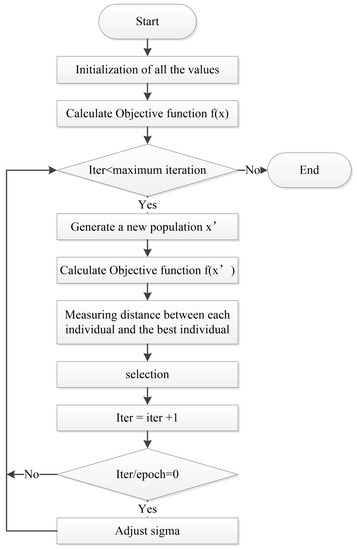
The negatively correlated search (NCS) was first proposed by Tang et al. [30] and has shown to deliver excellent performance for continuous optimization problems. The core logic of NCS is divide-and-conquer; the search domain is divided into several parts and each part is a random local search (RLS) which helps to avoid trapping into local optimum. However, NCS is rarely applied to binary or mixed-integer optimization problems such as UC. Furthermore, the computation time of the search process is too long, due to the calculation of correlations between individuals. Therefore, a binary, negatively correlated search (BNCS) is proposed in this paper which uses a rounding transfer function to convert real-valued variables into binary ones. To improve the efficiency of BNCS, the global best solution is introduced to BNCS, leading to the proposal of the global best inspired binary negatively correlated search (GBNCS) algorithm. These two algorithms were first tested on eight benchmark instances of the knapsack problem and then applied to UC problems.
The remainder of the paper is organized as follows: Section 2 presents the formulation of the unit commitment problem, followed by the proposed global-best inspired negative correlated search (GBNCS) and its implementation for a UC problem in Section 3, and the numerical results and analysis are given in Section 4. Finally, Section 5 concludes the paper.
2. Problem Formulation
The unit commitment problem, including the basic unit commitment and the unit commitment with electrical vehicles can be formulated as follows.
2.1. Basic Unit Commitment
The unit commitment problem can be modeled as a kind of optimization problem which aims at minimizing the objective function while equality and inequality constraints at the system level such as power balance limit and minimum up/down time limit have to be met.
2.1.1. Objective Function
The objective function of basic unit commitment problem consists of two parts including the fuel cost and the start-up cost.
Fuel cost
The committed units in power system usually have different power and efficiency. To dispatch these units economically, the fuel cost becomes a significant factor which can be expressed by a quadratic equation.
where and present the fuel cost and the power of unit at time t respectively, and , , and are the fuel cost coefficients associated to the unit.
Start-up cost
The start-up cost is also an important part of the objective function which can be divided into cold start-up cost and hot start-up cost. If the unit has not been off for too long time, it may take less time and cost to start up, whereas if the unit has been off for enough time, it may take much longer to start up the unit. The start-up cost related to unit is given by:
where is the hot start-up cost and is the cold start-up cost. is the minimum down time, is the off-line duration time, and is the cold-start hour of unit.
Therefore, the objective function of the unit commitment problem combining both the fuel cost and start-up cost can be expressed as follows, where is a binary variable representing the on/off state of unit at time t, and represents the on/off state of the generating unit at time .
2.1.2. Constraints
In the following, various constraints that need to be considered at the unit commitment stage are presented to ensure the adequacy of the system after implementation, while other constraints which are often considered at lower system operation and control levels relating to power system adequacy, contingency, vulnerability, and stability, are not included.
Power balance constraint
The power generated by all the units at time t needs to meet the power demand, which is given in Equation (4), where is the demand power, and is the generation power of unit i at time t.
Generation limit
The power of each unit should be within its rated generation range, as defined in Equation (5), where and respectively represent the minimum and maximum power outputs of the unit.
Minimum up and minimum down time constraint
To maintain the unit in good condition, the generation unit should not be turned on or off too frequently and has to meet the following constraints.
where and represent the off-line time and on-line time of unit n; and represent the minimum up/down time of unit n.
Ramp rates constraint
The power output of each unit cannot be changed violently, and it has to meet the ramp rate constraint given below,
where and in Equation (7) are the minimum and maximum outputs of unit i at time t, which are defined as follows, where and are the ramp-up/down rates of the unit and representing the output of unit i at time .
Spinning reserve constraint
To meet with the uncertainty of power demand forecast and unexpected failure of generating units, the spinning reserve constraint is considered, which is given by,
where is the maximum output of unit, is the power demand at t time, and is the spinning reserve factor for controlling the reserve capacity of the system.
2.2. Unit Commitment Integrated with EV
The unit commitment integrated with electric vehicles model is based on the basic unit commitment problem and the objective function associated with the fuel cost and start-up cost remains the same as before, but the integration of electric vehicles introduces new and more complex constraints.
2.2.1. Constraints of UC Combined with EVs
Power Balance Constraint
The charging load is added to the demand load due to additional load of EVs charging. Therefore, the power balance constraint in the unit commitment with EVs is given by:
where is the additional load for charging electric vehicles at time t.
Spinning reserve constraint
In order to solve the instantaneous demand changes brought by electric vehicle charging, the reserved capacity needs to increase.
where is the maximum power required for electric vehicle charging.
2.2.2. Different Charging Models
Since different EV users often have different charging habits which increase the complexity and stochasticity of the problem, four charging modes were introduced to reflect different charging portfolios; those included the off-peak charging mode (OPCM), peak charging mode (PCM), Electric Power Research Institute Charging Mode (EPRICM) and the stochastic charging mode (SCM).
Off-peak charging mode (OPCM)
In off-peak charging mode users usually charge EVs between 23:00 to 6:00; in this period of time the demand power is usually not high and the impact on the grid caused by the charging of EV is not significant. Foley et al. assumed a plain load curve to simulate the 10% EV charging load curve in Ireland in 2013 [23]. According to [23], research on the probability distribution of 24 h off-peak charging mode given in Table 1 and Figure 1 represents the probability distribution more intuitively.

Table 1.
The probability of charging electric vehicles (EVs) in off-peak mode.
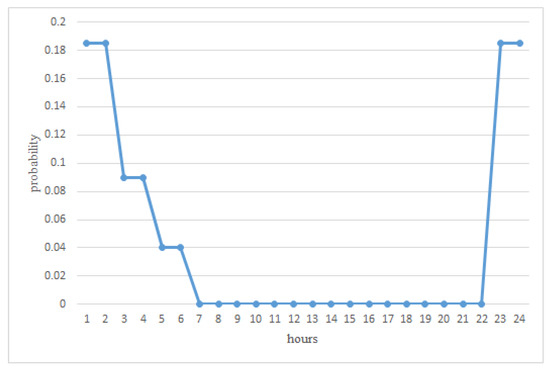
Figure 1.
The probability of charging EVs in off-peak mode.
Peak charging mode (PCM)
Different from the off-peak charging mode, the peak charging mode considers the most extreme situations. In the peak charging Mode, it is assumed that almost all EVs are charged during peak hours, which will bring a huge impact and burden to the power system. Table 2 and Figure 2 [23] give the probability distribution of 24 h peak charging Mode; the charging peak is mainly concentrated during the period from 13:00 to 20:00.

Table 2.
The probability of charging EVs in peak mode.
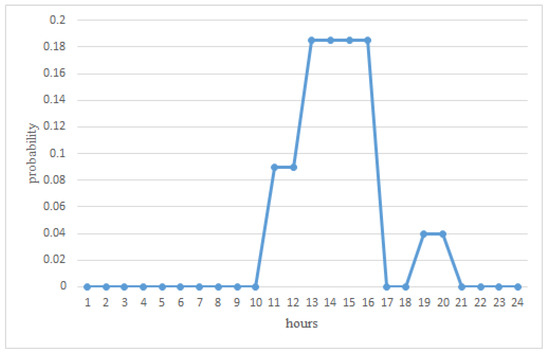
Figure 2.
The probability of charging EVs in PEAK mode.
Electric Power Research Institute Charging Mode (EPRICM)
The Electric Power Research Institute Charging Mode (EPRICM) is an electric vehicle charging mode proposed by the Electric Power Research Institute (EPRI). The research work of EPRI in 2007 [31] integrated the 24 h daily charging probability distribution of electric vehicles in the United States, which is shown in Table 3, and the fitting curve of this model is illustrated in Figure 3. It can be concluded from the curve that three-quarters of the EVs are charged between 23:00 and 6:00, and the remaining EVs are charged at other periods.

Table 3.
The probability of charging EVs in Electric Power Research Institute Charging Mode (EPRI) mode.
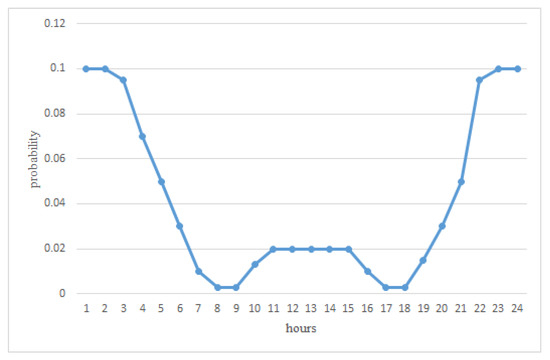
Figure 3.
The probability of charging EVs in EPRI mode.
Stochastic charging mode (SCM)
The off-peak charging mode and the peak charging Mode are usually assumed with ideal conditions. However, due to different charging habits, users of electric vehicles often change with daily activities, resulting in stochastic charging periods and charging duration. Therefore, the stochastic charging mode may be closer to the actual charging situation. In stochastic charging mode, five scenarios are randomly generated by a Gaussian operator where the mean value and standard deviation are respectively set as 4.16% (1/24) and 0.01. The probability distribution of five cases is given in Table 4 and Figure 4.

Table 4.
The probability of charging EVs in stochastic mode.
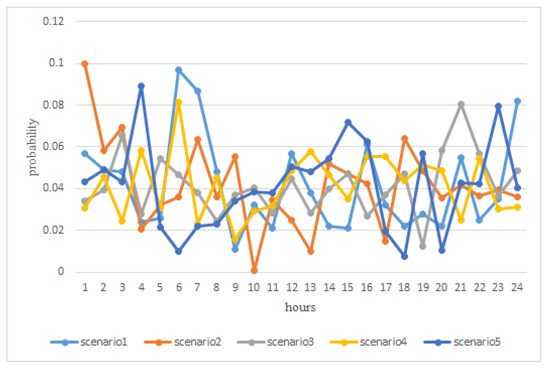
Figure 4.
The probability of charging EVs in stochastic mode.
4. Experimental Results
In this section, the proposed BNCS and GBNCS is first tested on the knapsack problem [37], and then applied to the basic UC problem and the UC problem integrated with the EV problem. The experiments were conducted using MATLAB2016a on an Intel Core i7-8700k CPU with 3.7 GHz, a personal computer with 32 GB of RAM. The unit data and load demand, which were obtained from the IEEE-10-unit system, are given in Table 5 [15], and the spinning reserve was assumed to be 10% of the demand.

Table 5.
The characteristics of units in the 10-unit base system.
4.1. Knapsack Problem
The knapsack problem is a classical, binary, NP-hard optimization problem which has many practical applications in many fields, such as the finance, engineering, and computing. The Knapsack problem can be modeled as a maximum optimization problem given by Equation (21), where and represent the quality and value of ith item respectively, and M is the maximum capacity of the backpack. The aim is to get the maximum total value of the items without exceeding the capacity of the backpack.
Although the knapsack problem has already been thoroughly studied, the benchmark functions of the knapsack problem are still often used to test the performance of binary algorithms. In this paper, ten benchmark functions of the knapsack problem are used to test the performance of BNCS and GBNCS. The dimension and parameters of ten test problems are listed in Table 6 [37]. To test the convergence of these algorithms, the total number of cost function evaluations (FES) was set as 10,000.

Table 6.
Numerical results of binary, negatively correlated search (BNCS) and global best inspired binary negatively search (GBNCS) approaches for Knapsack problem.
It is shown from the results in Table 6 that GBNCS produces the best performance of the two algorithms. The GBNCS is always able to find the best solution of almost all test cases except for F8 in 10,000 FES, and the BNCS’s performance is not ideal due to the slow convergence. Figure 6 gives the converge curve in different dimensions of F1, F2, F5, and F8.
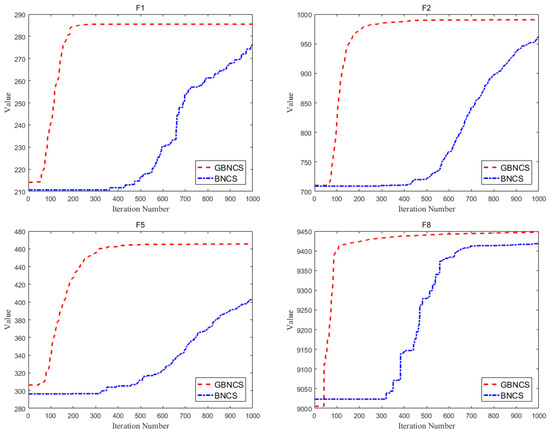
Figure 6.
Convergence characteristics of BNCS and GBNCS in F1, F2, F5 and F8.
4.2. Basic UC
The BNCS and GBNCS methods are applied to the 10 generating unit power systems over a 24 h scheduling horizon. The parameters of units in 10-unit system and the load demand in 24 h are listed in ref. [15] and given in Table 5 and Table 7.

Table 7.
Load demand for 24 h scheduling horizon.
To comparatively study the performance of the BNCS and GBNCS, the best value, worst value, and mean value obtained by the two algorithms proposed in this paper were compared with several popular algorithms which were applied to the UC problem. These algorithms include dynamic programming [15], Lagrangian relaxation [15], the genetic algorithm (GA) [15], NS evolutionary programming (EP) [38], simulate anneal (SA) [18], improved particle swarm optimization (IPSO) [39] binary particle optimization (BPSO) [40], quantum-inspired PSO (QPSO) [41], improved quantum evolutionary algorithm (IQEA) [42], quantum-inspired evolutionary algorithm (EQA-UC) [43] binary differential evolution algorithm (BDE) [44], binary real-coded GA (brGA) [45], harmony search algorithm (HAS) [46], hybrid harmony search (HHS) [47], binary gravitational search algorithm (BGSA) [36], and binary symmetric particle swarm optimization (BSPSO) [48]. The total number of cost function evaluations (FES) was set as 30,000. Table 8 shows the experimental results over 30 independent runs.

Table 8.
Comparison of BNCS and GBNCS with other approaches for 10 unit systems.
According to Table 8, it was found that GBNCS, BNCS, BGSA, HHS, EQA-UC, BDE, and BSPSO(2–5) were all capable of achieving the best value 563,937 $/day, which was also the best result among state-of-the-art UC results (some are illustrated as 563,938 $/day.) Meanwhile, GBNCS had the best performance in mean value, and worst value. Due to the great performance in seeking optimum, GBNCS is always able to achieve the best solution in all 30 independent runs. Figure 7 shows the convergence process of GBNCS and BNCS; it was revealed that the GBNCS and BNCS algorithms converge within around 2000 iterations and GBNCS has better performance than BNCS in convergence.
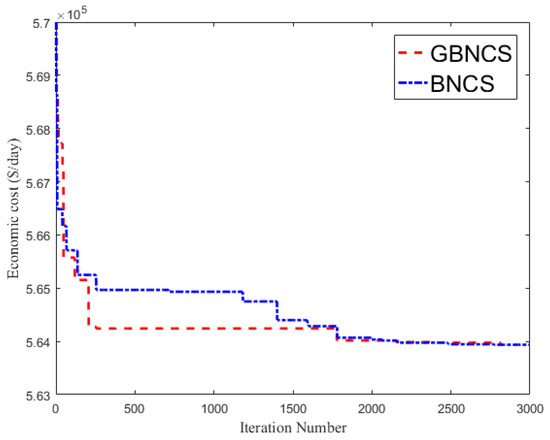
Figure 7.
Convergence curve of basic unit commitment (UC) problem.
According to the above experiment, GBNCS and BNCS are competitive in dealing with the 10 unit UC benchmark problem. These two algorithms were applied to the unit commitment problem integrated with electric vehicles, which is more complex.
4.3. UC with EVs
Intelligent charging helps to relieve the peak load and fills the valley load, which not only reduces the fuel cost but also avoids to start-up or shut-down the generators frequently. To study the EV charging impact on the power systems, 30,000 electric vehicles were integrated into the basic 10-unit benchmark power system, and the number of electric vehicles in Equation (22) is denoted as N. The EV parameters are given in Table 9 [49], and the maximum battery capacities of these EVs were within the range of 0.01–0.25 MW. It was assumed that the average capacity was 0.015MV and departure state of charge was set to 50%. The efficiency of charging is related to temperature. Here, the charging efficiency of all electric vehicles was set as 85%. The total charging load and maximum charging load of electric vehicles can be obtained from the following equation, where PV is the battery capacity.

Table 9.
Parameters of electric vehicles.
Hence, the total charging load was 191.25 MW, and the maximum charging load was 318.75 MW. Thus, the EV charging load within 24 h can be obtained from the total charging load and the probability distribution of four charging modes. The maximum charging load was added to the reserved constraint to consider the worst situation. Figure 8 shows the load curve after integrating electric vehicles in off-peak, peak, and EPRI modes, and basic UC loads.
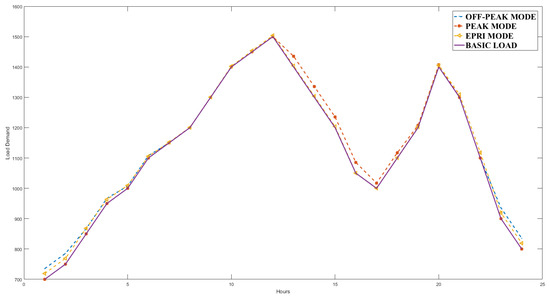
Figure 8.
Load demand curve for 24 h scheduling horizon in different charging modes.
To investigate the impact of EV charging on power systems and test the performance of BNCS and GBNCS, these two algorithms were applied to the 10-unit UC problem integrated with EVs. The results including best values, worst values, and mean values are given in Table 10. Similar to the experiment in the basic 10 unit UC benchmark problem, the FES was set as 30,000 and the results were obtained from 30 individual runs. The population size was set to 10.

Table 10.
Performance comparison of the proposed algorithms for UC with EVs problem.
As shown in Table 10, the results obtained by BNCS and GBNCS were far better than those obtained by GAD and GAH. GBNCS is always able to get the best solutions in four modes and eight scenarios. Table 10 also reflects the impact of EV charging on power systems. In the peak charging mode and the off-peak charging mode, the mean results obtained by GBNCS were 568,370 $/day and 568,894 $/day, respectively; peak charging costs 524 $/day more than off-peak charging, and the reason can be found in the unit commitment schedule and reserve available for 10-unit system under peak charging mode and off-peak charging mode obtained by GBNCS given in Table 11 and Table 12. Compared with the schedule of the off-peak charging mode, the charging of EV in peak charging mode caused a sudden start-up of unit 8 at 20:00; this unit was connected to the grid for only one hour and then shut down immediately at 21:00, which greatly increased the cost. But off-peak charging mode is not the most economical way to charge: the EPRI charging mode is cheaper than the off-peak charging mode; that is because off-peak charging mode as an ideal charging mode where all the EVs are charged in the off-peak period which forms a new peak of charging, but EPRI charging mode charges most of the EVs off-peak; only a quarter of EVs are charged at home.

Table 11.
Unit commitment schedule available for 10 unit system using GBNCS in Peak charging mode.

Table 12.
Unit commitment schedule available for 10 unit system using GBNCS in Off-Peak charging mode.
Figure 9 shows the computation time for solving the unit commitment integrated with electric vehicle problem and knapsack problem. GBNCS only uses about half of the calculation time of BNCS in all these four modes. Furthermore, when solving the knapsack problem, the calculation time of GBNCS is almost one tenth that of BNCS. The efficiency of GBNCS is more obvious when dealing with simple optimization problems, such as the knapsack problem. That is because the object function of the knapsack problem is much simpler then UC’s, so when dealing with knapsack problem, the objective function evaluation time is much less than the Bhattacharyya distance calculation time. GBNCS optimized the problem with significantly reduced computation time; therefore, the efficiency of the algorithm was greatly enhanced.
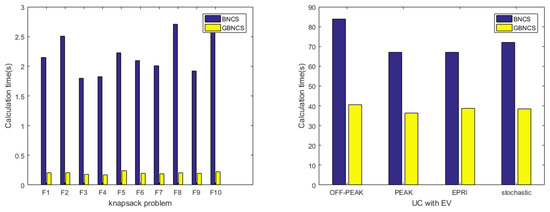
Figure 9.
Computational time of BNCS and GBNCS for the knapsack problem and UC with EVs problem.
5. Conclusions
This paper has proposed a unit commitment problem integrated with electric vehicles. Two algorithms, namely, the binary negatively correlated search and the global best inspired, binary, negatively correlated search have been proposed, for which a rounding transfer function to convert real-valued variables to binary ones was proposed. Furthermore, the GBNCS uses the global best information to improve the efficiency and convergence of the algorithm. The proposed algorithm was first tested on a benchmark knapsack problem and a basic unit commitment problem, and then applied to the unit commitment integrated with an electric vehicle model.
To comprehensively study the charging model, four charging modes were used to simulate different charging scenarios. The results confirmed that the proposed BNCS and GBNCS are very competitive in dealing with the traditional knapsack benchmark problem and the UCEV problem. The GBNCS is not only able to achieve good quality solutions to dispatch the committed units economically but also has great performance in convergence and computation time.
Our future work will consider other practical constraints of EV charging and discharging in real-world applications.
Author Contributions
Q.N. proposed the idea; K.J. and Z.Y. collected the data, designed the experiments and implemented the experiments; Q.N., K.J. analyzed the data and wrote the paper.
Funding
This paper was supported by the National Natural Science Foundation of China (61773252) and Natural Science Foundation of Guangdong Province (2018A030310671).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- U.S. Energy Information Administration (EIA). International Energy Outlook 2019. Available online: https://www.eia.gov/ (accessed on 1 July 2019).
- Mohammadi, F. Hybridization of an Electric Vehicle Using Lithium-ion Batteries. In Proceedings of the 1st International Conference on Modern Approaches in Engineering Science(ICMAES), Tbilisi, Georgia, 28–29 August 2018. [Google Scholar]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Lead Acid. In Proceedings of the 9th Iranian Conference on Electrical and Electronics Engineering (ICEEE), Gonabad, Iran, 28–29 August 2018. [Google Scholar]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Nickel Metal Hydride. In Proceedings of the 9th Iranian Conference on Electrical and Electronics Engineering (ICEEE), Gonabad, Iran, 28–29 August 2018. [Google Scholar]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Lithium-ion. In Proceedings of the 1st International Conference on Modern Approaches in Engineering Science (ICMAES), Tbilisi, Georgia, 28–29 August 2018. [Google Scholar]
- Fernández, R.A. A more realistic approach to electric vehicle contribution to greenhouse gas emissions in the city. J. Clean. Prod. 2018, 172, 949–959. [Google Scholar] [CrossRef]
- Mohammadi, F. Design and Electrification of an Electric Vehicle Using Lithium-ion Batteries. In Proceedings of the 1rd International Conference on Electrical Engineering, Zurich, Switzerland, 28–29 August 2018. [Google Scholar]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Systems 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Fernandes, C.; Frías, P.; Latorre, J.M. Impact of vehicle-to-grid on power system operation costs: The Spanish case study. Appl. Energy 2012, 96, 194–202. [Google Scholar] [CrossRef]
- Zhou, N.; Xiong, X.; Xiong, Q. Probability Model and Simulation Method of Electric Vehicle Charging Load on Distribution Network. J. Power Sources 2014, 42, 879–888. [Google Scholar] [CrossRef]
- Go, H.; Cho, I.; Kim, C. A Study on EV Charging Scheme Using Load Control. J. Electr. Eng. Technol. 2017, 12, 1789–1797. [Google Scholar]
- Snyder, W.; Powell, D.; Rayburn, J. Dynamic programming approach to unit commitment. IEEE Trans. Power Syst. 1987, 2, 339–348. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhou, B.; Zhang, M. Parallel augment Lagrangian Relaxation method for transient stability constrained unit commitment. IEEE Trans. Power Syst. 2013, 28, 1140–1148. [Google Scholar] [CrossRef]
- Kazarlis, S.A.; Bakirtzis, A.G.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Sasaki, H.; Watanabe, M.; Kubokawa, J. A solution method of unit commitment by artificial neural networks. IEEE Trans. Power Syst. 1992, 7, 974–981. [Google Scholar] [CrossRef]
- Rajan, C.C.A.; Mohan, M.R. An evolutionary programming-based tabu search method for solving the unit commitment problem. IEEE Trans. Power Syst. 2004, 19, 577–584. [Google Scholar] [CrossRef]
- Simopoulos, D.N.; Kavatza, S.D.; Vournas, C.D. Unit Commitment by an Enhanced Simulated Annealing Algorithm. 2006 IEEE PES Power Syst. Conf. Expo. 2006, 1, 193–201. [Google Scholar]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Alemany, J.; Magnago, F.; Moitre, D. Symmetry issues in mixed integer programming based Unit Commitment. Int. J. Electr. Power Energy Syst. 2014, 54, 86–90. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D. Particle Swarm Optimization for unit commitment problem. 2010 IEEE 11th Int. Conf. Probabilistic Methods Appl. Power Syst. 2010, 1, 642–647. [Google Scholar]
- Saber, A.Y.; Venayagamoorthy, G.K. Intelligent unit commitment with vehicle-to-grid—A cost-emission optimization. Electr. Power Compon. Syst. 2010, 195, 898–911. [Google Scholar] [CrossRef]
- Foley, A.; Tyther, B.; Calnan, P.; Gallachoir, B.O. Impacts of electric vehicle charging under electricity market operations. Appl. Energy 2013, 101, 93–102. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Z.; You, P. Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging. J. Sol. Energy Res. 2018, 3, 293–299. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Botterud, A. Assessment of Impacts of PHEV Charging Patterns on Wind-Thermal Scheduling by Stochastic Unit Commitment. IEEE Trans. Smart Grid 2012, 3, 675–683. [Google Scholar] [CrossRef]
- Mohammadi, F. Design, Analysis, and Electrification of a Solar-Powered Electric Vehicle. J. Solar Energy Res. 2018, 3. [Google Scholar]
- Yang, Z.; Li, K.; Niu, Q. A comprehensive study of economic unit commitment of power systems integrating various renewable generations and plug-in electric vehicles. Energy Convers. Manag. 2017, 132, 460–481. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Nazri, M. A Bidirectional Power Charging Control Strategy for Plug-in Hybrid Electric Vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef]
- Yang, L.; Li, K.; Xu, X. A hybrid meta-heuristic method for unit commitment considering flexible charging and discharging of plug-in electric vehicles. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2014–2020. [Google Scholar]
- Tang, K.; Yang, P.; Yao, X. Negatively Correlated Search. IEEE J. Select. Areas Commun. 2016, 34, 542–550. [Google Scholar] [CrossRef]
- EPRI executive summary: Environmental assessment of plug-in hybrid electric vehicles. In United States air quality Analysis Based on AEO-2006 Assumptions for 2030; Electric Power Research Institute: Palo Alto, CA, USA, 2007; Volume 2.
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
- Niu, Q.; Jiang, K.; Liu, B. A Novel Binary Negatively Correlated Search for Wind Farm Layout Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 191–196. [Google Scholar]
- Brier, E.; Clavier, C.; Olivier, F. Correlation power analysis with a leakage model. Lect. Notes Comput. Sci. 2004, 3156, 16–29. [Google Scholar]
- Rechenberg, I. Evolutionsstrategie Optimierung Technischer Systeme nach Prinzipien der Biologischen Evolution. Ph.D. Thesis, Universität zu Berlin, Berlin, Germany, 1973. [Google Scholar]
- Yuan, X.; Ji, B.; Zhang, S. A new approach for unit commitment problem via binary gravitational search algorithm. Appl. Soft Comput. 2014, 22, 249–260. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0–1 knapsack problem by a novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Juste, K.A.; Kita, H.; Tanaka, E.; Hasegawa, J. An evolutionary programming solution to the unit commitment problem. IEEE Trans. Power Syst. 1999, 14, 1452–1459. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.; Bai, B.; Cao, Y. An improved particle swarm optimization algorithm for unit commitment. Int. J. Electr. Power Energy Syst. 2006, 28, 482–490. [Google Scholar] [CrossRef]
- Gaing, Z. Discrete particle swarm optimization algorithm for unit commitment. 2003 IEEE Power Eng. Soc. Gener. Meet. 2003, 1, 418–424. [Google Scholar]
- Jeong, Y.; Park, J.; Jang, S.; Lee, K.Y. A New Quantum-Inspired Binary PSO: Application to Unit Commitment Problems for Power Systems. IEEE Trans. Power Syst. 2010, 25, 1486–1495. [Google Scholar] [CrossRef]
- Jeong, Y.; Park, J.; Shin, J.; Lee, K.Y. A thermal unit commitmentapproach using an improved quantum evolutionary algorithm. Electr. Power Compon. Syst. 2009, 37, 770–786. [Google Scholar] [CrossRef]
- Lau, T.W.; Chung, C.Y.; Wong, K.P.; Chung, T.S.; Ho, S.L. Quantum-Inspired Evolutionary Algorithm Approach for Unit Commitment. IEEE Trans. Power Syst. 2009, 24, 1503–1512. [Google Scholar] [CrossRef]
- Ghasemi, A.; Farsangi, M.M.; Nezamabadi-pour, H. Unit commitment scheduling using binary differential evolution algorithm. OPSEARCH 2009, 46, 108–122. [Google Scholar] [CrossRef]
- Datta, D. Unit commitment problem with ramp rate constraint using a binary-real-coded genetic algorithm. Appl. Soft Comput. 2013, 13, 3873–3883. [Google Scholar] [CrossRef]
- Afkousi-Paqaleh, M.; Rashidinejad, M.; Pourakbari-Kasmaei, M. An implementation of harmony search algorithm to unit commitment problem. Appl. Soft Comput. 2010, 92, 212–225. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Bath, S.K.; Dhillon, J.S. Hybrid HS–random search algorithm considering ensemble and pitch violation for unit commitment problem. Neural Comput. Appl. 2017, 28, 1123–1148. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Feng, S.; Niu, Q. A binary symmetric based hybrid meta-heuristic method for solving mixed integer unit commitment problem integrating with significant plug-in electric vehicles. Energy 2019, 170, 889–905. [Google Scholar] [CrossRef]
- Ehsan, T.; Masoud, R.; Amir, A. Evaluation of plug-in electric vehicles impact on cost-based unit commitment. Power Sources 2014, 248, 545–552. [Google Scholar]
- Zhang, L.; Niu, Q.; Yang, Z. Integration of electric vehicles charging in unit commitment. Int. J. Comput. Sci. Electron. Eng. 2015, 3, 22–27. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).