Analytical and Experimental Investigation of the Critical Length in Casing–Liner Overlap
Abstract
:1. Introduction
2. Literature Review
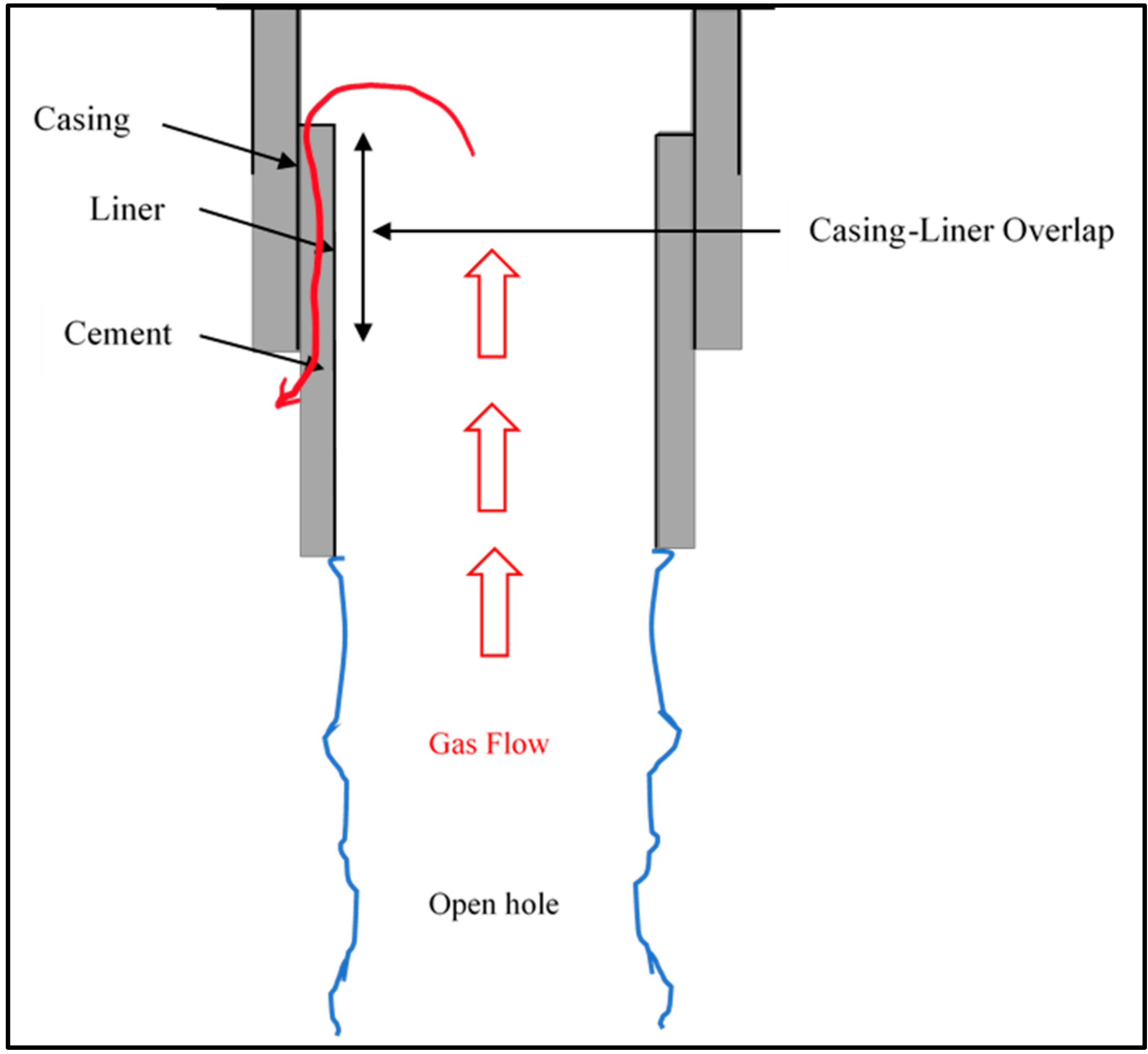
3. Development of Leakage Scenarios
- The last casing shoe was set at 1000 ft (304.8 m).
- Casing diameter was 22 inches (0.56 m).
- Liner hanger diameter was 18 inches (0.46 m).
- Temperature was 100 °F (37.7 °C).
- Four permeability values of 0.01, 0.1, 0.3, and 0.5 mD.
- Faulty elastomers in the liner hanger.
4. Experimental Methodology
5. Results and Discussion
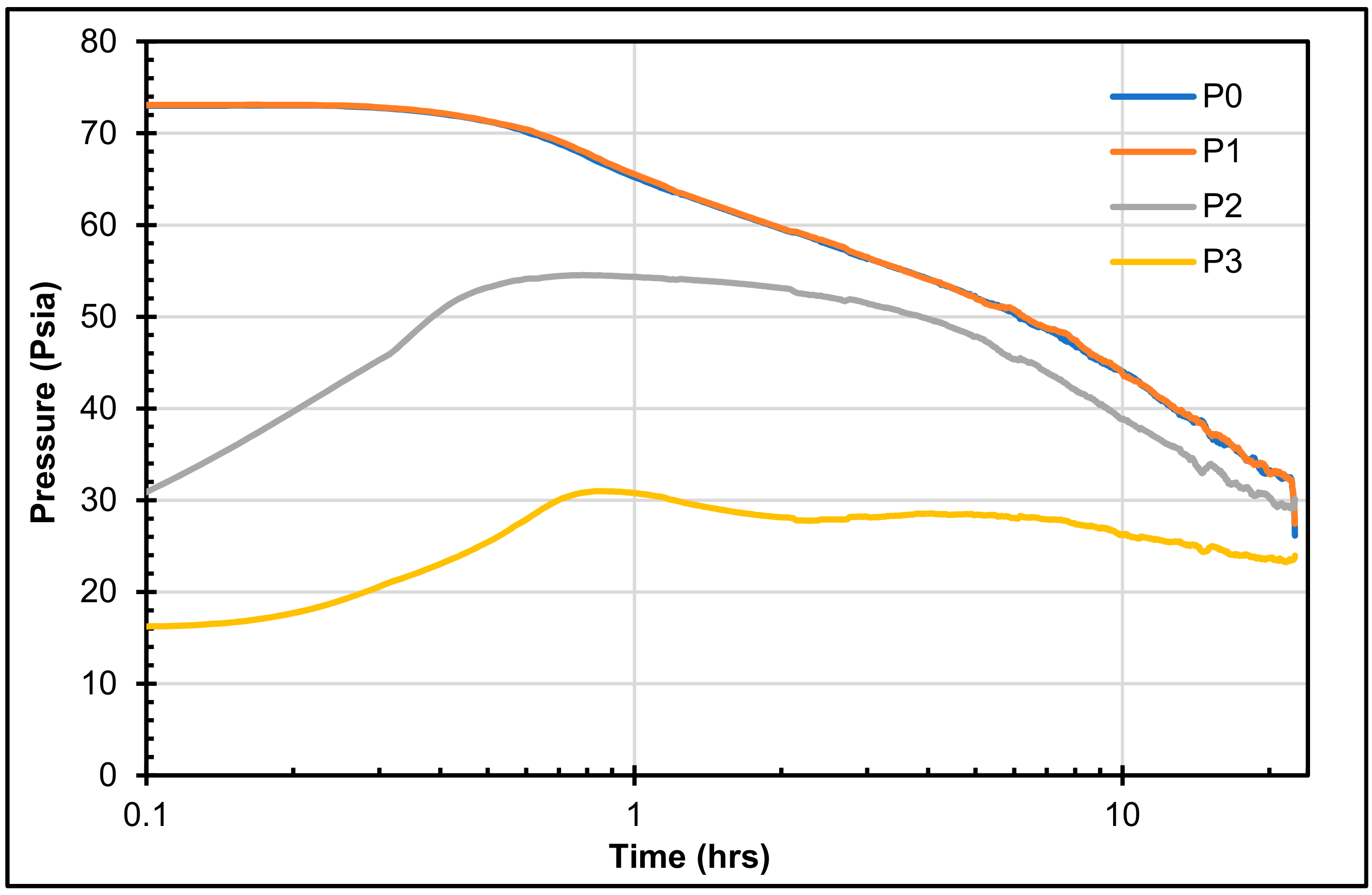
5.1. Experimental Results
5.2. Leakage Scenarios
6. Summary, Conclusions, and Recommendations
6.1. Conclusions
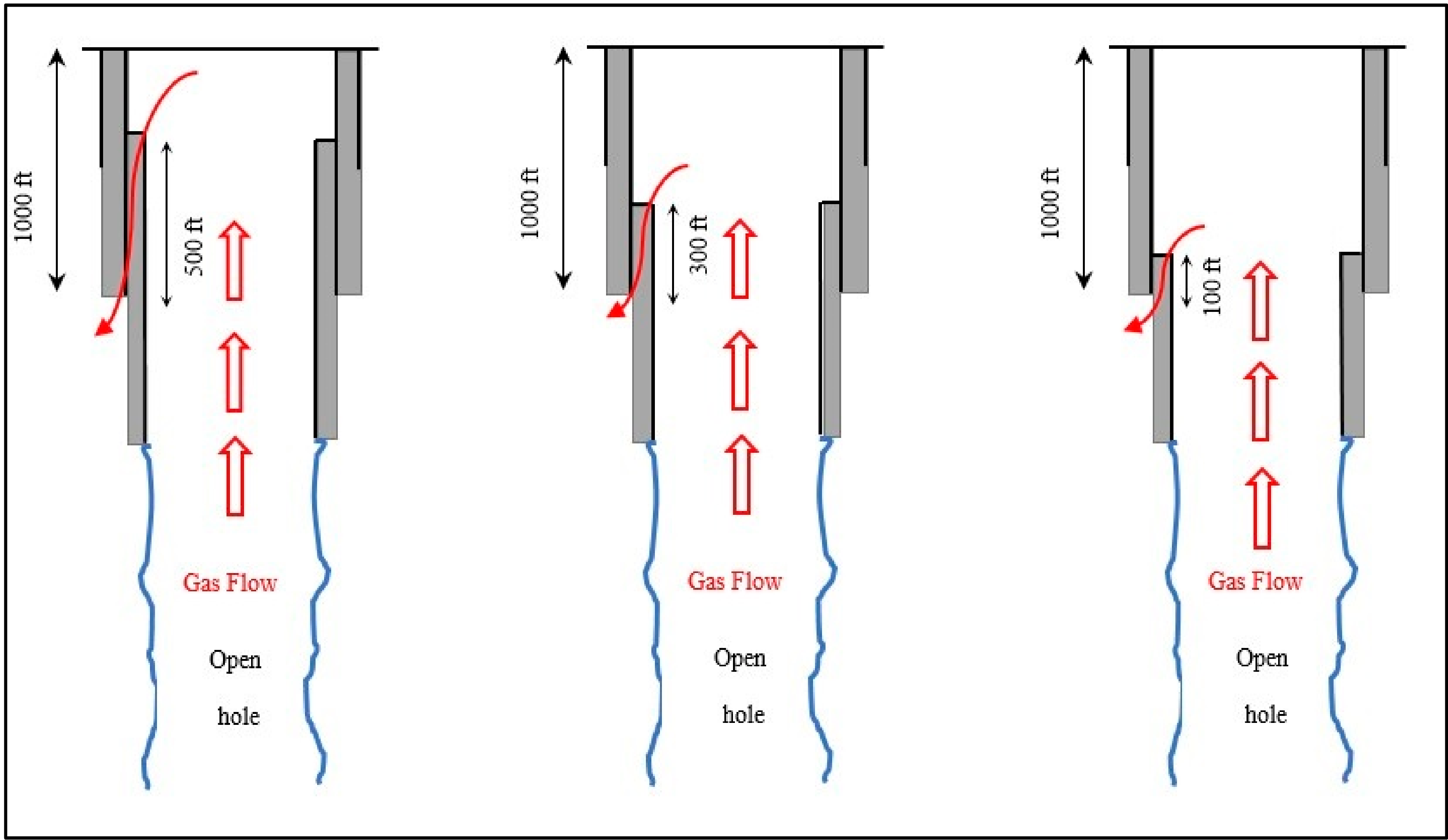
- A simple but effective methodology was proposed to estimate the leak time through a casing–liner overlap.
- The developed leakage scenarios showed that the leakage time increases as the length of the casing–liner overlap increases.
- The cement sheath sealability plays a critical role in maintaining the well integrity. The results showed that as the cement permeability increases, the leakage time decreases.
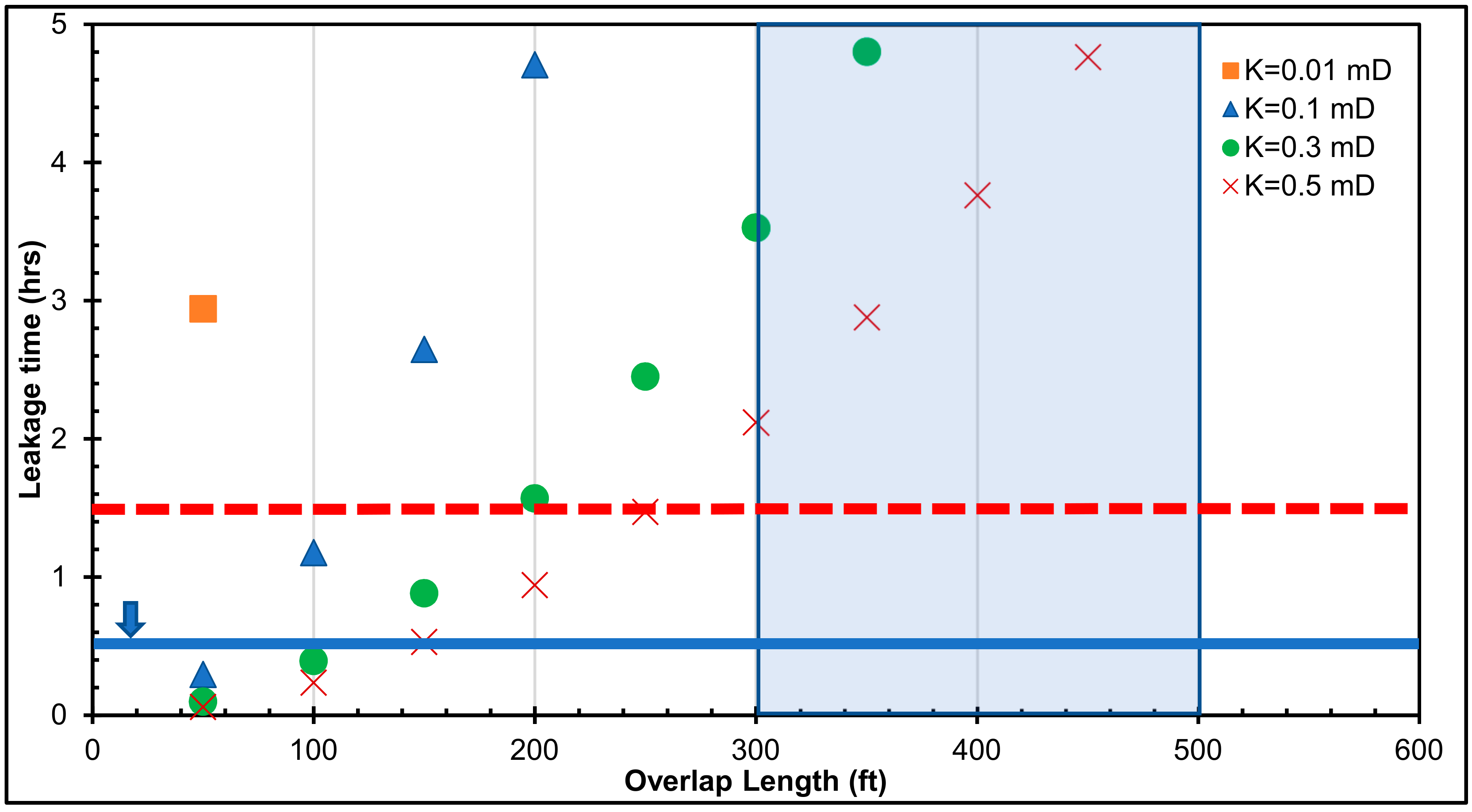
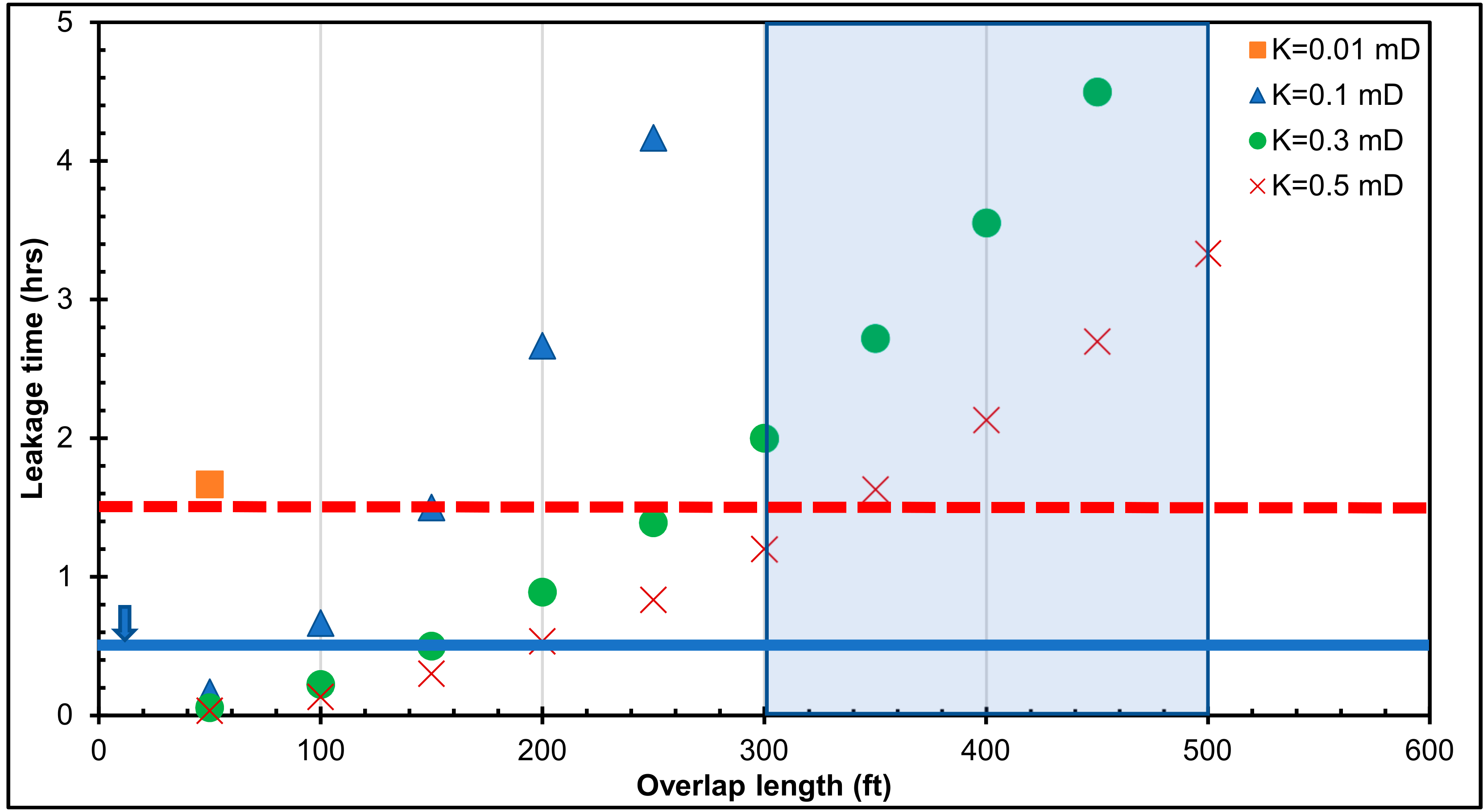
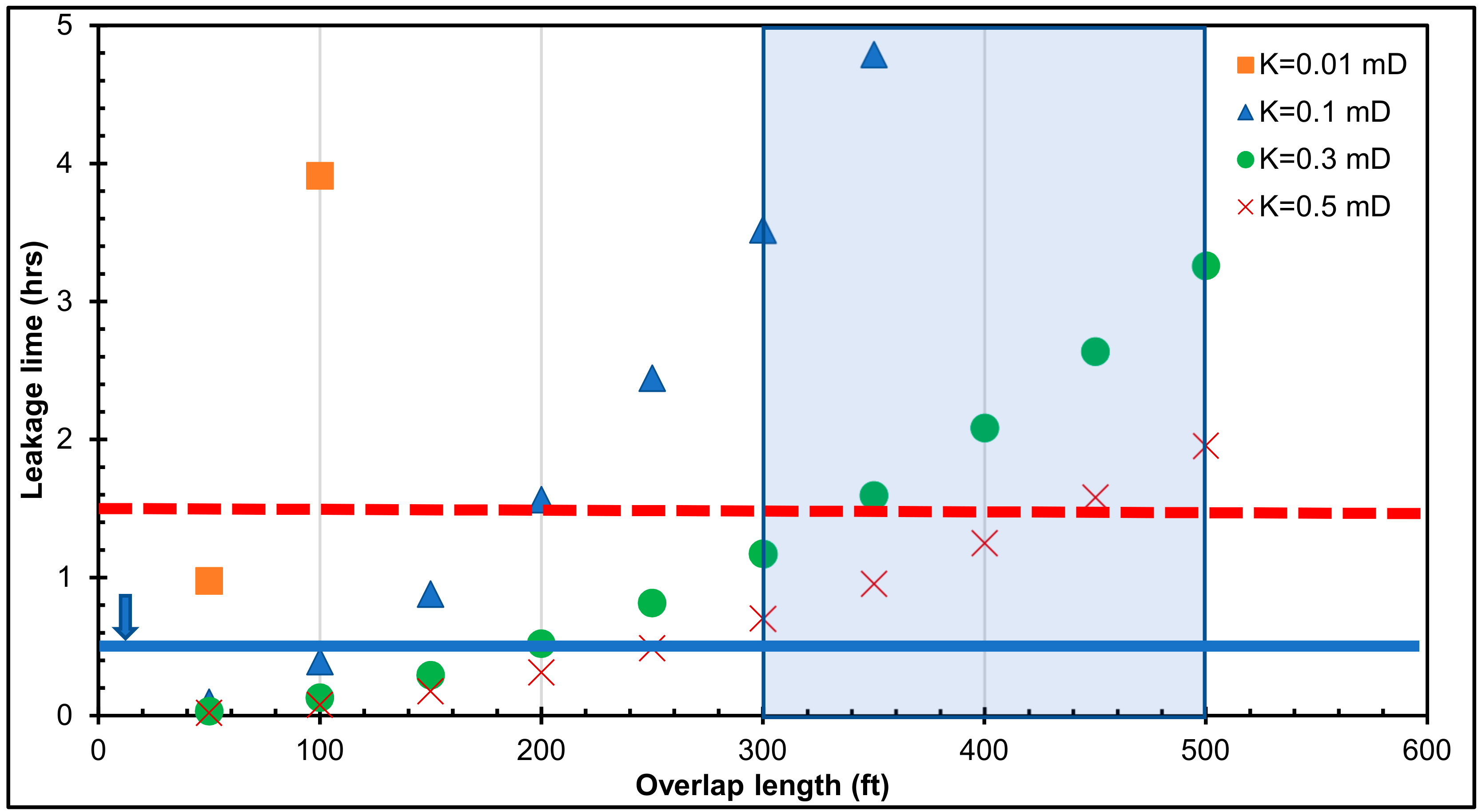
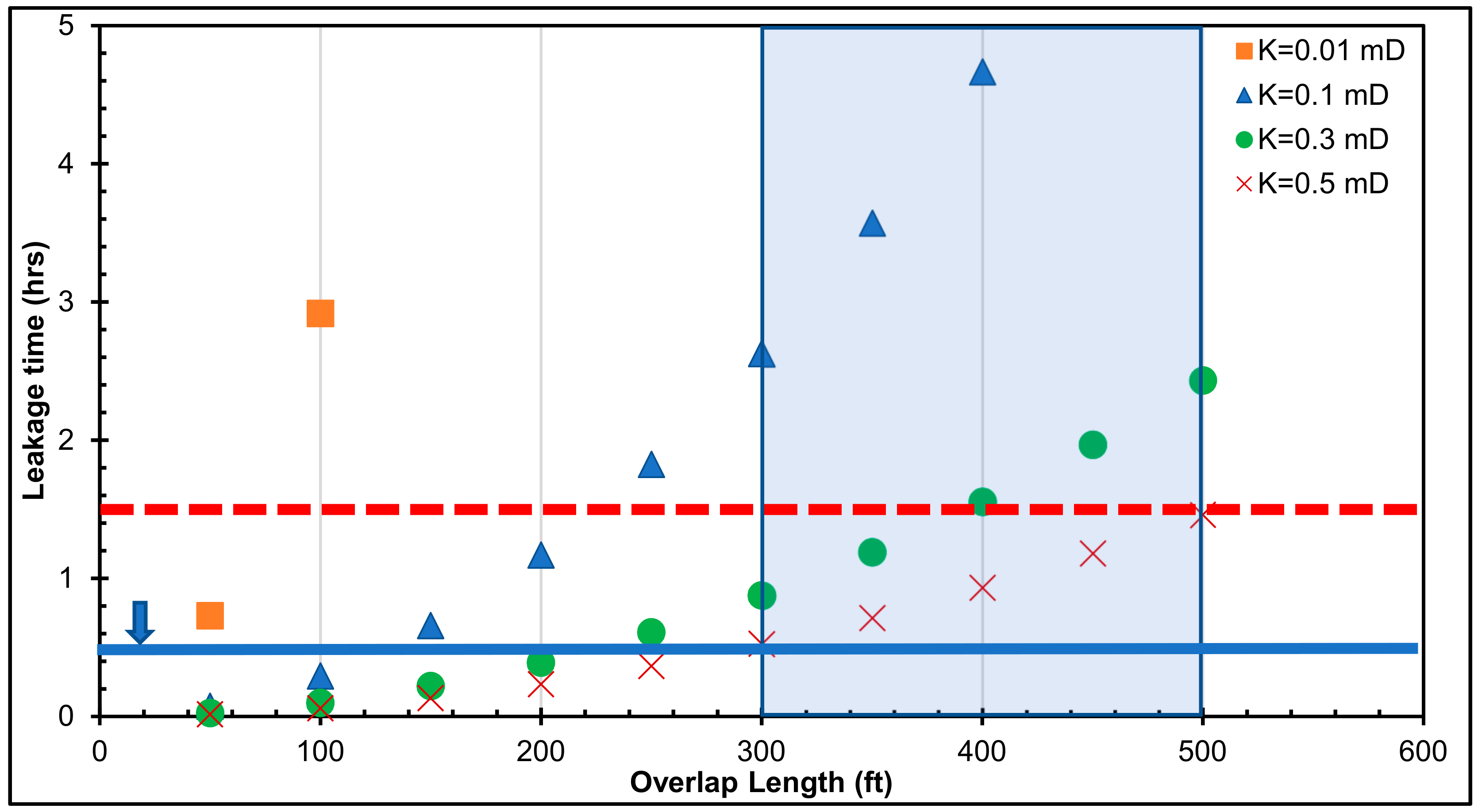
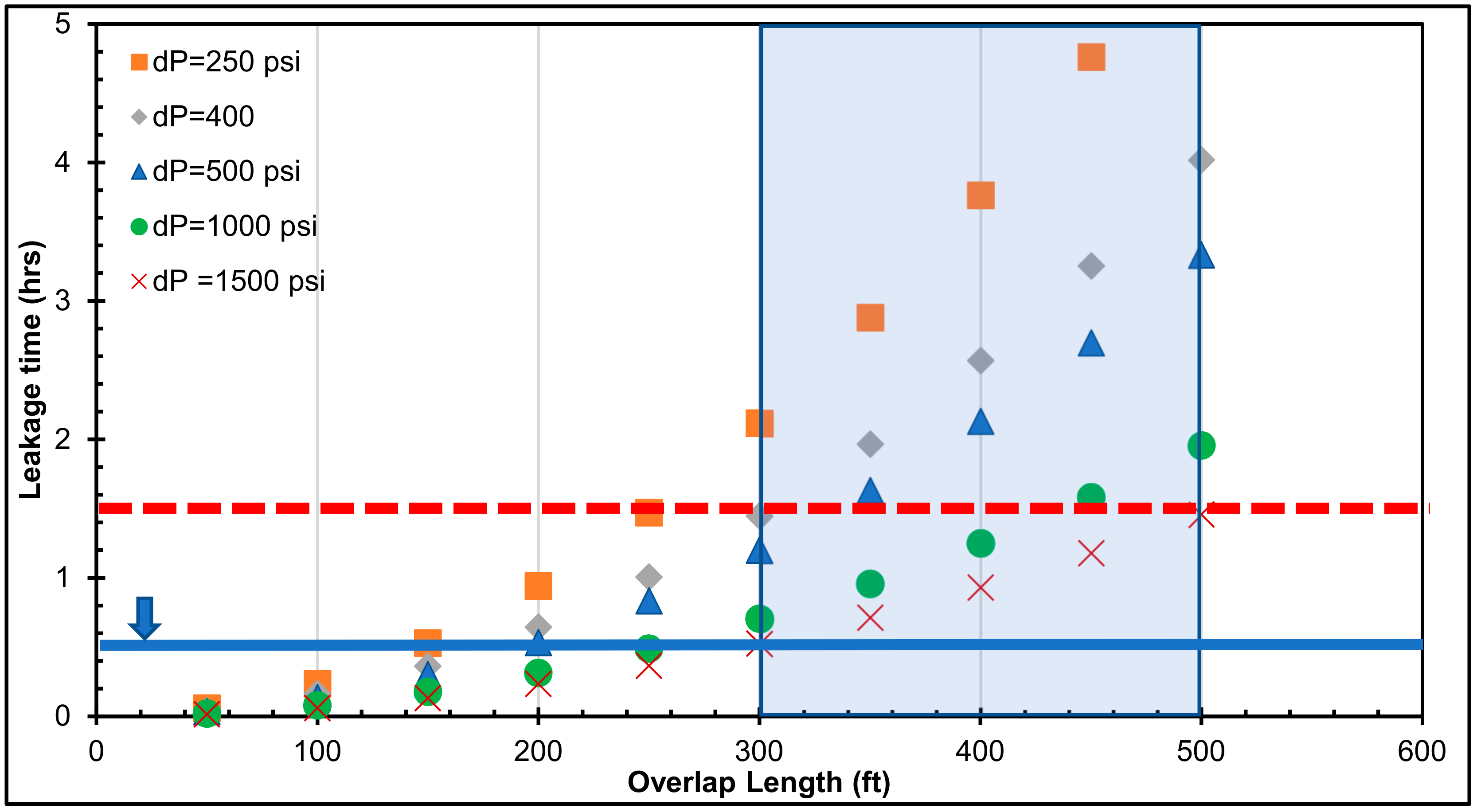
- The leakage scenario results revealed that 62% of the total leakage time falls under the casing–liner overlap range between 50 and 250 ft. This overlap range may not permit a longer duration for the detection and control of gas influx, when the cement sheath is faulty.
- The leakage scenario results suggest that only 35% of the leakage times are between 1 and 30 min. The current casing pressure test duration of 30 min may not be enough to verify the integrity of the cement sheath in the liner hanger overlap.
6.2. Recommendations
- It is recommended that the pressure test duration is increased beyond 30 min, depending on the cement column length in the casing–liner overlap. As shown from Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the dashed-red horizontal line (which represents 90 min) is the proposed pressure test duration for a cement column length ≥300 ft in the casing–liner overlap.
- It is recommended that the cement column in the casing–liner overlap is not less than 300 ft. The leakage times for all the differential pressure values in Figure 10 are less than 1 h for a 50-ft to 200-ft overlap. Shorter overlaps (50 to 200 ft) can be beneficial because pressure tests may quickly identify leaks if the cement and elastomer in the liner hanger are faulty. Cost may also be a contributing factor for the use of shorter overlaps. However, the leakage scenarios suggest that shorter overlaps have shorter leakage times, which implies a shorter time for gas migration through a faulty cement and elastomer in the overlap. To err on the side of caution, particularly in gas zones, the light-blue shaded area in Figure 10. represents the proposed cement column length in the casing–liner overlap (300 to 500 ft). This proposed range shows longer leakage times for a gas kick to migrate to the end of the overlap. In practice, the increase in leakage time can translate to a longer duration required for the detection and control of gas influx and migration.
- The experiments performed in this study were not at high temperatures. It is recommended that future experimental setups should consider the high temperature effect.
- The analytical method did not account for the cement’s mechanical properties. It is recommended that numerical methods are applied to compensate for the limitations of the analytical method.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| °F | Degree Fahrenheit |
| °K | Degree Kelvin |
| ∇P | Pressure gradient in Pa/m |
| 3D | Three dimensional |
| µ | Viscosity of fluid in Pa s |
| A | Cross sectional area of the cement plug in m2 |
| Am | Flow area in m2 |
| BOP | Blow-out preventer |
| BSEE | The Bureau of Safety and Environmental Enforcement |
| CO2 | Carbon dioxide |
| DAQ | Data acquisition system |
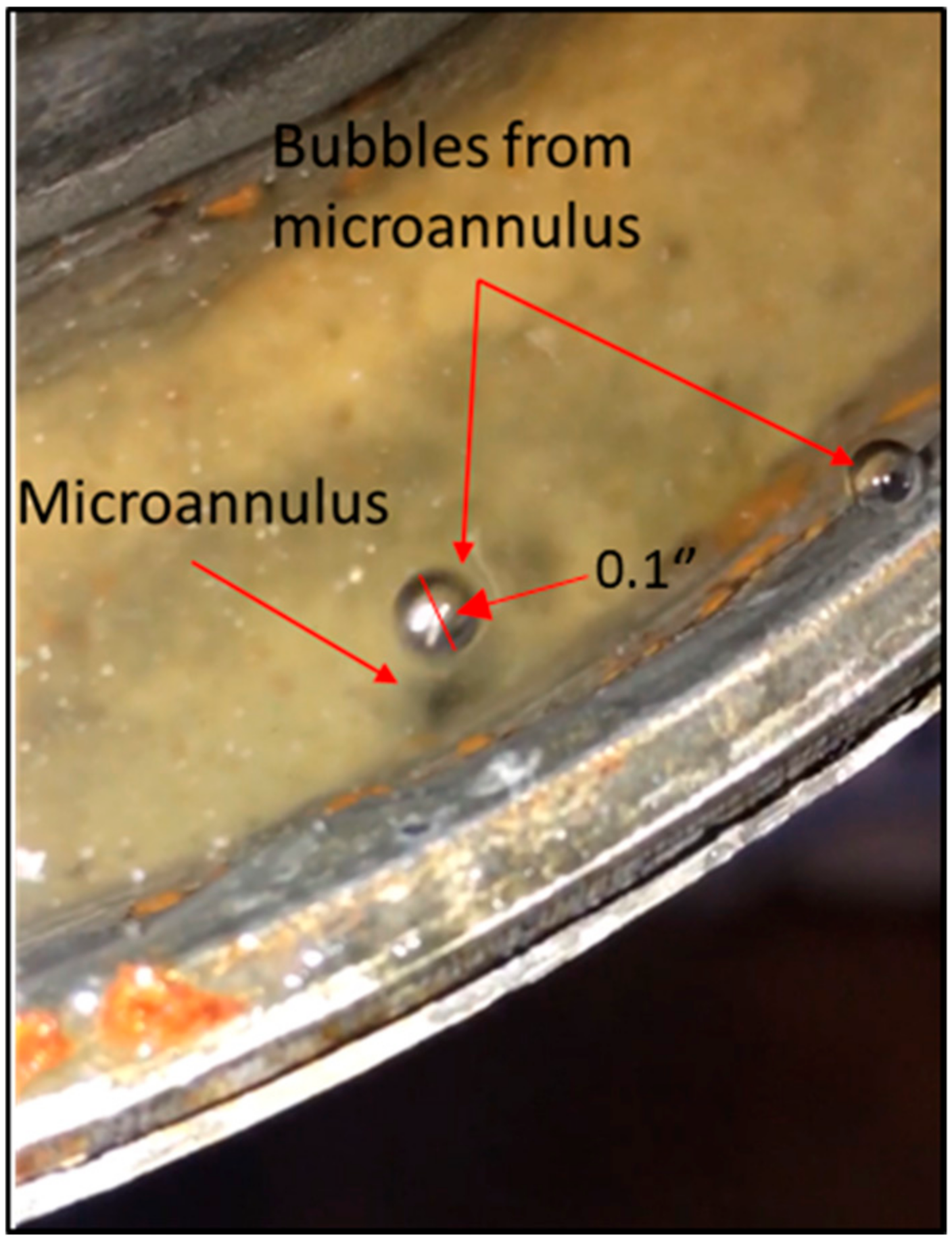
| ẟR | Microannulus gap in m |
| ft | Foot |
| GOM | Gulf of Mexico |
| h | Fracture aperture in m (Equation (3)) |
| h | Hydraulic aperture in m (Equation (4)) |
| H2S | Hydrogen sulfide |
| k | Cement permeability in m2 |
| K | Kalvin |
| Kg | Kilogram |
| L | Length of the cement column in m |
| M | Gas molecular weight in kg/mole |
| m | Meters |
| m2 | Square meter |
| m3 | Cubic meter |
| mD | milli-Darcy |
| N2 | Nitrogen gas |
| NVR | Network video recorder |
| θ | Inclination of well corresponding the cement plug in (°) |
| P&A | Plug and abandonment |
| Pa | Pascals |
| Pd | Downstream pressure in Pa |
| Pu | Upstream pressure in Pa |
| psi | Pound per square inch |
| psia | Pound per square inch absolute |
| psig | Pound per square inch gauge |
| Q | Flow rate in m3/sec |
| R | Universal gas constant in m3 Pa/mole K |
| Rc | Outer casing radius in m |
| Ri | Inner casing radius in m |
| Rm | Microannulus radius in m |
| SCP | Sustained casing pressure |
| s | Seconds |
| t | Leakage time in s |
| T | Temperature in Kelvin |
| W | Fracture width in m |
| W/C | Water to cement ratio |
| WOC | Wait on cement |
| z | Gas compressibility factor |
| α | Fracture orientation in (°) |
| ΔP | Pressure difference across the cement in Pa |
| ρ | Fluid density in kg/m3 |
| ω | Length of hydraulic aperture in m |
References
- Davies, R.J.; Almond, S.; Ward, R.S.; Jackson, R.B.; Adams, C.; Worrall, F.; Herringshaw, L.G.; Gluyas, J.G.; Whitehead, M.A. Oil and gas wells and their integrity: Implications for shale and unconventional resource exploitation. Mar. Pet. Geol. 2014, 56, 239–254. [Google Scholar] [CrossRef]
- Nygaard, R.; Salehi, S.; Weideman, B.; Lavoie, R.G. Effect of Dynamic Loading on Wellbore Leakage for the Wabamun Area CO2-Sequestration Project. J. Can. Pet. Technol. 2014, 53, 69–82. [Google Scholar] [CrossRef]
- Kiran, R.; Teodoriu, C.; Dadmohammadi, Y.; Nygaard, R.; Wood, D.; Mokhtari, M.; Salehi, S. Identification and evaluation of well integrity and causes of failure of well integrity barriers (A review). J. Nat. Gas Sci. Eng. 2017, 45, 511–526. [Google Scholar] [CrossRef]
- Al Ramadan, M.; Salehi, S.; Teodoriu, C. Robust Leakage Modeling for Plug & Abandonment Applications. In Proceedings of the ASME 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Ahmed, S.; Salehi, S.; Ezeakacha, C.; Teodoriu, C. Experimental investigation of elastomers in downhole seal elements: Implications for safety. Polym. Test. 2019, 76, 350–364. [Google Scholar] [CrossRef]
- Phi, T.; Elgaddafi, R.; Al Ramadan, M.; Ahmed, R.; Teodoriu, C. Well Integrity Issues: Extreme High-Pressure High-Temperature Wells and Geothermal Wells a Review. In Proceedings of the SPE Thermal Well Integrity and Design Symposium, Banff, AB, Canada, 19–21 November 2019. [Google Scholar]
- NORSOK. Standard D-010: Well Integrity in Drilling and Well Operations; NORSOK: Lysaker, Norway, 2014. [Google Scholar]
- Bogaerts, M.; De Bruijn, G.G.; Khalilova, P.R.; Moretti, F.; Voon, E. Identifying and Mitigating the Risks of Shallow Flow in Deepwater Cementing Operations. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 20–21 June 2012. [Google Scholar]
- Murray, S.J.; Williamson, M.D.; Gilham, S.; Thorogood, J.L. Well Design for Shallow Gas. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 28 February–2 March 1995. [Google Scholar]
- Adams, N.J.; Kuhlman, L.G. Case History Analyses of Shallow Gas Blowouts. In Proceedings of the SPE/IADC Drilling Conference, Houston, TX, USA, 27 February–2 March 1990. [Google Scholar]
- Prince, P.K. Current Drilling Practice And The Occurrence Of Shallow Gas. In Proceedings of the International Conference on Safety in Offshore Engineering, London, UK, 25–16 April 1990. [Google Scholar]
- Ahmed, S.; Salehi, S.; Ezeakacha, C.P.; Teodoriu, C. Evaluation of liner hanger seal assembly and cement sheath as a dual barrier system: Implications for industry standards. J. Pet. Sci. Eng. 2019, 178, 1092–1103. [Google Scholar] [CrossRef]
- Patel, H.; Hariharan, H.; Bailey, G.; Jung, G. Advanced Computer Modelling for Metal-to-Metal Seal in API Flanges. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24 September 2018; p. 21. [Google Scholar]
- Patel, H.; Salehi, S.; Ahmed, R.; Teodoriu, C. Review of elastomer seal assemblies in oil & gas wells: Performance evaluation, failure mechanisms, and gaps in industry standards. J. Pet. Sci. Eng. 2019, 179, 1046–1062. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S.; Teodoriu, C.; Ahmed, R. Performance evaluation and parametric study of elastomer seal in conventional hanger assembly. J. Pet. Sci. Eng. 2019, 175, 246–254. [Google Scholar] [CrossRef]
- Ahmed, S.; Ezeakacha, C.P.; Salehi, S. Improvement in Cement Sealing Properties and Integrity Using Conductive Carbon Nano Materials: From Strength to Thickening Time. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. [Google Scholar]
- Al-Yami, A.S.; Nasr-El-Din, H.A.; Al-Humaidi, A.S. An Innovative Cement Formula To Prevent Gas-Migration Problems in HT/HP Wells. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 20–22 April 2009. [Google Scholar]
- Grinrod, M.; Vassoy, B.; Dingsoyr, E.O. Development and Use of a Gas-Tight Cement. In Proceedings of the SPE/IADC Drilling Conference, Dallas, TX, USA, 28 February–2 March 1988. [Google Scholar]
- Kwatia, G.; Al Ramadan, M.; Salehi, S.; Teodoriu, C. Enhanced Cement Composition for Preventing Annular Gas Migration. In Proceedings of the ASME 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Khalifeh, M.; Saasen, A.; Hodne, H.; Godøy, R.; Vrålstad, T. Geopolymers as an alternative for oil well cementing applications: A review of advantages and concerns. J. Energy Resour. Technol. 2018, 140, 092801. [Google Scholar] [CrossRef]
- Salehi, S.; Khattak, M.J.; Ali, N.; Ezeakacha, C.; Saleh, F.K. Study and Use of Geopolymer Mixtures for Oil and Gas Well Cementing Applications. J. Energy Resour. Technol. 2017, 140, 012908. [Google Scholar] [CrossRef]
- Salehi, S.; Khattak, M.J.; Rizvi, H.; Karbalaei, S.F.; Kiran, R. Sensitivity analysis of fly ash geopolymer cement slurries: Implications for oil and gas wells cementing applications. J. Nat. Gas Sci. Eng. 2017, 37, 116–125. [Google Scholar] [CrossRef]
- Fakoya, M.; Patel, H.; Shah, S. Nanotechnology: Innovative applications in the oil and gas industry. Int. J. Glob. Adv. Mater. Nanotechnol. 2018, 1, 16–30. [Google Scholar]
- Kimanzi, R.; Patel, H.; Khalifeh, M.; Salehi, S.; Teodoriu, C. Potentials of nano-designed plugs: Implications for short and long term well integrity. In Proceedings of the 38th International Conference on Ocean, Offshore & Artic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar]
- Patel, H. Effect of Nanoparticles and Solvent Based Emulsion on Heavy Oil Viscosity; University of Oklahoma: Norman, OK, 2016. [Google Scholar]
- Patel, H.; Salehi, S.; Teodoriu, C. Assessing Mechanical Integrity of Expanding Cement. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium, Oklahoma City, OK, USA, 9–10 April 2019. [Google Scholar]
- Saleh, F.K.; Rivera, R.; Salehi, S.; Teodoriu, C.; Ghalambor, A. How Does Mixing Water Quality Affect Cement Properties. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Lafayette, LA, USA, 7–9 February 2018. [Google Scholar]
- Nath, F.; Kimanzi, R.J.; Mokhtari, M.; Salehi, S. A novel method to investigate cement-casing bonding using digital image correlation. J. Pet. Sci. Eng. 2018, 166, 482–489. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S. Development of an Advanced Finite Element Model and Parametric Study to Evaluate Cement Sheath Barrier. J. Energy Resour. Technol. 2019, 141, 092902. [Google Scholar] [CrossRef]
- Rocha-Valadez, T.; Hasan, A.R.; Mannan, S.; Kabir, C.S. Assessing Wellbore Integrity in Sustained-Casing-Pressure Annulus. SPE Drill. Completion 2014, 29, 131–138. [Google Scholar] [CrossRef]
- Xu, R. Analysis of Diagnostic Testing of Sustained Casing Pressure in Wells. Ph.D.Thesis, Louisiana State University, Baton Rouge, LA, USA, 2002. [Google Scholar]
- Xu, R.; Wojtanowicz, A.K. Pressure buildup test analysis in wells with sustained casing pressure. J. Nat. Gas Sci. Eng. 2017, 38, 608–620. [Google Scholar] [CrossRef]
- Nishikawa, S. Mechanism of Gas Migration after Cement Placement and Control of Sustained Casing Pressure. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, May 1999. [Google Scholar]
- Xu, R.; Wojtanowicz, A.K. Diagnosis of Sustained Casing Pressure from Bleed-off/Buildup Testing Patterns. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 24–27 March 2001. [Google Scholar]
- Xu, R.; Wojtanowicz, A.K. Diagnostic Testing of Wells With Sustained Casing Pressure-An Analytical Approach. In Proceedings of the Canadian International Petroleum Conference, Calgary, AB, Canada, 10–12 June 2003. [Google Scholar]
- Huerta, N.J.; Checkai, D.; Bryant, S.L. Utilizing Sustained Casing Pressure Analog to Provide Parameters to Study CO2 Leakage Rates Along a Wellbore. In Proceedings of the SPE International Conference on CO2 Capture Storage, and Utilization, San Diego, CA, USA, 2–4 November 2009. [Google Scholar]
- Tao, Q.; Checkai, D.; Bryant, S.L. Permeability Estimation for Large-Scale Potential CO2 Leakage Paths in Wells Using a Sustained-Casing-Pressure Model. In Proceedings of the SPE International Conference on CO2 Capture Storage, and Utilization, New Orleans, LA, USA, 10–12 November 2010. [Google Scholar]
- Salehi, S. Modeling Near Wellbore Leakage Pathways in Shale Gas Wells: Investigating Short and Long Terms Wellbore Integrity. In Proceedings of the US EPA Technical Workshop on Well Construction/Operation and Subsurface Modelling, Research Triangle Park, NC, USA, 16–17 April 2013. [Google Scholar]
- Aas, B.; Sørbø, J.; Stokka, S.; Saasen, A.; Statoil, R.G.; Lunde, Ø.; Phillips, C.; Vrålstad, T. Cement Placement with Tubing Left in Hole during Plug and Abandonment Operations. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 1–3 March 2016. [Google Scholar]
- Ford, E.P.; Moeinikia, F.; Lohne, H.P.; Arild, Ø.; Majoumerd, M.M.; Fjelde, K.K. Leakage Calculator for Plugged and Abandoned Wells. In Proceedings of the SPE Bergen One Day Seminar, Bergen, Norway, 5 April 2017. [Google Scholar]
- Godoy, R.; Fontan, M.; Capra, B.; Kvalsund, R.; Poupard, O. Well Integrity Support by Extended Cement Evaluation—Numerical Modeling of Primary Cement Jobs. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 9–12 November 2015. [Google Scholar]
- Sarkar, S.; Toksoz, M.N.; Burns, D.R. Fluid Flow Modeling in Fractures; Massachusetts Institute of Technology, Earth Resources Laboratory: Cambridge, MA, USA, 2004. [Google Scholar]
- Stormont, J.C.; Fernandez, S.G.; Taha, M.R.; Matteo, E.N. Gas flow through cement-casing microannuli under varying stress conditions. Geomech. Energy Environ. 2018, 13, 1–13. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- API. API BULLETIN E3: Environmental Guidance Document: Well Abandonment and Inactive Well Practices for U.S. Exploration and Production Operations, 1st ed.; API: Washington, DC, USA, 1993. [Google Scholar]
- API. API RP 10A: Specification for Cements and Materials for Well Cementing, 24th ed.; API: Washington, DC, USA, 2010. [Google Scholar]
- Carey, J.W. Geochemistry of wellbore integrity in CO2 sequestration: Portland cement-steel-brine-CO2 interactions. Rev. Mineral. Geochem. 2013, 77, 505–539. [Google Scholar] [CrossRef]
- Carroll, S.; Carey, J.W.; Dzombak, D.; Huerta, N.J.; Li, L.; Richard, T.; Um, W.; Walsh, S.D.C.; Zhang, L. Review: Role of chemistry, mechanics, and transport on well integrity in CO2 storage environments. Int. J. Greenh. Gas Control 2016, 49, 149–160. [Google Scholar] [CrossRef]
- Huerta, N.J.; Hesse, M.A.; Bryant, S.L.; Strazisar, B.R.; Lopano, C.L. Experimental Evidence for Self-Limiting Reactive Flow through a Fractured Cement Core: Implications for Time-Dependent Wellbore Leakage. Environ. Sci. Technol. 2013, 47, 269–275. [Google Scholar] [CrossRef]
- Al Ramadan, M.; Salehi, S.; Kwatia, G.; Ezeakacha, C.; Teodoriu, C. Experimental investigation of well integrity: Annular gas migration in cement column. J. Pet. Sci. Eng. 2019, 179, 126–135. [Google Scholar] [CrossRef]
- BSEE. QC-FIT Evaluation of Seal Assembly & Cement Failures Interim Summary of Findings; Internal QC-FIT Report #2014-02; Bureau of Safety and Environmental Enforcement: Washington, WA, USA, 2014.
- API. API SPEC 17 D: Specification for Design and Operation of Subsea Production Systems-Subsea Wellhead and Tree Equipment, 2nd ed.; API: Washington, DC, USA, 2011. [Google Scholar]
- CFR-250.425. What are the Requirements for Pressure Testing Liners. In A Special Edition of the Federal Register; Office of the Federal Register National Achieves and Records Administration: Dallas, TX, USA, 2004. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Ramadan, M.; Salehi, S.; Ezeakacha, C.; Teodoriu, C. Analytical and Experimental Investigation of the Critical Length in Casing–Liner Overlap. Sustainability 2019, 11, 6861. https://doi.org/10.3390/su11236861
Al Ramadan M, Salehi S, Ezeakacha C, Teodoriu C. Analytical and Experimental Investigation of the Critical Length in Casing–Liner Overlap. Sustainability. 2019; 11(23):6861. https://doi.org/10.3390/su11236861
Chicago/Turabian StyleAl Ramadan, Mustafa, Saeed Salehi, Chinedum Ezeakacha, and Catalin Teodoriu. 2019. "Analytical and Experimental Investigation of the Critical Length in Casing–Liner Overlap" Sustainability 11, no. 23: 6861. https://doi.org/10.3390/su11236861
APA StyleAl Ramadan, M., Salehi, S., Ezeakacha, C., & Teodoriu, C. (2019). Analytical and Experimental Investigation of the Critical Length in Casing–Liner Overlap. Sustainability, 11(23), 6861. https://doi.org/10.3390/su11236861





