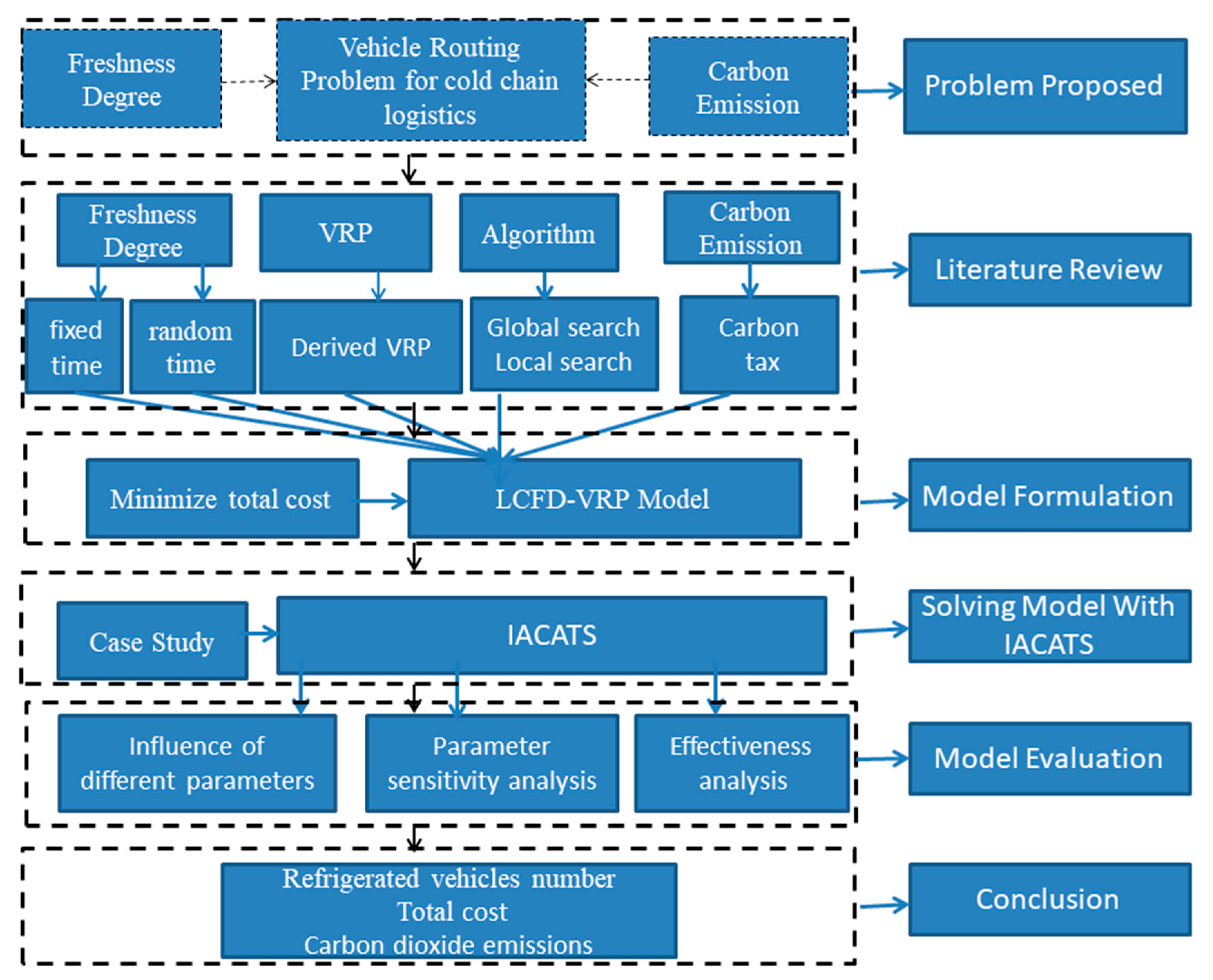
Optimization of Transportation Routing Problem for Fresh Food by Improved Ant Colony Algorithm Based on Tabu Search
Abstract
1. Introduction
2. Literature Review
2.1. Research Considering the VRP Model in Cold Chain Logistics
2.2. Research Considering Fresh Degrees
2.3. Research Considering Carbon Emissions
2.4. Research Considering the Optimization Algorithms
3. Model
3.1. Problem Description
- (1)
- Each customer can only be distributed to by one distribution center (DC), and all vehicles have the same loading ability.
- (2)
- The fresh products would deliver from DC and then to customers, with the assumption that each route begins and ends at the same DC.
- (3)
- We do not need to consider the customer’s request ahead of time. The demand of the customers is known or can be estimated in advance.
3.2. Objective Function of the LCFD-VRP
3.3. Factors Considered in the Model
3.3.1. Cost Profile
3.3.2. Fixed Cost
3.3.3. Fuel Cost and Carbon Cost
3.2.4. Penalty Cost for Freshness Degradation
3.2.5. Time Window Penalty Cost
4. Solving the Model Using IACATS
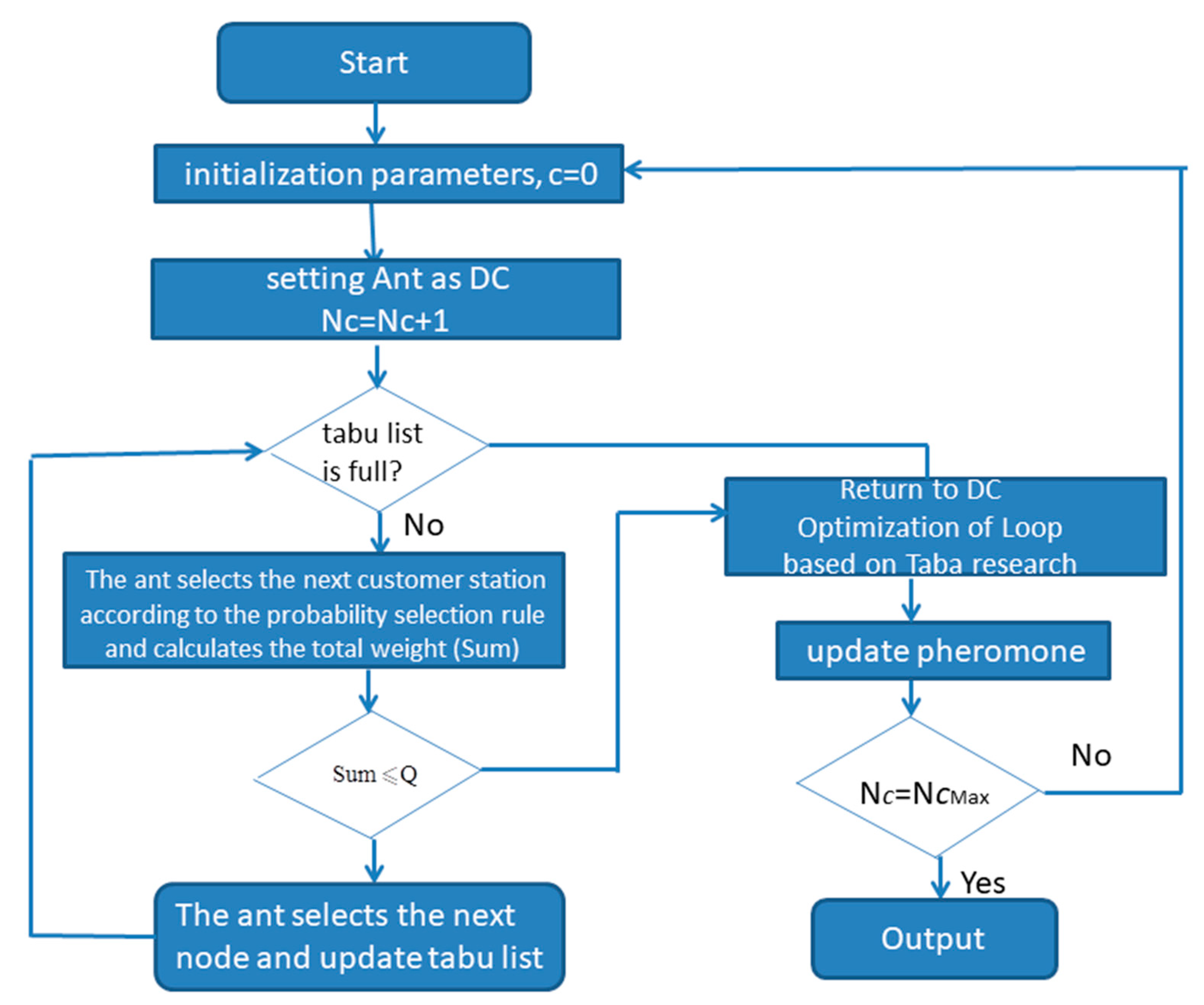
4.1. Improved Ant Colony Algorithm
Resetting the Rules of Updated Pheromone
4.2. Local Optimization and Improvement
4.3. Calculation Steps of the Algorithm
5. Case Study
Parameter Profile
6. Results
6.1. The Influences of Different Parameters on the Stability Performance of IACATS
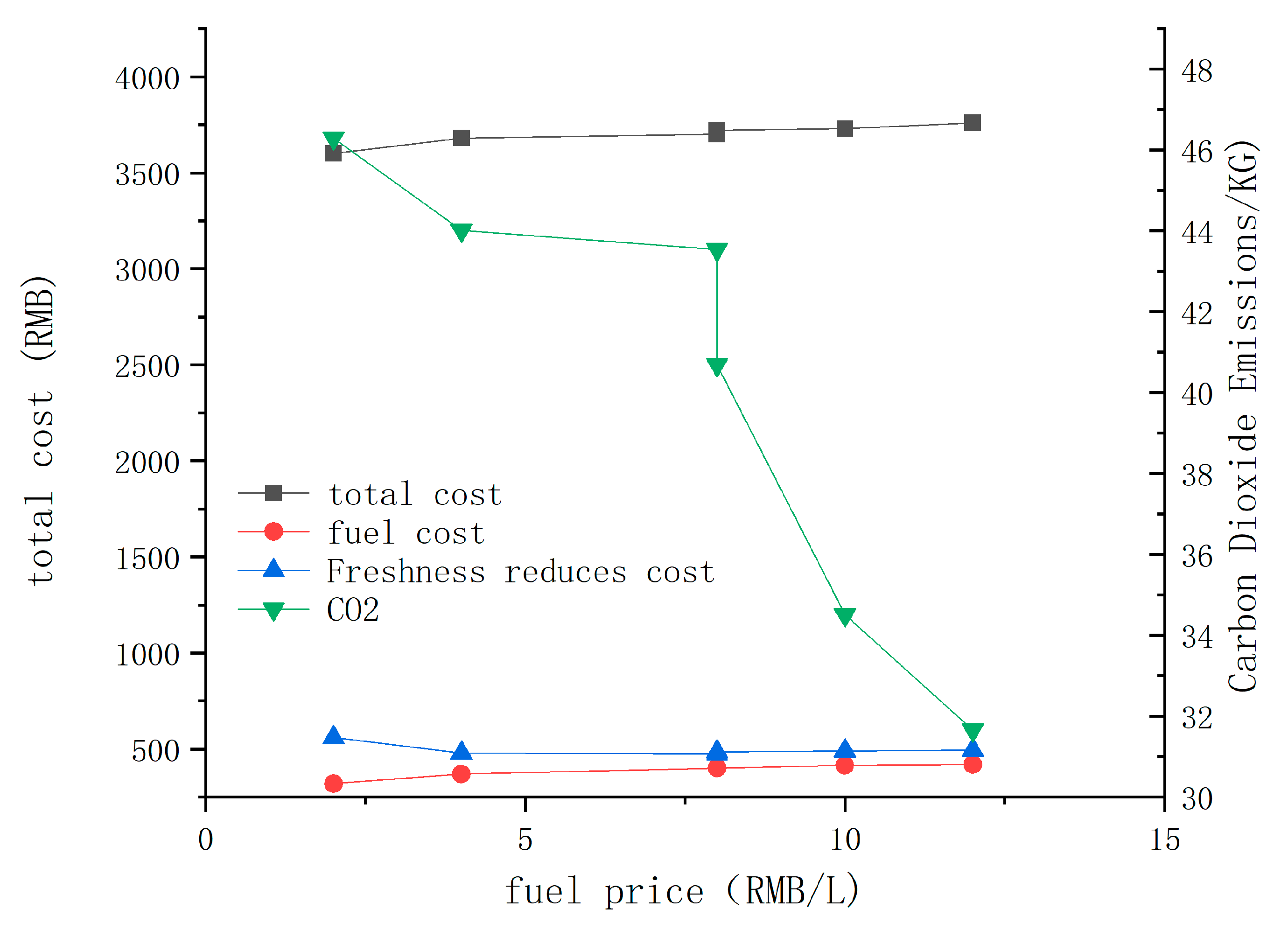
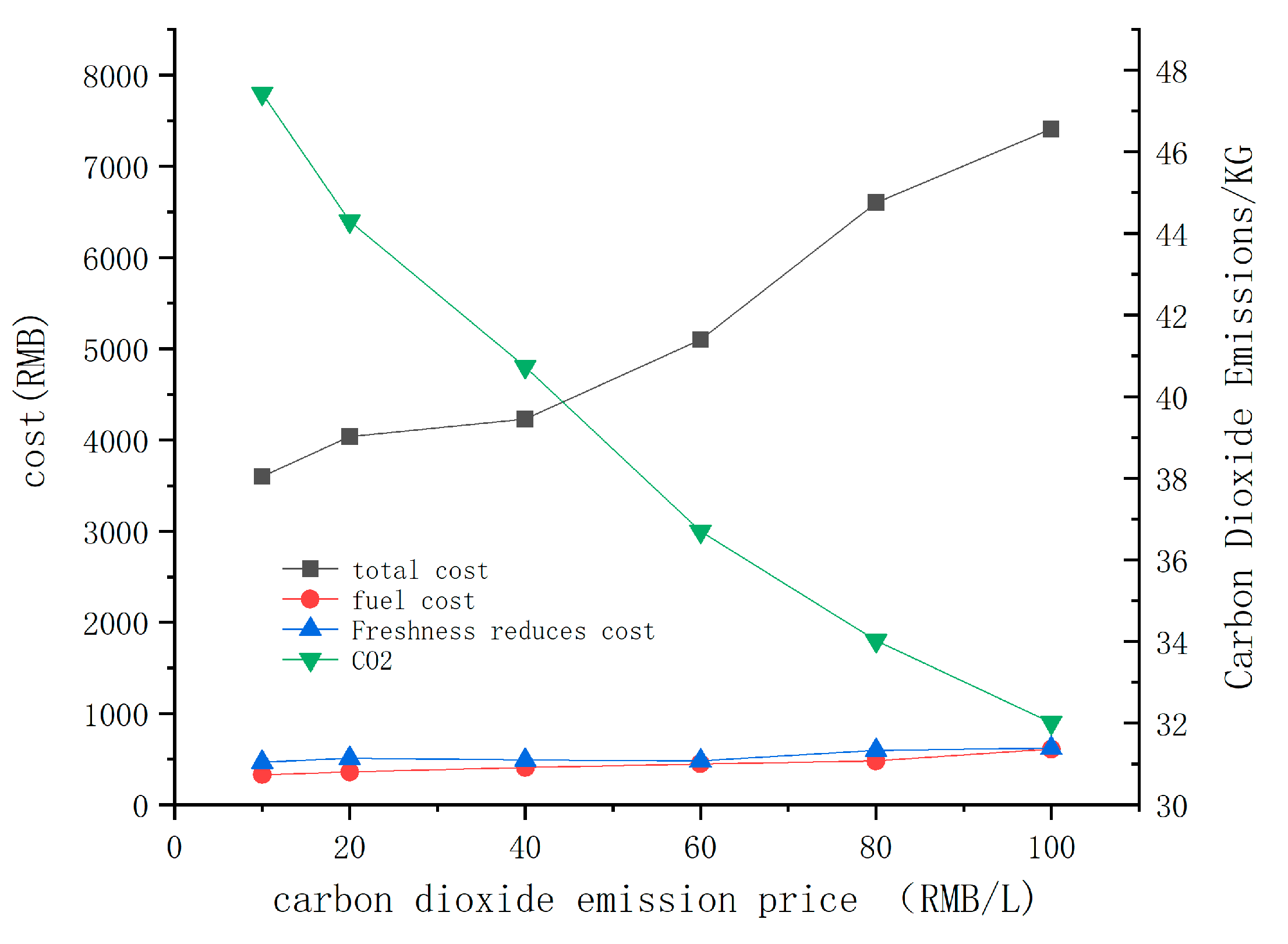
6.2. Parameter Sensitivity Analysis
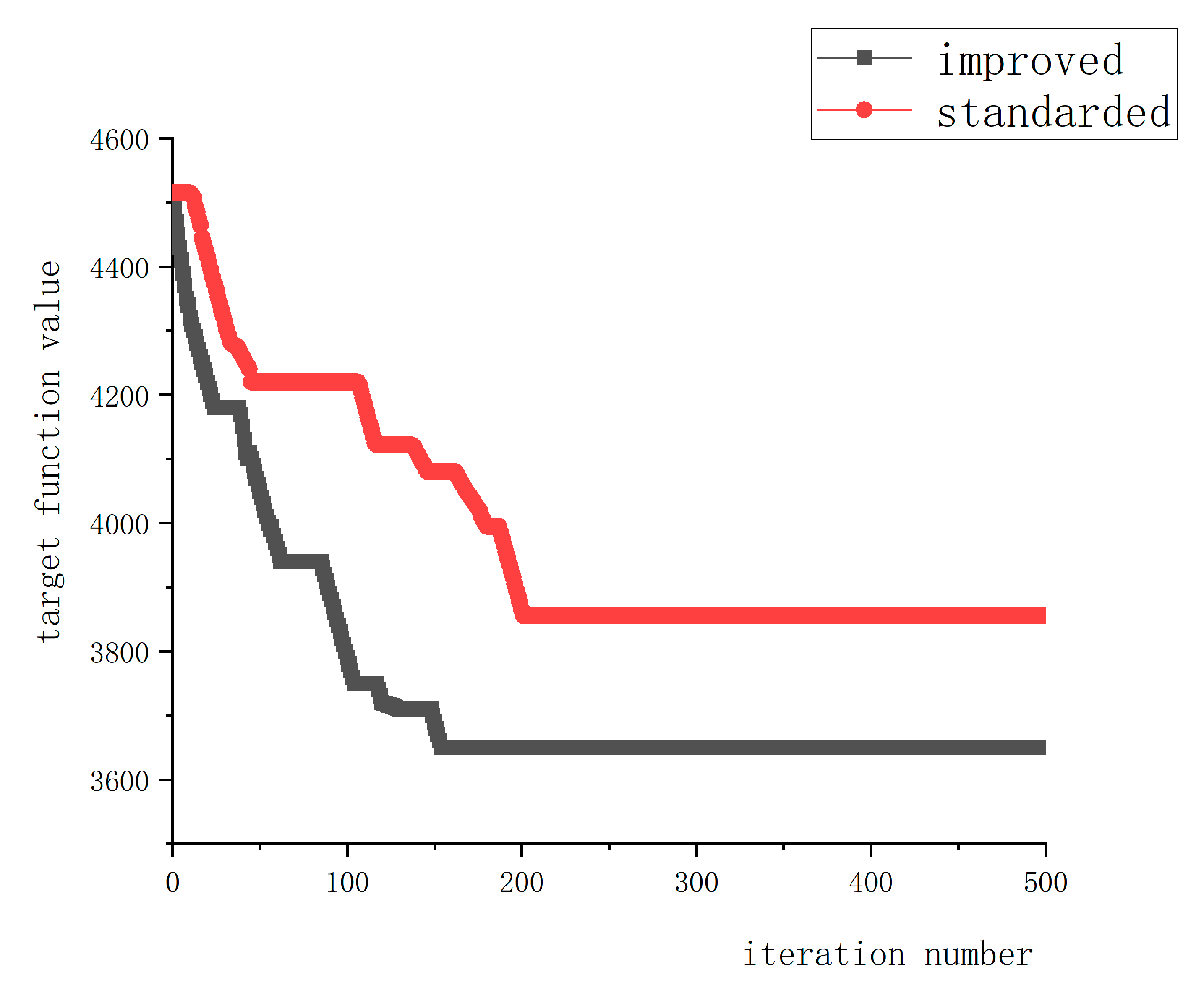
6.3. Effectiveness Analysis of IACATS Algorithm
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montanari, R. Cold chain tracking: A managerial perspective. Trends Food Sci. Technol. 2008, 19, 425–431. [Google Scholar] [CrossRef]
- Fan, J.; Li, J.; Wu, Y.; Wang, S.; Zhao, D. The effects of allowance price on energy demand under a personal carbon trading scheme. Appl. Energy 2016, 170, 242–249. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, X.; Wei, Y.-M.; Yu, S. Regional allocation of CO2 emissions allowance over provinces in China by 2020. Energy Policy 2013, 54, 214–229. [Google Scholar] [CrossRef]
- Verbič, M. Discussing the parameters of preservation of perishable goods in a cold logistic chain model. Appl. Econ. 2006, 38, 137–147. [Google Scholar] [CrossRef]
- Ho, W.; Ang, J.; Lim, A. A hybrid search algorithm for the vehicle routing problem with time windows. Int. J. Artif. Intell. Tools 2001, 10, 431–449. [Google Scholar] [CrossRef]
- Wang, S.; Tao, F.; Shi, Y.; Wen, H. Optimization of Vehicle Routing Problem with Time Windows for Cold Chain Logistics Based on Carbon Tax. Sustainability 2017, 9, 694. [Google Scholar] [CrossRef]
- Chameides, W.; Oppenheimer, M. Carbon trading over taxes. Science 2007, 315, 1670. [Google Scholar] [CrossRef]
- Maden, W.; Eglese, R.W.; Black, D. Vehicle routing and scheduling with time-varying data: A case study. J. Oper. Res. Soc. 2010, 61, 515–522. [Google Scholar] [CrossRef]
- Iv, J.H.W.; Cavalier, T.M. A Genetic Algorithm for the Split Delivery Vehicle Routing Problem. Am. J. Oper. Res. 2012, 2, 207–216. [Google Scholar]
- Archetti, C.; Bianchessi, N.; Speranza, M.G. Branch-and-cut algorithms for the split delivery vehicle routing problem. Eur. J. Oper. Res. 2014, 238, 685–698. [Google Scholar] [CrossRef]
- Dror, M.; Trudeau, P. Savings by split delivery routing. Transp. Sci. 1989, 23, 141–145. [Google Scholar] [CrossRef]
- Thongwan, T.; Kangrang, A.; Prasanchum, H. Multi-objective future rule curves using conditional TS algorithm and conditional genetic algorithm for reservoir operation. Heliyon 2019, 5, e02401. [Google Scholar] [CrossRef] [PubMed]
- Berbotto, L.; Garcia, S.; Nogales, F. A randomized granular TS heuristic for the split delivery vehicle routing problem. Ann. Oper. Res. 2014, 222, 153–173. [Google Scholar] [CrossRef]
- Ho, S.; Haugland, D. A TS heuristic for the vehicle routing problem with time windows and split deliveries. Comput. Oper. Res. 2004, 31, 1947–1964. [Google Scholar] [CrossRef]
- Hsiao, Y.; Chen, M.; Chin, C. Distribution planning for perishable foods in cold chains with quality concerns: Formulation and solution procedure. Trends Food Sci. Technol. 2016, 61, 80–93. [Google Scholar] [CrossRef]
- Cheng, R.; Gen, M. Fuzzy vehicle routing and scheduling problem using genetic algorithm. In Genetic Algorithms and Soft Computing; Herrera, F., Verdegay, J., Eds.; Springer: Berlin, Germany, 1996; pp. 683–709. [Google Scholar]
- Zhang, J.; Wang, W.; Zhao, Y.; Cattani, C. Multiobjective Quantum Evolutionary Algorithm for the Vehicle Routing Problem with Customer Satisfaction. Math. Probl. Eng. 2012, 2012, 1–19. [Google Scholar] [CrossRef]
- Comodi, G.; Renzi, M.; Rossi, M. Energy efficiency improvement in oil refineries through flare gas recovery technique to meet the emission trading targets. Energy 2016, 109, 1–12. [Google Scholar] [CrossRef]
- Hsu, C.-I.; Hung, S.-F.; Li, H.-C. Vehicle routing problem with time-windows for perishable food delivery. J. Food Eng. 2007, 80, 465–475. [Google Scholar] [CrossRef]
- Amorim, P.; Parragh, S. A rich vehicle routing problem dealing with perishable food: A case study. Top 2014, 22, 489–508. [Google Scholar] [CrossRef]
- Lai, M.; Cao, E. An improved differential evolution algorithm for vehicle routing problem with simultaneous pickups and deliveries and time windows. Eng. Appl. Artif. Intell. 2010, 23, 188–195. [Google Scholar]
- Anderson, E.W.; Sullivan, M.W. The Antecedents and Consequences of Customer Satisfaction for Firms. Mark. Sci. 1993, 12, 125–143. [Google Scholar] [CrossRef]
- Chung, L.M.; Wirtz, J. Book Review: Satisfaction: A Behavioral Perspective on the Consumer. Asia Pac. J. Manag. 1998, 15, 285–286. [Google Scholar] [CrossRef]
- Qin, Q.; Liu, Y.; Li, X.; Li, H. A multi-criteria decision analysis model for carbon emission quota allocation in China’s east coastal areas: Efficiency and equity. J. Clean. Prod. 2017, 168, 410–419. [Google Scholar] [CrossRef]
- Wang, X. Changes in CO2 Emissions Induced by Agricultural Inputs in China over 1991–2014. Sustainability 2016, 8, 414. [Google Scholar] [CrossRef]
- Yi, W.-J.; Zou, L.-L.; Guo, J.; Wang, K.; Wei, Y.-M. How can China reach its CO2 intensity reduction targets by 2020? A regional allocation based on equity and development. Energy Policy 2011, 39, 2407–2415. [Google Scholar] [CrossRef]
- Drezner, Z.; Scott, C.H. Location of a distribution center for a perishable product. Math. Methods Oper. Res. 2013, 78, 301–314. [Google Scholar] [CrossRef]
- GhannadPour, S.F.; Noori, S.; Tavakkoli-Moghaddam, R. Multiobjective Dynamic Vehicle Routing Problem with Fuzzy Travel Times and Customers’ Satisfaction in Supply Chain Management. IEEE Trans. Eng. Manag. 2013, 60, 777–790. [Google Scholar] [CrossRef]
- Wang, S.; Tao, F.; Shi, Y. Optimization of Inventory Routing Problem in Refined Oil Logistics with the Perspective of Carbon Tax. Energies 2018, 11, 1437. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Wang, S. Multi-Depot Incomplete Open Vehicle Routing Problem with Time Windows Based on Carbon Trading. Int. J. Environ. Res. Public Health 2018, 15, 2025. [Google Scholar] [CrossRef]
- Niu, Y.; Yang, Z.; Chen, P.; Xiao, J. Optimizing the green open vehicle routing problem with time windows by minimizing comprehensive routing cost. J. Clean. Prod. 2017, 171, 962–971. [Google Scholar] [CrossRef]
- Guo, J.; Liu, C. Time-Dependent Vehicle Routing of Free Pickup and Delivery Service in Flight Ticket Sales Companies Based on Carbon Emissions. J. Adv. Transp. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Naderipour, M.; Alinaghian, M. Measurement, evaluation and minimization of CO2, NOx, and CO emissions in the open time dependent vehicle routing problem. Measurement 2016, 90, 443–452. [Google Scholar] [CrossRef]
- Liao, T. On-Line Vehicle Routing Problems for Carbon Emissions Reduction. Comput. Civ. Infrastruct. Eng. 2017, 32, 1047–1063. [Google Scholar] [CrossRef]
- Liu, J. A national customer satisfaction barometer: The Swedish experience. J. Mark. 1992, 56, 6–21. [Google Scholar]
- Fornell, C.; Johnson, M.D.; Anderson, E.W.; Cha, J.; Bryant, B.E. The American Customer Satisfaction Index: Nature, Purpose, and Findings. J. Mark. 1996, 60, 7. [Google Scholar] [CrossRef]
- Zeng, Z.; Jiang, Z.; Xu, X. Research on the performance evaluation model of logistic company’s distribution. Ind. Eng. Manag. 2003, 3, 40–44. [Google Scholar]
- Parasuraman, A.; Zeithaml, V.A.; Berry, L.L. A Conceptual Model of Service Quality and Its Implications for Future Research. J. Mark. 1985, 49, 41. [Google Scholar] [CrossRef]
- Wang, S.; Tao, F.; Shi, Y. Optimization of Location–Routing Problem for Cold Chain Logistics Considering Carbon Footprint. Int. J. Environ. Res. Public Health 2018, 15, 86. [Google Scholar] [CrossRef]
- Bao, C.; Zhang, S. Route optimization of cold chain logistics in joint distribution: With consideration of carbon emission. Ind. Eng. Manag. 2018, 23, 95–107. [Google Scholar]
- Gao, J.; Yuan, Z.; Liu, X.; Xia, X.; Huang, X.; Dong, Z. Improving air pollution control policy in China—A perspective based on cost-benefit analysis. Sci. Total. Environ. 2016, 543, 307–314. [Google Scholar] [CrossRef]
- Lin, W.; Ma, Z.; Tsay, M. An improved TS for economic dispatch with multiple minima. Power Eng. Rev. IEEE 2002, 22, 70. [Google Scholar] [CrossRef]
- Zheng, G.; Liu, L.; Deng, L. Location-Routing Optimization of Cold Chain Distribution Center Based on Hybrid Genetic Algorithm-TS. In Proceedings of the 14th COTA International Conference of Transportation Professionals, Changsha, China, 4–7 July 2014. [Google Scholar]
- Shi, Z.; Zhuo, F. Distribution location routing optimization problem of food cold chain with time window in time varying network. Appl. Res. Comput. 2013, 30, 183–188. [Google Scholar]
- Karaoglan, I.; Altiparmak, F.; Kara, I.; Dengiz, B. A branch and cut algorithm for the location-routing problem with simultaneous pickup and delivery. Eur. J. Oper. Res. 2011, 211, 318–332. [Google Scholar] [CrossRef]
- Afshar, A.; Haghani, A. Modeling integrated supply chain logistics in real-time large-scale disaster relief operations. Socio-Econ. Plan. Sci. 2012, 46, 327–338. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J. Study on the effect of carbon emission trading mechanism on logistics distribution routing decisions. Syst. Eng. Theory Pract. 2014, 34, 1779–1787. [Google Scholar]
- Guo, H.; Ming, S. Process reengineering of cold chain logistics of agricultural products based on low-carbon economy. Asian Agric. Res. 2012, 5, 59–62. [Google Scholar]
- Meneghetti, A.; Monti, L. Greening the food supply chain: An optimisation model for sustainable design of refrigerated automated warehouses. Int. J. Prod. Res. 2015, 53, 6567–6587. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Ji, Y. Decision Optimization for Cold Chain Logistics of Fresh Agricultural Products under the Perspective of Cost-Benefit. Open Access Libr. J. 2019, 6, 1–17. [Google Scholar] [CrossRef]
- You, H.; Wang, X. Interactive genetic algorithm based on tournament selection and its application. J. Chin. Comput. Syst. 2009, 30, 1824–1827. [Google Scholar]
- Brandão, J. A TS algorithm for the open vehicle routing problem. Eur. J. Oper. Res. 2004, 157, 552–564. [Google Scholar] [CrossRef]
- Fan, J. The Vehicle Routing Problem with Simultaneous Pickup and Delivery Based on Customer Satisfaction. Procedia Eng. 2011, 15, 5284–5289. [Google Scholar] [CrossRef]
- Cheng, R.; Gen, M.; Tozawa, T. Vehicle Routing Problem with Fuzzy Due-time Using Genetic Algorithms. J. Jpn. Soc. Fuzzy Theory Syst. 1995, 7, 1050–1061. [Google Scholar] [CrossRef]
- Afshar-Bakeshloo, M.; Mehrabi, A.; Safari, H.; Maleki, M.; Jolai, F. A green vehicle routing problem with customer satisfaction criteria. J. Ind. Eng. Int. 2016, 12, 529–544. [Google Scholar] [CrossRef]
- Xia, Y.; Fu, Z. A TS algorithm for distribution network optimization with discrete split deliveries and soft time windows. Clust. Comput. 2018, 18, 586–597. [Google Scholar]
- Masson, R.; Røpke, S.; Lehuédé, F.; Péton, O. A branch-and-cut-and-price approach for the pickup and delivery problem with shuttle routes. Eur. J. Oper. Res. 2014, 236, 849–862. [Google Scholar] [CrossRef]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the European Conference on Artificial Life, ECAL’91, Paris, France, 11–13 December 1991; pp. 134–142. [Google Scholar]
- Osvald, A.; Stirn, L.Z. A vehicle routing algorithm for the distribution of fresh vegetables and similar perishable food. J. Food Eng. 2008, 85, 285–295. [Google Scholar] [CrossRef]
- Bogataj, M.; Bogataj, L.; Vodopivec, R. Stability of perishable goods in cold logistic chains. Int. J. Prod. Econ. 2005, 93, 345–356. [Google Scholar] [CrossRef]
- Chen, H.-K.; Hsueh, C.-F.; Chang, M.-S. Production scheduling and vehicle routing with time windows for perishable food products. Comput. Oper. Res. 2009, 36, 2311–2319. [Google Scholar] [CrossRef]
- Boventer, E.V. The relationship between transportation costs and location rent in transportation problems. J. Reg. Sci. 2010, 3, 27–40. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Shi, Y.; Qin, R. Optimization of Location-Routing Problem in Emergency Logistics Considering Carbon Emissions. Int. J. Environ. Res. Public Health 2019, 16, 2982. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Peng, Y.; Alsaadi, F.E. Location-Routing Problem for Relief Distribution in the Early Post-Earthquake Stage from the Perspective of Fairness. Sustainability 2019, 11, 3420. [Google Scholar] [CrossRef]
- Rath, S.; Gutjahr, W.J. A math-heuristic for the warehouse location–routing problem in disaster relief. Comput. Oper. Res. 2014, 42, 25–39. [Google Scholar] [CrossRef]
- Prins, C.; Prodhon, C.; Ruiz, A.; Soriano, P.; Calvo, R.W. Solving the Capacitated Location-Routing Problem by a Cooperative Lagrangean Relaxation-Granular Tabu Search Heuristic. Transp. Sci. 2007, 41, 470–483. [Google Scholar] [CrossRef]
- Cooper, L. The Transportation-Location Problem. Oper. Res. 1972, 20, 94–108. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, J.; Liang, B.; Zhang, L. Evaluation of Sustainable Livelihoods in the Context of Disaster Vulnerability: A Case Study of Shenzha County in Tibet, China. Sustainability 2019, 11, 2874. [Google Scholar] [CrossRef]
- Ting, J.; Chen, H. A multiple ant colony optimization algorithm for the capacitated location routing problem. Int. J. Prod. Econ. 2013, 141, 34–44. [Google Scholar] [CrossRef]
- Toro, E.M.; Franco, J.F.; Echeverri, M.G.; Guimarães, F.G. A multi-objective model for the green capacitated location-routing problem considering environmental impact. Comput. Ind. Eng. 2017, 110, 114–125. [Google Scholar] [CrossRef]
| Symbols | Descriptions |
|---|---|
| 0–1 are decision variables. If k car serves customer point i, and goes to serve customer point j, = 1, otherwise = 0. | |
| dij | The distance from customer point i to customer point j/km |
| P1 | The price of fresh agricultural products transported/(RMB t−1) |
| P2 | The price of fuel used by distribution vehicles/(RMB L−1) |
| P3 | Real-time carbon trading prices on the carbon exchange/(RMB t−1) |
| P4 | Fixed cost of the delivery vehicle/(RMB car number−1) |
| Si | Service time/min of the delivery vehicle at customer point i |
| Time window requirements of customer point i. Particularly, is the best receiving time for customers, and is the latest receiving time that customers can tolerate. | |
| Distribution vehicle collection = {1,2,3, ⋯,Κ}, where K represents the maximum number of vehicles in the distribution center | |
| Q | Maximum load of the distribution vehicle/t |
| qi | Quantity demanded/t at customer point i |
| ρ | CO2 emissions index |
| Fi | Requirement of customers order i on fresh agricultural products |
| v0 | Delivery vehicle speed/(km h−1) |
| ∂ | The freshness decreasing coefficient of produce |
| θ | Time window penalty coefficient |
| Parameter | Description |
|---|---|
| ξ | Fuel to air mass ratio |
| κ | Calorific value of the fuel engine/(kJ g−1) |
| ψ | Conversion coefficient/(from g s-1 to L s−1) |
| b | Engine friction coefficient |
| M | Engine speed |
| ω | Without loading in the vehicle/kg |
| g | Acceleration of gravity |
| ε | Road slope |
| Cr | Rolling resistance coefficient |
| v | Vehicle speed |
| Cd | Air resistance coefficient |
| ntf | Vehicle transmission efficiency |
| η | Fuel engine efficiency parameters |
| τ | Vehicle acceleration |
| Load when vehicle k reaches customer point j | |
| P | Air density/(kg m−3) |
| V | Engine capacity/VL |
| S | Frontal surface area |
| No. | Horizontal Axis/m | Vertical Axis/m | Fixed Time Window | Acceptable Time Window | Quantity Demanded/t | Service Time/min |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 5:30–17:00 | 5:00–17:00 | 0 | 0 |
| 1 | −189.2 | 455 | 6:00–7:00 | 6:00–7:30 | 0.8 | 15 |
| 2 | 103.8 | 1452 | 6:20–7:30 | 6:20–8:00 | 3.35 | 19 |
| 3 | 1103.5 | 426 | 6:00–6:50 | 6:00–7:20 | 2.95 | 17 |
| 4 | 1264.7 | 1289 | 7:00–8:00 | 7:00–8:20 | 2.4 | 11 |
| 5 | 1221.2 | −1842 | 6:40–7:30 | 6:40–8:00 | 2.75 | 14 |
| 6 | 1436.6 | −2025 | 6:00–7:00 | 6:00–7:40 | 3.3 | 20 |
| 7 | 245.6 | −672 | 6:30–7:00 | 6:30–7:30 | 2.8 | 15 |
| 8 | 2350.0 | −1189 | 6:20–7:30 | 6:20–8:00 | 3.25 | 10 |
| 9 | 1148.7 | −425 | 6:00–7:30 | 6:00–8:30 | 2.15 | 15 |
| 10 | 1025.2 | −27 | 6:20–8:00 | 6:20–9:00 | 3.05 | 18 |
| 11 | 863.6 | −1214 | 6:20–7:40 | 6:20–8:00 | 3.2 | 16 |
| 12 | 1785.6 | −957 | 7:30–8:50 | 7:30–9:20 | 3.5 | 11 |
| 13 | 682.4 | −3356 | 6:00–7:30 | 6:00–8:00 | 0.55 | 15 |
| 14 | 134.6 | −2879 | 6:40–7:50 | 6:40–8:30 | 2.7 | 19 |
| 15 | −485.4 | −1689 | 6:20–7:00 | 6:20–8:00 | 1.7 | 14 |
| 16 | 423.1 | −2196 | 6:00–7:00 | 6:00–7:30 | 2.25 | 10 |
| 17 | 444.3 | −983 | 6:00–6:40 | 6:00–7:10 | 2.75 | 15 |
| 18 | 1168.7 | −1786 | 7:00–8:00 | 7:00–9:00 | 1.9 | 20 |
| 19 | −568.3 | −622 | 6:00–6:50 | 6:00–7:20 | 3.15 | 14 |
| 20 | −722.4 | −2089 | 6:50–7:30 | 6:50–8:10 | 1 | 11 |
| Parameter | Implication | Value |
|---|---|---|
| ω | Vehicle weight/kg | 6350 |
| ξ | Fuel-to-air-mass ratio | 1 |
| b | Engine friction coefficient | 0.2 |
| M | Engine speed | 33 |
| V | Engine capacity/L | 5 |
| g | Acceleration of gravity | 9.81 |
| Cr | Rolling resistance coefficient | 0.01 |
| η | Fuel engine efficiency parameters | 0.9 |
| κ | Calorific value of fuel engine/(kJ·g−1) | 44 |
| ψ | Conversion coefficient | 737 |
| ntf | Vehicle transmission efficiency | 0.4 |
| Cd | Coefficient of air resistance | 0.7 |
| P | Air density/(kg m−3) | 1.2041 |
| S | Frontal surface are/m2 | 3.912 |
| Number of Vehicles | Distribution Routing | Cost/RMB | Loading Rate/% | CO2 Emissions/kg | Total Time/min |
|---|---|---|---|---|---|
| 1 | 0-19-2-8-0 | 528.22 | 96.87 | 9.23 | 63.78 |
| 2 | 0-17-15-14-0 | 534.25 | 72.52 | 5.01 | 66.89 |
| 3 | 0-1-10-6-20-0 | 658.72 | 83.20 | 8.96 | 83.56 |
| 4 | 0-16-11-4-0 | 632.02 | 79.68 | 7.25 | 74.25 |
| 5 | 0-13-5-12-0 | 589.36 | 68.79 | 7.95 | 105.23 |
| 6 | 0-9-3-7-18-0 | 657.85 | 99.03 | 7.02 | 83.87 |
| (α,β) | K | Z |
|---|---|---|
| (1,1) | 4 | 3587 |
| (1,2) | 3 | 3581 |
| (1,3) | 3 | 3576 |
| (2,1) | 3 | 3590 |
| (2,2) | 3 | 3586 |
| (2,3) | 3 | 3598 |
| Type | Research Time/s | Search Success Rate/% | Average Numberof Iterations |
|---|---|---|---|
| NSGA | 2 722.6 | 76 | 48 |
| MACOA | 2 692.8 | 85 | 30 |
| this work | 2534.3 | 98 | 16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Gui, P.; Ding, T.; Na, S.; Zhou, Y. Optimization of Transportation Routing Problem for Fresh Food by Improved Ant Colony Algorithm Based on Tabu Search. Sustainability 2019, 11, 6584. https://doi.org/10.3390/su11236584
Chen J, Gui P, Ding T, Na S, Zhou Y. Optimization of Transportation Routing Problem for Fresh Food by Improved Ant Colony Algorithm Based on Tabu Search. Sustainability. 2019; 11(23):6584. https://doi.org/10.3390/su11236584
Chicago/Turabian StyleChen, Jing, Pengfei Gui, Tao Ding, Sanggyun Na, and Yingtang Zhou. 2019. "Optimization of Transportation Routing Problem for Fresh Food by Improved Ant Colony Algorithm Based on Tabu Search" Sustainability 11, no. 23: 6584. https://doi.org/10.3390/su11236584
APA StyleChen, J., Gui, P., Ding, T., Na, S., & Zhou, Y. (2019). Optimization of Transportation Routing Problem for Fresh Food by Improved Ant Colony Algorithm Based on Tabu Search. Sustainability, 11(23), 6584. https://doi.org/10.3390/su11236584





