Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm
Abstract
1. Introduction
- (1)
- We proposed a multi-objective Water Cycle Algorithm for optimal allocation of the hybrid power system model in distribution systems. Also, an NSGA-III algorithm is performed and the simulation results between two algorithms are compared with each other
- (2)
- Studying the impact of different load models in summer day and winter day on the optimum placement of the hybrid power system model in radial distribution systems
- (3)
- Considering the uncertainty of renewable energy sources by using Hong’s 2m +1 PEM method.
- (4)
- Studying the impact of the hybrid power system model to enhance the technical, economic and environmental issues of distribution systems.
- (5)
- Reducing the power loss is considered as a technical benefit for achieving the improve system performance, reliability, and efficiency.
- (6)
- Minimizing energy costs because of the reduction in power loss can also be translated into economic benefits by using multiple distributed energy resources (DER) placements.
- (7)
- Minimizing the greenhouse gas emission is considered as environmental benefit.
- (8)
- Eventuality of the aforesaid approach is conducted on the standard IEEE 33 and IEEE 69 bus power system.
2. Load, Uncertainty and Distributed Energy Resources Modeling
2.1. Load Models
2.2. Modeling of DistributedEnergy Resources
2.2.1. Fuel Cell (FC)
2.2.2. Micro-Turbine (MT)
2.2.3. Photovoltaic System (PVS)
2.2.4. Wind Turbine (WT)
2.3. Fundamental of Point Estimated Method (PEM)
- Step 1:
- Calculate the statistical information of the input variables.
- Step 2:
- Calculate the concentrations for each input variable .
- Step 3:
- Evaluate the F function at the points , by theweighted probability factor. is themean value of the input variable . The points includethe kth location and the meanvalue of m − 1 remaining input variables .
- Step 4:
- Compute the statistical information of the output variable (Z)
3. Mathematical Problem Formulation
3.1. Objective Functions
3.1.1. Power Loss (Technical Benefit):
3.1.2. Total Annual Energy Cost (Annual Economic Benefit)
3.1.3. Total Greenhouse Gas Emission (Environmental Benefit)
3.2. Constraints
3.2.1. Equality Constraints
3.2.2. Inequality Constraints
4. Preliminaries of Proposed Algorithm
4.1. Review of WaterCycle Algorithm
- Step 1:
- Choose the initial parameters for the MOWCA: Nsr, dmax, Npop, Max Iteration, and Pareto archive size.
- Step 2:
- Generate a random initial population and form the initial streams, rivers, and sea by using equations as below.
- Step 3:
- Calculate the value of multi-objective functions for each stream using Equation (36).
- Step 4:
- Determine the non-dominated solutions in the initial population and save them in the Pareto archive.
- Step 5:
- Determine the non-dominated solutions among the feasible solutions and save them in the Pareto archive
- Step 6:
- Calculate the crowding-distance for each Pareto archive member.
- Step 7:
- Select a sea and rivers based on the crowding-distance value.
- Step 8:
- Determine the intensity of the flow for rivers and sea-based on the crowding distance values using Equation (37).
- Step 9:
- Streams flow into the rivers using Equation (38).
- Step 10:
- Exchange positions of the river with a stream which gives the best solution.
- Step 11:
- Some streams may directly flow into the sea using Equation (39).
- Step 12:
- Exchange positions of the sea with a stream which gives the best solution.
- Step 13:
- Rivers flow into the sea using Equation (40).
- Step 14:
- Exchange positions of the sea with a river which gives the best solution.
- Step 15:
- Check the evaporation condition.
- Step 16:
- If the evaporation condition is satisfied, the raining process will occur using Equation (41).
- Step 17:
- Reduce the value of dmax which is a user-defined parameter using Equation (42).
- Step 18:
- Determine the new feasible solutions in the population.
- Step 19:
- Determine the new non-dominated solutions among the feasible solutions and save them in the Pareto archive.
- Step 20:
- Eliminate any dominated solutions in the Pareto archive.
- Step 21:
- If the number of members in the Pareto archive is more than the determined Pareto archive size, go to Step 22, otherwise, go to Step 23.
- Step 22:
- Calculate the crowding-distance value for each Pareto archive member and remove as many members as necessary with the lowest crowding-distance value.
- Step 23:
- Calculate the crowding-distance value for each Pareto archive member to select new sea and rivers.
- Step 24:
- Check the convergence criteria. If the stopping criterion is satisfied, the algorithm will be stopped, otherwise return to Step 9.
4.2. Non-Dominated Sorting Genetic Algorithm (NSGA-III)
4.3. Best Compromise Solution
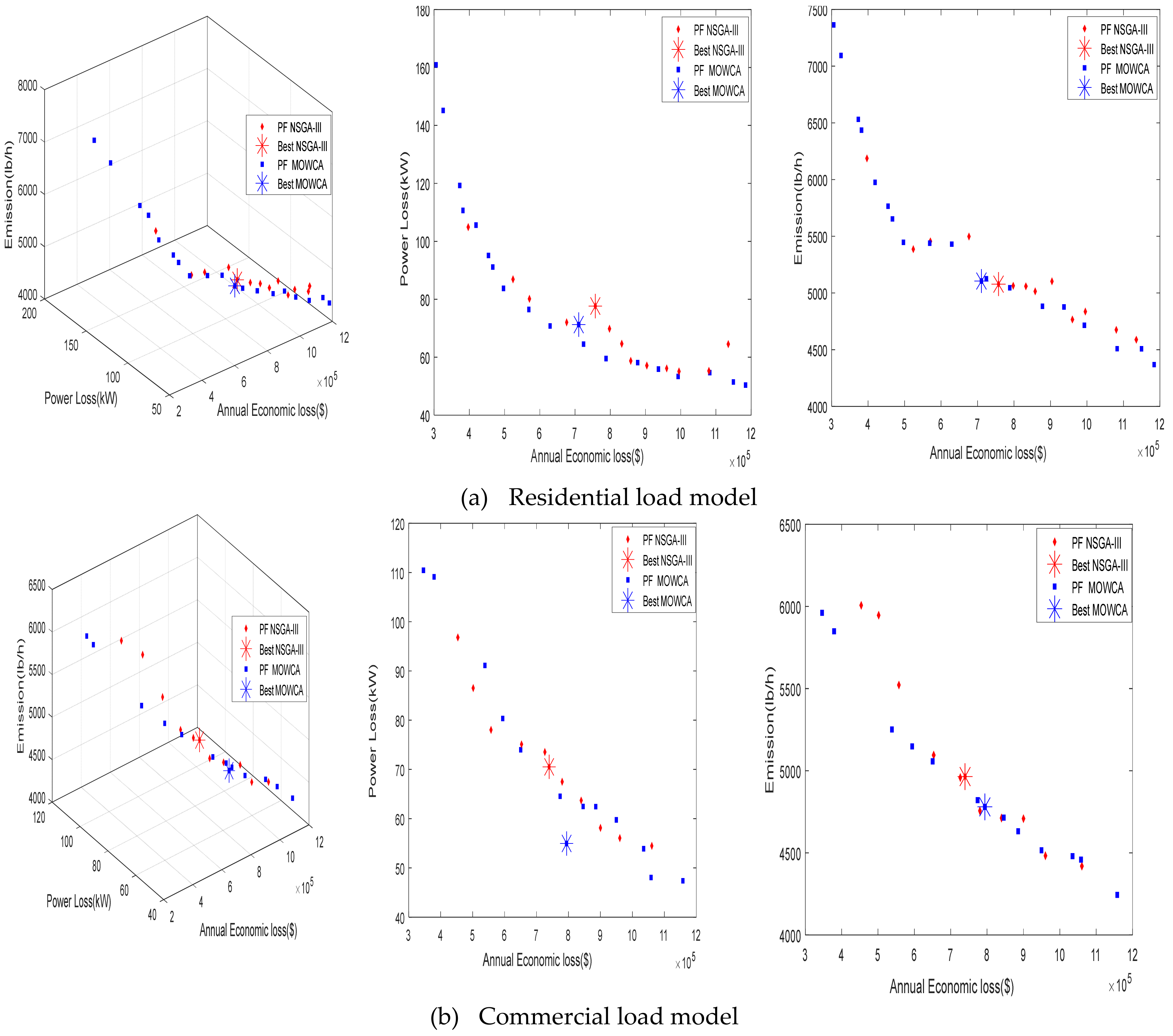
5. Results and Discussion
5.1. IEEE 33- Bus System
5.1.1. Case 1: Constant Load Model
5.1.2. Case 2: Summer Day Load Model (SDM)
5.1.3. Case 3: Winter Day Load Model (WDM)
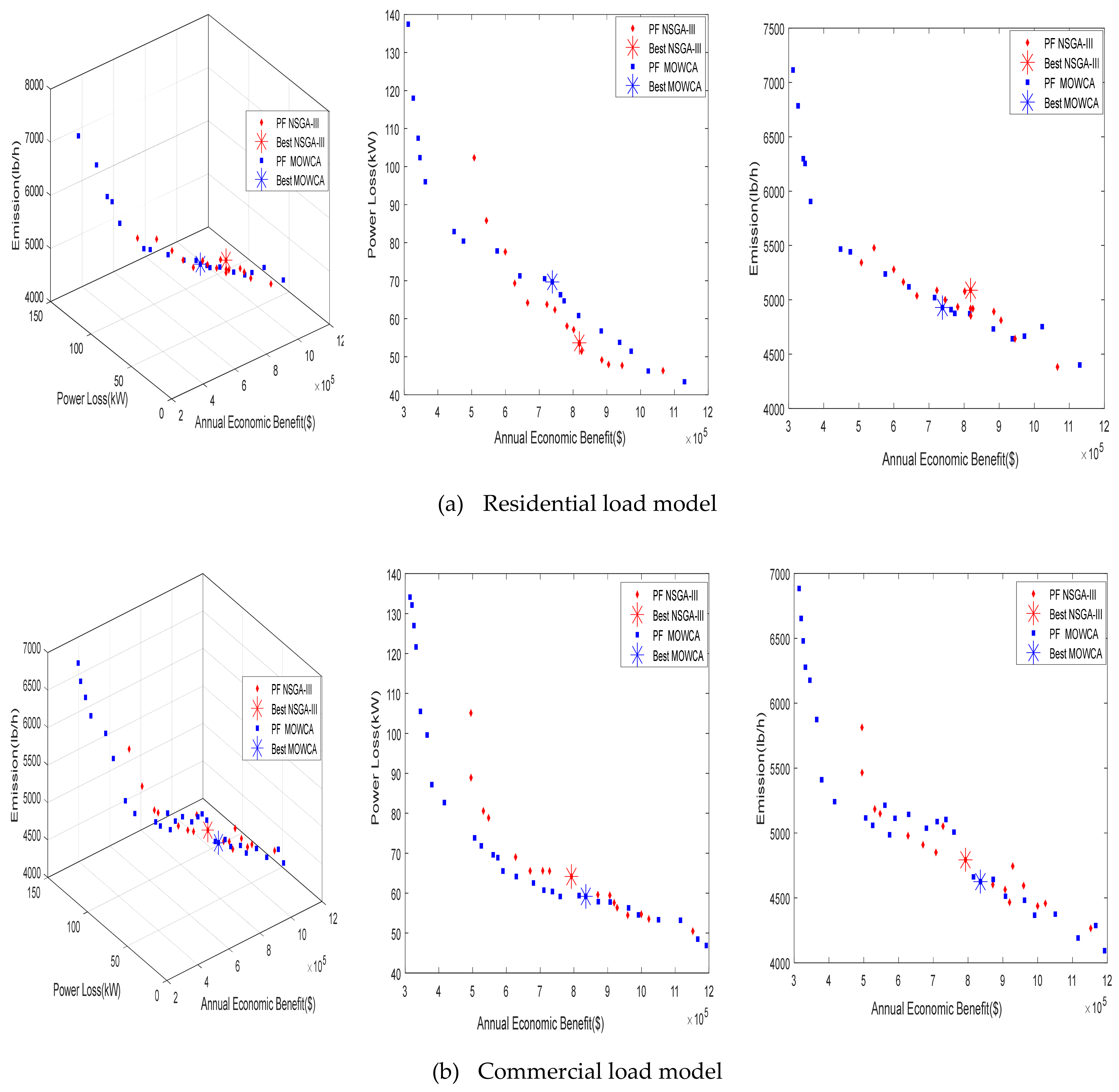
5.2. IEEE 69- Bus System
5.2.1. Case 4: Constant Load Model
5.2.2. Case 5: Summer Day Load (SDM)
5.2.3. Case 6: Winter Day Load Model (WDM)
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Fuel consumption cost of a fuel cell ($/h) | Substation active power | ||
| Price of natural gas supplied to fuel cell | Real power limit of the th generator | ||
| Fuel consumption cost of micro-turbine ($/h) | Output power of fuel cell | ||
| Natural gas price supplied to micro-turbine | Output power of micro-turbine | ||
| The th objective function | Wind turbine output power | ||
| Fuel cell efficiency | Rated/nominal power of the wind turbine | ||
| Micro-turbine efficiency | Substation active power | ||
| The current of th branch | l,k | Standard location of th point | |
| Annual conversion factor | pl | Mean deviation of random input variable | |
| The load factor | Load demand reactive power at th bus | ||
| Number of branches | Resistance of th branch | ||
| n | Nominal output power of photovoltaic panel | sn | Nominal illumination intensity of the photovoltaic |
| Numbers of the micro-turbine | Wind cut-in speed | ||
| Numbers of the fuel cell | Wind cut-out speed | ||
| Numbers of the Photovoltaic | Wind rated speed | ||
| Numbers of the wind turbine | Actual speed of the wind turbine | ||
| Ploss | Total system active power losses | Upper voltage limits of th bus | |
| Real output power of the th micro-turbine | Lower voltage limits of th bus | ||
| Real output power of the ith Photovoltaic | |||
| Real output power of the ith wind turbine | |||
| Active powers of the ith energy source |
References
- Sawle, Y.; Gupta, S.C.; Bohre, A.K. Review of hybrid renewable energy systems with comparative analysis of off-grid hybrid system. Renew. Sustain. Energy Rev. 2018, 81, 2217–2235. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A.; Liu, J. Optimization with a simulated annealing algorithm of a hybrid system for renewable energy including battery and hydrogen storage. Energy 2018, 163, 191–207. [Google Scholar] [CrossRef]
- Diemuodeke, E.O.; Addo, A.; Oko, C.O.C.; Mulugetta, Y.; Ojapah, M.M. Optimal mapping of hybrid renewable energy systems for locations using multi-criteria decision-making algorithm. Renew. Energy 2019, 134, 461–477. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Sun, J.; Jin, H. A review on the utilization of hybrid renewable energy. Renew. Sustain. Energy Rev. 2018, 91, 1121–1147. [Google Scholar] [CrossRef]
- Buch, H.; Trivedi, I.N. A new non-dominated sorting ions motion algorithm: Development and applications. Decis. Sci. Lett. 2019, 9, 59–76. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Savsani, V. Multi-objective sine-cosine algorithm (MO-SCA) for multi-objective engineering design problems. Neural Comput. Appl. 2019, 31, 915–929. [Google Scholar] [CrossRef]
- Bhadoria, V.S.; Pal, N.S.; Shrivastava, V. Artificial immune system based approach for size and location optimization of distributed generation in distribution system. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 339–349. [Google Scholar] [CrossRef]
- Mobin, M.; Mousavi, S.M.; Komaki, M.; Tavana, M. A hybrid desirability function approach for tuning parameters in evolutionary optimization algorithms. Measurement 2018, 114, 417–427. [Google Scholar] [CrossRef]
- Veeramani, C.; Sharanya, S. Analyzing the Performance Measures of Multi-Objective Water Cycle Algorithm for Multi-Objective Linear Fractional Programming Problem. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 297–306. [Google Scholar]
- Devabalaji, K.R.; Ravi, K. Optimal size and sitting of multiple DG and DSTATCOM in radial distribution system using Bacterial Foraging Optimization Algorithm. Ain Shams Eng. J. 2016, 7, 959–971. [Google Scholar] [CrossRef]
- Melgar-Dominguez, O.D.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Mantovani, J.R. Voltage-Dependent Load Model-Based Short-Term Distribution Network Planning Considering Carbon Tax Surplus. IET Gener. Transm. Distrib. 2019, 13, 3760–3770. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Discrete harmony search based size optimization of integrated renewable energy system for remote rural areas of Uttarakhand state in India. Renew. Energy 2016, 94, 587–604. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Olatomiwa, L.; Hazelton, J. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia. EnergyConvers. Manag. 2017, 144, 322–339. [Google Scholar] [CrossRef]
- Guangqian, D.; Bekhrad, K.; Azarikhah, P.; Maleki, A. A hybrid algorithm based optimization on modeling of grid independent biodiesel-based hybrid solar/wind systems. Renew. Energy 2018, 122, 551–560. [Google Scholar] [CrossRef]
- Peng, W.; Maleki, A.; Rosen, M.A.; Azarikhah, P. Optimization of a hybrid system for solar-wind-based water desalination by reverse osmosis: Comparison of approaches. Desalination 2018, 442, 16–31. [Google Scholar] [CrossRef]
- Singh, S.S.; Fernandez, E. Modeling, size optimization and sensitivity analysis of a remote hybrid renewable energy system. Energy 2018, 143, 719–731. [Google Scholar] [CrossRef]
- Ikeda, S.; Takeda, A.; Ohmori, H. Optimal sizing of photovoltaic systems for loss minimization in distribution network. In Proceedings of the 2018 SICE International Symposium on Control Systems (SICE ISCS), Tokyo, Japan, 9–11 March 2018; pp. 185–192. [Google Scholar]
- Nadjemi, O.; Nacer, T.; Hamidat, A.; Salhi, H. Optimal hybrid PV/wind energy system sizing: Application of cuckoo search algorithm for Algerian dairy farms. Renew. Sustain. Energy Rev. 2017, 70, 1352–1365. [Google Scholar] [CrossRef]
- Samy, M.M.; Barakat, S.; Ramadan, H.S. A flower pollination optimization algorithm for an off-grid PV-Fuel cell hybrid renewable system. Int. J. Hydrog. Energy 2019, 44, 2141–2152. [Google Scholar] [CrossRef]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Tran, H.V. Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies 2019, 12, 174. [Google Scholar] [CrossRef]
- Yahiaoui, A.; Benmansour, K.; Tadjine, M. Control, analysis and optimization of hybrid PV-Diesel-Battery systems for isolated rural city in Algeria. Sol. Energy 2016, 137, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Li, G.; Qi, J.; Zhao, D.; Mu, Y. Optimal distributed generation planning in active distribution networks considering integration of energy storage. Appl. Energy 2018, 210, 1073–1081. [Google Scholar] [CrossRef]
- Asmi, R.Y.; Salama, M.; Ahmad, I.A. Distributed generation’s integration planning involving growth load models by means of genetic algorithm. Arch. Electr. Energy 2018, 67, 667–682. [Google Scholar]
- Singh, B.; Mukherjee, V.; Tiwari, P. GA-based multi-objective optimization for distributed generations planning with DLMs in distribution power systems. J. Electr. Syst. Inf. Technol. 2017, 4, 62–94. [Google Scholar] [CrossRef][Green Version]
- Moradi, M.H.; Eskandari, M.; Hosseinian, S.M. Operational strategy optimization in an optimal sized smart micro grid. IEEE Trans. Smart Grid 2015, 6, 1087–1095. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Demand side management in a smart micro-grid in the presence of renewable generation and demand response. Energy 2017, 126, 622–637. [Google Scholar] [CrossRef]
- Esmaeili, M.; Sedighizadeh, M.; Esmaili, M. Multi-objective optimal reconfiguration and DG (Distributed Generation) power allocation in distribution networks using Big Bang-Big Crunch algorithm considering load uncertainty. Energy 2016, 103, 86–99. [Google Scholar]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Imran, M.; Kowsalya, M. Optimal size and siting of multiple distribution generators in distribution system using bacterial foraging optimization. Swarm Evol. Comput. 2014, 15, 58–65. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Rao, B.H.; Sivanagaraju, S. Optimum allocation and sizing of distributed generations based on clonal selection algorithm for loss reduction and technical benefit of energy savings. In Proceedings of the 2012 International Conference on Advances in Power Conversion and Energy Technologies (APCET), Mylavaram, Andhra Pradesh, India, 2–4 August 2012; pp. 1–5. [Google Scholar]
- Sadollah, A.; Eskandar, H.; Kim, J.H. Water cycle algorithm for solving constrained multi-objective optimization problems. Appl. Soft Comput. 2015, 27, 279–298. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based non-dominated sorting approach, part I: Solving problems with boxconstraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Hashim, H.A.; Abido, M.A. Location management in lte networks using multi-objective particle swarm optimization. Comput. Netw. 2019, 157, 78–88. [Google Scholar] [CrossRef]





| Ref. no. | Solution Method | DER Type | Objective Function | Multi Objective | Uncertainty Effect | Different Load Models | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | WT | MT | FC | Bat | DE | PLoss | TC | EM | |||||
| [18] | a second-order cone programming model | ✓ | ✓ | ✓ | |||||||||
| [19] | Cuckoo search algorithm | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [20] | The Flower Pollination Algorithm (FPA) | ✓ | ✓ | ✓ | |||||||||
| [21] | biogeography-based optimization algorithm | ✓ | ✓ | ✓ | |||||||||
| [22] | PSO algorithm | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [23] | Multi-objective ant lion optimizer | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [24] | Breeder genetic algorithm (BGA). | ✓ | ✓ | ||||||||||
| * | Proposed algorithms | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Load Type | Residential Load | Commercial Load | |||
|---|---|---|---|---|---|
| α | β | α | β | ||
| Summer | SDM | 0.72 | 2.96 | 1.25 | 3.5 |
| Winter | WDM | 1.04 | 4.19 | 1.5 | 3.15 |
| Generation | Capacity (kW) | Capacity Factor | Life Time (Year) | Capital Cost ($/kW) | Maintenance Cost ($/kWh) | Annual Conversion Factor |
|---|---|---|---|---|---|---|
| FC | 400 | 0.4 | 10 | 3674 | 0.001 | 0.1006 |
| MT | 250 | 1 | 10 | 750 | 0.039 | 0.2152 |
| PV | 300 | 0.25 | 20 | 6675 | 0.005 | 0.0843 |
| WT | 300 | 0.2 | 20 | 1500 | 0.005 | 0.1006 |
| Parameter | NSGA-III | Parameter | MOWCA |
|---|---|---|---|
| Population size N | 80 | Population size | 80 |
| Evaluation generation | 50 | Evaluation generation | 50 |
| Crossover probability (pc) | 0.5 | Nsr (Number of rivers + sea) | 4 |
| Mutation probability (pm) | 0.5 | dmax (Maximum allowable distance between river and sea) | 1×10−16 |
| Distribution index for a crossover (ηc) | 30 | ||
| Distribution index for mutation (ηm) | 20 |
| Case Study | Load Models | System | |
|---|---|---|---|
| Case 1 | Constant load | IEEE- 33 bus system | |
| Case 2 | Residential load Commercial load | At summer day | |
| Case 3 | Residential load Commercial load | At winter day | |
| Case4 | Constant load | IEEE-69 bus system | |
| Case5 | Residential load Commercial load | At summer day | |
| Case 6 | Residential load Commercial load | At winter day | |
| Method | Type of DG | Constant | Summer Day Load Model (SDM) | Winter Day Load Model (WDM) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residential Load | Commercial Load | Residential Load | Commercial Load | ||||||||||||
| Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | ||||||
| MOWCA method | MT | (27) (13) (13) | 89.751 73.116 0 | (13) (26) (27) | 135.25 150 129.85 | (9) (5) (24) | 250 172.95 100 | (6) (9) (19) | 198.37 121.99 153.42 | (32) (27) (27) | 241.53 116.8 0 | ||||
| FC | (19) (13) (29) | 205.74 0 210.71 | (16) (6) (27) | 137.14 186.18 0 | (5) (10) (18) | 0 323.36 400 | (19) (11) (24) | 0 152.96 191.82 | (4) (24) (20) | 146.76 220.32 200 | |||||
| PV | (18) (14) (26) | - | (21) (28) (14) | - | (30) (8) (28) | - | (15) (10) (22) | - | (13) (8) (30) | - | |||||
| WT | (16) (28) (8) | - | (24) (29) (12) | - | (32) (6) (29) | - | (14) (26) (16) | - | (17) (23) (15) | - | |||||
| F1 (kW) | 103.9202 | 71.2596 | 54.95523 | 69.68398 | 59.18302 | ||||||||||
| F2 ($) | 683.595.915 | 710.536.85 | 793,960.79887 | 738.466.285 | 835.280.76 | ||||||||||
| F3 (Ib/h) | 5489.94691 | 5105.50415 | 4779.93565 | 4928.2749 | 4624.96045 | ||||||||||
| NSGA-III method | MT | (31) (32) (23) | 58.58 247 134.5 | (27) (5) (9) | 2.161 59.053 116.97 | (21) (17) (2) | 0.23526 0.021001 0.032842 | (33) (28) (11) | 223.4 101.4 175.99 | (17) (11) (18) | 19.834 242.84 133.4 | ||||
| FC | (7) (7) (25) | 17.24 0343.6 | (14) (18) (14) | 218.51 324.28 0 | (17) (33) (15) | 0 0.33302 0.12261 | (21) (15) (9) | 109.5 162.5 191.4 | (11) (12) (23) | 0 229.63 251.36 | |||||
| PV | (4) (15) (12) | - | (22) (16) (30) | - | (18) (14) (19) | - | (25) (26) (31) | - | (3) (27) (31) | - | |||||
| WT | (12) (28) (17) | - | (12) (2) (32) | - | (4) (30) (25) | - | (31) (6) (28) | - | (21) (24) (14) | - | |||||
| F1(kW) | 96.54708 | 77.65119 | 70.53227 | 53.64945 | 64.16248 | ||||||||||
| F2 ($) | 744204.37 | 757584.55805 | 739478.40639 | 818483.8614 | 792.522.977 | ||||||||||
| F3(Ib/h) | 5520.95828 | 5078.22182 | 4964.23913 | 5087.94170 | 4793.43071 | ||||||||||
| Method | Type of DG | Constant | Summer Day Load Model(SDM) | Winter Day Load Model(WDM) | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residential Load | Commercial Load | Residential Load | Commercial Load | |||||||||||||||||||
| Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | Location (bus no) | Size (kW) | |||||||||||||
| Proposed MOWCA | MT | (6) (62) (45) | 123.6 197.44 61.991 | (45) (39) (37) | 98.874 131 24.193 | (54) (35) (59) | 204.1 100.58 0.17812 | (19) (15) (47) | 187.33 75.74 149.42 | (28) (53) (21) | 164.19 30.188 85.132 | |||||||||||
| FC | (62) (20) (7) | 0 136.72 302.2 | (38) (62) (44) | 50.602 392.54 173.06 | (21) (61) (30) | 216.05 274.91 65.198 | (56) (60) (36) | 2.3104 355.13 96.482 | (24) (32) (55) | 257.94 65.586 207.26 | ||||||||||||
| PV | (24) (41) (65) | - | (15) (65) (68) | - | (7) (38) (11) | - | (63) (32) (33) | - | (64) (23) (67) | - | ||||||||||||
| WT | (15) (12) (44) | - | (20) (21) (5) | - | (27) (64) (53) | - | (41) (64) (31) | - | (62) (46) (31) | - | ||||||||||||
| F1 (kW) | 135.852 | 88.02824 | 87.47904 | 78.90383 | 96.37189 | |||||||||||||||||
| F2 ($) | 653.778.637 | 713.190.23449 | 689.160.668 | 669.380.049 | 661.212.176 | |||||||||||||||||
| F3 (Ib/h) | 5622.082 | 5270.99823 | 5066.35384 | 5094.87203 | 4991.83448 | |||||||||||||||||
| NSGA-III method | MT | (55) (45) (33) | 46.52 173.36 111.68 | (50) (20) (6) | 96.838 0 149.14 | (37) (36) (46) | 109.69 19.288 17.67 | (37) (24) (51) | 0 116.5 116.5 | (43) (6) (43) | 0 0 0 | |||||||||||
| FC | (11) (60) (54) | 117.83 331.41 184.07 | (50) (19) (31) | 0 201.44 147.54 | (52) (52) (29) | 75.316 0 262.41 | (26) (26) (33) | 296.54 0 0 | (40) (500) (28) | 0 300 0 | ||||||||||||
| PV | (51) (15) (40) | - | (23) (24) (60) | - | (62) (51) (33) | - | (65) (21) (35) | - | (33) (47) (63) | - | ||||||||||||
| WT | (46) (38) (47) | - | (27) (34) (39) | - | (16) (54) (25) | - | (4) (7) (38) | - | (26) (18) (7) | - | ||||||||||||
| F1 (kW) | 152.73747 | 127.309 | 116.14785 | 111.44034 | 120.86334 | |||||||||||||||||
| F2 ($) | 744.761.744 | 537.874.808 | 495.466.135 | 499.478.626 | 418.812.277 | |||||||||||||||||
| F3 (Ib/h) | 5498.66641 | 5437.09658 | 5311.83193 | 5473.49029 | 5411.5537 | |||||||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-A.A.; Ali, S.; Alkhalaf, S.; Senjyu, T.; Hemeida, A.M. Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability 2019, 11, 6550. https://doi.org/10.3390/su11236550
Mohamed A-AA, Ali S, Alkhalaf S, Senjyu T, Hemeida AM. Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability. 2019; 11(23):6550. https://doi.org/10.3390/su11236550
Chicago/Turabian StyleMohamed, Al-Attar Ali, Shimaa Ali, Salem Alkhalaf, Tomonobu Senjyu, and Ashraf M. Hemeida. 2019. "Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm" Sustainability 11, no. 23: 6550. https://doi.org/10.3390/su11236550
APA StyleMohamed, A.-A. A., Ali, S., Alkhalaf, S., Senjyu, T., & Hemeida, A. M. (2019). Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability, 11(23), 6550. https://doi.org/10.3390/su11236550








