Optimal Energy Management of Railroad Electrical Systems with Renewable Energy and Energy Storage Systems
Abstract
:1. Introduction
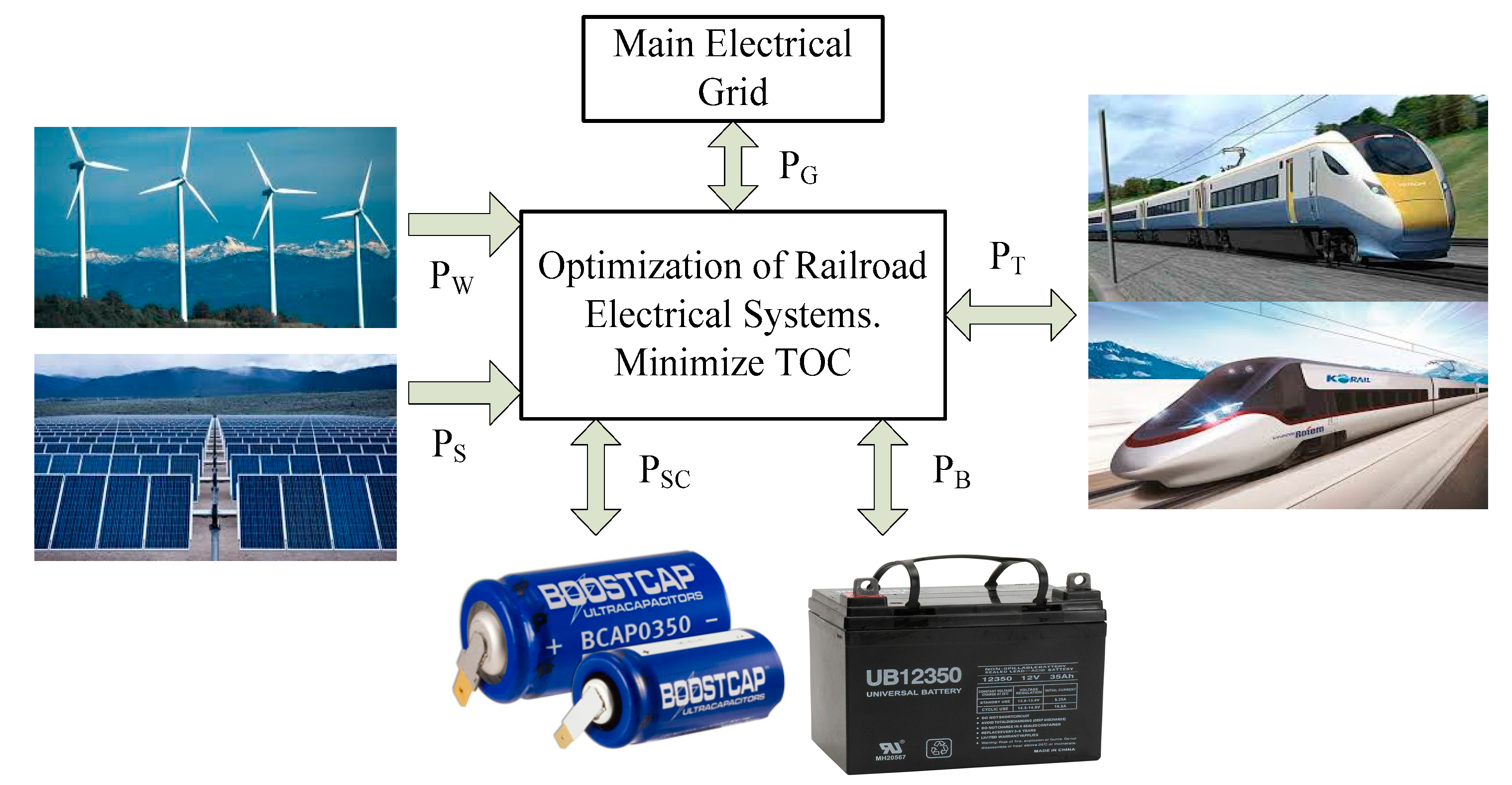
- Proposes an optimal operation of a railroad electrical system including renewable energy resources (RERs), a hybrid energy storage system (battery storage and supercapacitors), and the regenerative braking capabilities of trains.
- Formulates an AC optimal power flow (AC-OPF) problem by considering the total operating cost minimization objective of a railroad electrical system subjected to various equality and inequality constraints.
- Handles the uncertainties associated with wind and solar PV powers by using probability distribution functions.
- Solves the proposed optimization problem by using the differential evolution algorithm (DEA).
- Simulates four different case studies by considering the RERs and hybrid energy storage systems.
2. Modeling of Renewable Energy Resources and Energy Storage Systems
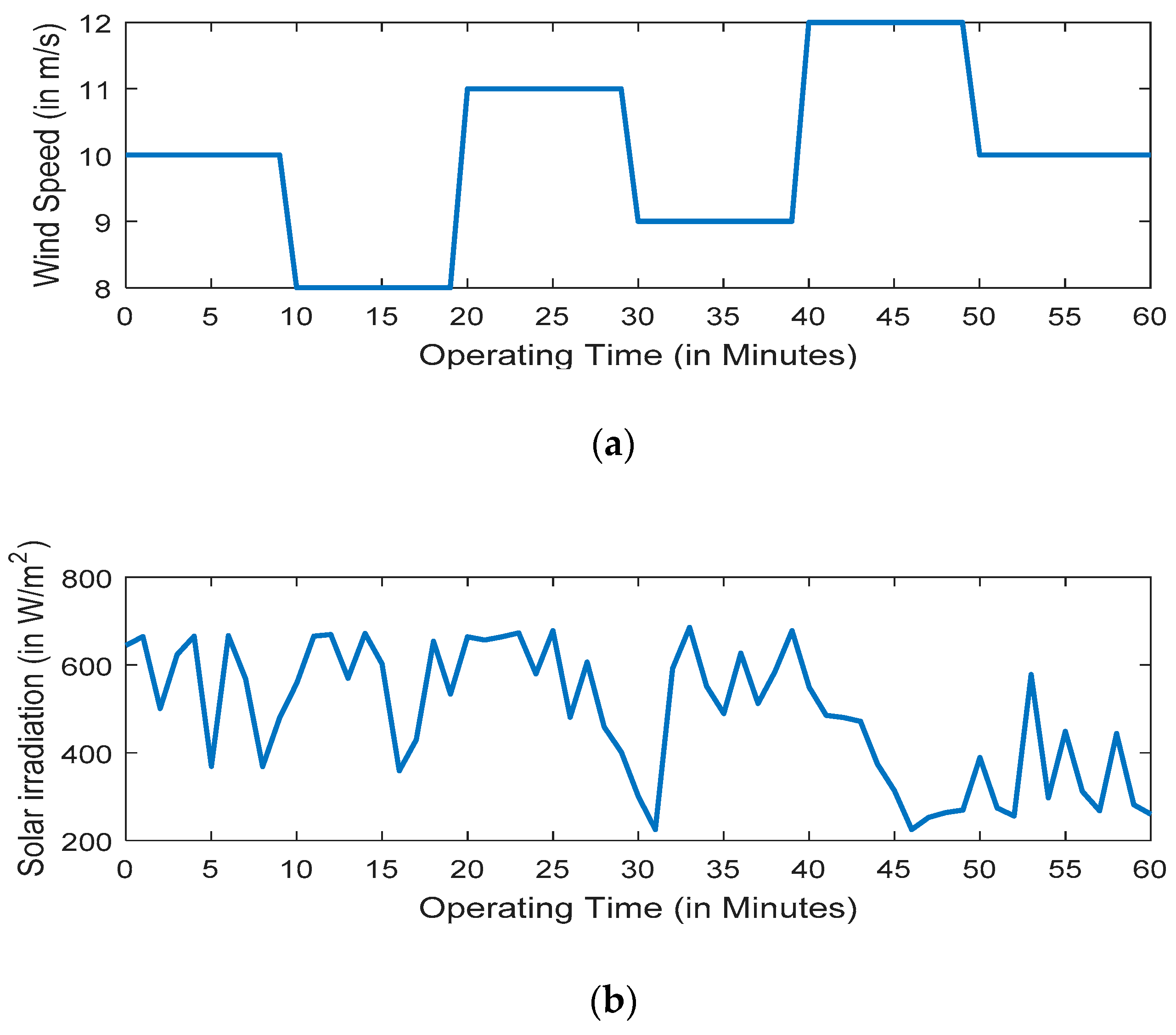
2.1. Modeling and Uncertainty Handling of Wind Energy System
2.2. Modeling and Uncertainty Handling of Solar Energy System
2.3. Modeling of Hybrid Energy Storage System
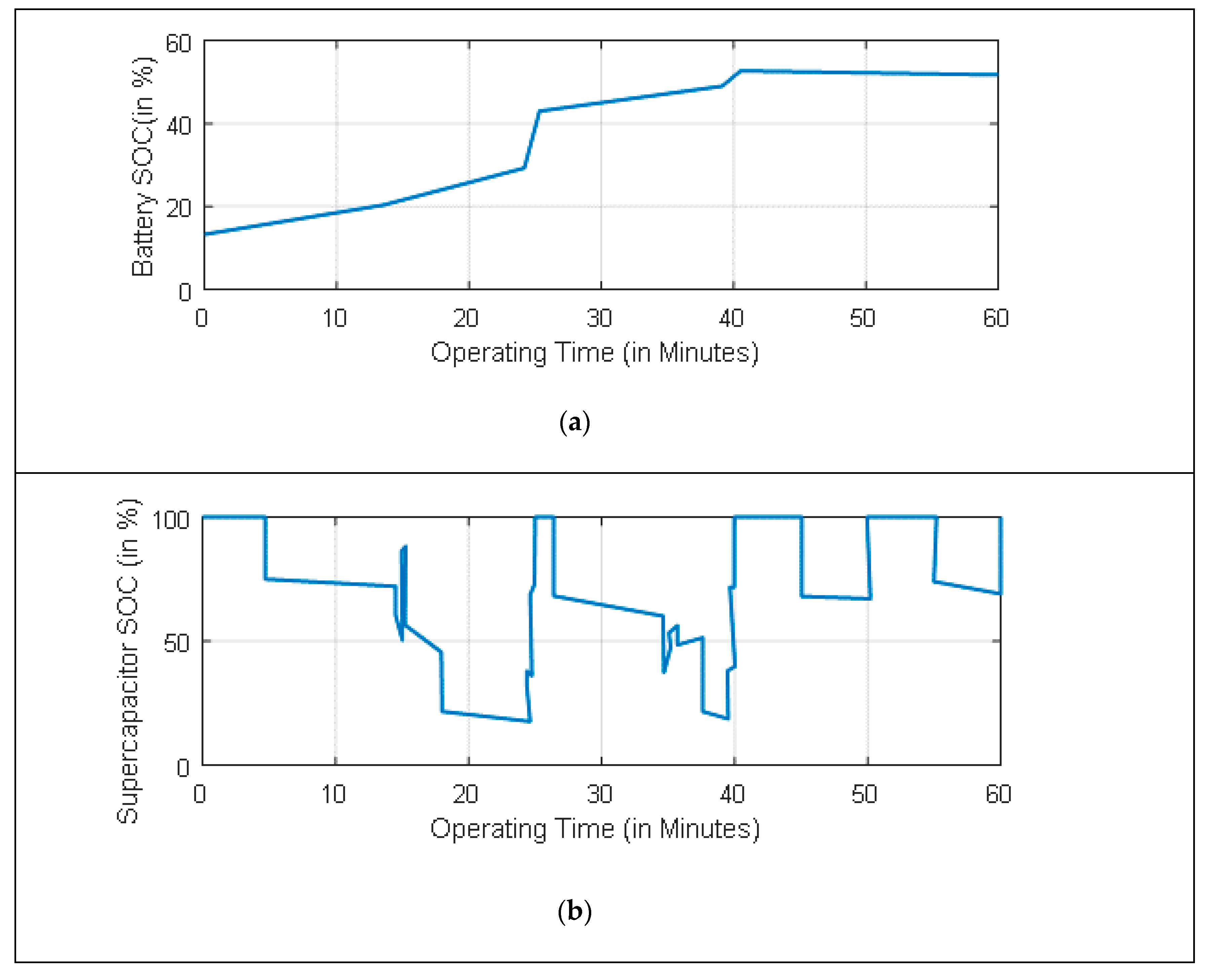
2.3.1. Modeling of Battery Storage
2.3.2. Modeling of Supercapacitors
3. Proposed Problem Formulation
3.1. Equality Constraints
3.2. Inequality Constraint
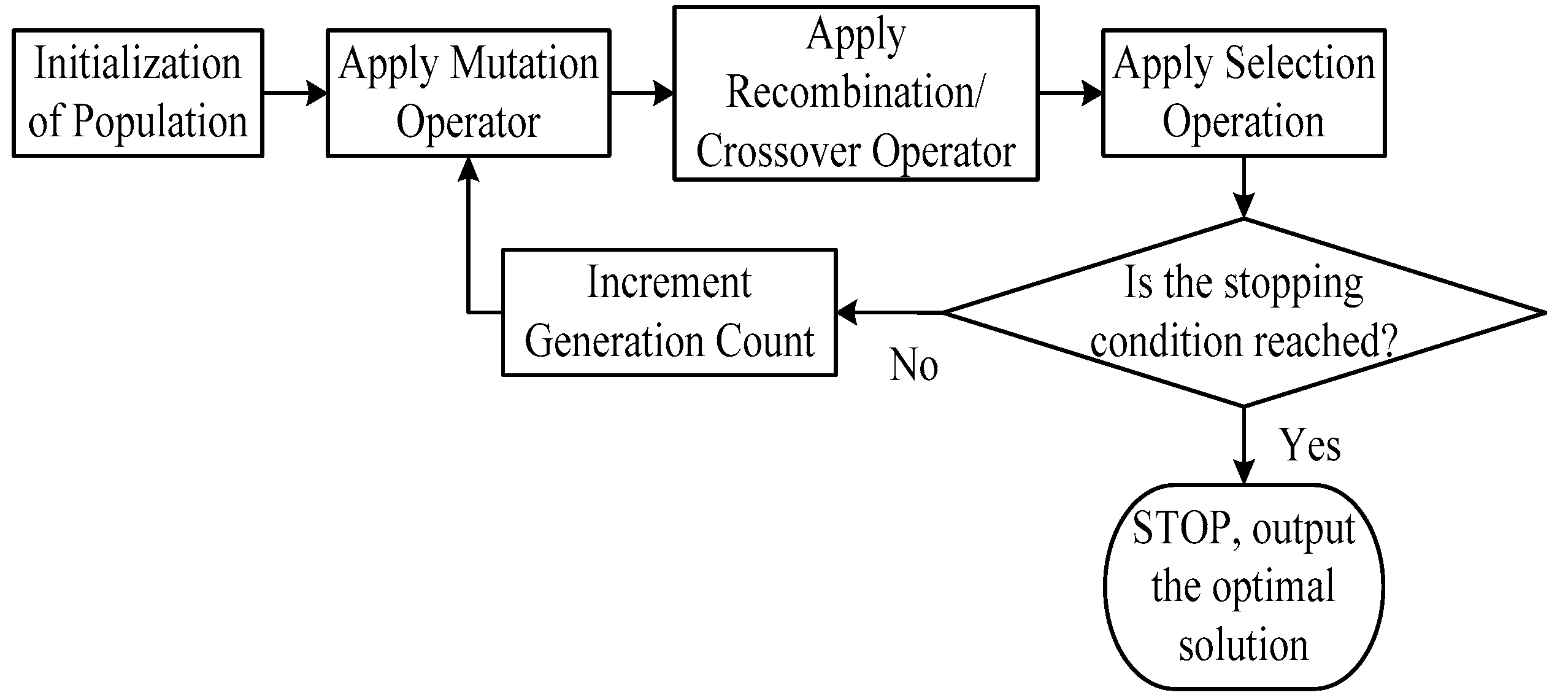
4. Differential Evolution Algorithm (DEA)
4.1. Initialization
4.2. Mutation Operation
4.3. Crossover Operation
4.4. Selection Operation
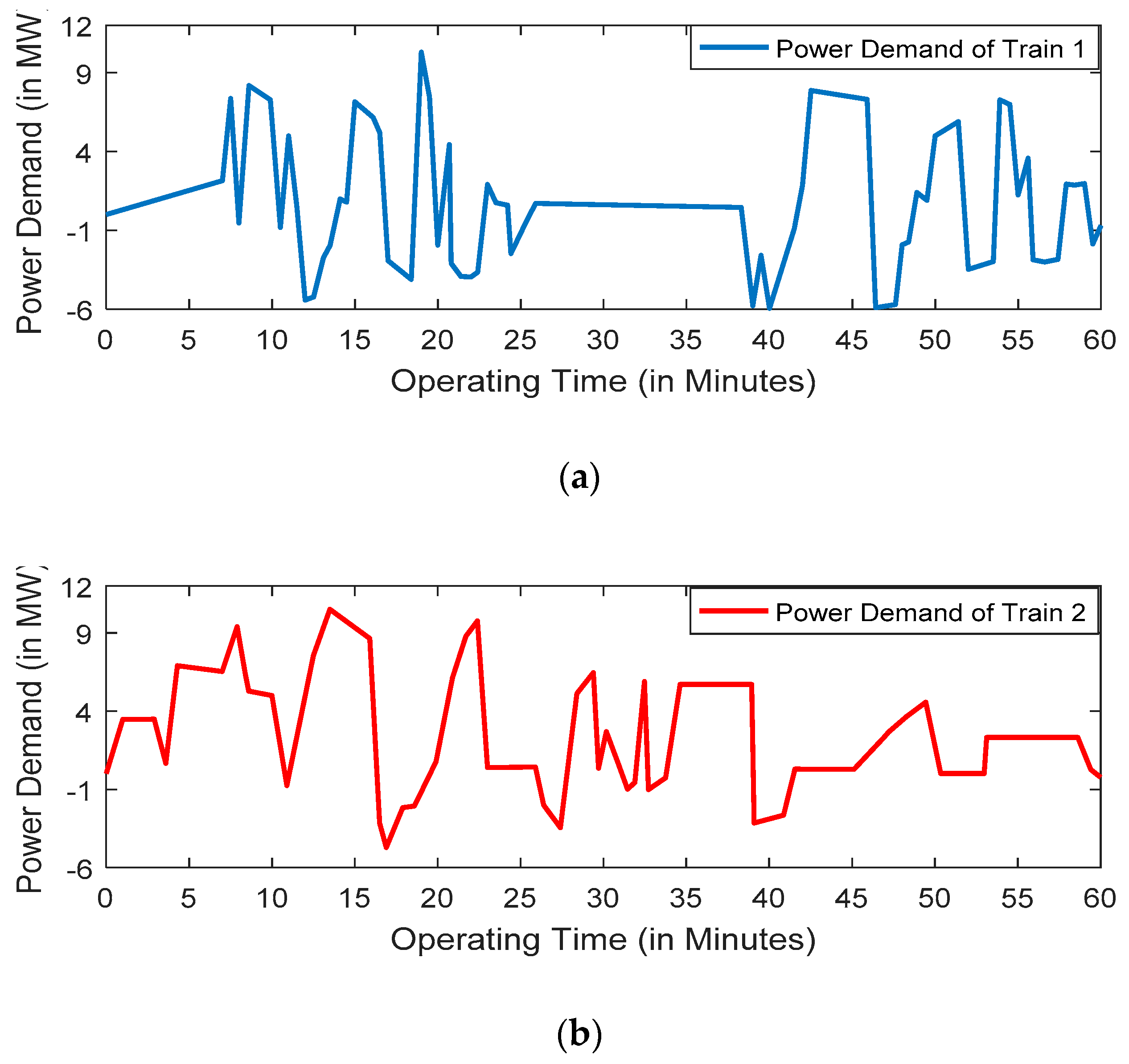
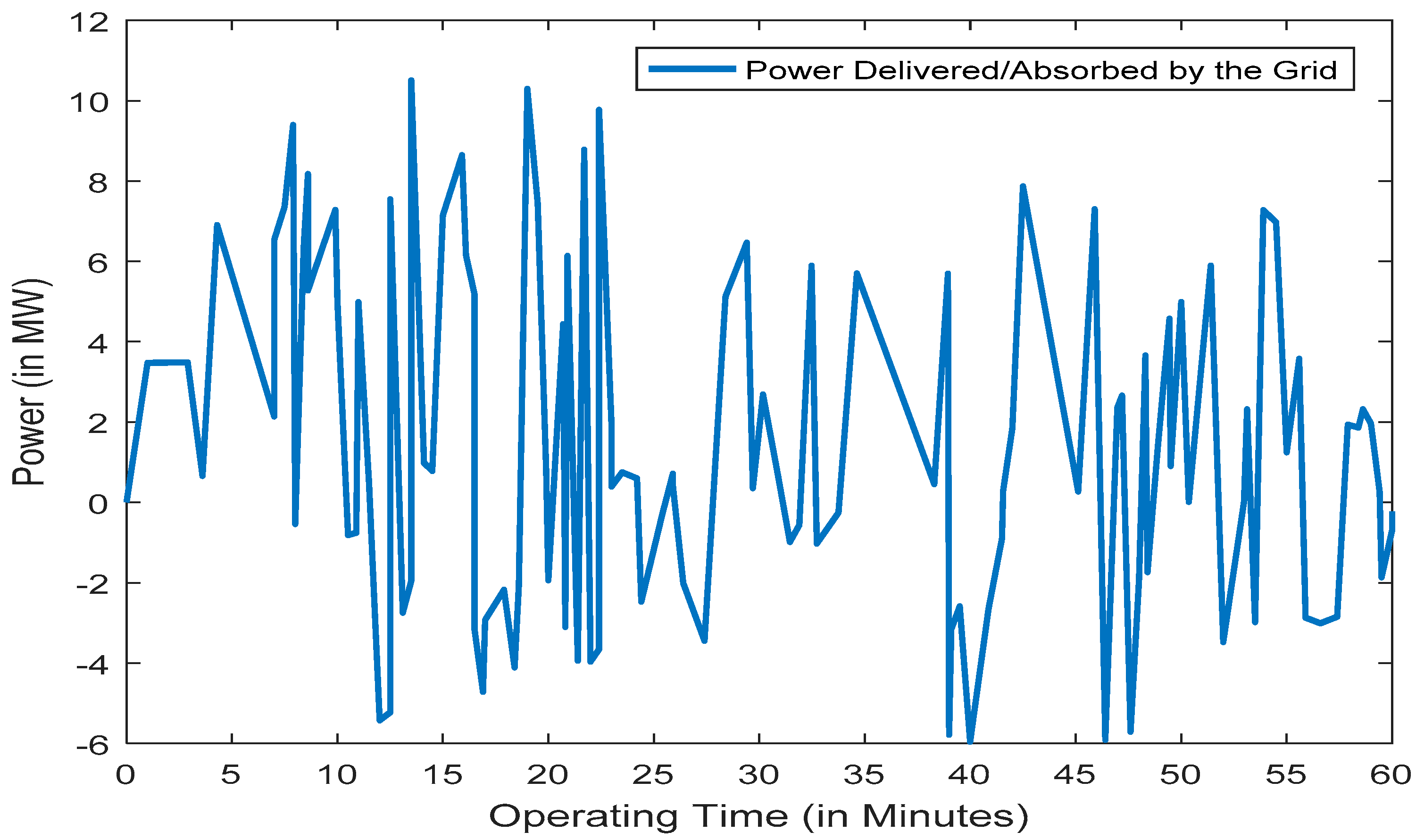
5. Results and Discussion
- Case Study 1: Railroad operation without considering RERs and energy storage systems (base case).
- Case Study 2: Railroad operation considering RERs.
- Case Study 3: Railroad operation considering hybrid energy storage systems.
- Case Study 4: Railroad operation considering RERs and hybrid energy storage systems.
5.1. Case Study 1
5.2. Case Study 2
5.3. Case Study 3
5.4. Case Study 4
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Nomenclature | Define |
| Cost of active power generation (in $/MWh). | |
| Active power output/generation from the network at the ith node. | |
| Cost of wind power generation (in $/MWh). | |
| Wind power output at the jth node. | |
| Cost of solar photovoltaic (PV) power generation (in $/MWh). | |
| Solar power output at the kth node. | |
| Selling price of excess power (in $/MWh). | |
| Available excess power at the lth node. | |
| Charging power of storage battery at the bth node. | |
| Discharging power of storage battery at the bth node. | |
| Charging power of supercapacitor at the uth node. | |
| Discharging power of supercapacitor at the uth node. | |
| Power returned to the grid. | |
| Power consumed from the grid. | |
| Active and reactive power demand of the Tth train. | |
| Active and reactive power demand at the ith node. | |
| Line flow of the ith line. | |
| Thermal limit of the ith line. |
References
- Reddy, S.S. Multi-Objective Optimal Power Flow for a Thermal-Wind-Solar Power System. J. Green Eng. 2017, 7, 451–476. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P. Sustainable urban rail systems: Strategies and technologies for optimal management of regenerative braking energy. Energy Convers. Manag. 2013, 75, 374–388. [Google Scholar] [CrossRef]
- Arboleya, P.; Mohamed, B.; El-Sayed, I. DC Railway Simulation Including Controllable Power Electronic and Energy Storage Devices. IEEE Trans. Power Syst. 2018, 33, 5319–5329. [Google Scholar] [CrossRef]
- Aguado, J.A.; Racero, A.J.S.; de la Torre, S. Optimal Operation of Electric Railways with Renewable Energy and Electric Storage Systems. IEEE Trans. Smart Grid 2018, 9, 993–1001. [Google Scholar] [CrossRef]
- Amrouche, S.O.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrogen Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Arboleya, P. Heterogeneous Multiscale Method for Multirate Railway Traction Systems Analysis. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2575–2580. [Google Scholar] [CrossRef]
- Arboleya, P.; Bidaguren, P.; Armendariz, U. Energy Is On Board: Energy Storage and Other Alternatives in Modern Light Railways. IEEE Electrif. Mag. 2016, 4, 30–41. [Google Scholar] [CrossRef]
- Arboleya, P.; Mohamed, B.; González-Morán, C.; El-Sayed, I. BFS Algorithm for Voltage-Constrained Meshed DC Traction Networks with Nonsmooth Voltage-Dependent Loads and Generators. IEEE Trans. Power Syst. 2016, 31, 1526–1536. [Google Scholar] [CrossRef]
- Frilli, A.; Meli, E.; Nocciolini, D.; Pugi, L.; Rindi, A. Energetic optimization of regenerative braking for high speed railway systems. Energy Convers. Manag. 2016, 129, 200–215. [Google Scholar] [CrossRef]
- Ghaviha, N.; Campillo, J.; Bohlin, M.; Dahlquist, E. Review of Application of Energy Storage Devices in Railway Transportation. Energy Procedia 2017, 105, 4561–4568. [Google Scholar] [CrossRef]
- Itani, K.; Bernardinis, A.D.; Khatir, Z.; Jammal, A. Comparative analysis of two hybrid energy storage systems used in a two front wheel driven electric vehicle during extreme start-up and regenerative braking operations. Energy Convers. Manag. 2017, 144, 69–87. [Google Scholar] [CrossRef]
- Ceraoloa, M.; Lutzembergera, G.; Melib, E.; Pugib, L.; Rindib, A.; Pancaric, G. Energy storage systems to exploit regenerative braking in DC railway systems: Different approaches to improve efficiency of modern high-speed trains. J. Energy Storage 2018, 16, 269–279. [Google Scholar] [CrossRef]
- De la Torre, S.; Sánchez-Racero, A.J.; Aguado, J.A.; Reyes, M.; Martínez, O. Optimal Sizing of Energy Storage for Regenerative Braking in Electric Railway Systems. IEEE Trans. Power Syst. 2015, 30, 1492–1500. [Google Scholar] [CrossRef]
- Ratniyomchai, T.; Hillmansen, S.; Tricoli, P. Recent developments and applications of energy storage devices in electrified railways. IET Electr. Syst. Transp. 2014, 4, 9–20. [Google Scholar] [CrossRef]
- Pankovits, P.; Pouget, J.; Robyns, B.; Delhaye, F.; Brisset, S. Towards railway-smartgrid: Energy management optimization for hybrid railway power substations. IEEE PES Innov. Smart Grid Technol. 2014, 1–6. [Google Scholar] [CrossRef]
- Reddy, S.S. Optimization of Railroad Electrical Systems with the Integrated Smart Grid. International J. Appl. Eng. Res. 2017, 12, 1027–1030. [Google Scholar]
- Nasr, S.; Iordache, M.; Petit, M. Smart micro-grid integration in DC railway systems. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Liu, H.; Tang, T.; Lv, J.; Chai, M. A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems. Energies 2019, 12, 1876. [Google Scholar] [CrossRef]
- Hiramatsu, S.; Kumada, Y.; Toukai, K.; Sugimoto, S.; Kawamura, J.; Kageyama, M. Study of practical energy-saving operation for electric railway vehicle. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–5. [Google Scholar]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An Economic Dispatch Model Incorporating Wind Power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Wang, M.Q.; Gooi, H.B. Spinning Reserve Estimation in Microgrids. IEEE Trans. Power Syst. 2011, 26, 1164–1174. [Google Scholar] [CrossRef]
- Reddy, S.S.; Momoh, J.A. Realistic and Transparent Optimum Scheduling Strategy for Hybrid Power System. IEEE Trans. Smart Grid 2015, 6, 3114–3125. [Google Scholar] [CrossRef]
- Pankovits, P.; Ployard, M.; Pouget, J.; Brisset, S.; Abbes, D.; Robyns, B. Design and operation optimization of a hybrid railway power substation. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–8. [Google Scholar]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Day-Ahead Energy Scheduling of a Smart Residential User under Uncertainty. In Proceedings of the 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 935–940. [Google Scholar]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Smart microgrid energy and reserve scheduling with demand response using stochastic optimization. Int. J. Electr. Power Energy Syst. 2014, 63, 523–533. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. Decentralized control for residential energy management of a smart usersʼ microgrid with renewable energy exchange. IEEE/CAA J. Autom. Sin. 2019, 6, 641–656. [Google Scholar] [CrossRef]
- Abrahamsson, L. Optimal Railroad Power Supply System Operation and Design. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
- Nayak, M.R.; Krishnanand, K.R.; Rout, P.K. Modified differential evolution optimization algorithm for multi-constraint optimal power flow. In Proceedings of the International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 1–7. [Google Scholar]
- El Ela, A.A.A.; Abido, M.A.; Spea, S.R. Optimal power flow using differential evolution algorithm. Electr. Power Syst. Res. 2010, 80, 878–885. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Novak, H.; Vašak, M.; Lešić, V. Hierarchical energy management of multi-train railway transport system with energy storages. In Proceedings of the IEEE International Conference on Intelligent Rail Transportation (ICIRT), Birmingham, UK, 23–25 August 2016; pp. 130–138. [Google Scholar]
- Novak, H.; Vašak, M.; Gulin, M.; Lešić, V. Railway transport system energy flow optimization with integrated microgrid. In Proceedings of the 12th International Conference on Modern Electrified Transport, Trogir, Croatia, 1 October 2015; pp. 1–6. [Google Scholar]
- Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
- Sperstad, I.B.; Korpås, M. Energy Storage Scheduling in Distribution Systems Considering Wind and Photovoltaic Generation Uncertainties. Energies 2019, 12, 1231. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. Cooperative Distributed Control for the Energy Scheduling of Smart Homes with Shared Energy Storage and Renewable Energy Source. IFAC-Pap. 2017, 50, 8867–8872. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Model Predictive Control for Real-Time Residential Energy Scheduling under Uncertainties. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 1386–1391. [Google Scholar]
- Touretzky, C.R.; Baldea, M. Integrating scheduling and control for economic MPC of buildings with energy storage. J. Process Control 2014, 24, 1292–1300. [Google Scholar] [CrossRef]
| Time (Min.) | Energy Price ($/MWh) | Time (Min.) | Energy Price ($/MWh) |
|---|---|---|---|
| (0–5) | 75 | (30–35) | 80 |
| (5–10) | 80 | (35–40) | 88 |
| (10–15) | 85 | (40–45) | 75 |
| (15–20) | 70 | (45–50) | 78 |
| (20–25) | 76 | (50–55) | 70 |
| (25–30) | 82 | (55–60) | 85 |
| Case Study 1 | Case Study 2 | Case Study 3 | Case Study 4 | |
|---|---|---|---|---|
| Total Generation (MWh) | 4.748 | 4.051 | 4.247 | 3.862 |
| Wind Power Generation (MWh) | - | 1.230 | - | 1.160 |
| Solar PV Power Generation (MWh) | - | 0.832 | - | 0.816 |
| Battery Energy Storage (MWh) | - | - | 0.421 | 0.382 |
| Supercapacitor Energy Storage (MWh) | - | - | 0.293 | 0.241 |
| Excess Energy (MWh) | 1.142 | 1.496 | 1.237 | 1.318 |
| Total Cost ($/h) | 325.94 | 306.82 | 290.22 | 283.40 |
| Cost Saving (%) | - | 5.87 | 10.96 | 13.05 |
| Computational Time (s) | 18.26 | 18.90 | 19.05 | 19.22 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Salkuti, S.R. Optimal Energy Management of Railroad Electrical Systems with Renewable Energy and Energy Storage Systems. Sustainability 2019, 11, 6293. https://doi.org/10.3390/su11226293
Park S, Salkuti SR. Optimal Energy Management of Railroad Electrical Systems with Renewable Energy and Energy Storage Systems. Sustainability. 2019; 11(22):6293. https://doi.org/10.3390/su11226293
Chicago/Turabian StylePark, Seunghyun, and Surender Reddy Salkuti. 2019. "Optimal Energy Management of Railroad Electrical Systems with Renewable Energy and Energy Storage Systems" Sustainability 11, no. 22: 6293. https://doi.org/10.3390/su11226293
APA StylePark, S., & Salkuti, S. R. (2019). Optimal Energy Management of Railroad Electrical Systems with Renewable Energy and Energy Storage Systems. Sustainability, 11(22), 6293. https://doi.org/10.3390/su11226293






