Partial Node Failure in Shortest Path Network Problems
Abstract
1. Introduction
2. Background
2.1. The Shortest Paths Network Model
- Ωsq = objective function at status quo,
- s = index of origin,
- t = index of destination,
- i, j = index of operable node,
- Ni = set of nodes connected directly to node i by an arc (i, j),
- Wst = amount of flow to be delivered from s to t,
- Cij = travel cost of arc (i, j),
- Xstij = 1: if arc (i, j) is the member of the shortest path from s to t; 0: otherwise.
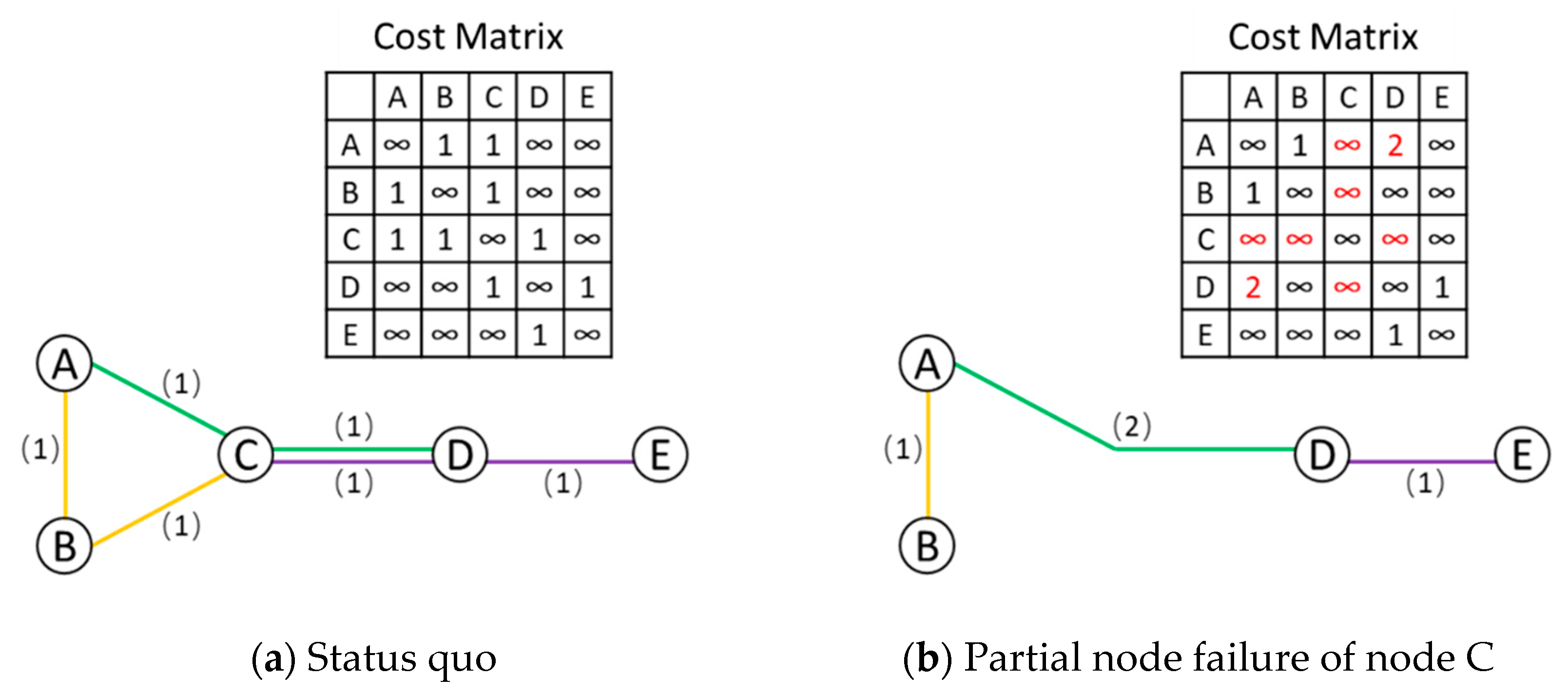
2.2. Partial Node Failure and Mandatory Transfer (MT)
3. Methodology and Formulations
3.1. Updating Cost Matrix and Link Attribute
- i, j = index of operable node,
- r = index of partially failed node,
- Nr = a set of nodes directly connected to the partially failed node r,
- d’ij = travel cost between node i and j when node r partially fails,
- dij = travel cost between node i and j at status quo,
- lij = link attribute between node i and j,
- Lir = a set of links between nodes i and r.
- Step 1.
- The set of nodes directly connected to node C (i.e., Nc) is identified as follows to decide the travel cost of the node pairs to be updated: NC = {A, B, D}.
- Step 2.
- The sets of links between node C and the three nodes in NC are as follows:
- LAC = {green}; LBC = {yellow}; LDC = {green, purple}.
- Step 3.
- The node pairs among the three nodes contained in NC are AB, AD, and BD. The link attributes of the three node pairs are identified and stored as follows:
- lAB = 0 (LAC and LBC do not contain the same value);
- lAD = 1 (LAC and LDC contain the same value of “green”);
- lBD = 0 (LBC and LDC do not contain the same value).
- Step 4.
- According to Equations (4) and (5), the updated cost matrix is obtained as follows:
- when i = r or j = r:d’ij = ∞; therefore, d’AC = ∞, d’BC = ∞, d’DC = ∞, d’CA = ∞, d’CB = ∞, d’CD = ∞.
- when i ≠ j ≠ r
- (1)
- If dij =∞
- If lij = 0, d’ij = ∞; therefore, d’BD = ∞, and d’DB = ∞,
- If lij = 1, d’ij = dir + drj; therefore, d’AD = dAC + dCD = 2, and d’DA = dDC + dCA = 2,
- (2)
- If dij ≠ ∞, dij = d’ij; therefore, d’AB = dAB = 1, d’BA = dBA = 1.
3.2. The SPN Model for Partial Node Failure (SPNPr)
- ΩPr = objective function when node r partially fails,
- r = index of disabled node(s),
- CijPr = travel cost of arc (i, j) when node r partially fails (i ≠ j ≠ r),
- XstijPr = 1: if arc (i, j) is the member of the shortest path from s to t; 0: otherwise when node r partially fails.
3.3. Assessment Indicators
- CostPrreroute = flow reroute cost when node r partially fails,
- ΩSq-r = total network cost at status quo, excluding the network cost related with node r, calculated by the following equation;
- ΩSq-r = ΩSq.
- k = index of operable node,
- ViaFlowkPr = amount of flow to be passed through node k when node r partially fails,
- ViaFlowkSq = amount of flow to be passed through node k at status quo,
- RidershipkSq = amount of flow at node k at status quo,
- RidershipkPr = amount of flow at node k when node r partially fails. The ridership is calculated by RidershipkPr = RidershipkSq −
- NodeFlowkPr = sum of inbound and outbound flow at node k when node r partially fails,
- NodeFlowkSq = sum of inbound and outbound flow at node k at status quo.
4. Numerical Experiments
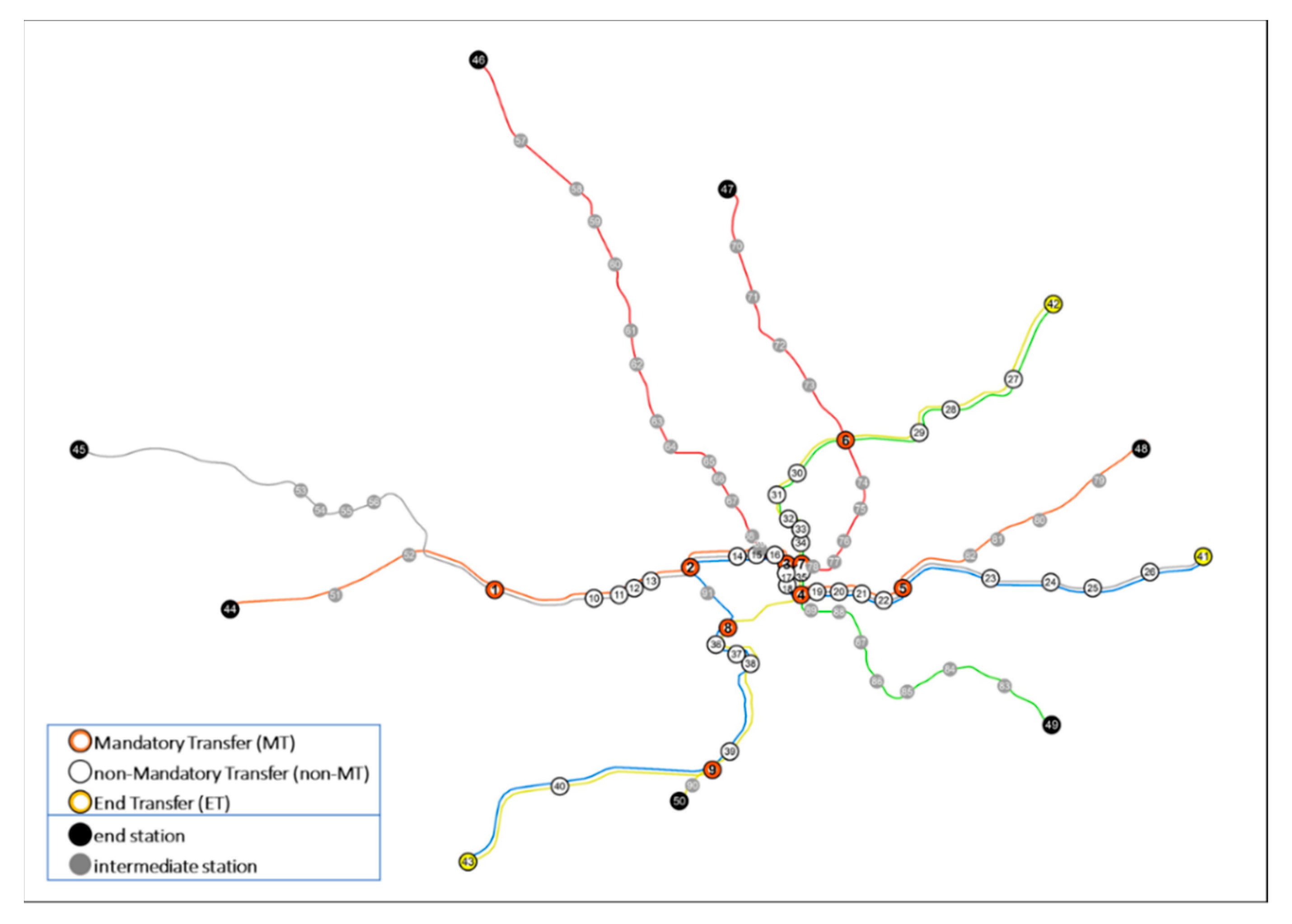
4.1. The WMATA Network
4.2. Computational Results: The Impact of Partial Node Failure of MTs in the WMATA Network
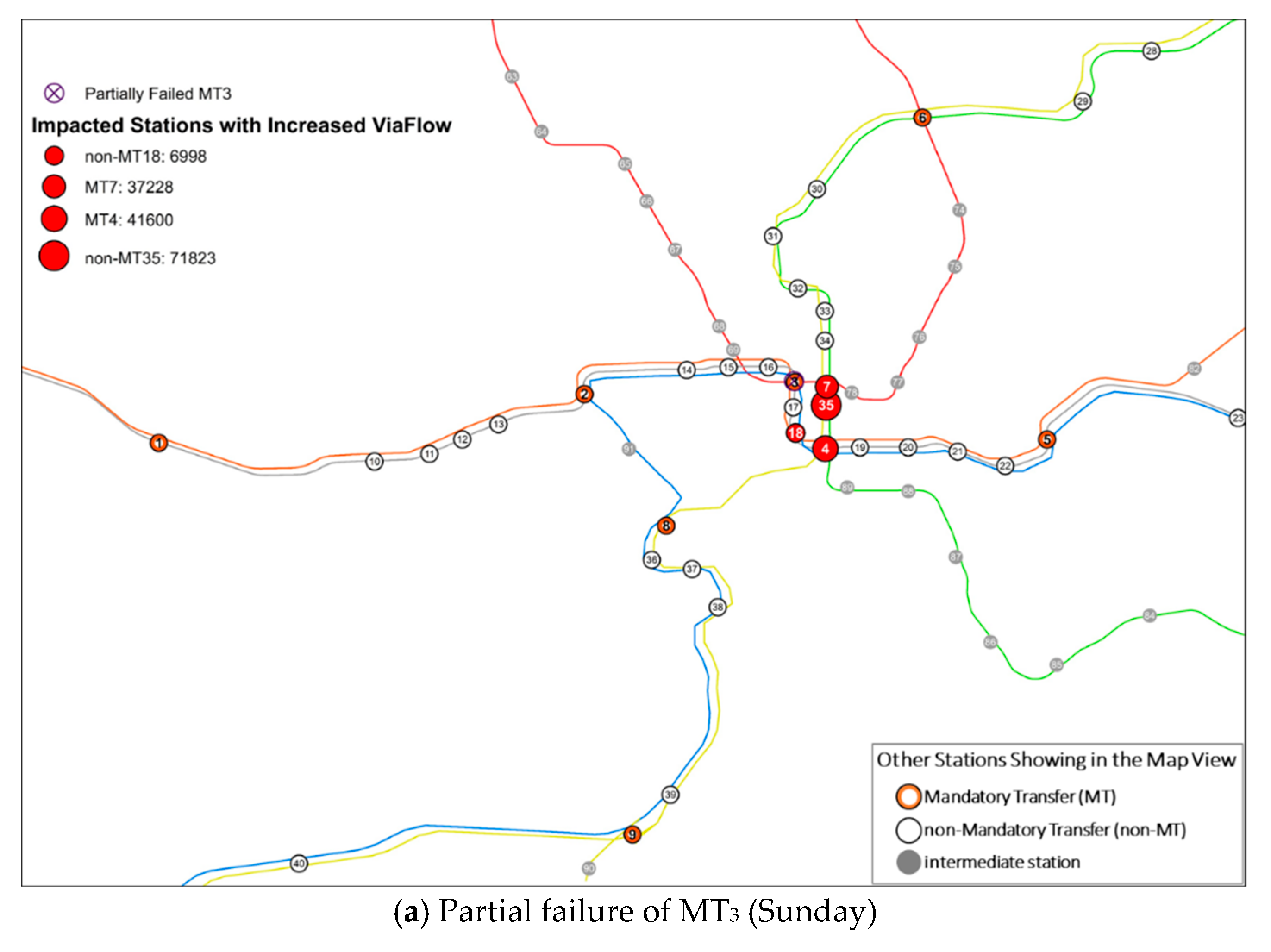
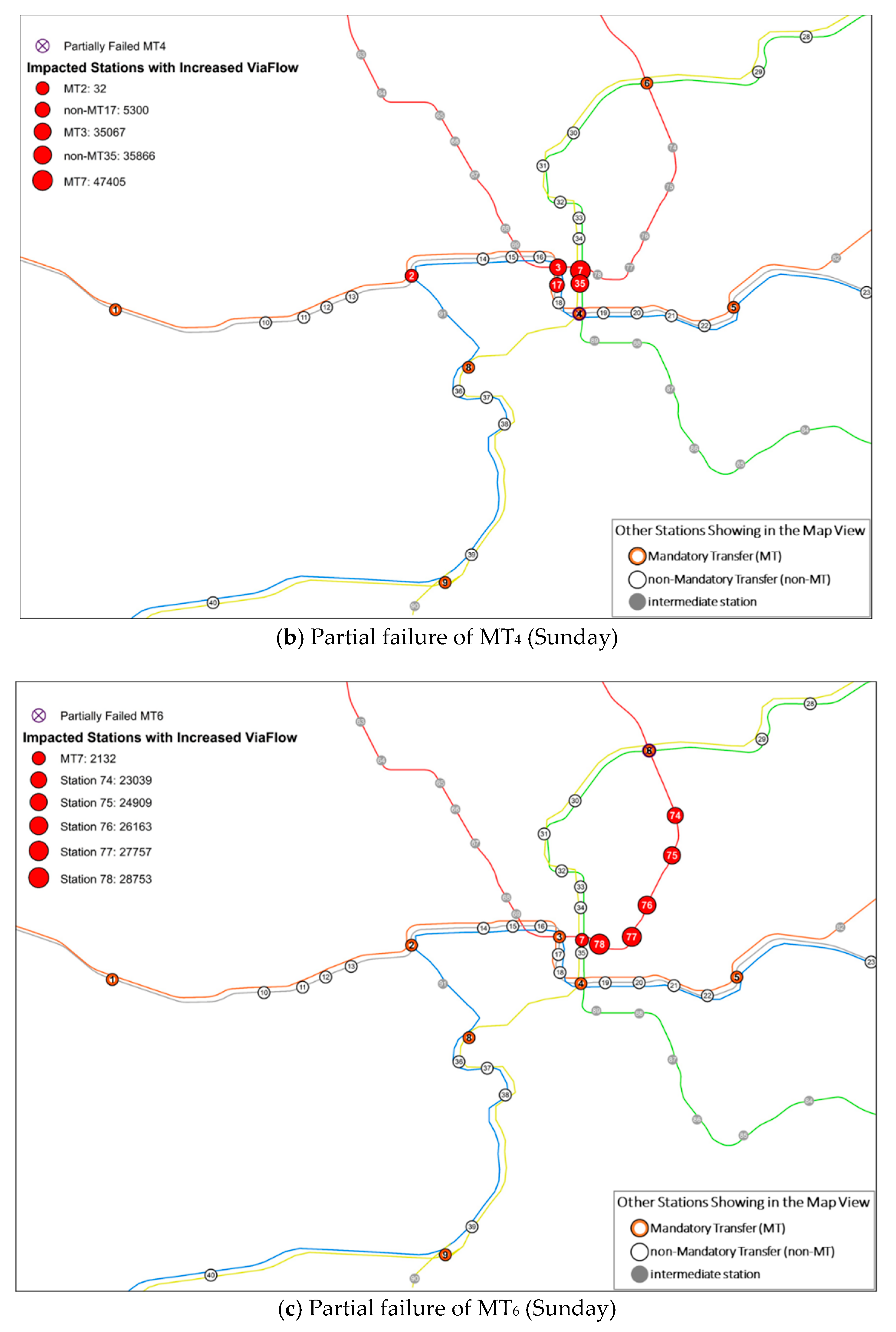
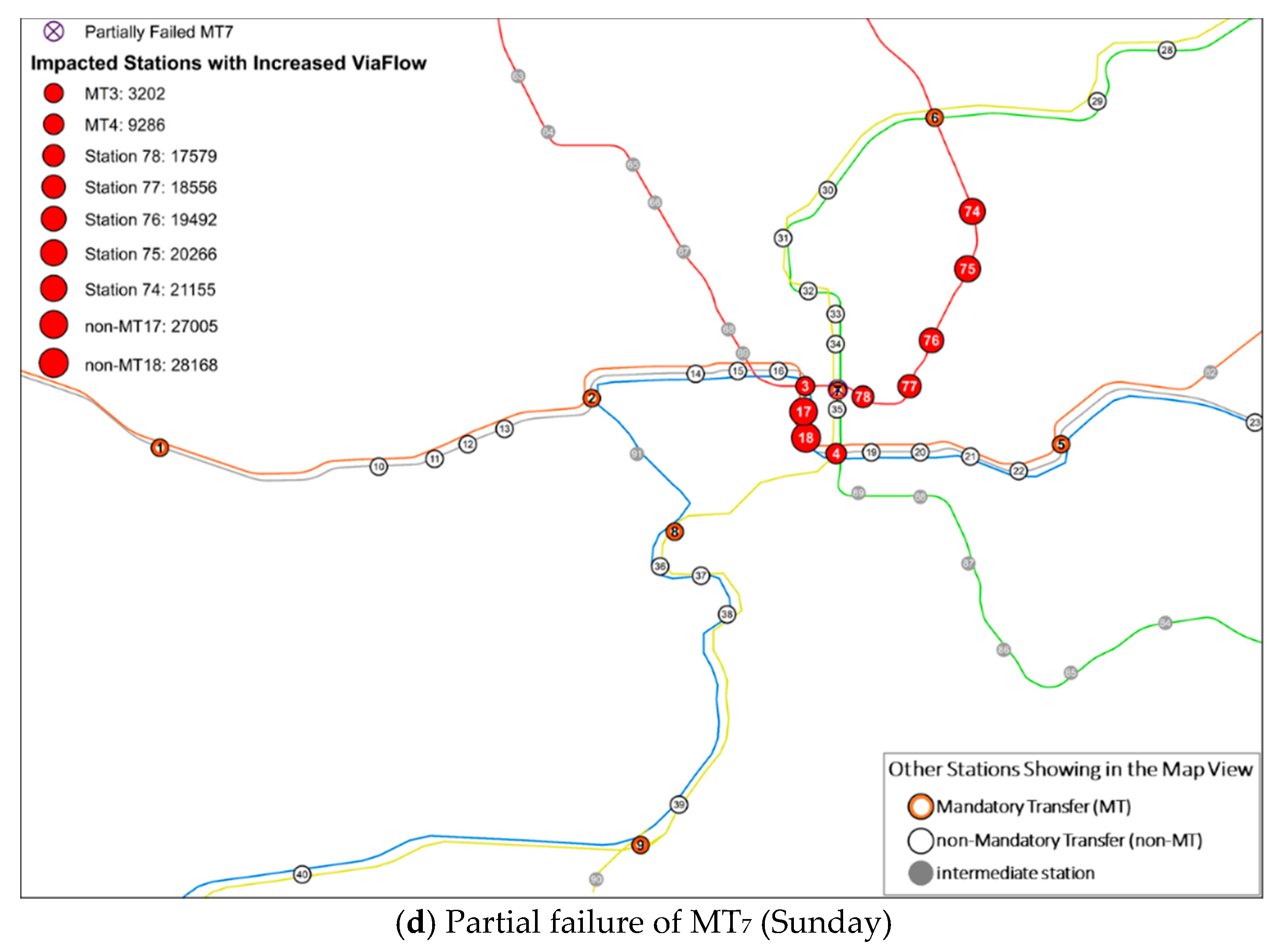
4.3. Impacted Stations with Increased ViaFlow
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
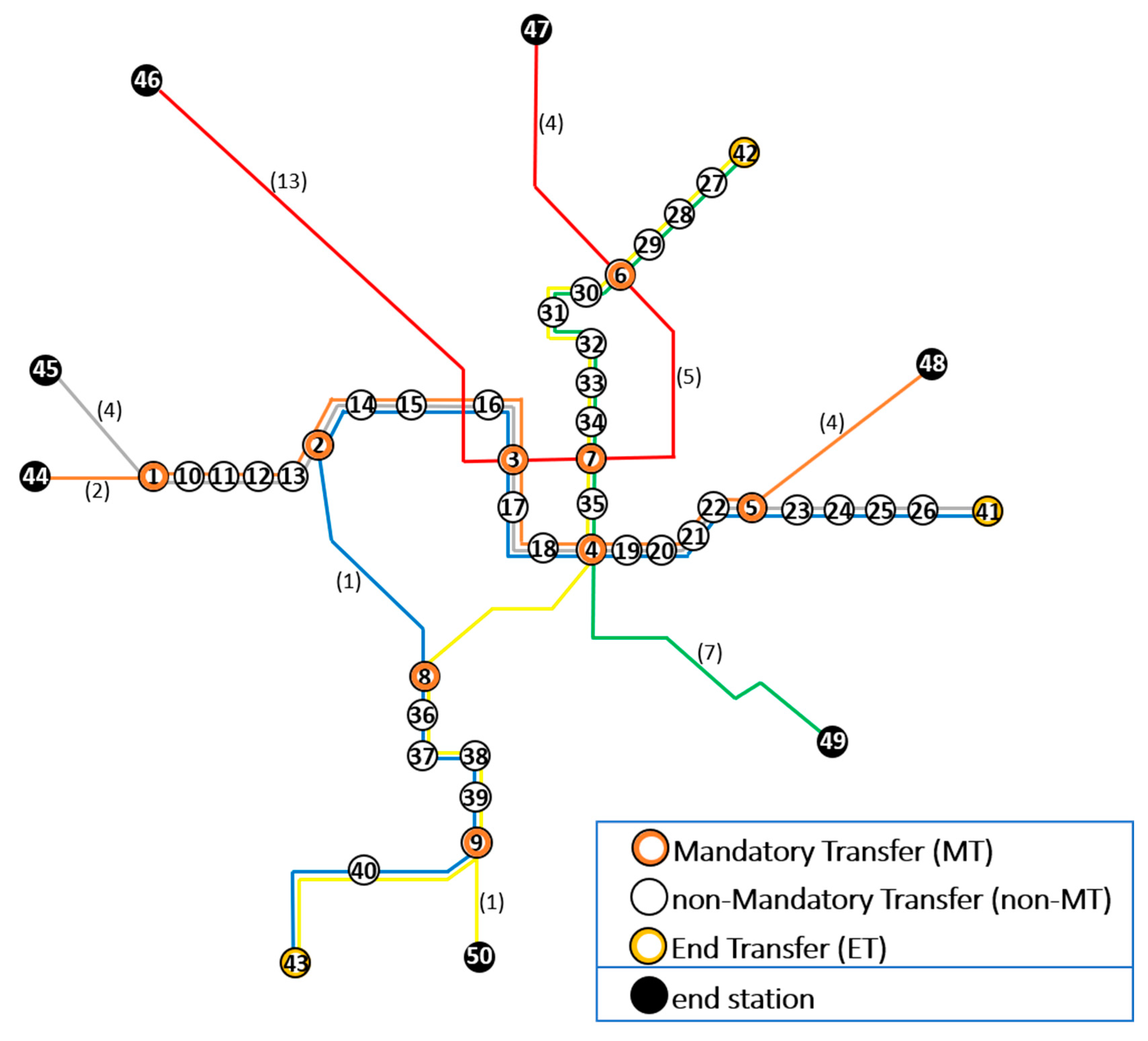
| Station ID | Station Name | Type | Link Attribute * |
|---|---|---|---|
| 1 | East Falls Church | MT | O, S |
| 2 | Rosslyn | MT | B, O, S |
| 3 | Metro Center | MT | B, O, R, S |
| 4 | L’Enfant Plaza | MT | B, G, O, S, Y |
| 5 | Stadium-Armory | MT | B, O, S |
| 6 | Fort Totten | MT | G, R, Y |
| 7 | Gallery Place/Chinatown | MT | G, R, Y |
| 8 | Pentagon | MT | B, Y |
| 9 | King St-Old Town | MT | B, Y |
| 10 | Ballston-MU | non-MT | O, S |
| 11 | Virginia Square-GMU | non-MT | O, S |
| 12 | Clarendon | non-MT | O, S |
| 13 | Court House | non-MT | O, S |
| 14 | Foggy Bottom-GWU | non-MT | B, O, S |
| 15 | Farragut West | non-MT | B, O, S |
| 16 | McPherson Square | non-MT | B, O, S |
| 17 | Federal Triangle | non-MT | B, O, S |
| 18 | Smithsonian | non-MT | B, O, S |
| 19 | Federal Center SW | non-MT | B, O, S |
| 20 | Capitol South | non-MT | B, O, S |
| 21 | Eastern Market | non-MT | B, O, S |
| 22 | Potomac Ave | non-MT | B, O, S |
| 23 | Benning Rd | non-MT | B, S |
| 24 | Capitol Heights | non-MT | B, S |
| 25 | Addison Rd/Seat Pleasant | non-MT | B, S |
| 26 | Morgan Blvd | non-MT | B, S |
| 27 | College Park-U of Md | non-MT | G, Y |
| 28 | Prince George’s Plaza | non-MT | G, Y |
| 29 | West Hyattsville | non-MT | G, Y |
| 30 | Georgia Ave-Petworth | non-MT | G, Y |
| 31 | Columbia Heights | non-MT | G, Y |
| 32 | U St/African-Amer Civil War Memorial/Cardozo | non-MT | G, Y |
| 33 | Shaw-Howard Univ | non-MT | G, Y |
| 34 | Mt Vernon Sq/7th St-Convention Center | non-MT | G, Y |
| 35 | Archives/Navy Memorial-Penn Quarter | non-MT | G, Y |
| 36 | Pentagon City | non-MT | B, Y |
| 37 | Crystal City | non-MT | B, Y |
| 38 | Ronald Reagan Washington National Airport | non-MT | B, Y |
| 39 | Braddock Rd | non-MT | B, Y |
| 40 | Van Dorn St | non-MT | B, Y |
| 41 | Largo Town Center | ET | B, S |
| 42 | Greenbelt | ET | G, Y |
| 43 | Franconia-Springfield | ET | B, Y |
| 44 | Vienna/Fairfax-GMU | ES | O |
| 45 | Wiehle-Reston East | ES | S |
| 46 | Shady Grove | ES | R |
| 47 | Glenmont | ES | R |
| 48 | New Carrollton | ES | O |
| 49 | Branch Ave | ES | G |
| 50 | Huntington | ES | Y |
| 51 | Dunn Loring/Merrifield | IS | O |
| 52 | West Falls Church/VT/UVA | IS | O |
| 53 | Spring Hill | IS | S |
| 54 | Greensboro | IS | S |
| 55 | Tysons Corner | IS | S |
| 56 | McLean | IS | S |
| 57 | Rockville | IS | R |
| 58 | Twinbrook | IS | R |
| 59 | White Flint | IS | R |
| 60 | Grosvenor-Strathmore | IS | R |
| 61 | Medical Center | IS | R |
| 62 | Bethesda | IS | R |
| 63 | Friendship Heights | IS | R |
| 64 | Tenleytown-AU | IS | R |
| 65 | Van Ness-UDC | IS | R |
| 66 | Cleveland Park | IS | R |
| 67 | Woodley Park/Zoo/Adams Morgan | IS | R |
| 68 | Dupont Circle | IS | R |
| 69 | Farragut North | IS | R |
| 70 | Wheaton | IS | R |
| 71 | Forest Glen | IS | R |
| 72 | S Spring | IS | R |
| 73 | Takoma | IS | R |
| 74 | Brookland-CUA | IS | R |
| 75 | Rhode Island Ave/Brentwood | IS | R |
| 76 | NoMa-Gallaudet U | IS | R |
| 77 | Union Station | IS | R |
| 78 | Judiciary Square | IS | R |
| 79 | Landover | IS | O |
| 80 | Cheverly | IS | O |
| 81 | Deanwood | IS | O |
| 82 | Minnesota Ave | IS | O |
| 83 | Suitland | IS | G |
| 84 | Naylor Rd | IS | G |
| 85 | Southern Ave | IS | G |
| 86 | Congress Heights | IS | G |
| 87 | Anacostia | IS | G |
| 88 | Navy Yard-Ballpark | IS | G |
| 89 | Waterfront | IS | G |
| 90 | Eisenhower Ave | IS | Y |
| 91 | Arlington Cemetery | IS | B |
References
- O’Kelly, M.E. Network hub structure and resilience. Netw. Spat. Econ. 2015, 15, 235–251. [Google Scholar] [CrossRef]
- Matisziw, T.; Murray, A.; Grubesic, H. Exploring the vulnerability of network infrastructure to interdiction. Ann. Reg. Sci. 2009, 43, 307–321. [Google Scholar] [CrossRef]
- Kim, H. Geographical analysis on network reliability of public transportation systems: A case study of subway network system in Seoul. J. Korean Geogr. Soc. 2009, 44, 187–205. [Google Scholar]
- Ye, Q.; Kim, H. Assessing network vulnerability of heavy rail systems with the impact of partial node failures. Transportation 2019, 46, 1591–1614. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C.; Chun, Y. Network reliability and resilience of rapid transit systems. Prof. Geogr. 2016, 68, 53–65. [Google Scholar] [CrossRef]
- Cats, O.; Jenelius, E. Beyond a complete failure: The impact of partial capacity degradation on public transport network vulnerability. Transportmetrica B 2016, 6, 77–96. [Google Scholar] [CrossRef]
- Duggan, P.; Siddiqui, F.; Aratani, L. Washington Post: For Metro Riders, Summer Starts with Partial Shutdown of 3 Rail Lines. Available online: https://www.washingtonpost.com/local/trafficandcommuting /for-metro-riders-summer-starts-with-a-partial-shutdown-of-three-rail-lines-as-part-of-safetrack/2016/06/20/b932e62e-3668-11e6-a254-2b336e293a3c_story.html (accessed on 17 October 2019).
- Nagurney, A.; Qiang, Q. Robustness of transportation networks subject to degradable links. Europhys. Lett. 2007, 80, 68001. [Google Scholar] [CrossRef]
- Sullivan, J.L.; Novak, D.C.; Aultman-Hall, L.; Scott, D.M. Identifying critical road segments and measuring system-wide robustness in transportation networks with isolating links: A link-based capacity-reduction approach. Transp. Res. Part A 2010, 44, 323–336. [Google Scholar] [CrossRef]
- Burgholzer, W.; Bauer, G.; Posset, M.; Jammernegg, W. Analysing the impact of disruptions in intermodal transport networks: A micro simulation-based model. Decis. Support Syst. 2013, 54, 1580–1586. [Google Scholar] [CrossRef]
- Ye, Q.; Kim, H. Assessing network vulnerability using shortest path network problems. J. Transp. Saf. Secur. 2019. [Google Scholar] [CrossRef]
- O’Kelly, M.E.; Kim, H.; Kim, C. Internet reliability with realistic peering. Environ. Plan. B 2006, 33, 325–343. [Google Scholar] [CrossRef]
- Matisziw, T.; Murray, A.; Grubesic, H. Strategic network restoration. Netw. Spat. Econ. 2010, 10, 345–361. [Google Scholar] [CrossRef]
- Kim, H.; Ryerson, M. The q-Ad hoc hub location problem for multi-modal networks. Netw. Spat. Econ. 2017, 17, 1015–1041. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H. Shortest paths in traffic-light networks. Transp. Res. Part B 2000, 34, 241–253. [Google Scholar] [CrossRef]
- Sherali, H.D.; Hobeika, A.G.; Kangwalklai, S. Time-Dependent, Label-Constrained Shortest Path Problems with Applications. Transp. Sci. 2003, 37, 278–293. [Google Scholar] [CrossRef]
- Santosa, L.; Coutinho-Rodrigues, J.; Current, J.R. An improved solution algorithm for the constrained shortest path problem. Transp. Res. Part B 2007, 41, 756–771. [Google Scholar] [CrossRef]
- Cappanera, P.; Scaparra, M.P. Optimal allocation of protective resources in shortest-path networks. Transp. Sci. 2011, 45, 64–80. [Google Scholar] [CrossRef]
- Wang, L.; Yang, L.; Gao, Z. The constrained shortest path problem with stochastic correlated link travel times. Eur. J. Oper. Res. 2016, 255, 43–57. [Google Scholar] [CrossRef]
- Shi, N.; Zhou, S.; Wang, F.; Tao, Y.; Liu, L. The multi-criteria constrained shortest path problem. Transp. Res. Part E 2017, 101, 13–29. [Google Scholar] [CrossRef]
- Strehler, M.; Merting, S.; Schwan, C. Energy-efficient shortest routes for electric and hybrid vehicles. Transp. Res. Part B 2017, 103, 111–135. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Whiting, P.D.; Hillier, J.A. A method for finding the shortest route through a road network. J. Oper. Res. Soc. 1960, 11, 37–40. [Google Scholar] [CrossRef]
- Ford, L.R., Jr. Network Flow Theory; Paper P-923; RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM. 1962, 5, 345. [Google Scholar] [CrossRef]
- Johnson, D.B. Efficient algorithms for shortest paths in sparse networks. J. ACM. 1977, 24, 1–13. [Google Scholar] [CrossRef]
- Bock, F.; Kantner, H.; Haynes, J. An Algorithm (the rh Best Path Algorithm) for Finding and Ranking Paths Through a Network; Research Report; Armour Research Foundation: Chicago, IL, USA, 1957. [Google Scholar]
- Bellman, R.; Kalaba, R. On kth best policies. J. Soc. Ind. Appl. Math. 1960, 8, 582–588. [Google Scholar] [CrossRef]
- Clarke, S.; Krikorian, A.; Rausan, J. Computing the N best loopless paths in a network. J. Soc. Ind. Appl. Math. 1963, 11, 1096–1102. [Google Scholar] [CrossRef]
- Kuby, M.; Xu, Z.; Xie, X. A minimax method for finding the k best “differentiated” paths. Geogr. Anal. 1997, 29, 298–313. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Matisziw, T.C.; Murray, A.T.; Snedicker, D. Comparative approaches for assessing network vulnerability. Int. Reg. Sci. Rev. 2008, 31, 88–112. [Google Scholar] [CrossRef]
- Washington Metropolitan Area Transit Authority API. Available online: https://developer.wmata.com (accessed on 11 November 2017).
- Haywood, L.; Koning, M. Estimating Crowding Costs in Public Transport. DIW Berlin Discussion Paper No. 1293. 2013. Available online: http://dx.doi.org/10.2139/ssrn.2256332 (accessed on 17 October 2019).
- PlanItMetro. Metrorail Ridership Data by Washington Metropolitan Area Transit Authority. Available online: https://planitmetro.com/?s=Metrorail+Ridership+Data+Download%2C+October+2015 (accessed on 11 November 2017).
- Open Data DC. Available online: https://opendata.dc.gov/datasets/metro-stations-regional; https://opendata.dc.gov/datasets/metro-lines-regional (accessed on 2 April 2018).
- WMATA. Available online: https://www.wmata.com/about/upload/Metro-Facts-2015.pdf (accessed on 11 November 2017).

| Key Elements | Value |
|---|---|
| ΩPc | 28 |
| 34 − 10 = 24 | |
| 28 − 24 = 4 | |
| NodeFlowASq | 8 |
| RidershipASq | 8 |
| NodeFlowAPc | 14 |
| RidershipAPc | 6 |
| ViaFlowASq | (8 − 8)/2 = 0 |
| ViaFlowAPc | (14 − 6)/2 = 4 |
| DiffViaFlowAPc-Sq | 4 − 0 = +4 |
| Type of Station | Station Name | Link (Line) Attribute |
|---|---|---|
| MT1 | East Falls Church | Orange, Silver |
| MT2 | Rosslyn | Blue, Orange, Silver |
| MT3 | Metro Center | Blue, Orange, Red, Silver |
| MT4 | L’Enfant Plaza | Blue, Green, Orange, Silver, Yellow |
| MT5 | Stadium–Armory | Blue, Orange, Silver |
| MT6 | Fort Totten | Green, Red, Yellow |
| T7 | Gallery Place/Chinatown | Green, Red, Yellow |
| MT8 | Pentagon | Blue, Yellow |
| MT9 | King St.–Old Town | Blue, Yellow |
| Partial Node Failure | Day | Obj. Values | Sol. Time (sec.) | # of Iterations | |
|---|---|---|---|---|---|
| Status quo | Monday | 8,938,458 | N/A | 9.91 | 50,742 |
| Tuesday | 7,011,337 | N/A | 9.95 | 50,929 | |
| Wednesday | 7,064,503 | N/A | 9.92 | 50,858 | |
| Thursday | 7,353,972 | N/A | 11.17 | 51,002 | |
| Friday | 7,408,573 | N/A | 10.13 | 50,742 | |
| Saturday | 4,816,424 | N/A | 11.36 | 50,609 | |
| Sunday | 3,526,568 | N/A | 11.16 | 49,939 | |
| MT1 | Monday | 8,823,267 | 6974 | 9.25 | 49,767 |
| MT1 | Tuesday | 6,918,687 | 5540 | 9.41 | 49,549 |
| MT1 | Wednesday | 6,971,922 | 5647 | 9.52 | 49,695 |
| MT1 | Thursday | 7,255,287 | 5992 | 9.38 | 49,775 |
| MT1 | Friday | 7,304,426 | 6702 | 9.58 | 49,789 |
| MT1 | Saturday | 4,703,423 | 3878 | 9.25 | 49,399 |
| MT1 | Sunday | 3,436,934 | 2051 | 9.58 | 48,607 |
| MT2 | Monday | 8,725,023 | 42,425 | 9.00 | 44,382 |
| MT2 | Tuesday | 6,856,648 | 34,840 | 9.08 | 44,289 |
| MT2 | Wednesday | 6,910,940 | 35,595 | 9.16 | 44,192 |
| MT2 | Thursday | 7,203,264 | 38,893 | 9.03 | 44,159 |
| MT2 | Friday | 7,262,983 | 40,325 | 9.30 | 44,400 |
| MT2 | Saturday | 4,730,392 | 25,003 | 9.06 | 43,911 |
| MT2 | Sunday | 3,356,169 | 32,273 | 9.27 | 43,394 |
| MT3 | Monday | 8,609,317 | 180,933 | 9.00 | 43,811 |
| MT3 | Tuesday | 6,785,886 | 146,572 | 9.00 | 43,759 |
| MT3 | Wednesday | 6,841,368 | 149,835 | 8.97 | 44,161 |
| MT3 | Thursday | 7,136,343 | 160,362 | 8.91 | 44,019 |
| MT3 | Friday | 7,218,614 | 171,308 | 9.78 | 43,665 |
| MT3 | Saturday | 4,729,130 | 121,566 | 8.89 | 43,350 |
| MT3 | Sunday | 3,472,257 | 82,516 | 9.13 | 43,013 |
| MT4 | Monday | 8,739,334 | 114,487 | 8.38 | 32,916 |
| MT4 | Tuesday | 6,815,577 | 96,767 | 8.45 | 32,954 |
| MT4 | Wednesday | 6,869,544 | 99,314 | 8.48 | 32,867 |
| MT4 | Thursday | 7,168,453 | 107,243 | 8.42 | 33,004 |
| MT4 | Friday | 7,286,959 | 116,125 | 9.16 | 33,049 |
| MT4 | Saturday | 4,778,639 | 90,138 | 8.41 | 32,736 |
| MT4 | Sunday | 3,491,884 | 60,286 | 8.53 | 32,329 |
| MT5 | Monday | 8,890,791 | 1891 | 9.66 | 49,911 |
| MT5 | Tuesday | 6,963,518 | 1550 | 9.34 | 49,716 |
| MT5 | Wednesday | 7,005,761 | 1466 | 9.72 | 49,863 |
| MT5 | Thursday | 7,302,765 | 1771 | 9.84 | 49,736 |
| MT5 | Friday | 7,287,289 | 1960 | 10.22 | 49,767 |
| MT5 | Saturday | 4,662,281 | 1583 | 9.64 | 49,322 |
| MT5 | Sunday | 3,473,958 | 1244 | 9.45 | 48,970 |
| MT6 | Monday | 8,848,170 | 94,301 | 6.39 | 27,903 |
| MT6 | Tuesday | 6,944,764 | 70,124 | 6.42 | 27,894 |
| MT6 | Wednesday | 6,995,616 | 70,229 | 6.41 | 27,863 |
| MT6 | Thursday | 7,282,473 | 72,870 | 6.59 | 27,949 |
| MT6 | Friday | 7,339,107 | 78,751 | 6.95 | 27,960 |
| MT6 | Saturday | 4,776,994 | 60,194 | 6.34 | 27,636 |
| MT6 | Sunday | 3,495,971 | 39,606 | 6.48 | 27,255 |
| MT7 | Monday | 8,607,383 | 91,978 | 8.77 | 47,265 |
| MT7 | Tuesday | 6,760,527 | 73,410 | 9.00 | 47,257 |
| MT7 | Wednesday | 6,818,075 | 74,345 | 9.38 | 47,220 |
| MT7 | Thursday | 7,100,146 | 77,862 | 9.34 | 47,179 |
| MT7 | Friday | 7,149,937 | 90,140 | 10.25 | 47,342 |
| MT7 | Saturday | 4,613,313 | 65,947 | 9.36 | 46,796 |
| MT7 | Sunday | 3,406,132 | 38,637 | 8.88 | 46,421 |
| MT8 | Monday | 8,724,544 | 1206 | 9.61 | 48,469 |
| MT8 | Tuesday | 6,813,712 | 805 | 9.44 | 48,547 |
| MT8 | Wednesday | 6,862,968 | 757 | 9.37 | 48,444 |
| MT8 | Thursday | 7,151,361 | 1057 | 9.36 | 48,610 |
| MT8 | Friday | 7,219,607 | 982 | 11.25 | 48,662 |
| MT8 | Saturday | 4,763,017 | 1320 | 9.61 | 48,255 |
| MT8 | Sunday | 3,309,214 | 1628 | 9.59 | 47,575 |
| MT9 | Monday | 8,662,722 | 715 | 9.38 | 49,706 |
| MT9 | Tuesday | 6,804,826 | 594 | 10.03 | 49,959 |
| MT9 | Wednesday | 6,854,973 | 611 | 9.52 | 49,627 |
| MT9 | Thursday | 7,136,922 | 612 | 9.72 | 49,809 |
| MT9 | Friday | 7,190,445 | 671 | 10.17 | 49,785 |
| MT9 | Saturday | 4,663,032 | 413 | 9.66 | 49,589 |
| MT9 | Sunday | 3,408,351 | 287 | 9.50 | 48,999 |
| Criticality * | Station | Mean of obj. Values | Station | Mean of |
|---|---|---|---|---|
| 1 | MT6 | 6,526,156 | MT3 | 144,727.4 |
| 2 | MT5 | 6,512,338 | MT4 | 97,765.7 |
| 3 | MT1 | 6,487,707 | MT7 | 73,188.4 |
| 4 | MT4 | 6,450,056 | MT6 | 69,439.3 |
| 5 | MT2 | 6,435,060 | MT2 | 35,622.0 |
| 6 | MT8 | 6,406,346 | MT1 | 5254.9 |
| 7 | MT3 | 6,398,988 | MT5 | 1637.9 |
| 8 | MT9 | 6,388,753 | MT8 | 1107.9 |
| 9 | MT7 | 6,350,788 | MT9 | 557.6 |
| MT | Day | ||
|---|---|---|---|
| Best Day for MT Maintenance | MT3 | Sunday | 82,516 |
| MT4 | Sunday | 60,286 | |
| MT6 | Sunday | 39,606 | |
| MT7 | Sunday | 38,637 | |
| MT2 | Saturday | 25,003 | |
| MT1 | Sunday | 2051 | |
| MT5 | Sunday | 1244 | |
| MT8 | Wednesday | 757 | |
| MT9 | Sunday | 287 | |
| Alternative Day for MT Maintenance | MT3 | Saturday | 121,566 (47.3%) |
| MT4 | Saturday | 90,138 (49.5%) | |
| MT7 | Saturday | 65,947 (70.7%) | |
| MT6 | Saturday | 60,194 (52.0%) | |
| MT2 | Sunday | 32,273 (29.1%) | |
| MT1 | Saturday | 3878 (89.1%) | |
| MT5 | Wednesday | 1466 (17.9%) | |
| MT8 | Tuesday | 805 (6.4%) | |
| MT9 | Saturday | 413 (43.9%) |
| Station ID | ViaFlowksq | ViaFlowkPr | DiffViaFlowkPr-sq | |
|---|---|---|---|---|
| MT3 Partially Fails (Sunday) | 35 | 60,854 | 132,677 | +71,823 |
| 4 | 153,684 | 195,284 | +41,600 | |
| 7 | 117,004 | 154,232 | +37,228 | |
| 18 | 65,233 | 72,231 | +6998 | |
| Total increase: +157,649 | ||||
| MT4 Partially Fails (Sunday) | 7 | 117,004 | 164,409 | +47,405 |
| 35 | 60,854 | 96,720 | +35,866 | |
| 3 | 148,726 | 183,793 | +35,067 | |
| 17 | 77,820 | 83,120 | +5300 | |
| 2 | 77,620 | 77,652 | +32 | |
| Total increase: +123,670 | ||||
| MT6 Partially Fails (Sunday) | 78 | 35,899 | 64,652 | +28,753 |
| 77 | 18,979 | 46,736 | +27,757 | |
| 76 | 15,921 | 42,084 | +26,163 | |
| 75 | 12,246 | 37,155 | +24,909 | |
| 74 | 6823 | 29,862 | +23,039 | |
| 7 | 117,004 | 119,136 | +2132 | |
| Total increase: +132,753 | ||||
| MT7 Partially Fails (Sunday) | 18 | 65,233 | 93,401 | +28,168 |
| 17 | 77,820 | 104,825 | +27,005 | |
| 74 | 6823 | 27,978 | +21,155 | |
| 75 | 12,246 | 32,512 | +20,266 | |
| 76 | 15,921 | 35,413 | +19,492 | |
| 77 | 18,979 | 37,535 | +18,556 | |
| 78 | 35,899 | 53,478 | +17,579 | |
| 4 | 153,684 | 162,970 | +9286 | |
| 3 | 148,726 | 151,928 | +3202 | |
| Total increase: +164,709 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Q.; Kim, H. Partial Node Failure in Shortest Path Network Problems. Sustainability 2019, 11, 6275. https://doi.org/10.3390/su11226275
Ye Q, Kim H. Partial Node Failure in Shortest Path Network Problems. Sustainability. 2019; 11(22):6275. https://doi.org/10.3390/su11226275
Chicago/Turabian StyleYe, Qian, and Hyun Kim. 2019. "Partial Node Failure in Shortest Path Network Problems" Sustainability 11, no. 22: 6275. https://doi.org/10.3390/su11226275
APA StyleYe, Q., & Kim, H. (2019). Partial Node Failure in Shortest Path Network Problems. Sustainability, 11(22), 6275. https://doi.org/10.3390/su11226275





