Abstract
This study presents a novel multi-attribute decision-making (MADM) model on the basis of Pythagorean fuzzy linguistic information measures. To do so, we first present a new concept of Pythagorean fuzzy linguistic sets to describe fuzziness and inconsistent information, in which the Pythagorean fuzzy linguistic values (PFLVs) are represented by the linguistic membership degree and linguistic non-membership degree. Then, we introduce two axiomatic definitions of information measures for PFLVs, including Pythagorean fuzzy linguistic entropy and the Pythagorean fuzzy linguistic similarity measure, to measure the uncertainty degree of PFLVs and the similarity degree between among PFLVs. In addition, based on the logarithmic function, we construct two new information measure formulas and verify that they satisfy the axiomatic conditions of the Pythagorean fuzzy linguistic entropy and similarity measure, respectively. We further explore the relationship between the Pythagorean fuzzy linguistic entropy and similarity measure. Finally, we present a novel Pythagorean fuzzy linguistic MADM model with the Pythagorean fuzzy linguistic entropy and similarity measure. A numerical example of selecting the most desirable sustainable blockchain product is given, and a comparison with the existing approach was performed to validate the reliability of the developed decision-making model.
1. Introduction
Multi-attribute decision-making (MADM) is an attractive and potentially useful approach in addressing complex decision situations. Due to the fuzziness in complex MADM problems, decision makers (DMs) tend to utilize fuzzy information to express their evaluation preference. Thus, fuzzy sets (FSs) [1] were first put forward by Zadeh and have been applied in various fields [2,3,4,5,6,7,8,9]. After this, various forms of uncertain fuzzy sets were generalized so as to satisfy actual demands, which included intuitionistic fuzzy sets (IFSs) [10,11,12], interval-valued intuitionistic fuzzy sets (IVIFSs) [13,14], hesitant fuzzy sets (HFSs) [15,16], and Pythagorean fuzzy sets (PFSs) [17,18]. Owing to the uncertainty and fuzziness of real-world decision-making problems, DMs are more comfortable providing their evaluation information linguistically rather than in terms of numerical values and, hence, typically lean toward linguistic term sets (LTSs) [19,20]. Considering the desirable characteristics of PFSs and LTSs, we introduce here a new concept of Pythagorean fuzzy linguistic sets (PFLSs), in which the decision-making evaluation information is described with Pythagorean fuzzy linguistic values (PFLVs), and each PFLV is represented by the degrees of linguistic membership and linguistic non-membership. It is obvious that PFLSs are more effective than PFSs in capturing the uncertainty and fuzziness in complex MADM problems.
Information measurement is an important research issue in MADM theory, and includes entropy, the similarity measure, and their transformation relationships [21,22]. Entropy is mainly used to determine the degree of uncertainty of objects, and the similarity measure is mainly utilized to determine the degree of similarity among objects. Based on the probability measures of fuzzy events, Zadeh [23] proposed fuzzy entropy to derive the uncertainty of assessment information. After that, De Luca and Termini [24] initially introduced some axiomatic definitions of entropy for FSs, and then discussed some mathematical properties of entropy. With the help of the distance between the FS and its negation FS, Yager [25] proposed several entropy measures to derive the fuzziness of FSs. By using the distances between the fuzzy message and its nearest and farthest non-fuzzy neighbors, Kosko [26] defined a novel non-probabilistic fuzzy entropy measure. Under the intuitionistic fuzzy information environment, Szmidt and Kacprzyk [27] developed an entropy measure for IFSs. Song et al. [28] investigated a new intuitionistic fuzzy similarity measure by utilizing the direct operation on the membership and non-membership functions of intuitionistic fuzzy values. For intuitionistic fuzzy MADM problems, Wu and Zhang [29] presented an intuitionistic fuzzy weighted entropy and developed a programming approach to derive the optimal attribute weights. Inspired by this intuitionistic fuzzy weighted entropy, Jin et al. [30] investigated an interval-valued intuitionistic fuzzy continuous weighted entropy to measure the degree of uncertainty for IVIFSs. Xu and Xia [31] defined the entropy and similarity measure for HFSs, which was followed by the construction of the interchangeable method. Owing to the existing information measures for HFSs having drawbacks and limitations, Hu et al. [32] designed several new effective and reliable distance, similarity, and entropy measures for HFSs. For MADM problems with interval-valued HFSs, Jin et al. [33] introduced three axiomatic definitions of interval-valued hesitant fuzzy information measures, and then established several formulas with a continuous ordered weighted averaging operator. Farhadinia [34] designed a linguistic term fuzzy entropy to calculate the attribute weights. Based on the intuitive geometric explanation, Wu and Mendel [35] developed the Jaccard similarity measure for closed general type-2 fuzzy sets. Majumdar and Samant [36] proposed the axiomatic conditions of single-valued neutrosophic entropy. In order to overcome the drawbacks of single-valued neutrosophic entropy in Majumdar and Samant [36], Jin et al. [37] constructed a novel single-valued neutrosophic entropy and similarity measure, and then investigated a new MADM method. In order to measure the vagueness and uncertainty of PFSs and interval-valued PFSs, Xue et al. [38] introduced the definitions of Pythagorean fuzzy entropy and interval-valued Pythagorean fuzzy entropy. Under the interval-valued Pythagorean fuzzy information environment, Peng and Li [39] presented new interval-valued Pythagorean fuzzy information measures, including entropy, distance, and similarity measures, and then applied these information measures to derive the ranking of alternatives. Zeng et al. [40] proposed a series of Pythagorean fuzzy similarity measures, and then established a Pythagorean fuzzy MADM method.
From the above analysis, it can be seen that entropy and similarity measures are useful tools for addressing the fuzziness and uncertainty characteristics of complex decision-making problems. More and more MADM methods have been constructed using the entropy and similarity measures. Under the Pythagorean fuzzy linguistic information environment, studying the axiomatic definitions of Pythagorean fuzzy linguistic entropy and similarity measures, constructing reliable information measurement formulas, and exploring the relationship of Pythagorean fuzzy linguistic information measures are significant and challenging issues. Although there exist reasonable methods to address Pythagorean fuzzy or Pythagorean fuzzy linguistic MADM problems, these methods have limitations. To this end, by considering the degrees of membership, non-membership, and hesitation, Wei and Wei [41] proposed a weighted similarity measure with a cosine function, and then developed a Pythagorean fuzzy MADM method. However, with the method developed by Wei and Wei [41], we use the Pythagorean fuzzy weighted similarity measure to calculate the weighted similarity degrees, in which some original decision-making information is lost. Thus, the decision-making results derived by the method of Wei and Wei [41] may be unreliable. Therefore, it is reasonable and necessary to propose a new method for generating decision-making results directly. Based on the weighted Pythagorean fuzzy Bonferroni mean (WPFBM) operator, Liang et al. [42] presented a new MADM method through which the ranking values of the alternatives could be obtained. However, the method by Liang et al. [42] cannot deal with MADM problems in which the information of attribute weights is completely unknown. Under the linguistic Pythagorean fuzzy information environment, Garg [43] developed a novel decision-making method on the basis of the linguistic Pythagorean fuzzy weighted average operator. It is known that the differences among these attributes and the type of attributes are different, thus the process of normalization for the decision-making matrix is necessary. However, Garg’s [43] method does not normalize the initial Pythagorean fuzzy linguistic decision-making matrix, and it directly uses the linguistic Pythagorean fuzzy weighted average operator [43] to generate the decision-making results (see details given in Section 5). Therefore, in this paper, we investigated a Pythagorean fuzzy linguistic MADM model to directly use the DM’s original evaluation information, in which the new Pythagorean fuzzy linguistic entropy and similarity measures are presented, and the DM’s original evaluation information can be preserved as much as possible.
Consequently, in order to overcome these limitations, the following research issues were studied:
- A new concept of PFLSs is introduced, which we believe to be more reasonable and convenient to express uncertain evaluation information;
- Two axiomatic definitions of information measures for PFLVs are presented;
- With the help of logarithmic functions, two new information measure formulas were constructed;
- A novel Pythagorean fuzzy linguistic multi-attribute decision-making model was developed to derive reliable ranking of the alternatives.
The rest of this paper is organized as follows. Section 2 reviews some basic concepts of LTSs and PFSs, and then introduces the new concept of PFLSs. In Section 3, two axiomatic definitions of information measures for PFLV are presented, and two new information measure formulas are constructed. We also explore the relationship between the Pythagorean fuzzy linguistic entropy and similarity measures in Section 3. Section 4 investigates a novel MADM model with Pythagorean fuzzy linguistic information measures. In Section 5, a numerical example is given to illustrate the application of the proposed decision-making model. Conclusions and further research are presented in the last section.
2. Preliminaries
In this section, the main concepts related to LTSs and PFSs are reviewed, and then the new concept of Pythagorean fuzzy linguistic sets is presented.
2.1. LTSs and PTSs
As a symbolic linguistic computing model, the concept of a virtual linguistic model is usually used as a linguistic computing model. Suppose that is a discrete LTS, where is a linguistic variable in . The LTS has the following characteristics [19,20]: (1) if , then ; and (2) the negation operator .
Example 1.
If the DM evaluates a supplier in a supply chain, a set of nine terms S can be expressed as follows:
to preserve the decision-making information, Xu [20] generalized the notion of a discrete LTS to a continuous one, , where is a sufficiently large positive integer. It is readily seen that these linguistic terms themselves map into the respective indices: , such that . Obviously, there exists an inverse function , such that .
Definition 1.
Reference [17] assumes that is a universe set, a PFS on is characterized by the membership function and the non-membership function , where , and , for . is called the hesitant degree of .
2.2. Pythagorean Fuzzy Linguistic Sets (PFLSs)
Definition 2.
Assume thatis a universe set,is a continuous LTS, and PFLSovercan be described as:
whereandrepresent the linguistic membership degree and linguistic non-membership degree of the elementto, respectively. For each,, and.
For convenience, we call a Pythagorean fuzzy linguistic value (PFLV). The complement of is denoted by . Let be the set of all the PFLVs.
3. The Pythagorean Fuzzy Linguistic Entropy and Pythagorean Fuzzy Linguistic Similarity Measure
This section first introduces two axiomatic definitions of Pythagorean fuzzy linguistic information measures, including the Pythagorean fuzzy linguistic entropy and Pythagorean fuzzy linguistic similarity measure, and then two new information measure formulas were constructed. We further explore the relationship between the Pythagorean fuzzy linguistic entropy and similarity measure.
3.1. Pythagorean Fuzzy Linguistic Entropy
Definition 3.
Assume thatis a PFLV with, if a mappingsatisfies the following four axiomatic conditions:
- (E1)
- if and only if or ;
- (E2)
- if and only if ;
- (E3)
- ;
- (E4)
- , if and when or and when ;
then, is called a Pythagorean fuzzy linguistic entropy on the set of .
Assume that is a PFLV, we constructed the following information measure formula for by utilizing the logarithmic function:
Theorem 1.
Letbe a PFLV with, then the information measure formula, constructed by Equation (2), is a Pythagorean fuzzy linguistic entropy of.
Proof.
According to Definition 3, we need to prove that the information measure formula meets the four axiomatic conditions in Definition 3.
As is a PFLV, then and , thus . Now, we first establish a continuous function on , as follows:
Thus, . It is obvious that when , when . Therefore, if , then is an increasing function with respect to ; if , then is a decreasing function with respect to . Furthermore, one can get that if and only if , if and only if . The graphical representation of is shown in Figure 1.
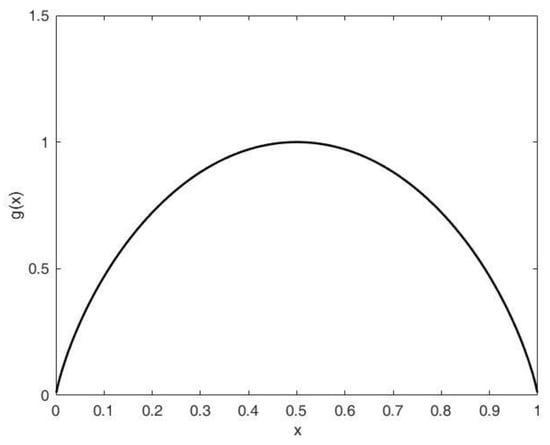
Figure 1.
The graphical representation of .
(E1) If , then we have or .
According to the above analysis and Equation (3), one can obtain that .
Suppose that ; that is, . From the above analysis, we have if and only if , then indicates that or :
While , thus or . Therefore, or , i.e., or .
(E2) By using the above analysis of function on [0,1], if :
(E3) Because , then:
(E4) Suppose that and when , we can derive that
and .
It follows that:
In addition, as , then , and one can obtain that:
Owing to being an increasing function with respect to when , thus:
that is, .
Similarly, if and when , one can get that .
Therefore, the proof of Theorem 1 is completed. ☐
3.2. Pythagorean Fuzzy Linguistic Similarity Measure
In order to measure the similarity degree among PFLVs, this subsection introduces the concept of the Pythagorean fuzzy linguistic similarity measure, and then a new kind of similarity measure formula was designed based on the logarithmic function.
Definition 4.
Assume thatandare two PFLVs, if a mappingsatisfies the following four axiomatic conditions:
- (S1)
- if and only if or ;
- (S2)
- if and only if ;
- (S3)
- ;
- (S4)
- if and or and ;
then, S is called a Pythagorean fuzzy linguistic similarity measure of .
Assume that and are two PFLVs, we constructed the following information measure formula by utilizing the logarithmic function:
Theorem 2.
Letandbe two PFLVs, then the information measure formula, constructed by Equation (10), is a Pythagorean fuzzy linguistic similarity measure of.
Proof.
As and are two PFLVs, then , for each . Thus, according to the proof of Theorem 1, Equation (10) can be rewritten as .
(S1) If or , then:
Thus, , and we have .
Assume that . Because , then for each , we have ; therefore, indicates that . According to the analysis of function on [0,1] in Theorem 1, we have or , for , and then or .
(S2) Owing to , for each , then ; therefore,
(S3)
(S4) If and , then and , thus:
As is an increasing function of , is a decreasing function of , and one can obtain that:
then we have . Similarly, one can prove that .
With the same reasoning, if and , one can get . Therefore, the proof of Theorem 2 is completed. ☐
3.3. Relationship Between the Pythagorean Fuzzy Linguistic Entropy and Similarity Measure
In this subsection, we explore the interchangeable method between the Pythagorean fuzzy linguistic entropy and similarity measure.
Theorem 3.
Assume thatis a PFLV with, then the Pythagorean fuzzy linguistic similarity measure betweenandis the Pythagorean fuzzy linguistic entropy of; that is,.
Proof.
Now, we prove that satisfies the four axiomatic conditions in Definition 3.
- (E1)
- or , i.e.,
- (E2)
- .
- (E3)
- .
- (E4)
- Let be a PFLV, if and when , then
Thus , .
Utilizing the axiomatic condition (S4) in Definition 2, one can obtain that , that is .
Similarly, if and when , one can obtain that . The proof of Theorem 3 is completed.
4. The MADM Model with Pythagorean Fuzzy Linguistic Information Measures
In this section, we investigate a new MADM model with Pythagorean fuzzy linguistic information measures to rank the alternatives and select the desirable alternative. The main steps of the proposed MADM model are as follows:
4.1. Step 1: Constructing the Initial Pythagorean Fuzzy Linguistic Decision-Making Matrix
Suppose that is a given set of alternatives, is an attribute set with the weight vector , satisfying and . Owing to the increasing complexity of the real decision-making environment, the information about attribute weights is completely unknown. Furthermore, in order to transform and express the evaluation information of experts comprehensively, we utilize the PFLV with to depict the evaluation information, where and are the linguistic membership degree and linguistic non-membership degree of alternative under the attribute , respectively. Based on this, a Pythagorean fuzzy linguistic decision-making matrix was constructed.
4.2. Step 2: Normalization of the Pythagorean Fuzzy Linguistic Decision-Making Matrix
Owing to there being a difference among these attributes and the type of attributes, we needed to normalize the initial Pythagorean fuzzy linguistic decision-making matrix . Generally, the alternative’s attributes can be divided into two types, including the benefit attribute and cost attribute. Therefore, we utilized the following transformation method to derive the normalized Pythagorean fuzzy linguistic decision-making matrix , in which all the attributes were benefit attributes:
4.3. Step 3: Determining the Attribute Weights with Pythagorean Fuzzy Linguistic Entropy
As we all know, information entropy is an effective method to measure information uncertainty. The greater the information entropy, the higher the degree of ambiguity; the smaller the information entropy, the higher the deterministic information. In Pythagorean fuzzy linguistic MADM problems, if the Pythagorean fuzzy linguistic entropy of all the attribute values under an attribute is smaller, it reflects that this attribute provides more valuable information for DMs in the process of decision-making, and the attribute weight of this attribute should be given a larger attribute weight. If the Pythagorean fuzzy linguistic entropy of all the attribute values under an attribute is larger, it means that this attribute can only provide less valuable information for DMs in the process of decision-making, thus the attribute weight of this attribute should be smaller. Therefore, the attribute weight is inversely proportional to the total Pythagorean fuzzy linguistic entropy under this attribute. As the information about attribute weights is completely unknown, we designed the following entropy-based method to calculate attribute weights:
where and:
4.4. Step 4: Obtaining the Weighted Similarity Degree for an Alternative with the Pythagorean Fuzzy Linguistic Similarity Measure
Let be the ideal alternative, be the anti-ideal alternative, where and indicate the ideal PFLV and anti-ideal PFLV, respectively. First, by using the proposed Pythagorean fuzzy linguistic similarity measure (i.e., Equation (10)), one can obtain the similarity degree between the evaluation information of alternative under the attribute and the ideal PFLV and the similarity degree between evaluation information and the ideal PFLV . Then, based on the attribute weight vector determined by Equation (14), we utilized the following methods to calculate the weighted similarity degrees and :
where and indicate the weighted similarity degrees of alternative with the ideal alternative and anti-ideal alternative .
4.5. Step 5: Deriving the Closeness Degrees of Alternatives
It is obvious that the greater the weighted similarity degree between alternative and ideal alternative , the smaller the weighted similarity degree between alternative and anti-ideal alternative , then the better comprehensive performance of the alternative . Therefore, the closeness degree of the alternative can be determined as follows:
4.6. Step 6: Ranking the Alternatives
According to the obtained closeness degrees , we can sort in descending order, and then the ranking order of the alternatives can be determined, which is followed by the selection of a desirable alternative.
5. Illustrative Example and Comparative Analysis
In the following, an applied case of a sustainable blockchain product assessment is given to illustrate the effect of the developed decision-making model, then we discuss the comparative analysis between the proposed model and existing method.
5.1. Application to Sustainable Blockchain Product Assessment
Blockchain is the underlying technology of Bitcoin [44]. Owing to the safety and convenience of blockchain, it has gradually attracted the attention of banks and the financial industry [45,46,47,48]. Blockchain is divided into three main categories, including public blockchain, joint blockchain, and private blockchain. Blockchain management is an important guarantee for the development of blockchain. Evaluating blockchain products is a key point for blockchain management research.
Suppose that there are five possible sustainable blockchain products to be evaluated. In order to evaluate and obtain the most desirable sustainable blockchain products, the expert evaluates the above five sustainable blockchain products by considering four attributes, including : the cost of products; : the lifetime of products; : the performance of products; and : the quality of after-sales service, while the attribute weight vector is completely unknown. The expert utilizes PFLV with to express the evaluation information, and then a Pythagorean fuzzy linguistic decision-making matrix is constructed as follows:
In the following, we utilized the developed Pythagorean fuzzy linguistic MADM model to rank the above five sustainable blockchain products and explore the most desirable sustainable blockchain product. The detailed steps are as follows.
5.1.1. Step 1
As is the cost attribute, we utilized Equation (13) to obtain the following normalized Pythagorean fuzzy linguistic decision-making matrix :
5.1.2. Step 2
By using Equations (14) and (15), one can obtain the attribute weights as follows:
5.1.3. Step 3
Applying Equations (10), (16), and (17), we obtained the weighted similarity degrees and of sustainable blockchain product :
5.1.4. Step 4
According to Equation (18), we calculated the closeness degrees of sustainable blockchain products :
5.1.5. Step 5
It was obvious that , then could determine that the ranking of the sustainable blockchain products was , and the most desirable sustainable blockchain product was .
5.2. Comparative Analysis and Discussion
In the following, we compare our proposed decision-making model with previous methods in the literature to verify the effectiveness of the developed MADM model, and then we explore the advantages of the developed model.
By considering the degrees of membership, non-membership, and hesitation, Wei and Wei [41] proposed a weighted similarity measure with a cosine function and then developed a Pythagorean fuzzy MADM method. For the same Pythagorean fuzzy linguistic decision-making matrix , we used the method in Wei and Wei [41] to derive the most desirable sustainable blockchain product.
5.2.1. Step 1
By using the decision-making matrix and Equation (14), we determined the normalized Pythagorean fuzzy linguistic decision-making matrix and attribute weight vector (See Section 5.1.1 and Section 5.1.2).
5.2.2. Step 2
By using the function , we could transform the normalized Pythagorean fuzzy linguistic decision-making matrix into the Pythagorean fuzzy decision-making matrix (where and ):
5.2.3. Step 3
Applying the following Pythagorean fuzzy cosine weighted similarity measures [41] to compute the weighted similarity degrees of the sustainable blockchain product xi:
Then we used Equation (18) to derive the closeness degrees of sustainable blockchain products as follows:
5.2.4. Step 4
It can be seen that . Therefore, the five sustainable blockchain products were ranked as: , and the most desirable sustainable blockchain product was x5.
5.3. The decision-making process with the method in Liang et al.
Liang et al. [42], based on the weighted Pythagorean fuzzy Bonferroni mean (WPFBM) operator, presented a new MADM method, following which the ranking values of the alternatives could be obtained. By using this method [42], the following steps are given to obtain the most desirable sustainable blockchain product:
5.3.1. Steps 1’ and 2’
See Section 5.1.1 and Section 5.1.2.
5.3.2. Step 3’
By using the following WPFBM operator [39] (let ):
To aggregate all into an overall Pythagorean fuzzy value of the sustainable blockchain products as follows: , .
5.3.3. Step 4’
Applying Definition 3 [42], one can obtain the following score values of the sustainable blockchain products :
5.3.4. Step 5’
Because , then we had , and the most desirable sustainable blockchain product was x5.
5.4. The decision-making process with the method in Garg
Under the linguistic Pythagorean fuzzy information environment, Garg [43] developed a novel decision-making method on the basis of the linguistic Pythagorean fuzzy weighted average operator. By using the method by Garg [43], the following steps are used to obtain the desirable sustainable blockchain product:
First, according to Section 5.1, one can construct the linguistic Pythagorean fuzzy matrix .
Owing to , then we can derive the same attribute weights with Step 2 by utilizing Equations (14) and (15):
Then, based on the following linguistic Pythagorean fuzzy weighted average operator [43]:
To fuse all the linguistic Pythagorean fuzzy values into the collective linguistic Pythagorean fuzzy value for each sustainable blockchain product :
Furthermore, by using Definition 3.2 [43], we derive the score functions of as follows:
Finally, as , and then the ranking of the sustainable blockchain products is . Therefore, the most desirable sustainable blockchain product is .
According to above analysis, the ranking results and the most desirable sustainable blockchain product can be summarized in Table 1.

Table 1.
The decision-making results by different methods.
From the above numerical example and comparison with other methods, the proposed MADM model with Pythagorean fuzzy linguistic information measures had the following characteristics:
(1) Because the decision-making methods in Wei and Wei [41], Liang et al. [42], and Garg [43] cannot deal with MADM problems in which the information of attribute weights is completely unknown, the application scope of the proposed MADM model is wider than the decision-making methods in those papers.
(2) Pythagorean fuzzy linguistic sets are a useful tool to depict the uncertainty and fuzziness of elements. Hence, the PFLSs are more reasonable and convenient as a technique to provide uncertain information. However, although there are many decision-making methods in the existing literature [41,42], these methods cannot address situations in which the input decision-making information takes the form of PFLVs. Our model can handle decision-making problems with PFLVs.
(3) Although the proposed MADM model generates the same decision-making result as the method by Wei and Wei [41], our model and the method in Wei and Wei [41] generate different ranking results among the sustainable blockchain products. In the MADM process, the developed model directly applies the original information of the decision-making matrix and derives the weighted similarity degrees of sustainable blockchain products, which can preserve the original information of the expert. However, with the method by Wei and Wei [41], Equations (19) and (20) are used to calculate the weighted similarity degrees of sustainable blockchain products, and some original decision-making information is lost. Therefore, our model is more reliable and scientific than the method by Wei and Wei [38].
(4) It can be observed that our model and the method in Garg [43] derive different ranking results for the sustainable blockchain products. Owing to differences existing among these attributes and the type of attributes being different, the process of normalization for the decision-making matrix is necessary. However, the method by Garg [43] does not normalize the initial Pythagorean fuzzy linguistic decision-making matrix, and it directly uses the linguistic Pythagorean fuzzy weighted average operator [43] to fuse the initial Pythagorean fuzzy linguistic information into collective linguistic Pythagorean fuzzy values. In contrast, with our MADM model, we first normalize the initial Pythagorean fuzzy linguistic decision-making matrix, then apply the Pythagorean fuzzy linguistic information measures to derive a decision-making result. In addition, according to the normalized Pythagorean fuzzy linguistic decision-making matrix , we have , and , which indicates that the sustainable blockchain product is better than , i.e., . Thus, our model can produce the correct ranking orders of these sustainable blockchain products. Therefore, the decision-making result derived by our model is more accurate.
6. Conclusions
This paper focused on the MADM model with the Pythagorean fuzzy linguistic entropy and similarity measure. First, based on the LTSs and PFSs, we proposed a new notion of Pythagorean fuzzy linguistic sets. Then, we presented the two axiomatic definitions of information measures for PFLVs, including Pythagorean fuzzy linguistic entropy and the Pythagorean fuzzy linguistic similarity measure. With the help of the logarithmic function, two new information measurement formulas were constructed. We further explored the inter-relationship between the Pythagorean fuzzy linguistic entropy and similarity measure. Finally, we developed a novel Pythagorean fuzzy linguistic MADM model. A numerical example of a sustainable blockchain product assessment was given to illustrate the reliability of the developed MADM model.
The main advantages of the proposed MADM model with Pythagorean fuzzy linguistic information are summarized as follows: (1) a new notion of PFLSs was introduced, in which the evaluation information is represented by a linguistic membership degree and a linguistic non-membership degree; (2) the Pythagorean fuzzy linguistic entropy and Pythagorean fuzzy linguistic similarity measure were investigated to measure the uncertainty degree of PFLV and similarity degree between PFLVs; (3) two new information measurement formulas were constructed to preserve DMs’ original decision-making information to the greatest extent possible; and (4) the developed MADM model can derive a reliable ranking of alternatives and extend the application scope of the decision-making model.
However, this paper did not discuss the situation in which some experts decide to not provide their assessment information; that is, how to construct a decision-making method with incomplete Pythagorean fuzzy linguistic information in decision-making problems. Therefore, in the future, we will focus on extending the proposed model for incomplete Pythagorean fuzzy linguistic multi-attribute decision-making problems, applying these models to solve practical applications in other areas, including knowledge recommendations, information fusion systems, and cooperative decision-making.
Author Contributions
All of the authors contributed to this research. F.J., L.P. and H.C. conceived the study and were responsible for the design and development of the data analysis. F.J. and H.C. were responsible for data collection and analysis. L.P., R.L. and J.L. were responsible for data interpretation. F.J. wrote the first draft of the article.
Funding
This research was funded by the National Natural Science Foundation of China (No. 71901001, No. 71871001, No. 11901150, No. 71771001, No. 71701001, No. 71972001, No. 71972002), the Construction Fund for Scientific Research Conditions of Introducing Talents in Anhui University (No. S020118002/085), the Natural Science Foundation for Distinguished Young Scholars of Anhui Province (No. 1908085J03), the Key Research Project of Humanities and Social Sciences in Colleges and Universities of Anhui Province (SK2019A0013).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Wu, N.; Xu, Y.; Kilgour, D.M. Water allocation analysis of the Zhanghe River basin using the graph model for conflict resolution with incomplete fuzzy preferences. Sustainability 2019, 11, 1099. [Google Scholar] [CrossRef]
- Li, G.X.; Kou, G.; Peng, Y. A group decision making model for integrating heterogeneous information. Ieee Trans. Syst. Man Cybern. Syst. 2018, 48, 982–992. [Google Scholar] [CrossRef]
- Kou, G.; Peng, Y.; Wang, G.X. Evaluation of clustering algorithms for financial risk analysis using MCDM methods. Inf. Sci. 2014, 275, 1–12. [Google Scholar] [CrossRef]
- Zhang, H.H.; Kou, G.; Peng, Y. Soft consensus cost models for group decision making and economic interpretations. Eur. J. Oper. Res. 2019, 277, 964–980. [Google Scholar] [CrossRef]
- Chao, X.; Kou, G.; Peng, Y.; Alsaadi, F.E. Behavior monitoring methods for trade-based money laundering integrating macro and micro prudential regulation: A case from China. Technol. Econ. Dev. Econ. 2019, 25, 1081–1096. [Google Scholar] [CrossRef]
- Kou, G.; Ergu, D.; Lin, C.S.; Chen, Y. Pairwise comparison matrix in multiple criteria decision making. Technol. Econ. Dev. Econ. 2016, 22, 738–765. [Google Scholar] [CrossRef]
- Wang, C.N.; Le, A.P. Application of multi-criteria decision-making model and GM (1,1) theory for evaluating efficiency of FDI on economic growth: A case study in developing countries. Sustainability 2019, 11, 2389. [Google Scholar] [CrossRef]
- Jin, F.F.; Ni, Z.W.; Chen, H.Y.; Li, Y.P. Approaches to group decision making with intuitionistic fuzzy preference relations based on multiplicative consistency. Knowl. -Based Syst. 2016, 97, 48–59. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Qu, G.H.; Qu, W.H.; Wang, J.M.; Zhou, H.S.; Liu, Z.L. Factorial-quality scalar and an extension of ELECTRE in intuitionistic fuzzy sets. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 183–207. [Google Scholar] [CrossRef]
- Luo, M.X.; Zhao, R.R. A distance measure between intuitionistic fuzzy sets and its application in medical diagnosis. Artif. Intell. Med. 2018, 89, 34–39. [Google Scholar] [CrossRef] [PubMed]
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P. Interval-valued intuitionistic fuzzy WASPAS method: Application in reservoir flood control management policy. Group Decis. Negot. 2018, 27, 1047–1078. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Wen, M.M.; Zhao, H.; Xu, Z.S. Hesitant fuzzy Lukasiewicz implication operation and its application to alternatives’ sorting and clustering analysis. Soft Comput. 2019, 23, 393–405. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Xing, Y.P.; Zhang, R.T.; Wang, J.; Zhu, X.M. Some new Pythagorean fuzzy Choquet-Frank aggregation operators for multi-attribute decision making. Int. J. Intell. Syst. 2018, 33, 2189–2215. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 99–249. [Google Scholar] [CrossRef]
- Xu, Z.S. Deviation measures of linguistic preference relations in group decision making. Omega 2005, 33, 249–254. [Google Scholar] [CrossRef]
- Bai, X.; Wang, Y.M.; Jin, J.L.; Qi, X.M.; Wu, C.G. Precondition cloud and maximum entropy principle coupling model-based approach for the comprehensive assessment of drought risk. Sustainability 2018, 10, 3236. [Google Scholar] [CrossRef]
- Kou, G.; Lu, Y.Q.; Peng, Y.; Shi, Y. Evaluation of classification algorithms using MCDM and rank correlation. Int. J. Inf. Technol. Decis. Mak. 2012, 11, 197–225. [Google Scholar] [CrossRef]
- Zadeh, L.A. Probability measures of fuzzy events. J. Math. Anal. Appl. 1968, 23, 421–427. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Yager, R.R. On the measure of fuzziness and negation Part I: Membership in the unit interval. Int. J. Gen. Syst. 1979, 5, 221–229. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy entropy and conditioning. Inf. Sci. 1986, 40, 165–174. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Song, Y.F.; Wang, X.D.; Quan, W.; Huang, W.L. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2019, 23, 1985–1998. [Google Scholar] [CrossRef]
- Wu, J.Z.; Zhang, Q. Multicriteria decision making method based on intuitionistic fuzzy weighted entropy. Expert Syst. Appl. 2011, 38, 916–922. [Google Scholar] [CrossRef]
- Jin, F.F.; Pei, L.D.; Chen, H.Y.; Zhou, L.G. Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making. Knowl. -Based Syst. 2014, 59, 132–141. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M.M. Hesitant fuzzy entropy and cross-entropy and their use in multi-attribute decision-making. International Journal of Intelligent Systems 2012, 27, 799–822. [Google Scholar] [CrossRef]
- Hu, J.H.; Zhang, X.L.; Chen, X.H.; Liu, Y.M. Hesitant fuzzy information measures and their applications in multi-criteria decision making. Int. J. Syst. Sci. 2015, 47, 1–15. [Google Scholar] [CrossRef]
- Jin, F.F.; Ni, Z.W.; Chen, H.Y.; Li, Y.P.; Zhou, L.G. Multiple attribute group decision making based on interval-valued hesitant fuzzy information measures. Comput. Ind. Eng. 2016, 10, 103–115. [Google Scholar] [CrossRef]
- Farhadinia, B. Determination of entropy measures for the ordinal scale-based linguistic models. Inf. Sci. 2016, 369, 63–79. [Google Scholar] [CrossRef]
- Wu, D.R.; Mendel, J.M. Similarity measures for closed general type-2 fuzzy sets: Overview, comparisons, and a geometric approach. Ieee Trans. Fuzzy Syst. 2019, 27, 515–526. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar]
- Jin, F.F.; Ni, Z.W.; Chen, H.Y.; Langari, R.; Zhu, X.H.; Yuan, H.J. Single-valued neutrosophic entropy and similarity measures to solve supplier selection problems. J. Intell. Fuzzy Syst. 2018, 35, 6513–6523. [Google Scholar] [CrossRef]
- Xue, W.T.; Xu, Z.S.; Zhang, X.L.; Tian, X.L. Pythagorean fuzzy LINMAP method based on the entropy theory for railway project investment decision making. Int. J. Intell. Syst. 2018, 33, 93–125. [Google Scholar] [CrossRef]
- Peng, X.D.; Li, W.Q. Algorithms for interval-valued Pythagorean fuzzy sets in emergency decision making based on multiparametric similarity measures and WDBA. IEEE Access 2019, 7, 7419–7441. [Google Scholar] [CrossRef]
- Zeng, W.Y.; Li, D.Q.; Yin, Q. Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int. J. Intell. Syst. 2018, 33, 2236–2254. [Google Scholar] [CrossRef]
- Wei, G.W.; Wei, Y. Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. Int. J. Intell. Syst. 2018, 33, 634–652. [Google Scholar] [CrossRef]
- Liang, D.C.; Zhang, Y.R.J.; Xu, Z.S.; Darko, A.P. Pythagorean fuzzy Bonferroni mean aggregation operator and its accelerative calculating algorithm with the multithreading. Int. J. Intell. Syst. 2018, 33, 615–633. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Xu, M.; Chen, X.T.; Kou, G. A systematic review of blockchain. Financ. Innov. 2019, 5, 27. [Google Scholar] [CrossRef]
- Nasir, M.A.; Huynh, T.L.D.; Nguyen, S.P.; Duong, D. Forecasting cryptocurrency returns and volume using search engines. Financ. Innov. 2019, 5, 2. [Google Scholar] [CrossRef]
- Kumar, A.S.; Ajaz, T. Co-movement in crypto-currency markets: evidences from wavelet analysis. Financ. Innov. 2019, 5, 33. [Google Scholar] [CrossRef]
- Khraisha, T.; Arthur, K. Can we have a general theory of financial innovation processes? A conceptual review. Financ. Innov. 2018, 4, 4. [Google Scholar] [CrossRef]
- Kou, G.; Chao, X.; Peng, Y.; Alsaadi, F.E.; Herrera-Viedma, E. Machine learning methods for systemic risk analysis in financial sectors. Technol. Econ. Dev. Econ. 2019, 25, 716–742. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).