Next Article in Journal
Effects of Transformational and Instructional Leadership on Organizational Silence and Attractiveness and Their Importance for the Sustainability of Educational Institutions
Next Article in Special Issue
Research on Field Reconstruction and Community Design of Living Settlements—An Example of Repairing a Fish Stove in the Hua-Zhai Settlement on Wang-An Island, Taiwan
Previous Article in Journal
Factors Influencing Matching of Ride-Hailing Service Using Machine Learning Method
Previous Article in Special Issue
Climate Change Challenges to Existing Cultural Heritage Policy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 11
Issue 20
10.3390/su11205616
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Use of GIS Tools in Sustainable Heritage Management—The Importance of Data Generalization in Spatial Modeling

by
Mateusz Ciski
*,
Krzysztof Rząsa
and
Marek Ogryzek
The Faculty of Geodesy, Geospatial and Civil Engineering, Institute of Geography and Land Management, University of Warmia and Mazury in Olsztyn, Prawocheńskiego Street 15, 10-720 Olsztyn, Poland
*
Author to whom correspondence should be addressed.
Sustainability 2019, 11(20), 5616; https://doi.org/10.3390/su11205616
Submission received: 2 August 2019 / Revised: 3 October 2019 / Accepted: 8 October 2019 / Published: 12 October 2019
(This article belongs to the Special Issue Sustainable Heritage Management)
Browse Figures
Versions Notes

Abstract

:
Cultural heritage is a very important element affecting the sustainable development. To analyze the various forms of spatial management inscribed into sustainable development, information on the location of objects and their concentration at specific areas is necessary. The main goal of the article was to show the possibility of using various GIS tools in modeling the distribution of historical objects. For spatial analysis, it is optimal to use the point location of objects. Often, however, it is extremely difficult, laborious, expensive, and sometimes impossible to obtain. Thus, various map content generalizations were analyzed in the article; the main goal was to find the level for which the data with an acceptable loss of accuracy can be generalized. Such analyses can be extremely useful in sustainable heritage management. Article also shows how cultural heritage fits into the sustainable heritage management. The research included non-movable monuments in Poland. The obtained results showed the universality of this type of research both in the thematic sense (can be used for various types of objects) and spatial sense (can be performed locally, at the country level, or even at the continental level).

1. Introduction

Sustainable development is nowadays one of the main components used in spatial development [1,2,3]. It is considered a Constitutional Principle of the Republic of Poland, as well as in another European countries. The definition of sustainable development can be found in Polish legislation—it is defined in the Environmental Protection Act [4] as the socio-economic development integrating political, economic, and social actions, balanced with environmental protection and a permanence of basic natural processes, in order to ensure the possibility of satisfying the basic needs of communities or individual citizens in both the present and future generations. In The Brundtland Report “Our Common Future” [5] sustainable development is defined as “development that meets the needs of the present without compromising the ability of future generations to meet their own needs”. The report highlighted three fundamental components of sustainable development: environmental protection, economic growth, and social equity. According to Pearce and Turner [6], sustainable development is associated with maximizing the benefits of economic development, in connection with protecting the quality and usability of natural resources. Such economic development must not only mean an increase in income per capita, but also the comprehensive improvement of other social aspects. Culture, as the basis of social life, is considered to be one of the four pillars of sustainable development [7,8,9,10]. Culture can be both the goal of development of a given society as well as the method of that development, but above all it is the development regulator [11]. Cultural heritage is one of the main elements of such described culture and it is understood much more broadly than just in the field of the protection of monuments, it also consists of: local traditions and customs, cultural affiliation or the sources of non-material values [12,13,14]. A greater sense of cultural identity can also contribute to the further development of social capital, because individuals and communities with a stronger sense of place are more actively involved in social matters. People living in places with a higher concentration of significant historical areas tend to have a stronger sense of place and/or increased social capital [15]. Cultural heritage is traditionally regarded as a non-economic factor of spatial development. However, treated as a resource and properly managed, it can be transformed into capital that can play an important role in the sustainable development strategies, both at the local and national level. The term “cultural heritage” covers a broad spectrum of meanings that are not obvious and can be ambiguous [16]. Cultural heritage is important as a source of remembrance and inspiration, and at the same time contributes to national and local identity, which is essential for sense of place and social cohesion [17]. Various studies have shown the influence of cultural heritage as an element of sustainable development on spatial planning [18,19], or tourism development [20,21,22].
To properly manage cultural heritage within sustainable development, regardless of the specific goal, knowledge of the location of objects constituting a material element of cultural heritage is necessary. In this article, the starting point for the conducted research and analyses were non-movable monuments in Poland. The legal basis for the protection of monuments in Poland is the Act of 23 July 2003 on the protection of monument and the care of monuments [23]. According to Article 3 of the above-mentioned Act, a non-movable monument is a real estate, its part or a complex of real estate, which is the work of humankind or is related to its activity, and is a testimony to a past era or event; whose protection is in the public interest because of its historical, artistic or scientific value. Article 6 of the Act indicates that non-movable monuments may include: cultural landscapes, urban and rural systems, building units, works of architecture and construction, works of defense construction; technical objects; cemeteries; parks, gardens, and other forms of designed greenery; as well as places commemorating historical events or the activities of remarkable characters or institutions. Non-movable monuments are registered by entry in “the register of objects of cultural heritage” (pol. rejestr zabytków), kept by the Voivodeship Conservators of Monuments. Voivodeship registers of objects of cultural heritage currently contain approx. 85 thousand entries on non-movable monuments, diversified in terms of type. A non-movable monument can be entered into the register on the basis of: an ex-officio decision issued by the Voivodeship Conservator of Monuments, or at the request of the owner of the non-movable monument or perpetual usufructuary of the land on which the non-movable monument is located. In the conducted research, the authors used data obtained from The National Heritage Board of Poland. The National Heritage Board of Poland (NHBP) is a cultural institution established by the Minister of Culture and National Heritage; its present structure was formed in 2007. NHBP is a state agency that gathers and disseminates information on heritage, sets standards for its protection and conservation, and aims to raise the social awareness on cultural heritage of Poland in order to save it for future generations in accordance with the strategy for sustainable development. The generic division of non-movable monuments used by NHBP is shown in the Figure 1.
When determining the location of individual monuments, reference was made to the administrative division of Poland. This division includes [26]:
  • 16 voivodeships,
  • 314 poviats and 66 cities with poviat rights,
  • 2477 municipalities (including 302 urban municipalities, 638 urban–rural municipalities, and 1537 rural municipalities).
The spatial distribution of the administrative division of Poland is shown in the Figure 2, and the quantitative data on the number of non-movable monuments in individual voivodeships in 2018—in Figure 3.
After obtaining location and generic data of all non-movable monuments in Poland, the authors continued the research using the Geographic Information System (GIS). GIS is an information system used to enter, collect, process, and visualize geographic data. It is a powerful tool; spatial analyses using GIS significantly support decision-making processes. Spatial data for GIS can be obtained by, among others: field measurements, digitalization of analog data (including historical data), or three-dimensional photogrammetry digitization and other methods of photogrammetry and remote sensing. Additional data entry functions include: entering descriptive data, geometric construction, interactive editing of objects (removal, modification). Data management can be defined as a set of processes with the main purpose of keeping the information resources of the system in good condition. It is also important that the data structures and search mechanisms provides efficient information sharing. The processing functions include transforming, analyzing, aggregating, and generalizing. GIS software allows spatial analysis using a variety of methods, the most popular include: overlay analysis, spatial interpolation, spatial data exploration, hot spot analysis, or kernel density estimation; this type of research finds application in a number of areas, e.g., bathymetry [29], spatial planning [30], location selection [31,32], environmental protection and disaster reduction capability [33,34,35,36,37], spatial and distribution patterns [38,39,40,41], demography [42], as well as many others. Using GIS software, the data can be visualized using many cartographic visualization methods, such as: cartogram, cartodiagram, range method, dot map, etc. [43].
Analyses related to management (including sustainable heritage management) requires a reference to the spatial location of objects [44,45]. The optimal solution is to acquire point data, however, as indicated in the Section 2 Materials and Methods, in practice, visualization is applied at different levels of generalization. The aim of the conducted research was to find the grid size for which the data with an acceptable loss of accuracy can be generalized. The goal was achieved using GIS tools, confirming its usefulness in such analyses.

2. Materials and Methods

When conducting spatial analysis, the use of precise point or linear data is in the most cases a model situation and gives the possibility to obtain the most accurate, flexible results [46]. Having information about the exact location of the analyzed phenomena allows for an in-depth examination of the issue. However, the availability of such data is often a problem [47]. Usually it is caused by the cost of acquisition, laboriousness, or impossibility to carry out measurements, but can also be related to the object’s specification. In the absence of precise data, some kind of generalization is introduced. Most often, data is collected for administrative division units. The smallest administrative division is usually sufficient for spatial analyses [48]. The main advantage of using administrative division units in spatial analysis is the availability of data collected in various types of offices (state, administrative)—it usually refers to administrative units [48]. The use of this type of units also simplifies the presentation of results to non-specialists (e.g., to local government authorities).
However, the administrative division units are spatially unequal, which increases difficulty of comparability (e.g., the smallest municipality in Poland has an area equal to 3.32 km2, the largest—6444 km2). The basic advantage of using geometric figures in spatial analyses is its identical surface, which facilitates comparability; it is also easy to develop it using digital techniques. The most popular geometric figures are: triangles, squares, and hexagons; these are the only regular shapes that tessellates the plane with no gaps [49]. In studies performed for the purposes of the article hexagonal grid was used—the higher usefulness of the hexagon over other figures has been repeatedly confirmed in the case of spatial analyses [50,51,52], as well as in other cases [53,54,55,56,57]. The aim of this research was to find the optimal size of the hexagonal grid, to the level of which the data can be generalized, without a significant decrease in the reliability of spatial modeling for various sustainable heritage management needs.
The practical part of the research was carried out in the Esri ArcGIS 10.6 software. All map attachments (as well as the entire practical part of the tests) were made in the Lambert Azimuthal Equal Area 52N 10E ETRS89 reference system. This projection accurately represents area in all regions of the sphere, but it does not accurately represent angles; it is commonly seen in atlases [58]. European Environment Agency (EEA) recommends the use of this reference system for storing raster data, for statistical analysis and for map display purposes (small scale mapping 1:500,000 or smaller applications) [59,60]. In the research, point data with the exact location of non-movable monuments in Poland, obtained from the National Heritage Board of Poland were used. The data has been verified and prepared for GIS analyses. The data describe the state on 1 August 2018, and contain the exact location and description of 85,891 non-movable monuments in Poland (Figure 4).
The research has been divided into three main stages:
  • Stage I—Creating the map of the density of non-movable monuments with kernel density estimation
  • Stage II—Choosing the optimal method of spatial interpolation
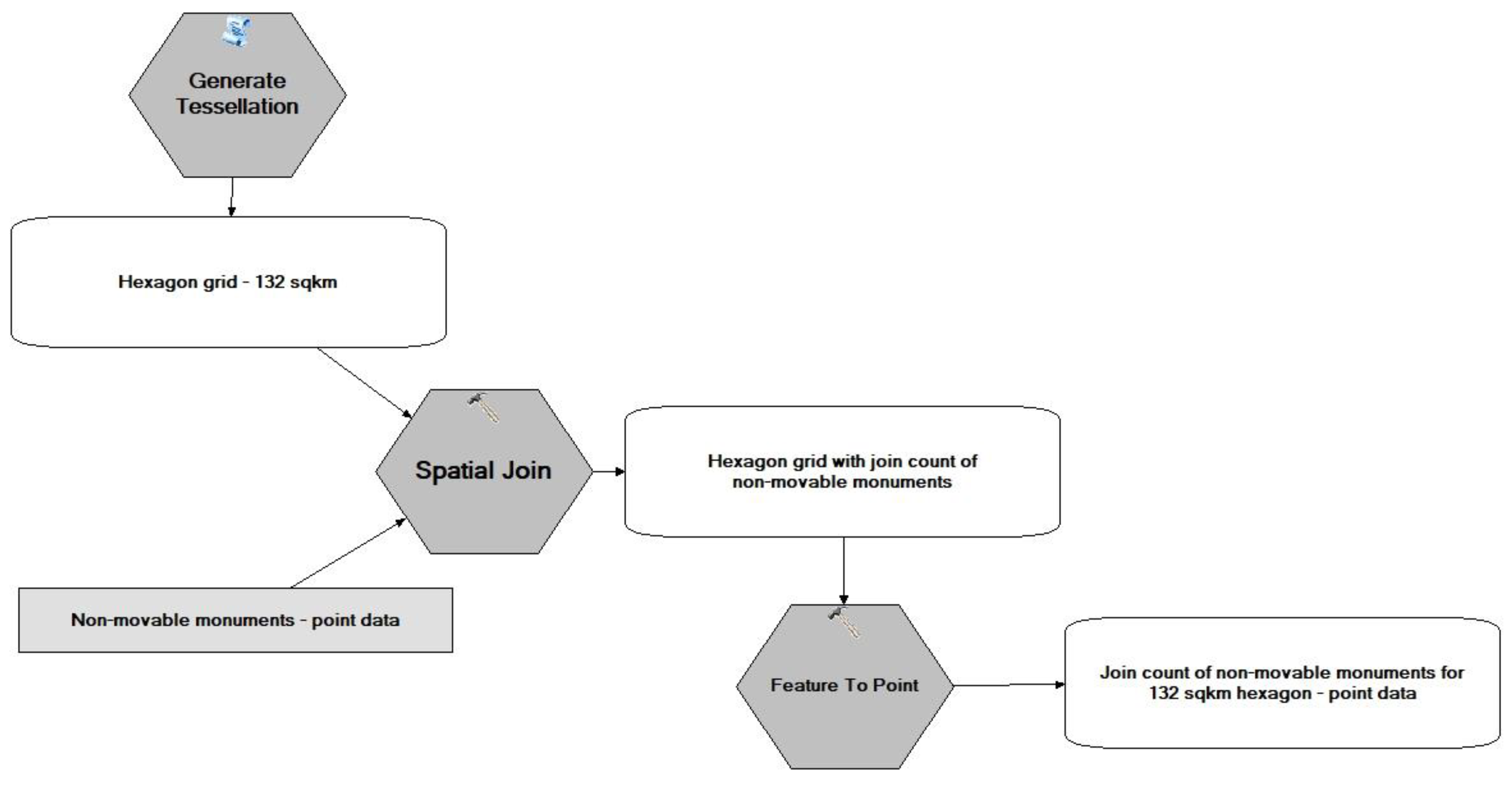
  • Stage III—Finding the optimal size of the geometric grid
In the first stage, using the point data, a map of the density of non-movable monuments in Poland was created using kernel density estimation. Kernel density estimation (KDE) is an important method of spatial data visualization; KDE presents the density of the analyzed points in a given spatial extent [61], thus showing spatial patterns [62,63]. This is a non-parametric estimation, it directly uses point data [64]. KDE calculates the density of point features around each output raster cell. The surface value is highest at the location of the point and diminishes with increasing distance from the point, reaching zero at the search radius (or ‘bandwidth’) distance from the point. The kernel function is based on the quartic kernel function described in [61]. This method finds application in many fields of science, such as: archaeology [65,66], astronomy [67,68,69,70,71], biology [72,73,74,75], forecasting [76,77], environmental protection [78,79], medicine and health studies [80,81,82,83], and many others. Choosing the appropriate bandwidth in KDE is the subject of many studies [84,85,86]. If the bandwidth is too low (the impact range of the kernels is too small), KDE can give unsmooth density; while too-large a bandwidth can over-generalize the data, giving inaccurate picture [64]. The created map of the density of non-movable monuments in Poland will serve as a model image, to which maps created using generalized hexagons will be compared.
The second stage was to determine the optimal data visualization method for the analyzed dataset. The point data was combined with administrative division units—points contained in polygons were summed up, and assigned to appropriate polygons. Polygons were then visualized with cartogram method in order to present a spatial distribution of data. A cartogram is a very good cartographic visualization method, but it has a significant disadvantage—the need to classify data gives a distorted view of the continuity of value across the entire polygon in a specific class [43]. In order to obtain more accurate view of continuity, polygon data were converted to point data (polygon centroids), and then interpolated using nine spatial interpolation methods, available in the “Geostatistical Analyst” add-on of ArcGIS software: inverse distance weighting (IDW), global polynomial interpolation (GPI), radial basis function (RBF), local polynomial interpolation (LPI), ordinary kriging (OK), simple kriging (SK), universal kriging (UK), disjunctive kriging (DK), and empirical Bayesian kriging (EBK). Spatial interpolation effectively generates a full spatial attribute pattern in a large spatial range. This tool accurately creates a spatial pattern of attributes with spatial continuity [87]. Spatial interpolation is found useful in many fields of science, such as: environmental and pollution studies [88,89,90,91], soil science/pedology [92,93,94,95], hydrology [96], bathymetry [97,98], medicine and health studies [99,100], as well as many others. Kriging interpolation is a geostatistical method for estimating values at unmeasured locations, based on empirical spatial structure quantified in a semivariogram model [101]. The aim of this part of the research was to determine the optimal method of spatial interpolation for the analyzed data using cross-validation. The values at the measured points of the analyzed point layer were interpolated—this way, maps (models) with spatial continuity were obtained. Comparing the accuracy of these maps is possible using the difference between measured points and modeled points (cross-validation). These differences are errors that constitute the basic determinant of model accuracy. Interpolation methods were compared on the basis of root-mean-square-error (RMSE). RMSE is recommended for comparing spatial interpolation methods [102], a smaller error value means a better adjusted model [91,97]. On the basis of cross-validation, the optimal method for visualizing the analyzed data was chosen.
In the third stage, a geometric grid composed of hexagons was generated. The hexagonal grid was created using the ArcGIS ‘Generate Tessellation’ tool. For different sizes of hexagons, polygons were combined with point data (same as in the second stage) and then visualized using the chosen interpolation method. The aim of the research was to find the optimal grid size, to the level of which the data can be generalized without a significant decrease in the credibility of spatial modeling. The Pearson correlation coefficient, calculated for the density map of non-movable monuments from the first part of the study and for maps created from subsequent hexagon sizes, was selected as the reliability indicator. KDE allows to obtain density values at any point within the analysis range [103], similarly for all methods of spatial interpolation [87]. This feature was used to obtain tabular data necessary to calculate Pearson’s correlation coefficient—but a point layer was needed, to collect the raster cell values. Test layers compose of randomly generated 8589 points (created using ‘Create Random Points’ tool), which corresponds with 10% of the complete set. To each particular point, the value of the chosen raster layer was assigned (from the model map created using KDE and a map created using the optimal interpolation method). Five test layers were applied, averaging Pearson’s correlation coefficients for five measurements, thus obtaining more reliable results. Received tabular data was compared using the Pearson’s correlation coefficient. In order to find the size of the hexagon for which the correlation coefficient is the highest, the above process was carried out for three levels of accuracy (every 10 km2, 5 km2, and 1 km2), narrowing the scope of the analysis with each level. By comparing successive values of Pearson’s correlation coefficient, one size of the hexagon was found, for which its value is the highest—it means finding the optimal grid size to which the data can be generalized without a significant decrease in reliability. Analyses carried out in this way allowed to draw conclusions in the field of the analyzed problem.

3. Results

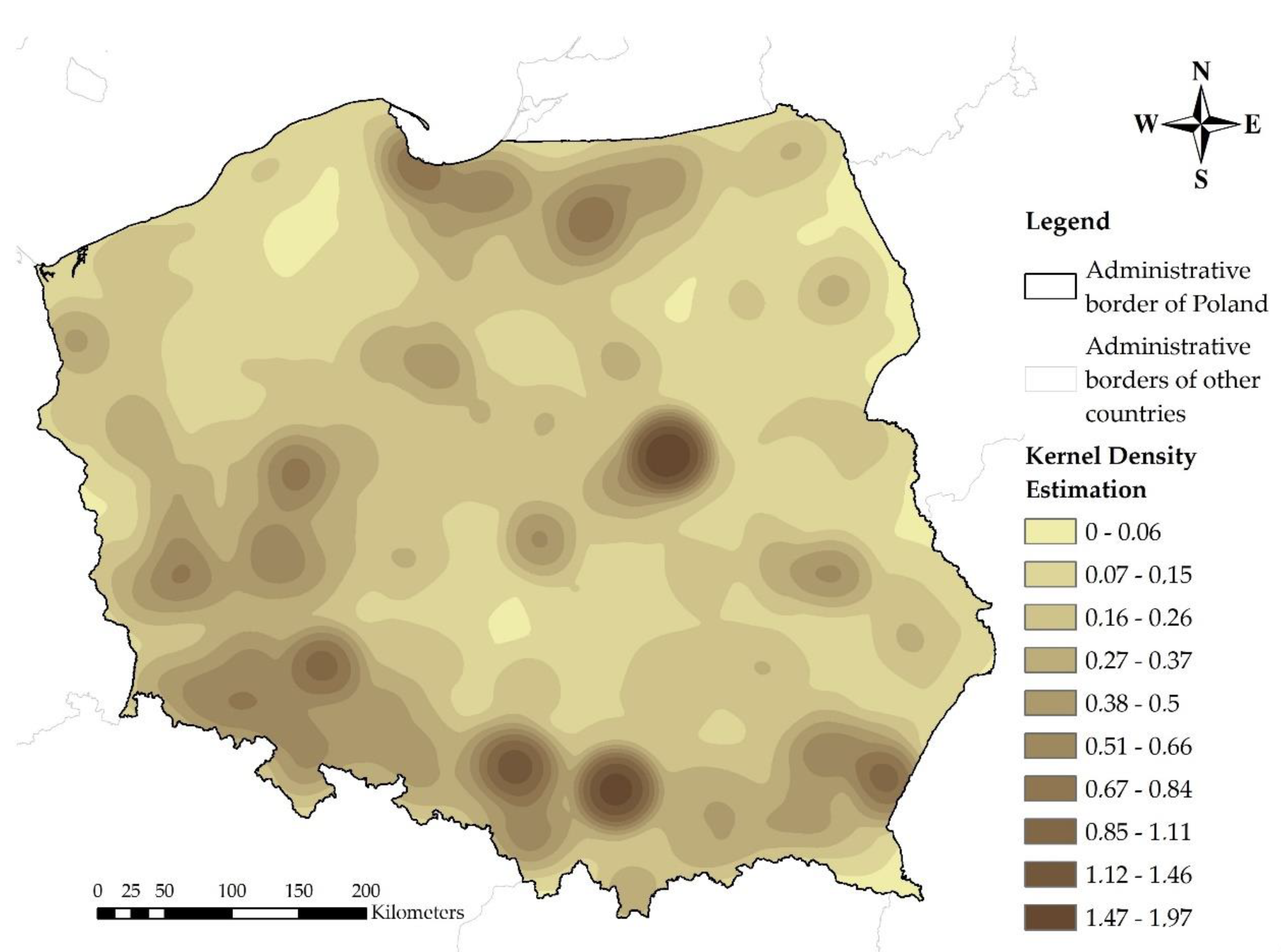
3.1. Map of the Density of Non-Movable Monuments—Kernel Density Estimation

The ‘Kernel Density’ tool from ArcGIS software was used to generate a density map of non-movable monuments in Poland. The built-in algorithm for determining the optimal bandwidth was used—it is (around rounded up to thousands) 40 km. Figure 5 shows the density map of non-movable monuments in Poland, generated on the basis of point data obtained from NHBP, using the ArcGIS ‘Kernel Density’ tool.
The generated Figure 5 will serve as a model image of the reality to which maps created using generalized hexagons will be compared. KDE allows to show the accurate spatial pattern, but as indicated in the Materials and Methods section, the availability of point data may be limited.

3.2. Optimal Method of Spatial Interpolation

Point data were combined with administrative division units, which were then visualized using a cartogram method (Figure 6).
For three levels of administrative division, data on the number of non-movable monuments in Poland were interpolated using the nine methods, as indicated in Materials and Methods. The information on RMSE was then collected, as shown in Table 1. Additional information on individual datasets is presented in Table 2.
The average size of the voivodeship in Poland is 19,543.82 km2; poviat—822.90 km2; and municipality—126.24 km2. Generalization in the case of the first two divisions is very large, which can be seen in the high error rates. When performing cross-validation and comparing obtained root-mean-square-errors, a clear result appears—the RMSE values are the lowest for simple kriging method (2223.73 for voivodeships, 215.70 for poviats, and 91.52 for municipalities). Simple kriging method demonstrates therefore the best adjustment of the model (values at the unmeasured locations are the closest to the values at the measured locations); this method was therefore chosen as optimal for subsequent tests. The results of spatial interpolation using the simple kriging method have been shown in the Figure 7.

3.3. Optimal Size of the Geometric Grid

The last stage of the research was the analysis of data generalized to the series of generated hexagonal grids, in order to find the optimal grid size, to the level of which the data can be generalized without a significant decrease in reliability. The hexagonal grid was created using the ArcGIS ‘Generate Tessellation’ tool. Then, using the ‘Spatial Join’ tool, the values of the total number of points within its boundaries were assigned to the appropriate polygons. Polygon data has been converted to point data (using the ‘Feature to Point’ tool), and then it was interpolated using the simple kriging method. The above process, described in the ArcGIS ModelBuilder component, is shown in the Figure 8.
The map created using the simple kriging method was compared to the map created using the ‘Kernel Density’ tool; The Pearson correlation coefficient was used as the indicator. The above process, described in the ArcGIS ModelBuilder component, is shown in the Figure 9.
In order to find the size of the hexagon for which the correlation coefficient is the highest, the processes described in Figure 8 and Figure 9 were performed for three levels of accuracy (ranges of values)—every 10 km2, 5 km2, and 1 km2—narrowing the scope of analysis with each level. On the first level of accuracy (10 km2), hexagons were generated in the range of 10–300 km2. The upper range was determined empirically on the basis of test research—higher values gave ever lower values of Pearson’s correlation coefficient. Values of the correlation coefficient for particular hexagon sizes with an accuracy of 10 km are shown in the Table 3, and the distribution of mean values of the correlation coefficient in the Figure 10.
All hexagon sizes are characterized by a high correlation coefficient, however, the range of 110–200 km contains values with a coefficient above 0.95 (rounded to the hundredth level). This range was chosen for the next stage—5 km2 accuracy. Values of the correlation coefficient for particular sizes of hexagons at the accuracy of 5 km2 are presented in the Table 4, and the distribution of the average values of the correlation coefficient in the Figure 11.
To the next level of accuracy (1 km2) a range with a correlation coefficient higher than 0.970 (rounded up to the thousandth level) was selected—hexagons with an area of 110–165 km2. Values of the correlation coefficient for particular sizes of hexagons at the accuracy of 5 km2 are presented in the Table 5, and the distribution of the average values of the correlation coefficient in the Figure 12.
By comparing successive values of Pearson’s correlation coefficient, one hexagon size was found, for which its value is the highest—132 km2. The value of the correlation coefficient for the measurement from the third test layer is in this case 0.9843, and the average value for this hexagon size for all five test layers is 0.9829. This is the optimal grid size, to which the data can be generalized without significant decrease in reliability. A hexagon grid with an area of 132 km2 is shown in the Figure 13, while a map of spatial distribution of non-movable monuments, generalized for this grid is shown in Figure 14.

4. Discussion

The conducted analyses showed the possibility of using various GIS tools in spatial analysis related to sustainable heritage management. The obtained results allowed us to formulate the following:
  • With the availability of point data containing detailed information about the location of objects, kernel density estimation gives an accurate picture of reality, as shown in the Results section. This is due to the fact that KDE is a non-parametric method, taking into account only the location of objects—not affected by a generalization error.
  • With the availability of point data, which does not contain detailed information about the location of objects, containing only parameters describing it quantitatively, spatial analyses require a different approach. Conducted research has shown that spatial interpolation should be performed; from the methods analyzed in the article, the simple kriging method proved to be optimal. This was confirmed by the smallest RMSE value.
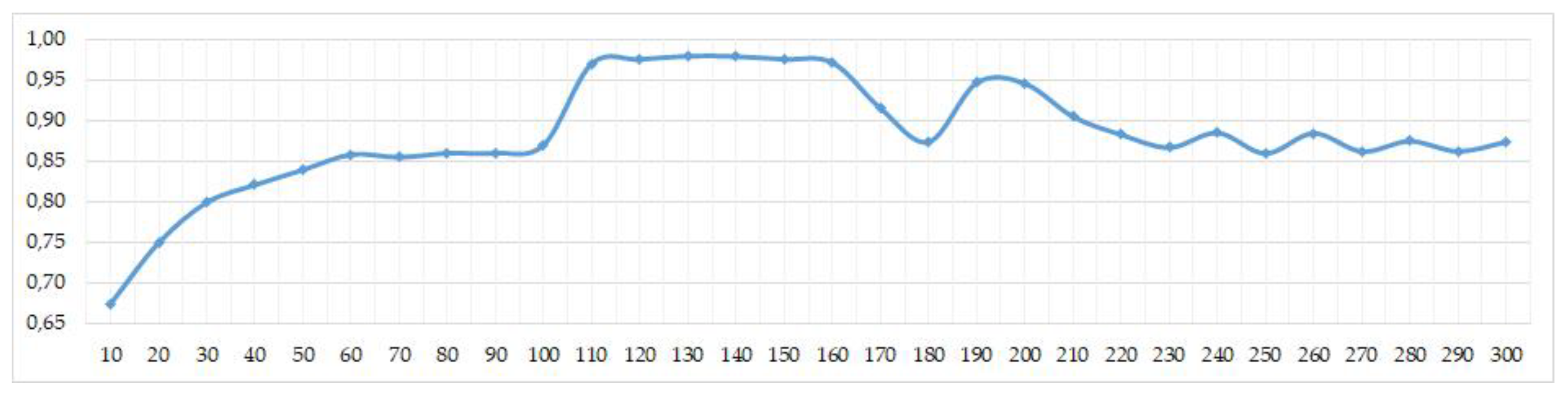
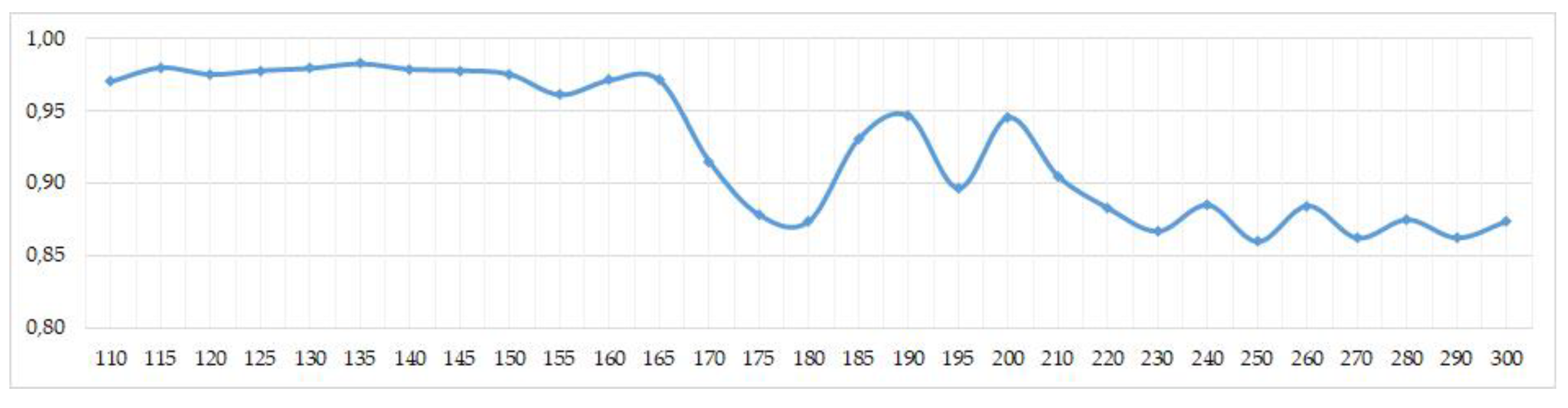
  • In the case of unavailability of point data, the literature analysis showed a solution in the form of data generalization through the use of a hexagonal grid. The research conducted in the article showed that in the range of 110–200 km2 hexagons, very satisfying results are obtained (Pearson’s correlation coefficient assumes values above 0.95). The 132 km2 hexagon proved to be an optimal one—the Pearson’s correlation coefficient after averaging for all five test layers is 0.9829.

5. Conclusions

  • To properly implement sustainable heritage management, thematic maps are required for various related analyses. Development of such maps (as indicated in the article) can be expensive, long, and not always possible to implement based on detailed location data. In the article, using data on non-moveable monuments in Poland, the methodology of creating more generalized maps using less data, is shown. Studies created in Poland (indicated in Conclusions, point 4) often require aggregated maps, without detailed location of the objects. The methodology presented in the article is a response to these needs.
  • The study was based on point data of non-movable monuments in Poland, and the result of the 132 km2 hexagonal grid is the result only for this specific data. The methodology proposed in the article gives the possibility of universal application. Further research may be based on a comparison of different types of data using the methodology developed in this article. The hexagonal grid gave a specific result, and a comparison of other geometric figures can also become the basis for further studies.
  • The scope of the analysis is also universal. The research in the article was carried out for the area of one country—Poland, including its administrative division units. Similar analyses can be made for any other country with a different administrative division, or even for larger areas (e.g., continents). The scope of the tests may also be limited to a smaller area (e.g., regions).
  • In Poland, some studies on spatial management (part of the sustainable heritage management) directly concern the administrative areas and the analysis closes within its borders. Such documents include: National Spatial Development Concept for the country level; Voivodeship Development Strategy, and Voivodeship Spatial Management Plan for the voivodeship level; and Municipality Development Strategy, Study Of The Conditions And Directions Of The Spatial Management Of Municipality, Local Spatial Management Plans for the municipality level. For such applications, the point level of detail may even be unnecessarily high. Generalization of data may end at the level of a given administrative unit (this is also shown in the article).
  • The research conducted in the article confirmed the wide possibilities of using GIS tools for various purposes, in this particular case concerning cultural heritage, and in particular sustainable heritage management.

Author Contributions

Conceptualization, M.C., K.R., and M.O.; Methodology, M.C., K.R., and M.O.; Formal analysis, M.C., K.R., and M.O.; Writing—original draft preparation, M.C. and K.R.; Writing—review and editing, M.C., K.R., and M.O.; Software, M.C. and M.O.; Visualization, M.C., K.R., and M.O.

Funding

This research received no external funding.

Acknowledgments

Authors would like to thank the National Heritage Board of Poland, for sharing data on non-movable monuments in Poland.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Alkhalidi, A.; Qoaider, L.; Khashman, A.; Al-Alami, A.R.; Jiryes, S. Energy and Water as Indicators for Sustainable City SiteSelection and Design in Jordan using smart grid. Sustain. Cities Soc. 2018, 37, 125–132. [Google Scholar] [CrossRef]
  2. Antonopoulos, E. Sustainable Urban Development in Greece Using Integrated Territorial Investments. Eur. Struct. Investig. Funds J. 2018, 6, 28–34. [Google Scholar]
  3. Bell, S.; Morse, S. Routledge Handbook of Sustainability Indicators; Routledge: London, UK, 2018; ISBN 9781138674769. [Google Scholar]
  4. Act of 27 April 2001 Environmental Protection Law; Journal of Laws: Warsaw, Poland, 2001; Volume 62.
  5. World Commission on Environment and Development: Our Common Future; Oxford University Press: Oxford, UK, 1987.
  6. Pearce, D.W. Sustainable development and developing country economies. In Sustainable Environmental Management; Turner, R.K., Ed.; Bellhaven Press: London, UK, 1993; pp. 70–105. [Google Scholar]
  7. Bogacz-Wojtanowska, E.; Góral, A.; Bugdol, M. The Role of Trust in Sustainable Heritage Management Networks. Case Study of Selected Cultural Routes in Poland. Sustainability 2019, 11, 2844. [Google Scholar] [CrossRef]
  8. Hawkes, J. The Fourth Pillar of Sustainability: Culture’s Essential Role in Public Planning; Cultural Development Network: Melbourne, Australia, 2001; ISBN 1 86335 050 0. [Google Scholar]
  9. James, P.; Magee, L.; Scerri, A.; Steger, M. Measuring Community Sustainability: The social Life Questionaire. In Urban Sustainability in Theory and Practice: Circles of Sustainability; Routledge: London, UK, 2015; pp. 161–180. ISBN 9781138025721. [Google Scholar]
  10. Soini, K.; Birkeland, I. Exploring the scientific discourse on cultural sustainability. Geoforum 2014, 51, 213–223. [Google Scholar] [CrossRef]
  11. Janikowski, R. Kultura osią zrównoważonego rozwoju. In Kultura a Zrównoważony Rozwój; Janikowski, R., Krzysztofek, K., Eds.; Polski Komitet do spraw UNESCO: Warsaw, Poland, 2009; pp. 17–39. ISBN 9788390293943. [Google Scholar]
  12. Barthel-Boucher, D. Cultural Heritage and the Challenge of Sustainability. Online J. Public Archaeol. 2018, 4, 163. [Google Scholar]
  13. Hall, S.; Evans, J.; Nixon, S. Representation. Cultural Representations and Signifying Practices, 2nd ed.; Sage/Open University: London, UK, 2013; ISBN 9781849205634. [Google Scholar]
  14. Kirshenblatt-Gimblett, B. Intangible heritage as metacultural production. Mus. Int. 2014, 66, 52–65. [Google Scholar] [CrossRef]
  15. Davies, J.; Whimster, R.; Clayton, L. Heritage Counts 2009, England; English Heritage: London, UK, 2009. [Google Scholar]
  16. Boryczka, E.M.; Michalak, J.; Rzeńca, P. Protection of valuable areas of local cultural heritage in sustainable development. Cultural parks in the Lodz region. Ekon. I Środowisko 2019, 1, 225–240. [Google Scholar]
  17. Pereira Roders, A.; van Oers, R. Editorial: Bridging cultural heritage and sustainable development. J. Cult. Herit. Manag. Sustain. Dev. 2011, 1, 5–14. [Google Scholar] [CrossRef]
  18. Bonenberg, W. The Role of Cultural Heritage in Sustainable Development. Values and Valuation as Key Factors in Spatial Planning of Rural Areas. In Advances in Intelligent Systems and Computing Book Series (AISC, Volume 966); Springer: Cham, Switzerland, 2019; pp. 124–134. [Google Scholar]
  19. Rzasa, K.; Ogryzek, M.; Kulawiak, M. Cultural Heritage in Spatial Planning. In Proceedings of the 2016 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 2–4 June 2016; pp. 85–89. [Google Scholar]
  20. Papoulias, E.; Zounis, T.-P. The Historic and Monumental Enhancement as a Tool for the Sustainable Development of Cultural Assets of Greece; Springer: Cham, Switzerland, 2019; pp. 271–278. [Google Scholar]
  21. Persson-Fischier, U. Sustainability in conflict: A study of cruise tourism to Gotland. In Proceedings of the MARE People and the Sea X, Amsterdam, The Netherlands, 24–28 June 2019. [Google Scholar]
  22. Ndiaye, M. Barriers to sustainable tourism in Senegal. Int. J. Innov. Educ. Res. 2019, 7, 258–274. [Google Scholar] [CrossRef]
  23. Act of 23 July 2003 on the Protection of Monuments and the Guardianship of Monuments; Journal of Laws: Warsaw, Poland, 2003; Volume 162.
  24. Regulation of the Minister of Culture of 9 February 2004 on the Model of an Information Sign Affixed to Non-Movable Monuments Entered in the Register of Monuments; Journal of Laws: Warsaw, Poland, 2004; Volume 30.
  25. Final act of the Intergovernmental Conference on the Protection of Cultural Property in the Event of Armed Conflict; UNESCO: Hague, The Netherlands, 1954; p. 83.
  26. Bielak, R.; Głowacka-Smolis, K.; Gustyn, J.; Kozera, A.; Kozłowska, J.; Lipowska, E.; Marikin, M.; Nowak, T.; Pilaszek, K.; Rybak-Nguyen, E.; et al. Statistical Yearbook of the Republic of Poland 2018; Statistics Poland: Warsaw, Poland, 2018. [Google Scholar]
  27. Database of Global Administrative Areas, GADM. Available online: https://gadm.org (accessed on 25 July 2019).
  28. Head Office of Geodesy and Cartography, Poland. Available online: http://www.gugik.gov.pl/pzgik/dane-bez-oplat/dane-z-panstwowego-rejestru-granic-i-powierzchni-jednostek-podzialow-terytorialnych-kraju-prg (accessed on 25 July 2019).
  29. Qi, L.; Huang, J.; Gao, J.; Cui, Z. Modelling the Impacts of Bathymetric Changes on Water Level in China’s Largest Freshwater Lake. Water 2019, 11, 1469. [Google Scholar] [CrossRef]
  30. Yang, B. Developing a Mobile Mapping System for 3D GIS and Smart City Planning. Sustainability 2019, 11, 3713. [Google Scholar] [CrossRef]
  31. Erdin, C.; Akbaş, H.E. A Comparative Analysis of Fuzzy TOPSIS and Geographic Information Systems (GIS) for the Location Selection of Shopping Malls: A Case Study from Turkey. Sustainability 2019, 11, 3837. [Google Scholar] [CrossRef]
  32. Layomi Jayasinghe, S.; Kumar, L.; Sandamali, J.; Layomi Jayasinghe, S.; Kumar, L.; Sandamali, J. Assessment of Potential Land Suitability for Tea (Camellia sinensis (L.) O. Kuntze) in Sri Lanka Using a GIS-Based Multi-Criteria Approach. Agriculture 2019, 9, 148. [Google Scholar] [CrossRef]
  33. Xiong, J.; Li, J.; Cheng, W.; Wang, N.; Guo, L.; Xiong, J.; Li, J.; Cheng, W.; Wang, N.; Guo, L. A GIS-Based Support Vector Machine Model for Flash Flood Vulnerability Assessment and Mapping in China. ISPRS Int. J. Geo-Inf. 2019, 8, 297. [Google Scholar] [CrossRef]
  34. Kartoziia, A. Assessment of the Ice Wedge Polygon Current State by Means of UAV Imagery Analysis (Samoylov Island, the Lena Delta). Remote Sens. 2019, 11, 1627. [Google Scholar] [CrossRef]
  35. Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide Susceptibility Mapping Using Different GIS-Based Bivariate Models. Water 2019, 11, 1402. [Google Scholar] [CrossRef]
  36. Tien Bui, D.; Khosravi, K.; Shahabi, H.; Daggupati, P.; Adamowski, J.F.; Melesse, A.M.; Thai Pham, B.; Pourghasemi, H.R.; Mahmoudi, M.; Bahrami, S.; et al. Flood Spatial Modeling in Northern Iran Using Remote Sensing and GIS: A Comparison between Evidential Belief Functions and Its Ensemble with a Multivariate Logistic Regression Model. Remote Sens. 2019, 11, 1589. [Google Scholar] [CrossRef]
  37. Kimsey, M.; Page-Dumroese, D.; Coleman, M.; Kimsey, M.; Page-Dumroese, D.; Coleman, M. Assessing Bioenergy Harvest Risks: Geospatially Explicit Tools for Maintaining Soil Productivity in Western US Forests. Forests 2011, 2, 797–813. [Google Scholar] [CrossRef]
  38. Song, B.; Park, K. Analysis of Spatiotemporal Urban Temperature Characteristics by Urban Spatial Patterns in Changwon City, South Korea. Sustainability 2019, 11, 3777. [Google Scholar] [CrossRef]
  39. Rząsa, K.; Ogryzek, M.; Ciski, M. Application of GIS technology in the protection of monuments on the example of Historic Monuments. E3s Web Conf. 2018, 63. [Google Scholar] [CrossRef]
  40. Rząsa, K.; Ciski, M. Archaeological monuments of the Warmian-Masurian voivodeship—Spatial analysis using GIS tools. E3s Web Conf. 2018, 63. [Google Scholar] [CrossRef]
  41. Rząsa, K.; Ciski, M.; Ogryzek, M. Application of GIS Tools in Spatial Distribution Modeling of Historical Monuments. Geomat. Environ. Eng. 2019, 13, 61. [Google Scholar] [CrossRef]
  42. Weichselbaum, J.; Papathoma, M. Sharpening census information in GIS to meet real-world conditions—The case for Earth Observation. Wit Trans. Ecol. Environ. 2005, 84. [Google Scholar] [CrossRef]
  43. Ogryzek, M.; Ciski, M. Cartographic Methods of Presentation the Average Transaction Prices of the Undeveloped Land. Civ. Environ. Eng. Rep. 2018, 28, 85–100. [Google Scholar] [CrossRef] [Green Version]
  44. Singh, A. Remote sensing and GIS applications for municipal waste management. J. Environ. Manag. 2019, 243, 22–29. [Google Scholar] [CrossRef] [PubMed]
  45. Peragón, J.M.; Pérez-Latorre, F.J.; Delgado, A.; Tóth, T. Best management irrigation practices assessed by a GIS-based decision tool for reducing salinization risks in olive orchards. Agric. Water Manag. 2018, 202, 33–41. [Google Scholar] [CrossRef]
  46. Kogure, K.; Takasaki, Y. GIS for empirical research design: An illustration with georeferenced point data. PLoS ONE 2019, 14, e0212316. [Google Scholar] [CrossRef] [PubMed]
  47. Escobar, F.; Williamson, I. Hierarchical Spatial Reasoning Applied To the Automated Design of Administrative Boundaries Using GIS. In Proceedings of the URISA 2000, Orlando, FL, USA, 19–23 August 2000; pp. 185–200. [Google Scholar]
  48. Estrada-Peña, A.; Venzal, J.M. A GIS framework for the assessment of tick impact on human health in a changing climate. Geospat. Health 2007, 1, 157–168. [Google Scholar] [CrossRef] [Green Version]
  49. Gullberg, J. Mathematics: From the Birth of Numbers; University of Denver: Denver, CO, USA, 1997; ISBN 039304002X. [Google Scholar]
  50. De Sousa, L.; Nery, F.; Sousa, R.; Matos, J. Assessing the accuracy of hexagonal versus square tilled grids in preserving DEM surface flow directions. In Proceedings of the 7th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Lisbon, Portugal, 5–7 July 2006; pp. 191–200. [Google Scholar]
  51. Golay, M.J.E. Hexagonal Parallel Pattern Transformations. IEEE Trans. Comput. 1969, 18, 733–740. [Google Scholar] [CrossRef]
  52. Mersereau, R.M. The processing of hexagonally sampled two-dimensional signals. Proc. IEEE 1979, 67, 930–949. [Google Scholar] [CrossRef]
  53. He, X.; Shen, G.; Xu, R.; Yang, W.; Zhang, C.; Liu, Z.; Chen, B.; Liu, J.; Song, M. Hexagonal and square patterned silver nanowires/PEDOT:PSS composite grids by screen printing for uniformly transparent heaters. Polymers 2019, 11, 468. [Google Scholar] [CrossRef]
  54. Uher, V.; Gajdoš, P.; Snášel, V.; Lai, Y.-C.; Radecký, M. Hierarchical Hexagonal Clustering and Indexing. Symmetry 2019, 11, 731. [Google Scholar] [CrossRef]
  55. Brimkov, V.E.; Barneva, R.P. “Honeycomb” vs Square and Cubic Models. Electron. Notes Theor. Comput. Sci. 2001, 46, 321–338. [Google Scholar] [CrossRef]
  56. Wen, W.; Khatibi, S. The impact of curviness on four different image sensor forms and structures. Sensors 2018, 18, 429. [Google Scholar] [CrossRef] [PubMed]
  57. Lee, G.; Chong, N.Y. A geometric approach to deploying robot swarms. Ann. Math. Artif. Intell. 2008, 52, 257–280. [Google Scholar] [CrossRef]
  58. Snyder, J.P. Flattening the Earth: Two Thousand Years of Map Projections; University of Chicago Press: Chicago, IL, USA, 1993; ISBN 9780226767475. [Google Scholar]
  59. Steenmans, C.; Lillethun, A.; Cryan, S.; Bliki, J.; Jessen, T.; Lund, M.; Bredahl, L.; Jeppesen, J. Guide to Geographical Data and Maps; European Environmental Agency: Copenhagen, Denmark, 2005. [Google Scholar]
  60. Annoni, A.; Bernard, L.; Lillethun, A.; Ihde, J.; Gallego, J.; Rives, M.; Sommer, E.; Poelman, H.; Condé, S.; Greaves, M.; et al. 1st Workshop on European Reference Grids. In Proceedings of the 1st European Reference Grid workshop and Proposal for a European Reference Grid Coding System; Annoni, A., Ed.; JRC-Institute for Environment and Sustainability: Ispra, Italy, 2004. [Google Scholar]
  61. Silverman, B.W. Density Estimation: For Statistics and Data Analysis; Routledge: London, UK, 2018; ISBN 9781351456173. [Google Scholar]
  62. Nie, K.; Wang, Z.; Du, Q.; Ren, F.; Tian, Q.; Nie, K.; Wang, Z.; Du, Q.; Ren, F.; Tian, Q. A Network-Constrained Integrated Method for Detecting Spatial Cluster and Risk Location of Traffic Crash: A Case Study from Wuhan, China. Sustainability 2015, 7, 2662–2677. [Google Scholar] [CrossRef] [Green Version]
  63. Yang, X.; Zhao, Z.; Lu, S. Exploring spatial-temporal patterns of urban human mobility hotspots. Sustainability 2016, 8, 674. [Google Scholar] [CrossRef]
  64. Qin, Z.; Li, W.; Xiong, X. Estimating wind speed probability distribution using kernel density method. Electr. Power Syst. Res. 2011, 81, 2139–2146. [Google Scholar] [CrossRef]
  65. Baxter, M.J.; Beardah, C.C.; Wright, R.V.S. Some archaeological applications of kernel density estimates. J. Archaeol. Sci. 1997, 24, 347–354. [Google Scholar] [CrossRef]
  66. Brigand, R.; Weller, O. Kernel density estimation and transition maps of Moldavian Neolithic and Eneolithic settlement. Data Brief 2018, 17, 452–458. [Google Scholar] [CrossRef]
  67. Fadda, D.; Slezak, E.; Bijaoui, A. Density estimation with non-parametric methods. Astron. Astrophys. Suppl. Ser. 1997, 127, 335–352. [Google Scholar] [CrossRef]
  68. Danese, M.; Lazzari, M.; Murgante, B. Kernel Density Estimation Methods for a Geostatistical Approach in Seismic Risk Analysis: The Case Study of Potenza Hilltop Town (Southern Italy). In Computational Science and Its Applications—ICCSA 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 415–429. [Google Scholar]
  69. Kremer, J.; Gieseke, F.; Steenstrup Pedersen, K.; Igel, C. Nearest neighbor density ratio estimation for large-scale applications in astronomy. Astron. Comput. 2015, 12, 67–72. [Google Scholar] [CrossRef] [Green Version]
  70. Jang, W.; Hendry, M. Cluster analysis of massive datasets in astronomy. Stat. Comput. 2007, 17, 253–262. [Google Scholar] [CrossRef] [Green Version]
  71. Vio, R.; Fasano, G.; Lazzarin, M.; Lessi, O. Kernel density estimators applied to gamma ray light curves. Astron. Astrophys. 1986, 289, 640–648. [Google Scholar]
  72. Worton, B.J. Kernel methods for estimating the utilization distribution in home- range studies. Ecology 1989, 70, 164–168. [Google Scholar] [CrossRef]
  73. Pittiglio, C.; Skidmorea, A.K.; van Gils, H.A.M.J.; Prins, H.H.T. Identifying transit corridors for elephant using a long time-series. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 61–72. [Google Scholar] [CrossRef]
  74. Maxwell, S.M.; Scales, K.L.; Bograd, S.J.; Briscoe, D.K.; Dewar, H.; Hazen, E.L.; Lewison, R.L.; Welch, H.; Crowder, L.B. Seasonal spatial segregation in blue sharks (Prionace glauca) by sex and size class in the Northeast Pacific Ocean. Divers. Distrib. 2019. [Google Scholar] [CrossRef]
  75. Niblett, M.; Church, R.; Sweeney, S.; Barber, K.; Niblett, M.R.; Church, R.L.; Sweeney, S.H.; Barber, K.H. Characterizing Habitat Elements and Their Distribution over Several Spatial Scales: The Case of the Fisher. Forests 2017, 8, 186. [Google Scholar] [CrossRef]
  76. Jeon, J.; Taylor, J.W. Using Conditional Kernel Density Estimation for Wind Power Density Forecasting. J. Am. Stat. Assoc. 2012, 107, 66–79. [Google Scholar] [CrossRef] [Green Version]
  77. Juban, J.; Fugon, L.; Kariniotakis, G. Probabilistic Short-Term Wind Power Forecasting Based on Kernel Density Estimators. In Proceedings of the European Wind Energy Conference and Exhibition, EWEC 2007, Milan, Italy, 7–10 May 2007. [Google Scholar]
  78. Wang, L.; Chen, Z.; Ma, D.; Zhao, P.; Wang, L.; Chen, Z.; Ma, D.; Zhao, P. Measuring Carbon Emissions Performance in 123 Countries: Application of Minimum Distance to the Strong Efficiency Frontier Analysis. Sustainability 2013, 5, 5319–5332. [Google Scholar] [CrossRef] [Green Version]
  79. Fan, Z.; Fan, X.; Crosby, M.K.; Moser, W.K.; He, H.; Spetich, M.A.; Shifley, S.R. Spatio-temporal trends of oak decline and mortality under periodic regional drought in the Ozark Highlands of Arkansas and Missouri. Forests 2012, 3, 614–631. [Google Scholar] [CrossRef]
  80. Stacciarini, J.M.R.; Vacca, R.; Mao, L. Who and where: A socio-spatial integrated approach for community-based health research. Int. J. Environ. Res. Public Health 2018, 15, 1375. [Google Scholar] [CrossRef] [PubMed]
  81. Wang, J.; Kwan, M.P.; Chai, Y. An innovative context-based crystal-growth activity space method for environmental exposure assessment: A study using GIS and GPS trajectory data collected in Chicago. Int. J. Environ. Res. Public Health 2018, 15, 703. [Google Scholar] [CrossRef] [PubMed]
  82. Wang, C.-C.; Chang, C.-D.; Jiang, B. Developing a Health Risk Evaluation Method for Triple H. Int. J. Environ. Res. Public Health 2019, 16, 1168. [Google Scholar] [CrossRef] [PubMed]
  83. Bonato, M.; Parazzini, M.; Chiaramello, E.; Fiocchi, S.; Le Brusquet, L.; Magne, I.; Souques, M.; Röösli, M.; Ravazzani, P.; Bonato, M.; et al. Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling. Int. J. Environ. Res. Public Health 2018, 15, 1963. [Google Scholar] [CrossRef] [PubMed]
  84. Chiu, S.-T. Bandwidth Selection for Kernel Density Estimation. Ann. Stat. 1991, 19, 1883–1905. [Google Scholar] [CrossRef]
  85. Sheather, S.J.; Jones, M.C. A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 53, 683–690. [Google Scholar] [CrossRef]
  86. Krisp, J.M.; Peters, S.; Murphy, C.E.; Fan, H. Visual Bandwidth Selection for Kernel Density Maps. Photogramm. Fernerkund. Geoinf. 2009, 2009, 445–454. [Google Scholar] [CrossRef]
  87. Di Piazza, A.; Conti, F.L.; Viola, F.; Eccel, E.; Noto, L.V. Comparative analysis of spatial interpolation methods in the Mediterranean area: Application to temperature in Sicily. Water 2015, 7, 1866–1888. [Google Scholar] [CrossRef]
  88. Xia, X.; Qi, Q.; Liang, H.; Zhang, A.; Jiang, L.; Ye, Y.; Liu, C.; Huang, Y. Pattern of Spatial Distribution and Temporal Variation of Atmospheric Pollutants during 2013 in Shenzhen, China. ISPRS Int. J. Geo-Inf. 2016, 6, 2. [Google Scholar] [CrossRef]
  89. Kethireddy, S.R.; Tchounwou, P.B.; Ahmad, H.A.; Yerramilli, A.; Young, J.H. Geospatial interpolation and mapping of tropospheric ozone pollution using geostatistics. Int. J. Environ. Res. Public Health 2014, 11, 983–1000. [Google Scholar] [CrossRef]
  90. Johnson, B.; Tateishi, R.; Kobayashi, T. Remote sensing of fractional green vegetation cover using spatially-interpolated endmembers. Remote Sens. 2012, 4, 2619–2634. [Google Scholar] [CrossRef]
  91. Huo, X.-N.; Li, H.; Sun, D.-F.; Zhou, L.-D.; Li, B.-G.; Huo, X.-N.; Li, H.; Sun, D.-F.; Zhou, L.-D.; Li, B.-G. Combining Geostatistics with Moran’s I Analysis for Mapping Soil Heavy Metals in Beijing, China. Int. J. Environ. Res. Public Health 2012, 9, 995–1017. [Google Scholar] [CrossRef] [PubMed]
  92. Chabala, L.M.; Mulolwa, A.; Lungu, O. Application of Ordinary Kriging in Mapping Soil Organic Carbon in Zambia. Pedosphere 2017, 27, 338–343. [Google Scholar] [CrossRef]
  93. Gharechelou, S.; Tateishi, R.; Sharma, R.; Johnson, B. Soil Moisture Mapping in an Arid Area Using a Land Unit Area (LUA) Sampling Approach and Geostatistical Interpolation Techniques. ISPRS Int. J. Geo-Inf. 2016, 5, 35. [Google Scholar] [CrossRef]
  94. Jia, Z.; Zhou, S.; Su, Q.; Yi, H.; Wang, J.; Jia, Z.; Zhou, S.; Su, Q.; Yi, H.; Wang, J. Comparison Study on the Estimation of the Spatial Distribution of Regional Soil Metal(loid)s Pollution Based on Kriging Interpolation and BP Neural Network. Int. J. Environ. Res. Public Health 2017, 15, 34. [Google Scholar] [Green Version]
  95. Zhang, Z.; Sun, Y.; Yu, D.; Mao, P.; Xu, L. Influence of sampling point discretization on the regional variability of soil organic carbon in the Red Soil Region, China. Sustainability 2018, 10, 3603. [Google Scholar] [CrossRef]
  96. Szcześniak, M.; Piniewski, M. Improvement of Hydrological Simulations by Applying Daily Precipitation Interpolation Schemes in Meso-Scale Catchments. Water 2015, 7, 747–779. [Google Scholar] [CrossRef]
  97. Curtarelli, M.; Leão, J.; Ogashawara, I.; Lorenzzetti, J.; Stech, J.; Curtarelli, M.; Leão, J.; Ogashawara, I.; Lorenzzetti, J.; Stech, J. Assessment of Spatial Interpolation Methods to Map the Bathymetry of an Amazonian Hydroelectric Reservoir to Aid in Decision Making for Water Management. ISPRS Int. J. Geo-Inf. 2015, 4, 220–235. [Google Scholar] [CrossRef]
  98. Dysarz, T. Development of RiverBox—An ArcGIS Toolbox for River Bathymetry Reconstruction. Water 2018, 10, 1266. [Google Scholar] [CrossRef]
  99. Jung, S.-W.; Lee, K.; Cho, Y.-S.; Choi, J.-H.; Yang, W.; Kang, T.-S.; Park, C.; Kim, G.-B.; Yu, S.-D.; Son, B.-S.; et al. Association by Spatial Interpolation between Ozone Levels and Lung Function of Residents at an Industrial Complex in South Korea. Int. J. Environ. Res. Public Health 2016, 13, 728. [Google Scholar] [CrossRef]
  100. Xi, Y.; Ren, F.; Liang, S.; Zhang, J.; Lin, D.-N.; Xi, Y.; Ren, F.; Liang, S.; Zhang, J.; Lin, D.-N. Spatial Analysis of the Distribution, Risk Factors and Access to Medical Resources of Patients with Hepatitis B in Shenzhen, China. Int. J. Environ. Res. Public Health 2014, 11, 11505–11527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  101. Cressie, N. Spatial prediction and ordinary kriging. Math. Geol. 1988, 20, 405–421. [Google Scholar] [CrossRef]
  102. Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
  103. Hernández-Ceballos, M.Á.; De Felice, L. Air Mass Trajectories to Estimate the “Most Likely” Areas to Be Affected by the Release of Hazardous Materials in the Atmosphere—Feasibility Study. Atmosphere 2019, 10, 253. [Google Scholar] [CrossRef]
Sustainability 11 05616 g001 550
Figure 1. Types of non-movable monuments in Poland. Own elaboration using information from [23] and information sign “Monument protected by law” (pol. Zabytek chroniony prawem). Non-movable monuments entered in the register of monuments are marked by this sign, it is an international symbol of cultural heritage protection, the sign of the Blue Shield [24]. The description of the sign was included in the 1954 Hague Convention [25], for the protection of monuments during armed conflicts, and the originator of the graphic form and its author was the Polish architect, prof. Jan Zachwatowicz.
Figure 1. Types of non-movable monuments in Poland. Own elaboration using information from [23] and information sign “Monument protected by law” (pol. Zabytek chroniony prawem). Non-movable monuments entered in the register of monuments are marked by this sign, it is an international symbol of cultural heritage protection, the sign of the Blue Shield [24]. The description of the sign was included in the 1954 Hague Convention [25], for the protection of monuments during armed conflicts, and the originator of the graphic form and its author was the Polish architect, prof. Jan Zachwatowicz.
Sustainability 11 05616 g001
Sustainability 11 05616 g002 550
Figure 2. Administrative divisions of Poland (with illustrative map of Poland’s location in Europe). Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28].
Figure 2. Administrative divisions of Poland (with illustrative map of Poland’s location in Europe). Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28].
Sustainability 11 05616 g002
Sustainability 11 05616 g003 550
Figure 3. The number of non-movable monuments in voivodeships in Poland. Own elaboration using Microsoft Excel software, on the basis of: polish administrative data from [28], point data from NHBP.
Figure 3. The number of non-movable monuments in voivodeships in Poland. Own elaboration using Microsoft Excel software, on the basis of: polish administrative data from [28], point data from NHBP.
Sustainability 11 05616 g003
Sustainability 11 05616 g004 550
Figure 4. Location of non-movable monuments in Poland. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Figure 4. Location of non-movable monuments in Poland. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Sustainability 11 05616 g004
Sustainability 11 05616 g005 550
Figure 5. Map of the density of non-movable monuments in Poland. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], point data from NHBP.
Figure 5. Map of the density of non-movable monuments in Poland. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], point data from NHBP.
Sustainability 11 05616 g005
Sustainability 11 05616 g006 550
Figure 6. Number of non-movable monuments in administrative division units: (a) voivodeships, (b) poviats, (c) municipalities. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Figure 6. Number of non-movable monuments in administrative division units: (a) voivodeships, (b) poviats, (c) municipalities. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Sustainability 11 05616 g006
Sustainability 11 05616 g007 550
Figure 7. Number of non-movable monuments in Poland, simple kriging method, generalization for administrative division units: (a) voivodeships, (b) poviats, (c) municipalities. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Figure 7. Number of non-movable monuments in Poland, simple kriging method, generalization for administrative division units: (a) voivodeships, (b) poviats, (c) municipalities. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of: world data from [27], polish administrative data from [28], point data from NHBP.
Sustainability 11 05616 g007
Sustainability 11 05616 g008 550
Figure 8. Model showing the process of generating a point layer to perform interpolation, based on a hexagon of a given size. Own elaboration using ArcMap component of ArcGIS 10.6.
Figure 8. Model showing the process of generating a point layer to perform interpolation, based on a hexagon of a given size. Own elaboration using ArcMap component of ArcGIS 10.6.
Sustainability 11 05616 g008
Sustainability 11 05616 g009 550
Figure 9. Model showing the process of assigning raster layer values to test points. Own elaboration using ArcMap component of ArcGIS 10.6.
Figure 9. Model showing the process of assigning raster layer values to test points. Own elaboration using ArcMap component of ArcGIS 10.6.
Sustainability 11 05616 g009
Sustainability 11 05616 g010 550
Figure 10. Mean values of Pearson’s correlation coefficient, accuracy level 10 km2. Own elaboration.
Figure 10. Mean values of Pearson’s correlation coefficient, accuracy level 10 km2. Own elaboration.
Sustainability 11 05616 g010
Sustainability 11 05616 g011 550
Figure 11. Mean values of Pearson’s correlation coefficient, accuracy level 5 km2. Own elaboration.
Figure 11. Mean values of Pearson’s correlation coefficient, accuracy level 5 km2. Own elaboration.
Sustainability 11 05616 g011
Sustainability 11 05616 g012 550
Figure 12. Mean values of Pearson’s correlation coefficient, accuracy level 1 km2. Own elaboration.
Figure 12. Mean values of Pearson’s correlation coefficient, accuracy level 1 km2. Own elaboration.
Sustainability 11 05616 g012
Sustainability 11 05616 g013 550
Figure 13. Hexagonal grid with an area of 132 km2. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of world data from [27].
Figure 13. Hexagonal grid with an area of 132 km2. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of world data from [27].
Sustainability 11 05616 g013
Sustainability 11 05616 g014 550
Figure 14. Map of spatial distribution of non-movable monuments, generalized for 132 km2 hexagon. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of world data from [27].
Figure 14. Map of spatial distribution of non-movable monuments, generalized for 132 km2 hexagon. Own elaboration using ArcMap component of ArcGIS 10.6, on the basis of world data from [27].
Sustainability 11 05616 g014
Table
Table 1. Collected root-mean-square errors. Own elaboration.
Table 1. Collected root-mean-square errors. Own elaboration.
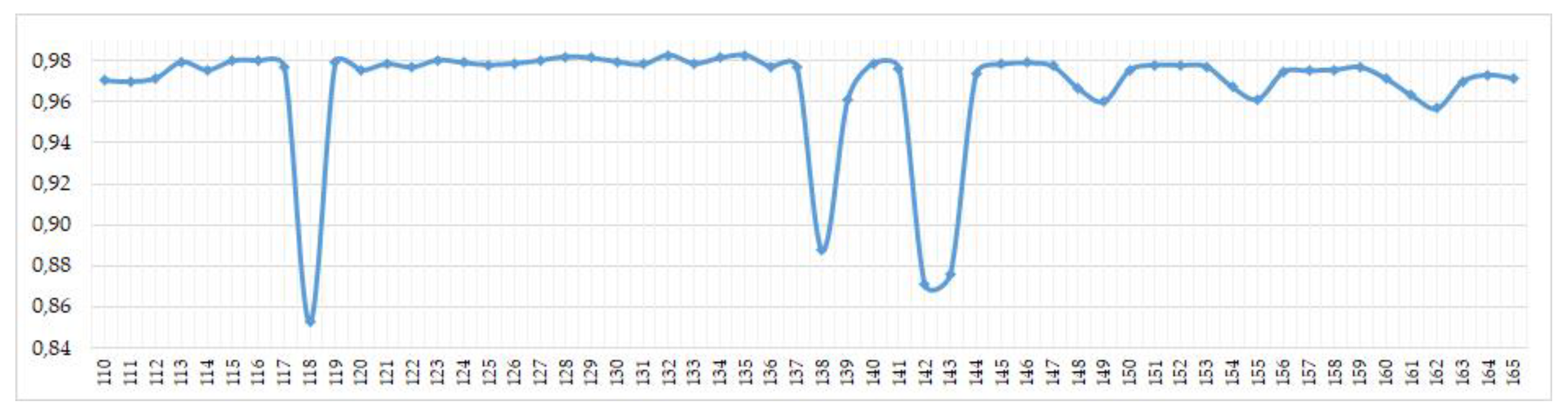
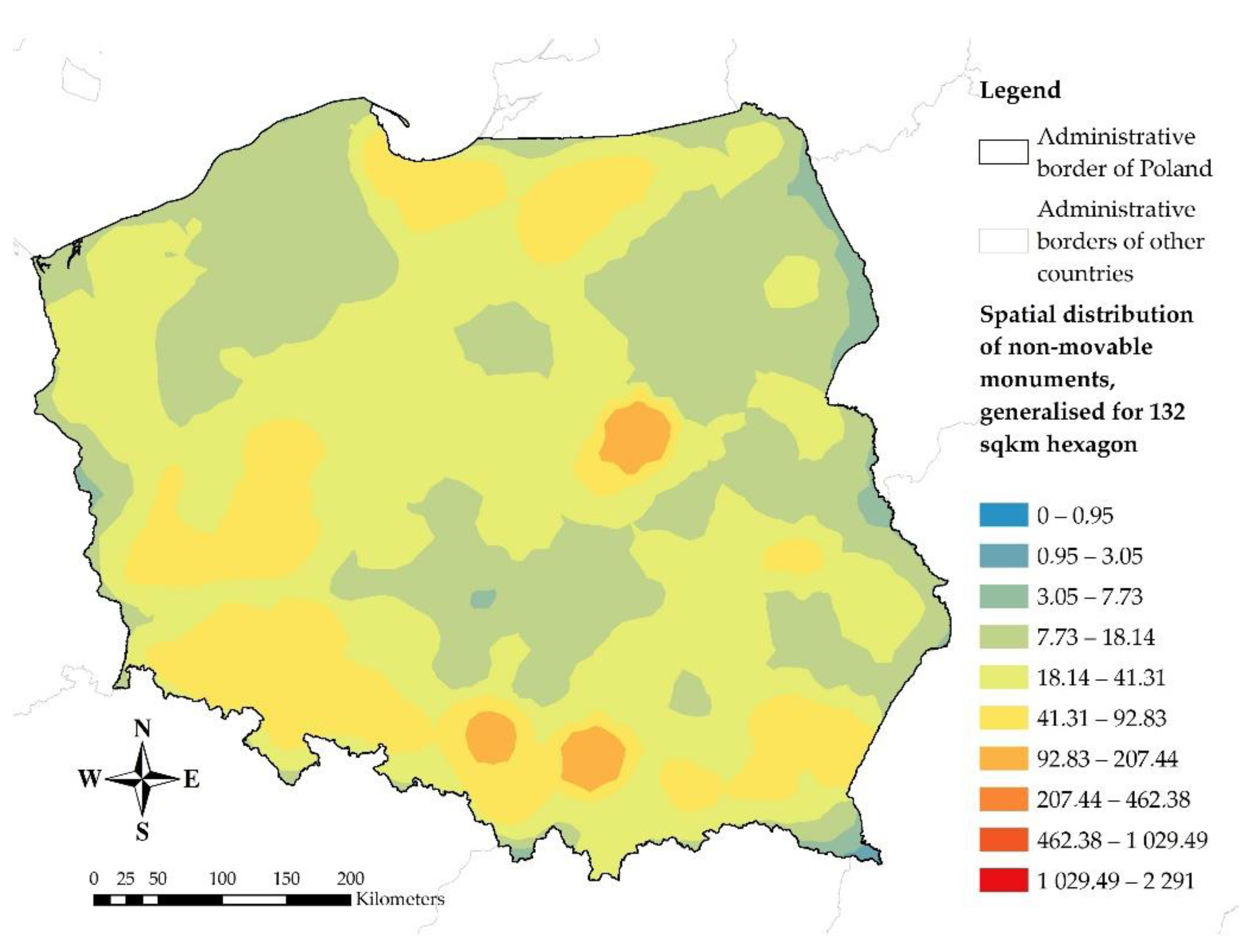
Interpolation MethodVoivodeshipsPoviatsMunicipalities
Inverse distance weighting (IDW)2735.33226.0694.42
Global polynomial interpolation (GPI)4709.37231.2391.86
Radial basis function (RBF)2813.37222.0694.14
Local polynomial interpolation (LPI)3672.84225.6491.77
Ordinary kriging (OK)2477.61230.3096.06
Simple kriging (SK)2223.73215.7091.52
Universal kriging (UK)2477.61228.8895.89
Disjunctive kriging (DK)2477.61217.6591.64
Empirical Bayesian kriging (EBK)2538.04226.0194.42
Table
Table 2. Additional information about individual data sets. Own elaboration.
Table 2. Additional information about individual data sets. Own elaboration.
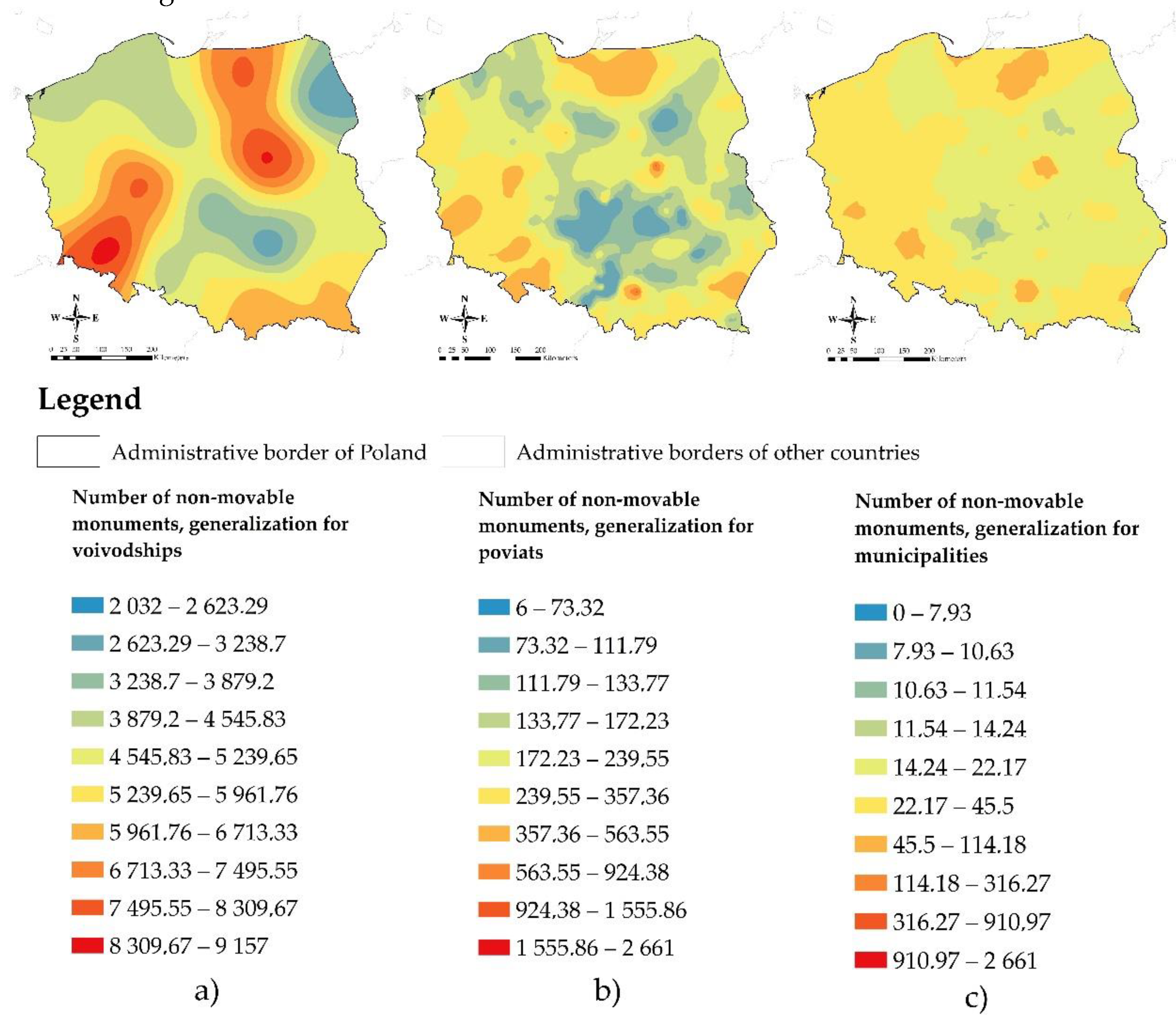
MeasureVoivodeshipsPoviatsMunicipalities
Skewness0.345.5017.08
Kurtosis1.8549.21408.73
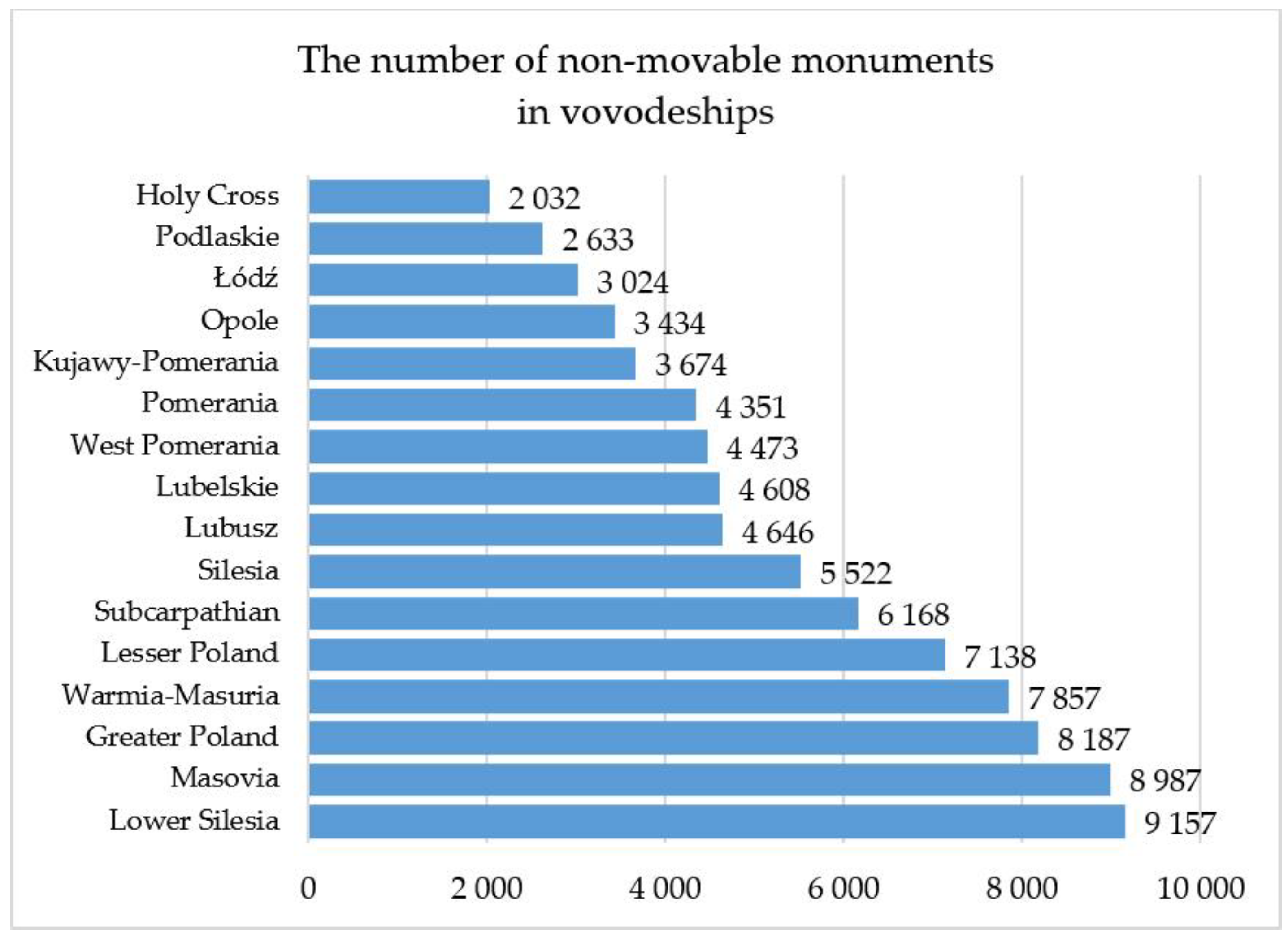
Minimum203260
Maximum915726612661
Mean5368.10226.0334.675
Standard deviation2295.40231.6892.358
Table
Table 3. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 10 km2. Own elaboration.
Table 3. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 10 km2. Own elaboration.
Hexagon SizeTest Layer 1Test Layer 2Test Layer 3Test Layer 4Test Layer 5Mean
100.680.680.670.670.670.67
200.760.750.750.750.750.75
300.800.810.800.790.800.80
400.820.820.820.820.820.82
500.840.840.840.840.840.84
600.860.860.860.860.860.86
700.860.860.860.850.850.85
800.860.860.860.860.860.86
900.860.860.860.850.860.86
1000.870.870.870.870.870.87
1100.970.970.970.970.970.97
1200.980.980.980.970.970.98
1300.980.980.980.980.980.98
1400.980.980.980.980.980.98
1500.980.980.980.980.970.98
1600.970.970.970.970.970.97
1700.910.920.920.910.910.92
1800.870.870.880.870.880.87
1900.950.950.950.940.950.95
2000.950.950.950.950.940.95
2100.900.910.910.900.900.90
2200.880.880.880.880.880.88
2300.870.870.870.860.870.87
2400.890.890.880.880.880.88
2500.860.860.860.860.860.86
2600.890.890.890.880.880.88
2700.860.860.860.860.860.86
2800.880.870.880.870.870.87
2900.860.870.870.860.860.86
3000.870.870.880.870.870.87
Table
Table 4. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 5 km2. Own elaboration.
Table 4. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 5 km2. Own elaboration.
Hexagon SizeTest Layer 1Test Layer 2Test Layer 3Test Layer 4Test Layer 5Mean
1100.9700.9720.9710.9710.9680.970
1150.9790.9790.9810.9810.9800.980
1200.9760.9760.9770.9740.9740.975
1250.9780.9790.9780.9780.9770.978
1300.9790.9810.9800.9800.9780.980
1350.9830.9840.9830.9830.9820.983
1400.9790.9800.9800.9790.9770.979
1450.9790.9780.9790.9780.9770.978
1500.9760.9750.9760.9770.9740.976
1550.9620.9630.9600.9620.9600.961
1600.9720.9720.9710.9710.9710.971
1650.9710.9700.9720.9720.9710.971
1700.9150.9180.9160.9120.9150.915
1750.8800.8780.8790.8760.8780.878
1800.8750.8710.8760.8700.8760.874
1850.9330.9330.9320.9290.9290.931
1900.9480.9500.9470.9440.9460.947
1950.8980.8940.8990.8960.8970.897
2000.9460.9470.9460.9450.9440.946
Table
Table 5. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 1 km2. Own elaboration.
Table 5. Values of the correlation coefficient for particular sizes of hexagons, accuracy level 1 km2. Own elaboration.
Hexagon SizeTest Layer 1Test Layer 2Test Layer 3Test Layer 4Test Layer 5Mean
1100.96990.97190.97110.97100.96850.9705
1110.96890.97170.97020.97080.96810.9699
1120.97170.97200.97260.97140.97050.9716
1130.98020.97910.97850.98010.97990.9796
1140.97620.97530.97550.97680.97420.9756
1150.97950.97930.98110.98110.97950.9801
1160.98090.98010.98100.97990.97860.9801
1170.97790.97740.97840.97660.97660.9774
1180.85640.85420.85320.84730.85140.8525
1190.97930.97930.98020.97900.97770.9791
1200.97610.97600.97670.97440.97380.9754
1210.97800.97800.97980.98020.97690.9786
1220.97780.97640.97790.97800.97460.9769
1230.98150.98030.98070.98150.97850.9805
1240.98040.97760.98050.97980.97740.9791
1250.97830.97850.97810.97840.97720.9781
1260.97950.97790.97890.98000.97770.9788
1270.98050.98030.98060.98110.97890.9803
1280.98270.98190.98240.98220.98110.9821
1290.98200.98210.98190.98130.98010.9815
1300.97920.98100.98040.97970.97790.9796
1310.97780.97880.97940.97870.97690.9783
1320.98220.98220.98430.98390.98210.9829
1330.97870.97910.97950.97880.97790.9788
1340.98110.98190.98190.98180.98080.9815
1350.98290.98370.98290.98250.98230.9828
1360.97700.97770.97760.97700.97660.9772
1370.97690.97690.97850.97790.97670.9774
1380.89020.88650.88830.88550.88730.8875
1390.96200.96360.96120.95940.96060.9614
1400.97880.98030.97970.97890.97720.9790
1410.97540.97890.97690.97560.97480.9763
1420.87260.86820.87380.87000.87180.8713
1430.87800.87490.87900.87330.87600.8762
1440.97300.97450.97400.97370.97250.9735
1450.97920.97770.97880.97830.97690.9782
1460.97970.97950.97940.97940.97720.9790
1470.97740.97840.97730.97770.97620.9774
1480.96650.96860.96650.96640.96470.9665
1490.96120.96190.96000.95950.95860.9602
1500.97560.97530.97570.97670.97440.9755
1510.97880.97770.97840.97900.97600.9780
1520.97820.97810.97830.97910.97590.9779
1530.97750.97710.97690.97780.97660.9772
1540.96740.96850.96590.96790.96670.9673
1550.96170.96280.96020.96160.96040.9613
1560.97470.97480.97540.97440.97370.9746
1570.97520.97480.97530.97590.97490.9752
1580.97640.97520.97540.97650.97520.9757
1590.97760.97660.97650.97730.97670.9769
1600.97160.97220.97120.97140.97060.9714
1610.96300.96410.96300.96380.96190.9632
1620.95750.95700.95630.95690.95640.9568
1630.97000.96990.97150.96920.96940.9700
1640.97360.97260.97450.97290.97230.9732
1650.97130.97040.97240.97230.97100.9715

Share and Cite

MDPI and ACS Style

Ciski, M.; Rząsa, K.; Ogryzek, M. Use of GIS Tools in Sustainable Heritage Management—The Importance of Data Generalization in Spatial Modeling. Sustainability 2019, 11, 5616. https://doi.org/10.3390/su11205616

AMA Style

Ciski M, Rząsa K, Ogryzek M. Use of GIS Tools in Sustainable Heritage Management—The Importance of Data Generalization in Spatial Modeling. Sustainability. 2019; 11(20):5616. https://doi.org/10.3390/su11205616

Chicago/Turabian Style

Ciski, Mateusz, Krzysztof Rząsa, and Marek Ogryzek. 2019. "Use of GIS Tools in Sustainable Heritage Management—The Importance of Data Generalization in Spatial Modeling" Sustainability 11, no. 20: 5616. https://doi.org/10.3390/su11205616

APA Style

Ciski, M., Rząsa, K., & Ogryzek, M. (2019). Use of GIS Tools in Sustainable Heritage Management—The Importance of Data Generalization in Spatial Modeling. Sustainability, 11(20), 5616. https://doi.org/10.3390/su11205616

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop