1. Introduction
In the 21st century, the low-carbon economy has entered the mainstream of world economic development. In recent decades, China’s rapid economic growth has relied heavily on a large amount of resources and energy consumption, which is accompanied by a sharp increase in carbon emissions. Since 2006, China has surpassed the United States to become the world’s largest carbon emitter. In response to the growing problem of greenhouse gas emissions, the Chinese government has drawn up a series of emission reduction plans. Besides, China has announced that by 2020 and 2030 its carbon dioxide emissions per unit of GDP will be reduced by 40–45% and 60–65%, respectively, on a 2005 basis at the 2009 United Nations Climate Change Conference in Copenhagen and the 2015 Paris Climate Conference. In order to achieve the above emission reduction goals and allocate the reduction tasks for various provinces and municipalities in a reasonable manner, it is necessary to deeply understand the change characteristics of regional carbon emissions and their influencing factors. Therefore, it is of great significance to explore the convergence of carbon emissions in China.
In recent years, scholars have carried out many studies on the convergence of carbon emissions in China. The common convergence test methods used are mainly based on the following three classical models: (1)
σ-convergence test. The value of
σ is used to measure the cross-sectional standard deviation of various regions. If the value becomes smaller with time, the inter-regional carbon emissions tend to converge. For example, Yu et al. (2018) uses the
σ-convergence test to study the convergence of carbon emissions intensity across 24 industrial sectors in China, and it is found that the various industrial sectors showed a trend of divergence after convergence [
1]. However, because the value of
σ only contains a little bit of information, the kernel density model is generally used for estimation; it is also a kind of
σ-convergence test in essence, but can provide more information (Stegman and Mckibbin, 2005) [
2]. Hu et al. (2015) find that the difference in carbon emissions between China’s provinces showed a trend of reduction through kernel density analysis [
3]; (2)
β-convergence test.
β-convergence mainly shows that the per capita carbon emission growth rate among different economic systems is negatively correlated with the initial carbon emission growth level, and according to whether the economy has heterogeneity, it can be divided into absolute convergence and conditional convergence. By using this method, Zhao et al. (2015) have found that China’s province-level CO
2 emission intensity exhibits the
β-convergence. Considering the spatial effect, Huang and Meng (2013) use the modified spatial
β-convergence test to analyze the convergence of per capita CO
2 emissions in Chinese cities, and conclude that the per capita carbon dioxide emissions in Chinese cities tend to converge [
4,
5]; (3) Stochastic convergence test. This method performs a unit root test on the sample observations to check whether the data is stable. If the answer is yes, it means the sample has stochastic convergence. For instance, Wang and Zhang (2014) analyzed the carbon emission convergence of six sectors in 28 provinces of China by using this method, and concluded that the carbon emission intensity of the six sectors have a stochastic convergence [
6]; Moreover, Li et al. (2017) focused on the study area in the Yangtze River Delta region of China, and also obtained similar convergence conclusions [
7].
The above research is of great value for understanding the changing trend and convergence characteristics of China’s carbon emissions, and it also provides an important reference for this article, but it still has two shortcomings: (1) as for the research objects, most of the literature is about China’s total carbon emissions, but less about the carbon emissions of individual sectors or industries. However, in order to implement emission reduction plans and policies, it is necessary to study the changes in carbon emissions of specific sectors and industries. In fact, transportation has become the second largest sector in energy consumption, ranking only after the industrial sector (Lin and Xie, 2014) [
8] and its carbon emissions account for 23.96% of the total global carbon emissions (International Energy Agency, 2017) [
9]. In China, transportation carbon emissions are also growing rapidly year by year, accounting for a large proportion of the total carbon emissions (Wang et al., 2011) [
10]; (2) As for the specific research approaches, the convergence test methods still have some defects in existing literature. First, the
σ-convergence only gives a little information. Second, the negative regression coefficient of initial per capita carbon dioxide emissions during convergence does not fully explain the existence of
β-convergence. Third, the stochastic convergence test requires that the individuals must be homogeneous (Herrerias, 2013) [
11]. Finally, in terms of exploring the club convergence characteristics, most of the literature (Yao et al., 2001; Zhang et al., 2001; Hao et al., 2015) usually subjectively classify clubs according to geographic or economic information, lacking a reasonable division criteria [
12,
13,
14], which would lead to inconsistencies in conclusions. In order to compensate the shortage of the traditional convergence test methods, Phillips and Sul (2007) propose a new convergence test method, i.e., the log
t regression test method based on the nonlinear time-varying factor model. This method considers the heterogeneity among individuals and allows this heterogeneity to change over time. Meanwhile, Phillips and Sul (2007) also develop a new clustering algorithm for club convergence, which can classify the sample into different convergence clubs according to the data characteristics, so as to avoid the deviation caused by artificial classification [
15]. Therefore, the log
t regression test method and the club clustering algorithm have been widely used in many different research fields such as environment (Wang et al., 2014; Herrerias, 2013; Apergis and Payne, 2017), income distribution (Ghosh et al., 2013; Tian et al., 2016), energy (Parker and Liddle, 2016), security investment (Apergis et al., 2014), etc [
11,
16,
17,
18,
19,
20,
21].
As one of China’s important basic industries, transportation is the target field of carbon emission reduction because of its huge energy consumption. However, at present, there are only a few studies concerning the convergence of the carbon emissions in the transportation sector (Apergis and Payne, 2017; Xiao et al., 2015) [
17,
22]. In view of this, this article analyzes the convergence of per capita transportation carbon emissions in China’s 30 provinces and municipalities over the period of 2005–2015. In order to avoid the defects (i.e., the convergence test and club classification methods), we use the log
t regression test and the club clustering algorithm proposed by Phillips and Sul (2007) to explore the convergence of per capita transportation carbon emissions in China [
15]. Moreover, previous studies on club convergence have focused on the identification and analysis of convergence (Burnett, 2016; Ulucak and Apergis, 2018), and less on the influencing factors of it; this article also uses the Ordered Logit model to further investigate these factors, and then conducts a more in-depth discussion on the evolution law of transportation carbon emission, in order to propose more effective policy recommendations for emission reduction [
23,
24].
This paper is organized into five sections. Specifically,
Section 2 is the method and data, mainly introducing the log
t regression test method, the data sources, and the processing procedure.
Section 3 is the convergence test, expounding the convergence of per capita transportation carbon emissions in China and the test results.
Section 4 analyzes factors influencing the club convergence.
Section 5 is the conclusion and policy suggestion.
3. Convergence Test
In order to identify the convergence characteristics of per capita transportation carbon emissions in China’s 30 provinces and municipalities, the log
t regression test results are shown in
Table 2.
As can be seen from
Table 2, the
t statistic obtained through the regression is −8.7790, which is much smaller than −1.65. Therefore, the null hypothesis on the convergence of the whole sample is rejected significantly, which indicates that the per capita transportation carbon emissions in China’s 30 provinces and municipalities does not converge on the whole. Then, we use the club clustering algorithm to check whether there may be club convergence within the sample, and the results are shown in
Table 3.
As can be seen from
Table 3, the per capita transportation carbon emissions across 28 provinces and municipalities initially converged to four clubs whose
statistics are significantly greater than −1.65, while Beijing and Liaoning form a divergent group. Next, in order to test whether there are potential clubs that can be merged, we continue to perform the club merging test. Then, we use the method modified by Schnurbus et al. (2017), and the results are shown in
Table 4 [
26].
As can be seen from
Table 4, the
statistics of the club merging tests on the initial clubs 1 and 2, as well as the initial clubs 2 and 3 are both smaller than −1.65, indicating that these initial clubs fail to pass the merging test. However, the
statistic of the clubs 3 and 4 is 0.2735, which means that they could be merged into the new club 3. Therefore, through the merging test, China’s 30 provinces and municipalities are classified into three convergence clubs and one divergent group, which is shown in
Table 5. For the three convergence clubs, their mean values of per capita transportation carbon emissions significantly varied. As can be seen from
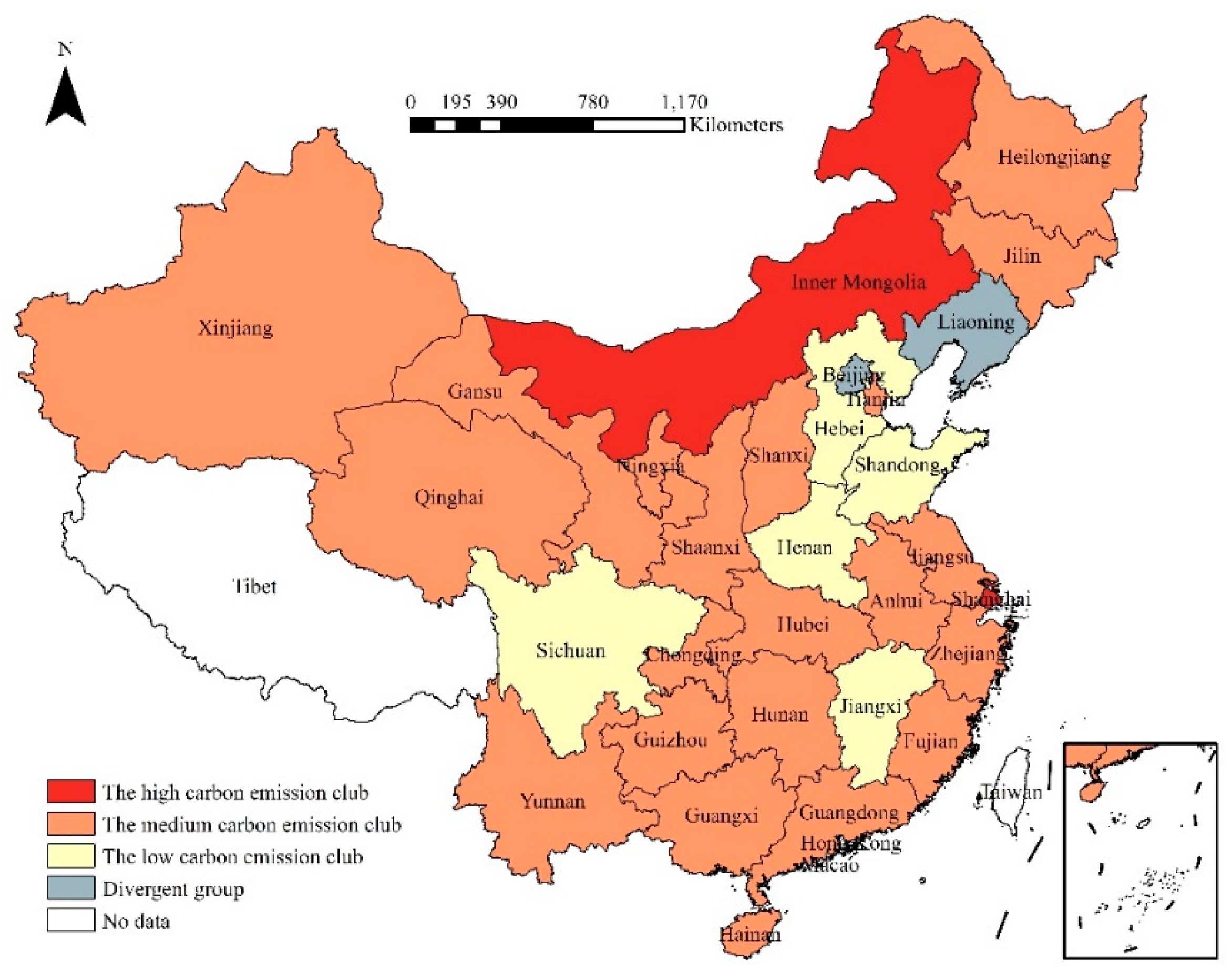
Table 6, Club 1, only consisting of 2 members, has the highest mean value of 0.3662; Club 2, consisting of 21 members, has the medium mean value of 0.1098; Club 3, consisting of 5 members, has the lowest mean value of 0.0716. Therefore, the convergence clubs 1, 2, and 3 are defined as the high carbon emission club, the medium carbon emission club, and the low carbon emission club, respectively. The spatial distribution of the three convergence clubs and one divergent group is shown in
Figure 1.
As can be seen from
Table 5, the high carbon emission club only consists of Inner Mongolia and Shanghai. The main reasons are as follows: (1) as the center of the economy in China, Shanghai is not only an important land transportation hub in eastern China, but also closely linked to the central and western provinces. Moreover, it is also an important port city connecting China to the world with huge flows of people and goods. According to the calculation results using statistical data, its traffic turnover volume ranks first in China from 2005 to 2015. (2) Inner Mongolia has a vast territory and is adjacent to various provinces. On the one hand, although it has a relatively low economic development level and relatively backward energy-saving and emission reduction technologies, its traffic infrastructure construction is relatively perfect. For instance, its railway operating mileage ranks first and highway mileage ranks ninth in China in 2016 (National Bureau of Statistics of the People’s Republic of China, 2018) [
29]. On the other hand, Inner Mongolia has rich mineral resources, thus increasing the freight turnover between it and the other provinces/municipalities. Obviously, its freight turnover volume is at the forefront of China. The above two reasons led to a large amount of transportation carbon emissions. Meanwhile, Inner Mongolia has a relatively small population, ultimately resulting in relatively high per capita transportation carbon emissions.
The medium carbon emission club consisted of 21 members covering the eastern, central and western regions in China. To be specific, the provinces in the western region have a relatively small population and a relatively low demand for transportation. However, its resources are rich in energy and its technology is relatively backward, which requires more energy to transport local resources. In this club, Hunan, Hubei, Anhui, and Shanxi provinces are located in the hinterland of China and easily accessible. Meanwhile, they are the main labor outflow provinces in China, thus resulting in relatively high transportation carbon emissions. Although the eastern coastal provinces, such as Jiangsu, Zhejiang, Guangdong, Tianjin, etc., have relatively advanced energy-saving and emission reduction technologies which can reduce transportation carbon emissions to some extent, they have a relatively developed economy, frequent foreign trade, and population movements. For example, Guangdong and Jiangsu have a relatively developed foreign trade, and attract large population inflows. In 2016, they respectively rank first and second with respect to the total import and export of goods in China. Therefore, the per capita transportation carbon emissions in those eastern coastal provinces converged to the medium carbon emission club.
The low carbon emission club consisted of 5 provinces including Hebei, Jiangxi, Shandong, Henan, and Sichuan with a large population. Among the top six provinces in population of China, four provinces are included in this club. Despite that they have a large amount of transportation carbon emissions due to the limitation of economy and technological development, they are affected by the average effect of the huge population, eventually converging to low-carbon clubs.
Different from the previous studies (Wang et al., 2014; Hao et al., 2015) [
14,
16], the classification of convergence clubs in this article does not overlap with the geographical division of China, which fully demonstrates that the log
t regression test method and the club clustering algorithm could identify the common characteristics of different regions. The geographical location is not the primary factor for the formation of convergence clubs in China.
4. Analysis of the Factors Influencing the Convergence
In order to further explore the reasons for the formation of the convergence clubs, we will analyze the factors influencing the club convergence of per capita transportation carbon emissions.
First, the dependent variable is the convergence club type of per capita transportation carbon emissions in China. According to the above results, the high carbon emission club, the medium carbon emission club, and the low carbon emission club are assigned the values of 1, 2, and 3, respectively. The higher the value, the better the performance of per capita transportation carbon emissions.
Second, we consider the following independent variables: (1) the development level of the transportation sector which is measured by the per capita transportation output; (2) the intensity of environmental regulation, measured by the proportion of industrial pollution control investment completion to local GDP; (3) the energy intensity of the transportation sector is measured by the ratio of regional transportation energy consumption to local GDP; (4) the energy structure of the transportation sector is represented by the consumption ratio of non-clean energy (specifically coke, raw coal, fuel oil, diesel, and crude oil) in energy consumption of the transportation industry; (5) the urbanization level which is measured by the ratio of the local urban population in the total population; (6) the relative price of energy is measured by the ratio of the purchasing price index of fuel and power to the ex-factory price indices of industrial products. The price is deflated to the price level of 2001; (7) and the fixed assets investment intensity of the transportation sector is measured by the per capita fixed assets investment of the transportation sector. In order to avoid the selection of defects such as outliers or statistical errors that may be caused by specific data for a certain year, all independent variables are the average of the 11-year data for 2005–2015. The above data is derived from the China Population and Employment Statistics Yearbook and China Statistical Yearbook, the provincial statistical yearbooks, and the National Bureau of Statistics of the People’s Republic of China.
Because the dependent variable is discrete ordered data, following the Mckelvey and Zavoina (1975) and Liu et al. (2018) [
30,
31], we use the Ordered Logit model to explore the factors influencing the club convergence of per capita transportation carbon emissions in China, as shown below:
Let
be an ordered dependent variable which is assigned with the values of
c (
c = 1, 2, 3), and
be the vector of the independent variables, where
i denotes the province/municipality
i. Let
be the probability that the individual
i is assigned with the dependent variable
c. Then, the cumulative probability distribution function can be defined as:
Based on the cumulative probability of the ordered dependent variable, the Ordered Logit model establishes the relationship between the independent variables and the club type probability sets:
where,
. Specifically,
is the estimate of coefficient. And the results are shown in
Table 7. The table also reports the regression coefficient and the marginal effects of independent variables.
As can be seen from
Table 7, the coefficient of the energy intensity of the transportation sector is significantly negative at the 1% confidence level, which shows that provinces with higher energy intensity of transportation will be more inclined to converge into high carbon emission clubs. The reason is that the energy intensity of transportation reflects the energy efficiency of the transportation industry in a region. The increase in energy consumption directly leads to an increase in carbon emissions, which results in the province tending to converge into clubs with high carbon emission levels.
The coefficient of the urbanization level is significantly negative at the 5% level. The provinces with higher urbanization levels tend to converge into clubs with high carbon emission levels, which is consistent with the findings of most of the existing literature (Wu et al., 2016; Li et al., 2017) [
7,
32]. On the one hand, the increase in urban population has increased demand for transportation in the region; on the other hand, with the improvement of the urbanization level, more economic exchange activities will be generated within regions and sufficient transportation capacity is needed to support the economic development of the city, which will eventually lead to the gradual convergence of the region into clubs with high carbon emission levels.
The coefficient of the fixed assets investment intensity of the transportation sector is significantly negative at the 5% confidence level, it is more likely that provinces with higher investment in fixed assets of transportation will converge to clubs with high carbon emission levels. The main reason is that the expansion of fixed assets investment of the transportation will promote the expansion of the transportation industry, which will consume more energy and generate a large amount of carbon emissions.
Finally, the coefficients of the development level and the energy structure of the transportation sector, as well as the relative price of energy are not significant; these variables do not affect the club convergence (see
Supplementary Materials).
5. Conclusions and Policy Implication
The CO
2 emissions from the transportation sector accounts for nearly a quarter of the total CO
2 emissions (International Energy Agency, 2017) [
9]. Since 1985, the average annual growth rate of the energy consumption in the transportation sector has been close to 8% in China, which is much higher than the average annual growth rate of the total energy consumption of 5.7% (Yuan et al., 2017), thereby driving the rapid growth of the transportation carbon emissions with an average annual growth rate of 10.56% (Wang et al., 2011) [
10,
33]. Therefore, studying the convergence of the transportation carbon emissions in China and its influencing factors is of great significance for the reduction of carbon emissions both in China and the world.
This article adopts the log
t regression test method and the club clustering algorithm proposed by Phillips and Sul (2007) to explore the convergence characteristics of per capita transportation carbon emissions in China’s provinces and municipalities [
12,
13,
14,
15]. Compared with the existing researches on club convergence of carbon emissions in China, this article not only identifies the characteristics of the club convergence of per capita transportation carbon emissions in China in a better manner, but also explores the factors influencing club convergence. Unfortunately, although this article has carried out a certain degree of improvement and innovation in research methods and research content, there are still some shortcomings. For example, due to the inability to obtain statistics on carbon emissions from transportation at the municipal level in China, when studying the factors affecting the convergence of China’s per capita transportation carbon emission clubs, there are only 28 provinces in the Ordered Logit regression model, and the sample size is too small. Moreover, the study period is relatively short. If there are official or authoritative organizations in the future to publish more comprehensive statistics on prefecture-level cities, we will conduct further in-depth research.
Based on the above conclusions, this article proposes the following policy suggestions on the reduction of the transportation carbon emissions in China:
First, the per capita transportation carbon emissions in China converged to three clubs with different carbon emission levels. Therefore, in order to reduce the transportation carbon emissions in China, Chinese governments should develop different emission reduction policies for different clubs. Specifically, for the high carbon emission club with only two members, rigorous environmental laws and regulations, as well as other related measures can be implemented, and the investment in environmental protection and governance should be increased; for the medium carbon emission club with many members, most of them have a relatively low economic development level and a relatively low science and technology level. Therefore, the government should strive to develop science and technology to promote the reduction of carbon emissions from the transportation sector and other sectors. The specific measures are as follows: (1) provide transportation enterprises with corresponding subsidies to purchase environmental protection equipment; (2) strengthen the cultivation of high-tech talents; (3) increase the investment in research and development of energy-saving and environmental protection technologies; (4) establish and perfect relevant institutions to promote the transformation and utilization of energy-saving and emission reduction technologies; for the low carbon emission club, its members have a large population. So, relevant policies should be formulated to improve public transportation facilities and control the number of private cars.
Second, there is a large gap between economic and technological development between clubs and members of the club. Therefore, it is necessary to improve the relevant institutions to promote clean energy and energy-saving technologies, as well as the flow of talents, and strengthen exchanges and cooperation between various clubs and members of the club in terms of transportation carbon emission reduction.
Finally, from the results of the Ordered Logit regression, we can know that the transportation department would adopt advanced energy-saving and emission reduction technologies to improve energy efficiency. At the same time, we must also innovate transportation tools, develop and promote new energy vehicles, and eliminate high-emission transportation vehicles. In terms of investment in transportation, the government cannot blindly expand the scale of transportation through investment, strive to improve transportation carrying capacity on the basis of the original scale through scientific management and planning. In addition, it is necessary to appropriately control the scale of the city, improve and rationally plan the various functional areas of the city, and promote the green and healthy development of the city.