Abstract
In a city, housing price varies with location. Thus, housing price plays an important role in detecting the spatial pattern of the city. Spatial interpolation methods have been widely used for simulating and predicting urban housing prices. In this paper, the Ordinary Kriging interpolation method is used for producing the digital elevation model (DEM) of urban housing prices. Based on the three-dimensional DEM of urban housing price, this paper develops a novel approach for geo–visual analytics of urban housing prices. To investigate and visualize the spatial morphology of housing price, we design the Water-flooding, Section-cutting and Belt-floating methods, and implement these methods with the 3D-analyst module in GIS environment. Then, we take Wuhan City as a case, apply this approach to analyze the complex spatial morphologic characteristics of the DEM for housing price and visualize the results from the multidimensional perspectives. The results show that the Water-flooding method effectively supports the investigation of the top areas of surface changes; Section-cutting method performs well in examining the profile or cross-section of the urban housing surface; and Belt-floating method is helpful for detecting the spatial variance of the urban housing surface through the routes of specific lines. The results demonstrate that the proposed approach works better than traditional methods in describing the complex spatial morphology of urban housing prices, and has an advantage in visualizing the analysis results.
1. Introduction
The relationships among residence location, commuting cost, and residence facility have always been the focus of much research, from urban location theory to residential location selection models [1] and the classical model for monocentric urban spatial structure built by Alonson (1964) [2], Mills (1967, 1972) [3,4] and Muth (1969) [5] (also known as the “AMM Model”). However, with the urban spatial structure becoming more and more complicated, it becomes difficult to describe and interpret urban spatial characteristics with the monocentric hypothesis and simple linear models [6]. Recent research has focused on the polycentric urban region in urban studies [7,8,9], as polycentric urban development morphology is becoming a trend [10]. The decentralization of urban factors provides a new dimension for depicting the urban spatial structure from the perspective of spatial morphology [11], functional heterogeneity [12,13], and housing price [14,15]. In particular, a large and growing amount of literature has employed various quantitative approaches to explore the number and morphology of the multiple centers of a city. For example, Adolphson (2009) [16] listed seven different methods for measuring the multicentricity of the Stockholm Region. Liu et al. (2015, 2016) [17,18] measured the polycentric structures of more than 300 Chinese cities based on intercity traffic network, population density, and other factors, and found that more than 90% of these Chinese cities have no more than four “centers”.
Based on the inherent linkage between housing and location as well as the sensitivity of housing price, the location and price of housing are typically one of the important factors for exploring the urban spatial structure [19]. In particular, with the rapid rise of housing prices in recent years, more and more attention has been paid to analyzing the sensitivity of housing price in Chinese cities [20]. The hedonic model is a common approach for quantitative analysis of spatial characteristics or gradient characteristics of the urban housing price or urban land price [19,21]. A lot of research has employed the hedonic model to analyze how urban housing prices are influenced by different factors, such as urban structure [14], subway traffic [22], lake landscape [23], waterfront resource [24], educational facility [25], central business district (CBD) location [19], waste-to-energy plants [26], urban improvement [27], agricultural land use [28], and proportion of household [29]. Several recent studies applied the hedonic model to examine the impact of environmental sustainability elements [30] and transit access [31,32] on urban housing price in Wuhan City, China. These models, however, do not perform well in depicting complex spatial morphologies and visualizing multiple dimensions. Besides which, previous research found that even if a city evolves from a monocentric structure to a polycentric structure, the variable of “distance to the urban center” can still interpret the urban spatial structure well. In some cases, the urban housing and land prices display complex spatial patterns, but these prices still tend to decline from the local CBD as the center to the ambient areas [33,34].
With the rapid development of GIS technologies and the gradual evolution towards Geographical Information Science [35], an increasing number of studies have introduced the GIS-based spatial analysis methods for analyzing spatial characteristics of urban housing. Spatial interpolation methods (such as Kriging method and Inverse Distance Weighted method) are often used to estimate the land price in an unknown area in a city [36,37]. An amount of literature uses Kriging and Co-Kriging for urban housing price prediction [38,39,40,41,42]. Some hedonic pricing models integrate different Kriging techniques for predicting house prices [43,44], and the performance of different semi-parametric spatial hedonic models have also been compared [45]. Previous research has indicated the limitations of Kriging and Co-Kriging techniques for housing market prices [46]. However, Kriging and Co-Kriging are constantly evolving, and new versions are constantly appearing [47]. Also, Kriging and Co-Kriging methods have been compared to traditional regression models, and the comparison has shown that they have the advantages of achieving quicker and better global prediction when the amount of the sample data is limited [48]. Meanwhile, the non-parameter-based spatial interpretation method can reduce the influence of subjective factors on the parameter model, and the smooth density surface produced by this method can support the analysis of urban spatial and structural characteristics. For example, McMillen and McDonald (1997) [33] designed the smooth density surface for employment with the non-parameter locally weighted regression model and identified the urban sub-center, and McMillen (2001, 2003) [49,50] further identified the urban employment center based on the non-parameter estimation model. Additionally, Redfearn (2007) [51] further improved and applied the identification method of the urban employment center. However, these studies do not focus on urban housing prices and are limited to geo–visual analytics.
Supported by GIS, the spatial interpolation methods have been widely used to produce the digital elevation model (DEM) and the digital terrain model (DTM). Most research uses limited topographic elevation data to estimate the digital expression of the topographic change, elevation change, and surface feature change [52]. The traditional digital terrain model has been widely used in natural science research fields such as land, hydrology, and meteorology, and surface roughness [53], slope [54], and curvature [55] are common indicators used to analyze and depict topographic characteristics. Over the past years, the DEM has also been successfully applied in social science areas, including the spatial distribution of urban factors and urban planning [20,42,52]. However, compared with the application of DEM in natural science, some application fields in the social sciences still need to be further explored, such as the characterization of complex spatial morphology, three-dimensional analysis, visualization, and so on. Thus, it is an area worth exploring in-depth of how to design new approaches in corresponding areas to conduct DEM-based analysis, depiction, and multidimensional visualization of urban housing price.
To sum up, since housing price is sensitive to urban location [56], its spatial distribution or gradient characteristics provides an important perspective to understand the urban spatial structure and identify the quantity and morphology of urban centers. Also, three-dimensional analysis methods have obvious advantages over two-dimensional approaches for urban studies, especially for multi-information presentation, result visualization, and complex spatial analysis. Previous research on urban housing prices mainly uses Kriging and Co-Kriging techniques for price prediction, while the application of geo–visual analytics is rare, especially for the analysis and visualization of non-linear complex urban spatial structures and spatial morphology. Further, in previous case studies in China, most of the housing price surface maps are two-dimensional, and few studies have conducted three-dimensional analysis. First, there is a lack of further refined treatment of the housing price surface, such as the elimination of unnecessary geographic elements. Second, there is a lack of profound analysis and visualization as to the tri-dimensional morphology of the DEM for housing price. Spatial interpretation methods (such as Kriging) provides the basis for producing urban housing price surface, while the DEM-based analysis indicators and methods in physical geography provide a good reference for housing price analysis. Illuminated by the idea of DEM-based terrain analysis, this article develops a geo–visual analytical method to investigate the complex spatial morphology of urban housing price. We will firstly produce a housing price DEM with spatial interpretation methods, which provides a basis for three-dimensional analysis and visualization. By using 3D-analyst components in ArcGIS and ArcScene, we propose a novel approach to geo–visual analytics of urban housing prices. Further, we take Wuhan City as a case, apply this approach to analyze complex spatial morphologic characteristics of the housing price DEM, and visualize the results from multidimensional perspectives.
2. Models and Methods
2.1. Digital Elevation Model for Urban Housing Price
Hedonic demand theory is the basis of hedonic housing price, which is a revealed preference method of estimating housing demand or value [57]. Previous studies on the hedonic housing price have concluded that the factors that influence housing price mainly include location, architectural structure, and neighborhood environment [58,59,60]. Urban housing price reflects the overall intent of consumers to pay for the characteristics implied in the housing price. We assume the housing price in any location i of the target city is Pi, then the location, structure, and neighborhood of location i can be expressed with the following formula:
where Li, Si, and Ni represent the location, structure, and neighborhood environment of location i, respectively. If the housing price in location i is higher than that in location j, we can infer that the location, structure, and neighborhood environment of houses in location i are superior to those of the houses in location j. If the architectural structures of houses in locations i and j are equivalent and the housing price in location i is higher than that in location j, we can infer the location and neighborhood in location i are superior to those in location j. In essence, the process of building the DEM for the urban housing price with the spatial interpolation method is to estimate the housing price value of an unknown space with known spatial data of the urban housing price, and finally obtain a continuous urban housing price surface (field).
In this paper, we use Ordinary Kriging to produce the spatial interpolation map and visualize the urban housing price surface (DEM). Ordinary Kriging is an interpolation method by which the interpolated values are modeled by a Gaussian process dominated by prior covariances. Based on the pioneer of the techniques [61], Matheron [62], and most recently Cressie [63], have laid out the statistical principles and theoretical basis of this method. This method can be expressed with the following formula [64]:
with the constraint of weights:
The expected value of the prediction error:
where P(xi) is the sample observation values, which correspond to locations xi in the study area of the city, x0 is a point that has not been sampled, and λi is the weight given to location i. It should be noted that does not represent the estimated value of the actual market transaction price in an unknown point, but can be seen as the “price index” under the specific assumption.
2.2. DEM-Based Analysis Method
In this study, we assume that the DEM for the urban housing price can be seen as a “housing price index surface” under the specific architectural structural standard in the global scope of the study area. The DEM for urban housing price constitutes the foundation for analyzing the spatial morphology and the variance of resident’s willingness to pay for the housing. It provides a perspective for understanding the urban spatial structure.
Different from the analysis and depiction of the DEM-based spatial morphology in the natural science area, the application of DEM for urban housing price need to be combined with urban space theory and the actual urban environment. Meanwhile, the approaches that can effectively analyze and express the spatial morphology of the DEM need to be adopted to address the actual study issues relating to the housing price. On the basis of previous studies, this paper undertakes geo–visual analytics of the morphological characteristics of the housing price DEM by using the 3D analyst module in ArcGIS and ArcScene (Figure 1).
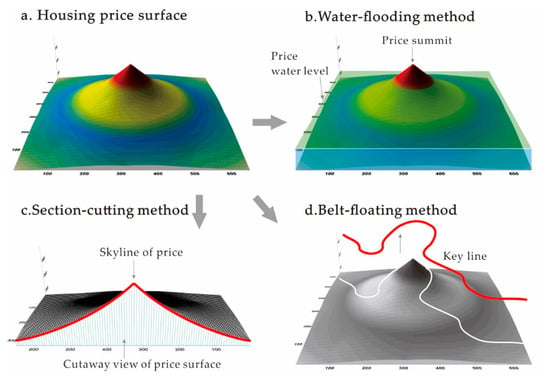
Figure 1.
Sketches of DEM-based analysis methods for urban housing price.
In order to visualize the analysis results and make them easier for understanding, we develop a novel approach by referring to the DEM and DTM-based analysis methods in geoscience, such as the river cross-section in flood model [65,66] and the terrain model for floodplain mapping [67]. We assume the housing price surface can be expressed as f(x, y, z). By integrating different modules in ArcGIS and ArcScene, we propose the DEM-based analysis methods as follows:
- -
- The Water-flooding method (see Table 1), which uses the “water level” (a given benchmark housing price) at a designated height to analyze the high values and characteristics of the top area on the urban housing price surface (see Figure 1b). We simulate the flooding result of housing price by vertically changing the basic level of the original DEM model in ArcScene.
 Table 1. Basic description of the DEM-based analysis methods.
Table 1. Basic description of the DEM-based analysis methods. - -
- The Section-cutting method (see Table 1), which analyzes the side-view price skyline and gradient characteristics through section cutting in the specific directions (see Figure 1c). We cut and split the original DEM model according to the directions we set in ArcScene, and examine the gradient characteristics of housing price along the cutting lines.
- -
- The Belt-floating method (see Table 1), which is used to analyze spatial variance of the urban housing price DEM on the route of a specific line, such as a subway line (see Figure 1d). Specifically, we build a covering relation between traffic lines and DEM model surfaces in ArcScene to obtain housing price changes along the traffic routes.
3. Case Study Area and Materials
3.1. Study Area
Wuhan is located in the middle reaches of the Yangtze River and its largest tributary, the Hanshui River, which pass through the city [68]. There are a large number of lakes in the urban area of Wuhan, including China’s largest urban lake, East Lake. Therefore, Wuhan is known as a “river city” and “city of lakes” (see Figure 2). Over the past century, Wuhan has been growing, with the intersection of the Yangtze River and the Hanshui River as the core (see Figure 3). The landscape of the city has gradually evolved from a monocentric mode to a polycentric mode. At present, the landscape of Wuhan City has the following characteristics [42]: (1) Urban ring roads form a basic framework with a radioactive structure; (2) multiple centers have made up an intensive road network area within the inner ring road; (3) different urban areas have gradually built respective sub-centers, constrained by natural geographic and environmental conditions. Figure 2a shows the location, topographical map, and study area of Wuhan City. The study area is mainly the central urban area of the city. For the study area, we have built the GIS analysis environment (see Figure 2c), including ring road, subway line, trunk road, water body, green land, and other geographic elements, based on the Open Platform of Baidu Map (lbsyun.baidu.com) and with reference to Wuhan City’s spatial regulation and implementation planning for urban development area and the city’s subway construction planning (www.whrt.gov.cn).
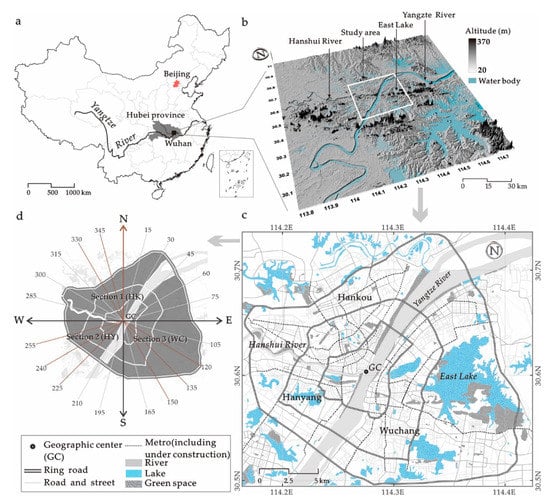
Figure 2.
Location of Wuhan city in China (a); and topographical map (b); spatial element distribution (c) and spatial pattern setting (d) of the study area (Note: Figure 2b was based on SRTM 90 m-resolution elevation data provided by the Consortium for Spatial Information, srtm.csi.cgiar.org. Figure 2c was collected from an online map (map.baidu.com). Figure 2d shows the division of sectors in downtown Wuhan by 15° intervals, with the GC as the center and the loop as the scale; 360, 345, 330, 255, 240, 225, 150, 135, and 120 in Figure 2d are main concerns in the empirical analysis).
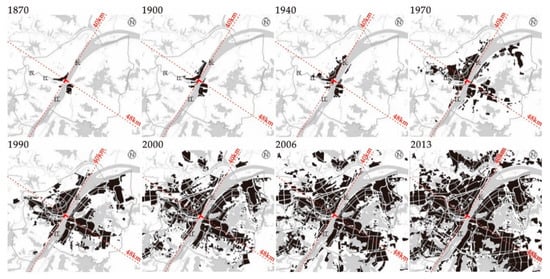
Figure 3.
The urban spatial changes of Wuhan City in different years (Note: The area colored black in the figures shows the built-up areas of Wuhan city in different years. The fundamental data were provided by Wuhan Land Resources and Planning Bureau).
The Yangtze River and Hanshui River divide the central urban area of Wuhan into three sectors, Hankou, Wuchang, and Hanyang [68]. Hankou is the center of business, finance, and urban administration, Wuchang is the center of education, new technology industries, and provincial administration, and Hanyang is the traditional industrial base [37,42]. Prior study has indicated that there exists spatial heterogeneity among the three sectors for the urban housing price [42,69] and urban residential land price [36,37]. To better understand the urban spatial structural characteristics, we define the center (gravitational center) of the region inside the inner ring road as the geographic center (GC) of Wuhan city (see Figure 2c). The GC turns out to be located at the intersection of the Yangtze River and the Hanshui River. Further, by setting the GC as the center of the circle and due north as the starting point, we defined 24 directions with an interval of 15 degrees as the reference for evaluating the spatial directional heterogeneity (see Figure 2d), and selected three representative directions for each sector as the major target of analysis.
3.2. Housing Price
To produce the DEM model that reflects the overall housing price surface in Wuhan, we collected samples and processed them as follows: Firstly, in order to reduce the influence of the market, we excluded second-hand housing and selected residential housing estates (including housing price, location, area, planned floor area ratio) in the study area as housing samples. We collected 386 new residential housing estate projects on sale from December 2011 to December 2014 and obtained housing price and some related information from Wuhan Housing Security and Management Bureau (fgj.wuhan.gov.cn). Secondly, we used the unit selling price (in CNY ¥ ▪ m−2) of estate projects to reflect urban housing price. To deal with the differences in transaction date, we corrected the sample prices into standardized prices. Specifically, all housing prices of selected samples were amended to the same trading day (December 2014) through real estate price indices of Wuhan.
Global spatial autocorrelation reflects the spatial characteristics of an attribute across the whole area and indicates whether there exists an evident correlation between the attribute information and its location. The spatial autocorrelation theory is usually applied in the fields of spatial economics and geo-statistics [70,71,72,73]. The Moran’s I Index, which is used to measure the correlation among spatial elements, is a correlation coefficient that is widely used to test the global spatial correlation [74]. After correction, the Moran’s I Index of commodity house price is 0.29 for the selected samples, with an expectancy value of −0.007, a Z test value of 7.964, and a p value below 0.01. With a confidence level of 99%, the multiple Z test value reflecting the standard deviation is above 2.5. Therefore, we can deny the null assumption that the random distribution of observed values and conclude that the housing price attributes of these observed samples are spatially correlated with one another. Besides, we employed a frequency distribution curve to test the sample’s normality and eliminate abnormal data points. Based on the quantile–quantile (Q-Q) plot (see Figure 4d) of the housing prices from 386 samples that follow a lognormal distribution, we removed luxury houses (such as villas) and affordable housing (policy-related house). Finally, the 318 remaining samples (positions), including 313,230 housing units (covering an area of about 32.26 million square meters), were used for geo–visual analysis (see Figure 4a).
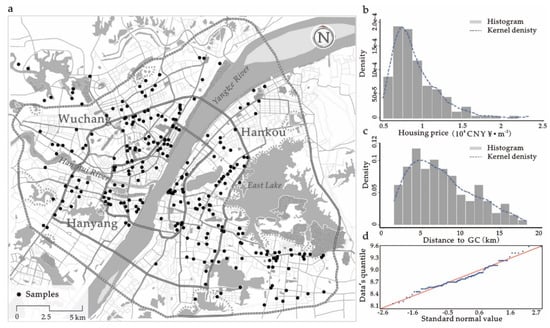
Figure 4.
Spatial distribution of housing price samples (a); price density distribution (b); distance density distribution (c) and log-transformed QQ-plot of samples (d).
We listed the statistical information of the sampling housing price in Table 2. Further, we calculated the distances between the samples and the GC with ArcGIS tools, and the average, the maximum, and the minimum distances were 7.45 km, 18.42 km, and 1.33 km, respectively (see Table 2).

Table 2.
Basic statistical description of revised samples.
4. Results
4.1. Urban Housing Price Surface
Based on the Ordinary Kriging method, we performed logarithmic transformation of the entered data and applied the spherical model to interpolate the samples. The prediction error of the average value is 0.032, which is close to 0, and the standard root-mean-square error is 0.898, which is close to 1. The results show that the interpolation method is reliable. Further, the housing price was visualized with color maps: when the housing price ranges from high to low, the color ranges from warm color (red) to cold color (blue). The results show that the overall housing price in Wuhan City presents a high-to-low trend from the GC to other areas; the housing price decreases with the increasing distance to the ring roads; this trend is more obvious in sector HK and sector HY. Besides, to avoid the influence of natural factors (such as lakes and rivers) on the model, we set these lake or river areas as no data areas (blanked area) in the GIS environment.
To better observe and understand the spatial characteristics of the calculation results from the model, we output the tridimensional visualization of the DEM for housing price, water bodies, and ring roads in GIS environment. The ring roads are displayed as floating on the DEM surface. Figure 5 displays the morphologies of the DEM surface for housing price under different perspectives. The tridimensional visible presentation of the DEM models makes it possible to interpret the spatial distribution of housing price in multiple dimensions and perspectives.
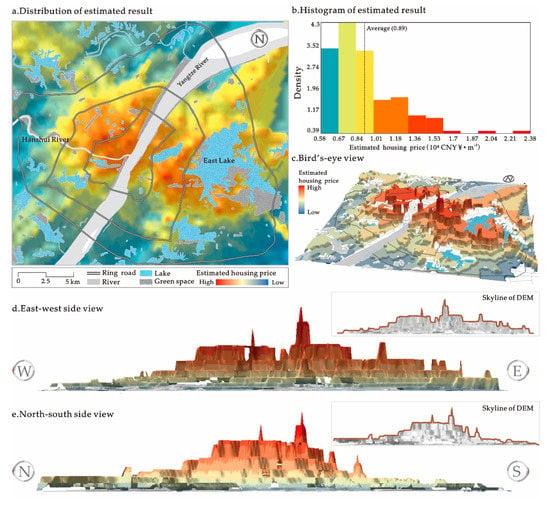
Figure 5.
Result of Wuhan housing prices DEM surface.
4.2. Water-Flooding: The Multi-Peak Changes of Surface
If we put the DEM for housing price in a “closed container”, and keep injecting “water” into the “container”, then as the “price water level” keeps rising, the area with a low price terrain will be gradually “flooded”, and the area exposed above the price water level will be the price highland, and the “island” that is finally be left will be the area where the top area exists. In the ArcScene 3D-analyst environment for the case under this paper, when the “water level” (benchmark price) arrives at 13,000, the characteristics of high-value areas that are still exposed above the benchmark (see Figure 6a) are basically concentrated and continuous in Hankou and Hanyang, but these areas in Wuchang are not continuous, but discrete. Considering spatial differences of the price level between different sectors, we have cut the housing price DEM by sectors and further flooded these sectors. When the price water level arrives at 13,800, Wuchang will become an “island” (see Figure 6c), while Hankou will not change a lot (see Figure 6b). When the price water level falls to 11,000, Hanyang will become an “island” (see Figure 6d). This shows that among the three sectors, the high-value area of the housing price is the lowest in Hanyang, and high-value area is relatively concentrated and larger in Hankou. The high-value areas in Hanyang and Hankou are distributed along the Yangtze River, which responses to the historical spatial expansion of Wuhan City as a port. The peak value in the global scope appears in Wuchang, but the high-value areas are relatively decentralized there. This can be explained by the influence of natural geographical elements and the rise of sub-centers and new high-technology districts in Wuchang.
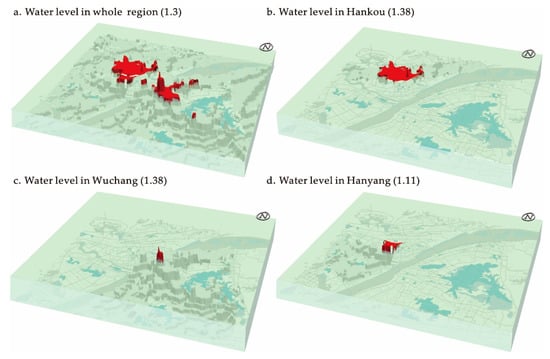
Figure 6.
Housing prices DEM under different scenarios with fluctuating “water levels” (Note: “water level” uses the unit selling price in 104 CNY ¥ ▪ m−2; (a) displays the global scope of the study area under the water level of 1.3; (b–d) represent Hankou Sector and Wuchang Sector under the water level of 1.38 as well as Hanyang Sector under the water level of 1.11).
4.3. Section-Cutting: Spatial Morphology of Gradient in Side Views
We cut along the section of the DEM surface for housing price in Wuhan City in the tri-dimensional spatial environment, obtained side-view morphological characteristics of the housing price surface in a given direction, and analyzed the gradient changes. Under the spatial landscape of Wuhan City, the Yangtze River and the Hanshui River are important geographical factors that influence the urban spatial landscape and can be considered as the key directions for spatial change characteristics of the housing price. By implementing the cutting process in ArcGIS, we got the side-view characteristic patterns of the housing price surfaces of Hankou, Hanyang, and Wuchang along the rivers. All side views present a similar trend of housing price variance: the housing price decreases with the distance increases from the GC. For example, the price decreases from the GC to the northwest direction (Figure 7a1) and from the GC to the northeast direction (Figure 7a2) in Hankou, and the price declines from the GC to the southwest direction (Figure 7b1) and from the GC to the northwest direction (Figure 7b2) in Hanyang; the price decreases from the GC to the northeast and the southwest direction (Figure 7c) in Wuchang. As for the overall gradient decline pattern, the housing prices fluctuate in any direction (Figure 7b1). Additionally, after all the sections are blackened, we can further analyze the price relationship between the riverfront areas and other areas from the horizontal side view. If the remote price surface is covered by the black section in the side view, this means the housing price in the riverfront areas stays at a higher level (Figure 7b2).
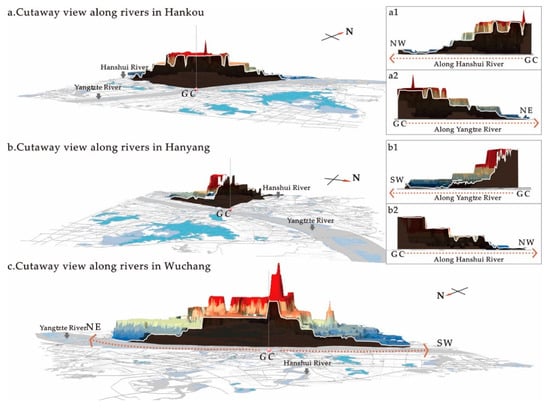
Figure 7.
Morphological characteristics of housing price DEM along the rivers.
To make a further quantitative analysis of the gradient change of the housing price surface in different directions, we observe the housing price changes when the distances from the GC rises. We define the GC as the starting point, selecting different directions and cutting the cross-sections of the DEM, according to the spatial landscape division and definition mentioned above. On the principle of typicality and maximum assurance of spatial continuity, we selected three representative directions in Hankou, Hanyang, and Wuchang (HK Sector: GC-330, GC-345, and GC-360; HY Sector: GC-225, GC-240, and GC-255; and WC Sector: GC-120, GC-135, and GC-150).
Figure 8 displays the housing price distribution along the sectional lines and in different directions, with the GC as the starting point. Since the ring roads constitute the skeleton of Wuhan City, we fitted a trend line in every diagram and marked the locations where the sectional line intersects with urban ring roads. It indicates the housing price curves tend to decrease when the distance to the GC increases. This can be explained by the radioactive concentric spatial structure of Wuhan City. However, the average price levels and the decline gradients of housing price show different characteristics in different sectors: (1) The average price level and gradient in HK Sector are relatively high in all directions, and present an obvious peak in the GC-360 direction; (2) in the HY Sector, the average price level is relatively high in the GC-240 direction and presents a lower peak in the GC-255 direction; and (3) the price curve fluctuates within a greater range in the WC Sector, and there is an obvious peak between B1 and B2, and between B2 and B3 in the GC-120 direction as well as between B1 and B2 in the GC-135 and GC-150 directions. This is possibly because there are many water bodies in Wuchang region and the land is rather scattered, which lead to multiple peaks of price distribution.
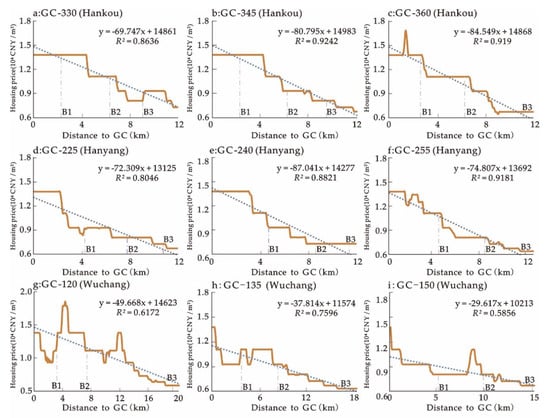
Figure 8.
Housing price distribution and fitted curves along the section-lines in different directions (B1, B2, and B3 are the intersections of the sectional line and three ring roads respectively).
4.4. Belt-Floating: Spatial Morphology along Key Traffic Lines
- (1)
- Spatial morphological visualization of housing prices along main subway lines. We consider the housing price as a proxy variable that reflects the spatial value, and intersect different subway lines and DEM surfaces for housing prices in the tri-dimensional space environment based on the DEM surface for housing prices in Wuhan City. Then, we further explore the characteristic morphology of spatial distribution along subway lines and complete visualization under different perspectives (see Figure 9). Globally, low-value areas appear on the starting point and the ending point of each line, while the high-value areas are usually distributed in the middle part of the line. Locally, different lines present complex multidimensional fluctuations.
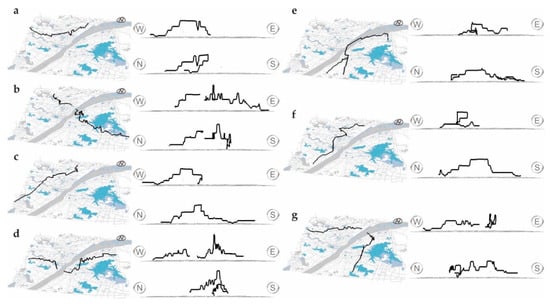 Figure 9. Spatial morphology of subway lines floating in housing price DEM (Note: (a–g) relate to subway lines 1–7, including completed and under construction, in Wuhan City).
Figure 9. Spatial morphology of subway lines floating in housing price DEM (Note: (a–g) relate to subway lines 1–7, including completed and under construction, in Wuhan City). - (2)
- Investigation of housing prices along subway lines. Considering the radioactive landscape of Wuhan City, we collected the price data on the DEM surface relating to different ring roads within the central urban area and compared these data. Through investigating the housing prices along different ring roads in different directions, we found that the prices tend to decrease from the first ring road to the third ring road in Hankou and Hanyang (see Figure 10a), which fits the radioactive spatial structure feature of Wuhan City. However, the housing price in Wuchang does not show a similar pattern. In some directions in Wuchang, the housing prices along the ring roads do not show a hierarchical distribution but display a fluctuation pattern. This feature is contrary to the spatial structure feature, but corresponding with the polycentric trends of the housing price morphology, as explored earlier. Besides, if sequenced from high to low along the ring roads, the housing prices also present an overall decline trend from first ring road to third ring road (see Figure 10b).
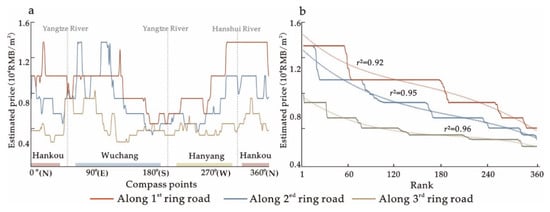 Figure 10. Comparison of housing prices along different ring roads (Note: The horizontal axis in (a) displays different directionalities, while that in (b) displays the price sequence).
Figure 10. Comparison of housing prices along different ring roads (Note: The horizontal axis in (a) displays different directionalities, while that in (b) displays the price sequence).
5. Concluding Discussion
To examine the spatial pattern housing price in a city is crucial to a better understanding of urban spatial structures and more rational urban planning. Urban planners, economists, and geographers have developed many models to investigate the urban spatial pattern, which greatly contributes to quantitative analysis and visualization of the analysis result. Previous studies have indicated both the strengths and limitations of spatial interpretation methods for housing price prediction. In this paper, we did not use spatial interpolation methods directly for housing price prediction, but employed the Kriging interpolation method for producing the DEM of urban housing price. The DEM for urban housing price in this paper provides the foundation for studying the spatial morphological characteristics of resident’s willingness to pay for the house at a certain location under the local housing market. Meanwhile, it provides a new dimension and perspective for understanding of the urban spatial structure.
Based on the three-dimensional DEM of urban housing price, this paper developed a new approach of geo–visual analytics for urban housing prices. Referring to the DEM/DTM-based analysis idea in hydrology and geosciences, we designed the Water-flooding method, the Section-cutting method, and the Belt-floating method for investigating and visualizing the spatial morphology of housing price. We implemented these methods with the 3D-analyst module in ArcGIS and ArcScene. Through analyzing the results, we found that the Water-flooding method effectively supports the investigation of the top areas of the housing price surface above a given horizontal plane; the Section-cutting method performs well in examining the profile or cross-section of the urban housing surface along a selected straight line or a series of straight line segments, and the Belt-floating method is highly helpful for detecting the spatial variance of urban housing surface through the routes of specific lines, such as subway lines.
The empirical analysis of the central urban areas of Wuhan City indicates that: (1) Under different perspectives, the “housing price skylines” on the DEM presents the complex features of multiple peaks and fluctuations; (2) Based on the Water-flooding method, the top surface of the housing price DEM shrinks and appears in different spatial forms as the “water level“(given benchmark price) continues to rise; (3) Based on the Section-cutting method, the fluctuation and gradient of the housing price in different directions indicate the spatial heterogeneity in different sectors in Wuhan City; (4) Based on the Belt-floating method, the housing price along different subway lines presents complex multidimensional fluctuations, while the housing price along the ring roads shows an overall downward trend from the inside to outside.
The empirical analysis of the spatial morphology of housing prices confirms the complex urban structure and spatial heterogeneity of Wuhan City. Due to the limitation of the study area, we did not examine how various spatial elements and geographical conditions impact the complex spatial pattern of urban housing prices. However, it is worth noting that previous related studies in Wuhan City found that the proximity to water bodies, green space, transit systems, or CBDs has positive effects on housing price, especially the proximity to the Yangtze River or the East Lake. However, in this paper, the geo–visual analytics of urban housing prices in Wuhan City indicate that housing prices in proximity to water bodies or transit show more complex changes. For example, the housing price is not higher in all directions with proximity to the Yangtze River or Hanshui River. Further, our research provides potential methodological support for the local government of Wuhan City to carry out spatial land allocation, measure housing space welfare, and achieve a spatial balance of housing affordability. At the same time, our three-dimensional visualization results provide a potential basis for a better understanding of the complex urban structures in the local urban planning process.
The research method proposed in this paper inherits the advantages of spatial interpretation technology, and also draws on the application of DEM in other natural science fields. Compared with the traditional two-dimensional model and linear analysis methods, the proposed approach works better in describing the complex spatial morphology of urban housing price and has an advantage in visualizing the results for analysis. However, the following issues need to be considered and handled when the approach is implemented: (1) In the process of spatial interpretation, some factors, especially non-location factors of the residential samples, must be controlled or revised to ensure the reference effect of the housing price surface; (2) the urban housing surface does not reflects real housing transaction prices but acts as a certain price index under the given condition.
Further, the limitations of this study and the directions for future research should be identified. Firstly, we collected the sample data manually, and the data were extracted from the statistical data sources. This limits the accuracy of the housing price DEM on a larger spatial scale. Big data and new data sources, such as POI (point of interest) data, provide the potential to improve model accuracy. Another possible area for future work would be to investigate the different sub-divides of the real estate market, obtain data separately, and produce corresponding DEMs. Secondly, we proposed the DEM-based analysis by referring to the application of DEM in other disciplines. Although it has achieved good visualization effects, the theoretical basis needs further exploration. Thirdly, the urban housing price DEM reflects the spatial characteristics of people’s willingness to pay for the house in a city, which provides a perspective for examining the urban spatial structure. However, a comprehensive investigation of the urban spatial structure requires DEM-based analysis of more variables, such as land price, human activities, or employment density.
Author Contributions
Z.Z. proposed and designed the study; M.Z. and B.K. were accountable for data collecting and the interpretation of results; Z.Z. wrote the paper; X.L. (Xinhai Lu), Y.S. and X.L. (Xiang Luo) were responsible for the further revision of this study; All authors have read and approved the final manuscript.
Funding
This study was financially supported by the National Natural Science Foundation of China (71774066, 41401631), Fundamental Research Funds for the Central Universities in China (2020516032116, CCNU18ZYTS05, CCNU18XJ019), China Postdoctoral Science Foundation (2018M642882, 2018M642883), and Self-determined Research Funds of CCNU from the Colleges’ Basic Research and Operation of MOE.
Acknowledgments
We would like to express our great appreciation to the reviewers for very constructive comments during the revision of the paper. In addition, we thank to Mingjie Song for her helps in English editing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haggett, P.; Cliff, A.D.; Frey, A. Locational Analysis in Human Geography; Edward Arnold: London, UK, 1977. [Google Scholar]
- Alonso, W. Location and Land Use; Harvard University Press: Cambridge, UK, 1964. [Google Scholar]
- Mills, E.S. An Aggregative Model of Resource Allocation in a Metropolitan Area. Am. Econ. Rev. 1967, 57, 197–210. [Google Scholar]
- Mills, E.S. Studies in the Structure of the Urban Economy; Jones Hopkins Press: Baltimore, MD, USA, 1972. [Google Scholar]
- Muth, R.F. Cities and Housing; The University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- Krugman, P.R. Development, Geography, and Economic Theory; MIT Press: Cambridge, MA, USA, 1995; pp. 595–599. [Google Scholar]
- Kloosterman, R.C.; Musterd, S. The Polycentric Urban Region: Towards a Research Agenda. Urban Stud. 2001, 38, 623–633. [Google Scholar] [CrossRef]
- Parr, J. The Polycentric Urban Region: A Closer Inspection. Reg. Stud. 2004, 38, 231–240. [Google Scholar] [CrossRef]
- Meijers, E.J.; Burger, M.J. Spatial structure and productivity in US metropolitan areas. Environ. Plan. A 2010, 42, 1383–1402. [Google Scholar] [CrossRef]
- Mori, T. Monocentric Versus Polycentric Models in Urban Economics. In The New Palgrave Dictionary of Economics; Palgrave Macmillan: London, UK, 2016; pp. 1–4. [Google Scholar]
- Burger, M.; Meijers, E. Form follows function? Linking morphological and functional polycentricity. Urban Stud. 2012, 49, 1127–1149. [Google Scholar] [CrossRef]
- Tian, G.; Wu, J.; Yang, Z. Spatial pattern of urban functions in the Beijing metropolitan region. Habitat Int. 2010, 34, 249–255. [Google Scholar] [CrossRef]
- Vasanen, A. Functional polycentricity: Examining metropolitan spatial structure through the connectivity of urban sub-centres. Urban Stud. 2012, 49, 3627–3644. [Google Scholar] [CrossRef]
- Wen, H.; Tao, Y. Polycentric urban structure and housing price in the transitional China: Evidence from Hangzhou. Habitat Int. 2015, 46, 138–146. [Google Scholar] [CrossRef]
- Qin, B.; Han, S.S. Emerging polycentricity in Beijing: Evidence from housing price variations, 2001–2005. Urban Stud. 2013, 50, 2006–2023. [Google Scholar] [CrossRef]
- Adolphson, M. Estimating a Polycentric Urban Structure. Case Study: Urban Changes in the Stockholm Region 1991–2004. J. Urban Plan. Dev. 2009, 135, 19–30. [Google Scholar] [CrossRef]
- Liu, X.; Derudder, B.; Wu, K. Measuring Polycentric Urban Development in China: An Intercity Transportation Network Perspective. Reg. Stud. 2015, 50, 1302–1315. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M. How polycentric is urban China and why? A case study of 318 cities. Landsc. Urban Plan. 2016, 151, 10–20. [Google Scholar] [CrossRef]
- Ottensmann, J.R.; Payton, S.; Man, J. Urban Location and Housing Prices within a Hedonic Model. J. Reg. Anal. Policy 2012, 38, 19–35. [Google Scholar]
- Zhang, Z.; Tang, W. Analysis of spatial patterns of public attention on housing prices in Chinese cities: A web search engine approach. Appl. Geogr. 2016, 70, 68–81. [Google Scholar] [CrossRef]
- Law, S. Defining Street-based Local Area and measuring its effect on house price using a hedonic price approach: The case study of Metropolitan London. Cities 2017, 60, 166–179. [Google Scholar] [CrossRef]
- Bajic, V. The Effects of a New Subway Line on Housing Prices in Metropolitan Toronto. Urban Stud. 2014, 20, 147–158. [Google Scholar] [CrossRef]
- Wen, H.; Bu, X.; Qin, Z. Spatial effect of lake landscape on housing price: A case study of the West Lake in Hangzhou, China. Habitat Int. 2014, 44, 31–40. [Google Scholar] [CrossRef]
- Lansford, N.H., Jr.; Jones, L.L. Recreational and aesthetic value of water using hedonic price analysis. J. Agric. Resour. Econ. 1995, 20, 341–355. [Google Scholar]
- Wen, H.; Zhang, Y.; Zhang, L. Do educational facilities affect housing price? An empirical study inHangzhou, China. Habitat Int. 2014, 42, 155–163. [Google Scholar] [CrossRef]
- Sun, C.; Meng, X.; Peng, S. Effects of Waste-to-Energy Plants on China’s Urbanization: Evidence from a Hedonic Price Analysis in Shenzhen. Sustainability 2017, 9, 475. [Google Scholar] [CrossRef]
- Rosato, P.; Breil, M.; Giupponi, C.; Berto, R. Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice. Buildings 2017, 7, 112. [Google Scholar] [CrossRef]
- Bilbao-Terol, C.; Cañal-Fernández, V.; Valdés, L.; Valle, E.D. Rural Tourism Accommodation Prices by Land Use-Based Hedonic Approach: First Results from the Case Study of the Self-Catering Cottages in Asturias. Sustainability 2017, 9, 1688. [Google Scholar] [CrossRef]
- Won, J.; Lee, J.S. Investigating How the Rents of Small Urban Houses are Determined: Using Spatial Hedonic Modeling for Urban Residential Housing in Seoul. Sustainability 2017, 10, 31. [Google Scholar] [CrossRef]
- Huang, H.; Yin, L. Creating sustainable urban built environments: An application of hedonic house price models in Wuhan, China. J. Hous. Built Environ. 2014, 30, 1–17. [Google Scholar] [CrossRef]
- Tao, X.; Ming, Z.; Aditjandra, P.T. The impact of urban rail transit on commercial property value: New evidence from Wuhan, China. Transp. Res. Part A Policy Pract. 2016, 91, 223–235. [Google Scholar]
- Xu, T.; Zhang, M. Tailoring empirical research on transit access premiums for planning applications. Transp. Policy 2016, 51, 49–60. [Google Scholar] [CrossRef]
- Mcmillen, D.P.; Mcdonald, J.F. A Nonparametric Analysis of Employment Density in a Polycentric City. J. Reg. Sci. 1997, 37, 591–612. [Google Scholar] [CrossRef]
- Mcmillen, D.P. The return of centralization to Chicago: Using repeat sales to identify changes in house price distance gradients. Reg. Sci. Urban Econ. 2003, 33, 287–304. [Google Scholar] [CrossRef]
- Openshaw, S. Computational Human Geography: Towards a Research Agenda. Environ. Plan. A 1994, 26, 499–505. [Google Scholar]
- Hu, S.; Cheng, Q.; Wang, L.; Xie, S. Multifractal characterization of urban residential land price in space and time. Appl. Geogr. 2012, 34, 161–170. [Google Scholar] [CrossRef]
- Hu, S.; Yang, S.; Li, W.; Zhang, C.; Xu, F. Spatially non-stationary relationships between urban residential land price and impact factors in Wuhan city, China. Appl. Geogr. 2016, 68, 48–56. [Google Scholar] [CrossRef]
- Chica-Olmo, J. Prediction of Housing Location Price By a Multivariate Spatial Method: Cokriging. J. Real Estate Res. 2007, 29, 95–114. [Google Scholar]
- Chica-Olmo, J.; CanoGuervos, R.; ChicaOlmo, M. A Coregionalized Model to Predict Housing Prices. Urban Geogr. 2013, 34, 395–412. [Google Scholar] [CrossRef]
- Martínez, M.G.; Lorenzo, J.M.M.; Rubio, N.G. Kriging methodology for regional economic analysis: Estimating the housing price in Albacete. Int. Adv. Econ. Res. 2000, 6, 438–450. [Google Scholar] [CrossRef]
- Olmo, J.C. Spatial Estimation of Housing Prices and Locational Rents. Urban Stud. 1995, 32, 1331–1344. [Google Scholar] [CrossRef]
- Zhang, Z.; Tan, S.; Tang, W. A GIS-based Spatial Analysis of Housing Price and Road Density in Proximity to Urban Lakes in Wuhan City, China. Chin. Geogr. Sci. 2015, 25, 775–790. [Google Scholar] [CrossRef]
- Dubin, R.A. Predicting House Prices Using Multiple Listings Data. J. Real Estate Financ. Econ. 1998, 17, 35–59. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. Geogr. Anal. 2005, 38, 5–22. [Google Scholar] [CrossRef]
- Montero, J.M.; Mínguez, R.; Fernández-Avilés, G. Housing price prediction: Parametric versus semi-parametric spatial hedonic models. J. Geogr. Syst. 2017, 20, 1–29. [Google Scholar] [CrossRef]
- Cellmer, R. The Possibilities and Limitations of Geostatistical Methods in Real Estate Market Analyses. Real Estate Manag. Svaluation 2014, 22, 54–62. [Google Scholar] [CrossRef]
- Montero, J.M.; Fernández-Avilés, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Montero-Lorenzo, J.M.; Larraz-Iribas, B.; Páez, A. Estimating commercial property prices: An application of cokriging with housing prices as ancillary information. J. Geogr. Syst. 2009, 11, 407–425. [Google Scholar] [CrossRef]
- Mcmillen, D. Identifying Sub-centres Using Contiguity Matrices. Urban Stud. 2003, 40, 57–69. [Google Scholar] [CrossRef]
- Mcmillen, D.P. Nonparametric Employment Subcenter Identification. J. Urban Econ. 2001, 50, 448–473. [Google Scholar] [CrossRef]
- Redfearn, C.L. The topography of metropolitan employment: Identifying centers of employment in a polycentric urban area. J. Urban Econ. 2007, 61, 519–541. [Google Scholar] [CrossRef]
- Lv, G.N.; Xiong, L.; Chen, M.; Tang, G.A.; Sheng, Y.H.; Liu, X.J.; Song, Z.Y.; Lu, Y.; Yu, Z.Y.; Zhang, K.; et al. Chinese progress in geomorphometry. J. Geogr. Sci. 2017, 27, 1389–1412. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Tang, G.A.; Li, F.Y.; Yuan, B.Y.; Lu, Z.C. Modeling the evolution of loess-covered landforms in the Loess Plateau of China using a DEM of underground bedrock surface. Geomorphology 2014, 209, 18–26. [Google Scholar] [CrossRef]
- Guo, W.Q.; Liu, S.Y.; Peng-Chun, Y.U.; Jun-Li, X.U. Automatic extraction of ridgelines using on drainage boundaries and aspect difference. Sci. Surv. Mapp. 2011, 6, 75. [Google Scholar]
- Dipasquale, D.; Wheaton, W.C. Urban Economics and Real Estate Markets; Prentice Hall: Upper Saddle River, NJ, USA, 1996; pp. 289–299. [Google Scholar]
- Xiao, Y. Hedonic Housing Price Theory Review. In Urban Morphology and Housing Market; Springer: Berlin, Germany, 2017; pp. 11–40. [Google Scholar]
- Kiel, K.A.; Zabel, J.E. Location, location, location: The 3L Approach to house price determination. J. Hous. Econ. 2008, 17, 175–190. [Google Scholar] [CrossRef]
- Shimizu, C. Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables. Sustainability 2014, 6, 2946–2960. [Google Scholar] [CrossRef]
- Meese, R.; Wallace, N. Nonparametric Estimation of Dynamic Hedonic Price Models and the Construction of Residential Housing Price Indices. Real Estate Econ. 2010, 19, 308–332. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data, Revised Edition; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Lloyd, C.D. Local Models for Spatial Analysis; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Gichamo, T.Z.; Popescu, I.; Jonoski, A.; Solomatine, D. River cross-section extraction from the ASTER global DEM for flood modeling. Environ. Model. Softw. 2012, 31, 37–46. [Google Scholar] [CrossRef]
- Schäppi, B.; Perona, P.; Schneider, P.; Burlando, P. Integrating river cross section measurements with digital terrain models for improved flow modelling applications. Comput. Geosci. 2010, 36, 707–716. [Google Scholar] [CrossRef]
- Tate, E.C.; Maidment, D.R.; Olivera, F.; Anderson, D.J. Creating a terrain model for floodplain mapping. J. Hydrol. Eng. 2002, 7, 100–108. [Google Scholar] [CrossRef]
- Han, S.S.; Wu, X. Wuhan. Cities 2004, 21, 349–362. [Google Scholar] [CrossRef]
- Jiao, L.; Liu, Y. Geographic Field Model based hedonic valuation of urban open spaces in Wuhan, China. Landsc. Urban Plan. 2010, 98, 47–55. [Google Scholar] [CrossRef]
- Tse, R.Y.C. Estimating Neighbourhood Effects in House Prices: Towards a New Hedonic Model Approach. Urban Stud. 2011, 39, 1165–1180. [Google Scholar] [CrossRef]
- Case, B.; Clapp, J.; Dubin, R.; Rodriguez, M. Modeling Spatial and Temporal House Price Patterns: A Comparison of Four Models. J. Real Estate Financ. Econ. 2004, 29, 167–191. [Google Scholar] [CrossRef]
- Dubin, R.; Pace, R.K.; Thibodeau, T.G. Spatial Autoregression Techniques for Real Estate Data. J. Real Estate Lit. 1999, 7, 79–96. [Google Scholar] [CrossRef]
- Pace, R.K.; Lesage, J.P. Spatial Statistics and Real Estate. J. Real Estate Financ. Econ. 1998, 17, 5–13. [Google Scholar] [CrossRef]
- Smith, M.J.D.; Goodchild, M.F.; Longley, P.A. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools, 2nd ed.; Troubador Publishing Ltd.: Leicester, UK, 2007. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).