Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach
Abstract
:1. Introduction
2. Review of Literature
3. Data and Methodology
3.1. Data
3.2. Methodology
3.3. Dynamic Conditional Correlation (DCC) GARCH Model
4. Empirical Results
4.1. Descriptive Statistics
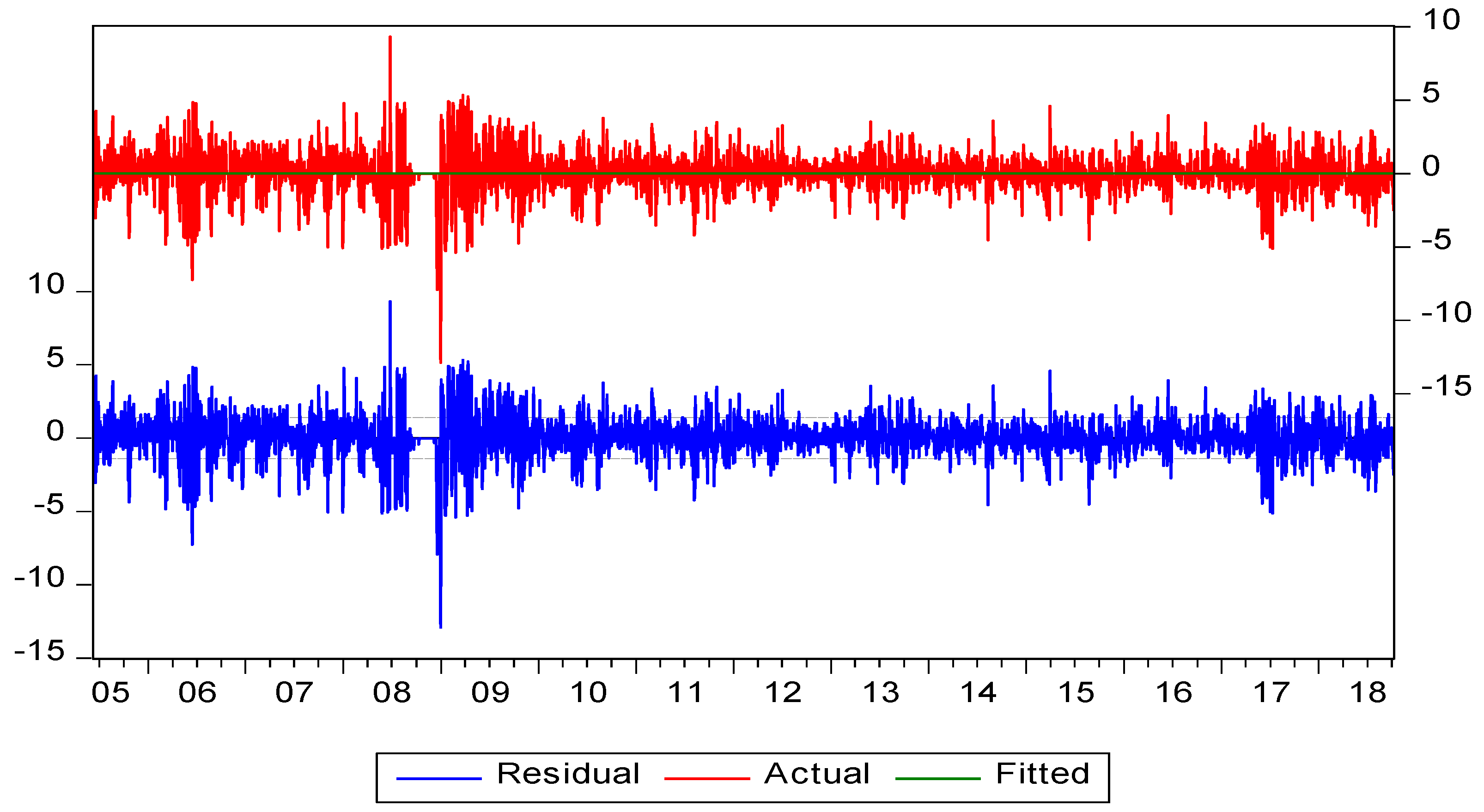
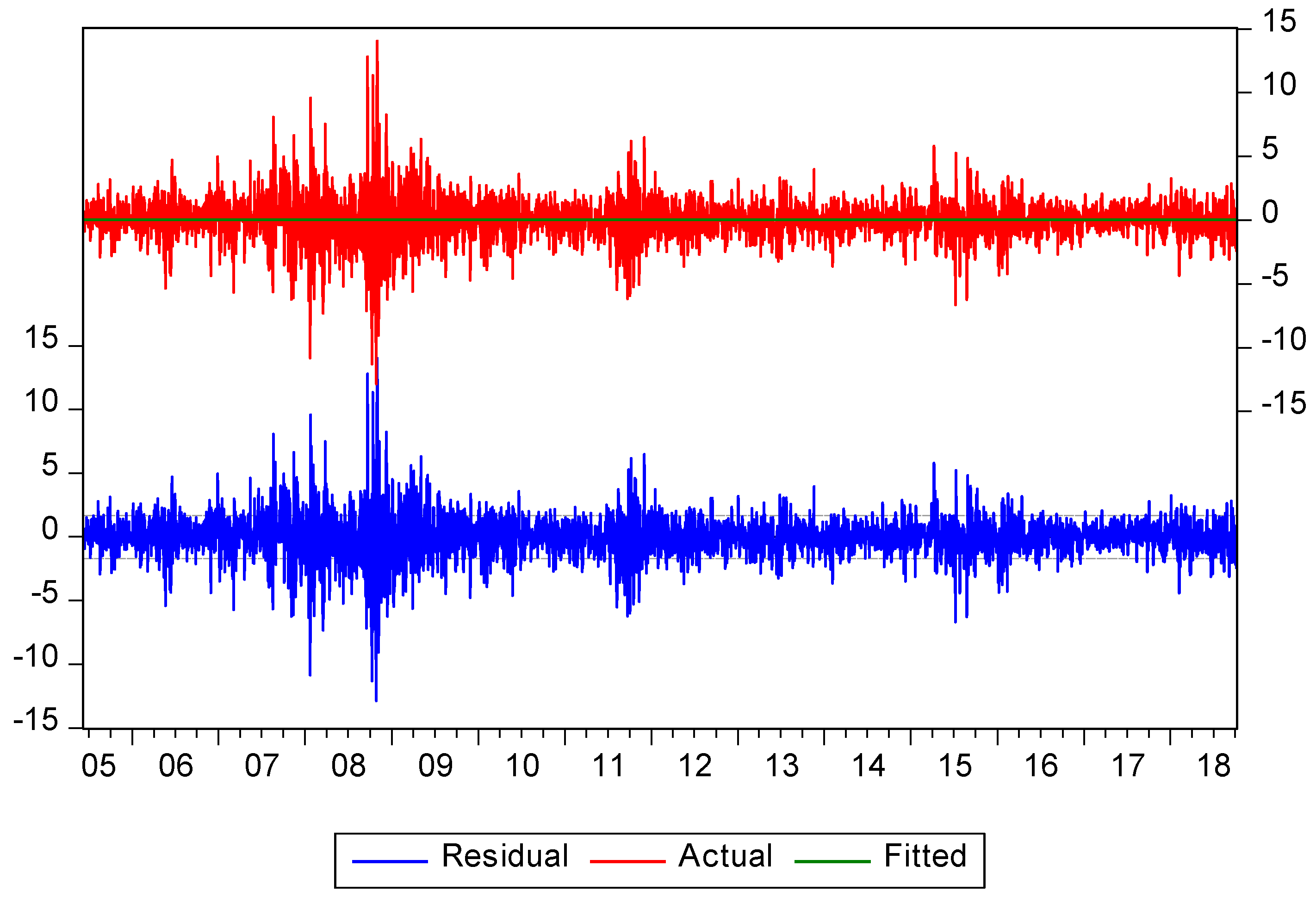
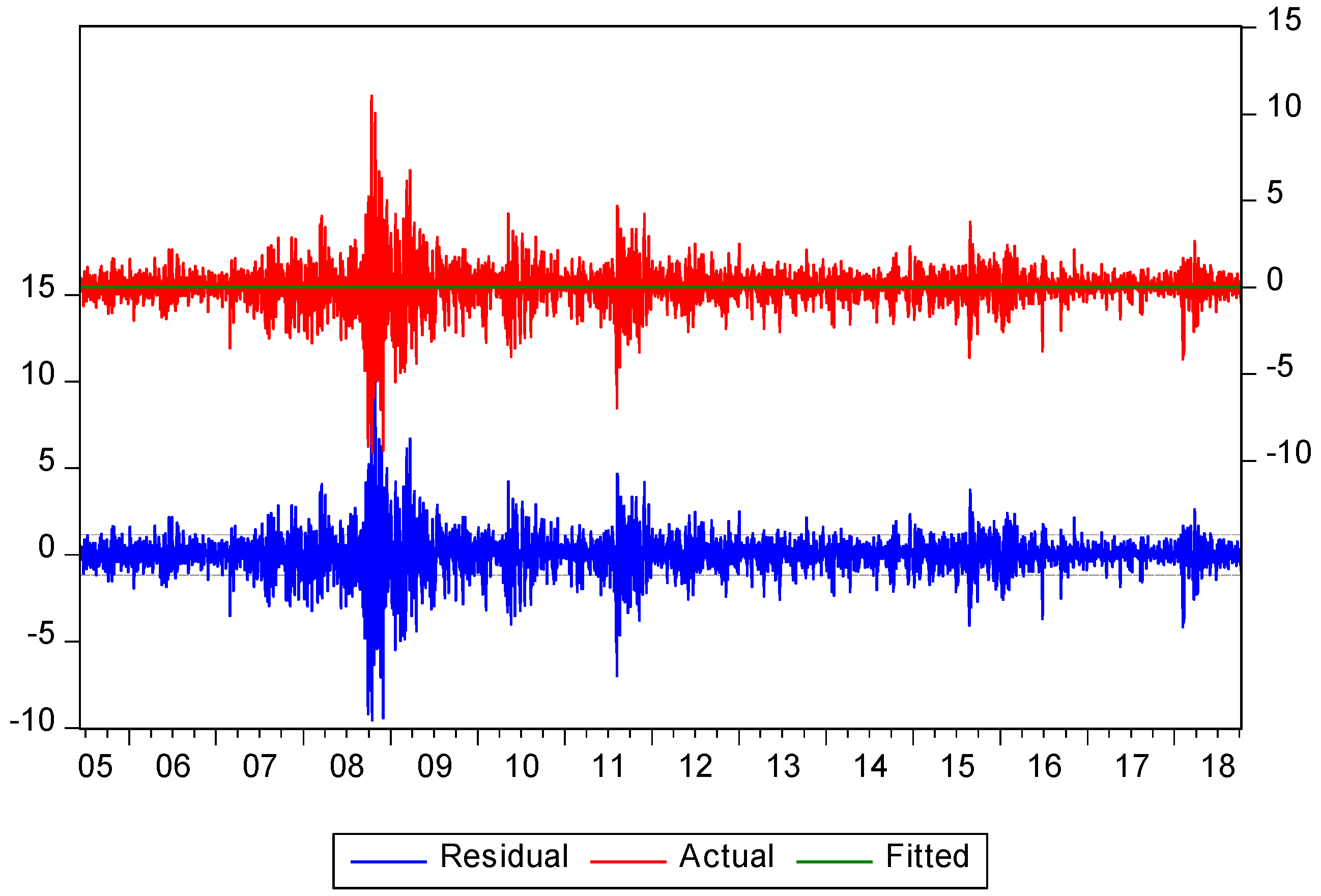
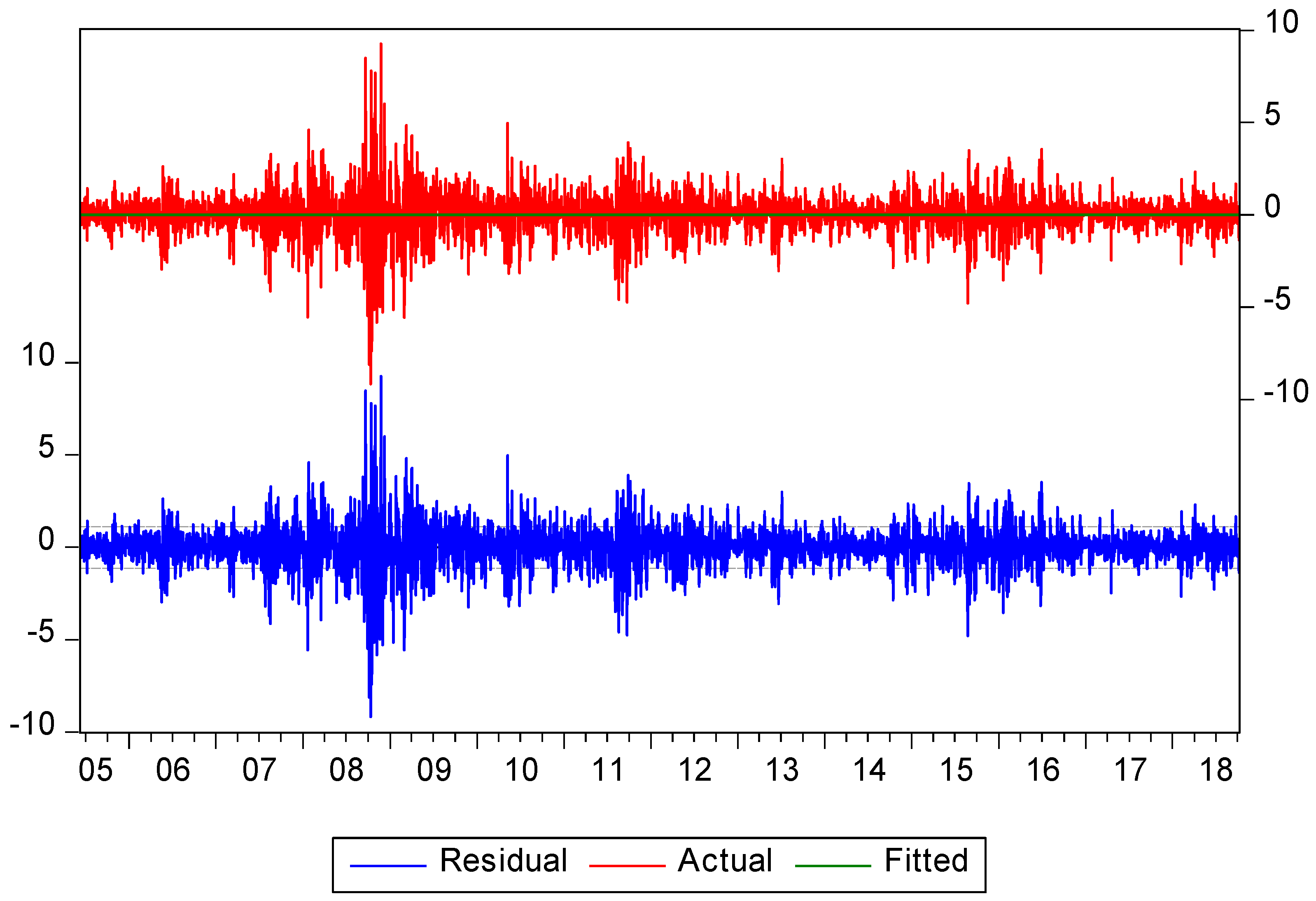
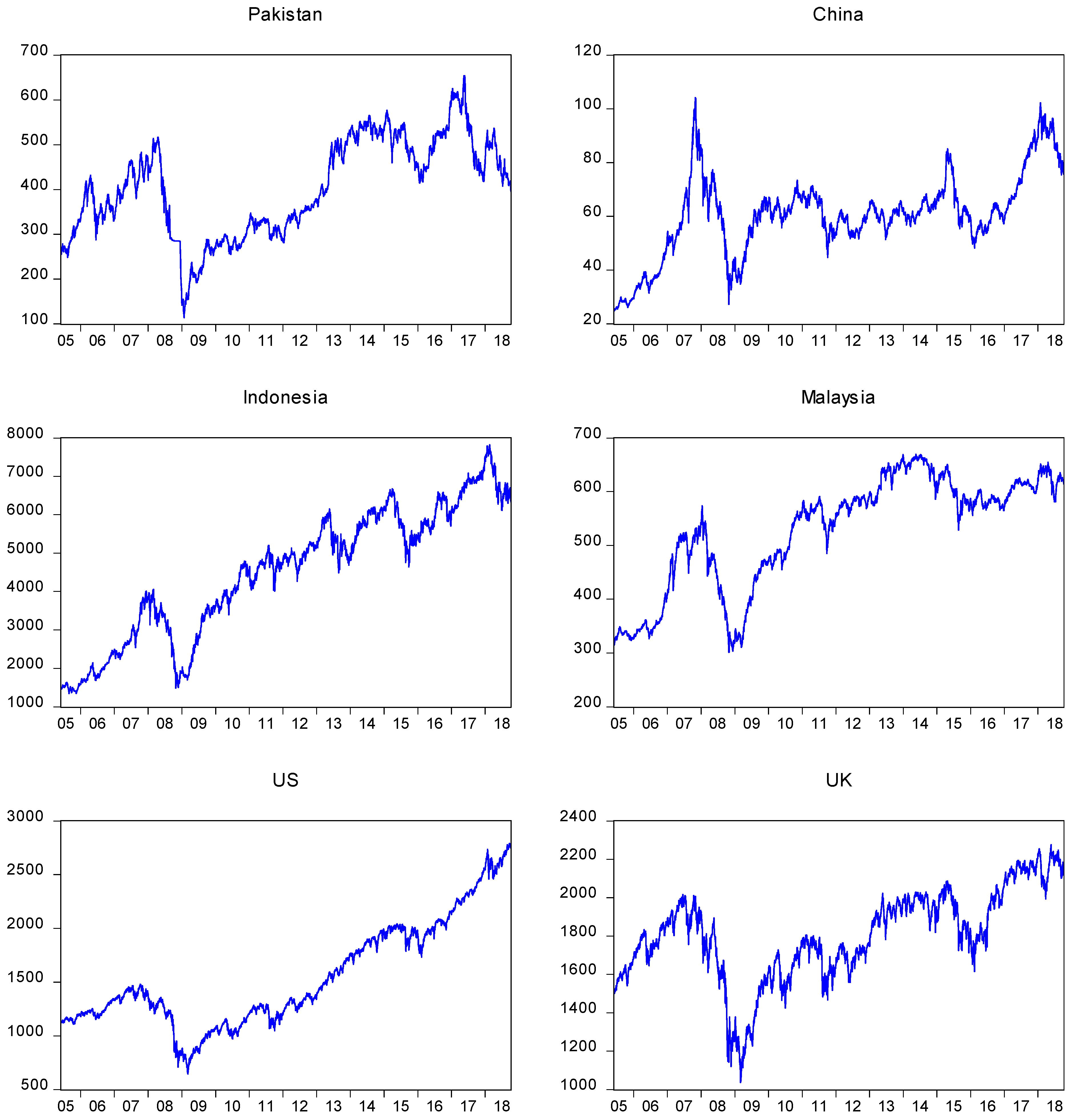
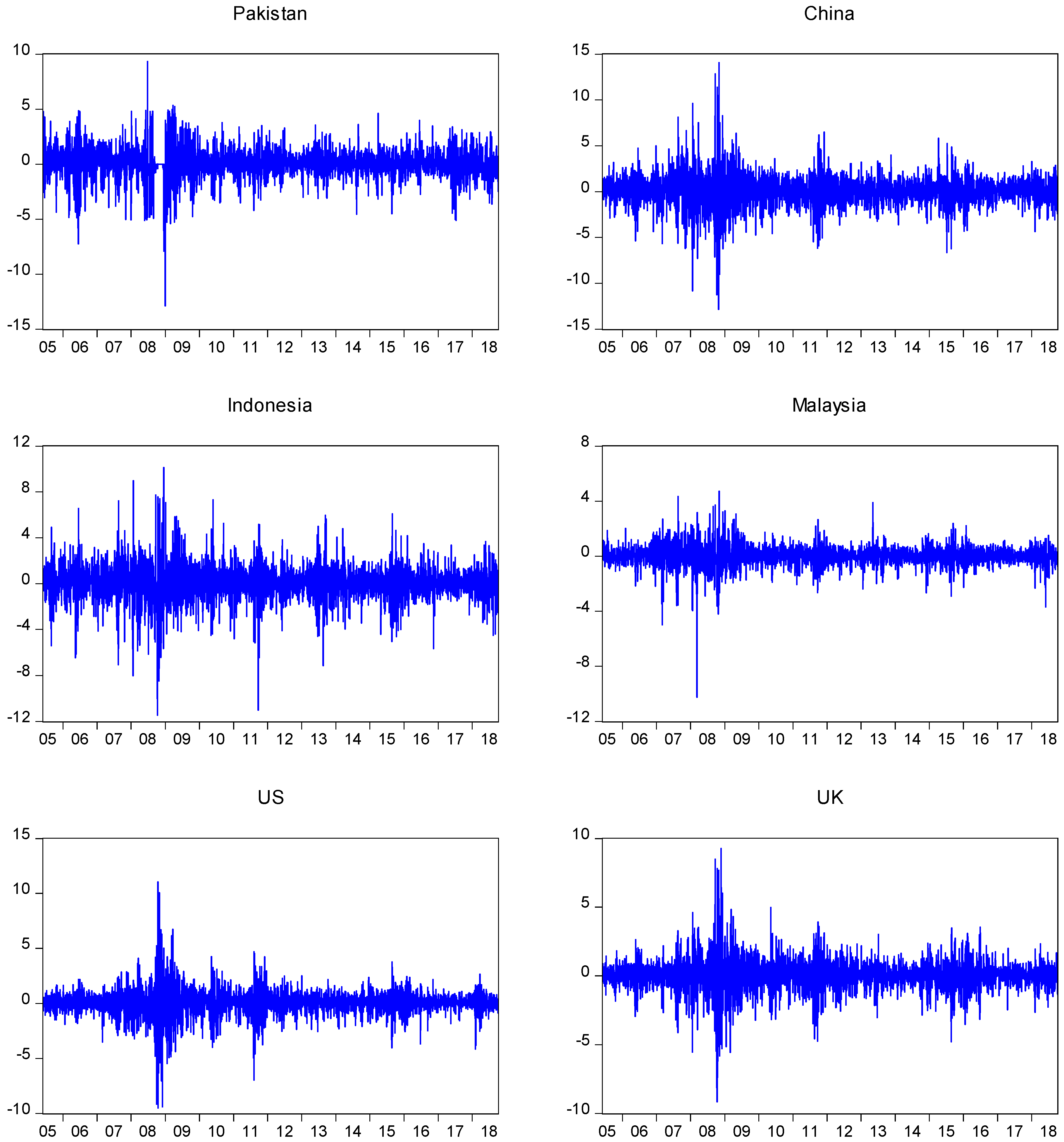
4.2. Dynamics of Daily Stock Prices and Returns
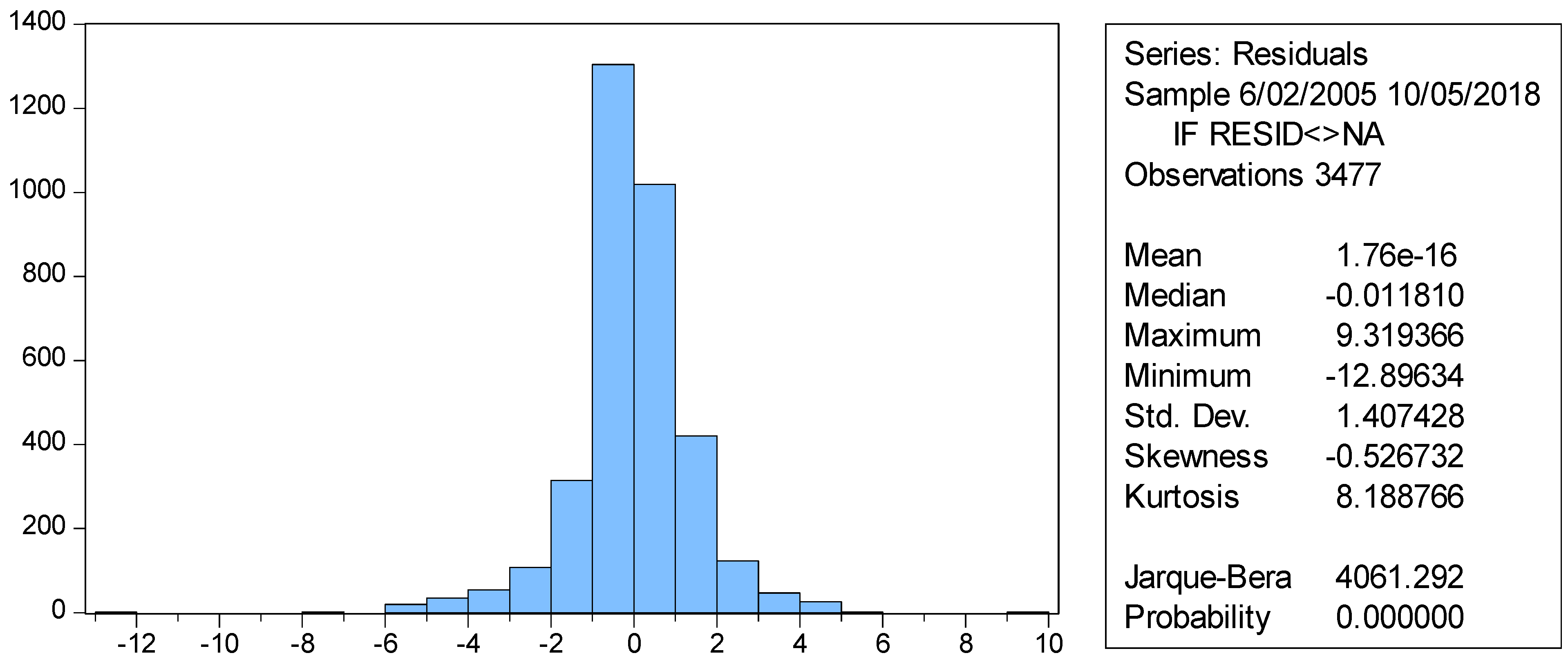
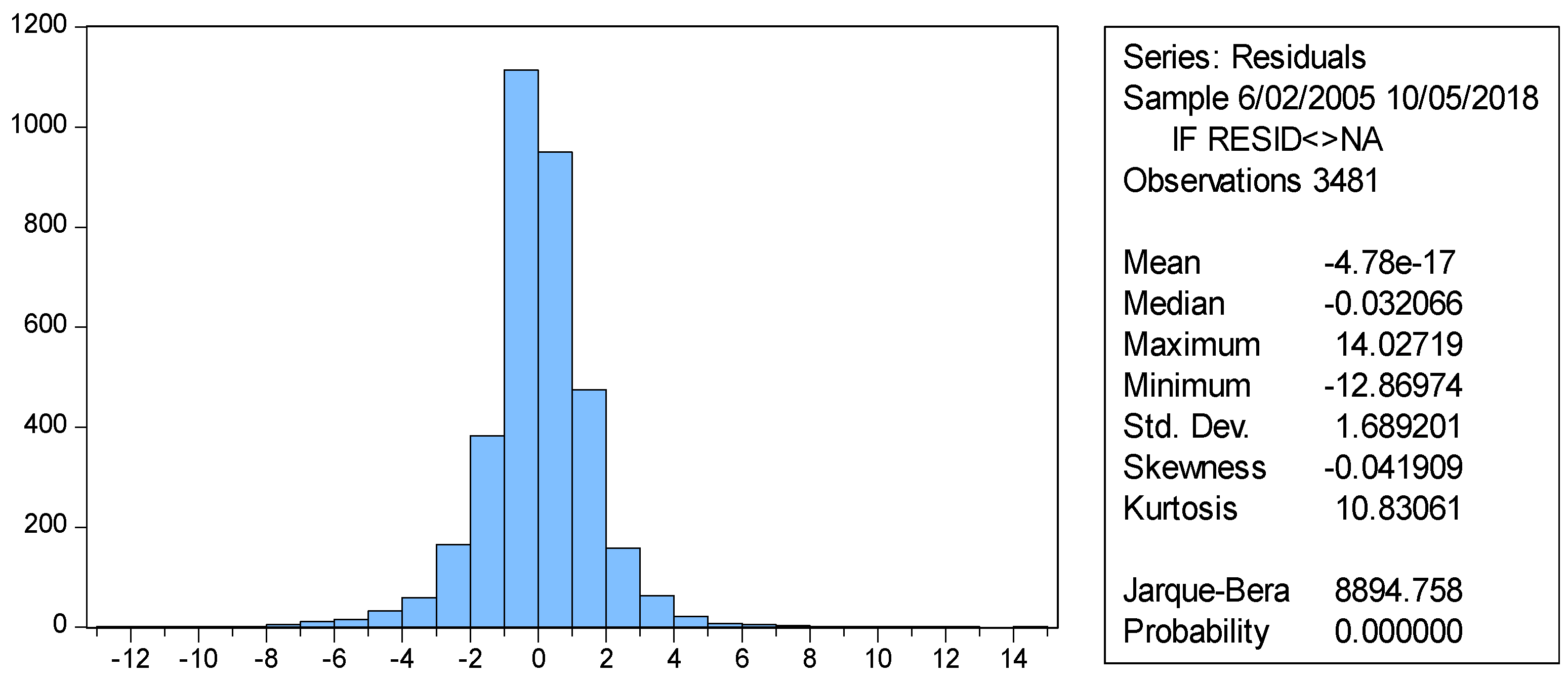
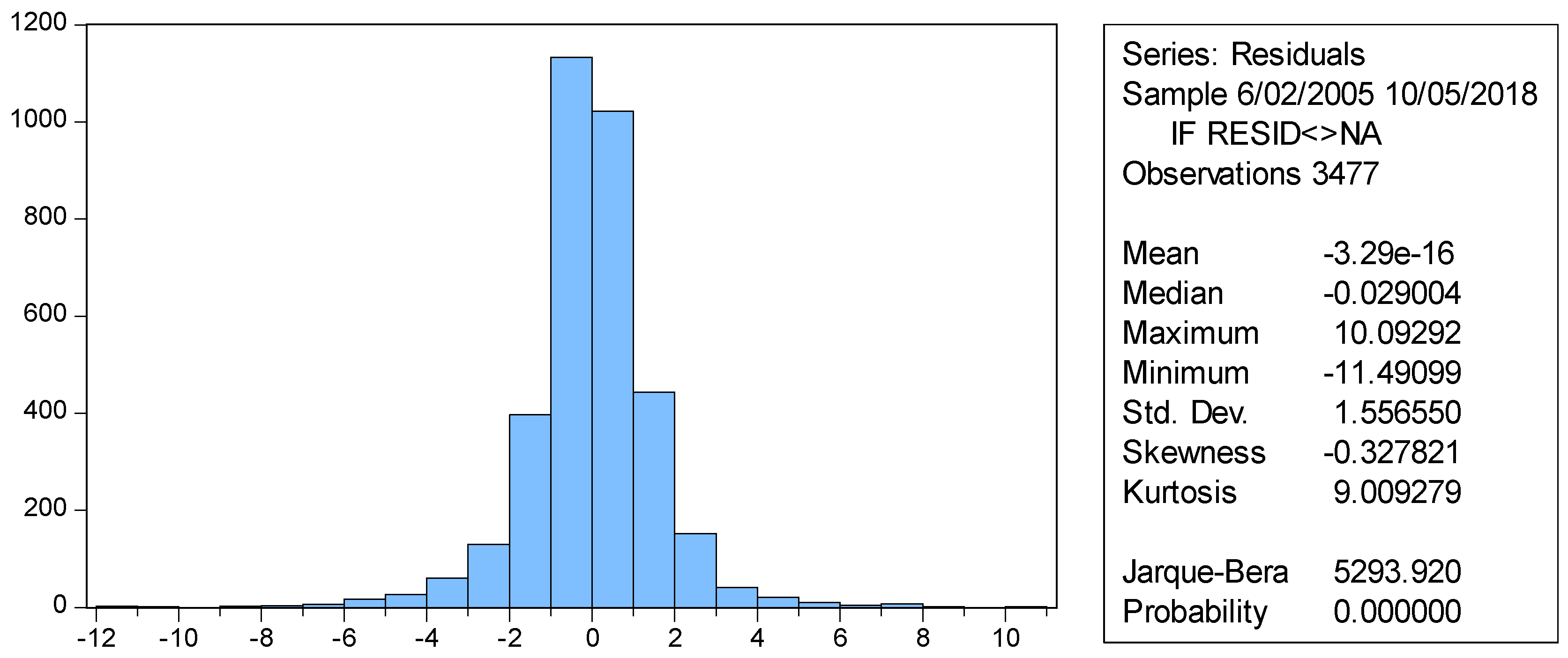
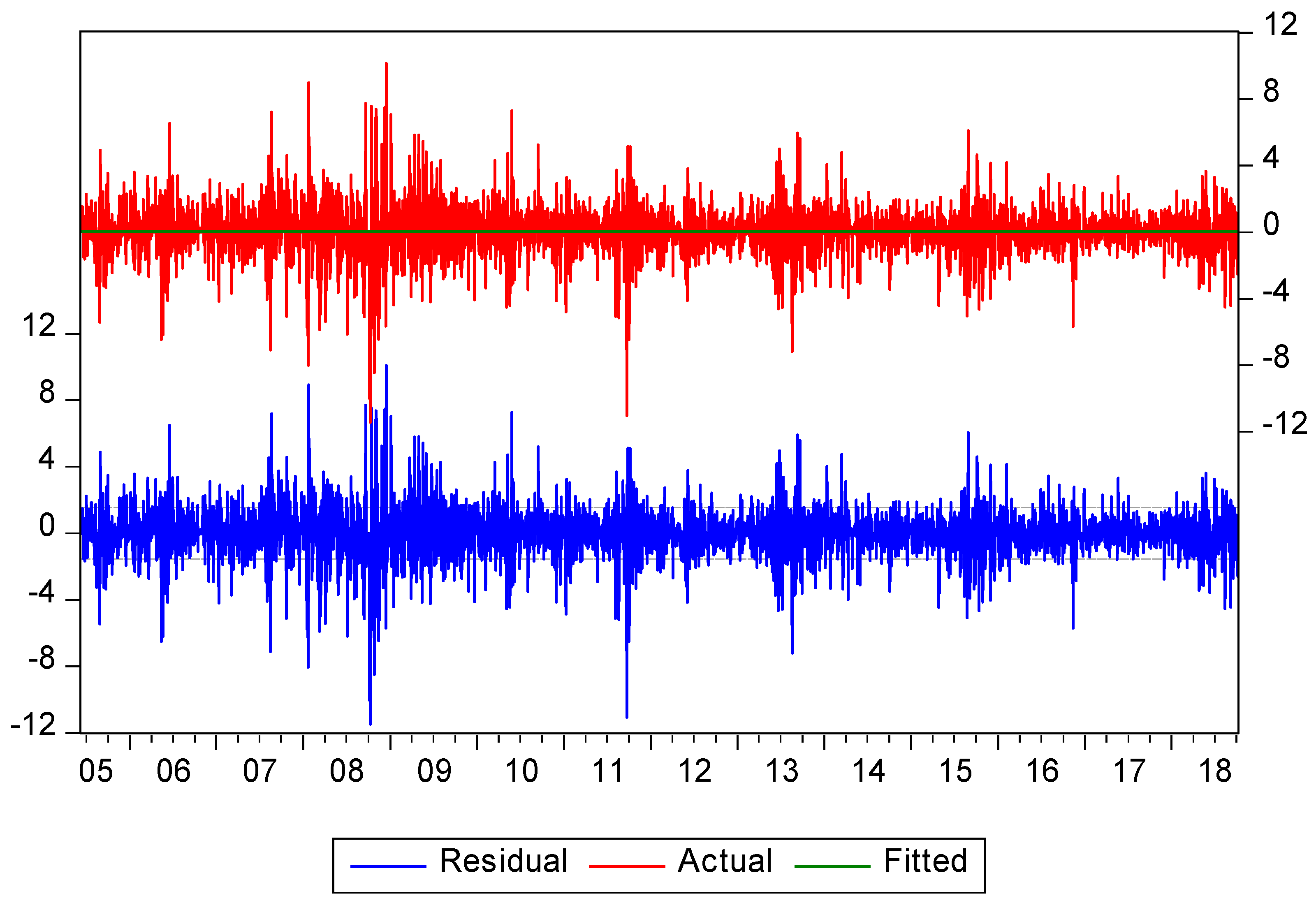
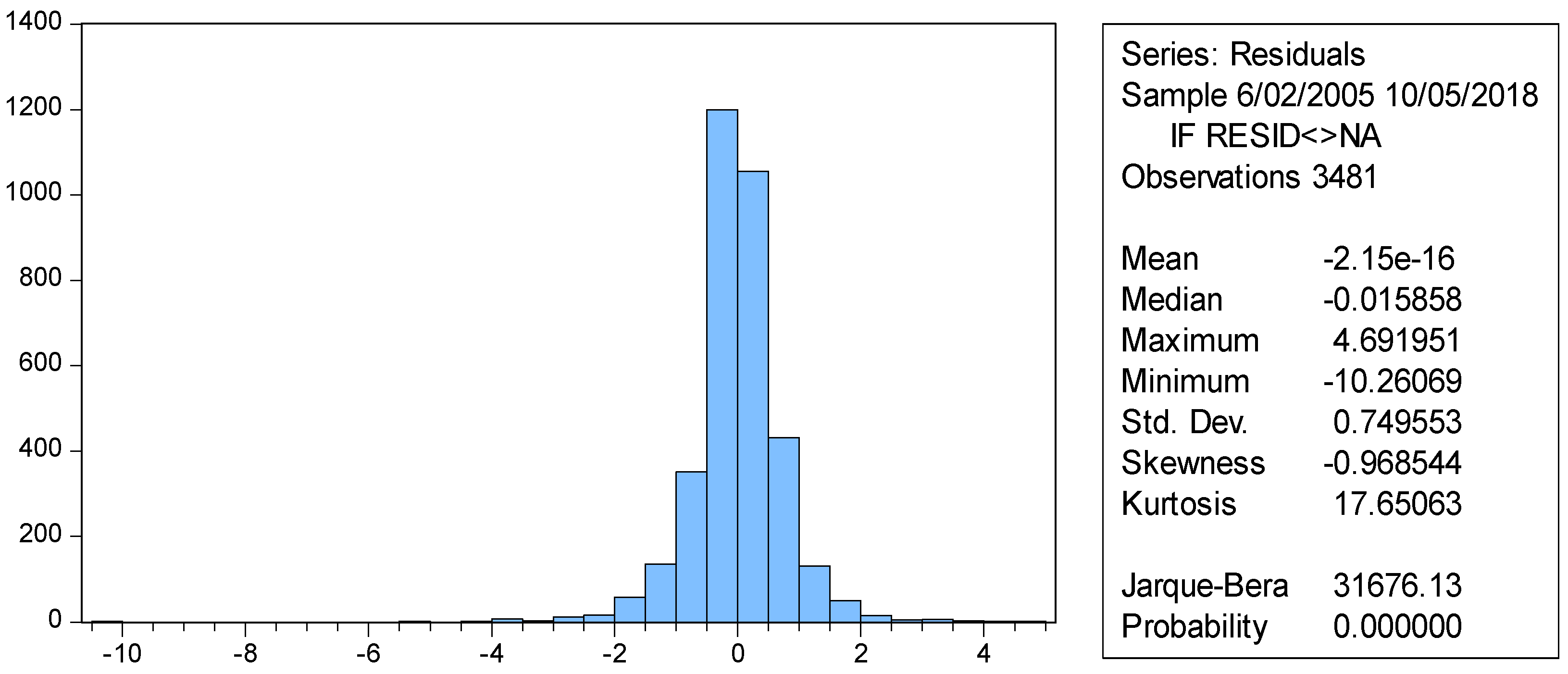
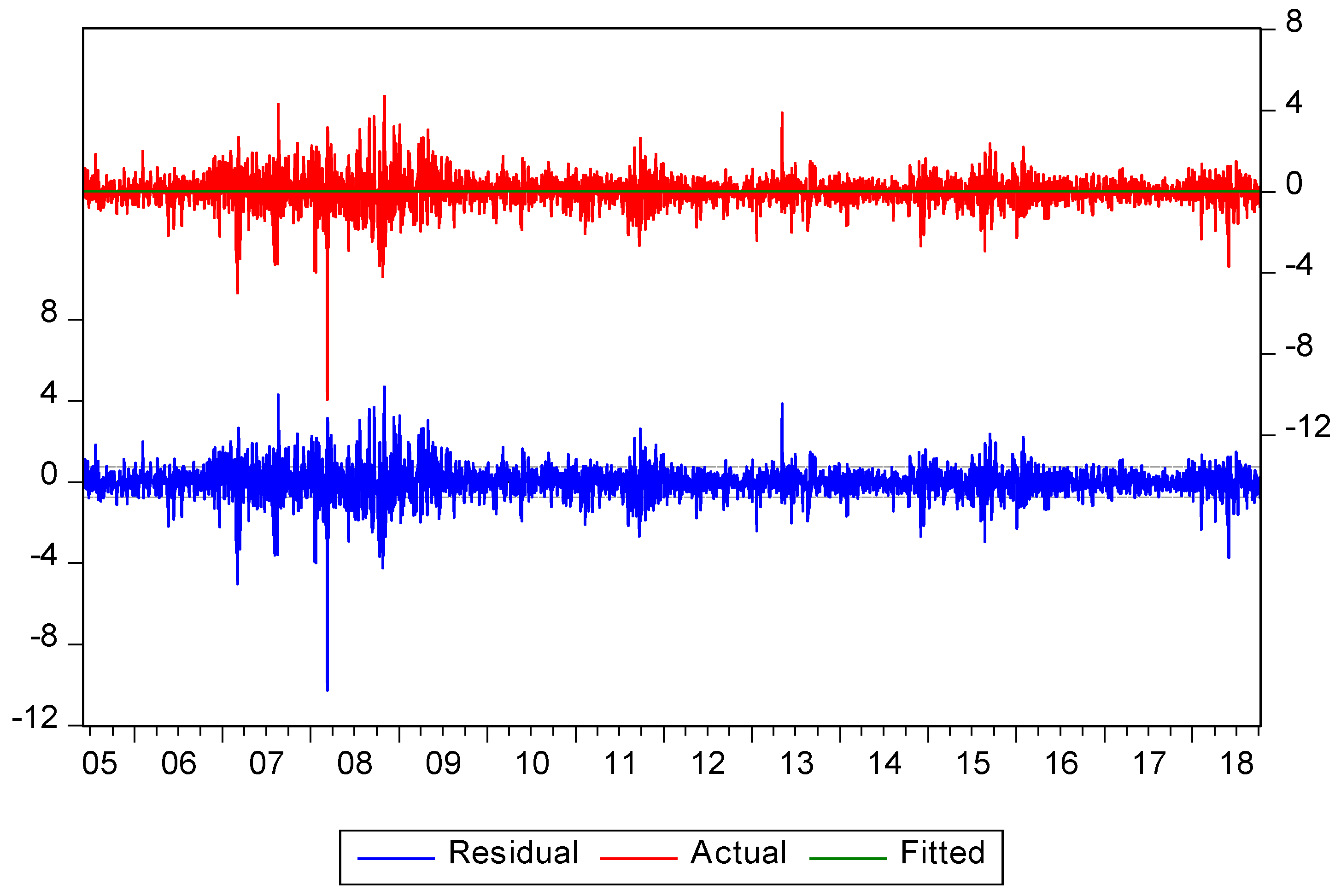
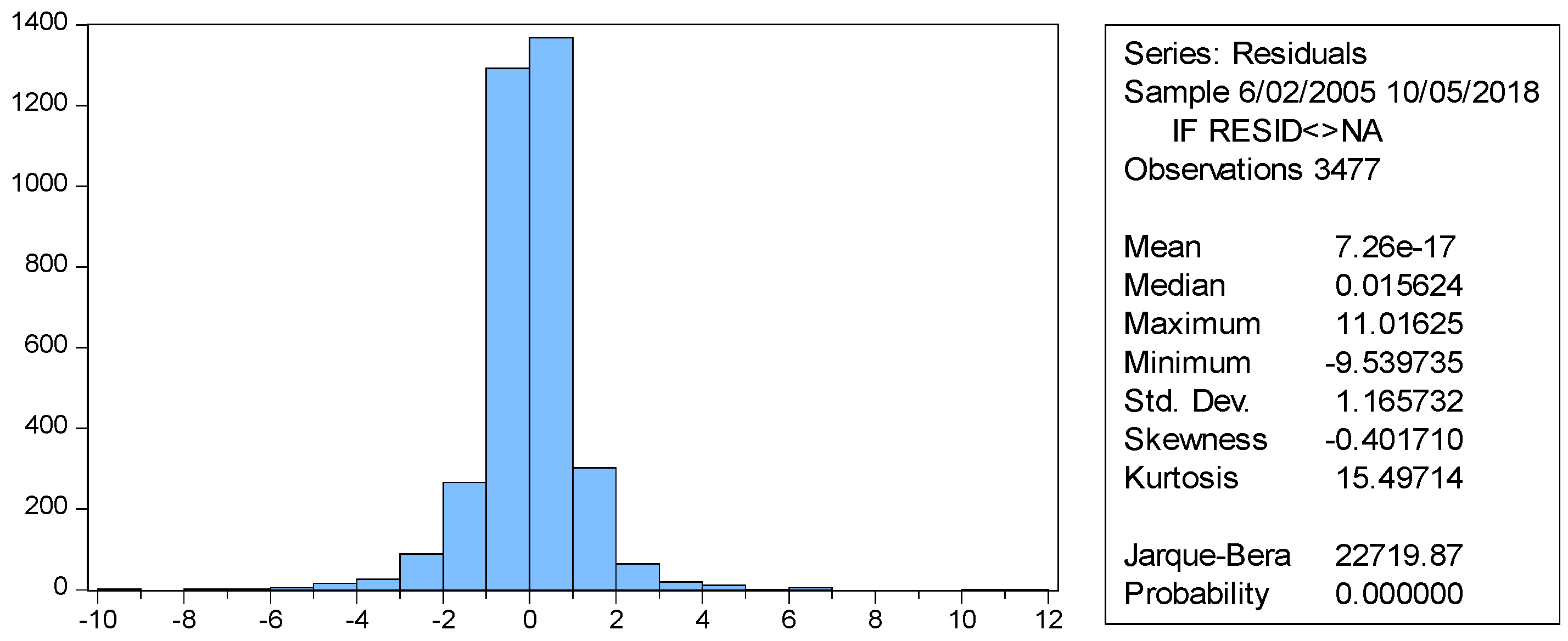
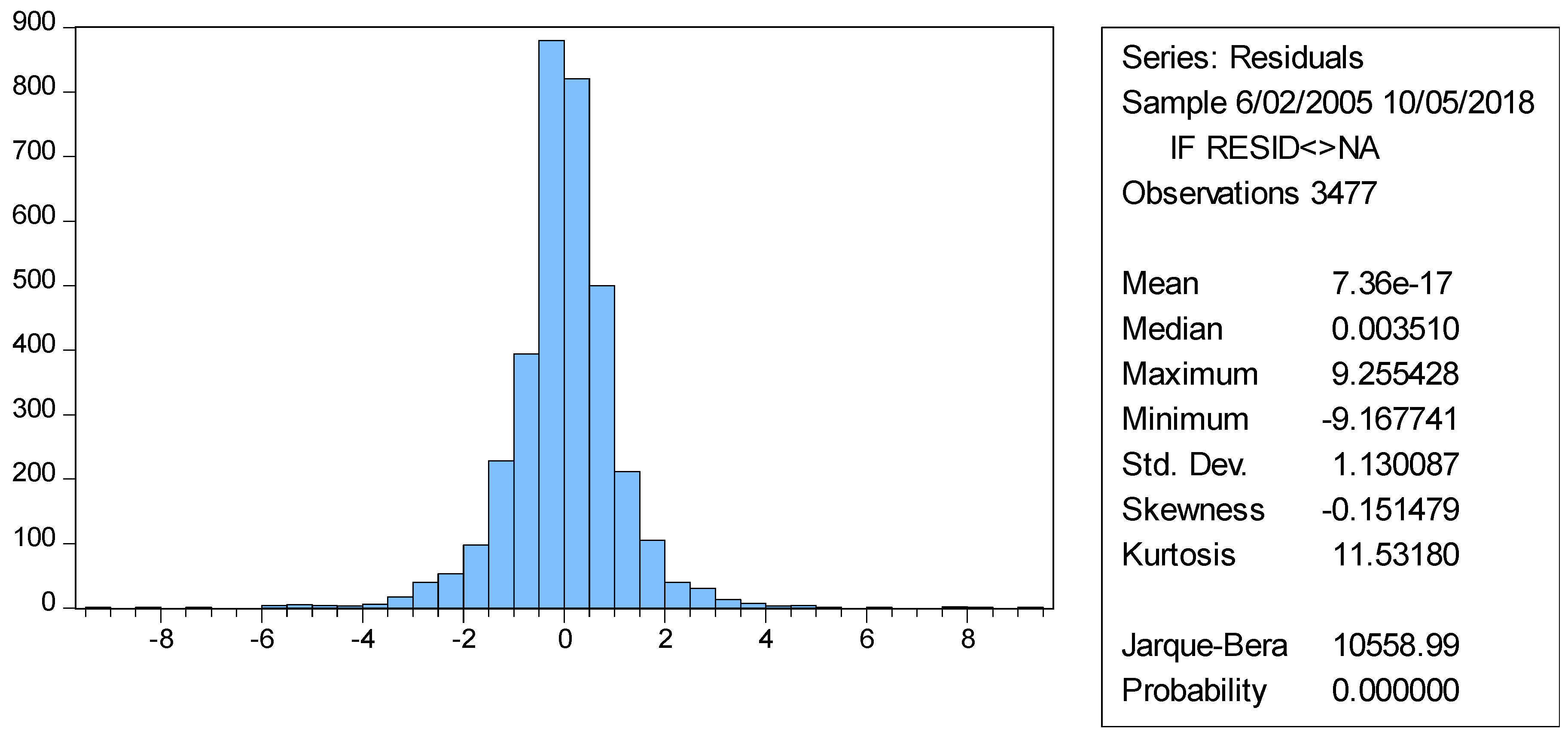
4.3. Stationarity and Residual Diagnostic Tests
4.4. Correlation Matrix
4.5. DCC-GARCH Model
4.6. The Unconditional Volatility and Correlations
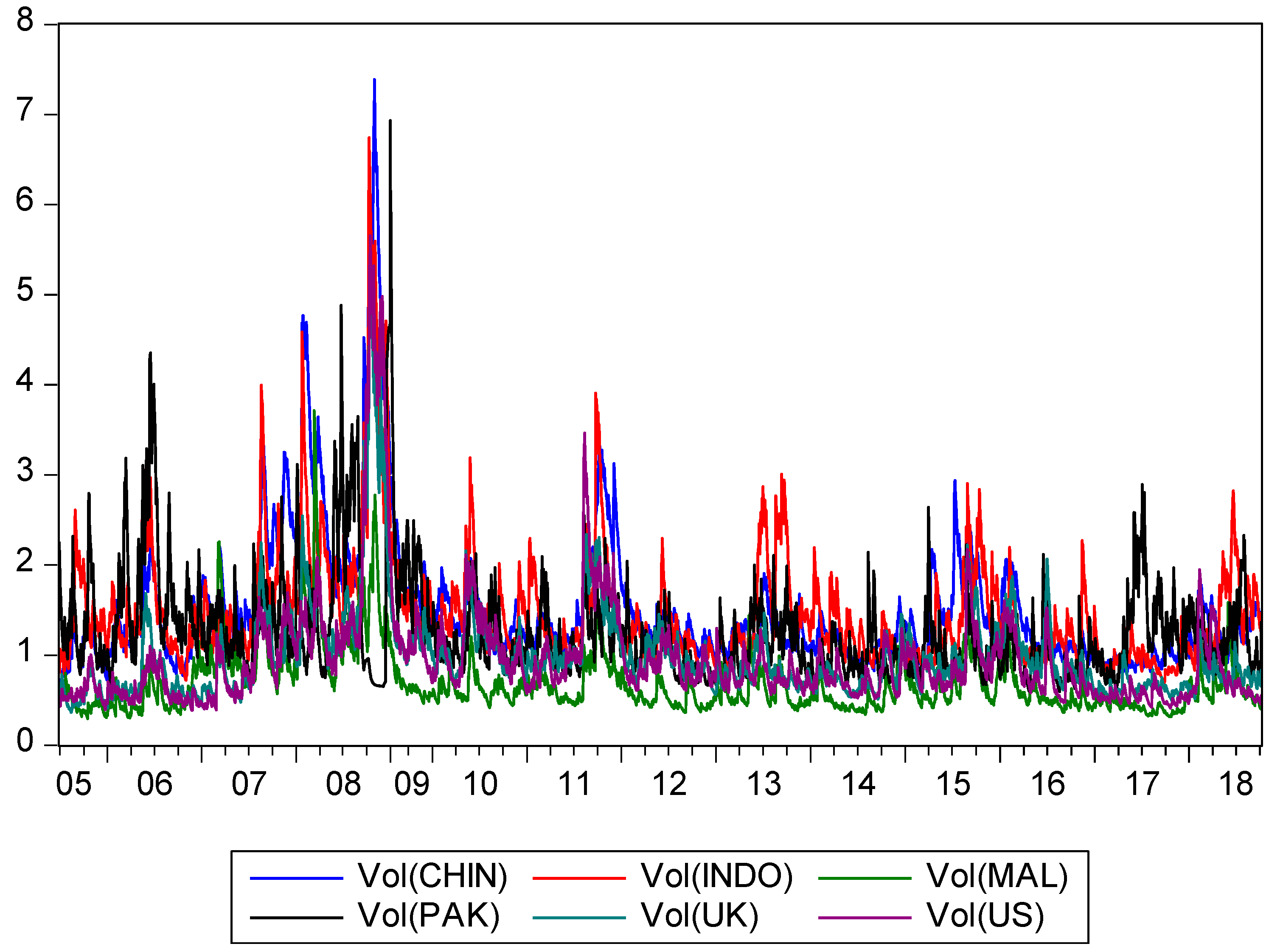
4.7. The Plots of Conditional Correlation and Conditional Volatility
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Johnson, R.; Soenen, L. Asian economic integration and stock market comovement. J. Financ. Res. 2002, 25, 141–157. [Google Scholar] [CrossRef]
- Forbes, K.J.; Chinn, M.D. A decomposition of global linkages in financial markets over time. Rev. Econ. Stat. 2004, 86, 705–722. [Google Scholar] [CrossRef]
- Chen, N.-F.; Zhang, F. Correlations, trades and stock returns of the Pacific-Basin markets. Pac.-Basin Financ. J. 1997, 5, 559–577. [Google Scholar] [CrossRef]
- Manopimoke, P.; Prukumpai, S.; Sethapramote, Y. Dynamic Connectedness in Emerging Asian Equity Markets; Puey Ungphakorn Institute for Economic Research: Bangkok, Thailand, 2018. [Google Scholar]
- Gupta, R.; Guidi, F. Cointegration relationship and time varying co-movements among Indian and Asian developed stock markets. Int. Rev. Financ. Anal. 2012, 21, 10–22. [Google Scholar] [CrossRef] [Green Version]
- Chien, M.-S.; Lee, C.-C.; Hu, T.-C.; Hu, H.-T. Dynamic Asian stock market convergence: Evidence from dynamic cointegration analysis among China and ASEAN-5. Econ. Model. 2015, 51, 84–98. [Google Scholar] [CrossRef]
- Al Nasser, O.M.; Hajilee, M. Integration of emerging stock markets with global stock markets. Res. Int. Bus. Financ. 2016, 36, 1–12. [Google Scholar] [CrossRef]
- Marashdeh, H.A. Financial Integration of the MENA Emerging Stock Markets; University of Wollongong: Wollongong, Australia, 2006. [Google Scholar]
- Wälti, S. Stock market synchronization and monetary integration. J. Int. Money Financ. 2011, 30, 96–110. [Google Scholar] [CrossRef]
- De Brouwer, G. Financial Integration in East Asia; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Obadan, M.I. Globalization of finance and the challenge of national financial sector development. J. Asian Econ. 2006, 17, 316–332. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Rogoff, K.S. The IMF Strikes Back. Available online: https://www.imf.org/en/News/Articles/2015/09/28/04/54/vc021003 (accessed on 11 August 2018).
- Chuluun, T. Global portfolio investment network and stock market comovement. Glob. Financ. J. 2017, 33, 51–68. [Google Scholar] [CrossRef]
- Vo, X.V.; Ellis, C. International financial integration: Stock return linkages and volatility transmission between Vietnam and advanced countries. Emerg. Mark. Rev. 2018, 36, 19–27. [Google Scholar] [CrossRef]
- Iqbal, A. Determinants of Political Governance and Investment Trends in Pakistan; Iqra University, Main Campus: Karachi, Pakistan, 2015. [Google Scholar]
- Siddiqui, S. Pakistan’s stock market: From Asia’s best to Asia’s worst|The Express Tribune. Pakistan Tribune, 19 December 2017. [Google Scholar]
- Siddiqui, S. PSX Ends as World’s Worst Market in 2017|The Express Tribune. The Express Tribune, 1 January 2018. [Google Scholar]
- Anwar, T.; Raza, M.Y. Economic Integration of Stock Markets: An Evidence from Pakistan, China and Malaysia Stock Exchanges. Manag. Organ. Stud. 2016, 3, 52. [Google Scholar] [CrossRef]
- Abdul Karim, B.; Shabri Abd. Majid, M. Does trade matter for stock market integration? Stud. Econ. Financ. 2010, 27, 47–66. [Google Scholar] [CrossRef]
- Paramati, S.R.; Gupta, R.; Hui, A. Trade and Investment Linkages and Stock Market Long-Run Relationship. Aust. Econ. Pap. 2016, 55, 149–169. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Grubel, H.G. Internationally diversified portfolios: Welfare gains and capital flows. Am. Econ. Rev. 1968, 58, 1299–1314. [Google Scholar]
- Ferreira, P. Portuguese and Brazilian stock market integration: A non-linear and detrended approach. Port. Econ. J. 2017, 16, 49–63. [Google Scholar] [CrossRef]
- Panda, A.K.; Nanda, S. Time-varying synchronization and dynamic conditional correlation among the stock market returns of leading South American economies. Int. J. Manag. Financ. 2018, 14, 245–262. [Google Scholar] [CrossRef]
- Das, D.; Bhowmik, P.; Jana, R. A multiscale analysis of stock return co-movements and spillovers: Evidence from Pacific developed markets. Phys. A Stat. Mech. Appl. 2018, 502, 379–393. [Google Scholar] [CrossRef]
- Bracker, K.; Docking, D.S.; Koch, P.D. Economic determinants of evolution in international stock market integration. J. Empir. Financ. 1999, 6, 1–27. [Google Scholar] [CrossRef]
- Pretorius, E. Economic determinants of emerging stock market interdependence. Emerg. Mark. Rev. 2002, 3, 84–105. [Google Scholar] [CrossRef] [Green Version]
- Elyasiani, E.; Perera, P.; Puri, T.N. Interdependence and dynamic linkages between stock markets of Sri Lanka and its trading partners. J. Multinatl. Financ. Manag. 1998, 8, 89–101. [Google Scholar] [CrossRef]
- Paramati, S.R.; Roca, E.; Gupta, R. Economic integration and stock market dynamic linkages: Evidence in the context of Australia and Asia. Appl. Econ. 2016, 48, 4210–4226. [Google Scholar] [CrossRef]
- Vo, X.V. Trade integration and International financial Integration-Evidence from Asia. Singap. Econ. Rev. 2018. [Google Scholar] [CrossRef]
- Dhanaraj, S.; Gopalaswamy, A.K.; Babu, M.S. Trade, Financial Flows and Stock Market Interdependence: Evidence from Asian Markets; Madras School of Economics: Chennai, India, 2017. [Google Scholar]
- Vithessonthi, C.; Kumarasinghe, S. Financial development, international trade integration, and stock market integration: Evidence from Asia. J. Multinatl. Financ. Manag. 2016, 35, 79–92. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.B.; Lam, A.H. Financial Development, International Trade, and Stock Market Integration: Evidence in Six Southeastern Asia Countries. J. Econ. Dev. 2017, 19, 5–17. [Google Scholar]
- Abdul Karim, Z.; Abdul Karim, B. Stock Market Integration: Malaysia and Its Major Trading Partners. Munich Personal RePEc Archive, MPRA Paper 2008. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/26976 (accessed on 10 August 2018).
- Daelemans, B.; Daniels, J.P.; Nourzad, F. Free Trade Agreements and Volatility of Stock Returns and Exchange Rates: Evidence from NAFTA. Open Econ. Rev. 2018, 29, 141–163. [Google Scholar] [CrossRef]
- Chiou, W.-J.P. Who benefits more from international diversification? J. Int. Financ. Mark. Inst. Money 2008, 18, 466–482. [Google Scholar] [CrossRef]
- Paramati, S.R.; Zakari, A.; Jalle, M.; Kale, S.; Begari, P. The dynamic impact of bilateral trade linkages on stock market correlations of Australia and China. Appl. Econ. Lett. 2018, 25, 141–145. [Google Scholar] [CrossRef]
- Chevallier, J.; Nguyen, D.K.; Siverskog, J.; Uddin, G.S. Market integration and financial linkages among stock markets in Pacific Basin countries. J. Empir. Financ. 2018, 46, 77–92. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring Financial Asset Return and Volatility Spillovers, with Application to Global Equity Markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Najeeb, S.F.; Bacha, O.; Masih, M. Does heterogeneity in investment horizons affect portfolio diversification? Some insights using M-GARCH-DCC and wavelet correlation analysis. Emerg. Mark. Financ. Trade 2015, 51, 188–208. [Google Scholar] [CrossRef]
- Jiang, Y.; Yu, M.; Hashmi, S.M. The Financial Crisis and Co-Movement of Global Stock Markets—A Case of Six Major Economies. Sustainability 2017, 9, 260. [Google Scholar] [CrossRef]
- Nath Mukherjee, K.; Mishra, R.K. Stock market integration and volatility spillover: India and its major Asian counterparts. Res. Int. Bus. Financ. 2010, 24, 235–251. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Seth, N. Literature review of stock market integration: A global perspective. Qual. Res. Financ. Mark. 2012, 4, 84–122. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Kenourgios, D.; Samitas, A. Equity market integration in emerging Balkan markets. Res. Int. Bus. Financ. 2011, 25, 296–307. [Google Scholar] [CrossRef]
- Bollerslev, T. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. Rev. Econ. Stat. 1990, 72, 498–505. [Google Scholar] [CrossRef]
- Su, J.-B.; Hung, J.-C. The Value-At-Risk Estimate of Stock and Currency-Stock Portfolios’ Returns. Risks 2018, 6, 133. [Google Scholar] [CrossRef]
- Ismail, M.T.; Audu, B.; Tumala, M.M. Comparison of forecasting performance between MODWT-GARCH(1,1) and MODWT-EGARCH(1,1) models: Evidence from African stock markets. J. Financ. Data Sci. 2016, 2, 254–264. [Google Scholar] [CrossRef]
- Hkiri, B.; Hammoudeh, S.; Aloui, C.; Shahbaz, M. The interconnections between US financial CDS spreads and control variables: New evidence using partial and multivariate wavelet coherences. Int. Rev. Econ. Financ. 2018, 57, 237–257. [Google Scholar] [CrossRef]
- Sakti, M.R.P.; Masih, M.; Saiti, B.; Tareq, M.A. Unveiling the diversification benefits of Islamic equities and commodities: Evidence from multivariate-GARCH and continuous wavelet analysis. Manag. Financ. 2018, 44, 830–850. [Google Scholar] [CrossRef]
- Jaffar, Y.; Dewandaru, G.; Masih, M. Exploring Portfolio Diversification Opportunities Through Venture Capital Financing: Evidence from MGARCH-DCC, Markov Switching, and Wavelet Approaches. Emerg. Mark. Financ. Trade 2018, 54, 1320–1336. [Google Scholar] [CrossRef]
- Pesaran, B.; Pesaran, M.H. Time Series Econometrics Using Microfit 5.0: A User’s Manual; Oxford University Press, Inc.: Oxford, UK, 2010. [Google Scholar]
- Buriev, A.A.; Dewandaru, G.; Zainal, M.-P.; Masih, M. Portfolio diversification benefits at different investment horizons during the Arab uprisings: Turkish perspectives based on MGARCH–DCC and wavelet approaches. Emerg. Mark. Financ. Trade 2018, 54, 3272–3293. [Google Scholar] [CrossRef]
- Lim, S.J.; Masih, M. Exploring Portfolio Diversification Opportunities in Islamic Capital Markets through Bitcoin: Evidence from MGARCH-DCC and Wavelet Approaches. Munich Personal RePEc Archive, MPRA Paper 2017. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/79752 (accessed on 10 August 2018).
- Arouri, M.E.H.; Jawadi, F.; Nguyen, D.K. The Dynamics of Emerging Stock Markets; Physica-Verlag HD: Heidelberg, Germany, 2010; ISBN 978-3-7908-2389-9. [Google Scholar]
- Balanda, K.P.; MacGillivray, H. Kurtosis: A critical review. Am. Stat. 1988, 42, 111–119. [Google Scholar]
- Saiti, B.; Noordin, N.H. Does Islamic equity investment provide diversification benefits to conventional investors? Evidence from the multivariate GARCH analysis. Int. J. Emerg. Mark. 2018, 13, 267–289. [Google Scholar] [CrossRef]
- Pesaran, M.H. Time Series and Panel Data Econometrics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Narayan, S.; Sriananthakumar, S.; Islam, S. Stock market integration of emerging Asian economies: Patterns and causes. Econ. Model. 2014, 39, 19–31. [Google Scholar] [CrossRef]

| Studies | Countries | Data and Frequency | Models | Results |
|---|---|---|---|---|
| Paramati, S. R., Roca, E., & Gupta, R. [30] | Australia and ten Asian trade partners. | MSCI weekly prices for the period 1999 to 2013. | Cointegration, AGDCC-GARCH, and Multiple regression models. | Increasing trade linkages have increased the stock market integration. |
| Paramati, S. R., Zakari, A., Jalle, M., Kale, S., & Begari, P. [38] | Australia and China. | MSCI weekly prices for the period January 1993 to December 2015. | OLS, DOLS, and, FMOLS models | Trade caused an increase in stock market integration and decreased the portfolio diversification. |
| Paramati, S. R., Gupta, R., & Hui, A. [21] | Australia, and 13 trade and investment partners. | Weakly closing prices from 1992 to 2013. | Cointegration, AGDCC-GARCH, and Multiple regression. | There are varying Cointegration and correlation which has changed before and after GFC. |
| Vithessonthi, C., & Kumarasinghe, S. [33] | Fifteen developed and the developing countries in Asia. | Daily MSCI stock returns 1985–2013 and other yearly economic indicators. | OLS Regression, Fixed Effect, Random effect, and correlation. | A country’s financial development has an impact on the stock market integration with international stock markets. |
| Thuy Bach Nguyen, T. H., & Huynh Lam, A. [34] | Vietnam and five ASEAN countries. | Daily MSCI stock returns 2000–2015 and other economic indicators. | OLS Regression, Fixed Effect, Random effect, and correlation. | Trade integration affect stock market integration. |
| Abdul Karim, B., & Shabri Abd. Majid, M. [20] | Major trading partners of Malaysia. | Weekly stock indices 1992–2008. | ARDL, and VAR models. | Malaysian stock market is found to be integrated with the stock markets of its trading partners. |
| Abdul Karim, Z., & Abdul Karim, B. [35] | Malaysia and its major trading partners. | Weekly data from 1998–2007. | Cointegration, VECM and Granger causality test. | The stronger the economic ties between the countries higher the stock market integration. |
| Chevallier, J., Nguyen, D. K., Siverskog, J., & Uddin, G. S. [39] | Fourteen countries from Pacific Basin. | Daily stock indices return for the period of 1993–2014. | Diebold and Yilmaz [40,41] Spillover index and impulse response. function (IRF). | ASEAN emerging markets are exposed to US shocks. Stock market interrelationship has increased over time which reduces the diversification benefits. |
| Daelemans, B., Daniels, J. P., & Nourzad, F. [36] | Canada, Mexico, and the United States. | Daily stock indices return for the period of 1994–2014. Bilateral exchange rates. | DCC-GARCH model. | Free-trade agreement affects differently to exchange rate and stock market returns. Canada and Mexico are more correlated as compared to the USA. |
| Najeeb, S. F., Bacha, O., & Masih, M. [42] | Different benchmark mark Islamic stock indices. | Daily closing prices for the period of 2006–2013. | DCC-GARCH, continuous wavelet transformation (CWT), and Maximum Overlap Discrete Wavelet Transform (MODWT) models. | There are portfolio diversification benefits for the investors in Islamic stock market for the short holding period. |
| Jiang, Yu, & Hashmi. [43] | Six Major Economies US, UK, mainland China, Hong Kong, Japan, and Germany. | Period divided into three sub-periods. Daily stock market prices June 2006 to July 2010. | VAR model, Granger causality tests and impulse response. | The GFC has increased the co-movements among the economies selected. |
| Ferreira, P. [24] | Portuguese and Brazilian. | Daily data from 1993 to 2016. The whole sample was divided into six sub-periods to make a comparison among the periods. | DFA, DCCA and DMCA. | The integration between the markets increased; however, the results showed that the Portuguese and Brazilian investors could gain as from the international portfolio diversification. |
| Panda, A. K., & Nanda, S. [25] | Six Leading South American countries. | Weekly stock indices from 1995 to 2015 | GJR-GARCH and DCC-GARCH. | Asymmetry in returns and the increasing integration among the countries is found. |
| Stock Market | Symbols | Benchmark Indices | MSCI Status |
|---|---|---|---|
| Pakistan | PAK | MSCI Pakistan Index | Emerging market |
| China | CHIN | MSCI China Index | Emerging market |
| Indonesia | INDO | MSCI Indonesia Index | Emerging market |
| Malaysia | MAL | MSCI Malaysia Index | Emerging market |
| United States | US | MSCI USA Index | Developed market |
| United Kingdom | UK | MSCI UK Index | Developed market |
| Pakistan | China | Indonesia | Malaysia | US | UK | |
|---|---|---|---|---|---|---|
| Mean | 0.0126 | 0.0319 | 0.0422 | 0.0192 | 0.0255 | 0.0097 |
| Median | 0.0000 | 0.0000 | 0.0121 | 0.0034 | 0.0410 | 0.0107 |
| Maximum | 9.3312 | 14.0593 | 10.1349 | 4.7111 | 11.0419 | 9.2652 |
| Minimum | −12.8845 | −12.8377 | −11.4490 | −10.2415 | −9.5141 | −9.1580 |
| Std. Dev. | 1.4120 | 1.6890 | 1.5556 | 0.7494 | 1.1650 | 1.1294 |
| Skewness | −0.5061 | −0.0417 | −0.3282 | −0.9687 | −0.4014 | −0.1513 |
| Kurtosis | 8.1403 | 10.8332 | 9.0177 | 17.6557 | 15.5153 | 11.5428 |
| Jarque–Bera | 3982.08 | 8903.23 | 5316.33 | 31707.11 | 22818.17 | 10601.26 |
| Probability | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Sum | 44.007 | 111.179 | 146.765 | 66.865 | 88.662 | 33.939 |
| Sum Sq. Dev. | 6940.66 | 9930.06 | 8424.09 | 1955.17 | 4724.24 | 4440.29 |
| Observations | 3482 | 3482 | 3482 | 3482 | 3482 | 3482 |
| Pakistan | China | Indonesia | Malaysia | US | UK | |
|---|---|---|---|---|---|---|
| ADF(Level) | −36.2750 | −57.2736 | −54.2688 | −53.1820 | −46.2989 | −28.2440 |
| Probability | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0000 |
| ADF (1st difference) | −24.3141 | −20.7381 | −20.8440 | −23.2532 | −22.9411 | −21.8649 |
| Probability | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0000 |
| Q-Statistics | 81.5660 | 3.0101 | 24.0910 | 36.9440 | 32.1610 | 3.4023 |
| Probability | 0.0000 | 0.0830 | 0.0000 | 0.0000 | 0.0000 | 0.0650 |
| LM test | 91.7990 | 3.0249 | 24.1519 | 37.0981 | 44.2551 | 13.0839 |
| Probability | 0.0000 | 0.2204 | 0.0000 | 0.0000 | 0.0000 | 0.0014 |
| ARCH effect | 441.1908 | 238.1075 | 140.3748 | 48.9674 | 169.3661 | 207.7931 |
| Probability | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Countries | Pakistan | China | Indonesia | Malaysia | US | UK |
|---|---|---|---|---|---|---|
| Pakistan | 1 | 0.089 | 0.111 | 0.145 | 0.022 | 0.052 |
| China | 1 | 0.542 | 0.502 | 0.233 | 0.408 | |
| Indonesia | 1 | 0.488 | 0.135 | 0.304 | ||
| Malaysia | 1 | 0.111 | 0.305 | |||
| US | 1 | 0.577 | ||||
| UK | 1 |
| Parameter | Probability | |||
|---|---|---|---|---|
| Pakistan | 0.77099 | 0.19485 | 0.000 | 0.03416 |
| China | 0.91925 | 0.07022 | 0.000 | 0.01052 |
| Indonesia | 0.86909 | 0.11007 | 0.000 | 0.02084 |
| Malaysia | 0.87530 | 0.10905 | 0.000 | 0.01565 |
| US | 0.87884 | 0.11006 | 0.000 | 0.01110 |
| UK | 0.89884 | 0.08730 | 0.000 | 0.01385 |
| Parameter | Probability | |||
|---|---|---|---|---|
| Pakistan | 0.78330 | 0.18530 | 0.000 | 0.03140 |
| China | 0.91792 | 0.07341 | 0.000 | 0.00866 |
| Indonesia | 0.87606 | 0.10457 | 0.000 | 0.01937 |
| Malaysia | 0.86978 | 0.11500 | 0.000 | 0.01522 |
| US | 0.87443 | 0.11311 | 0.000 | 0.01246 |
| UK | 0.87970 | 0.10420 | 0.000 | 0.01610 |
| Rank | Countries | Benchmark Indices | Unconditional Volatility |
|---|---|---|---|
| 1 | China | MSCI China Index | 1.6871 |
| 2 | Indonesia | MSCI Indonesia Index | 1.6005 |
| 3 | Pakistan | MSCI Pakistan Index | 1.3600 |
| 4 | US | MSCI USA Index | 1.1215 |
| 5 | UK | MSCI UK Index | 1.1065 |
| 6 | Malaysia | MSCI Malaysia Index | 0.7606 |
| Pakistan | China | Indonesia | Malaysia | US | UK | |
|---|---|---|---|---|---|---|
| Pakistan | 1.36000 | |||||
| China | 0.08813 | 1.68710 | ||||
| Indonesia | 0.11257 | 0.52269 | 1.60050 | |||
| Malaysia | 0.14648 | 0.47821 | 0.47924 | 0.76065 | ||
| US | 0.020233 | 0.23549 | 0.14842 | 0.09691 | 1.12150 | |
| UK | 0.053134 | 0.40849 | 0.31304 | 0.29587 | 0.56293 | 1.10650 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joyo, A.S.; Lefen, L. Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach. Sustainability 2019, 11, 303. https://doi.org/10.3390/su11020303
Joyo AS, Lefen L. Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach. Sustainability. 2019; 11(2):303. https://doi.org/10.3390/su11020303
Chicago/Turabian StyleJoyo, Ahmed Shafique, and Lin Lefen. 2019. "Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach" Sustainability 11, no. 2: 303. https://doi.org/10.3390/su11020303
APA StyleJoyo, A. S., & Lefen, L. (2019). Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach. Sustainability, 11(2), 303. https://doi.org/10.3390/su11020303





