1. Introduction
Renovation is a common means of maintaining buildings in order to serve their users. For example, the maintenance of campus buildings is important because they serve many students during their education and serve as a workplace for teachers and staff. The main function of building renovations is to control deterioration and maintain optimal performance of each building component [
1]. In the building life cycle, renovation is a prevailing activity carried out after the completion of the building construction phase. Because the building function continues to decrease every year [
2], it is necessary to take an effort to maintain its performance. In practice, taking the case of the university campus as an example, campus buildings may be subject to a wide variety of complex defects, such as peeling paint, wall cracks, and ceiling cracks [
3]. Renovation design on campus does not rely only on technical necessities but also has to provide a strategy to achieve multiple objectives and often conflicting under resource constraints. Therefore, renovation of university campuses have three main elements:
- (1).
Renovation projects are more difficult than new construction projects: The main characteristic that influences the complexity of renovation projects is the concurrent utilization of a building by both workers and users. It is usually not possible to close off an entire building or a whole area that has several buildings to carry out a single-phase renovation project [
4]. During the renovation, the owner usually requires that the building operates normally despite the renovation project. Generally, renovation projects involve multiple types of construction projects, including reconstruction, rehabilitation, and remodeling [
5]. The renovation project has a distinctive environment and creates larger limitations for the owner, the engineer, the contractor, the operator, and the user [
6]. Due to the complexity of existing building characteristics, such as limited work areas and shared utilization of space by workers and occupants, renovation projects have a large tendency towards reducing the convenience of the occupants, as well as safety issues and project delays. Hence, the impact on the occupants of the building as a result of the renovation activities should be kept to a tolerable extent [
5].
- (2).
Simultaneous renovation engineering and building operation: On the renovation project site, there are potentially conflicting activities between the workers and occupants. To address this problem, a renovation project is generally carried out in several segments in different periods or locations. As a result, it can reduce the unacceptable impact on occupants and the renovation activity can be performed as expected.
- (3).
Multiple decision factors: As a combination, primarily between the building conditions and the resource constraints on campus. Focusing on the building conditions, various factors influence the type of renovation, such as the degree of aging in the buildings, the urgency to repair the buildings, and the service life of the buildings. The resource constraints factors can be explained more broadly, such as financial capacity and the number of rooms available as temporary spaces. As a consequence of the many influencing factors, the decision of the type of renovation made by the planner can be diverse and can impact the entire renovation project in various ways; therefore, a strategy to assess the appropriate schedule is required. Furthermore, it allows decision-makers to be able to plan their future renovation schedule more accurately.
The building planners are responsible for planning and carrying out renovations. In general, the campus consists of several types of buildings of various conditions and ages, making the renovation planning process rather complicated. In the process of decision-making, the building planner must focus on fundamental objectives including functionality, feasibility, and accountability [
7].
Appropriate scheduling should be constructed in detail and consider key factors in building renovation [
7]. Generally, building planners focus attention on the cost and time needed for the renovations. As a result, a renovation plan is still lacking when it comes to the concept of long-term performance of the building. To obtain a comprehensive renovation plan, the decision-makers should develop a framework to assess building renovation performance [
7] and consider the renovation impact to the occupants during and after renovation. For instance, if a building planner carries out renovations in the classroom building, students and teachers will be disturbed, because some of, or possibly all, the rooms would close. Consequently, teaching and learning activities have to be performed in other locations during the renovation project.
The main goal of this study is to build a model that can help the planners to make the renovation schedule plan. The model has to provide performance-based decision support of renovation construction process scheduling by considering the long-term performance of the buildings. It will assist the planners in overcoming the complexity of constructing a renovation schedule.
To achieve the goal of this study, there are objectives. First, this study deals with the complexity of building renovation schedule. The schedule development process involves information related to the renovations, such as the age and the service life of the building, the renovation cost, the duration of the renovation, and the resource relationship. For this objective, this study takes a university campus as an example to make the analysis. Second, the complexity of build renovation schedule is analyzed and employed to form the key attributes in the model operation. For this objective, it is necessary to select and apply suitable mechanisms to operate the planning in the model. By the mechanisms, the model can provide good schedule solutions with high performance under the resources constraint. Finally, the demonstration of the model is implemented by an application case of a university campus in Taiwan. The model provides a worthwhile schedule plan for the administrators and planners of the university.
2. Methodology
The proper and feasible methodology for this study is essential. We need to identify the characteristics of long-term performance of the buildings according to previous research related to building renovation, maintenance, rehabilitation, and refurbishment. The key factors influencing the long-term performance of building are also necessary to collect, quantify, and combine as an evaluable index for the comparisons of plans’ performance.
To generate feasible plans for renovation construction process scheduling, this study analyzes the required resources and conditions. There are several important facets, including financial supply and limitation, spatial capacity, and the flexibility of occupant’s usage. These facets lead to the generation of candidate plans for renovation construction process scheduling.
Due to a large number of candidate plans to satisfy the requirements with different levels of plan performance, the integrated mechanism employed in the model is beneficial. For generating the candidate plans and calculating the plans’ performance, this study uses simulation engine as the mechanism. For searching the optimal schedule plan efficiently, this study uses genetic algorithm, one of the optimization methods, as another mechanism. The two combined mechanisms make up the model to provide the decision support of renovation construction process scheduling.
The final important part of the methodology is to demonstrate the proposed model. We selected a university campus as the application case. In the case, the model assists building planners as decision-makers in presenting the optimal renovation schedules on campus.
3. Long-Term Performance Assessment of Building Renovation
Many studies in different industries have focused on modeling decision-making and scheduling, such as building a decision support model for the maintenance and management of green areas [
8], renovation scheduling to minimize user impacts in a building that remains in operation [
5], and optimized maintenance and renovation scheduling in multifamily buildings [
1]. For instance, Lee et al. [
8] propose a model using a decision support system to provide an appropriate maintenance schedule of green areas on campus by optimizing manpower. Lee [
5] also proposes an integrated model to search for a near-optimal schedule by minimizing the impact on users by relying on calculating the work zones and the time delay. For a group of buildings in an area, Farahani et al. [
1] carried out partial dynamic modeling to provide a cost-optimal maintenance plan by simulating several scenarios. However, these models have not found a solution for the long-term performance of the building since these studies do not propose a schedule optimization strategy attributed to the occupant convenience rate and the quality of the building.
In a related study in building maintenance, Farahani et al. [
1] argued that the effects of renovations would improve the quality and extend the service life of the building. In this study, the quality of building space to be used (
QC) is the first item that would affect the performance index of the building. The quality of the building space for use (
QC) in our model is given by Equation (1), which considers influencing factors of the renovation project [
9],
In the above equation,
denotes the service life of the building in years,
is the age of the building in years,
is the extended lifespan of the building due to renovation in years, and
is the rate of depreciation for reinforced concrete structures per year, shown in
Table 1 [
9].
The second part of the performance function involves an inconvenience rate of occupants caused by the occupants’ movements during the renovation project. This study emphasizes the inconvenience rate of occupants as the main impact of renovation activities that cannot be avoided, which depends on temporary space relocation duration and the total number of relocated rooms. The inconvenience rate function is formulated in Equation (2) as the summation of the total duration per relocated room divided by the capacity of the temporary space,
where
is the average relocation duration per relocated room,
DR is the temporary space relocation duration,
is the summation of temporary space relocation duration, and
is the capacity of temporary space (the total amount of available space multiplied by the total renovation plan duration). Detailed formulations of these components are addressed in Equation (3) and Equation (4). Equation (3) is the summation of temporary space relocation duration, which depends on the amount of renovated room and the duration of the renovation,
where
is the room area associated with type
I, and
is the required duration of the renovation associated with a type
i room. Equation (4) formulates the capacity of temporary space (
CP) as the product of the total amount of available space (
AS) and the total duration of the renovation plan (
DP),
where
is the summation of available space associated with type
I, and
is the total duration of the renovation plan. According to the above equations, the lower the
DU index, the higher the level of performance in the renovation plan. Therefore, the objective function here is to minimize the inconvenience rate as a result of the renovation project.
The long-term performance assessment process for the renovation project considers the quality of the building space for use (
QC) and the occupant inconvenience rate (
DU) as the result of the renovation project. The goal of this assessment is to maximize the performance index (
PI) for a renovation project while considering resource constraints. Since the two factors that influence the performance values oppose each other, i.e.,
QC is maximized and
DU is minimized, the process of constructing assessment objectives is a challenge in developing an optimal schedule. In this study, two objective functions were normalized and combined with weights. The weighting factors (
and
) were applied to develop the final solutions. The values of the weights depended on the renovation planner’s goals and preferences. The objective function for the long-term performance assessment in our model is represented as Equation (5). However, since the second objective (
DU) is, in fact, a minimization function, the opposite formulation is introduced to create the composite objective maximization function by the performance index (
PI),
where
and
represent the weighting for objectives one and two, respectively,
represents the minimum value of the building space quality for use,
represents the maximum value of the building space quality for use,
represents the minimum value of the inconvenience rate, and
represents the maximum value of the inconvenience rate.
3.1. Space Requirement
The important distinguishing characteristic between renovation projects and new construction projects are the space resources required. In contrast to a new project that has sufficient flexibility in utilizing the work area, a renovation project has to share the work area with the occupants. Despite the fact that the building is being renovated, the occupants must be able to continue the usage of the building as usual. Therefore, the owner and contractor need to pay more attention to the disruption and inconvenience perceived by the occupants. The most important objective in determining the space available is that convenience of the occupants affected, and they should not be interrupted due to the renovation project. For instance, if a classroom is scheduled in the renovation plan, the contractor and the owner must prepare an available room as a temporary classroom before project commencement. In this study, the available space is defined as the resources which would affect the occupants’ inconvenience level. The following notations are used for the formulation.
Sets:
= {1,2,…,n}: Set of available space associated with type i
Parameter:
n: The total amount of available space
In addition to the number of rooms, another important thing that must be considered by the building planner is the similarity in size of the room that will be utilized as temporary space compared to the initial room. In this study, there is an assumption that all vacant rooms or underutilized space, including vacant labs, vacant offices, vacant classrooms, or spaces otherwise imperfect for occupancy are considered capable for use as resources. If the temporary room is larger or smaller than the initial room, an effort is required to maintain the level of convenience of the initial room. For instance, if renovation work is carried out in the laboratory, it is necessary to prepare a temporary room that is a similar size to the laboratory room. In addition, the convenience level in the room must be improved, such as through furniture installation, relocation of laboratory facilities, and evaluation of additional items for potential needs. Furthermore, expenditures to add temporary space for occupant convenience must be considered during the estimated cost of renovation.
3.2. Financial Capacity
Financial capacity for the renovation project is considered as the budget, which is the most crucial issue [
10] that faces the decision-maker, especially when it is limited. In other words, the decision-maker deals with the problem of managing the budget by allocating financial resources to renovate several buildings in a certain period. This issue is discussed by Luft and Shields [
11] who discuss how a budget needs to be managed optimally in an organization. Budget allocation is a complicated problem to resolve, since decision-makers should be able to achieve the goals and objectives of the renovation in a dynamic scope. The renovation project budget is a fiscal plan for a defined period as well as a resource, which expresses strategic plans in measurable terms. Effective methods are needed to allocate the limited budget of a renovation project to evaluate and prioritize the projects. The decision-makers should be able to allocate the budget effectively, putting the budget to the best use and maximizing its function. In this case, the decision-makers must emphasize efficiency, which is the key point in managing the budget. Practically, the result of the renovation should be to obtain the highest value and maximum function.
This study applies long-term financial capacity to provide strategic plans for several years. Considering that there are various departments’ buildings that need to be maintained, financial capacity must be flexible to meet the requirement of sufficient financial resources in multiple building renovations, hence it may integrate the different departments. In addition, long-term financial capacity is an essential tool for long-term planning to assist in planning strategy and actions that will contribute to the performance of the renovation project.
3.3. Level of Renovation Intervention
When the renovation is required, the main decision is to decide the best plan for the building and select a scenario that satisfies to the objectives under constraint. In previous research, Kamari et al. [
12] developed a decision support framework as a renovation “knowledge base” with the aim of managing the complexity of decision problems regarding the selection and use of various renovation alternatives. Kamari et al. [
12] classify renovation intervention into four levels, i.e., minor, moderate, deep, and nearly zero-energy buildings (NZEB). Their classification refers to the extent and size measures applied, as well as to the level of resulting energy and emissions reduction. Different from their study, our proposed model is project-based scheduling, which classifies renovation intervention into three levels [
13]—major, medium, and minor—to address the building deterioration problems. Minor renovation works involve maintenance or repair activities with the objective of extending service life. Medium renovation works usually involve the upgrading of existing building services, but do not involve any major structural alterations. Major renovation involves overall major structural alterations with the aim of making a building perform at a level similar to a new building [
13]. Furthermore, each renovation level will be linked to its cost [
10], selected approaches [
12] and the expected extension of the service life of the buildings of this case study. There are trade-off decisions when executing under budgetary constraints different levels of renovation for each building. First, performing a major-level renovation will lead to a longer service life of the buildings. However, because of the large scope of work items, it will be the costliest renovation that requires more resources and time, and hence will create the highest amount of inconvenience for occupants. On the contrary, performing a minor-level renovation will lead to a more convenient environment for the work crews of renovation construction and the building occupants. It is the cheapest renovation option because the scope of work is simple and the duration required is shorter. However, the improvement of the service life of buildings is the lowest. Hence, the different levels of renovation will affect the performance of the building.
4. Scheduling Simulation Network
In this study, a renovation scheduling simulation mechanism is constructed to assist decision-makers in developing renovation schedules by incorporating several factors in renovation decisions, such as resource allocation and the impact of the renovations. The scheduling simulation network is a process used to build a time-dependent model in order to present all the main elements and resources involved in a renovation process. As a result, it can broadly perceive the impact of potential decisions on the scheduling process. The model in the simulation visually shows what will occur in the process if modifications are made and records performance measures of the system under different scenarios. Simulation models are frequently used in the engineering field and can be classified as static or dynamic simulation models, continuous or discrete event simulation models, stochastic or deterministic simulation models, and as parallel or distributed simulations [
14]. One of the advantages of simulations is that they can model an actual process or phenomena. The types of systems that are typically modelled present dynamic (change over time), and stochastic (statistically variable) behavior. To date, simulation has generally been more convenient to use, with a more applicable outcome, for decision-makers in the industry [
14].
The sequence of renovation scheduling stages can be obtained through analysis in simulation networks. The key point in constructing a scheduling simulation network is connecting activities, timed events, and resources by managing the code in the simulation. All activity involved in the renovations should consider resource availability in both a financial capacity as well as available space, project duration, and a priority value. In other words, this research utilizes simulation networks to predict and review the interaction of the renovation type under resource constraints.
4.1. Applying SIMUL8
SIMUL8 is a software package of the SIMUL8 Corporation (
www.simul8.com) used for simulating systems that involve the processing of discrete entities at discrete times. This program is a tool for planning, design, optimization, and service provision systems. SIMUL8 allows its user to create a computer model that considers real-life constraints, capacities, failure rates, shift patterns, and other factors that affect the total performance and efficiency of production [
14]. In previous research, Debta et al. [
15] emphasized that SIMUL8 is advanced software used for the simulation of discrete events that allows the user to draw objects directly on the computer window, to create a visual model of the system under consideration. In this study, the problems that should be solved in the renovation schedule involve many activities, time, and resources that are in accordance with the SIMUL8 features. Moreover, this software is suitable for the discrete event simulation related to the scheduling issues and allows the user to establish logic that is similar to the real-life scenarios. Considering the factors that have been mentioned, this study applies SIMUL8 to find an optimal solution to a scheduling problem. The optimal renovation schedule can be obtained by extending the main components in SIMUL8 including probability, activities, project resources, and timed events.
4.2. Activities
The main component of a simulation network in SIMUL8 is activity. In this simulation network, an activity receives all the factors that influence the renovation as input and then processes it partially until it obtains the performance index. In general, activity is the main component of SIMUL8, which mostly processes and controls the work items. The work completed on activities takes time, sequences, logic function, and requires the availability of resources. In order to determine constraints and workflow, activity properties control work items by changing one or more labels and modifying the logic function, or Visual Logic. After the work item process is complete, activity will deliver it into another simulation object through a routing mechanism. Due to the flexibility of the activity function, the simulation frequently uses this component to represent the problem and the solution mechanism. In a whole model, another component, the routing arrow, will connect all activities according to the sequence and the direction of the work item movement. To develop a solution strategy, each activity is given a random priority value for obtaining its required resources. Therefore, activities compete with each other to receive limited resources.
4.3. Queues and Resources
In addition to activity as the main component in SIMUL8, other components, queue and resource, form the resource utilization in the simulation network. These components complement activity in forming a simulation network that is able to figure out the renovation scheduling problems. Work items wait in queue before the next process. Furthermore, Visual Logic will control a work item in a queue and link it into a spreadsheet. A queue is able to receive work items from activities and can define the queue capacity. In this study, a queue can organize the renovation schedule of each building.
The resource is a required component in the simulation model in order to process a work item. In the proposed model, an activity cannot start any work until certain resources are available. The resources used in this model are the financial capacity associated with capital and available space, which is divided into three parts: Large rooms, medium rooms, and small rooms. There are two mechanisms in the resource setting. First, it determines the amount of available capacity in resource properties. Second, it incorporates the resource requirements for an activity. Financial capacity in the model is a non-reusable resource, thus, in the resource properties, financial capacity used is set to not release after use in the activity. Meanwhile, available space is defined as a reusable resource. Hence, in the space resource properties, available space used is set to release to other components, such as another activity or queue. In practice, this works as follows: If available spaces have been used in certain renovation activities, these resources can be used again in other renovation activities.
4.4. Activity Priority for Resource Usage
In this study, priority is given to activities that are of prime concern and which take precedence over others. Priority for an activity shows that the activity is exceedingly important and requires the resources first. In this model, if a building has the highest priority value, it will receive resources, such as temporary room and financial capacity, according to the requirements of its renovation type. In other scheduling problems, multi-priority concepts have been used. Sauré et al. [
16] developed a model that focuses on patient schedule by developing a framework that incorporates stochastic service times into the advanced scheduling problem. The priority concept in the proposed model is time-dependent. Priority is dynamic and an activity has a different priority at each point in time. Thus, for each point in time, the priority of all activities will be compared together as a whole model. Priority will change over time according to the evolution of the importance of activities throughout the renovation project. For example, consider when the building that is the main teaching room is in a defective and inadequate condition. Hence, a renovation is urgently needed in this room. As a result, it will receive some resources first over other rooms.
Activity priority has many settings in SIMUL8. It can be set as a fixed value, a label value, be combined with multiple values or Visual Logic options. One activity in the simulation may have a higher priority than another for a number of different reasons. Priority could be the reference used for determining the sequence in which an activity receives a shared resource, the sequence in which work items are processed, or even which activity has control over the routing of work items [
14].
5. Integrated Model for Scheduling Planning
To address the complexity of the scheduling process, a number of optimization algorithms have been applied in different scheduling fields [
17,
18]. For instance, Xu et al. [
19] applied a hybrid simulated annealing algorithm for a large-scale problem in berth scheduling by considering traffic limitations in navigation channels. Xu et al. [
20] developed the modified heuristic algorithms to enhance repair sequence scheduling methods for post-disaster critical infrastructure systems. Imran Hossain et al. [
21] proposed the use of particle swarm optimization with selective search to optimize course scheduling. These studies demonstrated that applying optimization algorithms implements a more efficient searching process for a large number of candidate solutions in scheduling problems.
The optimization algorithms were also employed for the study issues of building renovation. For example, Kamari et al. [
22] present a decision support systems (DSS) by applying the genetic algorithm to generate and evaluate renovation scenarios especially for the early design stage of renovation projects. These scenarios are afterward selected in fitness using a crossover scheme, in which a mutation can be applied by applying random gene or renovation alternatives [
22]. The genetic algorithm process begins by determining the initial population, which consists of several chromosomes arranged by genes that are representations of solution candidates. The best candidates are chosen through a selection process, based on fitness values that have been calculated for each chromosome in the population. In this algorithmic approach, a population of chromosomes represents a potential solution set to a problem, and each chromosome represents a possible solution.
Motivated by prior research, this study proposes the use of genetic algorithm (GA), which has increasingly been applied by researchers to various fields. This is because the genes in chromosomes are a feasible frame to save and arrange the characteristics of different renovation projects, such as the priority and resource-using order. The crossover mechanism in the genetic algorithm can help us find out the better and better schedule solutions over iterations. Thus, this study employs genetic algorithm to search the optimal schedule more efficiently.
5.1. Integration of Simulation and the Genetic Algorithm
According to previous related studies, integration of simulation and the genetic algorithm can construct a satisfying search for optimal solutions. Many studies in various fields combine the simulations and the genetic algorithms to solve the specific problems. For example, Dzeng and Lee [
23] applied a system, which is an integration of simulation and a genetic algorithm to aid the scheduler in developing the optimal project schedule by calculating the net present value of each combination. In the proposed model, the application of the genetic algorithm is improved by generating the priority value of each building renovation type in each time step, instead of generating activities’ sequence directly, to develop the renovation schedules as related to the previous study [
23]. In construction operations, Cheng and Feng [
24] aimed to find the optimal combination of resources for construction applications. Their study provided a model that integrates simulation with a genetic algorithm, forming the genetic algorithms with construction operation simulation tool (GACOST), to evaluate construction operations to provide optimized solutions.
The main mechanism to obtain the optimal solution for the renovation schedule is to integrate SIMUL8 with a genetic algorithm. The priority value in SIMUL8 of each activity and each time step is expressed with genetic coding of chromosomes and influenced by polyploidy genes. One of the advantages of SIMUL8 is the flexibility of its operation. In this model, the variant of priority values for the renovation sequence type can be predetermined in the SIMUL8 function. Furthermore, the priority values are a basis in each simulation run. This framework can connect the activity with a spreadsheet containing priority values through the Visual Logic function. With reference to priority values, SIMUL8 will directly choose the renovation type sequence and calculate the performance index for each building renovation. In order to obtain a whole renovation schedule in each simulation, SIMUL8 will transfer a sequence of each renovation type to the bar chart in the spreadsheet.
5.2. The Model Applying Genetic Algorithms for Priority Optimization
This study establishes an integrated model for searching the optimal schedule plan for the building renovation projects.
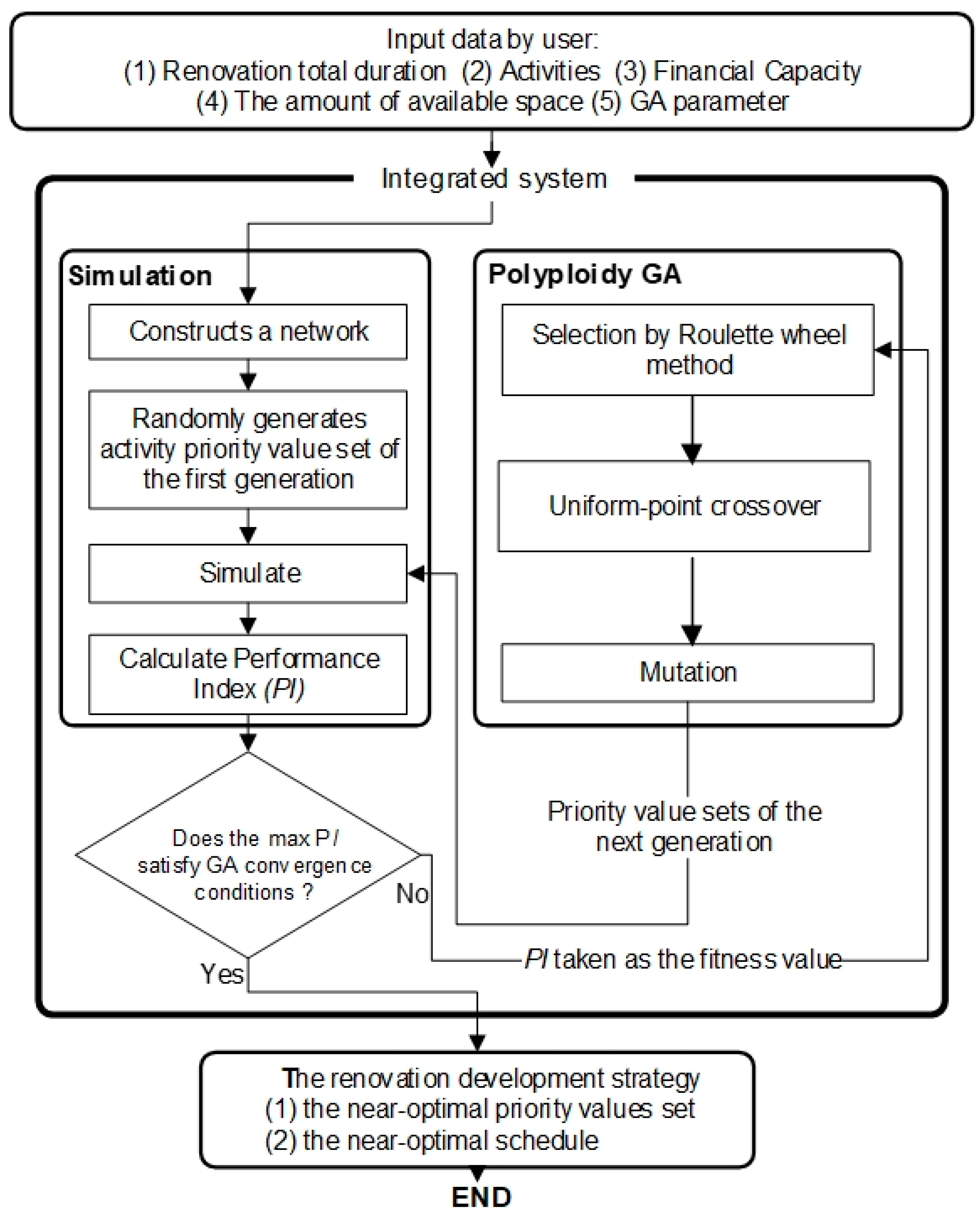
Figure 1 shows the flow chart integrating the simulation and the polyploidy genetic algorithm in the proposed model. In the proposed model, this study attempts to evaluate the renovation performance by simulation and obtain an optimal schedule by genetic algorithm.
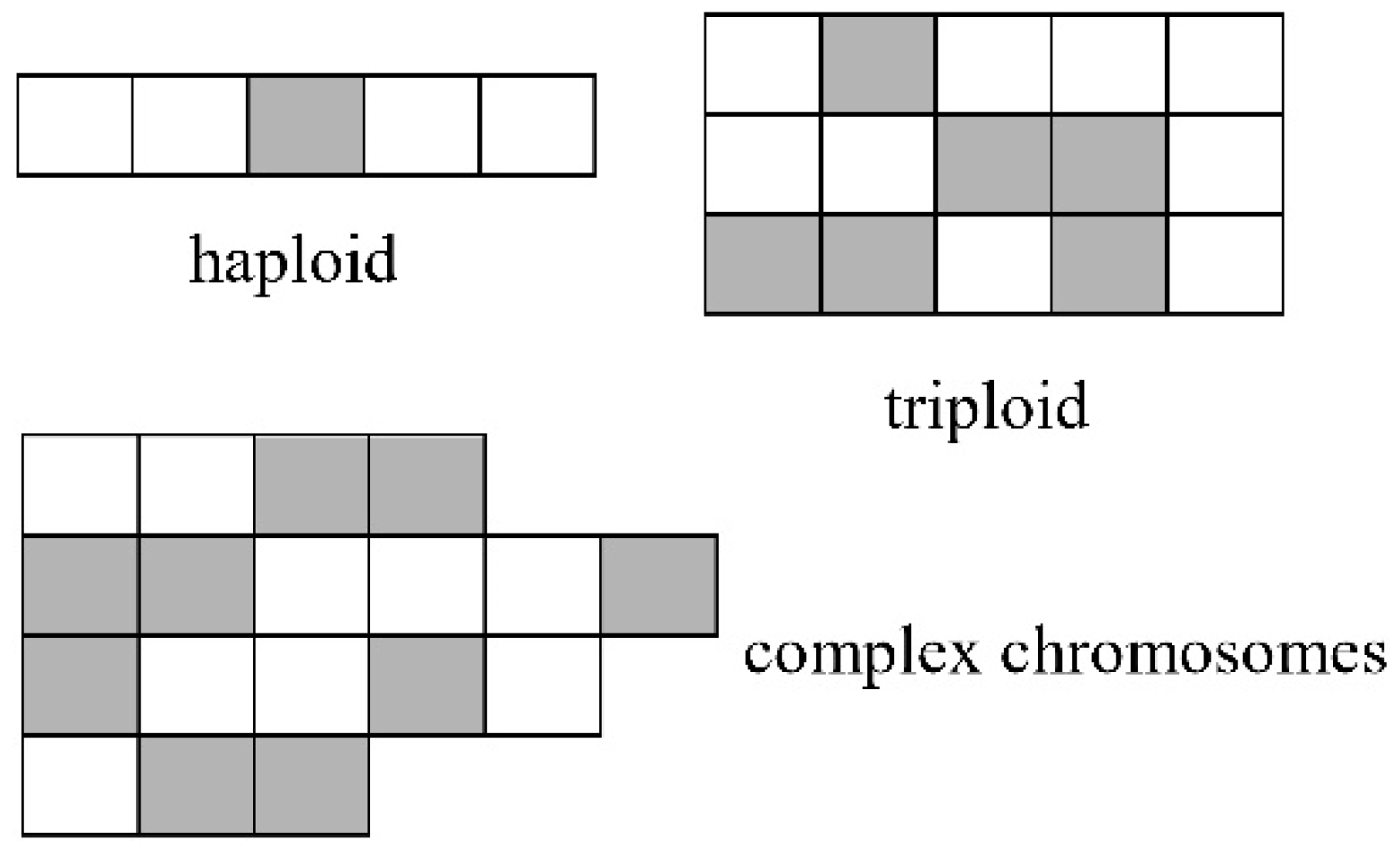
In this study, the formation of the genetic algorithm consists of many chromosomes to provide various potential solutions or phenotypes, called the polyploidy structure.
Figure 2 reflects haploidy, diploidy, triploidy, and complex chromosomes. Haploidy refers to only single chromosome for presenting the biological’s phenotype; diploidy refers to double sets of chromosomes in which one presents the phenotype and another is spare for utilization when the environment changes; triploidy refers to three sets of chromosomes for utilizations in different situations; the biological with complex chromosomes has a higher opportunity to survive in the nature. This biological approach provides a forward concept into the feasibility of the proposed model for the simulation of complex genetic structures [
25]. The proposed structure is different from the original genetic algorithm, which has limited possible solutions due to the structure of the haploid genetic mechanism. The main advantages of polyploidy in the genetic algorithm are the capability to acquire the beneficial chromosome sets in earlier iterations, and the maintenance of genetic diversity even in relatively small populations [
26]. In another study, applying polyploidy had an advantage over diploids because of their greater ability to mask deleterious mutations [
27].
As shown in
Figure 1, the proposed integrated model consists of two main mechanisms: The polyploidy genetic algorithm and the simulation mechanism. The polyploidy genetic algorithm is used to frame and sequence the renovation projects and search the optimal schedule solution by iterations. The simulation mechanism is used to estimate the performance index for each candidate schedule solution. The interface between the polyploidy genetic algorithm and the simulation mechanism is the transformation of the priority values of the renovation projects. In order to determine a renovation schedule sequence, the proposed model uses random numbers to generate priority values, which are set in the polyploidy genetic algorithm for each activity. If a resource is needed by several activities and one activity is more critical than the others are, then it is important that this activity receive the resource first. The proposed simulation model allows the random number streams of priority value to be changed in every timed event.
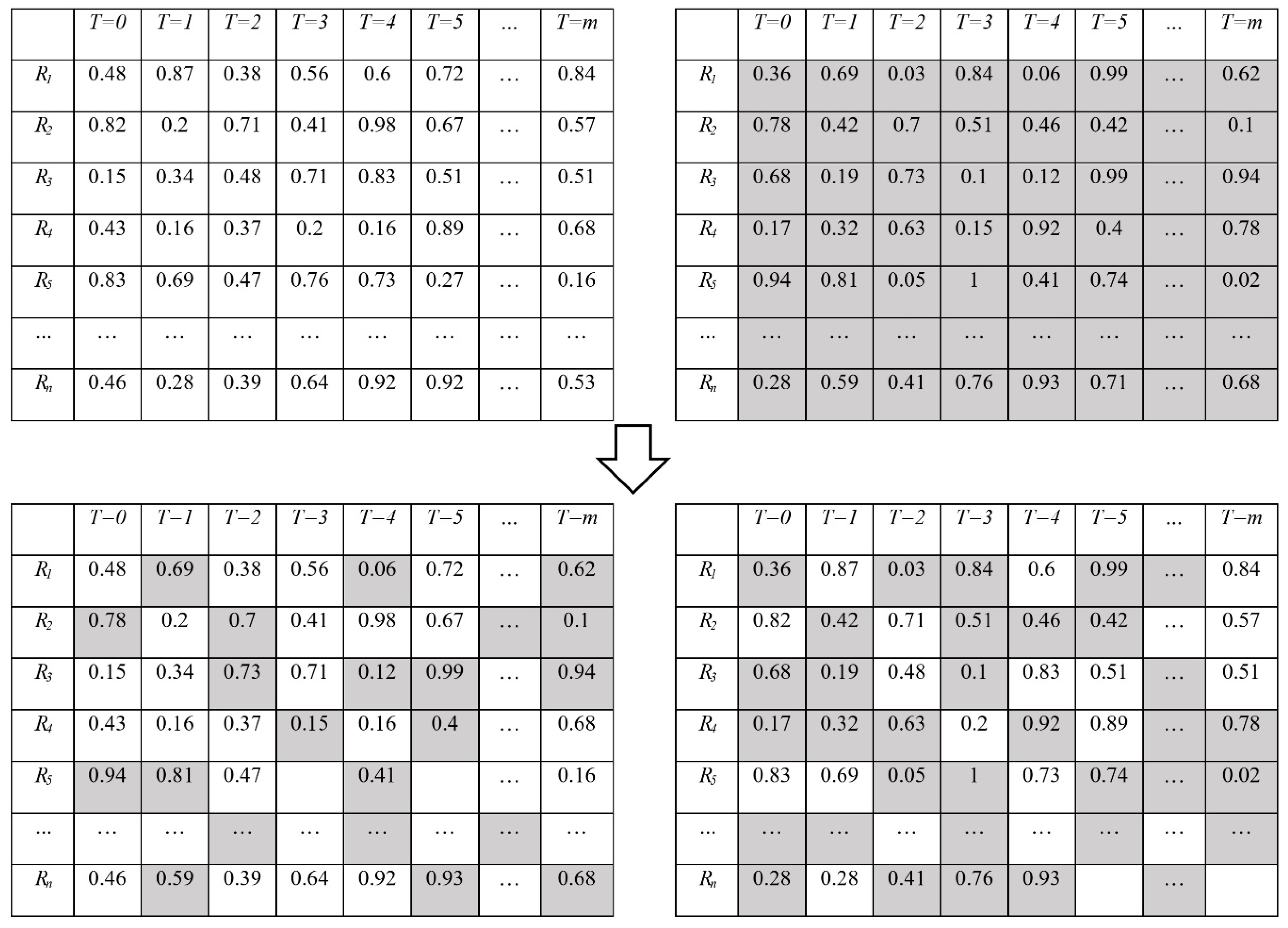
Table 2 shows the correlation of priority values to obtain resources for each renovation activity in a time step. Each activity has a priority value as genetic encoding in each time step
T. Using
T =
i, activity for renovation type
R1 has a priority value of
P1,i, and the priority value of a set of
n activities (
R1,
R2, …,
Rn) at
T =
i can be stated as
P1,i,
P2,i,
P3,i,…,
Pn,i, giving the genetic code of a chromosome. To determine a priority value set with an equal number to the population size, the “roulette wheel” method is applied in this integrated model. This mechanism preserves individuals with a top ten performance index ranking to avoid superior individuals from being dropped during the selection process. The priority values for the next generation are generated through crossover and mutation.
The polyploidy genetic algorithm has been applied in previous research. For example, Lee and Lin [
28] proposed the polyploidy structure in genetic algorithms with case studies optimizing the scheduling of exhibitions in art museums with a decision support model to provide a near-optimal exhibition schedule for the planner. In the solution-searching process, the genetic chromosomes in the polyploidy genetic algorithm are formed according to the priority value of the renovation activities’ resource-using. The structure of chromosomes can present the importance of the different renovation projects and provide a higher opportunity to allocate resource for necessary renovation projects at each time points. This indicates that complicated problems in this study can be solved under the structure of polyploidy genes, in order to record and improve the scheduling strategies of renovation in each time step.
Crossover is the important process in the polyploidy genetic algorithm.
Figure 3 illustrates the uniform-point crossover process performed on each individual gene independent of one another. This mechanism is continuously repeated until the maximum performance index reaches stability in line with genetic algorithm convergence. It is noteworthy that in this mechanism, it is possible to obtain several strategies due to the nature of polyploidy.
6. Case Study
This study demonstrates the proposed model by an application case of the university campus. National Taiwan University of Science and Technology was selected to evaluate the performance of the proposed model. In this campus, there are several buildings at various conditions that need to be renovated, as shown in
Table 3. Although a campus university has free periods in a year, these selected buildings continue to serve its users, such as classrooms that are used during summer courses, library, dormitories, research rooms, and laboratories. Hence, the planner should provide several renovation scenarios as strategic management tools in building maintenance. To obtain renovation scenarios from a wider perspective, previous research by Kamari et al. [
22,
29] identified a total of 139 renovation alternatives and classified them into 26 approaches as shown in
Table 4. In this case, these approaches [
22,
29] will be divided into three renovation levels [
13] corresponding to the cost (see
Table 5). Furthermore, the building planner can judge which level is suitable for certain building renovation project.
6.1. Case Introduction
As a campus case study, the National Taiwan University of Science and Technology is rather old, with the majority of buildings older than 20 years. The buildings on campus have mostly suffered a reduction in quality and function. However, the buildings should be able to function for any activities.
Table 6 provides detailed building information for the campus and several possible renovation options for each building. In this study, building planners not only must consider the budget constraints [
30] and duration of renovations but also must understand the essential factors of the impact and the value of the renovation. Building planners must flexibly be able to improve the quality of buildings.
To satisfy the occupants’ convenience rate, the requirement for temporary space became the main resource during the renovation project along with financial resources.
Table 6 and
Table 7 show the resource requirements and resources provided on campus in order to support the execution of the renovation project. In this study, all resources are available; however, the planning of the renovation schedule has limitations in time and cost. The campus only provides a 100 million NTD annual budget. The building planner must prepare a strategic renovation schedule that covers the next five years.
6.2. Modeling the Simulation Network
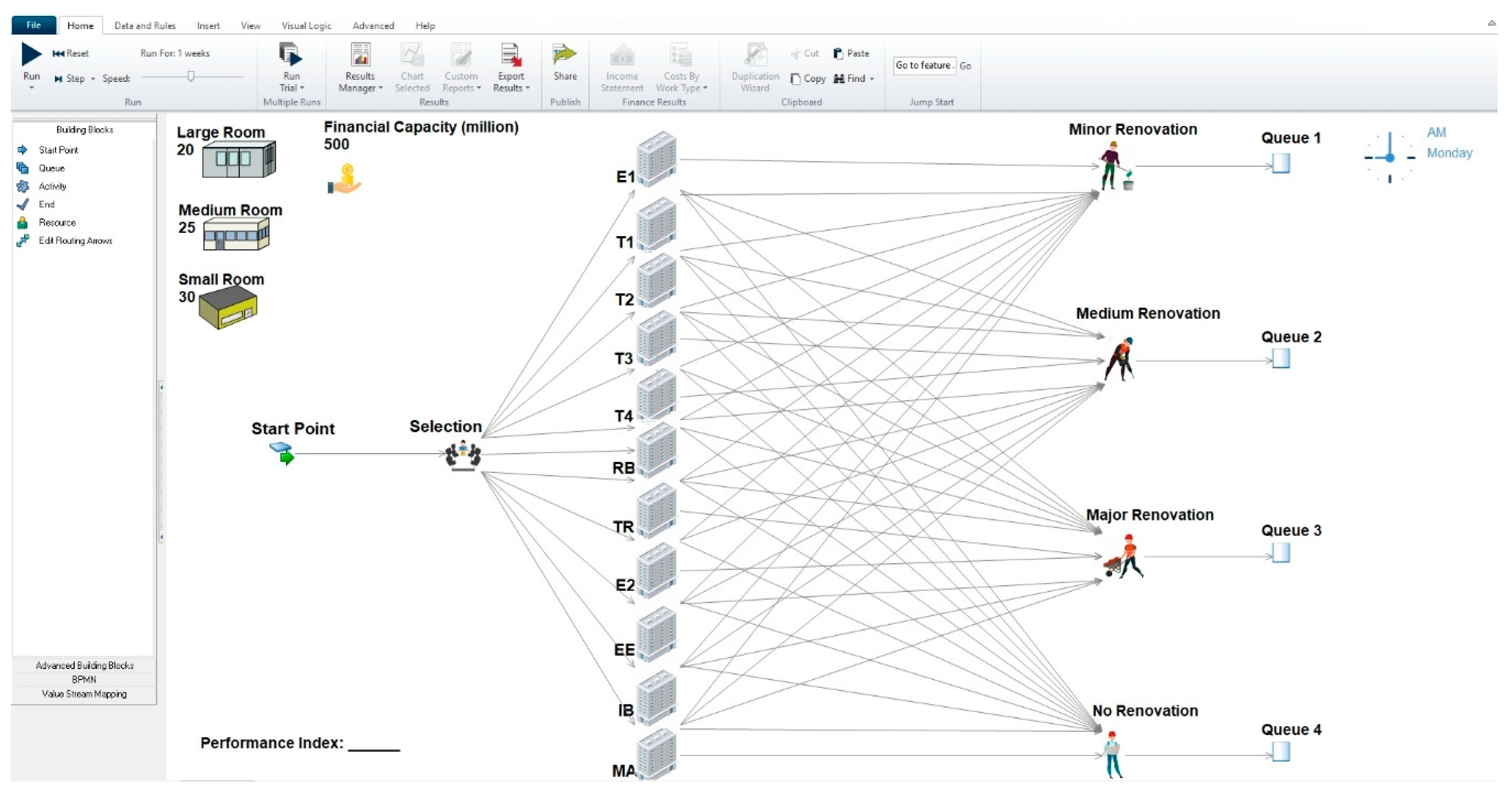
After acquiring building data and possible renovation options as shown in
Table 3, the subsequent step is to construct a simulation network in SIMUL8. In the simulation phase, the network is formed by connecting the main components in SIMUL8, such as activity, queue, and resource. The simulation network uses routing arrows to connect all the main components. In this model, activity is applied as a type of building and a type of renovation because its function is more adequate. Meanwhile, resource is applied to describe resource requirements, such as temporary space and financial capacity. In the resource component, the capacity and the characteristic of each resource were set according to the data. In contrast to activity and queue networks, the connection between the activity and resource network does not require routing arrows. The resource workflow mechanism is constructed by incorporating the required resources in each renovation type. Meanwhile, queue is applied to express the outcome of the renovation schedule and the performance index.
Figure 4 shows the simulation network of the campus renovation. The simulation networks clearly illustrate the major, medium, and minor renovation alternatives. Each alternative renovation option requires different resources and influences the outcomes of the renovation schedule plan. In addition, the Visual Logic function manages the workflow. Thus, the proposed model represents the real conditions.
After all the main items and work logic have been constructed, the next step is the calculation of the performance index for each renovation type. In the simulation network, the performance index is an accumulation of the sum of building space quality (QC) and the inconvenience rate (DU). The calculation is performed by incorporating values for each parameter in the queue component. For instance, building space quality (QC) is influenced by the service life of the building (SL), the building age (Ba), and the building’s extended lifespan due to renovation (Pr). At this stage, the value of all parameters is defined globally. Hereafter, Visual Logic is applied to describe the mathematical model of the calculation according to Equation (1). The same method also applied to the calculation of the inconvenience rate (DU). Visual Logic incorporated all parameters that influenced the inconvenience rate (DU), such as the duration of renovation (Di) and the amount of room (Ai). Then, a mathematical model is built according to Equation (2). If a timed renovation work is performed in the simulation, the outcomes only applies for one timed event. A different timed event might present minor or very different outcomes. Hence, the effect on the behavior and output of the model could be observed.
6.3. Searching the Schedule Plan
After the renovation
PI (performance index) is estimated by the simulation mechanism, the model operates the genetic algorithm mechanism to search the optimal schedule plan. After the iterations, the better schedule plans are reserved for the next generations.
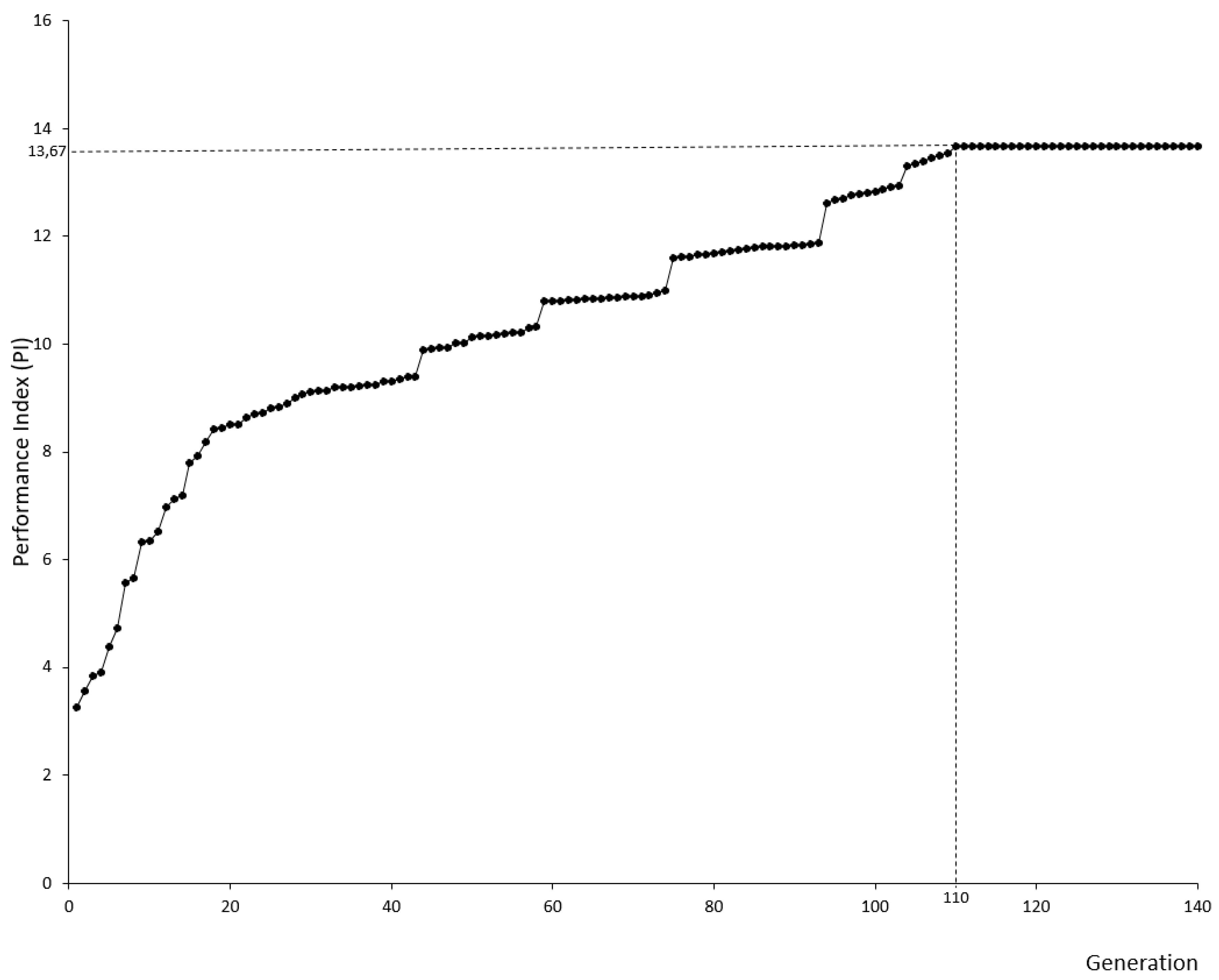
Figure 5 reflects the convergence nature of the method with generation, it shows that the performance index is very poor at the beginning (e.g., 5, 10) and improves over generations. As an example, for the fifth generation, the achieved performance index is 4.38. By applying a uniform crossover point in each generation, convergence is completed in the 110th generation with an optimal value of 13.67. During the process of finding the best solution, SIMUL8 delivers a schedule dynamically following the performance index as a result of the priority value set. According to the findings from this study, it is necessary to conduct minor and medium renovations on the university campuses. The renovation schedule as shown in
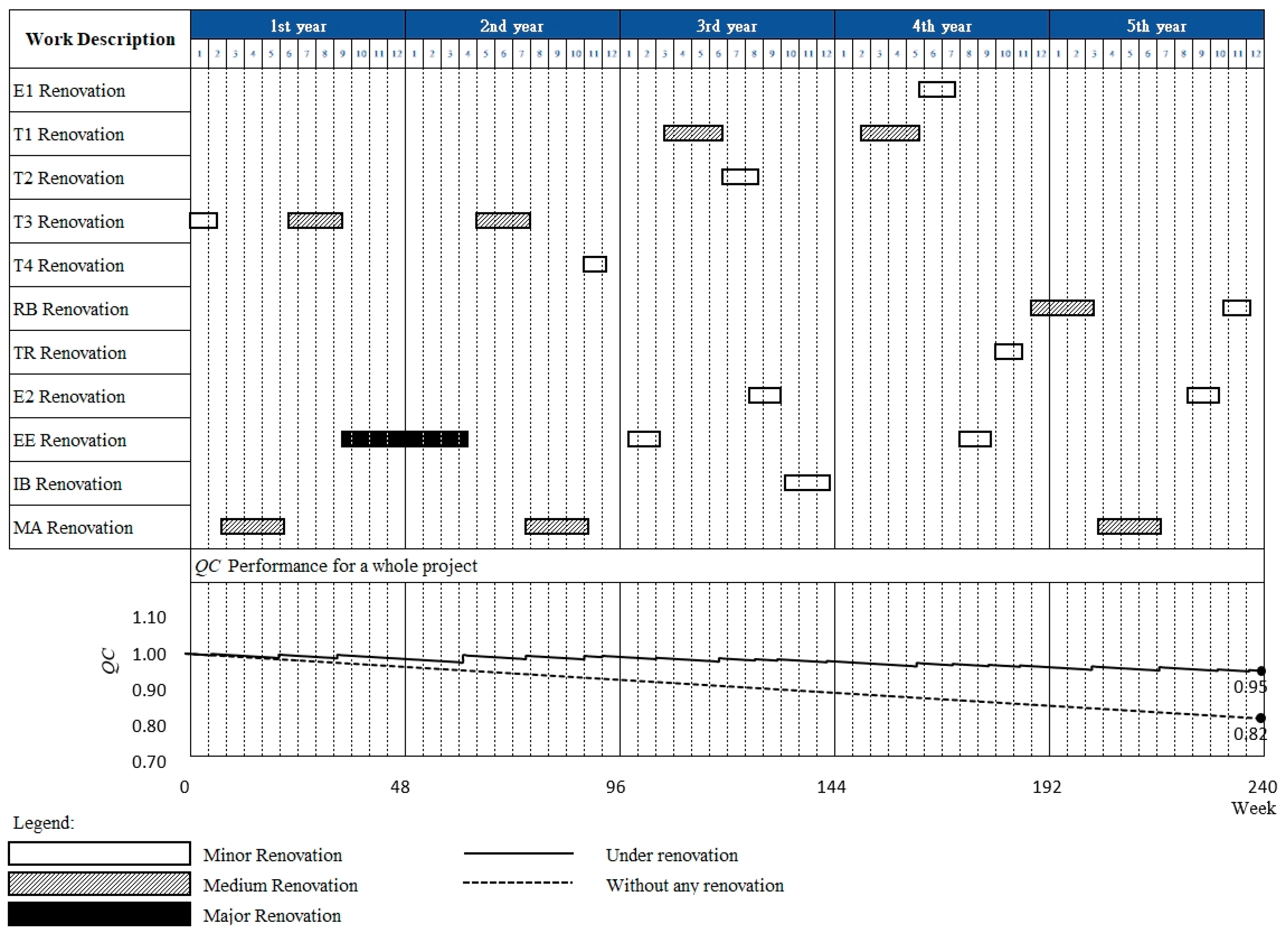
Figure 6 describes that there are 20 renovations during five years with the following details: 11 minor renovations, 8 medium renovations, and 1 major renovation. A major renovation leads to a longer service of the building; however, it is only necessary to conduct once in this case study. This is because a major renovation has high inconvenience rate and requires many resources. This clearly shows that the best renovation approaches are the ones in the minor level, such as ceiling repair, waste facilities maintenance, replacement for windows and furniture [
29]. From
Figure 6, there is a difference in the building quality index between the buildings when there has been no renovation and when they undergo renovation. The figure summarizes that the building quality delivery continues to decrease for five years. However, by implementing the renovation strategy that is the outcome of this study, the quality of the buildings will increase, and the service life of the buildings will be extended. The results of this study show that the building quality index (
QC) will naturally decrease from 1.00 to 0.82 in fifth year. On the contrary, if the buildings undergo renovation, the building quality index (
QC) would be 0.95 in the fifth year. Hence, the outcome of the case demonstrates the capability of the proposed model as a performance-based decision-making model, while previously the schedule plan only relied on subjective judgments and personal experiences.
7. Conclusions
This study presents renovation construction process scheduling in perspective of long-term performance by considering the occupant convenience and quality improvement to the buildings. An extensive list of building conditions, resources, renovation types, and renovation approaches was collected and incorporated with the intention of facilitating the building planners to understand the renovation framework as well as to obtain an optimal renovation schedule. In order to develop renovation scenarios, an integrated model for scheduling planning was constructed, which consists of simulation and polyploidy genetic algorithm. In the simulation process, factors affecting the performance of renovation and a set of priority values were involved. It facilitated the calculation of the occupant convenience rate and building quality. In addition, the simulation generated broadly renovation scenarios for five years. Meanwhile, the application of polyploidy genetic algorithm demonstrated in this study seems an effective method to obtain the highest performance index of renovation. However, the effectiveness of this application still needs to be compared. The main challenges to achieving an optimal schedule are how to select the renovation types in various building and how to calculate the interactions and trade-offs between resources and performances. The method developed in this study can help the building planners to create an optimal renovation scenario instead of a human’s experience. Moreover, this study is the main contribution in developing renovation scheduling strategy with quantitative information.
Even though this study provides innovative decision support to planners in obtaining an optimal schedule, the concept of this study is subject to limitations. There are two main limitations in this study that need to be considered: First, the affecting factors of the performance index only based on the convenience occupancy problem and the quality improvements of the buildings. Second, the scheduling algorithm presented in this study only uses polyploidy genetic algorithm. In order to obtain a better performance index of the building comprehensively, further studies need to incorporate other affecting factors such as noise and dust associated with environmental issues, as well as energy-efficient buildings. In addition, other algorithm optimization approaches can be applied to make the comparison of the efficiency of finding the best solution. Finally, improvements to the model are still open for further studies.