A Model-Based Estimation of Resource Use Efficiencies in Maize Production in Nigeria
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Description
2.2. Climate and Soil Data
2.3. Dataset for Model Calibration
- The mean relative error (MR) as:
- The mean residual error (ME) as:where n is the sample number, x is the observed value, and y is the simulated value. An ME value of 0 indicates no systematic bias between simulated and measured values. The mean relative error (MR) shows the mean magnitude of the error related to the observed value. Small values indicate little difference between simulated and measured values.
3. Results
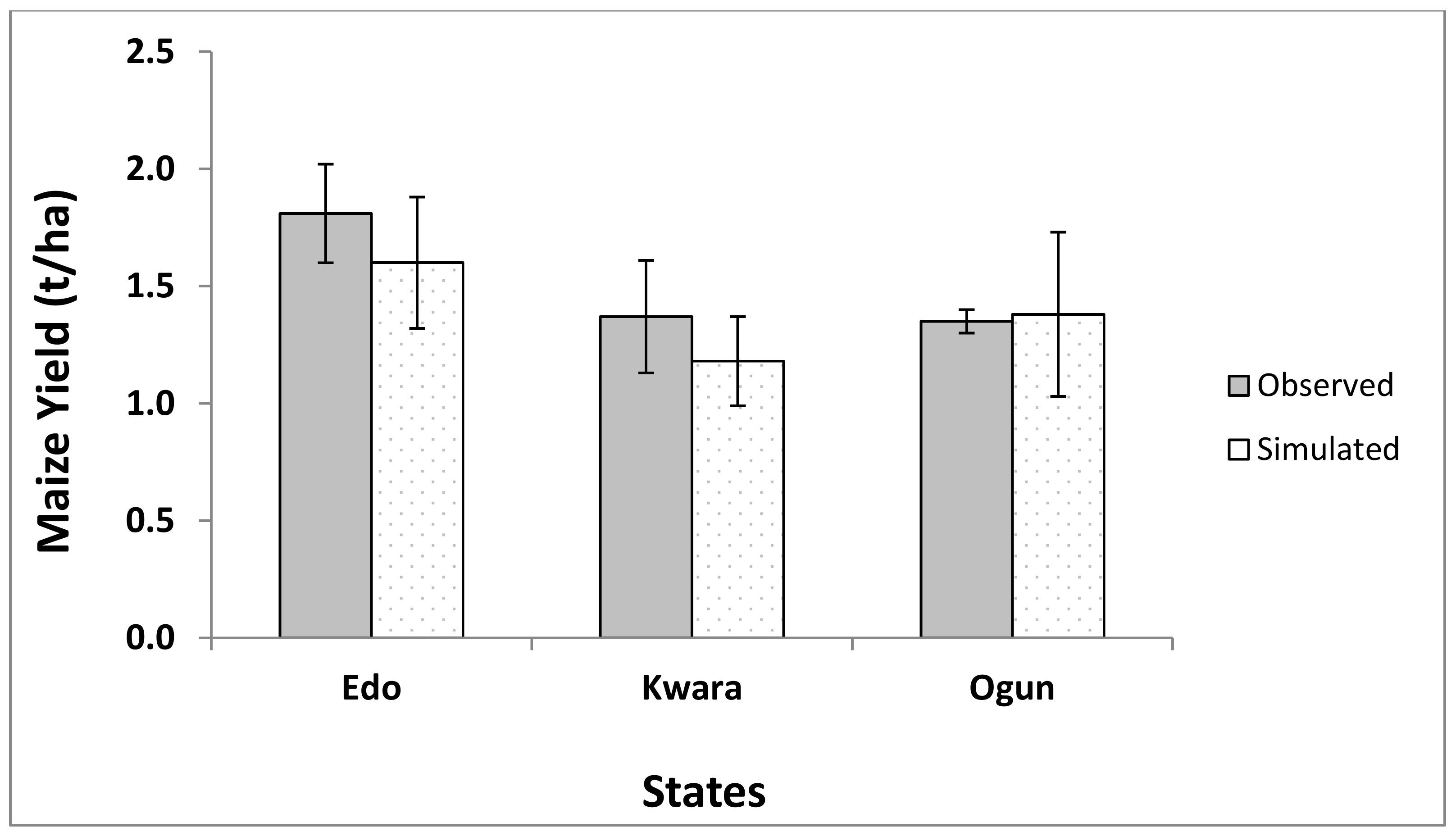
3.1. Model Calibration and Evaluation
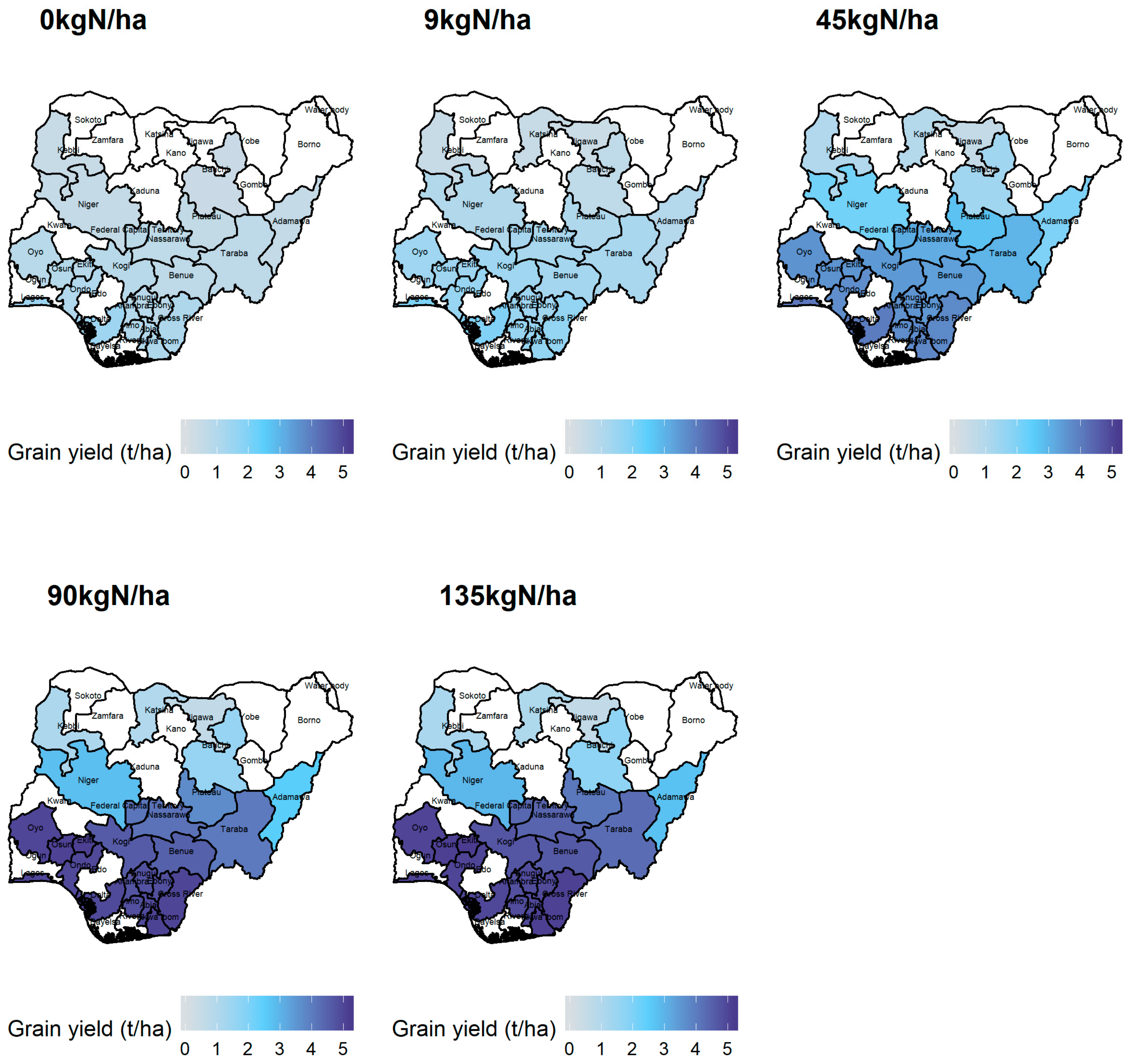
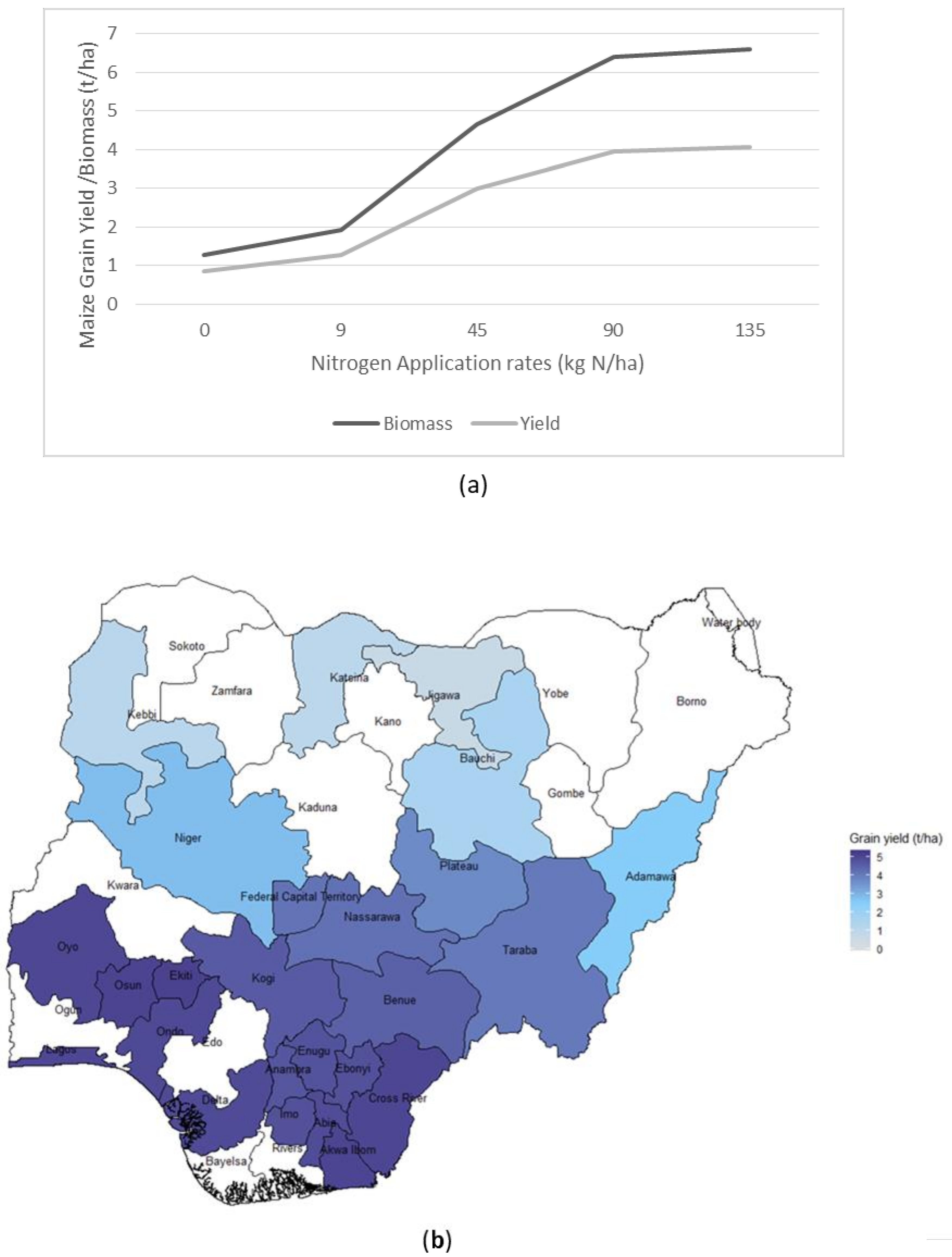
3.2. Simulated Yields and Biomass at Different Rates of Fertilizer Application
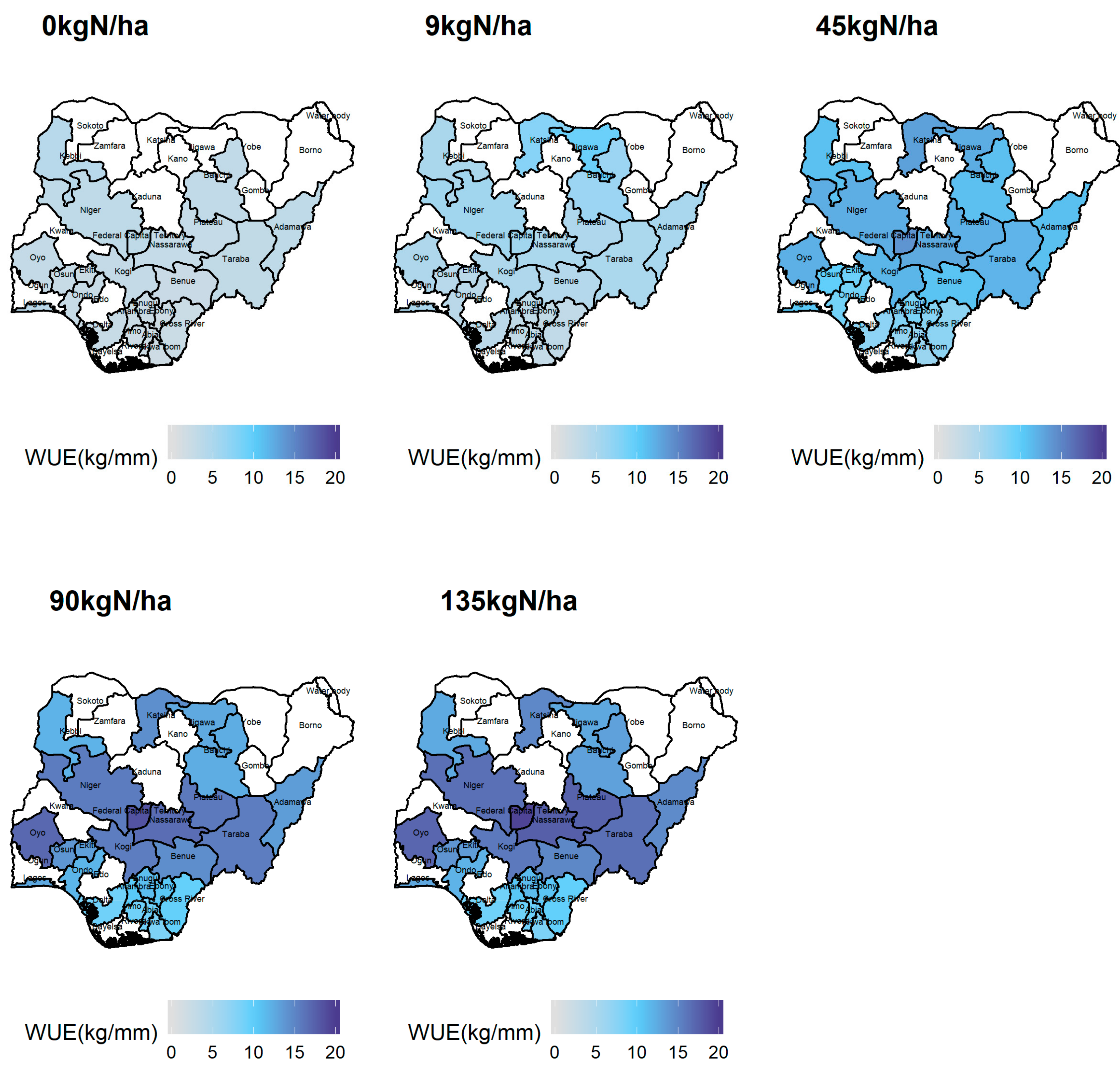
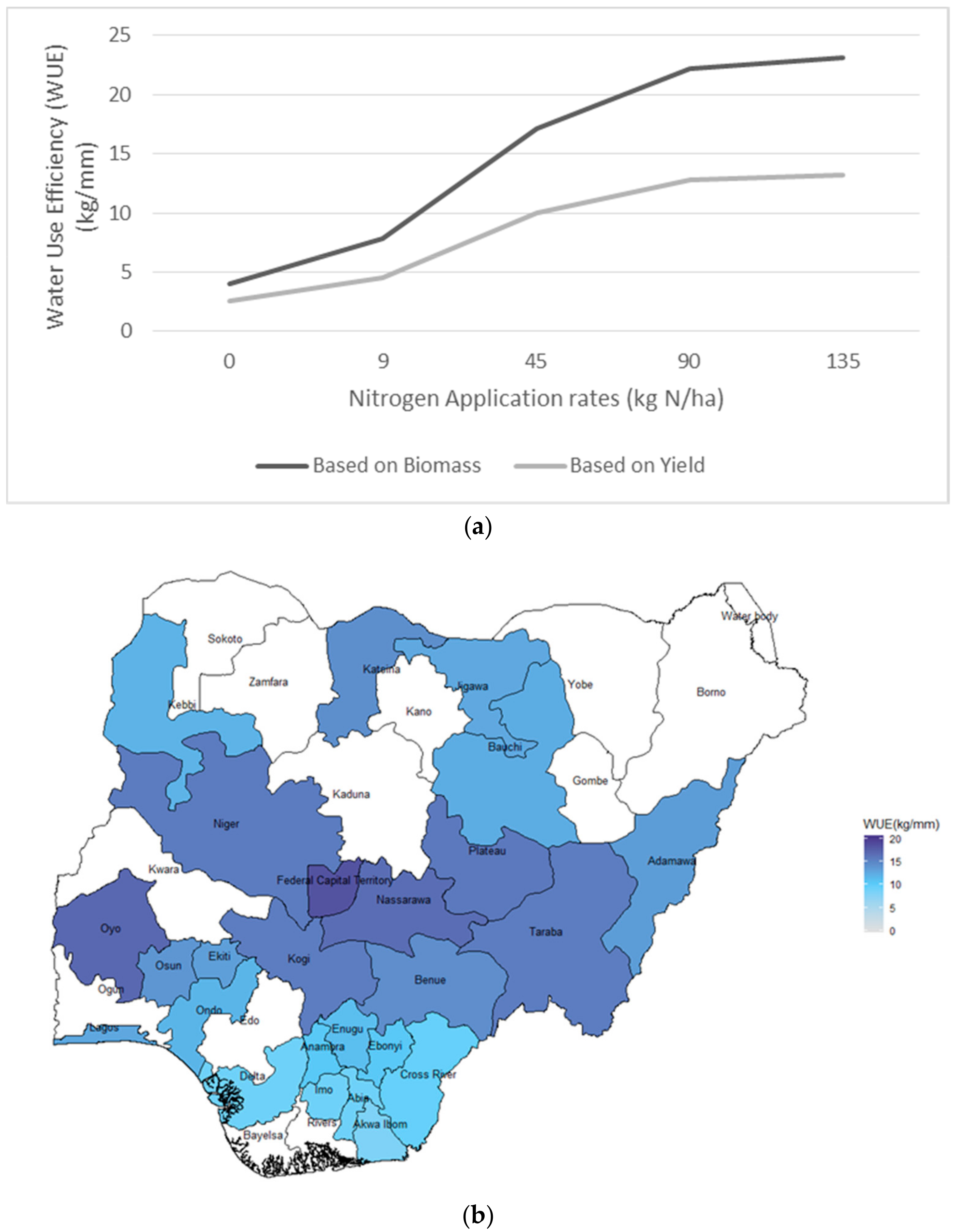
3.3. Simulated Water Use Efficiency under Different Rates of Fertilizer Application
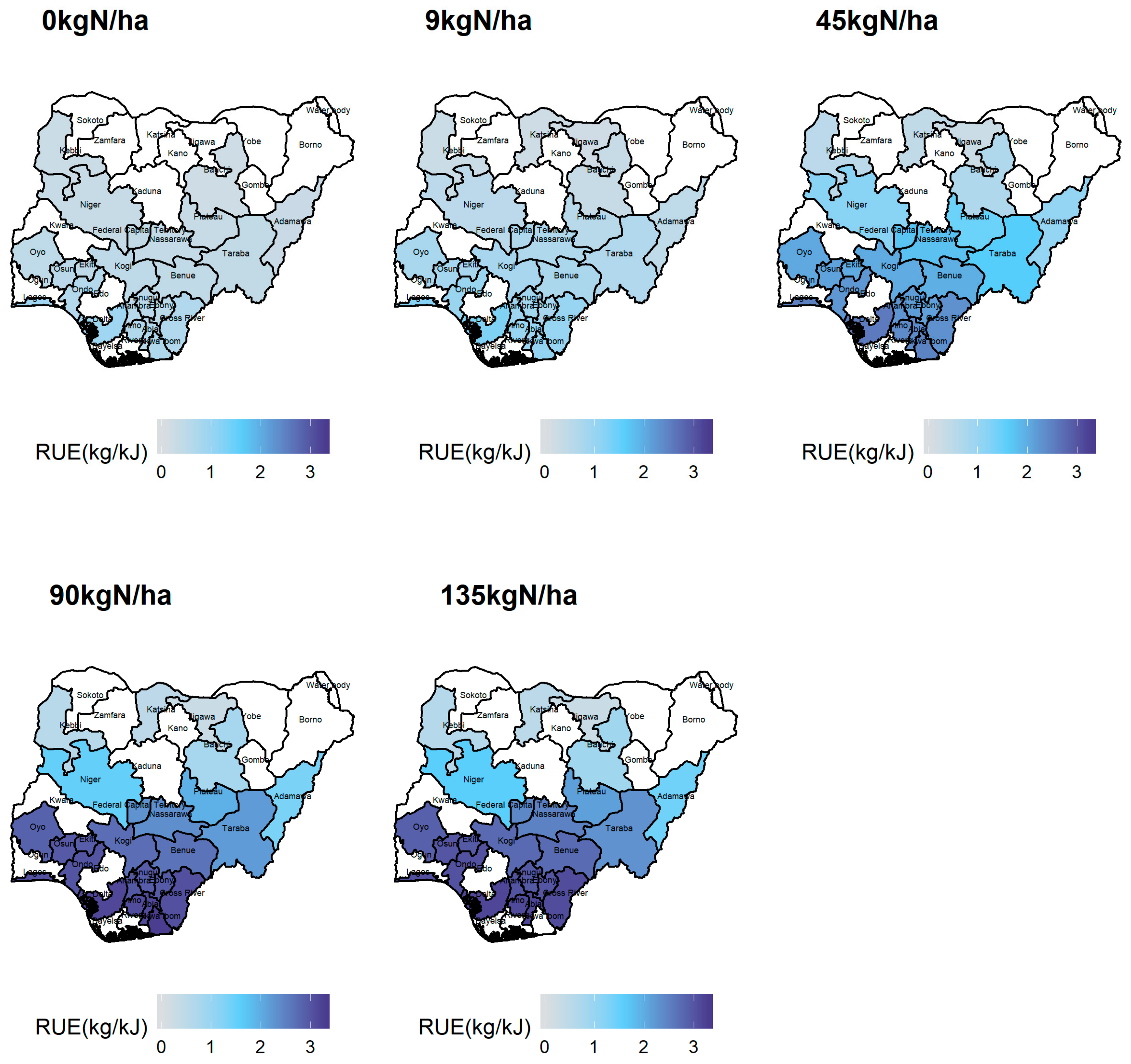
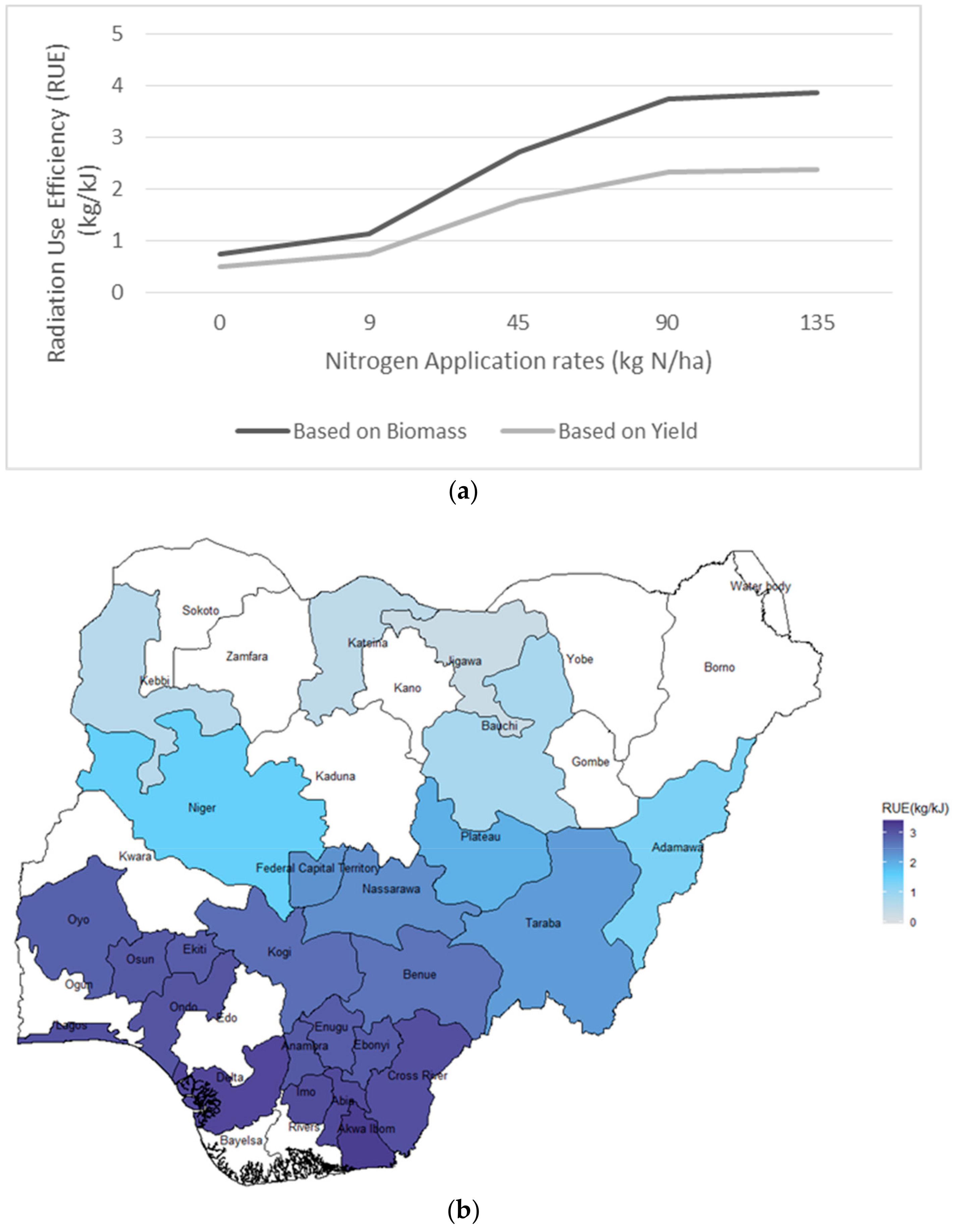
3.4. Simulated Radiation Use Efficiency RUE under Different Rates of Fertilizer Application
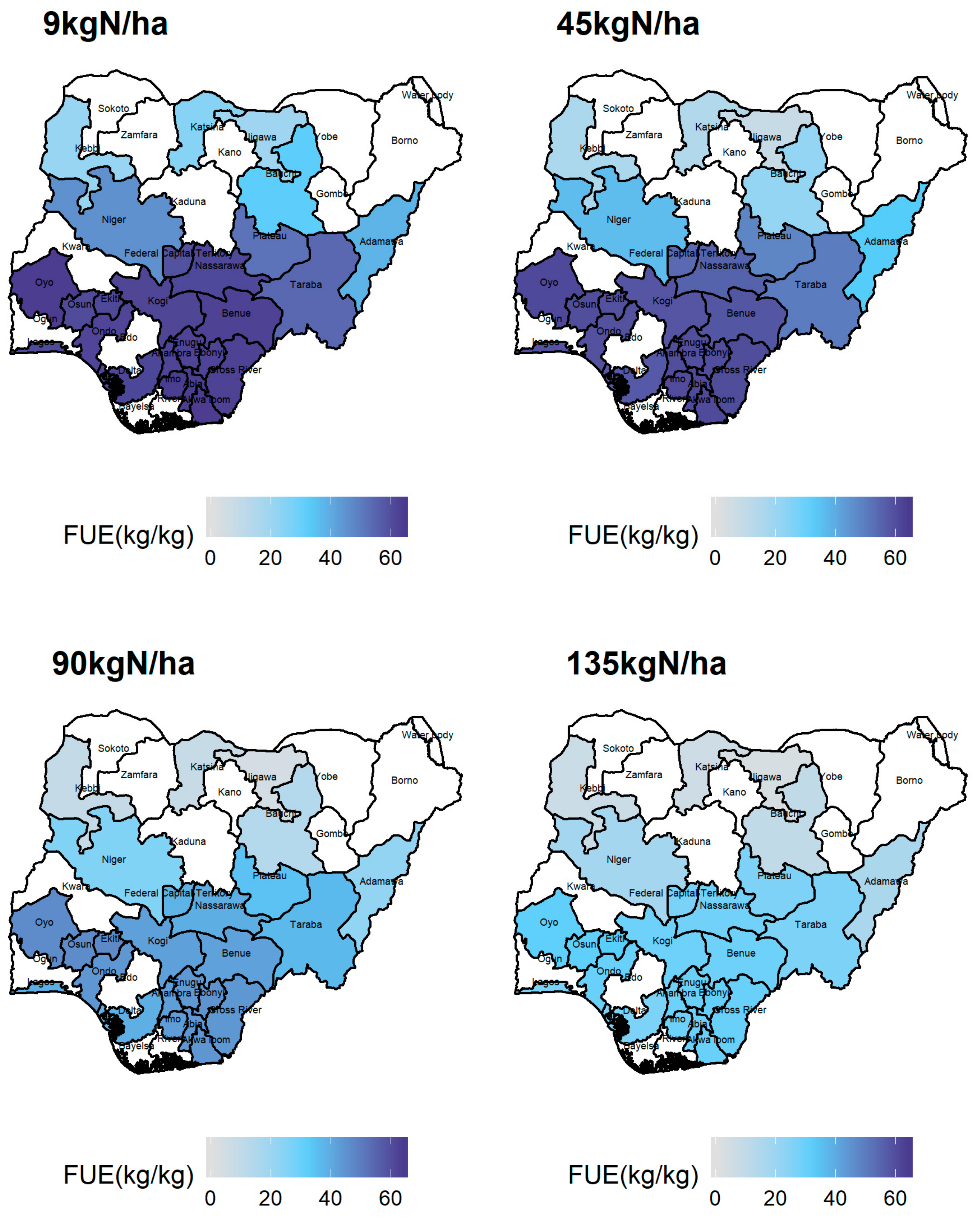
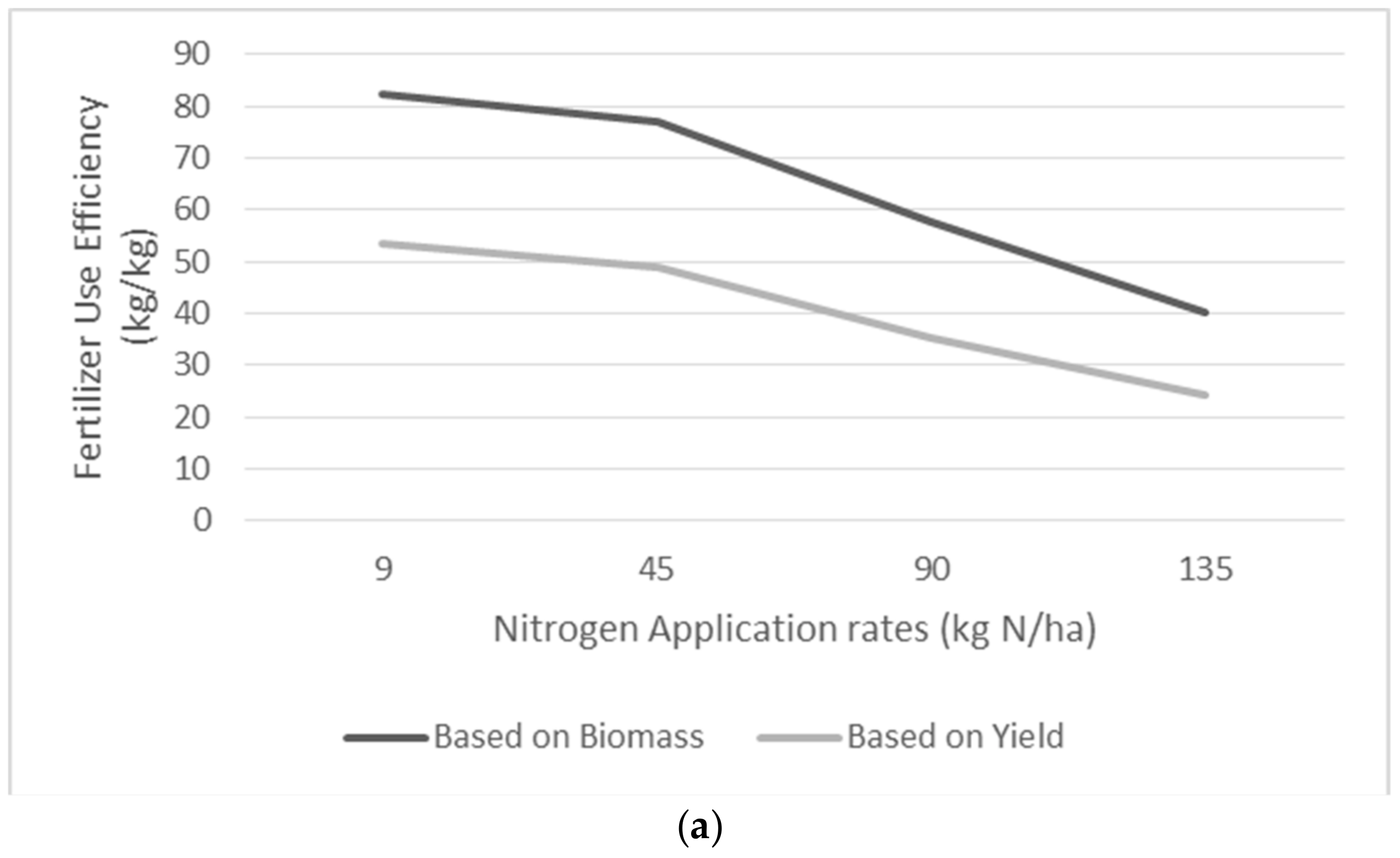
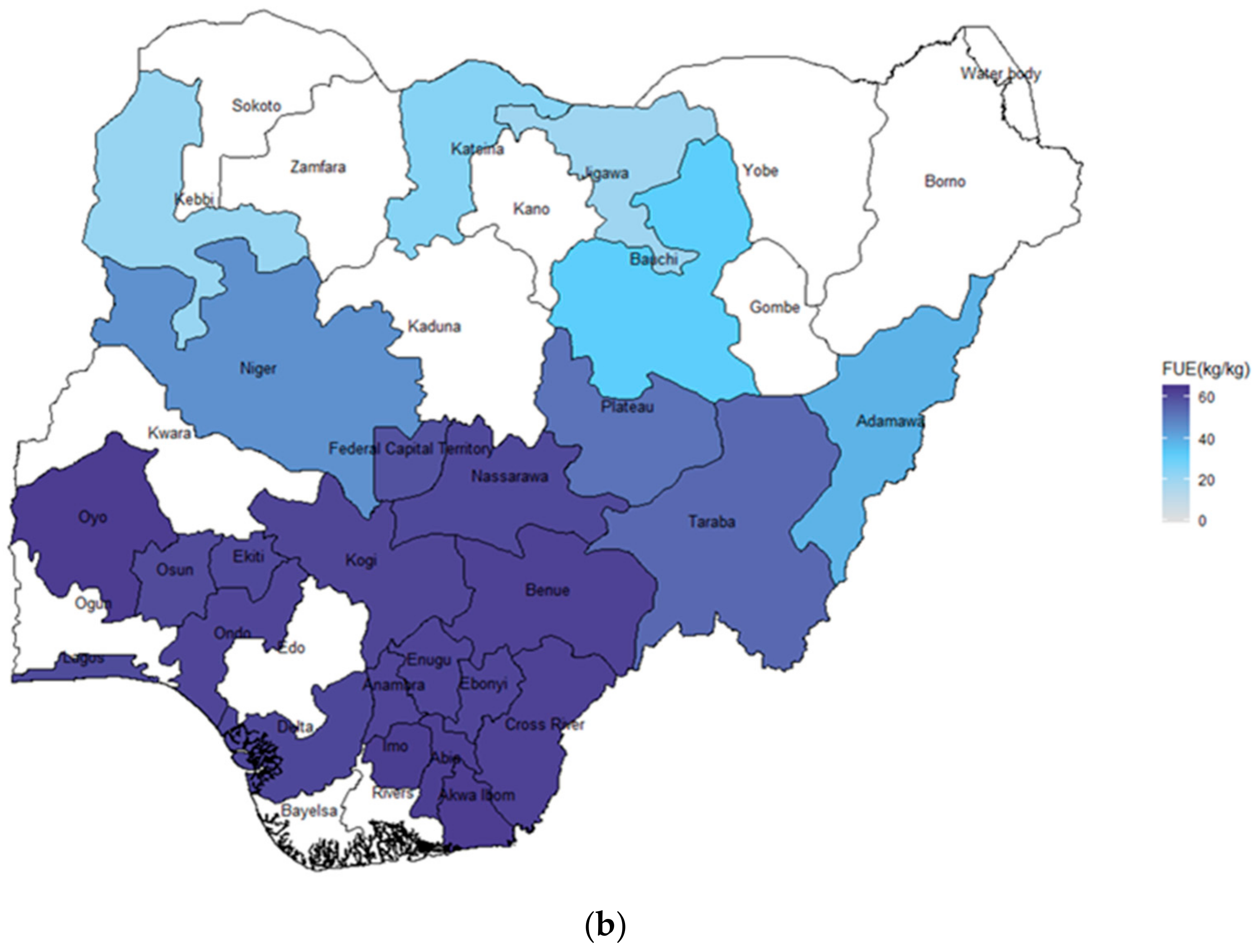
3.5. Simulated Fertilizer Use Efficiency FUE under the Different Rate of Fertilizer Application
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ranum, P.; Peña-Rosas, J.P.; Garcia-Casal, M.N. Global maize production, utilization, and consumption: Maize production, utilization, and consumption. Ann. NY Acad. Sci. 2014, 1312, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Vanlauwe, B.; Kihara, J.; Chivenge, P.; Pypers, P.; Coe, R.; Six, J. Agronomic use efficiency of N fertilizer in maize-based systems in sub-Saharan Africa within the context of integrated soil fertility management. Plant Soil 2011, 339, 35–50. [Google Scholar] [CrossRef]
- FAO. Country Brief: Nigeria. 2018. Available online: http://www.fao.org/giews/countrybrief/country.jsp?code=NGA (accessed on 15 February 2019).
- World Bank. Nigeria | Data. The World Bank. Available online: https://data.worldbank.org/country/nigeria?view=chart (accessed on 1 February 2019).
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ. 2010, 114, 1167–1177. [Google Scholar] [CrossRef]
- Morris, M.; Kelly, V.A.; Kopicki, R.J.; Byerlee, D. Fertilizer Use in African Agriculture: Lessons Learned and Good Practice Guidelines; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
- World Bank. Agricultural land (% of land area) | Data. The World Bank. Available online: https://data.worldbank.org/indicator/AG.LND.AGRI.ZS?contextual=default&end=2016&locations=NG&name_desc=false&start=1999http://www.fao.org/faostat/en/#data/RFBhttps://www.indexmundi.com/nigeria/area.html (accessed on 1 February 2019).
- FAO. FAOSTAT. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 15 February 2019).
- IITA. Transforming African Agriculture Through Research. IITA Annual Report; IITA: Ibadan, Nigeria, 2017; Available online: www.iita.org/annual-reports (accessed on 1 February 2019).
- Srivastava, A.K.; Mboh, C.M.; Gaiser, T.; Kuhn, A.; Ermias, E.; Ewert, F. Effect of mineral fertilizer on rain water and radiation use efficiencies for maize yield and stover biomass productivity in Ethiopia. Agric. Syst. 2019, 168, 88–100. [Google Scholar] [CrossRef]
- Umoh, G.S. Resource Use Efficiency in Urban Farming: An Application of Stochastic Frontier Production Function. Int. J. Agric. Biol. 2006, 8, 38–44. [Google Scholar]
- Adeyemo, R.; Kuhlmann, F. Resource Use Efficiency in Urban Agriculture in Southwestern Nigeria. Tropicultura 2009, 27, 49–53. [Google Scholar]
- Singh, B.; Singh, Y.; Sekhon, G.S. Fertilizer-N use efficiency and nitrate pollution of groundwater in developing countries. J. Contam. Hydrol. 1995, 20, 167–184. [Google Scholar] [CrossRef]
- Xu, G.; Fan, X.; Miller, A.J. Plant Nitrogen Assimilation and Use Efficiency. Annu. Rev. Plant Biol. 2012, 63, 153–182. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Sauer, T.J.; Prueger, J.H. Managing Soils to Achieve Greater Water Use Efficiency. Agron. J. 2001, 93, 271. [Google Scholar] [CrossRef]
- Varvel, G.E. Monoculture and Rotation System Effects on Precipitation Use Efficiency of Corn. Agron. J. 1994, 86, 204. [Google Scholar] [CrossRef]
- Condon, A.G. Breeding for high water-use efficiency. J. Exp. Bot. 2004, 55, 2447–2460. [Google Scholar] [CrossRef] [PubMed]
- Hassanli, A.M.; Ebrahimizadeh, M.A.; Beecham, S. The effects of irrigation methods with effluent and irrigation scheduling on water use efficiency and corn yields in an arid region. Agric. Water Manag. 2009, 96, 93–99. [Google Scholar] [CrossRef]
- Stockle, C.O.; Kiniry, J.R. Variability in crop radiation-use efficiency associated with vapor-pressure deficit. Field Crop. Res. 1990, 25, 171–181. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Mboh, C.M.; Gaiser, T.; Ewert, F. Impact of climatic variables on the spatial and temporal variability of crop yield and biomass gap in Sub-Saharan Africa—A case study in Central Ghana. Field Crop. Res. 2017, 203, 33–46. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Mboh, C.M.; Gaiser, T.; Webber, H.; Ewert, F. Effect of sowing date distributions on simulation of maize yields at regional scale—A case study in Central Ghana, West Africa. Agric. Syst. 2016, 147, 10–23. [Google Scholar] [CrossRef]
- Trawally, D.; Webber, H.; Agyare, W.A.; Fosu, M.; Naab, J.; Gaiser, T. Effect of heat stress on two varieties under irrigation in northern region of Ghana. Int. J. Biol. Chem. Sci. 2015, 9, 1571–1587. [Google Scholar]
- Eyshi Rezaei, E.; Siebert, S.; Ewert, F. Impact of data resolution on heat and drought stress simulated for winter wheat in Germany. Eur. J. Agron. 2015, 65, 69–82. [Google Scholar] [CrossRef]
- Zhao, G.; Webber, H.; Hoffmann, H.; Wolf, J.; Siebert, S.; Ewert, F. The implication of irrigation in climate change impact assessment: a European-wide study. Glob. Chang. Biol. 2015, 21, 4031–4048. [Google Scholar] [CrossRef]
- Webber, H.; Zhao, G.; Wolf, J.; Britz, W.; de Vries, W.; Gaiser, T.; Hoffmann, H.; Ewert, F. Climate change impacts on European crop yields: Do we need to consider nitrogen limitation? Eur. J. Agron. 2015, 71, 123–134. [Google Scholar] [CrossRef]
- Gaiser, T.; Perkons, U.; Küpper, P.M.; Kautz, T.; Uteau-Puschmann, D.; Ewert, F.; Endwers, A.; Krauss, G. Modeling biopore effects on root growth and biomass production on soils with pronounced sub-soil clay accumulation. Ecol. Model. 2013, 256, 6–15. [Google Scholar] [CrossRef]
- Franke, A.C.; Haverkort, A.J.; Steyn, J.M. Climate Change and Potato Production in Contrasting South African Agro-Ecosystems 2. Assessing Risks and Opportunities of Adaptation Strategies. Potato Res. 2013, 56, 51–66. [Google Scholar] [CrossRef]
- Wolf, J. User Guide for LINTUL5: Simple Generic Model for Simulation of Crop Growth Under Potential, Water Limited and Nitrogen, Phosphorus and Potassium Limited Conditions; Wageningen University: Wageningen, The Netherlands, 2012. [Google Scholar]
- Addiscott, T.M.; Whitmore, A.P. Simulation of solute leaching in soils of differing permeabilities. Soil Use Manag. 1991, 7, 94–102. [Google Scholar] [CrossRef]
- Corbeels, M.; Mcmurtrie, R.; Pepper, D.; O’Connell, A.M. A process-based model of nitrogen cycling in forest plantations: Part I. Structure, calibration and analysis of the decomposition model | Request PDF. Ecol. Model. 2005, 187, 426–448. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. 15. [Google Scholar]
- Ruane, A.C.; Goldberg, R.; Chryssanthacopoulos, J. Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation. Agric. For. Meteorol. 2015, 200, 233–248. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.; Chuang, H.; Iredell, M.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Amer. Meteor. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Rawls, W.J.; Ahuja, L.R.; Brakensiek, D.L.; Shirmohammadi, A. Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Boogaard, H.L.; van Diepen, C.A.; Rotter, R.P.; Cabrera, J.M.C.A.; van Laar, H.H. WOFOST 7.1; User’s Guide for the WOFOST 7.1 Crop Growth Simulation Model and WOFOST Control Center 1.5; Wageningen, SC-DLO, 1998. Techn. Doc. 52; Wageningen University: Wageningen, The Netherlands, 1998; p. 144. [Google Scholar]
- Boons-Prins, E.R.; PenningdeVries, F.W.T. Crop-Specific Simulation Parametersfor Yield Forecasting Across the European Community; Wageningen University: Wageningen, The Netherlands, 1993; p. 201. [Google Scholar]
- Ceglar, A.; Črepinšek, Z.; Kajfež-Bogataj, L.; Pogacar, T. The simulation of phenological development in dynamic crop model: The Bayesian comparison of different methods. Agric. For. Meteorol. 2011, 151, 101–115. [Google Scholar] [CrossRef]
- Papula, A. Mathematik Für Chemiker; Enke-Verlag: Stuttgart, Germany, 1982. [Google Scholar]
- Tsujimoto, Y.; Rakotoson, T.; Tanaka, A.; Saito, K. Challenges and opportunities for improving N use efficiency for rice production in sub-Saharan Africa. Plant Prod. Sci. 2019, 1–15. [Google Scholar] [CrossRef]
- Onasanya, R.O.; Aiyelari, O.P.; Onasanya, A.; Oikeh, S.; Nwilene, F.E.; Oyelakin, O.O. Growth and Yield Response of Maize (Zea mays L.) to Different Rates of Nitrogen and Phosphorus fertilizers in Southern Nigeria. World J. Agric. Sci. 2009, 5, 400–407. [Google Scholar]
- Bosede, A.J. Economic assessment of fertilizer use and integrated practices for environmental sustainability and agricultural productivity in Sudan savannah zone, Nigeria. AJAR 2010, 5, 338–343. [Google Scholar]
- Fowler, D.B.; Brydon, J.; Darroch, B.A.; Entz, M.H.; Johnston, A.M. Environment and Genotype Influence on Grain Protein Concentration of Wheat and Rye. Agron. J. 1990, 82, 655. [Google Scholar] [CrossRef]
- Cassman, K.G.; Dobermann, A.; Walters, D.T. Agroecosystems, Nitrogen-use Efficiency, and Nitrogen Management. AMBIO A J. Hum. Environ. 2002, 31, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Wang, G.; Yue, S.; Wu, L.; Zhang, W.; Zhang, F.; Chen, X. Closing the N-Use Efficiency Gap to Achieve Food and Environmental Security. Environ. Sci. Technol. 2014, 48, 5780–5787. [Google Scholar] [CrossRef]
- Bryan, B.A.; King, D.; Zhao, G. Influence of management and environment on Australian wheat: Information for sustainable intensification and closing yield gaps. Environ. Res. Lett. 2014, 9, 044005. [Google Scholar] [CrossRef]
- Li, G.; Zhao, B.; Dong, S.; Zhang, J.; Liu, P.; Vyn, T.J. Impact of controlled release urea on maize yield and nitrogen use efficiency under different water conditions. PLoS ONE 2017, 12, e0181774. [Google Scholar] [CrossRef] [PubMed]
- Reeves, D.W.; Wood, C.W.; Touchton, J.T. Timing Nitrogen Applications for Corn in a Winter Legume Conservation-Tillage System. Agron. J. 1993, 85, 98. [Google Scholar] [CrossRef]
- Huang, R.; Birch, C.J.; George, D.L. Water Use Efficiency in Maize Production—The Challenge and Improved Strategies. In Proceedings of the 6th Water to Gold Triennial Conference, Maize Ass, Griffith, NSW, Australia, 21–23 February 2006. [Google Scholar]
- Kröbel, R.; Campbell, C.A.; Zentner, R.P.; Lemke, R.; Steppuhn, H.; Desjardins, R.L.; De Jong, R. Nitrogen and phosphorus effects on water use efficiency of spring wheat grown in a semi-arid region of the Canadian prairies. Can. J. Soil Sci. 2012, 92, 573–587. [Google Scholar] [CrossRef]
- Bramley, H.; Turner, N.C.; Siddique, K.H.M. Water Use Efficiency. In Genomics and Breeding for Climate-Resilient Crops: Vol. 2 Target Traits; Kole, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 225–268. [Google Scholar]
- Miranzadeh, H.; Emam, Y.; Seyyed, H.; Zare, S. Productivity and Radiation Use Efficiency of Four Dryland Wheat Cultivars under Different Levels of Nitrogen and Chlormequat Chloride. J. Agric. Sci. Tech. 2011, 13, 339–351. [Google Scholar]
| Name | Description | Unit | Value |
|---|---|---|---|
| Crop parameters | |||
| TSUM1 | Temperature sum from emergence to anthesis | °C/day | 1060 |
| TSUM2 | Temperature sum from anthesis to maturity | °C/day | 990 |
| TBASEM | Lower threshold temperature for emergence | °C | 8.0 |
| TEFFMX | Maximum effective temperature for emergence | °C | 30.0 |
| TSUMEM | Temperature sum from sowing to emergence | °C | 56.0 |
| RUE-0.0 | Radiation use efficiency at development stage 0 | g/MJ | 3.8 |
| RUE-1.25 | Radiation use efficiency at development stage 1.25 | g/MJ | 3.8 |
| RUE-1.50 | Radiation use efficiency at development stage 1.50 | g/MJ | 3.0 |
| RUE-1.75 | Radiation use efficiency at development stage 1.75 | g/MJ | 2.0 |
| RUE-2.0 | Radiation use efficiency at development stage 2.0 | g/MJ | 1.4 |
| SLATB-0.0 | Specific leaf area at development stage 0 | m2/g | 0.022 |
| SLATB-0.9 | Specific leaf area at development stage 0.9 | m2/g | 0.03 |
| SLATB-1.0 | Specific leaf area at development stage 1.0 | m2/g | 0.032 |
| SLATB-2.0 | Specific leaf area at development stage 2.0 | m2/g | 0.02 |
| LAI critical | Critical leaf area beyond which leaves die due | m2/m2 | 4 |
| to self shading | |||
| RGRLAI | Maximum relative increase in LAI | ha/ha/day | 0.02 |
| ROOTDI | Initial rooting depth | m | 0.1 |
| ROOTDM | Maximum rooting depth | m | 1 |
| RRDMAX | Maximum rate of increase in rooting depth | m | 0.012 |
| TDWI | Initial total crop dry weight | kg/ha | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez, G.; Kolem, H.B.; Srivastava, A.K.; Gaiser, T.; Ewert, F. A Model-Based Estimation of Resource Use Efficiencies in Maize Production in Nigeria. Sustainability 2019, 11, 5114. https://doi.org/10.3390/su11185114
Lopez G, Kolem HB, Srivastava AK, Gaiser T, Ewert F. A Model-Based Estimation of Resource Use Efficiencies in Maize Production in Nigeria. Sustainability. 2019; 11(18):5114. https://doi.org/10.3390/su11185114
Chicago/Turabian StyleLopez, Gina, Hannah Beate Kolem, Amit Kumar Srivastava, Thomas Gaiser, and Frank Ewert. 2019. "A Model-Based Estimation of Resource Use Efficiencies in Maize Production in Nigeria" Sustainability 11, no. 18: 5114. https://doi.org/10.3390/su11185114
APA StyleLopez, G., Kolem, H. B., Srivastava, A. K., Gaiser, T., & Ewert, F. (2019). A Model-Based Estimation of Resource Use Efficiencies in Maize Production in Nigeria. Sustainability, 11(18), 5114. https://doi.org/10.3390/su11185114






