Bottlenecks, Shockwave, and Off-Ramp Blockage on Freeways
Abstract
1. Introduction
2. Analysis of Off-Ramp Blockage
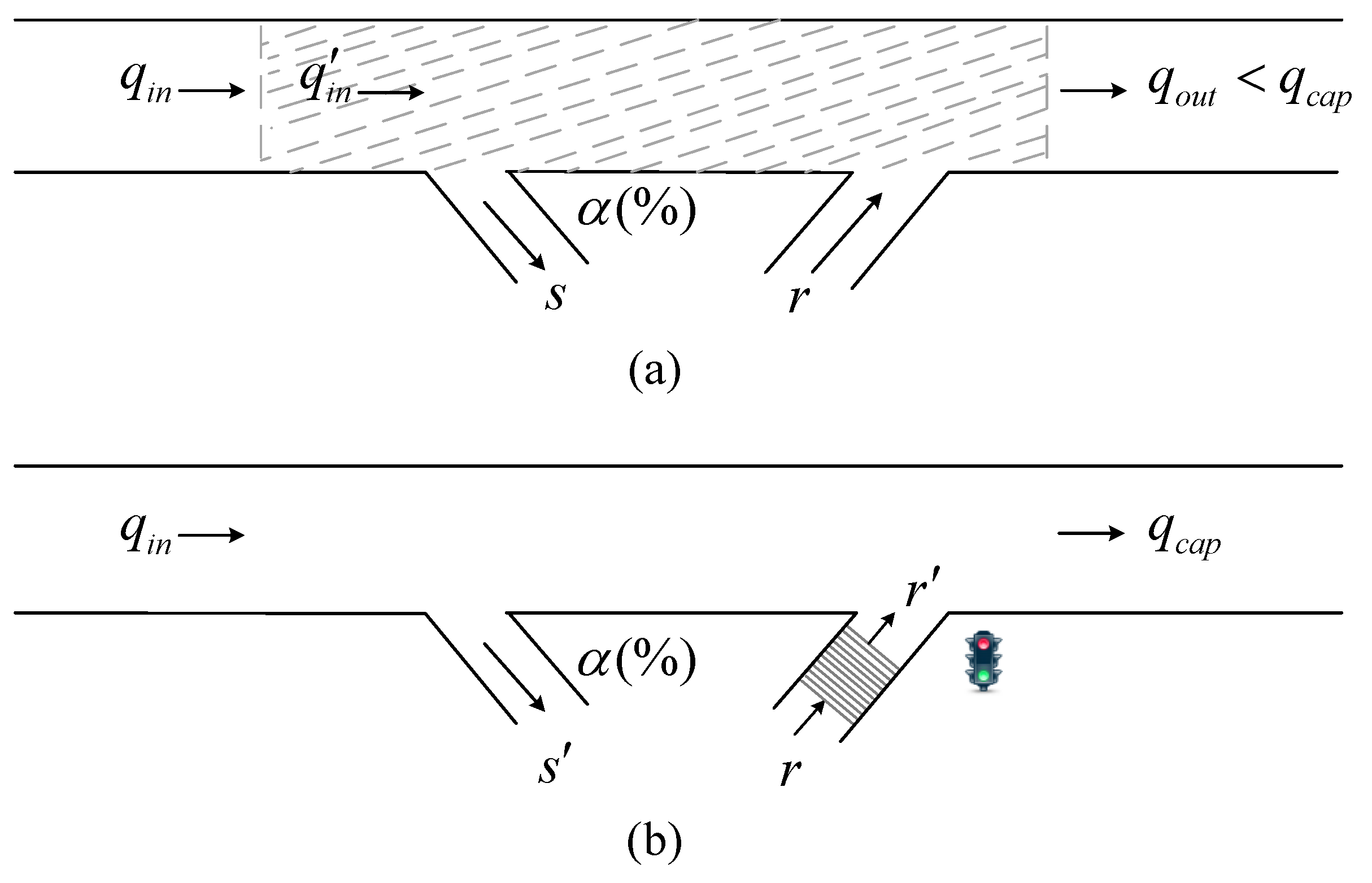
2.1. Problem Statement
- (i)
- the same traffic demands are considered for both cases, i.e., the mainstream demand is q, and the on-ramp demands are qm (m = 1, 2, …, n).
- (ii)
2.2. Flow Conditions for Bottleneck Activation and Congestion Propagation
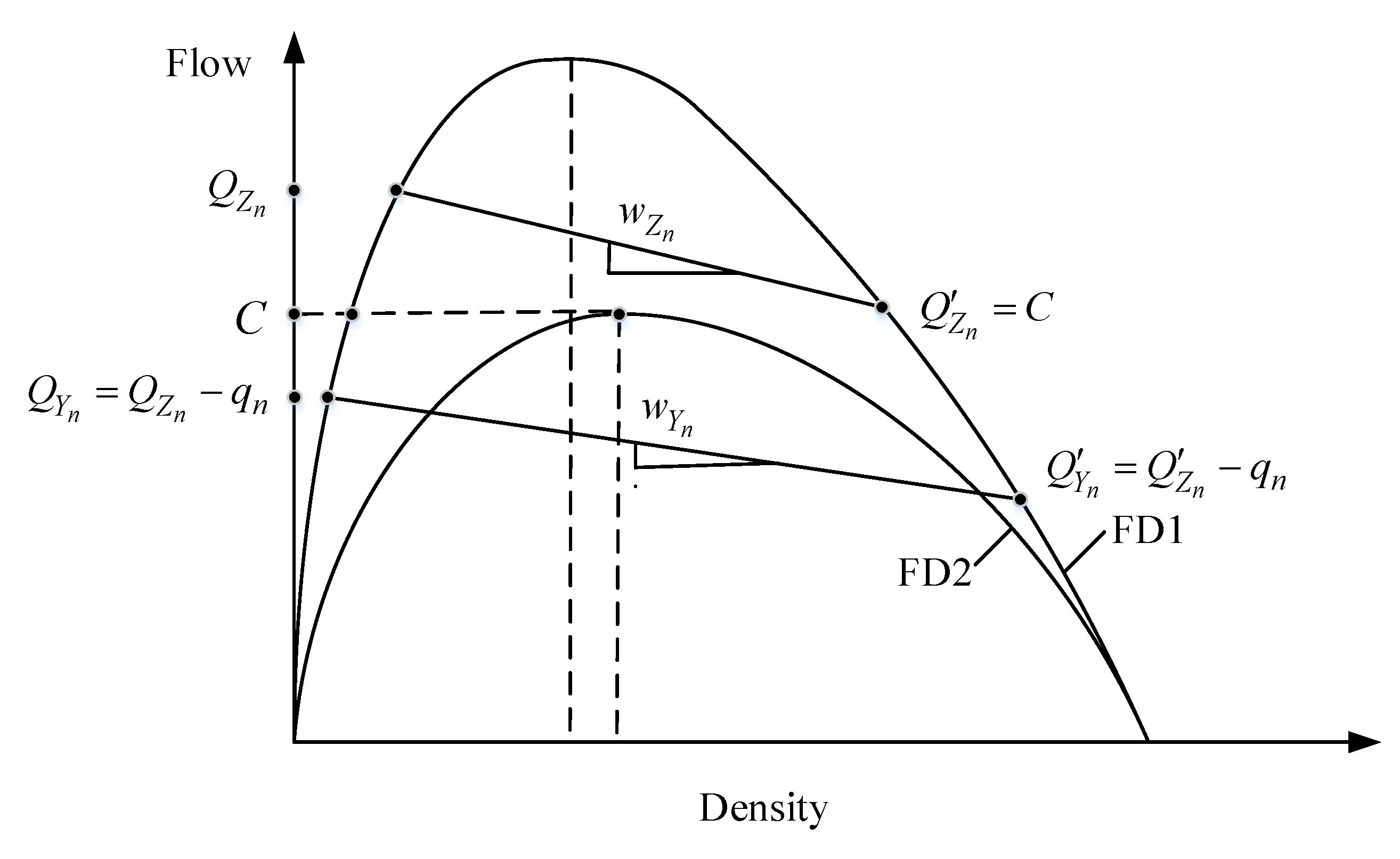
2.2.1. Basic Definitions and Relations
2.2.2. Mathematic Analysis
- (1)
- under an idealized condition were qm’ = qm and αm’ = αm (m = 1, 2, …, n) (i.e., on-ramp inflows and off-ramp exiting rates do not change under congestion), the resulting shockwave keeps spilling back if and only if it arises at the downstream bottleneck (Lemma 2 and Corollary 1);
- (2)
- under general conditions where and (m = 1, 2, …, n) (i.e., on-ramp inflows may drop and off-ramp exiting rates may increase under congestion), the resulting shockwave keeps propagating upstream if some additional conditions are satisfied (Theorem 1);
2.3. Off-Ramp Blockage
2.4. Further Discussions
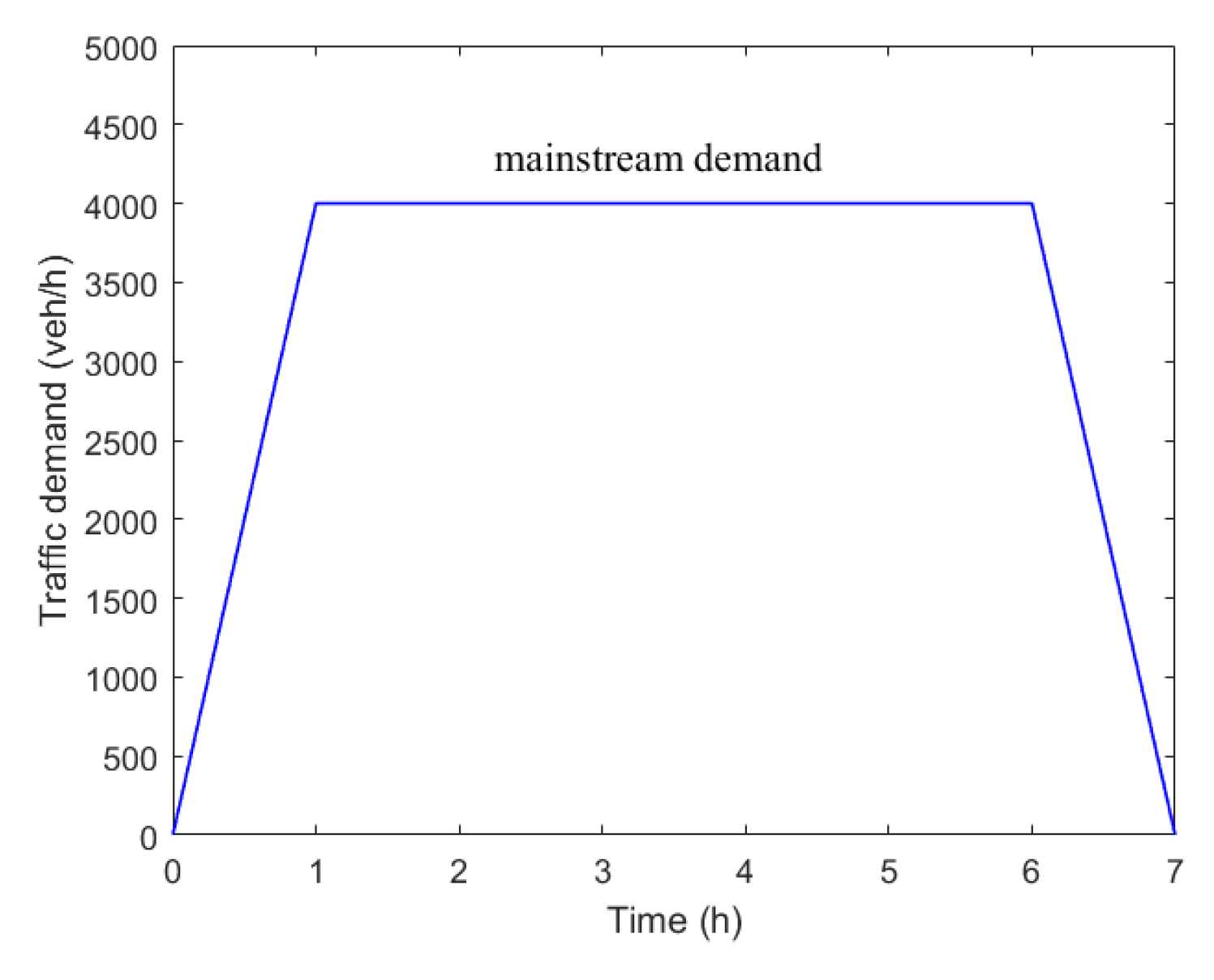
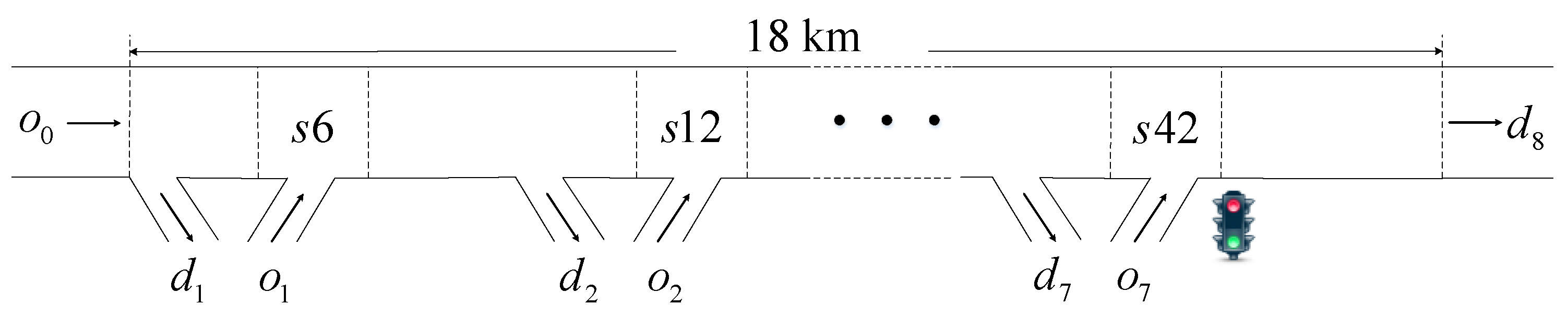
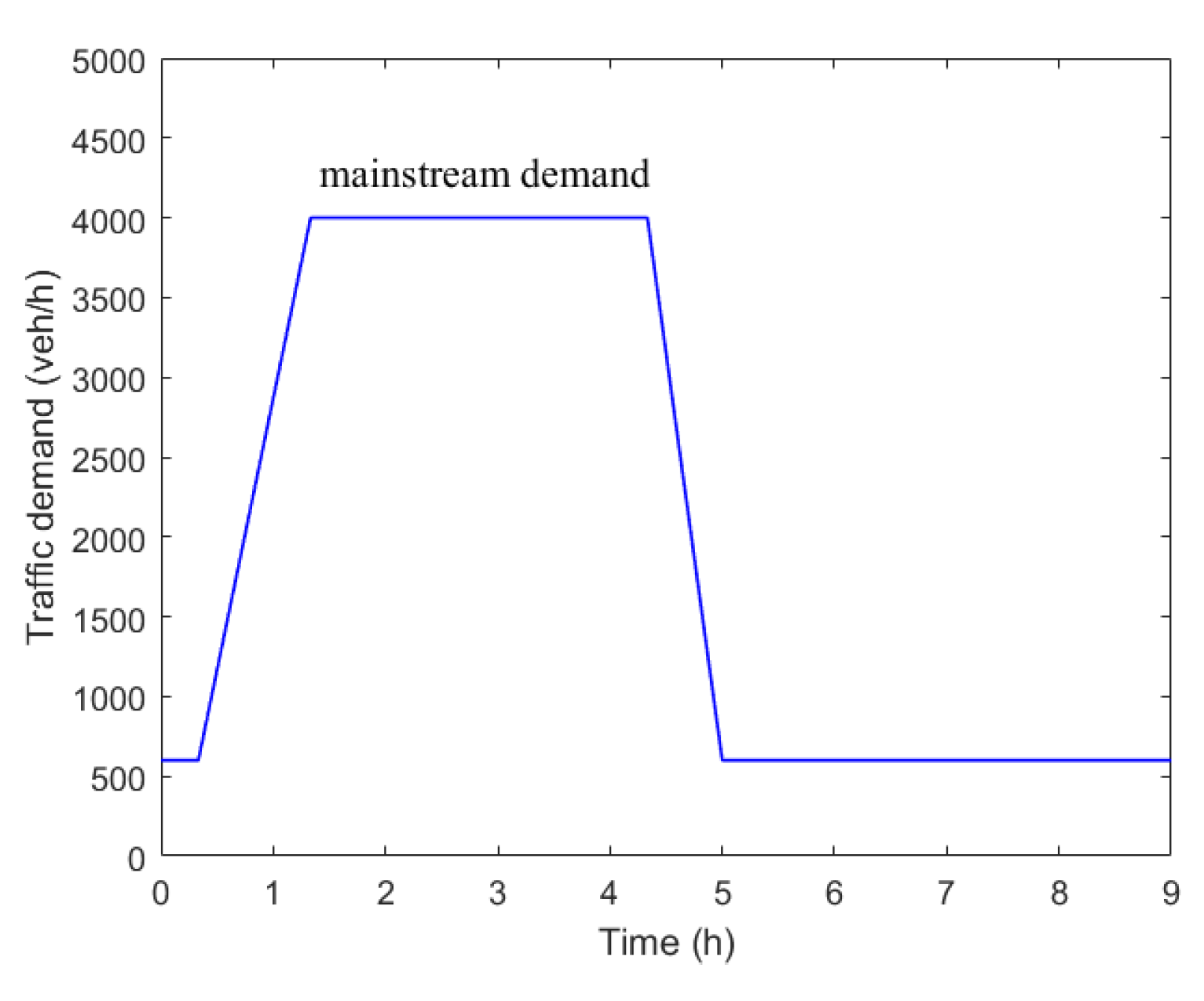
3. Simulation Investigations
3.1. Off-Ramp Blockage Effect
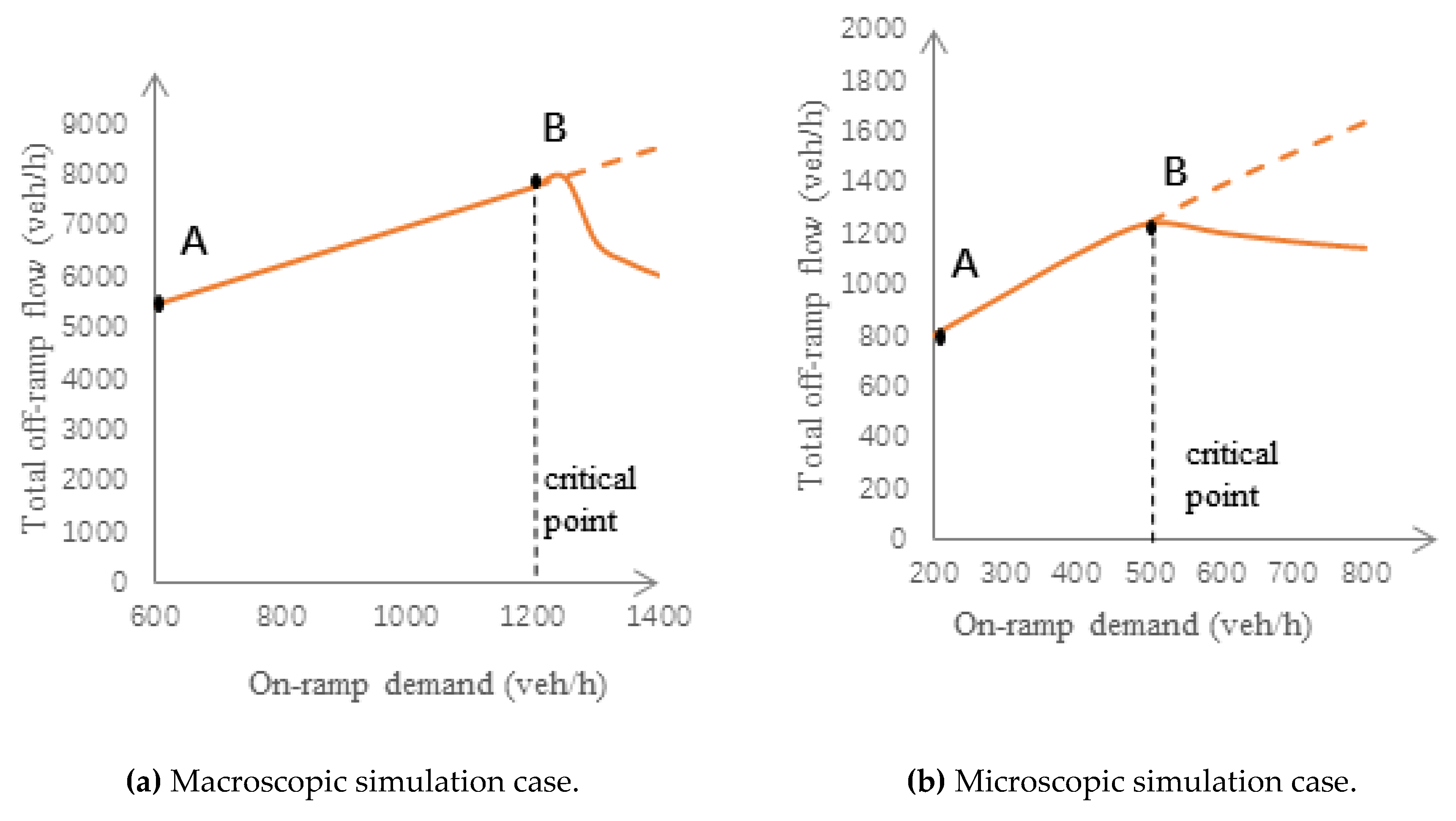
3.1.1. An Accident Case
3.1.2. A Ramp Merging Case
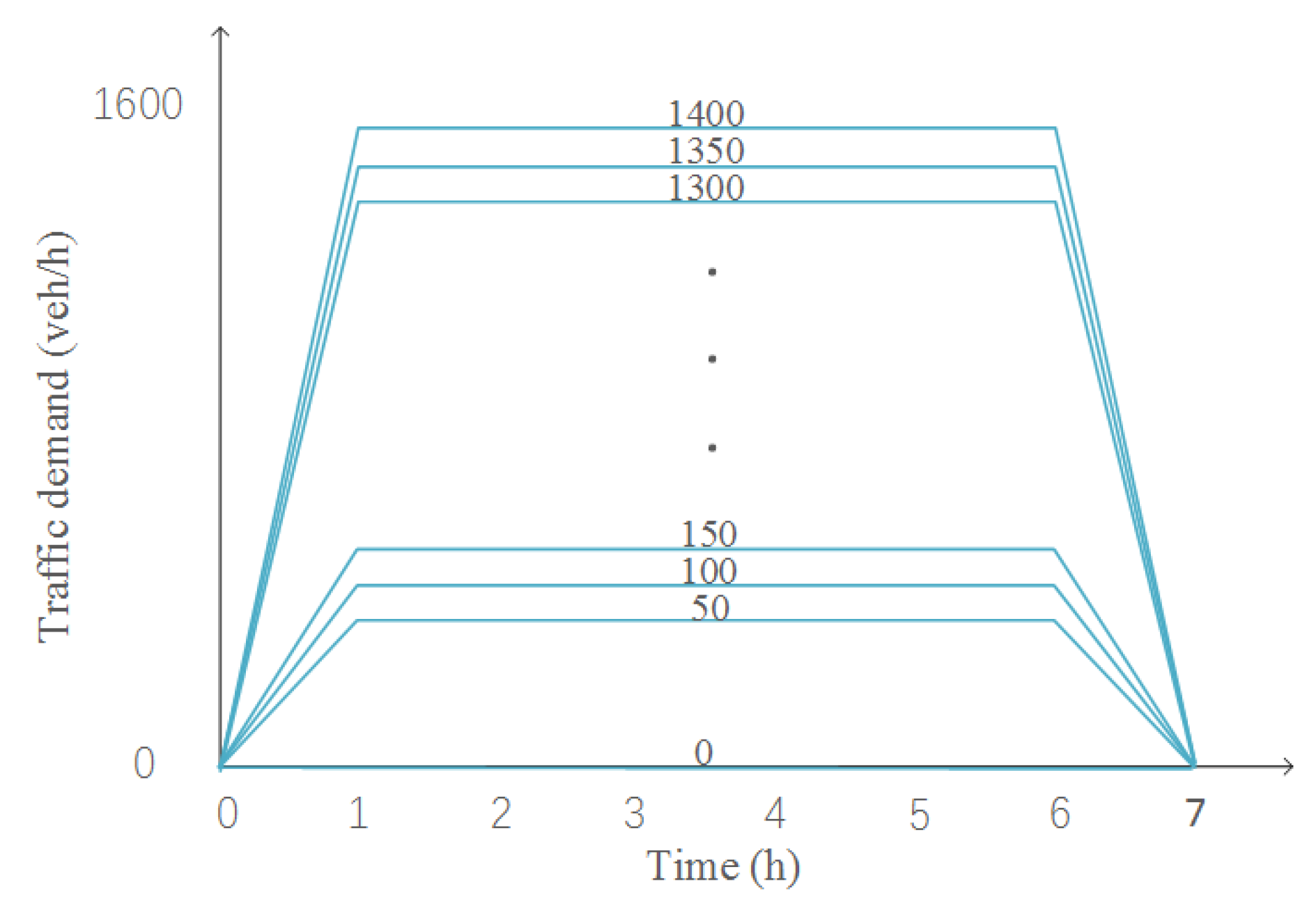
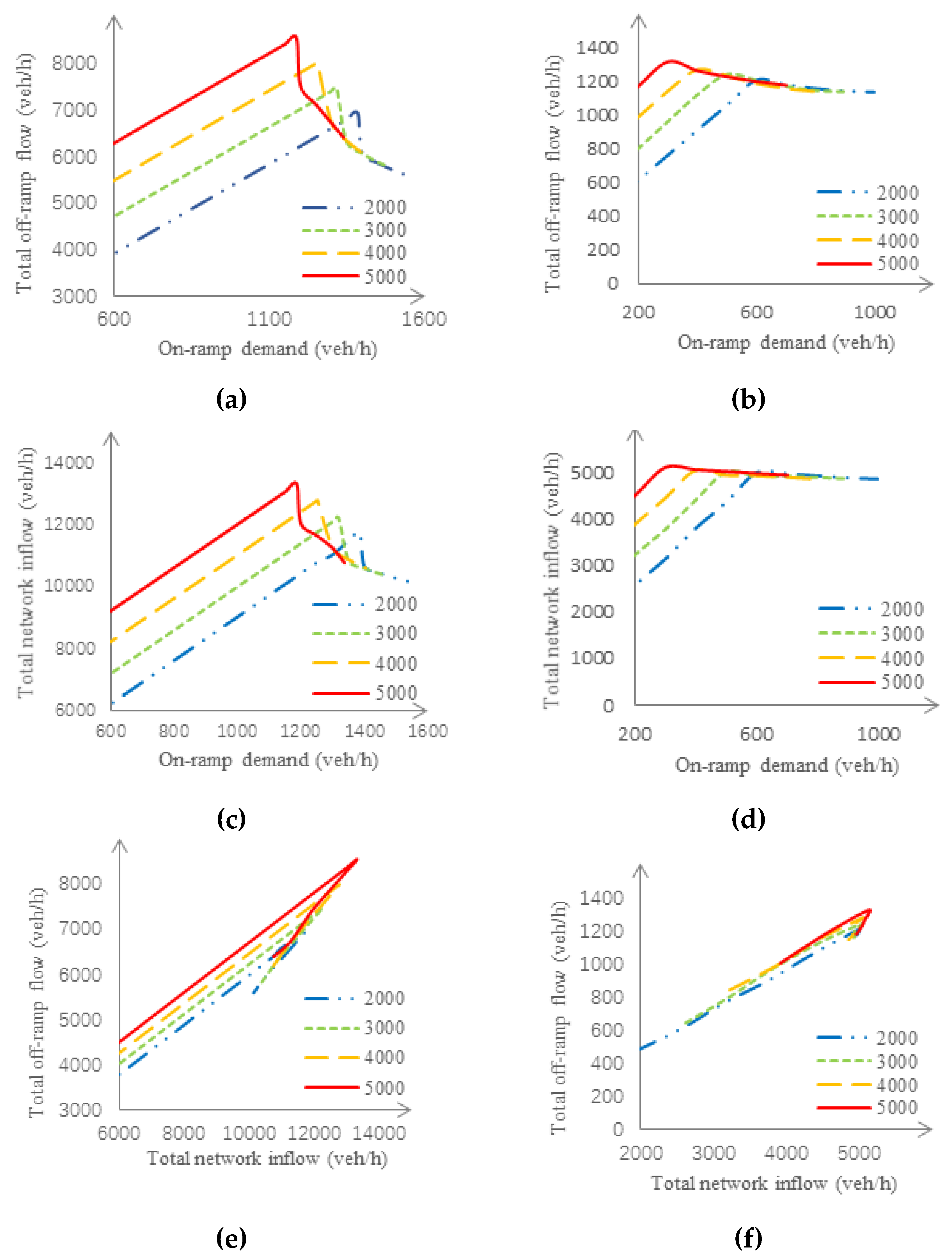
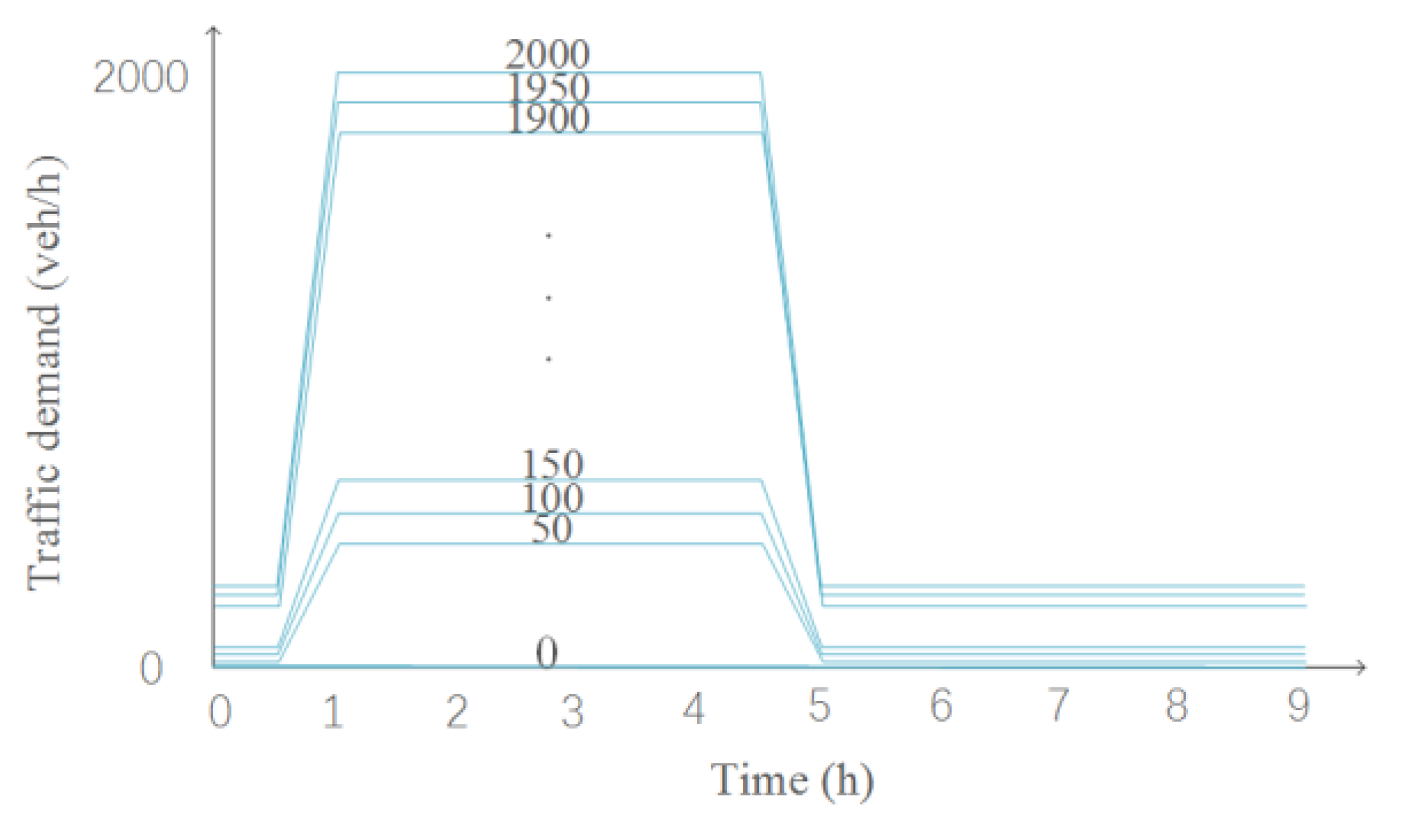
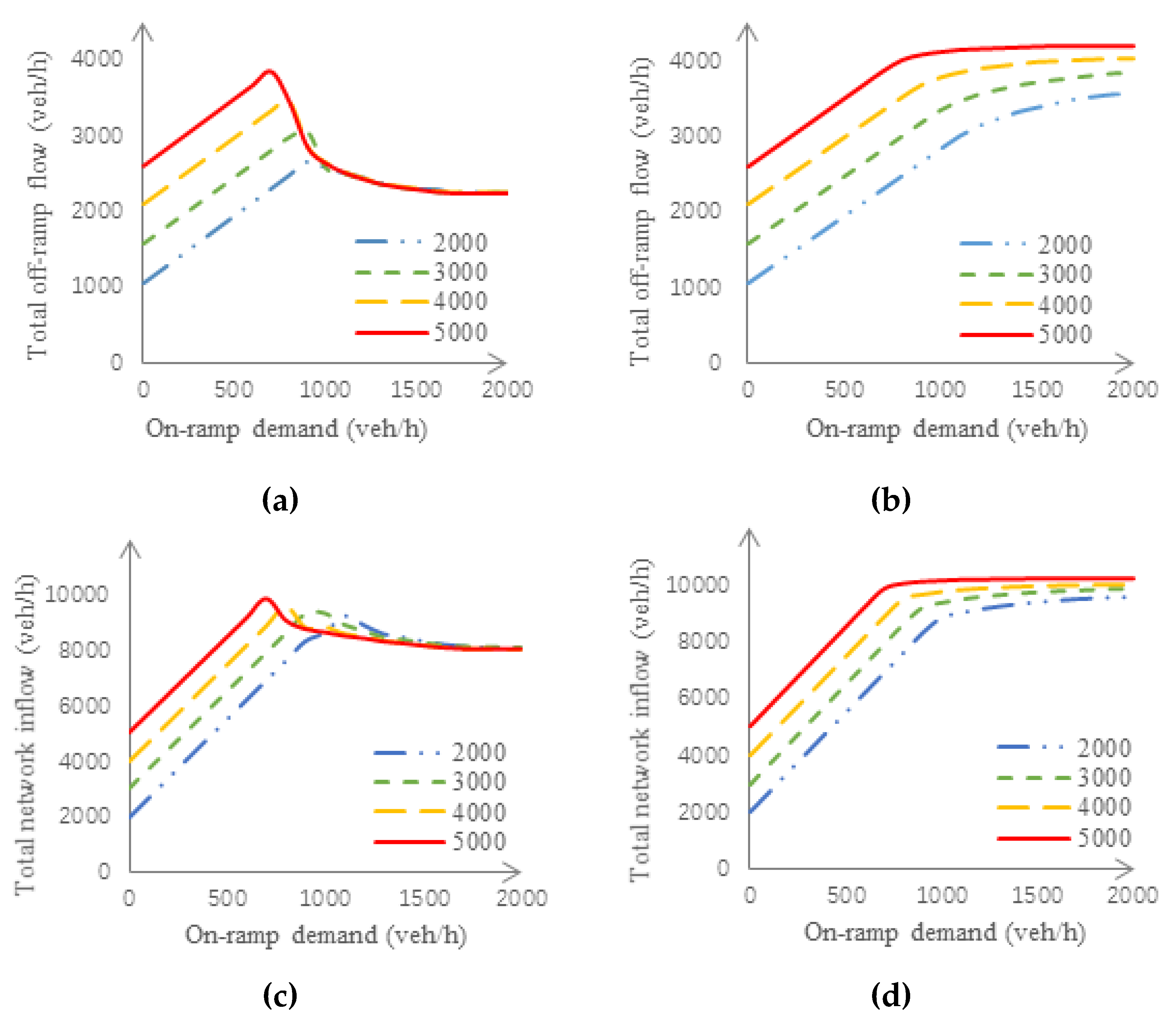
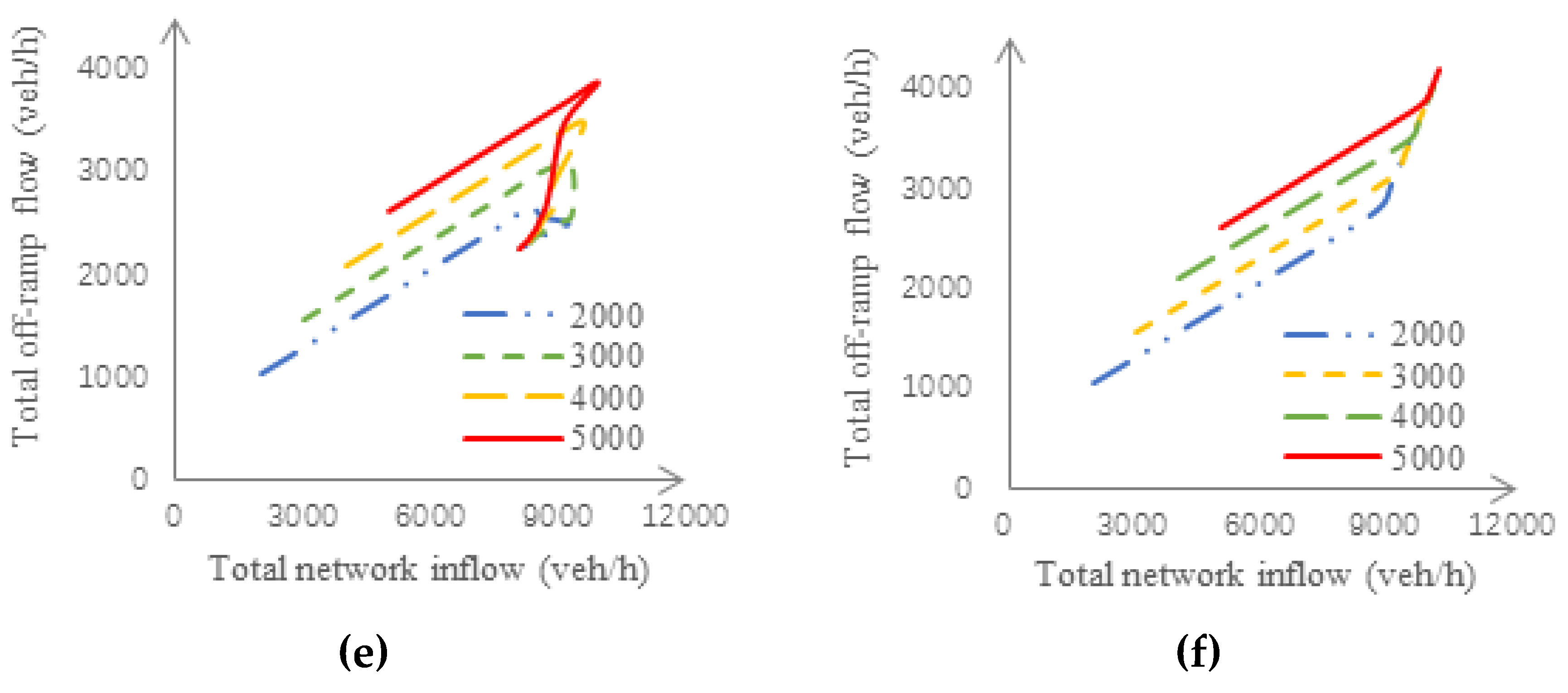
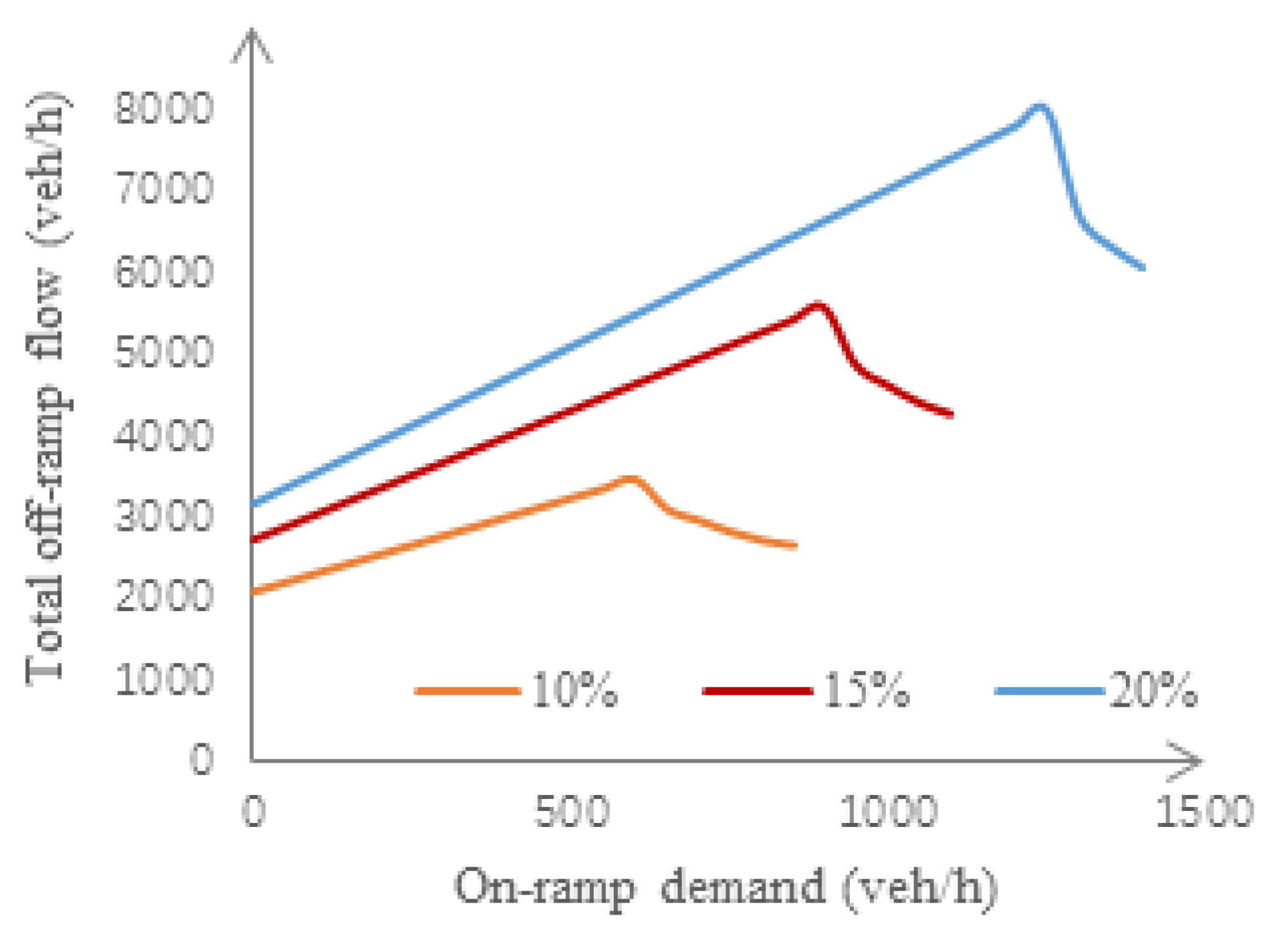
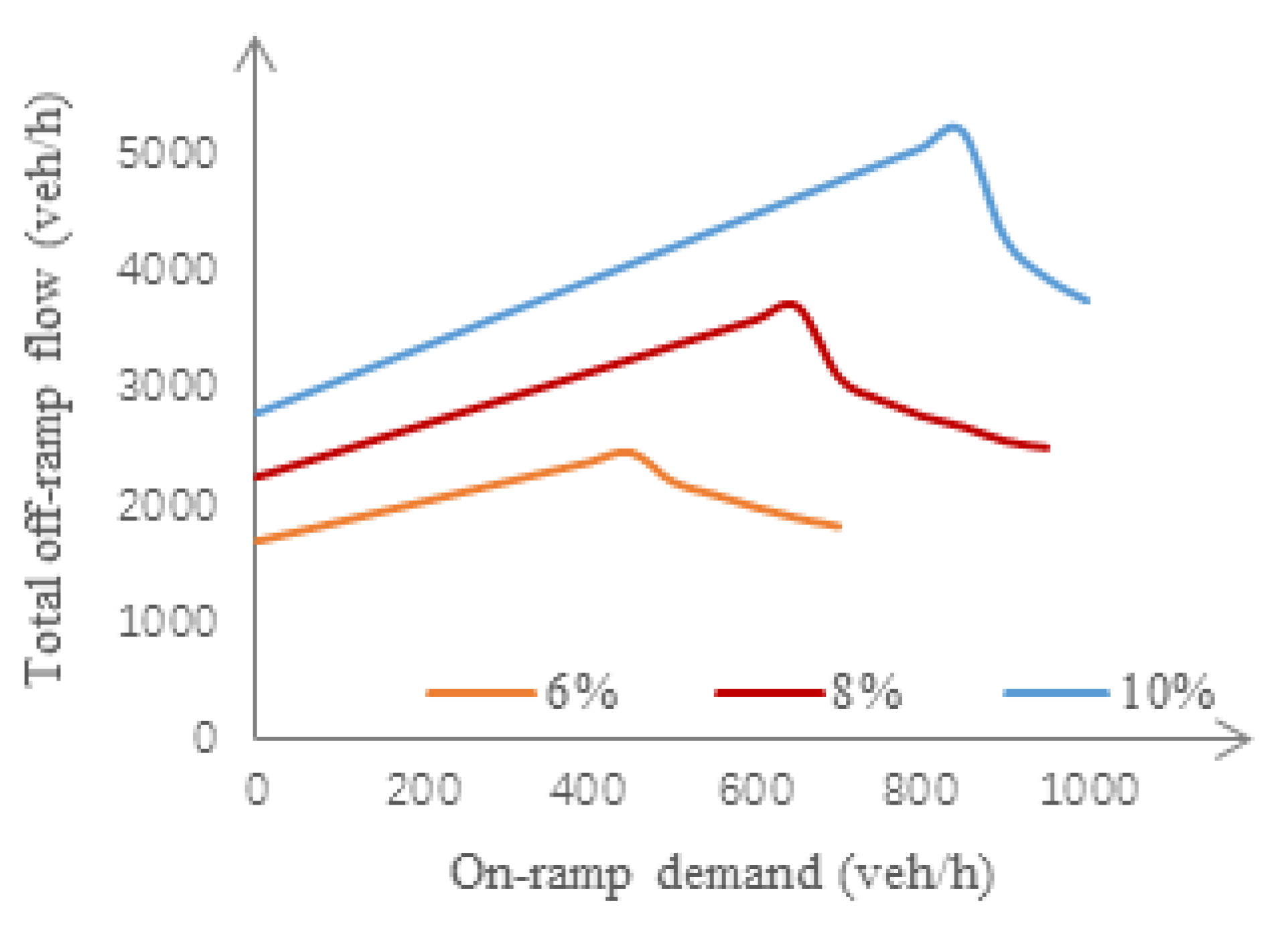
3.2. Sensitivity Studies
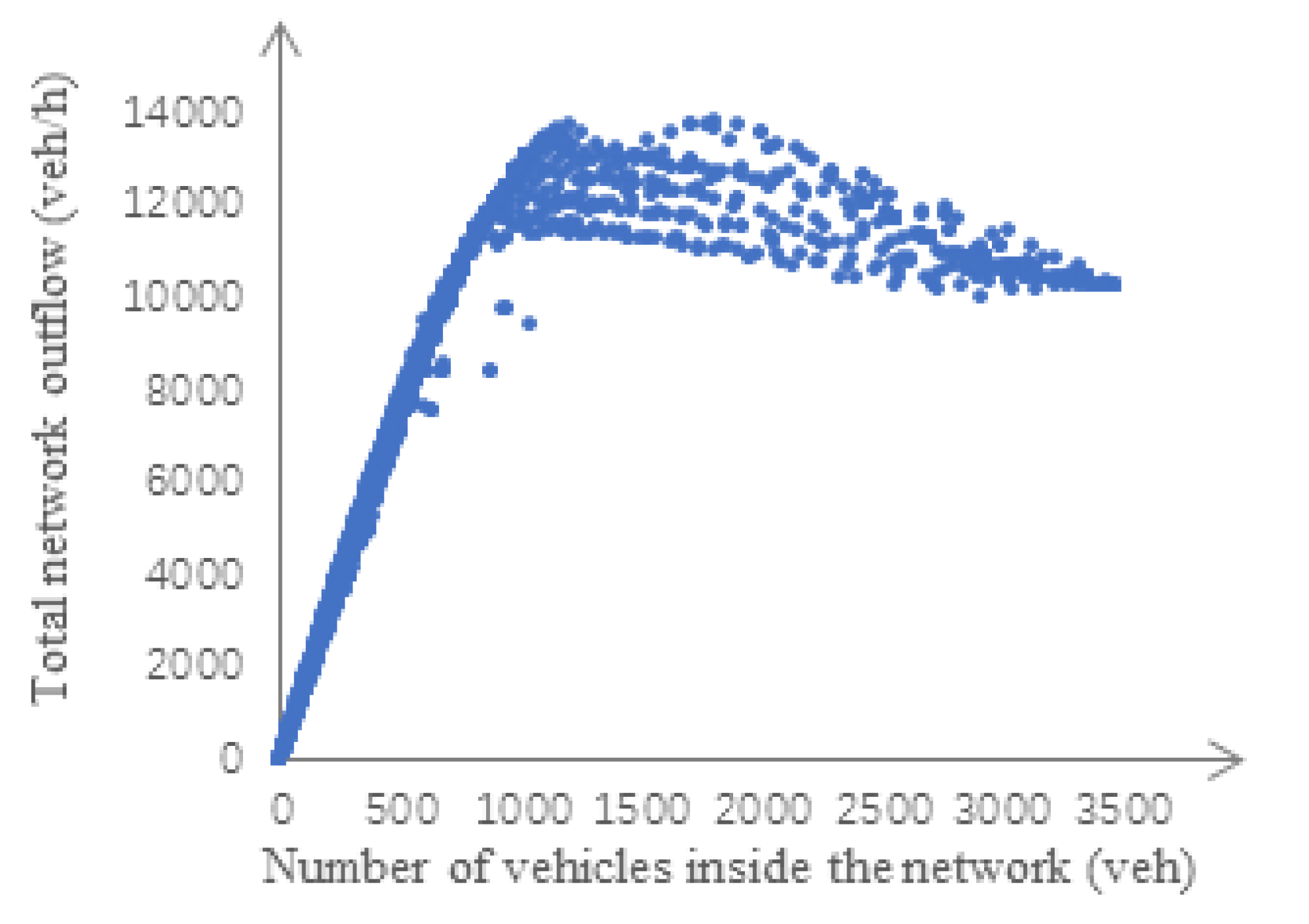
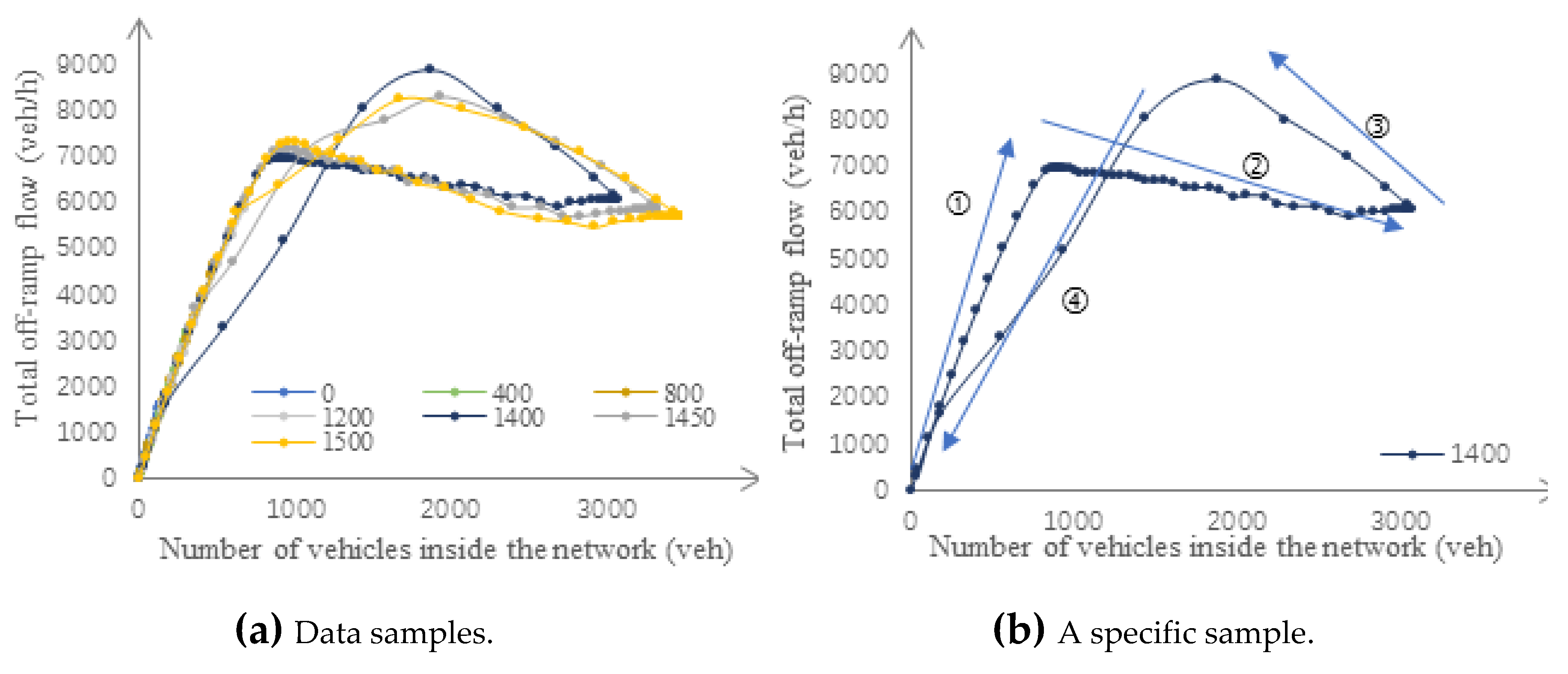
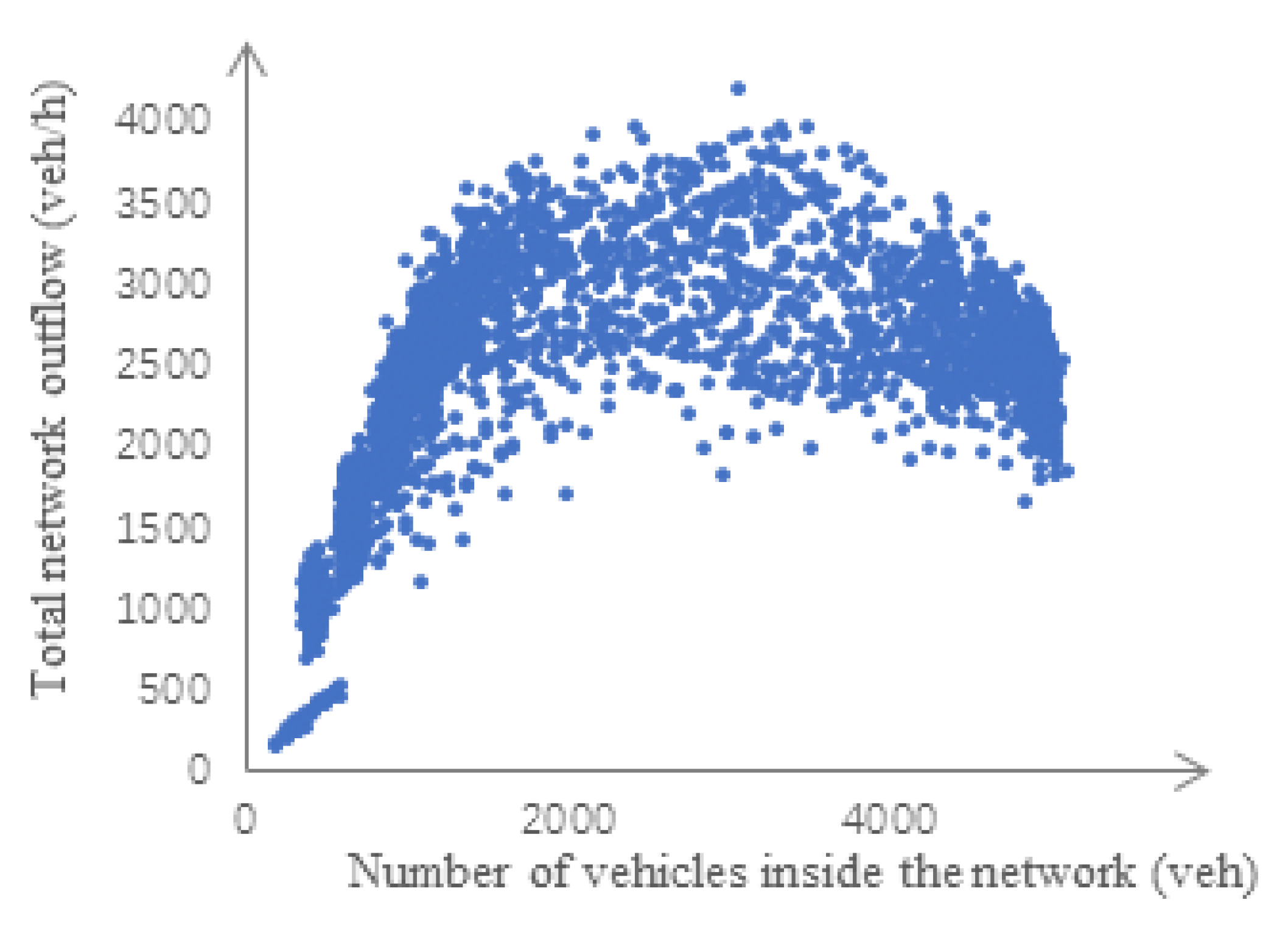
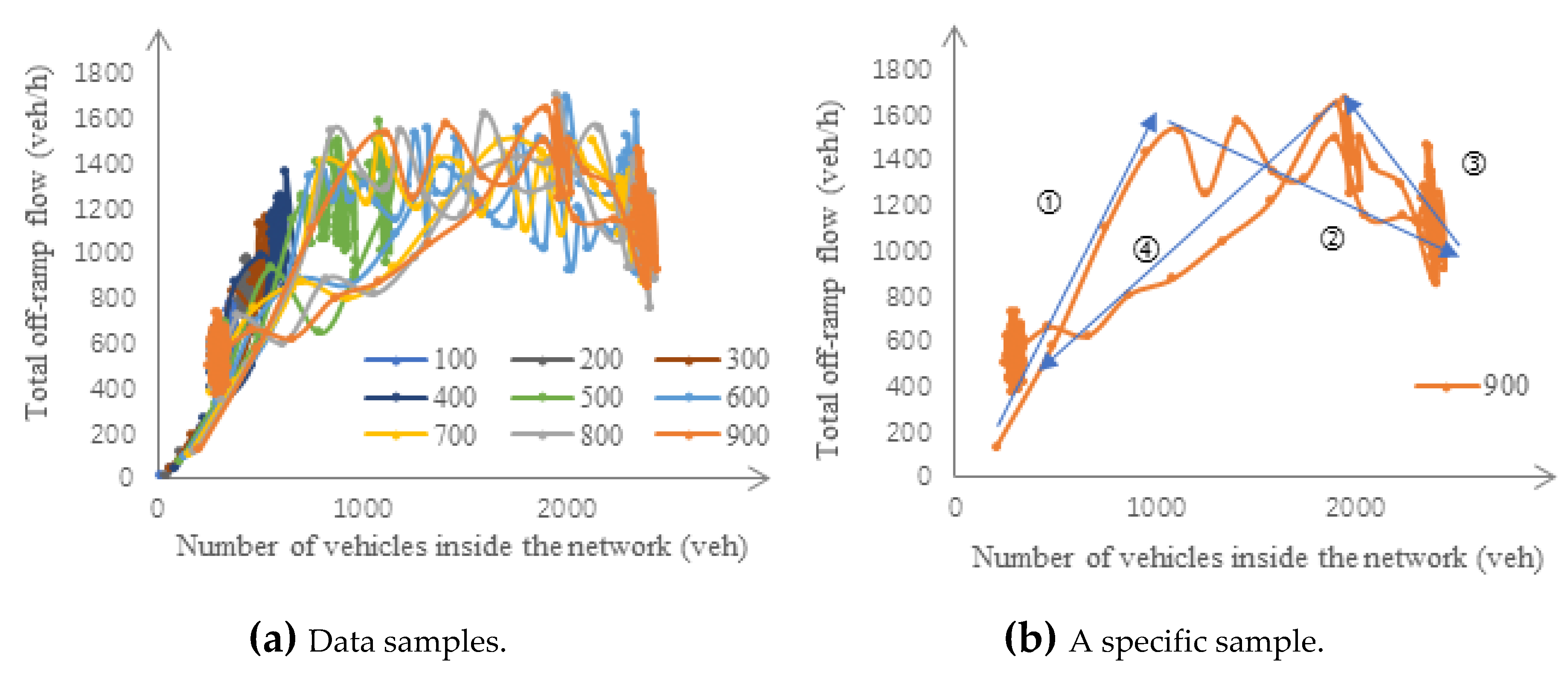
3.3. Macroscopic Fundamental Diagrams
4. Conclusions
- (1)
- Provided that on-ramp inflows and off-ramp exiting rates do not change under congestion, the shockwave keeps spilling back if and only if it arises at the downstream bottleneck as shown in Figure 3 (Lemma 2 and Corollary 1).
- (2)
- Considering that on-ramp inflows may drop and off-ramp exiting rates may increase under congestion, the shockwave keeps propagating upstream only if some additional conditions are satisfied (Theorem 1).
- (3)
- In consideration of the same condition as (2), the occurrence of off-ramp blockage depends on a special condition (Theorem 2).
- (4)
- On top of (3), assuming that off-ramp exiting rates do not change under congestion, then off-ramp blockages happens unconditionally (Corollary 3).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- European Environment Agency. Towards a Resource-Efficient Transport System; European Environment Agency: Copenhagen, Denmark, 2010. [Google Scholar]
- United States Environmental Protection Agency. Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990–2010; Tech. Rep. EPA 430-R-12-001; United States Environmental Protection Agency: Washington, DC, USA, 2012.
- EU Energy and Transport in Figures–Statistical Pocketbook 2010; EU: Brussels, Belgium, 2010.
- Schrank, D.; Lomax, T. Annual Urban Mobility Report; Tech. Rep. 10-09-019; Texas A&M Transportation Institute: College Station, TX, USA, 2011. [Google Scholar]
- Keep Europe Moving—Sustainable Mobility for Our Continent; Tech. Rep. COM/2006/0314; European Commission: Brussels, Belgium, June 2006.
- Guerrini, F. Traffic Congestion Costs Americans $124 Billion A Year, Report Says. Forbes, 14 October 2014. [Google Scholar]
- Daganzo, C.F. The nature of freeway gridlock and how to prevent it. In Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 24–26 July 1996; Lesort, J.B., Ed.; Pergamon-Elsevier: Tarrytown, NY, USA, 1996; pp. 629–646. [Google Scholar]
- Papageorgiou, M. Reduction of Total Time Spent in A Freeway System by On-Ramp Metering; Internal Report; Dynamic Systems and Simulation La: Chania, Greece, 1997. [Google Scholar]
- Daganzo, F. Improving City Mobility through Gridlock Control: An Approach and Some Ideas; UCB-ITS-VWP-2005-1; UC Berkeley Center for Future Urban Transport Working Paper; UC Berkeley: Berkeley, CA, USA, 2005. [Google Scholar]
- Geroliminis, N.; Daganzo, C.F. Existence of urban-scale macroscopic fundamental diagrams: Some experimental findings. Transp. Res. Part B Methodol. 2008, 42, 759–770. [Google Scholar] [CrossRef]
- Haddad, J.; Ramezani, M.; Geroliminis, N. Cooperative traffic control of a mixed network with two urban regions and a freeway. Transp. Res. Part B Methodol. 2012, 54, 17–36. [Google Scholar] [CrossRef]
- Arnott, R. A bathtub model of downtown traffic congestion. J. Urban Econ. 2013, 76, 110–121. [Google Scholar] [CrossRef]
- Ros, G.B.; Knoop, V.L.; van Arem, B.; Hoogendoorn, S.P. Mainstream Traffic Flow Control at Sags. Transport. Res. Rec. J. Transp. Res. Board 2014, 2470, 57–64. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Papamichail, I. High-Level Proof-of-Concept for the Application of the HERO Coordinated Ramp Metering Scheme to a Field Test at A10; Dynamic Systems and Simulations Laboratory, Technical Systems and Simulations Laboratory, Technical University of Crete: Chania, Greece, 2009. [Google Scholar]
- Newell, G.F. Delays caused by a queue at a freeway exit ramp. Transp. Res. Part B Methodol. 1999, 33, 337–350. [Google Scholar] [CrossRef]
- Spiliopouloua, A.; Kontorinakia, M.; Papageorgioua, M.; Kopelias, P. Macroscopic traffic flow model validation at congested freeway off-ramp areas. Transport. Res. Part C Emerg. Technol. 2014, 41, 18–29. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y. Integrated signal optimization and non-traditional lane assignment for urban freeway off-ramp congestion mitigation. Transp. Res. Part C Emerg. Technol. 2016, 73, 219–238. [Google Scholar] [CrossRef]
- Iordanidou, G.; Roncoli, C.; Papamichail, I.; Papageorgiou, M. Feedback-Based Mainstream Traffic Flow Control for Multiple Bottlenecks on Motorways. IEEE Trans. Intell. Transp. Syst. 2015, 16, 610–621. [Google Scholar]
- Pang, Y. Off-Ramp Blockage on Freeways. Master’s Thesis, School of Civil Engineering and Architecture, Zhejiang University, Zhejiang, China, 2017. [Google Scholar]
- Gomes, G.; Horowitz, R. Optimal freeway ramp metering using the asymmetric cell transmission model. Transp. Res. Part C Emerg. Technol. 2006, 14, 244–262. [Google Scholar] [CrossRef]
- Dabiri, A.; Kulcsar, B. Distributed Ramp Metering-A Constrained Discharge Flow Maximization Approach. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2525–2538. [Google Scholar] [CrossRef]
- Ferrara, A.; Sacone, S.; Siri, S. An overview of traffic control schemes for freeway systems. In Freeway Traffic Modelling and Control; Springer: New York, NY, USA, 2018. [Google Scholar]
- Newell, G.F. A simplified theory of kinematic waves in highway traffic. I: General theory. II: Queueing at freeway bottlenecks. III: Multi-destination flows. Transp. Res. Part B Methodol. 1993, 27, 281–313. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Bertini, R.L. Some traffic features at freeway bottlenecks. Transp. Res. Part B Methodol. 1999, 33, 25–42. [Google Scholar] [CrossRef]
- Messmer, A.; Papageorgiou, M. METANET: A macroscopic simulation program for motorway networks. Traffic Eng. Control 1990, 31, 466–470. [Google Scholar]
- Wang, Y.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part B Methodol. 2005, 39, 141–167. [Google Scholar] [CrossRef]
- VISSIM 5.20 User’s Manual; Planung Transprot Verkehr: Karlsruhe, Germany, 2009.
- Papageorgiou, M.; Kotsialos, A. Freeway ramp metering: An overview. IEEE Trans. Intell. Transp. Syst. 2002, 3, 271–281. [Google Scholar] [CrossRef]

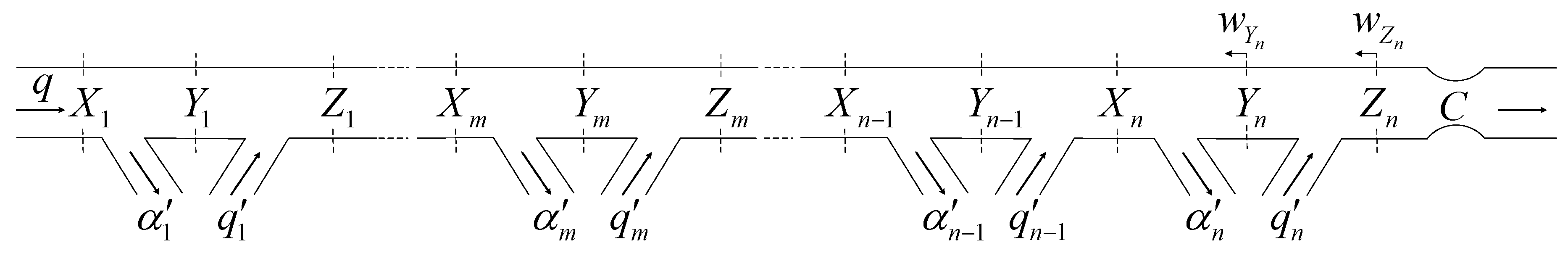



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Chen, X.; Pang, Y.; Wang, Y.; Zheng, P. Bottlenecks, Shockwave, and Off-Ramp Blockage on Freeways. Sustainability 2019, 11, 4991. https://doi.org/10.3390/su11184991
Guo J, Chen X, Pang Y, Wang Y, Zheng P. Bottlenecks, Shockwave, and Off-Ramp Blockage on Freeways. Sustainability. 2019; 11(18):4991. https://doi.org/10.3390/su11184991
Chicago/Turabian StyleGuo, Jingqiu, Xinyao Chen, Yuqi Pang, Yibing Wang, and Pengjun Zheng. 2019. "Bottlenecks, Shockwave, and Off-Ramp Blockage on Freeways" Sustainability 11, no. 18: 4991. https://doi.org/10.3390/su11184991
APA StyleGuo, J., Chen, X., Pang, Y., Wang, Y., & Zheng, P. (2019). Bottlenecks, Shockwave, and Off-Ramp Blockage on Freeways. Sustainability, 11(18), 4991. https://doi.org/10.3390/su11184991




