Generalizing Predictive Models of Admission Test Success Based on Online Interactions

Abstract

To start medical or dentistry studies in Flanders, prospective students need to pass a central admission test. A blended program with four Small Private Online Courses (SPOCs) was designed to support those students. The logs from the platform provide an opportunity to delve into the learners’ interactions and to develop predictive models to forecast success in the test. Moreover, the use of different courses allows analyzing how models can generalize across courses. This article has the following objectives: (1) to develop and analyze predictive models to forecast who will pass the admission test, (2) to discover which variables have more effect on success in different courses, (3) to analyze to what extent models can be generalized to other courses and subsequent cohorts, and (4) to discuss the conditions to achieve generalizability. The results show that the average grade in SPOC exercises using only first attempts is the best predictor and that it is possible to transfer predictive models with enough reliability when some context-related conditions are met. The best performance is achieved when transferring within the same cohort to other SPOCs in a similar context. The performance is still acceptable in a consecutive edition of a course. These findings support the sustainability of predictive models.

1. Introduction

In most countries, entry into medical or dentistry schools is restricted by a high-stake admission test. In Flanders, this test consists of a scientific part with questions on chemistry, physics, mathematics, and biology and an information processing part. The passing rate fluctuates around 20% (i.e., approximately 20% of learners pass the test). One of the most influential success predictors is the prior educational track, giving students with a science and/or mathematics background an advantage [1]. Students train intensively for the admission test to be optimally prepared.

In the digital era, technologies have enabled new ways to provide learning that can support students. With the popularity of online learning (and particularly with MOOCs (Massive Open Online Courses) because of its flexibility [2], new kind of courses have appeared that use new learning facilities such as quizzes and video interactions. Small Private Online Courses (SPOCs) [3] have emerged as a way to use MOOC technology for specific on-campus training (e.g., for students enrolled in a course) or for more targeted courses. Moreover, these digital platforms not only serve as a repository to upload teaching materials but also allow us to get comprehensive traces about learners’ interactions. These interactions can be useful to detect patterns about students’ behaviors and to predict trends on advance (e.g., who will pass the course) [4].

Prediction in education has a special relevance because stakeholders (e.g., teachers and students) can anticipate what will happen in the course so they can adapt their teaching/learning behavior to improve learning outcomes. Furthermore, predictions can be presented through dashboards and/or feedback systems (similar to, e.g., the learning tracker to inform about learners’ behaviors [5]) to aid sensemaking [6], e.g., presenting information about students’ success or students at risk [7] to make students self-reflect on their learning. At this point, stakeholder engagement is very important and course builders and instructors should be involved in the design of visualizations, predictions, etc. (without neglecting students). However, although many people are involved and accurate and meaningful predictions are obtained, it should be noted that the particular course context can considerably affect the results. Particularly, the course context and course design have special relevance in online or blended courses where learners are more at risk to procrastinate and need good self-regulation skills for success [8]. That is the case for the SPOCs KU Leuven developed to support last-year high-school students to prepare for the sciences part of the admission test. In these courses, any student can enroll to access videos, theoretical background, and exercises to prepare for the admission test. In particular, the SPOC format would allow learners to study at their own pace. However, it is not clear how learners’ interactions in a SPOC to prepare for a high-stake admission test can influence success of the student and how early it is possible to forecast learning outcomes with predictive models.

Due to the impact of the course context, the generalizability of models developed for particular courses is challenging and still an open issue. As mentioned by Gašević, Dawson, and Siemens [9], few contributions actually evaluate the impact and transferability of the models in different contexts. While this fact is often neglected, it is very important to obtain models that could scale beyond the course where they were developed to ensure the sustainability of prediction models [10]. For example, as it was mentioned before, predictive models can be used to identify learners at risk and to make impact on learning [11]. However, if models are only developed for a specific course and cannot be reused for other courses or different cohorts, then their applicability will be limited. This also applies to research findings, which can be limited if they are not valid in other contexts. As a result, the analysis of the generalizability becomes very relevant as this generalizability is a condition for sustainability of the models and findings. While the analysis can be limited because of the large number of different contexts, it is very useful to provide insight about how models can be generalized and under which conditions (related to the context). In this direction, this work aims to address the following objectives:

O1.

Analyze the moment in which success on the admission test can be accurately predicted using SPOC activity and in which variables are the best predictors in the developed predictive models;

O2.

Analyze to what extent the best predictors of success in the admission test generalize when developing predictive models in other courses;

O3.

Analyze to what extent predictive models can be transferred to other courses with the same cohort, to the same courses but different cohorts, and to both different courses and cohorts;

O4.

Discuss which conditions have to be met to achieve generalizability of the predictive models.

This paper is an extension of the paper “Predicting admission test success using SPOC interactions” [12], which was published in the Companion Proceedings of the Learning Analytics and Knowledge Conference 2019. In that paper, only one SPOC was considered for the analysis. As a result, the conclusions about the best predictors and the best moment to predict were limited to one SPOC, without an evaluation of the generalizability. In this paper, data about three more SPOCs are used, and it is analyzed, evaluated, and discussed whether these models can be transferred to other courses and cohorts. Moreover, the discussion of generalizability is also improved based on the data, and the conditions to achieve the generalizability are pointed out. The problem of generalizability is very important and significant since, once we create a model, this model could also be applied to other courses, thus increasing the target and the potential benefit. There is recent research tackling this issue. For example, a recent special issue in 2019 related to predictive learning included a total of five different articles that are focused on generalization, i.e., trying to transfer predictive models to other courses [13]. However, the contexts used to evaluate generalizability (e.g., educational stages, platform, and interactions) are different in our article, as is the approach. Our approach is focused on analyzing the generalizability in courses with different conditions (same/different courses, same/different cohorts, etc.), to compare what happens in each case, and to obtain global conclusions. The aim is to provide insight about the conditions needed to achieve generalizability (through different scenarios), which have not been covered before.

The structure of the paper is as follows. Section 2 presents a background of research on prediction and particularly on the generalizability and sustainability of the predictive models. Section 3 details the context and the methodology used in the study. Results of the analysis are provided in Section 4, while the discussion of them in terms of generalizability is detailed and justified in Section 5. Finally, the main conclusions are pointed out in Section 6.

2. Related Work

This section first provides a general background of prediction in education. Next, articles that specifically address and/or consider the generalizability of predictive models are discussed to justify the main contributions of the article.

2.1. Prediction in Education

In literature, there is an increasing interest in developing predictive models in education. These models can be useful to anticipate learners’ behaviors and/or outcomes so as to improve both engagement and performance. In order to develop those models, one of the important aspects is the variables used to predict, i.e., prediction features. Research has currently focused on the use of variables related to learners’ activity; interactions with videos, exercises, and the forum; and demographic variables. However, the latter usually achieve worse predictive power than the variables obtained from the tracking logs [14]. Among the variables obtained from the logs, for example, Ruipérez-Valiente et al. [15] predicted certificate earners by using variables related to activity (e.g., number of days the student accessed), interactions with videos (e.g., total time invested in videos), and interactions with exercises (e.g., grade in the assignments). They found that the grade in the assignments was the best predictor. Apart from those variables, Moreno-Marcos et al. [16] indicated that there can be many possible prediction features and that new ones could be introduced (e.g., self-regulated learning variables, as used by Maldonado-Mahauad et al. [17] to forecast success). Nevertheless, it is important to note that not all variables are always available. Alamri et al. [18] experienced this issue when some courses did not have quizzes every week, so they could not gather information about how students performed in the quizzes. However, they achieved good accuracies with just the time spent in the platform and the number of accesses.

Another important aspect when developing the models is the variable to predict, i.e., prediction outcome. Some of the most typical cases are related to predicting dropout (e.g., References [19,20]) and student success (e.g., References [21,22,23,24]). For the first case, Aguiar et al. [19] predicted dropouts in engineering students and found that variables related to performance, such as the Cumulative Grade Point Average (CPGA), were not enough to predict and that variables related to activity increased the predictive power. Regarding student success, which will be the focus of this paper, Polyzou and Karypis [21], for example, considered several classifications to identify undergraduate students with poor performance at the University of Minnesota (i.e., failing students, students achieving grades considerably lower than their Grade Point Average, etc.). A particular case of student success is the prediction of test scores. For example, Okubo et al. [22] used a Recurrent Neural Network (RNN) to predict the grade (between A–F) in a university course about information science and compared the predictive power during the 15 weeks of the course. Moreover, Ashenafi, Riccardi, and Ronchetti [23] predicted exam scores in two programming courses based on the results of the tasks carried out throughout the course.

While it has been shown that there can be many possible prediction features and outcomes, the context where predictions are carried out is also important. Many researchers have analyzed prediction in MOOCs, which have a similar format to SPOCs, although their contexts and learner characteristics are different. SPOCs offer a similar structure of videos, exercises, etc. in a digital platform, and the content can be even the same as used in a MOOC (some MOOCs can also be offered for university students as a SPOC). However, SPOCs are intended for closed courses, and the fact that students are part of a closed group, which usually have face-to-face lessons, allows for their combination methodologies such as blended learning or flipped classroom. Particularly in MOOCs, a literature review [16] showed that dropout is the most used outcome variable (e.g., Reference [25]), followed by final or assignment scores (e.g., Reference [26]) and certificate earners (e.g., Reference [27]). The high interest of dropout prediction can be due to the high attrition rates that are typical for MOOCs [28]. As an example, Xing and Du [29] predicted dropouts in a project management MOOC. Their work showed strong predictive power from week 1, and it also highlighted the importance of providing intervention personalization using drop out probabilities to make impact on learners.

Despite the high number of contributions in MOOCs, fewer contributions focus on SPOCs. Yu [30] used combined linear regression and deep neural network (DNN) to predict the final score of a computer science course. Moreover, Ruipérez-Valiente et al. [31] predicted learning gains in a preparatory course for freshmen students. This article presents a similar kind of study, although the variables related to learners’ interactions and context (e.g., course duration and objective, pedagogy, etc.) are different. Finally, regarding state exams, Feng, Heffernan, and Koedinger [32] developed a regression model to forecast grades in the exam based on interactions with an Intelligent Tutoring System (ITS). More recently, Fancsali et al. [33] also predicted a math state exam from logs of their ITS (MATHia), such as solving time, knowledge components (KC) mastered, etc.

This paper presents a study that analyzes how admission test success can be predicted from learners’ interactions in a SPOC and which variables affect the prediction. One of the differences with previous research is the analysis of the best moment to predict in order to analyze at which moment in the course it is possible to anticipate students’ success. Moreover, this paper includes new variables (e.g., variables related to the run of consecutive actions, pauses in videos, and whether a student asks for the answer) and particularly the analysis of which variables have a higher effect on the predictive models (related to objective O1). In addition, the context of the SPOCs is different (e.g., sequence of activities, pedagogy, purpose of the SPOCs, etc.) from other contributions in the literature, which will be useful to get insight on the study of prediction. Nevertheless, the main contributions of this paper are related to the analysis of generalizability, which are justified in Section 2.2.

2.2. Generalizability and Sustainability of Predictions

Many researchers have developed predictive models in many different contexts, as presented in Section 2.1. The intention is that these models can be widely used or, at least, that they can be used in new courses in real time, as models are usually developed using past data. However, an important issue is how to ensure that models can be transferred to new courses with a high degree of reliability [10]. One of the problems to make models transferrable and generalizable is that the context can be different across courses, which can cause a model to not be applicable to another course. Ocumpaugh, Baker, and Gowda [34] already experienced this problem when they developed predictive models to detect affective states with different populations and found that detectors trained on one population could not generalize to other populations. Moreover, Olivé et al. [35] developed predictive models with neural network, and although they achieved good accuracy in their models, they concluded that results can vary depending on how institutions and instructors use the Learning Management System (LMS). Merceron [36] also recognized this issue and pointed out that models should be checked regularly to evaluate their validity, which can slow down the adoption of learning analytics.

While this problem can suppose an important challenge in the development of predictive models, very few studies have addressed how it is possible to transfer models to other courses. Some contributions have mentioned the sample size as a factor for the generalizability (e.g., Reference [37]) and/or have acknowledged the generalizability as a limitation of the paper (e.g., Reference [38]), but they do not analyze this issue in detail. Among those articles that have specifically analyzed this issue, Boyer and Veeramachaneni [39] evaluated different methods to transfer models and found that models performed worse when transferred. Particularly, they found a drop of at least 0.1 in Area Under the Curve (AUC) when transferring from a previous edition of the MOOC. He et al. [40], however, found that predictive models trained on a first edition performed well on a second edition of a MOOC. In addition, Gitinabard et al. [41] analyzed the generalizability in four courses and found accurate results when transferring models, although they were better when the course was the same but in another offering. Furthermore, Hung et al. [42] proposed three models to predict successful students and at-risk students and a third model to optimize the thresholds of the previous models. They used K–12 and high-school contexts and found important differences in the context as well as the best predictors.

Kidzinsk et al. [43] also analyzed how to generalize models in other instances of the same course and other courses and concluded that there is a trade-off between specificity and generalizability. They also indicated that, in order to achieve high performance in a small variety of courses, it was best to use variables that depend on the context but that, at the same time, the use of these variables can affect generalizability. Therefore, in order to achieve generalizability, the predictive power should be compromised with course independent variables. In order to achieve generalizability across many courses, Kizilzec and Halawa [44] trained predictive models with data from 20 MOOCs: they also mentioned that a large number of courses could improve the transferability. This resulted in a high predictive power (AUC over 0.92). While this positive result suggests that it is possible to make models generalizable, other studies (as seen previously) show the opposite (e.g., References [34,39]). In order to make predictions sustainable, some researchers (e.g., Reference [45]) have proposed in situ models, i.e., models that use the available data in an ongoing course (e.g., using data from the first week in week 2), so that there are no differences in the course context. For example, Whitehill et al. [46] concluded that post hoc models (those using past data of only one course) can overestimate accuracy whereas in situ models could achieve high performance. However, a limitation of those models is that they cannot be used when the dependent variable is only available at the end of the course, such as the grade of an admission test, which will be analyzed in this paper. They can be used, for example, to predict engagement [45] as this can be measured each week.

Taking this into account, this paper will focus on transferring models to other courses and will analyze the generalizability of the findings. Particularly, this article will contribute with an analysis of the best predictors in different courses with the same target audience to check whether they differ or generalize (related to objective O2). This is also important because many articles just consider one course [16], and although some articles, as shown before, have focused on transferring models to other courses, it is also relevant to analyze the generalizability of the predictors. A similar work in this line was made by Hung et al. [42], who analyzed this issue in several educational stages, although this article will analyze different contexts within the same stage.

Moreover, this paper innovates with an analysis of how models can be transferred to other courses in different contexts (different cohort, different course, etc.) to delve into the generalizability issue (related to objective O3). Previous contributions, such as the article by Kidzinsk et al. [43], only focused on a single context (e.g., transferring the model to another edition of the same course) or developed models joining data from several MOOCs [44]. This work, however, analyzes generalizability with different contexts (same/different cohort, same/different course, etc.). One of the most similar works is the article by Gitinabard et al. [41]. They had two courses with two offerings each, so they could evaluate transferability in another edition and in another course. They could not, however, analyze the differences of the cohorts (i.e., the effect of having another course with the same students). Their data were also very specific and was mainly about social information and activity on sessions, while this work focuses on edX data (particularly Edge edX data), which allows for the gathering of more interactions, and can be more easily extended to other courses given the popularity of the Open edX platform. Another difference, which is also an innovation of this work, is the discussion about the conditions to achieve generalizability of the models and what can be done to make the use of predictive models sustainable in the long term (related to objective O4). While previous articles have provided some results about generalizability, there is still a need to discuss when models may be generalized (which is why the analysis of different contexts is also relevant) in order to design future interventions that make impact learners. Our paper contributes to this discussion.

3. Materials and Methods

3.1. Context and Data Collection for the Initial Course of Chemistry

The study was carried out using data from SPOCs developed in Edge edX as a joint project of the Faculty of Science and Faculty of Medicine at KU Leuven. These SPOCs were part of a blended learning support program to prepare for the medicine and dentistry admission test in Flanders. This entrance exam consists of several tests, including physics, chemistry, mathematics, and biology (they comprise the sciences part and communication/information skills part), and students need to pass them in order to be admitted in the university programs of medicine or dentistry. Therefore, the target users were students in the last year of secondary school who wanted to enter medicine or dentistry in any university in Flanders and who paid a registration fee for the blended learning program. In the SPOCs, online modules were released gradually every fortnight (from September to May) and alternated with face-to-face interactive sessions that used a flipped classroom approach with the intention to stimulate SPOC learners to spread their learning activities over the year. Nevertheless, in practice, many students enrolled late and they studied at their own pace. Attendance to those face-to-face sessions was not mandatory, since one of the goals was to allow time- and place-independent study, which implied flexibility of the learning process.

The first analysis focused on the chemistry SPOC. This primary SPOC is about chemistry. It was run in the academic year 2016/2017 and consists of 11 modules including 66 videos and 121 exercises, which cover the required contents for the chemistry component of the medicine and dentistry admission test in Flanders. For this SPOC, three interactive face-to-face sessions were organized during which additional exercises were made. A total of 1062 students accessed the online course, although only 680 completed at least one exercise and only 750 had interactions with videos.

For the analysis of data, two main sources were used. The first one includes the tracking logs from Edge edX [47]. Particularly, the following events have been considered: (1) problem_check, (2) problem_show, (3) play_video, (4) pause_video, (5) seek_video, and (6) stop_video. The second source consists of the information collected by means of a questionnaire sent to all SPOC participants after the course and contains the self-reported results of 133 students on the science part of the admission test. The limited number of students completing the survey is a clear limitation of the study. All learners who accessed the platform at least once (regardless of whether they have attempted exercises and watched videos) and completed the survey are initially included in the study. This means that, when developing models at the beginning of the course, fewer students are considered as some students have not enrolled yet or have not accessed the platform yet. Nevertheless, the main constraint is the availability of the results of the admission test and, because of that, all students are included provided they have accessed the platform and their results of the test are available.

After the initial analysis, which can be found in a previous contribution [12], it was found that there were many differences between the students from educational tracks with sciences and math (traditional students, TR) and those who do not have this background (nontraditional students, NTR). When conducting Mann–Whitney tests between traditional and nontraditional students who passed and failed, statistically significant differences were found in most of the variables. In addition, NTR were more active as they lacked the background knowledge, and in several cases, NTR who failed worked harder than TR who passed. As the behavior and activity was very different between TR and NTR, they will be separated for the predictive models to avoid bias. Therefore, students in the same group should cover about the same contents in high school, which reduces background diversity. Due to the too low number of NTR to develop models with representative samples with the current data, models will only focus on TR. Nevertheless, it will be interesting to develop models for NTR students as more students will appear in future SPOC editions. To sum up, the sample selection criteria will consider all traditional learners who had at least one access to the platform and who completed the survey (n = 114 in the chemistry SPOC in 2016/2017).

3.2. Variables and Techniques

In order to carry out the analysis, low-level variables obtained from the two abovementioned sources of data had to be processed. With regard to the tracking logs, a first filtering was carried out to select information about the main events. This initial filtering allowed for the retrieval of the following information of the aforementioned events: (1) user id; (2) event type; (3) agent (device used for the interactions); (4) time; (5) session id; (6) element id (id of the course component the student is interacting); (7) grade (not-normalized); (8) maximum grade; (9) id of the attempt of the exercise; (10) old time (for video interactions, it represents the initial point of interaction, e.g., when a user plays a video, it indicates the point from which the video is reproduced); (11) new time (for video interaction, it represents the final point of the interaction); and (12) YouTube id, which indicates the id of the video in YouTube.

With this information of the events, high-level variables are derived to be used in the prediction models after processing the data using R and libraries such as dplyr (https://www.rdocumentation.org/packages/dplyr/versions/0.7.8). These high-level variables are similar to those used in previous contributions (e.g., Reference [4]), and their intent was to gather information about the main kind of features (according to Reference [16]): accesses to the platform, videos, and exercises. In this studio, forum variables are not considered because of the very low level of forum interactions. Following these categories of variables,

Table 1. Features used in the study.

ID	Variable	Description
Variables related to accesses to the platform
1	streak_acc	Longest consecutive run of accesses to the platform
2	ndays	Number of days the student has access to the platform
3	avg_con	Average number of consecutive days that the student accesses the platform
4	per_pc	Percentage of accesses from a PC (not from a mobile, tablet, etc.)
5	per_wk	Percentage of accesses during weekend
6	per_night	Percentage of accesses during evening/night
Variables related to interactions with videos
7	per_vtotal	Viewed percentage of total video time
8	per_compl	Percentage of completed videos
9	per_open	Percentage of opened videos
10	avg_rep	Average number of repetitions per video
11	avg_pause	Average number of pauses per video
Variables related to interactions with exercises
12	per_attempt	Percentage of attempted exercises over the total
13	avg_grade	Average grade of formative exercises (only using the first attempts)
14	avg_attempt	Average number of attempts in the exercises attempted
15	per_correct	Percent of correctness using all attempts (average grade). This variable matches with the percentage of correct exercises over attempted when exercises are binary.
16	CFA	Number of 100% correct exercises in the first attempt
17	streak_ex	Longest consecutive run of correct exercises
18	nshow	Number of times the user asks for the solution of an exercise (without submitting an answer)

shows the list of features included in the analysis. The dependent variable is the binary result of passing/failing the test.

Predictive models are created using the library caret (http://topepo.github.io/caret/index.html) of R, and four of the most common algorithms are considered: Random Forest (RF), Generalized Linear Model (GLM), Support Vector Machines (SVM), and Decision Trees (DT). With these models, results are obtained using 10-fold cross validation and 10 repetitions. AUC is used to evaluate the quality of the prediction as this metric is widely used, is generally appropriate for student behavior classification problems [48], and is avoids some problems that other metrics face (e.g., accuracy) in imbalanced datasets [49].

3.3. Courses and Experiments for the Generalization

In order to evaluate the generalizability of the predictive models, data from three other SPOCs apart from the chemistry SPOC mentioned in Section 3.1 are used. The three other SPOCs (apart from the chemistry SPOC) are a SPOC on physics in the academic year 2016/2017 and both SPOCs on chemistry and physics in the academic year 2017/2018. A summary of the number of students who participated in these SPOCs can be found in

Table 2. Summary of the number of students who participated in the Small Private Online Courses (SPOCs).

Course	Year	No. Students	Students Who Watched at Least 1 Video	Students Who Attempted at Least 1 Exercise
Chemistry	2016/2017	1062	750	680
Physics			730	606
Chemistry	2017/2018	1131	936	834
Physics			856	767

. It is important to note that the students who took the chemistry SPOC were the same as those who took the physics SPOC in the same academic year, since students got access to both SPOCs when they registered in the preparation program. Therefore, students who enrolled in the same academic year are in the same cohort, and when we refer to different cohorts, we always refer to different academic years. Moreover, note that Table 2 provides some statistics about the level of activity of the SPOCs, although in the analysis, all students are included provided they accessed the platform and they indicated their results of the admission test in the survey (regardless of whether they had interactions with videos and exercises).

The physics SPOC is more focused on conceptual understanding. The number of students who actually watched at least one video and attempted at least one exercise was very similar to the SPOC on chemistry. This SPOC will serve as a basis to analyze how the predictive model can be transferred to another SPOC where the topic is different but the cohort is the same (in both directions, i.e., from chemistry to physics, and vice versa) as well as the dependent variable (passing the admission exam).

The SPOCs on chemistry and physics of the academic year 2017/2018 had almost the same content as the SPOCs of the previous years, but there was a different timing of the supporting face-to-face sessions. In this year, more SPOCs participants registered early since more students were aware of the existence of the blended learning program and the online activity was also higher. For these SPOCs, the number of learners who watched at least a video and attempted at least one exercise was also higher than in 2016/2017, as well as the total enrollment. Nevertheless, the number of students who completed the survey was similar and 116 students are considered for this cohort (while 114 were considered in 2016/2017). In this academic year, nine face-to-face lessons were offered with an average registration of 351 attendants per session. One of the possible reasons for the increased activity is that the second session of the admission test in August was abolished, and as a result, students had only one attempt in July. Moreover, a numerus fixus was introduced this year and only a predefined number of best-scoring students who passed both the sciences and communication/information skills part of the exam were admitted.

In terms of generalizability, these courses will serve to analyze how the predictive models can be transferred from one cohort to another with and without changing the course. This means that a predictive model is generated using data from a SPOC in one cohort and used to predict the outcome for a different cohort and the same/different course (e.g., train with the chemistry SPOC 2016/2017 and predict with both chemistry and physics 2017/2018). Moreover, the transferability in the same cohort within those courses is challenged by building a model with combined data from different courses from the same cohort and then by transferring to another cohort. That is, we can generate a single model with both SPOCs of the same cohort and predict using data of the following cohort.

In summary, the following experiments will be carried out to analyze the generalizability of the models:

• Within the same cohort: It consists of building a model using data of one SPOC and of predicting using data of another SPOC taken by the same cohort.
• Within the same course but different cohort: It consists of training using data of one SPOC and of predicting using data of the same SPOC but in a different cohort.
• Using a different course and cohort: It consists of training using data of one SPOC and of predicting using data of another course in a different cohort.
• Using the combination of SPOCs in different cohorts: It consists of training a model with the interactions of the learners in both chemistry and physics SPOCs in the same cohort and of predicting using the interactions of both SPOC in a different cohort.

4. Results

This section is divided into three parts, which address the first three objectives (O1, O2, and O3) that were introduced in Section 1.

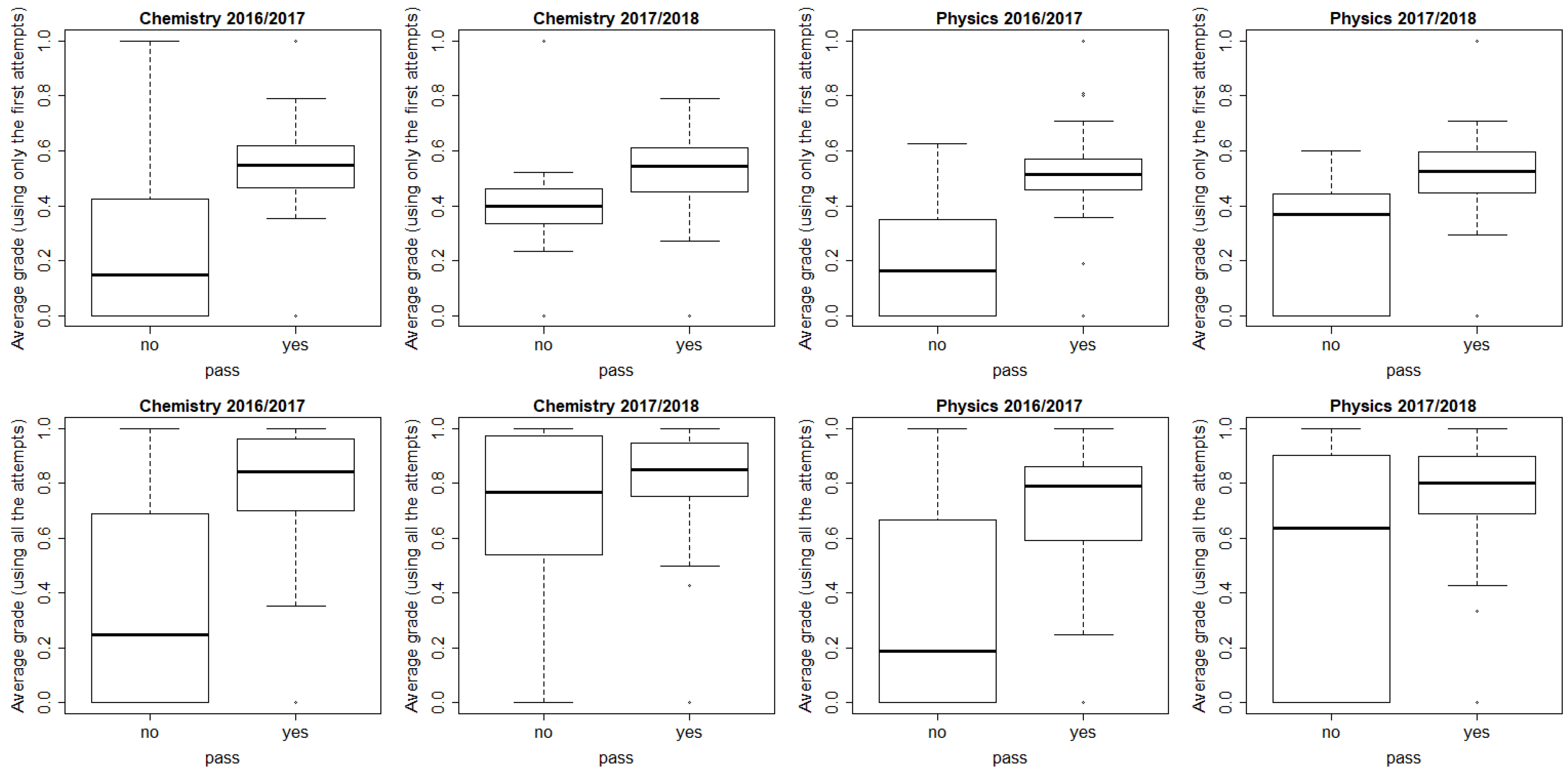
4.1. O1: Anticipation of Grades and Influence of Variables for the Initial Course of Chemistry

This section focuses on how success in the sciences part of the admission test can be predicted and, more importantly, how early it can do so. For that purpose, seven dates were selected (T_i) corresponding to crucial deadlines in the blended learning program of chemistry 2016/2017 (specific dates are in

Table 3. Results of the predictive models (in area under the curve (AUC)).

Period	T1	T2	T3	T4	T5	T6	T7
End date of the period	22/10	14/01	07/04	06/05	05/07	30/08
Students included	33	79	104	107	113	114	114
% activity included	2.2%	13.4%	31.0%	42.6%	77.6%	99.8%	100%
RF	0.46	0.45	0.70	0.78	0.84	0.87	0.87
GLM	0.59	0.71	0.72	0.73	0.74	0.77	0.77
SVM	0.55	0.51	0.72	0.73	0.84	0.85	0.85
DT	0.50	0.50	0.70	0.71	0.78	0.80	0.80

Note: Best model for each period is highlighted in bold. RF, Random Forest; GLM, Generalized Linear Model; SVM, Support Vector Machines; and DT, Decision Trees.

). T1, T2, and T4 correspond to the face-to-face interactive sessions that were organized to discuss problems on specific topics of the SPOC. At T3, traditional lectures were organized on topics that were not part of the chemistry SPOC but that were crucial for the admission exam. The first session of the admission test was organized at T5, and the second was organized at T6 (there were two sessions of the test to give a second chance to students who failed the exam). T7 includes all the interactions in the SPOC. With these dates, predictive models were from the beginning of the course (September 7th) to each T_i. Table 3 shows the results of the models.

Results show that, at the beginning of the course, the predictive power is poor. With an AUC threshold of 0.8 (as used by Moreno-Marcos et al. [16]), the predictive power of the model is only considered good from T5, the first session of the exam. A possible reason is the low activity at the beginning of the SPOC (57.4% of interactions occur after T4). If medium predictive performance (AUC = 0.7) is acceptable (there is always a trade-off between anticipation and predictive power), the prediction from T3 can be considered. In that case, at least 31% of interactions are included, which is much more than the 13.4% in T2 (where many learners had not enrolled yet), which is not enough to predict. The low level of activity may also indicate that the learners do not use the SPOC in the synchronous way it was planned. That may affect prediction as the activity is not uniform among students during the course. This invites reflection about the setup of the SPOC. Within the blended setup, it would be advisable to enhance the relevance of the early face-to-face sessions to ensure that more learners are engaged online from the early stages and attend all the face-to-face sessions. Nevertheless, with this setup and considering the trade-off between anticipation and predictive power, a good moment to predict may be T3 (with either GLM or SVM) or T4 (with RF). On the one hand, the predictive power is acceptable, and on the other hand, there would be 2–3 months before the admission test, granting students enough time to change their learning behavior.

In terms of the algorithms, the best model from T4 (included) onwards is RF, which achieves an AUC of 0.87 at the end of the course. While differences are not big in some periods, this algorithm seems to be more consistent in this context when there is enough data to predict. However, if the continuous grade was predicted and the Root Mean Square Error (RMSE) was used, SVM would be better (0.110 vs. 0.119), although both SVM and RF also perform better than the others.

After evaluating the predictive power of the models, the next challenge is to determine the best predictors, i.e., the variables that contribute most to the prediction. These best predictors identify the activities that are important for success. From the best model (RF in T7), the importance of the variables has been evaluated using the Mean Decrease Gini, which is often used to evaluate importance in RF [50].

The results in

Table 4. Variable importance (VI) and correlation of variables with the learning outcome (CR).

Variable	VI	CR	Variable	VI	CR
streak_acc	0.35	0.14	avg_rep	1.55	0.26
ndays	2.67	0.26	avg_pause	1.41	0.07
avg_con	0.64	0.04	per_attempt	1.33	0.30
per_pc	1.08	0.12	avg_grade	8.42	0.44
per_wk	1.13	0.14	avg_attempt	1.41	0.38
per_night	1.96	0.08	per_correct	2.14	0.47
per_vtotal	1.11	0.21	CFA	1.15	0.35
per_compl	0.62	0.19	streak_ex	2.12	0.40
per_open	2.10	0.24	nshow	2.34	0.21

indicate that the average grade of exercises using only the first attempt (avg_grade) is the best predictor. This is reasonable as correct answers at first attempt indicate successful processing of the learning material and, after several attempts, the correctness of the answer can be affected by chance. Next, the number of days the user accesses (ndays) and the number of times the user asks for the solution (nshow) stand out. The last variable represents that students who request the explanation of answers are more likely to pass. Regarding the variables about streaks, the results show that long consecutive runs of correct exercises (streak_ex) have a strong effect on success, unlike long consecutive runs of accesses to the platform (streak_acc). Finally, regarding video interactions, the variables that have more effect on success are the percentage of videos opened (per_open) and the number of times learners repeat the videos (avg_rep).

4.2. O2: Analysis of the Influence of Variables in Prediction for Different Courses

In order to validate whether the best predictors also have a strong predictive power in other courses, predictive models were also developed for the other three SPOCs using RF at the end of the course and the importance of variables was also evaluated using the same criteria. Moreover, predictive models were also developed with a combination of the interactions of both physics and chemistry SPOCs in the same cohort to discover which variables are better predictors. The results of these models and the best predictors are presented in

Table 5. Best predictors and predictive power of the models generated with different SPOCs ¹.

Course	AUC	Top 5 Predictors (in Order)
Chemistry 2016/2017	0.87	avg_grade (100), ndays (29), nshow (25), per_correct (22), streak_ex (22)
Physics 2016/2017	0.87	avg_grade (100), avg_pause (29), per_attempt (23), avg_rep (21), per_correct (18)
Physics + Chemistry 2016/2017	0.88	avg_grade (100, PH), avg_grade (97, CH), per_correct (33, CH), steak_ex (33, CH), per_open (31, CH)
Chemistry 2017/2018	0.77	avg_grade (100), avg_rep (53), avg_attemp (40), CFA (34), ndays (27)
Physics 2017/2018	0.86	avg_grade (100), per_correct (54), avg_attempt (35), per_compl (32), CFA (28)
Physics + Chemistry 2017/2018	0.84	avg_grade (100, PH), avg_grade (65, CH), avg_rep (41, CH), per_correct (39, PH), avg_attempt (38, CH)

¹ The importance of variables, scaled from 0 to 100, is mentioned between brackets. For the combined models, PH means physics and CH chemistry.

.

Results show that the best predictor is always the average grade using the first attempt (avg_grade), which implies that past performance is the best way to predict future performance. Moreover, grades with only the first attempts are confirmed to be more important. A possible reason is that activities can sometimes be correct when using trial and error strategies, which does not reflect learning [51]. Even in the combined models, the average grade in physics and the average grade in chemistry are the two best variables (with the average in physics being the better of the two). Nevertheless, the average grade using all attempts (per_correct) is also among the best predictors in all of the SPOCs, except chemistry 2017/2018, which achieves a weaker predictive power. In order to explain this fact, an analysis of the variables of each SPOC was carried out. Results showed that the average grade was similar in all the SPOCs, although the activity had increased considerably in 2017/2018. For example, the viewed percentage of videos increased 7% in chemistry and 11% in physics, while the percentage of attempted exercises increased 11% in chemistry and 10% in physics. Comparing those students who passed and failed in both cohorts, the results showed that those students who failed in 2017/2018 had a higher activity, particularly in chemistry, which can indeed make predictions more difficult (i.e., it is easier to predict when students who pass and fail have more differences in their indicators). Figure 1 shows the differences in the average grade (using only the first attempt and all the attempts) for those who passed and failed in all the SPOCs.

Figure 1 shows that the average grade using all the attempts can be a good variable for classifying students (as shown in the importance of variables). However, the difference is smaller in 2017/2018 because students who failed got a higher grade in the SPOC and the effect is stronger in chemistry. Correlations between average grade and passing the exam are also weaker in chemistry. While from all the variables, the highest correlation with passing the exam is observed for the avg_grade, these correlations are between 0.51–0.52 in all the SPOCs, except in chemistry, where the correlation is 0.40. A similar effect can be observed with the average grade of all attempts, which is less influential in 2018 and particularly in chemistry, which is in concordance with the importance of variables. The correlation between average grade of all attempts and passing the exam is also lower in 2018 (i.e., 0.26 in chemistry and 0.35 in physics) than in 2017 (i.e., 0.54 in chemistry and 0.42 in physics). The fact that the correlation is lower in chemistry 2018 may affect the predictive power, but a general conclusion is that variables related to correctness of exercises are the best predictors, although other variables related to videos and activity (as shown in Table 5) can also contribute to the model.

Finally, we explored a couple of variables that were available in 2017/2018 but not in 2016/2017 to see if they could enhance the predictive power. The first one is the percentage of registered face-to-face sessions, which serves to measure attendance, although only registration information is considered (for each session, students had to register, but no information is available about actual attendance). The second one is the enrollment date. However, none of these variables enhanced the models. A Mann–Whitney test between those students who passed and failed also showed no statistical difference between both groups in terms of attendance (p-value 0.10) or enrollment date (p-value 0.31). A possible reason for this result is that students who enroll later are not necessarily worse students. Furthermore, as the SPOCs are support materials for the exam and students can have their notes from their high school classes, they can get good grades even when enrolling late. A similar effect may happen with the attendance and particularly for those students who lived far from the place where sessions were held. Therefore, the best predictors can be found in the online interactions, which are common for all the students.

4.3. O3: Analysis of the Generalizability and Transferrability of the Models

In the previous section, separate models were developed for each SPOC. In this section, the generalizability will be analyzed by using these models (those developed in Section 4.2 using RF with all the available data) to predict outcomes in different courses to those used for training.

The first experiment consists of predicting using data from students in the same cohort but in different courses. Since for each cohort data are available from physics and chemistry SPOCs, it is possible to train with one course and to predict with the other. Results of this experiment can be found in row(a) in

Table 6. Results of the experiments to evaluate the generalizability of the predictive models.

Experiment	Course Used for Training	Course Used for Prediction	AUC
(a) Within the same cohort	Chemistry 16/17	Physics 16/17	0.88
	Physics 16/17	Chemistry 16/17	0.89
	Chemistry 17/18	Physics 17/18	0.87
	Physics 17/18	Chemistry 17/18	0.83
(b) Within the same course but different cohort	Chemistry 16/17	Chemistry 17/18	0.79
	Physics 16/17	Physics 17/18	0.79
(c) Using a different course and cohort	Chemistry 16/17	Physics 17/18	0.75
	Physics 16/17	Chemistry 17/18	0.63
(d) Using the combination of SPOCs in different cohorts	Physics + Chemistry 16/17	Physics + Chemistry 17/18	0.74

and they reflect a very good transferability as the predictive power is similar and even slightly better than the predictive power obtained when training and predicting with data from the same course. This means that the model can adapt to new data and can be perfectly transferred to another SPOC (with different topic) during the same year. A possible explanation is that, since the students are the same, their learning behavior is also similar in different courses. Another factor can be the fact that what it is predicted is not the result of the physics or chemistry exam separately but the result (pass/fail) of the admission test, which comprises the results of exams related to the different courses.

The second experiment is more common in the literature and consists of training the model with data of one edition of the course and of predicting with data from a different edition (e.g., in a future edition of the course). Particularly, data from one cohort will be used to train and data from the next cohort will be used to predict. This approach had already been explored in the literature (e.g., Reference [39]) because it is the common application of a post hoc prediction. By using trained models in future editions, learning can be affected based on the predictions calculated while the course is developing (e.g., on a daily-basis). Results of this analysis (see row (b) in Table 6) show that predictive power, both from transferring the physics and chemistry SPOC from 2016/2017 to 2017/2018, is 0.79, which is in the limit between fair and good. This entails that it is possible to use the predictive model in a future edition, although predictive power decreases. Thus, changing the cohort has a more negative effect on the predictive power compared to changing the course, as the predictive power did not decrease when transferring within courses in the same cohort. While there can be many factors that change from one course to another, this result suggests that changing the cohort has a more profound effect on the generalizability, although it is possible to use a trained model to predict with a future edition of a SPOC.

The third experiment consists of predicting using data from one course and cohort, by using training data from another course in a different cohort, so both the course and students are different. While in most cases, one will probably use data from the same course to predict learning behavior in a future edition, this experiment is interesting to completely analyze generalizability. Also, it can also be practical because you might have different courses in the next years and/or you might only have one trained model (with a specific course) to predict, so you may need to predict using a model trained with a different course and cohort. Results in this case (see row(c) in Table 6) show that the predictive power is worse than in the previous experiments. When transferring chemistry 16/17 to physics 17/18, the predictive power is fair (0.75), but when transferring physics 16/17 to chemistry 17/18, the predictive power is poor (0.63). This entails that transferring models from different courses and students can be more difficult because there are many factors that change, limiting the generalizability of the model.

The fourth and last experiment consists of combining the variables of the two different SPOCs of the same cohort. In the literature, models are typically developed using data from one course. However, as the SPOCs are taken by the same students, it is possible to develop models with the combination of indicators of two SPOCs. While the predictive power did not differ as much compared to the predictive power of the best course alone when training and predicting using the same combination of SPOCs in a post hoc approach (see Table 5), we want to analyze the predictive power of the combination in the following cohort. Results (see row(d) in Table 6) show that the AUC is 0.74 when transferring the combination from 16/17 to 17/18. This is similar to the best AUC obtained in the third experiment but worse than the AUC obtained when using data from only one course. This entails that the combination is not better and that it is preferable to use models trained with one course for transferability, although this approach could be sometimes useful (and the predictive power is fair) if there is little information about each single course in case data are limited.

To summarize, results show that it is possible to transfer the predictive models into other courses, but the predictive power depends on how the context changes. The best results were obtained for the same cohort in different courses, whereas results were acceptable when the course was the same but different cohorts were used.

5. Discussion about the Generalizability

Section 4.3 shows an analysis of under which contexts predictive models can be transferred to other courses. Although our study was limited to four courses, our results show that the course context is very important for transferring models, which was also suggested by Gašević et al. [52]. In particular, from an exploratory analysis, we believe that certain conditions in the context need to be met to achieve the generalizability. This section presents and discusses these conditions in order to meet objective O4 of the article. Particularly, from our analysis, these conditions are as follows:

• Student characteristics should be as similar as possible: When one model is generated with one course and used in another course with the same students, the predictive power was very high. This may imply that, if students’ behaviors are similar, it is possible to transfer the models. While it is not always possible to use the model with the same cohort, results show that it would be possible because of the high predictive power. However, when changing the cohorts (students), the predictive power is worse but can be still acceptable.
• Courses should be as similar as possible: Results showed that the predictive power dropped considerably when predicting using a model with different students in a different course. This fact can hinder the generalizability, although the predictive power may be acceptable if the course is similar. If the course is the same but in a different edition, it may be possible to achieve a reasonable performance. Therefore, it would be better to generate a model from the same course in another edition (if available) than to use a trained model from another course.

Apart from these conditions, which could be evaluated when using different SPOCs, there are other conditions that were shared by the four SPOCs, which could contribute to achieving generalizability because they were very related to the course context. These conditions are as follows:

• The methodology: The four SPOCs were taught using blended learning, and they were organized in a similar way. All the SPOCs were run in the same period (from September to the dates of the admission test) each year, and face-to-face sessions were organized following a similar approach for all the SPOCs. With regard to the face-to-face sessions, a positive result in the analyzed SPOCs was that the variables obtained from them were less strong predictors. While this may change in another context and should not be neglected, it can be good if the offline part of the blended program is less important for the generalizability, as it is often harder to measure.
• Delivery mode: All SPOCs were synchronous (instructor paced), which means that materials were released every fortnight. Changes in the delivery mode may affect the way students behave (e.g., students may face more problems in self-regulation in self-paced settings [17]) and thus the generalizability.
• Perceived importance of the course: In this case, all the SPOCs were supporting materials for the admission test, although they were perceived as an important tool for the exam preparation. Even if two courses are the same, there can be differences if the perceived importance of the SPOC is different. For example, if one instructor does not strengthen the importance of the SPOC and only considers it as extra material, results may differ from a similar SPOC in which the instructor encourages its use frequently.
• Course duration: All the SPOCs were launched at the beginning of the academic year, and they were intended to be used until the end of the academic year when the admission test was held.
• Relationship between the dependent variable among courses: The dependent variable in this case is the overall pass/fail result of the sciences part of the exam, which includes both chemistry and physics. That may contribute to the generalizability across courses which are part of the final result.

When all these conditions are met, this will increase the options to make the models generalizable. However, if only some of the conditions are met, the predictive power may be good enough to be used. For example, the experiment showed that the predictive power was acceptable when transferring the model to the same course in a future edition, and therefore, it could be used to obtain information that could be useful in improving the learning processes in the following edition. This finding matches with other contributions where models were found to be transferrable (e.g., References [40,44]), although the precision can vary depending on the context. Nevertheless, this finding is positive because, if predictive models could not be used outside the course that is used to train the models, which is often finished, the use of prediction would not be sustainable. Because of that, models should be developed to be used in similar contexts.

This fact also means that it is not possible to find a one-size-fits-all model, trained with a single course, that can be used for all contexts, as generalizability cannot always be achieved (e.g., References [34,39]). Instead, existing models need to be taken and adapted to the specific context. This means that part of the process to make predictive models sustainable should rely on the reuse and adaptation of models. Whenever the context is similar enough, the same model could be used. Otherwise, a new model should be generated for this context. For example, in this case, we should develop a model for physics and another for chemistry. While this task may seem tedious, in fact, it is not if the models are designed to be adapted easily. For example, when the courses are held in the same platform (Edge edX in this case), it is possible to use the same or similar algorithms to collect the indicators and to train the model, so the only change for the model generation would be the input raw data. Nevertheless, if there is an analysis of the results for the new course, the methodology and pedagogical background should be considered. In addition, if the course has some special features, perhaps some new indicators could be included as part of the adaptation. Following the abovementioned approach, each model would be specific for each context while the generation of the models will be easy, and models from a similar context would be used in future editions. This way, the use of predictive models can produce effects on future students and can be sustainable over time.

Related to this, there is also a question about the validity of the research results. If models are not transferrable, the results may be different. However, in this case, results show that the trend is similar with respect to the most important variables and that variables related to exercises are the best predictors. This was also shown in other contexts, such as in the article by Moreno-Marcos et al. [4], which entails that research results can be applicable in other contexts, although they may change if they are very different. Because of that, it is important to analyze different contexts and to compare the results to obtain global conclusions about how students learn and about what behaviors have relevant effects on their success, although current results can actually provide insight in effective learning behaviors.

To summarize, there are certain conditions to achieve generalizability of the models. If some of these conditions are met, it is possible to achieve models with enough predictive power to be used; for example, this may happen with future editions of the same course. However, in order to address the limitation of transferability, it is encouraged to reuse and adapt the model to new courses. This way, several models will be developed easily that can be adapted and they can be used for future students in the same course, making the predictions sustainable.

6. Conclusions

In this paper, an analysis of SPOC data, including predictions for success on a high-stake admission test, has been done. One interesting finding was that predictive models only behaved reasonably well in the last three months, which were also the months with more than half of the activity. Among the variables, the average grade using first attempts stands out as the best predictor, and this result is also validated with three other SPOCs. Moreover, average grade using all attempts is also a very good predictor, which entails that the best indicators to predict future performance are those related to performance in the past. This finding matches with the contribution by Ruipérez-Valiente et al. [15], who found that progress with problems was the strongest predictor. Nevertheless, other variables related to interactions with videos and the overall activity also showed positive relationships with success. These findings contribute to the analysis of how early it is possible to predict (contribution related to O1), what are the best predictors, and how they generalize across courses (contribution related to O2).

With regard to generalizability, the analysis showed that course context is very important, which was also suggested in previous contributions (e.g., References [36,52]). Although it was possible to transfer the model in some cases, some conditions need to be met. The predictive power got worse when conditions were changed, which matches with findings by Boyer and Veeramachaneni [39]. Nevertheless, the predictive power can still sometimes be acceptable to be used. For example, the predictive power of the model trained with the same course in a previous edition was acceptable (as reported by Gitinabard et al. [41]), which is useful in ensuring sustainability of the models. Nevertheless, as discussed, it is important to reuse and adapt the models whenever possible, and therefore, the process of generation of the models should be generalizable as far as possible to guarantee the scalability of the models when models cannot be transferred. These findings contribute to the analysis of generalizability across different contexts (contribution related to O3) and to the discussion about how to achieve generalizability and sustainability in the long term (contribution related to O4).

Despite the abovementioned findings, there are some limitations that are worth mentioning. It is noteworthy that the dataset was limited due to lack of information about the admission test results (few students answered the survey). Moreover, that information was self-reported data and, although it appeared reliable, it could only partially be verified (62% of the cases). In addition, the generalizability was only evaluated with three other courses. While they served to analyze different cases because they comprised different academic years (cohorts) and courses, more courses should be analyzed to evaluate more conditions to achieve generalizability of the models.

As future work, it would be interesting to include data about more different courses (with different methodologies, thematic areas, etc.) and more cohorts to delve more deeply into the generalizability. The addition of data would also serve to develop models for nontraditional students and to analyze how they change. Moreover, it would be relevant to analyze the importance of variables across courses at different temporal points to see how they could vary over time. Furthermore, it would be interesting to design and evaluate some visualizations based on the prediction results to provide SPOC learners with useful interventions based on their interactions. Finally, it would be relevant to put the models into practice by reusing/adapting models or by transferring previous models to analyze the impact they can produce in the learning process, which is very important to guarantee the sustainability of learning analytics in the long term.