1. Introduction
Gold is an underlying asset in which volatility is an important factor for option pricing. The issue of gold return volatility has been empirically discussed. There have been many insightful investigations published previously that use various sorts of econometric models to study the gold return volatility and the asymmetric effect of positive and negative shocks [
1,
2,
3,
4,
5].
The core idea of sustainable investing has two elements. Firstly, it has value in helping investors to spot reputational risk threat and offset such a risk in advance. Secondly, it is an economic moat helping investors to identify what makes a company sustainable in the financial sense, leading to strong brands and healthy end-markets. If investors concern themselves with long-term future trends, the sustainable invest rating can help them to decide whether or not the investment target is worth the long-term investment and whether it will provide stable profits. Investors should definitely consider the target of sustainable investing, ethical investing, or socially responsible investing [
6,
7,
8].
Only in an efficient market would the price of gold momentarily adjust and completely reflect the new information. As such, no tendency of future increases and decreases is predicted [
3,
5]. Sustainable Enterprise Resource Planning (S-ERP) systems could be a robust multi-function platform providing real-time and integration services and finding the most up-to-the-minute information available on trading metrics throughout the trading day [
9,
10,
11,
12,
13]. Based on the principle of diversification, a multiple-asset portfolio has almost no unsystematic risk. Gold is known as the anti-complex asset. It could be the safe haven or hedge asset in times of an unstable economy or a highly adverse environment. During market fluctuation periods, it might be a good time to invest in the gold market [
2,
4,
14]. In this context, we conclude that gold is more sustainable than many other financial assets in an investment portfolio.
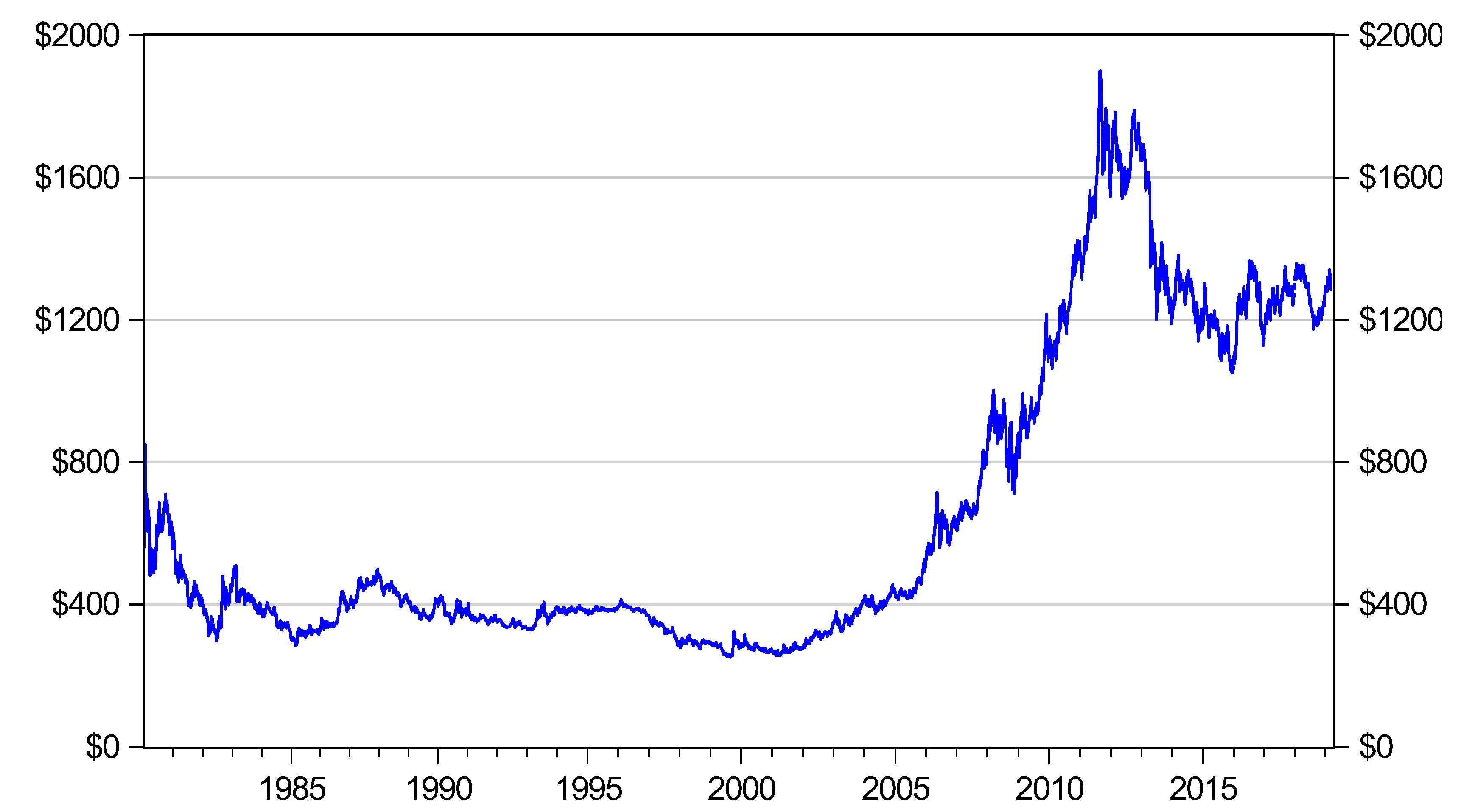
Figure 1 shows the evolution of the price of gold over a 40 year sample period.
ARCH-GARCH (autoregressive conditional heteroskedasticity - generalized autoregressive conditional heteroskedasticity) models are applied to account for empirical nonlinear time-series properties of gold return. Furthermore, the GJR (Glosten-Jagannathan-Runkle) -GARCH model has been widely applied to determine the asymmetric effects of positive or negative shocks to conditional volatility in financial research. The GJR-GARCH model uses the positive or negative previous residual term as a threshold to measure the asymmetric effect due to innovation shocks. The difference between the GARCH (p,q) and GJR-GARCH (p,q) models is the additional assumption that all leverage terms are equal to zero. However, using zero as a cut-off threshold in general does not guarantee an overall optimization fit in empirical estimation, according to the abovementioned studies [
1,
15,
16,
17].
The GARCH model can capture thick-tailed returns and volatility clustering. However, neither the ARCH model, which examines variance or volatility clustering, nor the GARCH model, which examines the dependence on the forecast variance of the previous period, can capture volatility asymmetry. To further account for the asymmetric and steepness asymmetric effects of the inter-period gold return’s change and volatility, the threshold autoregressive (TAR) and the momentum threshold autoregressive (MTAR or momentum TAR) econometric models could be jointly applied with the GARCH model [
18,
19,
20].
The TAR and MTAR econometric models have been well documented as tools for measuring the asymmetric and nonlinear phenomenon in time-series analyses. However, in most cases both models are estimated separately, resulting in unbiased but inefficient estimators. The TAR dummy variable could measure asymmetric effects due to past residual shocks to the system, while the MTAR dummy variable tries to capture residual difference effects for measuring the incremental momentum (nonlinearity) during a highly volatile period. This paper thus proposes a hybrid integrated mean equation so that both asymmetric and nonlinear properties can be measured simultaneously [
21,
22,
23].
Therefore, this paper proposes a hybrid momentum TAR/MTAR-GARCH (HMTAR-GARCH) model to explore a better functional fit in empirical estimation. A new programming algorithm is proposed for simulating two random thresholds for both TAR and MTAR components in the equations of mean and variance simultaneously. The paper also aims to investigate the gold return volatility in the following circumstances. First, the gold return volatility is greater during the financial tsunami period (i.e., extreme market conditions) than the non-financial tsunami period. Second, the effect on gold return volatility is greater whenever the lagged residual falls below its threshold during the financial tsunami period (TAR effect). Third, the effect on gold return volatility is greater whenever the first differencing of the lagged residual falls below its momentum threshold during the financial tsunami period (MTAR effect). Forth, the MTAR effect is even stronger than the TAR effect on gold return volatility.
The rest of the paper is organized as follows:
Section 2 introduces the hypotheses, data set, and methodology;
Section 3 provides the empirical results; and
Section 4 summarizes the discussion and concludes the paper.
3. Results
The sample in this study was the daily data from 3 January 2000 to 30 December 2016, and thus contains the low-volatility period as well as the high-volatility period [
2,
3,
4,
5]. In order to observe the variation of the gold return (RET) in different sorts of periods, the original time-series data set was divided into three periods (pre-financial tsunami, financial tsunami, and post-financial tsunami), as shown in
Table 1.
Table 2 reports a summary of RET descriptive statistics over each sample period. During the financial tsunami period, the RET, in contrast to other periods, obviously displays a larger dispersion, ranging from a high of 10.7883 to a low of −6.9149, with a mean of 0.0921. The mean value is positive and approaches zero over time. These statistics are similar to other financial markets’ performance, with a standard deviation larger than the mean.
Furthermore,
Table 3 reports a summary of statistics of the structural break test between the financial tsunami period and the non-financial tsunami period. The coefficient
(=0.0732) is significantly positive, while the t-statistic of Chow test are significant at less than the 5% implying the beta difference between financial tsunami and non-financial tsunami periods. The total gold return volatility effect would be 0.0338 (i.e.,
) during the financial tsunami period. This indicates the structural break exists during the financial tsunami periods [
24,
25].
The mean model extended from Equation (9) is as follows:
where
is the dummy of the financial tsunami period.
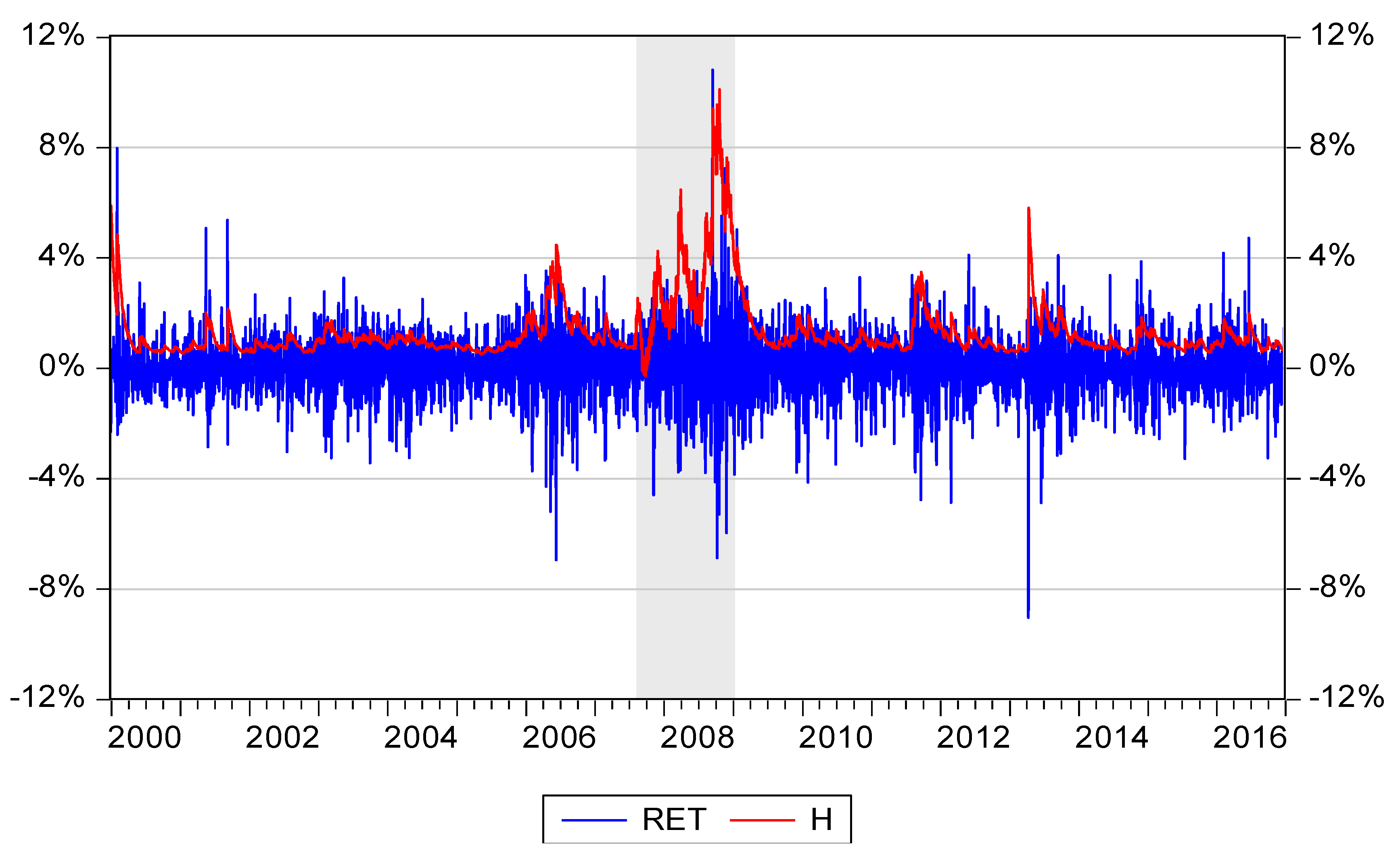
Figure 2 illustrates the daily gold return (RET) denominated in US
$ over a 17 year period.
Figure 3 shows the daily conditional volatility HMTAR-GARCH (1, 1) estimates of the gold return (H) denominated in US
$ over a 17 year period.
Figure 4 illustrates the gold return (RET) and the daily conditional volatility HMTAR-GARCH (1, 1) estimates of the gold return (H) denominated in US
$ over a 17 year period.
As many financial variables are not stationary or are not residual stationary of regression and may lead to spurious regression, the ADF, PP, KPSS, and KSS unit root tests were conducted for the level of gold prices (GP) and the RET [
26,
27,
28,
29,
30].
Table 4 shows the results of the ADF, PP, KPSS and KSS tests and concludes that GP is non-stationary.
Furthermore,
Table 5 shows the results of the ADF, PP, KPSS and KSS tests and concludes that RET is stationary.
The presence of ARCH (autoregressive conditional heteroscedasticity) effects in the residuals was also checked. The test statistic is highly significant, as shown in
Table 6, proving the existence of ARCH effects [
19,
21].
For comparison purposes, three models are proposed. Model 1 is the GARCH model without a threshold. Model 2 is GJR-GARCH (1,1), which is similar to the model with the TAR threshold () and the MTAR threshold () set to zero. Model 3 is the HMTAR-GARCH model, with random thresholds and .
Table 7 illustrates the results of our estimations between the gold return of current and previous trading days and demonstrates that the HMTAR-GARCH (1,1) model has the best minimum AIC, SBC, and maximum log-likelihood. In other words, Model 3 is better than Model 1 and Model 2.
Table 7 also confirms the notion that a hybrid random threshold model might be superior to a zero threshold model.
Table 7 also provides the residual diagnostic and the
p-values of the Ljung–Box test of autocorrelation in the standardized residuals with 5, 10, and 20 lags [
32]. For all series, the null hypothesis of no autocorrelation left cannot be rejected at the 5% level, indicating that the HMTAR-GARCH specifications are successful in modeling the serial correlation in the conditional mean and variance. In addition, the four hypotheses of the study were verified as follows.
First, in the HMTAR-GARCH model, the coefficient of ) is positive and highly significant, showing that the gold return volatility is greater during the financial tsunami period (i.e., extreme market conditions) than the stable or tranquil regime.
Second, the coefficient (=−0.4359) is significantly negative, revealing that the effect on gold return volatility would be greater whenever the lagged residual falls below its threshold (=−0.8261) during the financial tsunami period. The gold return volatility model exhibits the TAR effect during a highly volatile period.
Third, the coefficient (=−0.7068) is significantly negative, denoting that the effect on gold return volatility would be greater whenever the first differencing of lagged residual falls below its momentum threshold during the financial tsunami period. This might imply that unexpected negative market shocks would tend to increase the gold return volatility. The gold return volatility model exhibits the MTAR effect during a highly volatile period.
Forth, to test whether the MTAR effect is even stronger than TAR effect (), the Wald Chi-square statistics for alternative H4a: is 3.0197 (p-value = 0.0411); and for alternative H4b: is 5.3393 (p-value = 0.0104), demonstrating statistically significant results. This might suggest that the MTAR dummy variable has a substantially greater impact on the conditional variance during the financial tsunami period and the MTAR specification could capture residual difference effects for measuring the incremental momentum (nonlinearity) during a highly volatile period.
Finally, the total TAR volatility effect would be −0.3530 (i.e., ) and the total MTAR volatility effect would be −0.7148 (i.e., ) during the financial tsunami period. By comparing the total volatility effects of both TAR and MTAR, this might imply that unexpected negative first difference in market shocks would tend to increase the gold return volatility even stronger.
The HMTAR-GARCH model is superior to the GJR-GARCH model and could better capture the asymmetric and nonlinear natures of gold return volatility. The empirical findings might contribute to gold return volatility forecasting for accurate hedging and arbitrage decisions, especially during severe market fluctuation periods. Traders of derivatives can be categorized three types: hedgers, speculators, or arbitrageurs. Hedgers and speculators are either betting a gold price that will go up or betting a gold price that will go down. Arbitrage involves locking in a riskless profit by entering simultaneously transactions in two or more markets including spot and future gold markets. Therefore, gold dealers, traders, and manufacturers could make better hedging and investing decisions by adopting the HMTAR-GARCH model into the risk management module of S-ERP systems [
6,
7,
9,
10,
11,
12,
13,
20].
On the other hand, this study estimated the TAR threshold (
) and the MTAR threshold (
) directly with other parameters instead of searching for each value (not reported here). The coefficients of the
and
are large and outside of the reasonable boundary. The result of the estimates does not match the practice of the gold market. A single optimal threshold either in the TAR or MTAR model is identified using Chan’s method. Chan [
33] set the reasonable boundary and used the searching method to estimate
or
, constraining the feasible solutions over the possible range. Based on [
33], this study modified and designed a new grid search algorithm not only to estimate two random thresholds (
and
) but also to improve the problem of over-estimated residuals.
Additionally, this study obtained alternative data from Reuters.com, which has daily gold spot prices from 3 January 2000 to 30 December 2016, including a total of 4427 observations. The results for the robustness test, given in
Table 8, confirm the hypothesis above.
Table 8 also provides the residual diagnostic and the
p-values of the Ljung–Box test of autocorrelation in the standardized residuals with 5, 10, and 20 lags [
32]. For all series, the null hypothesis of no autocorrelation left cannot be rejected at the 5% level, indicating that the HMTAR-GARCH specifications are successful in modeling the serial correlation in the conditional mean and variance.
4. Discussion and Conclusions
The contribution of this paper is its combination of TAR, MTAR, and GARCH for gold return volatility forecasting. This was a novel attempt to construct a hybrid momentum TAR/MTAR-GARCH econometric model by studying the gold return prediction and examining two issues. One issue was to integrate TAR and MTAR dummy interaction terms in the mean and variance equations to avoid a econometric problem of model misspecification, and the other was to expand the traditional GJR-GARCH model by designing two random thresholds for the TAR and MTAR components in the variance equation so that random threshold values other than zero could be traced. The algorithm for simulating two random thresholds was proposed and tested.
By estimating asymmetric threshold parameters, the HMTAR-GARCH model has more explanatory power than the GJR-GARCH model. Four major hypothetical tests were verified. First, the gold return volatility was found to be greater during the financial tsunami period (i.e., extreme market conditions) than non-financial tsunami period. Second, it was confirmed that the effect on gold return volatility would be greater whenever the lagged residual falls below its threshold during the financial tsunami period. Third, it was confirmed that the effect on gold return volatility would be greater whenever the first differencing of lagged residual falls below its momentum threshold during the financial tsunami period. Finally, it was shown that the MTAR effect is even stronger than the TAR effect during the financial tsunami period.
Our findings suggest that whenever there is a downtrend in the market, traders could earn extra profits by simultaneously holding a long position in the underlying gold spot and a short position in the gold options, futures, Exchange Traded Funds (ETFs), or other derivatives. Taken together, the above results demonstrate that our new HMTAR-GARCH model is superior to the GJR-GARCH model and can better capture the asymmetric and nonlinear natures of gold return volatility. The empirical findings contribute to gold return volatility forecasting for accurate hedging and arbitrage decisions, especially during severe market fluctuation periods.
On the financial market, the HMTAR-GARCH model helps dealers and traders make better speculation and arbitrage trading decisions, concerning options and futures, ETFs, etc. In terms of the physical gold demand and supply, the HMTAR-GARCH model could enable customers and suppliers to establish better hedging decisions to gain non-operating income from the financial trades, such as through total global jewelry fabrication and consumption, retail investment, industrial fabrication, government official sector, and mine production and scrap. Gold dealers, traders, and manufacturers could make better hedging and investing decisions by adopting the HMTAR-GARCH model into the risk management module of S-ERP systems.