Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia
Abstract
1. Introduction
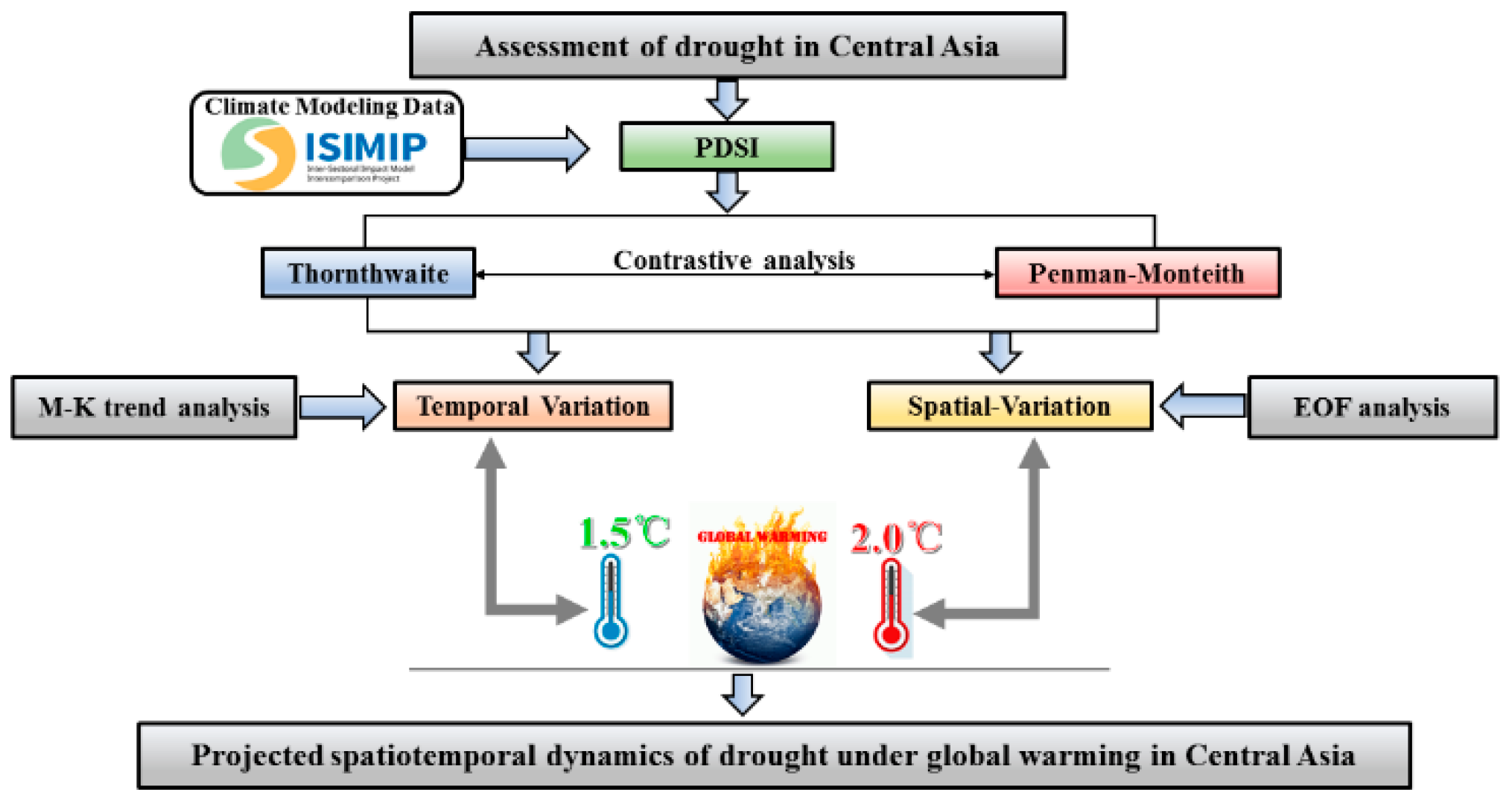
2. Materials and Methods
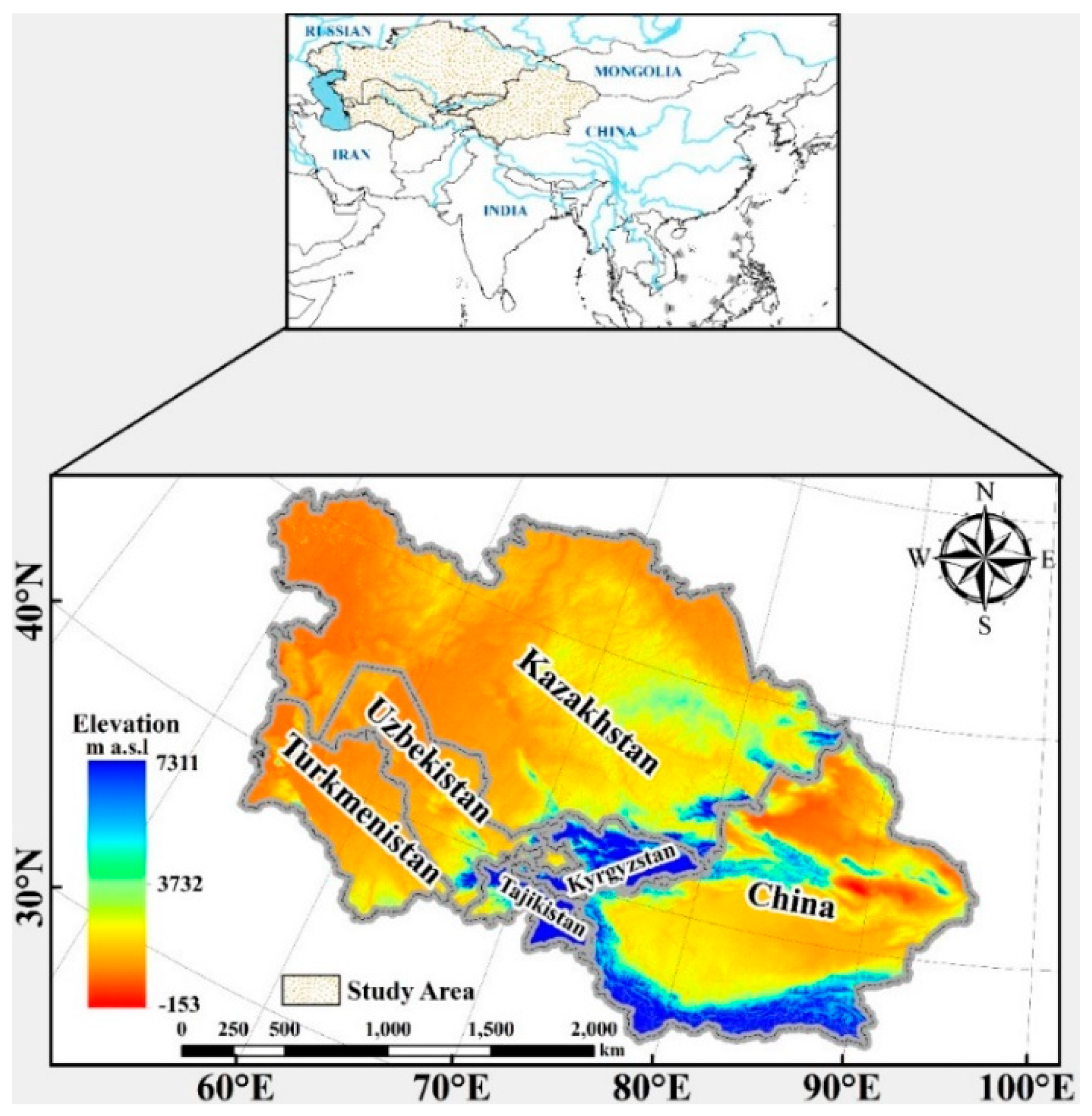
2.1. Study Area
2.2. Global Warming Scenarios of 1.5 °C and 2.0 °C
2.3. Climate Modeling Data
2.4. Drought Index Calculation
2.5. Statistical Analysis
3. Results
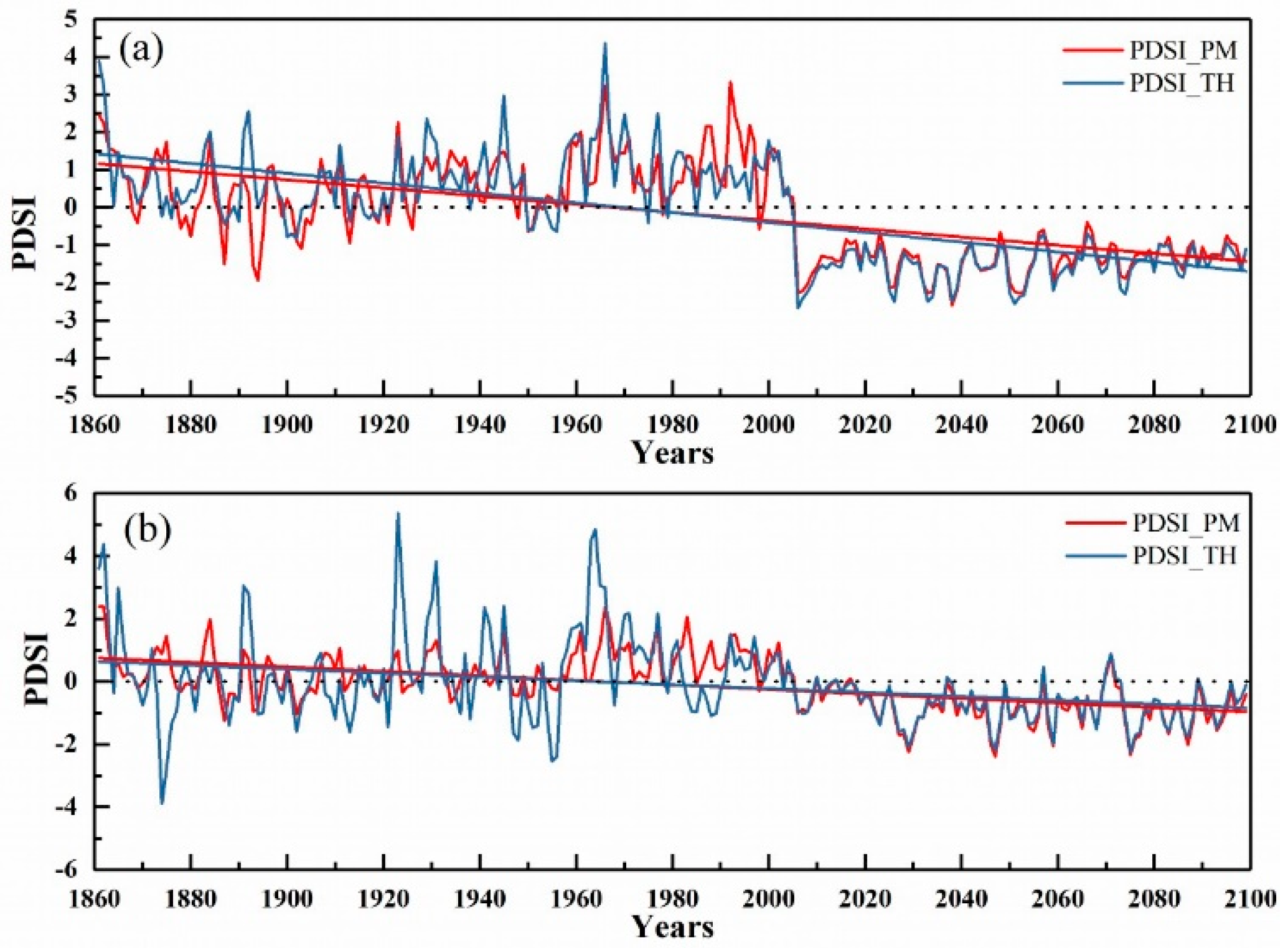
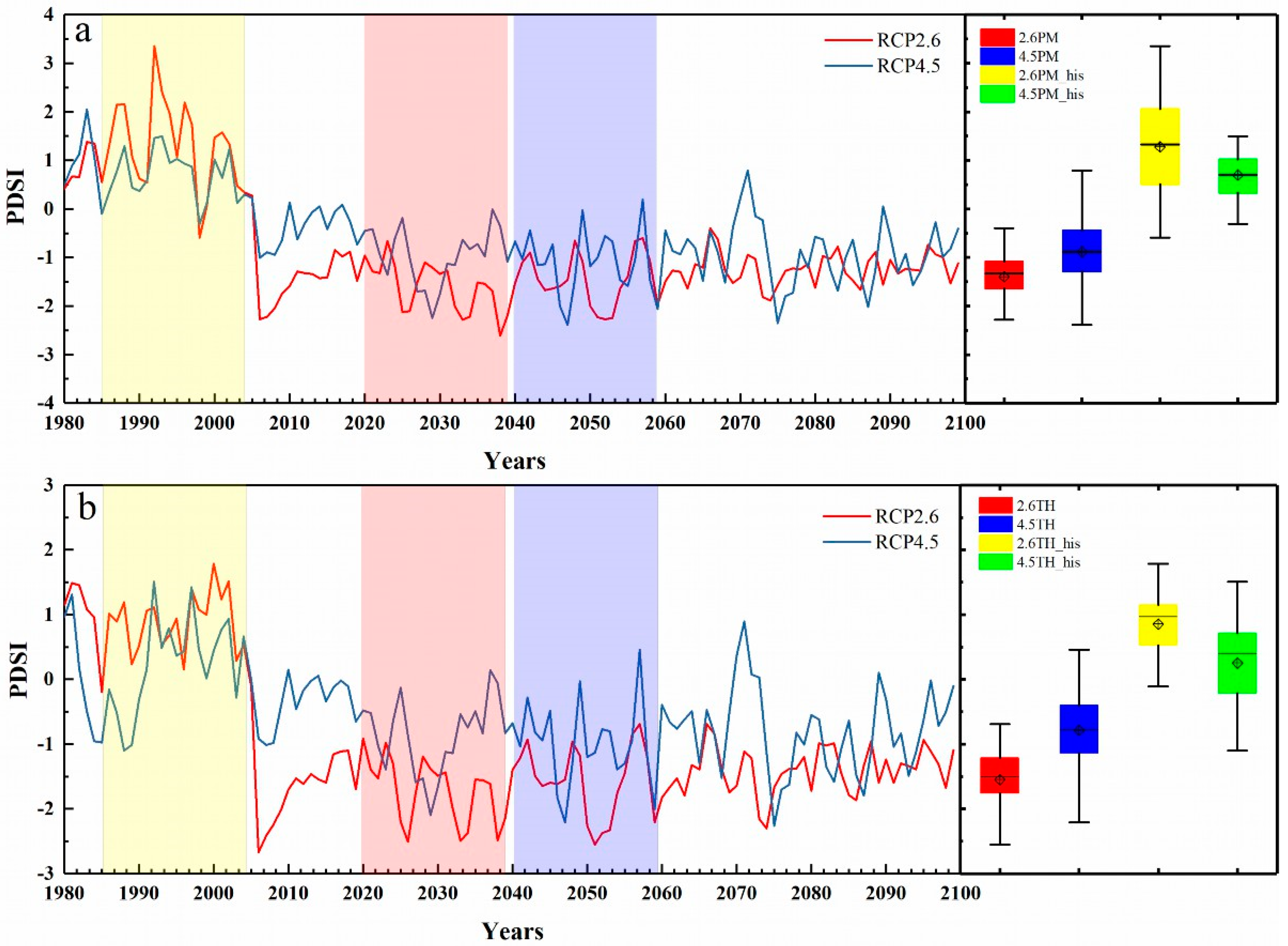
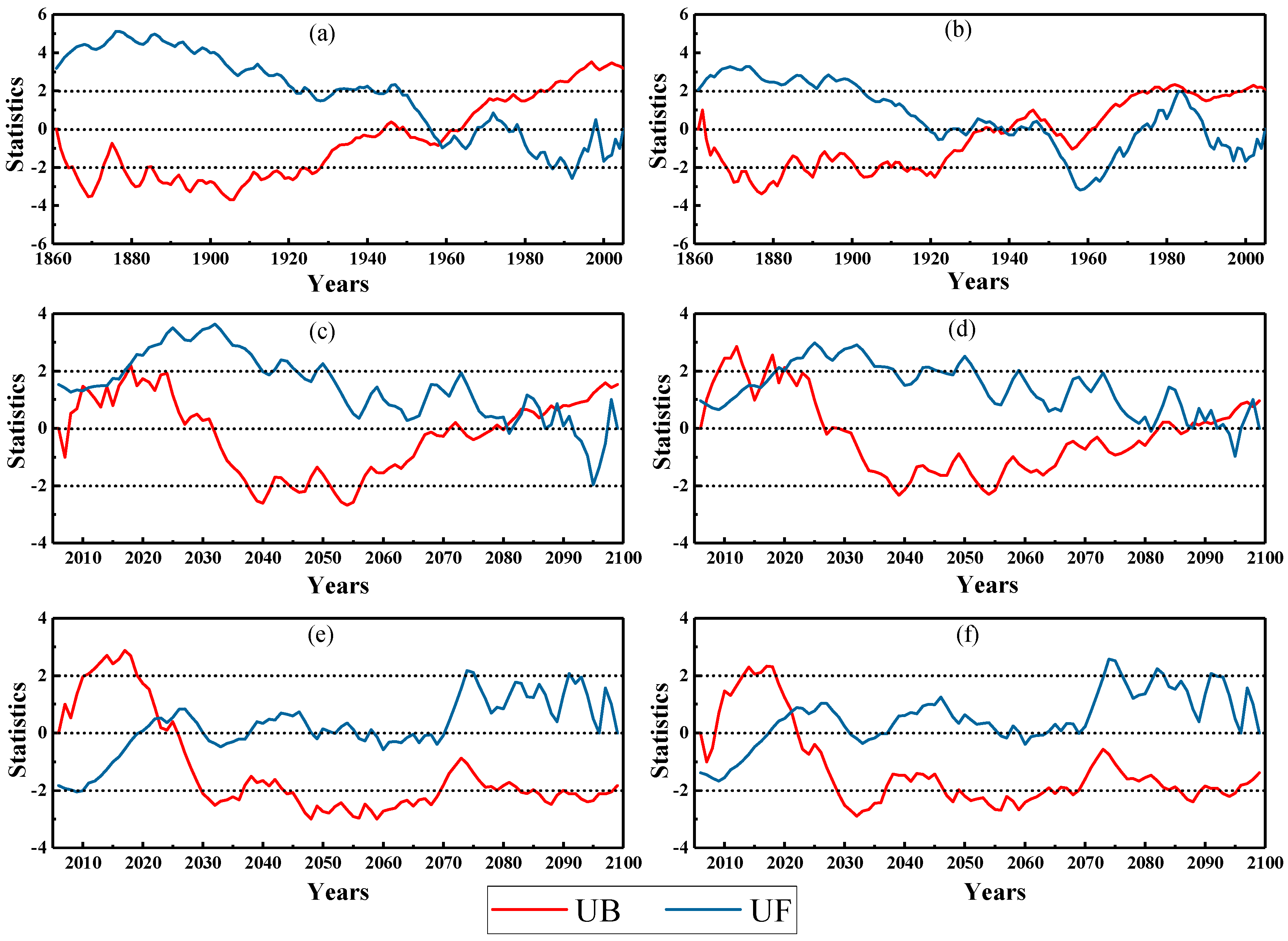
3.1. Temporal Variation in the Palmer Drought Severity Index (PDSI)
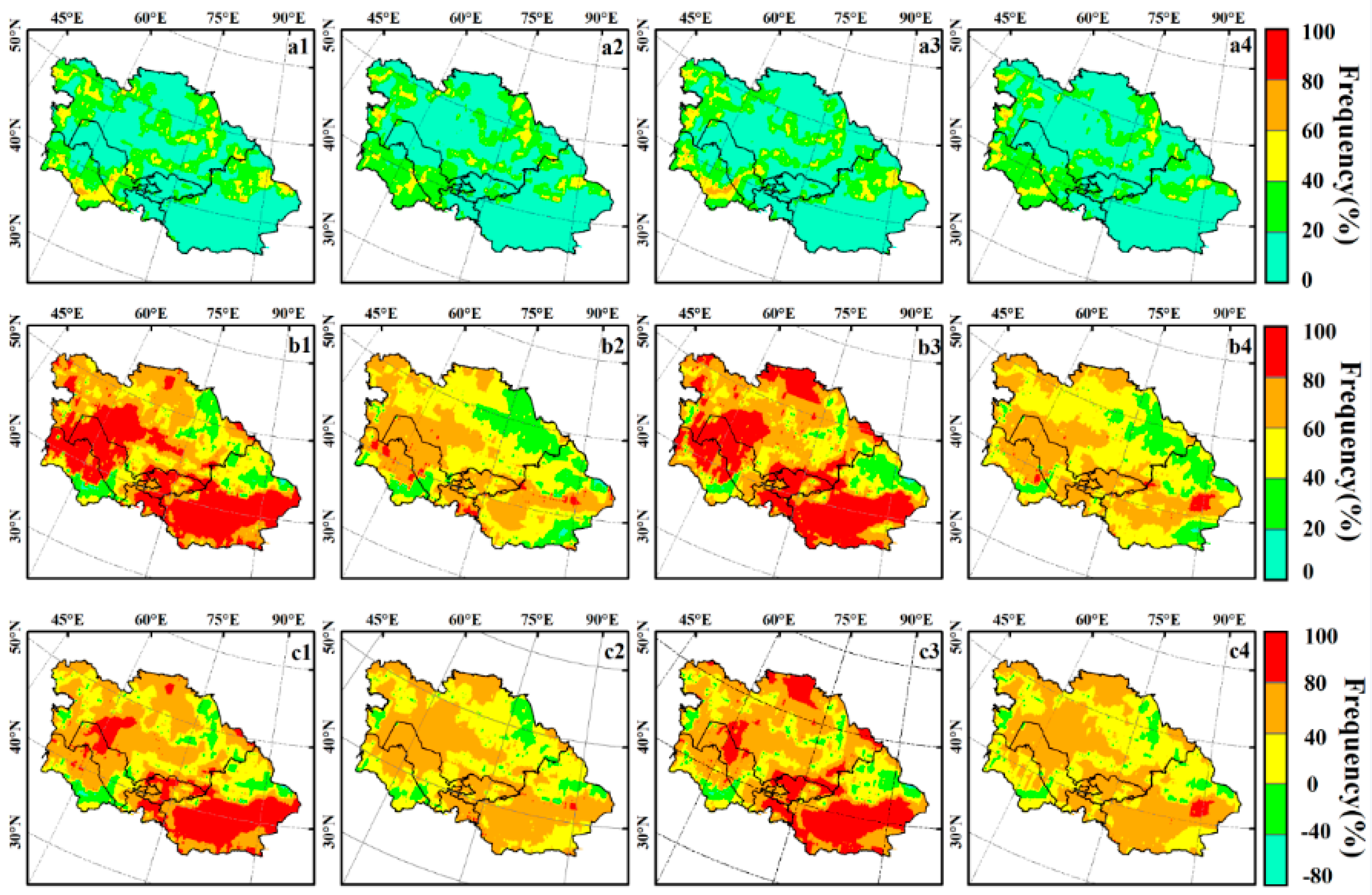
3.2. Spatial Variation in the PDSI
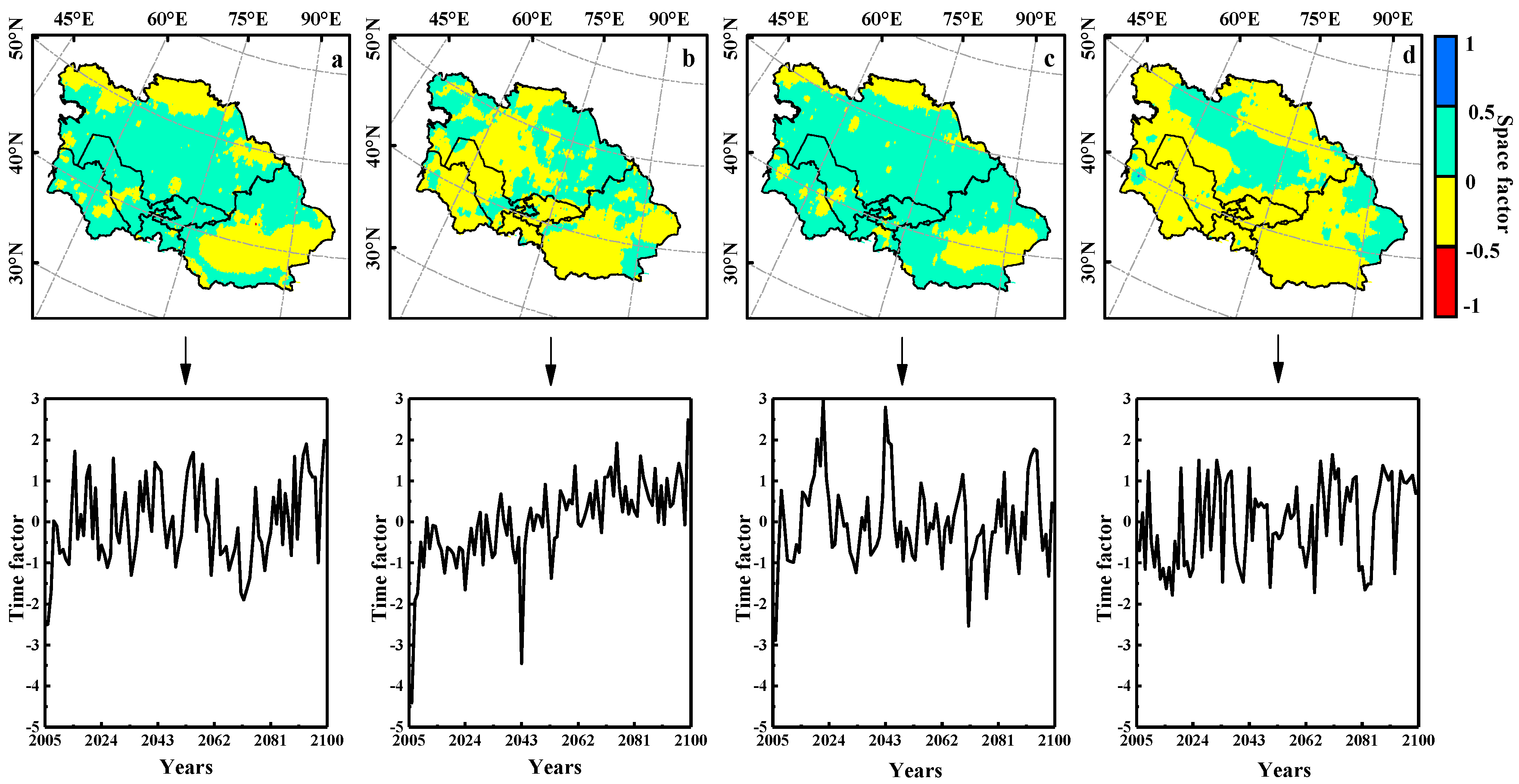
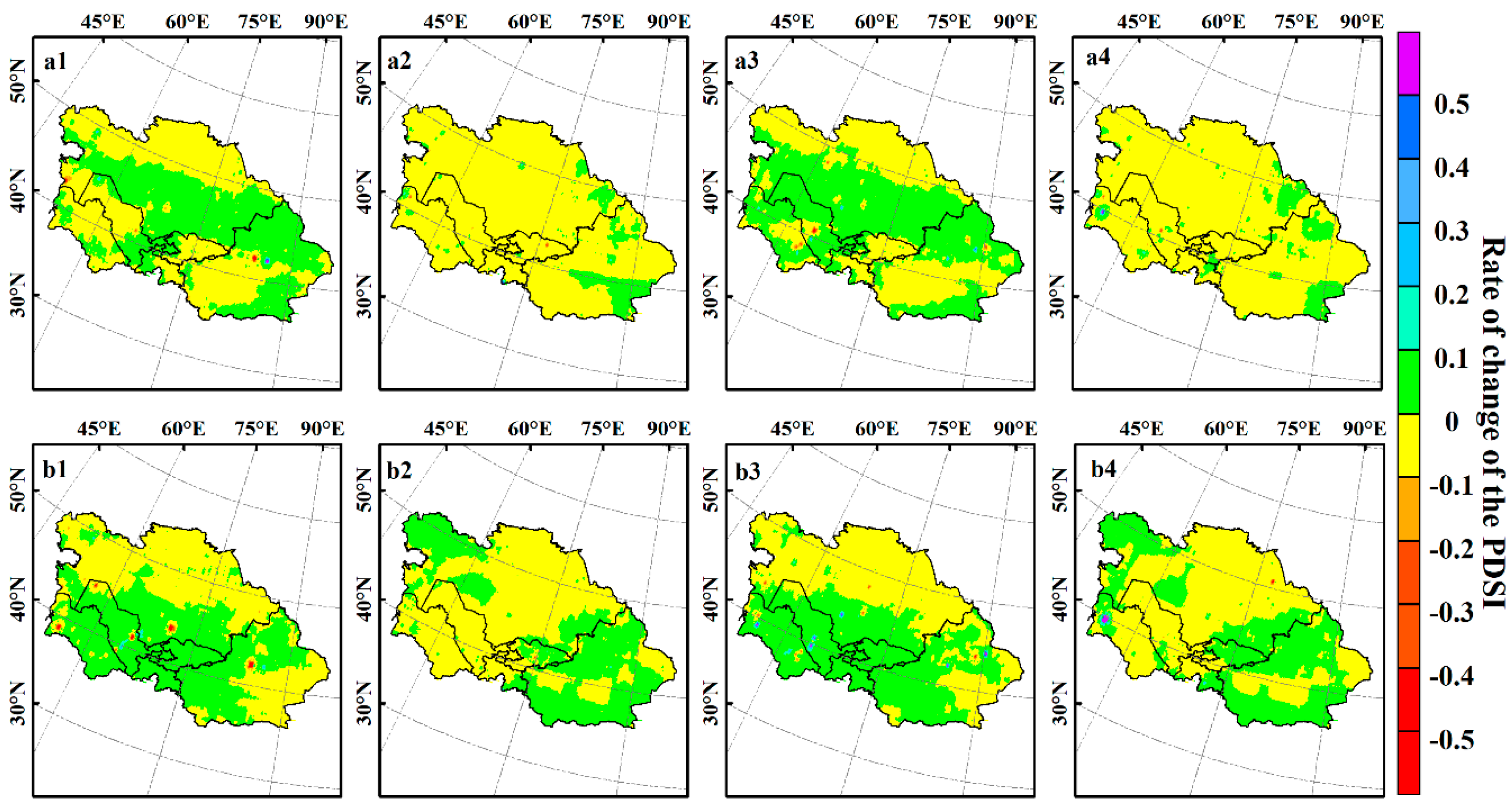
3.3. Spatiotemporal Trend in the PDSI
4. Discussion
4.1. Influence of Different Evapotranspiration Calculation Methods on the PDSI
4.2. Characteristics of Drought Variation in Central Asia under Different Warming Scenarios
5. Conclusions
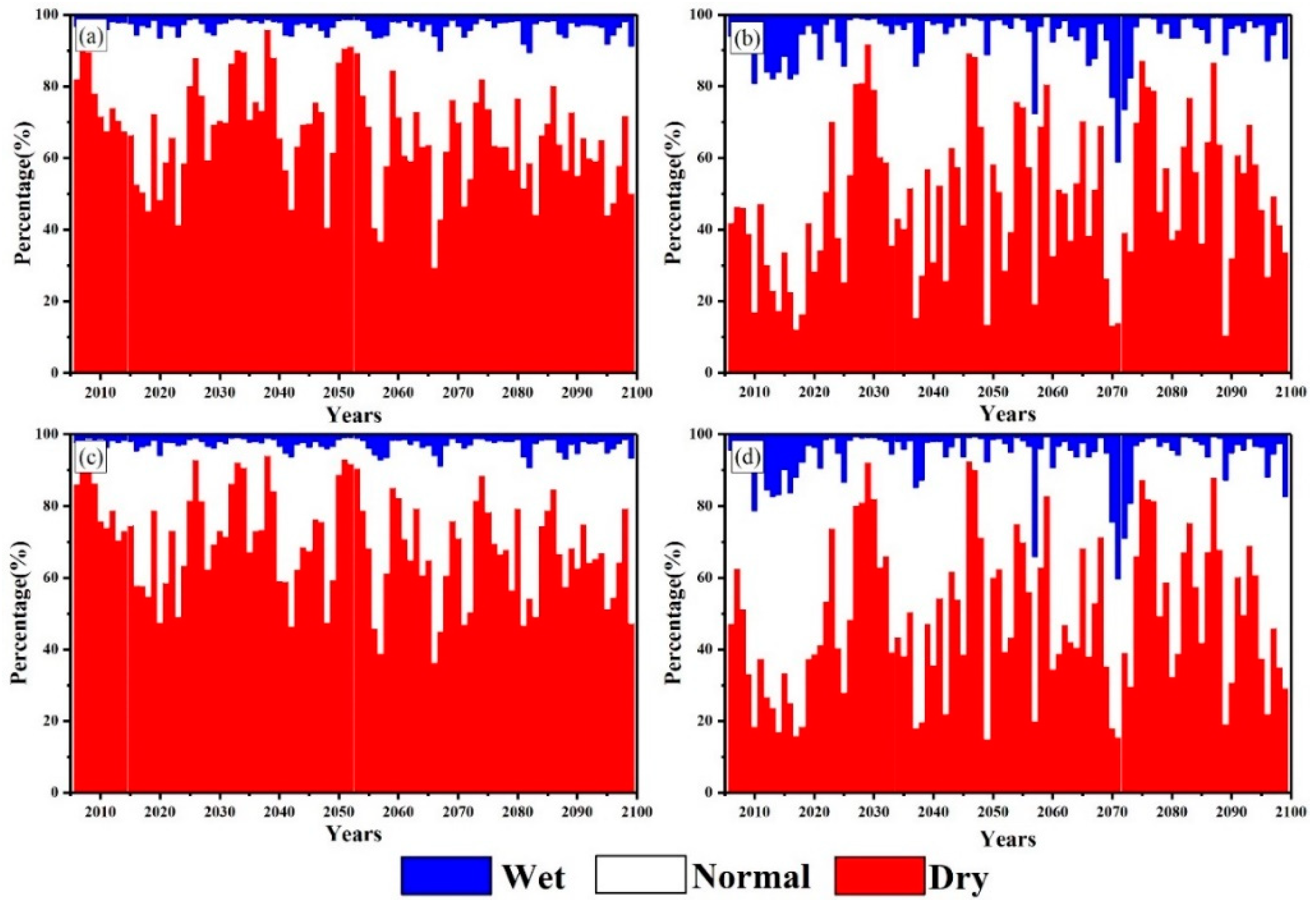
- Under the 1.5 °C and 2.0 °C warming scenarios, the PDSI of Central Asia showed a decreasing trend, indicating worsening drought conditions. The annual average PDSI value in Central Asia under the 1.5 °C warming scenario was −1.36, which was lower than the value of −0.98 obtained for the 2.0 °C warming scenario. The PDSI variation trend obtained using the two calculation methods (PDSI_PM and PDSI_TH) was similar: that is, under both warming scenarios, the PDSI in Central Asia showed a significant decrease compared to the base period, and the future drought trend was significant. The M–K trend analysis also indicated that the PDSI initially increased and then decreased for the four scenarios (the 1.5 °C warming scenario using the PM formula, the 1.5 °C scenario using the TH formula, the 2.0 °C scenario using the PM formula, and the 2.0 °C scenario using the TH formula). After 2050, a downward trend in the PDSI was observed (α = 0.05). Under the two warming scenarios, the change point of the PDSI in Central Asia appeared in 2080–2090 and 2020–2025, respectively. The change rates in the PDSI under the 1.5 °C and 2.0 °C warming scenarios were −0.0164/per decade and −0.0135/per decade, respectively. The change rates of the PDSI were similar for the PDSI_PM and PDSI_TH methods. Under the 1.5 °C and 2.0 °C warming scenarios, the proportion of arid areas (PDSI < −1) in Central Asia was 54.2% and 38.9%, respectively.
- The EOF analysis showed that there were large differences in the spatial distribution of drought in Central Asia under the two warming scenarios. Under the 1.5 °C warming scenario, most parts of Central Asia would be in a humid state, while southern Xinjiang, parts of northern Kazakhstan, and parts of Turkmenistan would experience drought. The distribution of dry and wet areas in Central Asia was predicted to change frequently in the future. Under the 2.0 °C warming scenario, most parts of Kazakhstan and northern parts of Xinjiang showed a wet state, while other regions in Central Asia presented a dry state. The different PDSI calculation methods (PDSI_PM and PDSI_TH) showed significantly different spatial distributions of drought in Central Asia. The spatial distribution characteristics of drought in Central Asia were predicted to change frequently in the future. Under the 1.5 °C warming scenario, the drought frequency in most parts of Central Asia was 60–80%, with an average of 67.6%, whereas under the 2.0 °C warming scenario, the average drought frequency was 54.8%.
- The PDSI values obtained using different calculation formulas for potential evapotranspiration were different. There were some differences in the drought conditions obtained by the two PDSI calculation methods (PDSI_PM and PDSI_TH) in Central Asia for the two future warming scenarios. The average annual PDSI values for Central Asia obtained using PDSI_PM and PDSI_TH were −1.35 and −1.51, respectively. The drought frequency (71.3%) and the proportion of arid areas (55.4%) obtained for Central Asia using the TH formula were higher than those obtained using the PM formula (drought frequency and proportion of arid areas of 67.6% and 54.8%, respectively). Under the warming scenarios, the use of the TH formula led to an error in the calculation of potential evapotranspiration, which in turn led to problems in the calculation of the PDSI. Compared to the PM formula, the TH formula led to an overestimation of the drought situation in Central Asia under both warming scenarios.
- The drought situation in Central Asia would be further aggravated under both warming scenarios. Under the 1.5 °C warming scenario, the calculated PDSI value in Central Asia was lower than that under the 2.0 °C warming scenario, while the drought frequency and proportion of arid areas were significantly higher than those under the 2.0 °C warming scenario. Compared to the 2.0 °C warming scenario, the drought situation in Central Asia may be more serious under the 1.5 °C warming scenario. This research improves human cognition of the drought process in Central Asia under global warming and enhances regional security and construction of the Silk Road Economic Belt.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tian-Jun, Z.; Tao, H. Projected changes of palmer drought severity index under an RCP8. 5 scenario. Atmos. Ocean. Sci. Lett. 2013, 6, 273–278. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhang, Y.Y.; Zhan, C.S.; Qiao, Y.F. Comprehensive assessment of drought risk in the arid region of Northwest China based on the global palmer drought severity index gridded data. Sci. Total Environ. 2018, 627, 951–962. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.P.; Yu, H.P.; Dai, A.G.; Wei, Y.; Kang, L.T. Drylands face potential threat under 2 degrees C global warming target. Nat. Clim. Chang. 2017, 7, 417–422. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a Natural Hazard: Concepts and Definitions. 2000. Available online: https://digitalcommons.unl.edu/droughtfacpub/69 (accessed on 14 August 2019).
- Trenberth, K.; Jones, P.; Ambenje, P.; Bojariu, R.; Easterling, D.; Klein Tank, A.; Parker, D.; Rahimzadeh, F.; Renwick, J.; Rusticucci, M. Observations: Surface and Atmospheric Climate Change. Chapter 3. Climate change. 2007, pp. 235–336. Available online: https://www.ipcc.ch/report/ar4/wg1/observations-atmospheric-surface-and-climate-change/ (accessed on 5 August 2019).
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- UNFCCC. UNFCCC Conference of the Parties: Adoption of the Paris Agreement; FCCC/CP/2015/10Add. 1; UNFCCC: Paris, France, 2015. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Vicenteserrano, S.M.; Beguería, S.; Lorenzolacruz, J.; Camarero, J.J.; Lópezmoreno, J.I.; Azorinmolina, C.; Revuelto, J.; Morántejeda, E.; Sanchezlorenzo, A. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef]
- Tsakiris, G.; Nalbantis, I.; Vangelis, H.; Verbeiren, B.; Huysmans, M.; Tychon, B.; Jacquemin, I.; Canters, F.; Vanderhaegen, S.; Engelen, G. A system-based paradigm of drought analysis for operational management. Water Resour. Manag. 2013, 27, 5281–5297. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- Yan, H.X.; Zarekarizi, M.; Moradkhani, H. Toward improving drought monitoring using the remotely sensed soil moisture assimilation: A parallel particle filtering framework. Remote Sens. Environ. 2018, 216, 456–471. [Google Scholar] [CrossRef]
- Yan, H.X.; Moradkhani, H.; Zarekarizi, M. A probabilistic drought forecasting framework: A combined dynamical and statistical approach. J. Hydrol. 2017, 548, 291–304. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Yan, H.; Zarekarizi, M. Remote Sensing of Drought: Vegetation, Soil Moisture, and Data Assimilation. In Remote Sensing of Hydrological Extremes; Lakshmi, V., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 121–149. [Google Scholar]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Lorenzo-Lacruz, J.; El Kenawy, A.; Azorin-Molina, C.; Morán-Tejeda, E.; Pasho, E.; Zabalza, J.; Beguería, S.; Angulo-Martínez, M. The NAO impact on droughts in the Mediterranean region. In Hydrological, Socioeconomic and Ecological Impacts of the North Atlantic Oscillation in the Mediterranean Region; Springer: Dordrecht, The Netherlands, 2011; pp. 23–40. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought, Research Paper no. 45; US Weather Bureau: Washington, DC, USA, 1965; Volume 58. [Google Scholar]
- Barling, R.D.; Moore, I.D.; Grayson, R.B. A quasi-dynamic wetness index for characterizing the spatial distribution of zones of surface saturation and soil water content. Water Resour. Res. 1994, 30, 1029–1044. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 Drought Using the Standardized Precipitation Index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Karl, T.R.; Koscielny, A.J. Drought in the united states: 1895–1981. J. Climatol. 1982, 2, 313–329. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Global variations in droughts and wet spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Briffa, K.; Osborn, T.; Cook, E. Summer moisture availability across North America. J. Geophys. Res. Atmos. 2006, 111, D11. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008. J. Geophys. Res. Atmos. 2011, 116, D12. [Google Scholar] [CrossRef]
- Gao, L.; Gou, X.; Deng, Y.; Yang, M.; Zhao, Z.; Cao, Z. Dendroclimatic response of Picea crassifolia along an altitudinal gradient in the eastern Qilian Mountains, northwest China. Arct. Antarct. Alp. Res. 2013, 45, 491–499. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Li, W. Spatial and temporal variability of drought in the arid region of China and its relationships to teleconnection indices. J. Hydrol. 2015, 523, 283–296. [Google Scholar] [CrossRef]
- Wondie, M.; Terefe, T. Assessment of drought in Ethiopia by using self-calibrated Palmer Drought Severity Index. Int. J. Eng. Manag. Sci. 2016, 7, 108–117. [Google Scholar]
- Heddinghaus, T.R.; Sabol, P. A review of the Palmer Drought Severity Index and where do we go from here. In Proceedings of the 7th Conference on Applied Climatology, Salt Lake City, UT, USA, 10–13 September 1991; American Meteorological Society: Boston, MA, USA, 1991; pp. 242–246. [Google Scholar]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Jones, P.D.; Briffa, K.R. The sensitivity of the PDSI to the Thornthwaite and Penman-Monteith parameterizations for potential evapotranspiration. J. Geophys. Res. Atmos. 2011, 116, 16. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, C.; Tao, H.; Zhu, J.; Kundzewicz, Z.W. Projections of actual evapotranspiration under the 1.5 °C and 2.0 °C global warming scenarios in sandy areas in northern China. Sci. Total Environ. 2018, 645, 1496–1508. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Fischer, T.; Wang, Y.; Kundzewicz, Z.W.; Zhai, J.; Sun, H.; Wang, A.; Zeng, X.; Wang, G. Drought losses in China might double between the 1.5 °C and 2.0 °C warming. Proc. Natl. Acad. Sci. USA 2018, 115, 10600–10605. [Google Scholar] [CrossRef]
- Huang, J.P.; Ji, M.X.; Xie, Y.K.; Wang, S.S.; He, Y.L.; Ran, J.J. Global semi-arid climate change over last 60 years. Clim. Dyn. 2016, 46, 1131–1150. [Google Scholar] [CrossRef]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.-L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G. Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013-The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 1029–1136. Available online: https://www.ipcc.ch/report/ar5/wg1/ (accessed on 14 August 2019).
- Kim, D.-W.; Byun, H.-R. Future pattern of Asian drought under global warming scenario. Theor. Appl. Climatol. 2009, 98, 137–150. [Google Scholar] [CrossRef]
- Fang, K.; Gou, X.; Chen, F.; Davi, N.; Liu, C. Spatiotemporal drought variability for central and eastern Asia over the past seven centuries derived from tree-ring based reconstructions. Quat. Int. 2013, 283, 107–116. [Google Scholar] [CrossRef]
- Touma, D.; Ashfaq, M.; Nayak, M.A.; Kao, S.-C.; Diffenbaugh, N.S. A multi-model and multi-index evaluation of drought characteristics in the 21st century. J. Hydrol. 2015, 526, 196–207. [Google Scholar] [CrossRef]
- Sun, H.; Wang, A.; Zhai, J.; Huang, J.; Wang, Y.; Wen, S.; Zeng, X.; Su, B. Impacts of global warming of 1.5 C and 2.0 C on precipitation patterns in China by regional climate model (COSMO-CLM). Atmos. Res. 2018, 203, 83–94. [Google Scholar] [CrossRef]
- Jahani, B.; Mohammadi, B. A comparison between the application of empirical and ANN methods for estimation of daily global solar radiation in Iran. Theor. Appl. Climatol. 2019, 137, 1257–1269. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Wu, F.; Fang, X.; Herrmann, M.; Mosbrugger, V.; Miao, Y. Extended drought in the interior of Central Asia since the Pliocene reconstructed from sporopollen records. Glob. Planet. Chang. 2011, 76, 16–21. [Google Scholar] [CrossRef]
- Burke, E.J.; Brown, S.J.; Christidis, N. Modeling the recent evolution of global drought and projections for the twenty-first century with the hadley centre climate model. J. Hydrometeorol. 2006, 7, 1113–1125. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.; Pan, J.; Xu, Y. Projected changes in temperature extremes in China using PRECIS. Atmosphere 2017, 8, 15. [Google Scholar] [CrossRef]
- Jiang, D.; Sui, Y.; Lang, X. Timing and associated climate change of a 2 C global warming. Int. J. Climatol. 2016, 36, 4512–4522. [Google Scholar] [CrossRef]
- Schlaepfer, D.R.; Bradford, J.B.; Lauenroth, W.K.; Munson, S.M.; Tietjen, B.; Hall, S.A.; Wilson, S.D.; Duniway, M.C.; Jia, G.; Pyke, D.A. Climate change reduces extent of temperate drylands and intensifies drought in deep soils. Nat. Commun. 2017, 8, 14196. [Google Scholar] [CrossRef]
- Davi, N.K.; Jacoby, G.C.; Curtis, A.E.; Baatarbileg, N. Extension of drought records for central Asia using tree rings: West-central Mongolia. J. Clim. 2006, 19, 288–299. [Google Scholar] [CrossRef]
- Shahabfar, A.; Ghulam, A.; Conrad, C. Understanding hydrological repartitioning and shifts in drought regimes in Central and South-West Asia using MODIS derived perpendicular drought index and TRMM data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 983–993. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Otto, I.M.; Adams, S.; Albrecht, T.; Baarsch, F.; Cartsburg, M.; Coumou, D.; Eden, A.; Ludi, E.; Marcus, R.; et al. Climate change impacts in Central Asia and their implications for development. Reg. Environ. Chang. 2017, 17, 1639–1650. [Google Scholar] [CrossRef]
- Chen, F.; Huang, W.; Jin, L.; Chen, J.; Wang, J. Spatiotemporal precipitation variations in the arid Central Asia in the context of global warming. Sci. China Earth Sci. 2011, 54, 1812–1821. [Google Scholar] [CrossRef]
- Huang, J.; Qin, D.; Jiang, T.; Wang, Y.; Feng, Z.; Zhai, J.; Cao, L.; Chao, Q.; Xu, X.; Wang, G. Effect of Fertility Policy Changes on the Population Structure and Economy of China: From the Perspective of the Shared Socioeconomic Pathways. Earth’s Future 2019, 7, 250–265. [Google Scholar] [CrossRef]
- King, A.D.; Karoly, D.J.; Henley, B.J. Australian climate extremes at 1.5 degrees C and 2 degrees C of global warming. Nat. Clim. Chang. 2017, 7, 412–416. [Google Scholar] [CrossRef]
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP): Project framework. Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef] [PubMed]
- Dai, A.; Trenberth, K.E.; Qian, T.T. A global dataset of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Jacobi, J.; Perrone, D.; Duncan, L.L.; Hornberger, G. A tool for calculating the Palmer drought indices. Water Resour. Res. 2013, 49, 6086–6089. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Letsinger, S.L.; Gholizadeh, H.; Maxwell, J.T. Incorporation of the Penman–Monteith potential evapotranspiration method into a Palmer Drought Severity Index tool. Comput. Geosci. 2015, 85, 136–141. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Montroy, D.L. Linear relation of central and eastern North American precipitation to tropical Pacific sea surface temperature anomalies. J. Clim. 1997, 10, 541–558. [Google Scholar] [CrossRef]
- Hannachi, A.; Jolliffe, I.T.; Stephenson, D.B. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int. J. Climatol. 2010, 27, 1119–1152. [Google Scholar] [CrossRef]
- Jiang, L.L.; Jiapaer, G.; Bao, A.M.; Kurban, A.; Guo, H.; Zheng, G.X.; De Maeyer, P. Monitoring the long-term desertification process and assessing the relative roles of its drivers in Central Asia. Ecol. Indic. 2019, 104, 195–208. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21 st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Burke, E.J.; Brown, S.J. Evaluating uncertainties in the projection of future drought. J. Hydrometeorol. 2008, 9, 292–299. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. On the importance of including vegetation dynamics in Budyko’s hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 983–995. [Google Scholar] [CrossRef]
- Lockwood, J. Is potential evapotranspiration and its relationship with actual evapotranspiration sensitive to elevated atmospheric CO2 levels? Clim. Chang. 1999, 41, 193–212. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435. [Google Scholar] [CrossRef]
- Huang, J.P.; Yu, H.P.; Guan, X.D.; Wang, G.Y.; Guo, R.X. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Sherwood, S.; Fu, Q. A drier future? Science 2014, 343, 737–739. [Google Scholar] [CrossRef] [PubMed]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Hobbins, M.T.; Dai, A.; Roderick, M.L.; Farquhar, G.D. Revisiting the parameterization of potential evaporation as a driver of long-term water balance trends. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate change and drought: From past to future. Curr. Clim. Chang. Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Smirnov, O.; Zhang, M.; Xiao, T.; Orbell, J.; Lobben, A.; Gordon, J. The relative importance of climate change and population growth for exposure to future extreme droughts. Clim. Chang. 2016, 138, 41–53. [Google Scholar] [CrossRef]
- Lehner, F.; Coats, S.; Stocker, T.F.; Pendergrass, A.G.; Sanderson, B.M.; Raible, C.C.; Smerdon, J.E. Projected drought risk in 1.5 C and 2 C warmer climates. Geophys. Res. Lett. 2017, 44, 7419–7428. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Scherer, M.; Ashfaq, M. Response of snow-dependent hydrologic extremes to continued global warming. Nat. Clim. Chang. 2013, 3, 379–384. [Google Scholar] [CrossRef]
- Liu, W.; Sun, F.; Lim, W.H.; Zhang, J.; Wang, H.; Shiogama, H.; Zhang, Y. Global drought and severe drought-affected populations in 1.5 and 2 °C warmer worlds. Earth Syst. Dyn. 2018, 9, 267–283. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global changes in drought conditions under different levels of warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
| Model | Institution | Country | Original Resolution (Lat × Lon) |
|---|---|---|---|
| GFDL-ESM2 M | Geophysical Fluid Dynamics Laboratory | USA | 2.5° × 2.0° |
| HadGEM2-ES | Met Office Hadley Center | UK | 1.875° × 1.258° |
| IPSL-CM5A-LR | Institute Pierre Simon Laplace | France | 3.75° × 1.98° |
| MIROC5 | Model for Interdisciplinary Research on Climate | Japan | 1.4° × 1.4° |
| PDSI | Wet and Dry Grade | PDSI | Wet and Dry Grade |
|---|---|---|---|
| ≥4 | Extremely wet | ≥−2~−1 | Mild drought |
| ≥3~4 | Very wet | ≥−3~−2 | Moderate drought |
| ≥2~3 | Moderately wet | ≥−4~−3 | Severe drought |
| ≥1~2 | Slightly wet | <−4 | Extreme drought |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhao, C.; Ma, X.; Brindha, K.; Han, Q.; Li, C.; Zhao, X. Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia. Sustainability 2019, 11, 4421. https://doi.org/10.3390/su11164421
Zhang R, Zhao C, Ma X, Brindha K, Han Q, Li C, Zhao X. Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia. Sustainability. 2019; 11(16):4421. https://doi.org/10.3390/su11164421
Chicago/Turabian StyleZhang, Ruiwen, Chengyi Zhao, Xiaofei Ma, Karthikeyan Brindha, Qifei Han, Chaofan Li, and Xiaoning Zhao. 2019. "Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia" Sustainability 11, no. 16: 4421. https://doi.org/10.3390/su11164421
APA StyleZhang, R., Zhao, C., Ma, X., Brindha, K., Han, Q., Li, C., & Zhao, X. (2019). Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia. Sustainability, 11(16), 4421. https://doi.org/10.3390/su11164421







