1. Introduction
In the first decades of the 21st century, the air cargo market has grown rapidly due to the spread of information technology (IT) products, the expansion of e-commerce, and high value-added products. The world’s air traffic will increase by 4.7 percent annually over the next 20 years, and it will double by 2035. In order to reduce the delay, airports and airlines can adjust their flight schedules, expand airport terminals, and introduce weather observation equipment to reduce such delays [
1]. Cargo exports in South Korea amounted to US
$175 billion in 2017, an increase of 30.3% over the previous year. The industry also recorded a high annual growth rate of 8.1% across a preceding period of five years. During that period of growth, wireless communication equipment and computers accounted for 70% of total cargo exports, mainly in semiconductors, and cargo exports of high value-added products such as pharmaceuticals and cosmetics also increased significantly. Among trading partners, Vietnam grew strongly, and China and Hong Kong topped the list. These three countries accounted for 64% of total cargo exports in South Korea during the period of observation [
2,
3,
4].
Experts predict that cargo exports will continue to increase as the demand for semiconductors, IT products, and special cargo expansions on the back of global economic recovery and the growth of the reverse-purchase market. Therefore, Korean exporters have the potential to continue to expand the export of high-end consumer goods by positively utilizing air cargo transportation [
5,
6].
Air cargo transportation has the advantages of maintaining constant quality in products during transportation with low risks of damage due to a promptness of delivery and supply chain timeliness. However, because air cargo costs are relatively high, air cargo mainly operates in a small sector of transportation centered on IT, high value-added products, and products sensitive to physical environmental conditions. High value-added products, such as semiconductors, computers, and wireless communication devices, are usually transported by air because the longer the period of transportation, the greater the risk of breakage in these types of products. In the case of medicines, cosmetics, or dangerous goods (such as lithium batteries), air transportation is preferred because it allows for greater control over certain aspects of the external environment, including temperature [
7,
8].
In recent years, as consumers’ desire for rapid delivery has increased and the development of comprehensive logistics has reduced cargo rates in comparison to the past, air transportation has expanded around small consumer goods. As the link between air transport and land transport closes, consumer needs can be met by the rapid delivery of products at lower fares. ICB is the official partner of Cainiao, the logistics company of China’s Alibaba Group. This partnership has made possible the construction of a logistics warehouse close to the airport to shorten the distance between land transportation and air transportation and has allowed for the use of China’s extensive logistics system by way of professional cooperation [
9,
10].
According to the International Air Transport Association (IATA), freight ton kilometers (FTK) handled by airlines around the world in September 2018 fell 0.3% from the previous month, and global air cargo growth was 2.0% higher than in September 2017 [
11,
12]. Air cargo volume has been reported to have maintained a robust growth due to strong consumer confidence, investment growth, and e-commerce activity. Additionally, air cargo competition is increased, and cargo market itself is becoming important for a sustainability of the airport industry [
13,
14]. Delays incur costs, so airlines’ management plan operations to minimize delay time. There are several delays such as weather, internal, passenger/baggage, cargo/mail, handling, technical, damage/failure, operation, air traffic control, and others. There are various reasons to delay, such as due to late arrival (about 40%), air carrier (about 32%), aviation system (about 23%), weather (about 5%) and security (about 0.1%). The weather accounts for about 5% of the total delay, but 58% of the cancellation [
15,
16]. Thus, weather deterioration around airports has substantial effects on cargo transportation. However, few previous studies have explored predicting delay times and costs caused by weather.
The purpose of this study is to develop a forecasting model to predict delay times and costs caused by the delayed arrival of cargo due to low visibility environments, especially low visibility by fog. Weather deterioration due to low visibility by fog around airports occasionally prohibits the use of airports, potentially causing crises for companies in the global supply chain environment. If the arrival of cargo is delayed, supply chain delays occur. Because delays are directly linked to costs, companies need precise predictions of cargo transportation. Costs that are caused by delay are extra air cargo fuel, air cargo maintenance cost, air crew cost, airport usage cost, and compensation cost. Thus, airport corporation and airline companies need to cooperate to build strategies of airline scheduling, terminal expansions, and weather forecasting facilities for proper cargo transportation in order to minimize the related costs. Thus, this study will provide business decision-makers with strategic insights in order to improve the quality of service and sustainable operations in current airports, airline companies, and other similar settings.
2. Literature Review
2.1. ARIMA Model and Seasonal ARIMA Model
Our method involves a seasonal autoregressive integrated moving average (SARIMA) model, which is used when there are trends and seasonalities in time series data. The SARIMA incorporates seasonal terms in a general autoregressive integrated moving average (ARIMA) model. The ARIMA model combines an autoregressive (AR) model with a moving average (MA) model, starting from the concept that recent observations have a strong influence on future predictions.
The ARIMA model is more suitable for short-term prediction than long-term prediction because it gives more weight to historical observations that are closer to recent times than to the distant past. More recent weight for events observed in the near past means that long-term predictive values obtained from the ARIMA model are less reliable than short-term predictive values. The ARIMA model can also be used to predict seasonal or periodic fluctuations in time series data. The work of Box and Jenkins [
17] suggests that an appropriate sample size is required to set up the ARIMA model and that at least 50 observations are required for the sample to be used. Particularly in cases involving seasonal fluctuations, larger samples are required.
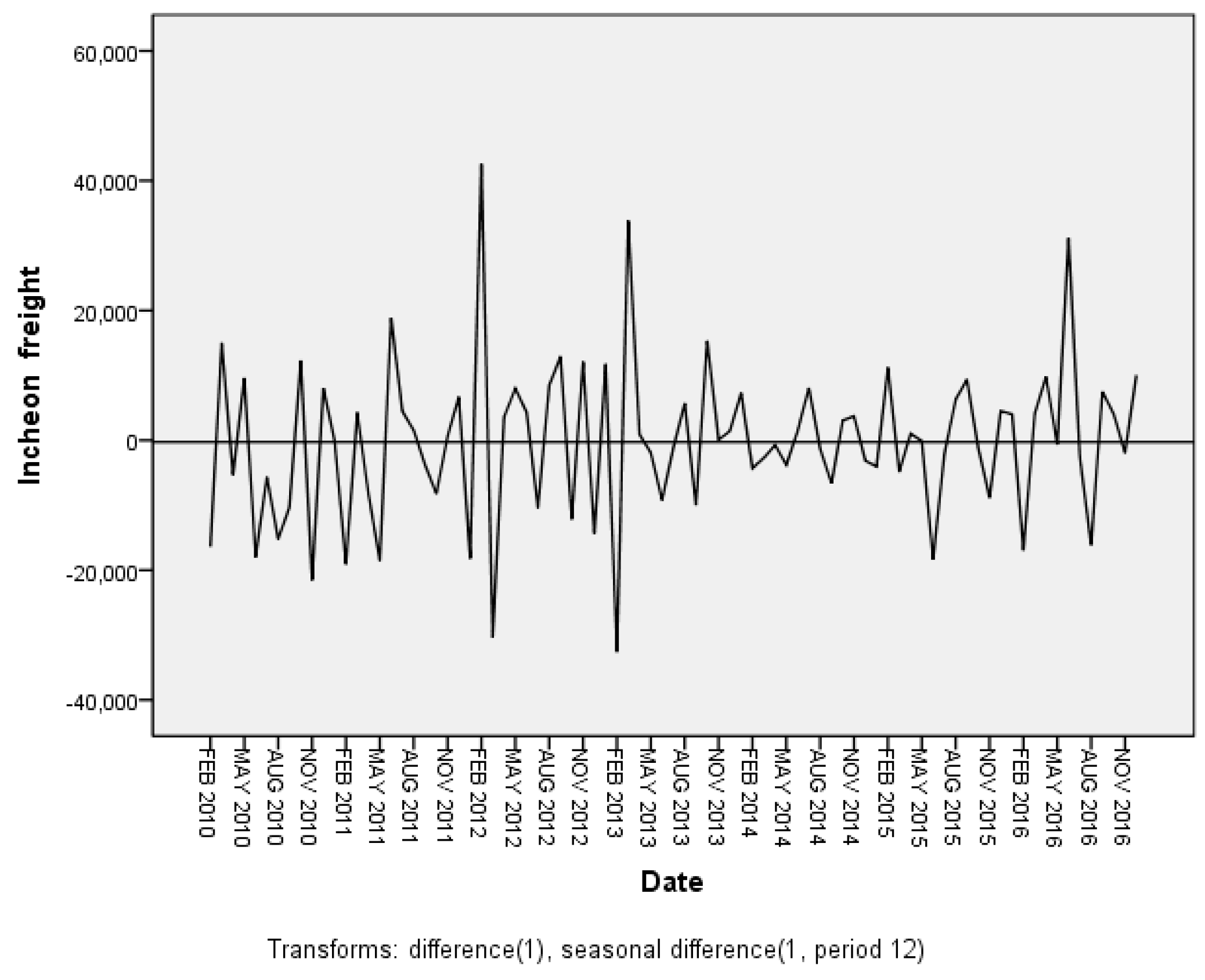
In order to construct the ARIMA model, the first step is to satisfy the stationarity of the average and the variance of data. In the presence of non-stationarity and seasonality, non-seasonal differences (d) and seasonal differences (D) ensure a steady state. The difference is obtained by subtracting the value of a past specific time from the value of the present time point and replacing the value with the new value. Thus, the more the number of times of the difference (d, D), the more the data are damaged.
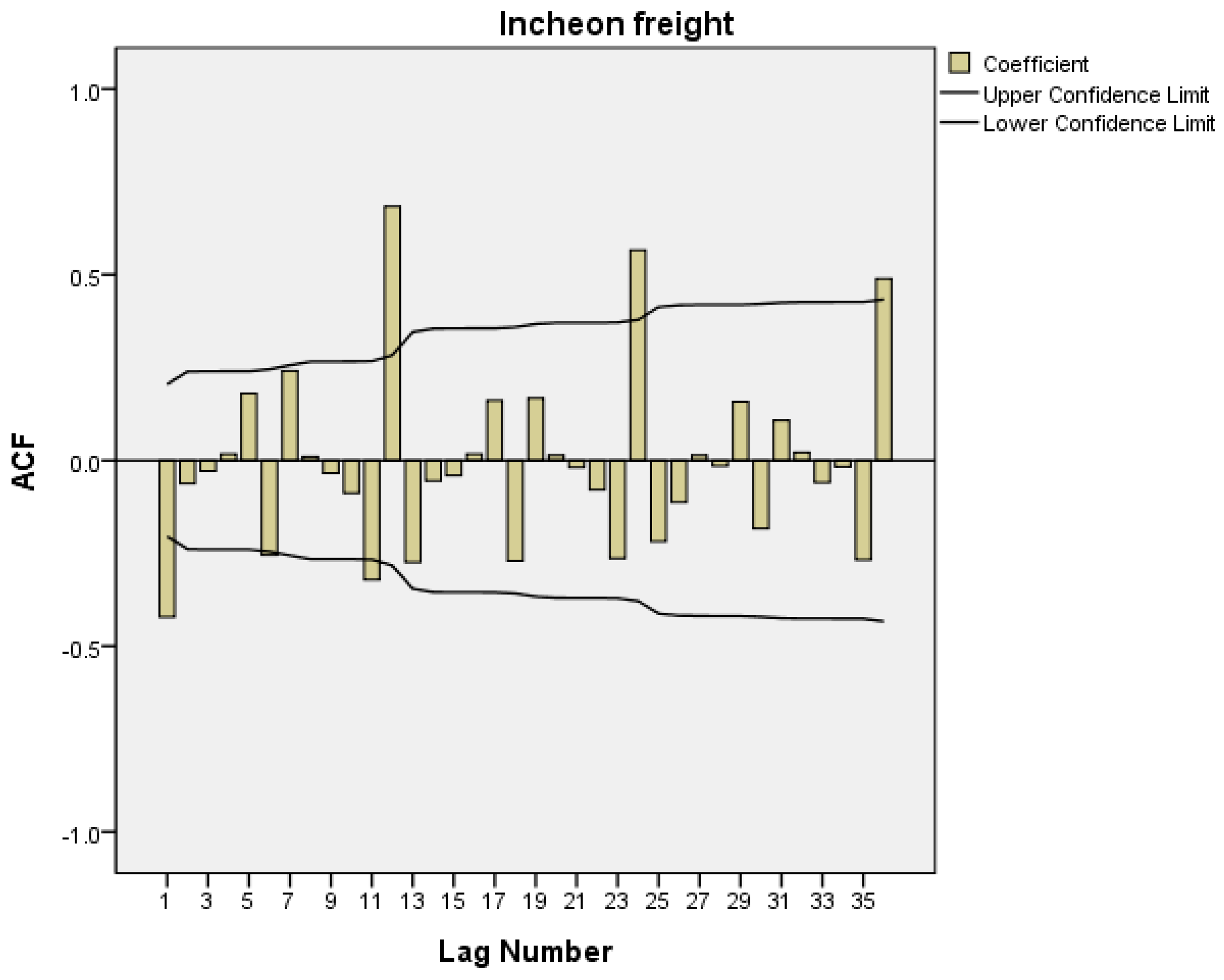
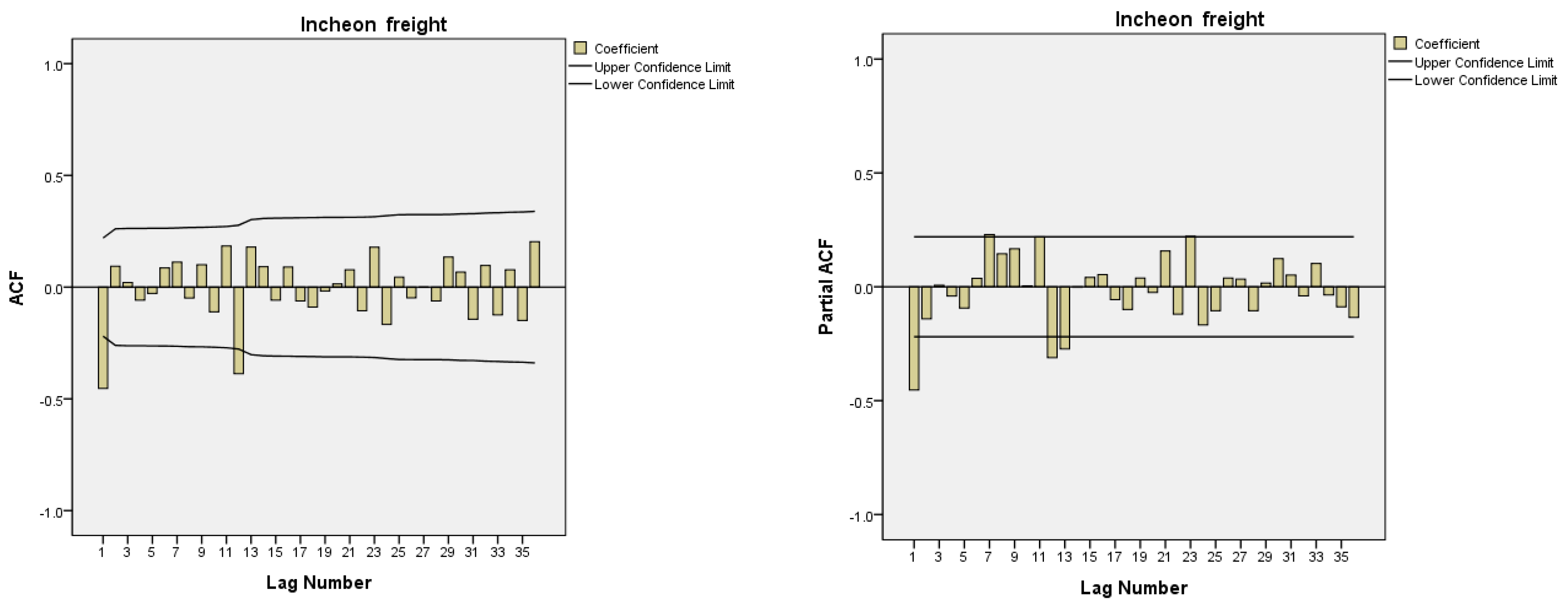
The second step is an identification step in which the correlation between observed values in the time series is measured to temporarily determine autoregressive (AR) elements, p, P, and moving average (MA) elements, q, Q. Correlation is measured by an autocorrelation function (ACF) and a partial autocorrelation function (PACF). The third step is an estimation step which estimates the coefficients of the model selected in the identification step and determines the statistical significance of the estimated parameters. Here, if the estimated parameters are not statistically significant, we must go back to the identification step and temporarily select another ARIMA model. The fourth step is to determine whether the estimated model is statistically appropriate. The fourth step validates the independence of white noise through verification methods such as residual autocorrelation functions, t-test statistics, and chi-squared tests (Ljung–Box Q-tests). The model that matches the verification results is rejected, and the three steps of identification, estimation, and model verification are repeated until a final model is found. Predicted values are obtained based on the model that is finally confirmed.
Lim and McAleer [
18] predicted travel demand in Asia–Australia routes through the traditional ARIMA model and the seasonal ARIMA (SARIMA) model. Coshall [
19] predicted UK passenger demand for routes connecting 16 main countries to Japan, Canada, the United States, and the Canary Islands. Yüksel [
20] predicted the demand for five-star hotel rooms in Ankara, Turkey, based on an ARIMA model.
The seasonal ARIMA (SARIMA) model involves the addition of seasonal terms to the ARIMA model. The process of constructing the model is almost the same as the process of constructing the non-seasonal ARIMA model. In the identification step, two estimated correlation functions are calculated and one or more temporal models are selected by comparing them with two theoretical correlation functions. After estimating the parameters included in the model, the independence of white noise is verified through the residual autocorrelation function. If the null hypothesis is rejected, then another model is temporarily re-identified through the residual autocorrelation function. Unlike non-seasonal time series data, seasonal time series data are correlated with each other at intervals of the length of periodicity (s). By adding seasonality to the general ARIMA model, the SARIMA model is expressed as
where
represent non-seasonal orders and
represent seasonal orders. This is expressed in the following Equation (1).
Here, is the non-seasonal AR part, is the seasonal AR part, is the seasonal MA part, is the non-seasonal MA part, d is the non-seasonal difference order, D is the seasonal difference order, and s is the length of the cycle. The term follows a white noise process with a mean of 0 and a variance of , assuming that and , are independent of each other. The term denotes a normalized time series obtained through non-seasonal and seasonal differential methods to normalize the abnormal time series .
2.2. Delay Time and Delay Cost Analysis
2.2.1. Delay Reduction Model
There are three typical methods for analyzing delay times in flight service due to dangerous weather. First, the delay time may be calculated from the actual departure/arrival time of the flight schedule of any flight corresponding to alarm times announced by the Meteorological Administration. However, there are dozens and dozens of alarms per airport, leading to difficulties in calculation because dozens (hundreds) of aircrafts arrive and depart from various airports during the course of each alarm. The second method is to calculate the actual departure/arrival delay time of a delayed flight from data classified as dangerous aircraft data according to causes of aircraft delay announced by the Korea Airports Corporation (KAC). These data are limited, however, in that they only include cases where the delay time is more than one h. Finally, the delayed model is used as a representative delay analysis model. The method involves a calculation based on time, which affects the number of airports handling departures and arrivals of aircraft in dangerous conditions together with the number of arrivals and departures of aircraft in dangerous conditions. This is an effective method to analyze time-based delay times affecting the number of arrivals/departures and the number of flights under conditions of severe weather [
21,
22].
This study looks at the basics of the delay reduction model proposed by Evans [
23] using the delay reduction model. Delays occur due to several reasons, resulting in aircraft turnaround, industrial actions and operational efficiency. Weather conditions reduce the capacity of an airport terminal for a certain period of time. Fog is main low visibility source, and other main sources are gale, snowfall, rainfall and typhoon. If severe weather lasts for two h, causing aircraft that need to depart from the airport not to depart, as well as situations where landing aircraft cannot land as scheduled, then the resulting “aircraft delay” lasts until grounded aircraft take off and arrive at set destinations [
24,
25,
26].
At this time, if the minimum flight time of the aircraft on the ground is 1 h, then the total delay time is 3 h. The sum of these aircraft delay times can be expressed by the following Equation (2).
where
(h/month)
(monthly fights/operating time)
(no. of fights/h)
(no. of fights/h)
(h/month)
The term T is the square; thus, if we can reduce alert times for severe weather via more accurate weather forecasts, then delay times of flights will be greatly reduced. The delay reduction model is effective in responding to air traffic management and terminal capacity reduction at airports, and it is advantageous in various studies for its easy calculation of delay times. The work of Allan et al. [
27] used a delay reduction model to calculate the economic benefits of flight delays when using the Integrated Terminal Weather System (ITWS) at LaGuardia and John F. Kennedy International airports in New York City. Allan and Evans [
28] used this model to calculate operating profits generated when using the ITWS at Atlanta International Airport. Robinson et al. [
29] used a delay reduction model to measure delay reduction effects caused by a Route Availability Planning Tool (RAPT) in New York City airports.
2.2.2. Delay Cost Analysis
The cost of flight delays in South Korea is calculated by assigning weights to the frequency of occurrence and setting a representative value in a scenario under the standards of consumer dispute resolution. South Korea’s delay costs are not analyzed according to precise criteria and do not include the opportunity costs of passengers, which is insufficient to produce a clear picture of total economic loss. In general, the method of calculating flight delay costs is mainly based on a method proposed by the European Organization for the Safety of Air Navigation (commonly known as Eurocontrol) that analyzes delay costs by dividing delay costs into three situations [
30].
The first situation is a delay situation in which network effects are not reflected. This means that the scenario does not take into account that chain delays are caused by a single original delay. The second situation is a delay situation that reflects network effects. This is a case where chain delays occur due to network effects, such as a delay in a preceding flight affecting a delay in a subsequent flight. The third and final delay situation aims to adjust flight plans by predicting delays. This means that delays are minimized by predicting delays and adjusting flight schedules in advance. Here, delays are categorized as ground delays or in-flight delays, with ground delays defined as delays before and after the landing of flights. In-flight delays refer to delays in route and arrival. In a study on the economic loss of aircraft based on Eurocontrol standards, Cook and Tanner [
31] compared the management costs of takeoff delays and in-flight delays. The work of Ferguson et al. [
32] used Eurocontrol criteria to analyze delays over a period of time at 19 major airports in the United States by type of aircraft, time of day, and route.
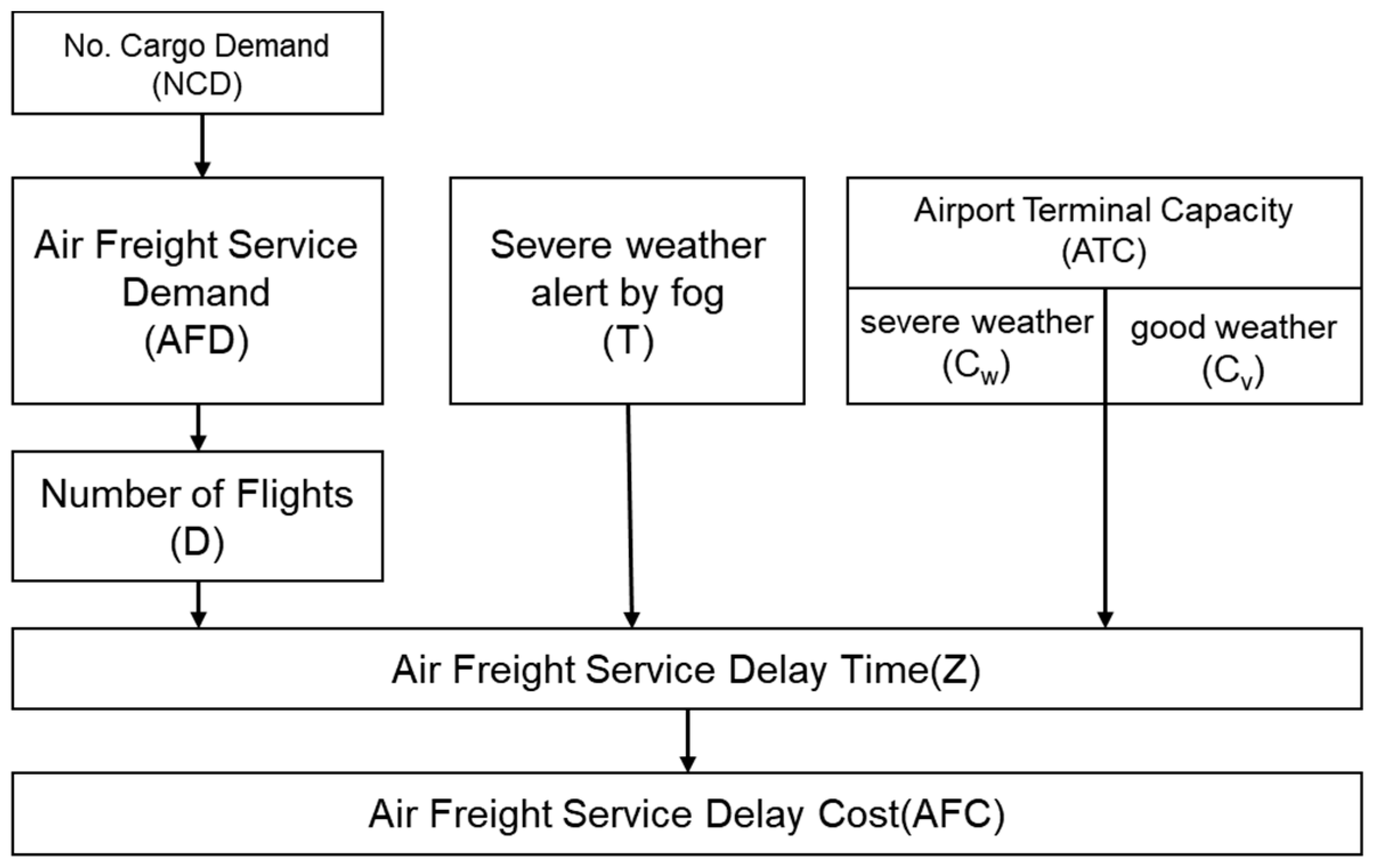
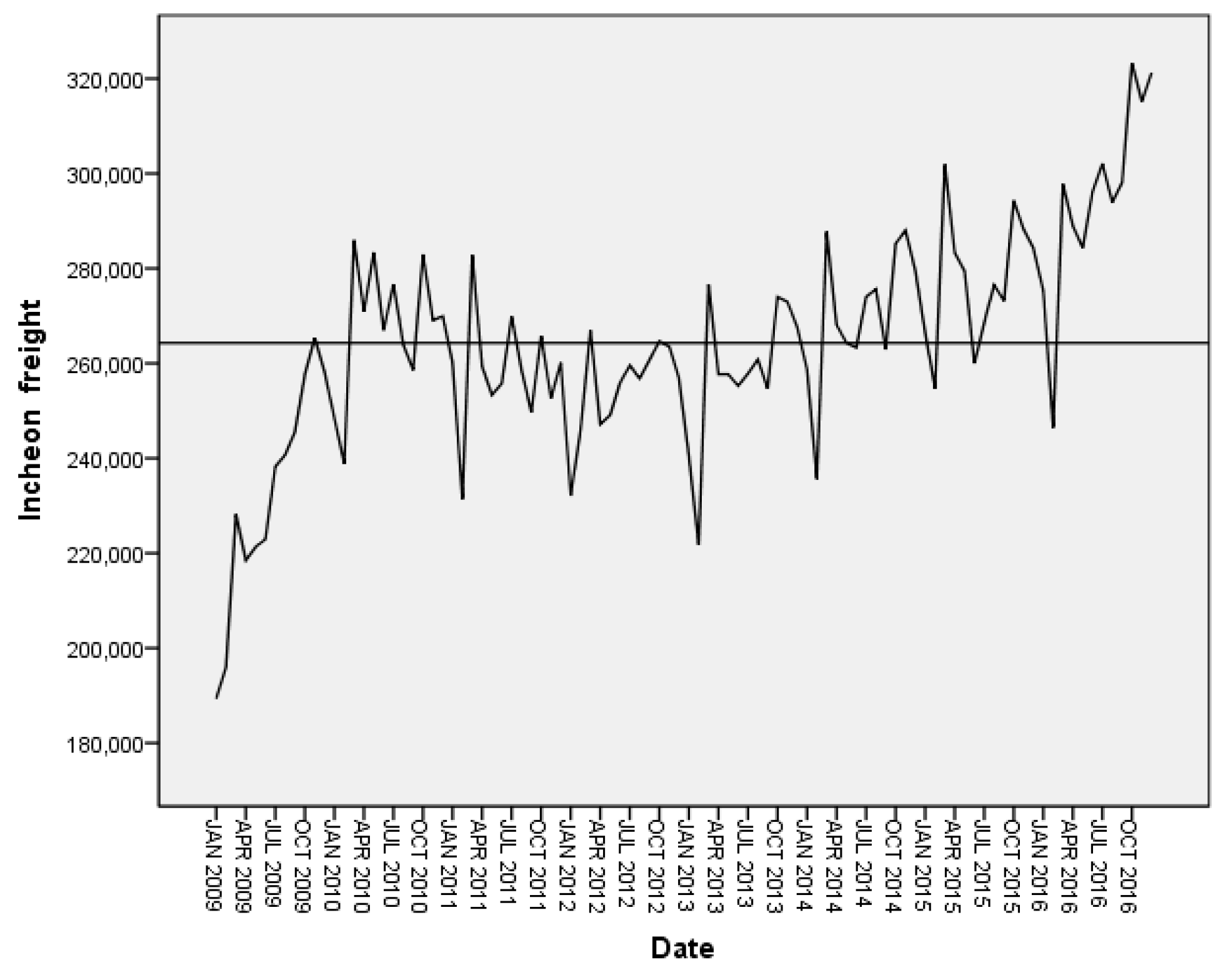
In the current study, demand for air cargo service (cargo throughput) at Incheon International Airport, selected because it has the largest terminal capacity in South Korea, was inputted into the seasonal ARIMA (SARIMA) model for forecasting purposes. We also developed a regression model that predicts the number of flights by regression analysis between air cargo service demand and number of flights. We predicted the delay times of flights by substituting the predicted number of flights and severe weather (i.e., low visibility) alert times into a delay reduction model. This delayed time was calculated according to the delay cost calculation criterion of Eurocontrol, and a model was developed to quantitatively calculate delay costs in air cargo service caused by severe weather conditions.
5. Conclusions
In recent years, consumer demand for rapid delivery has grown, and the development of comprehensive logistics has led to an increase in air cargo transportation. In the past, the cost of air cargo was relatively high, mainly operated by a small sector of transportation centered on IT and high-value products. Today, however, the connection between air transportation and land transportation has been enhanced to improve the speed and timeliness of cargo transportation.
In an environment where supply chain globalization has expanded and the importance of air cargo transportation has increased, weather factors are very important factors affecting operating costs. This study selected low visibility due to fog as a representative factor affecting air cargo transportation delay for analysis. The purpose of this study was to suggest implications for the cost aspect of air cargo operation by predicting delay costs based on delay times caused by low visibility.
In airports, multitudinous delays in flight service are due to many types of dangerous conditions for aviation operation. This study developed a model that quantitatively calculates and predicts delay costs in air navigation service at a South Korean airport (i.e., the Incheon airport complex due to low visibility). In this study, we estimated and forecasted delay costs based on weather factors in order to make strategic decisions about operational costs to improve air cargo service. The model for the prediction of delay costs developed herein can be further utilized to quantitatively estimate economic loss due to delays caused by factors other than low visibility. March of 2018 had a heavy influence on total delay of 2018 and therefore on the cost of delay. This value was very exceptionally high, but it was not a persistent situation of low visibility. Incheon International Airport is located in the western part of Korea. In March 2018, the Meteorological Administration and Incheon International Airport (KICA) confirmed that a number of low-visibility alerts of Incheon were issued due to the heavy fog and fine dust caused by the west coast, resulting in high delay time. There are several ways to improve the service delay in an air transportation. One way is to properly utilize the ILS (instrumental landing system) category possessed by the airport, which obviously influences the total amount of delay. The ILS is the most popular landing aid in the world. It is a distance-angled support system for landing in reduced visibility, and its task is the safe conduct of the aircraft from the prescribed course landing on the approach path. Additionally, a target operation under low visibility conditions may be allowed, depending on the lowest figure among airport ILS, aircraft onboard equipment and pilot certification.
In conclusion, delay costs caused by low visibility have been shown to increase, depending on air cargo service. Thus, service delays due to low visibility should be improved. Our proposed model estimates economic losses for strategic decisions aiming to improve air cargo service. This model is applicable to other similar settings as well.