3.3.1. Simplified Yield Response Function
The impact of increasing rates of typically used mineral fertilizer on Rain water use efficiency (WUE) and Radiation use efficiency (RUE) of maize grain yield and stover biomass productivity was estimated across the Agro-Ecological zones (AEZs) using the crop model LINTUL5 which is later embedded into a general modeling framework. LINTUL5 is a bio-physical model that simulates plant growth, biomass, and yield as a function of climate, soil properties, and crop management using experimentally derived algorithms. The applied version LINTUL5 simulates potential crop growth (limited by solar radiation only) under well-watered conditions, ample nutrient supply and the absence of pests, diseases, and weeds. To simulate a continuous cropping system, the model was embedded into a general modeling framework, SIMPLACE (Scientific Impact Assessment and Modelling Platform for Advanced Crop and Ecosystem Management) [
43]. The SIMPLACE<LINTUL5-SLIM-SoilCN solution of the modeling platform was used in this study. SLIM is a conceptual soil water balance model subdividing the soil in a variable number of layers, substituting the two layer approach in Lintul5 [
44]. In this modeling framework, water, nutrients (NPK), temperature, and radiation stresses restrict the daily accumulation of biomass, root growth, and yield.
Spatial resolution was at the 1 km grid cell level, where cropland and soil data are available. Long maturing cycle maize variety was used in the simulations in AEZ1 and AEZ2 where the length of crop growing season is more than 160 days, elsewhere (AEZ 3) a medium maturing cycle variety was used in the simulations. The simulated yield from all the simulation units within each administrative zone was averaged to obtain a representative value for a specific year to compare with the observed yield.
Two sets of parameters for hybrid maize cultivars, namely BH660 (a long maturing cycle variety) and BH540 (a medium maturing cycle variety) were calibrated against experimental data (yield and phenology) under rain-fed conditions collected from Melko (Jimma Agricultural Centre) for the years 2008 to 2012. Fertilizer application rates used in the experiments were 23 kg ha-1 of urea and 217 kg ha-1 DAP (Di-Ammonium Phosphate) at planting and 150 kg ha-1 urea after 35 days of planting. According to Jaleta et al. [
45], both BH660 and BH540 are the most popular and widely grown maize varieties in the country. The maize crop parameter dataset (provided with the LINTUL5 model and Srivastava et al. [
46]), was used as a starting point to establish a new parameter set for these maize varieties. Further details on the crop modeling effort can be found in Srivastava et al. [
47].
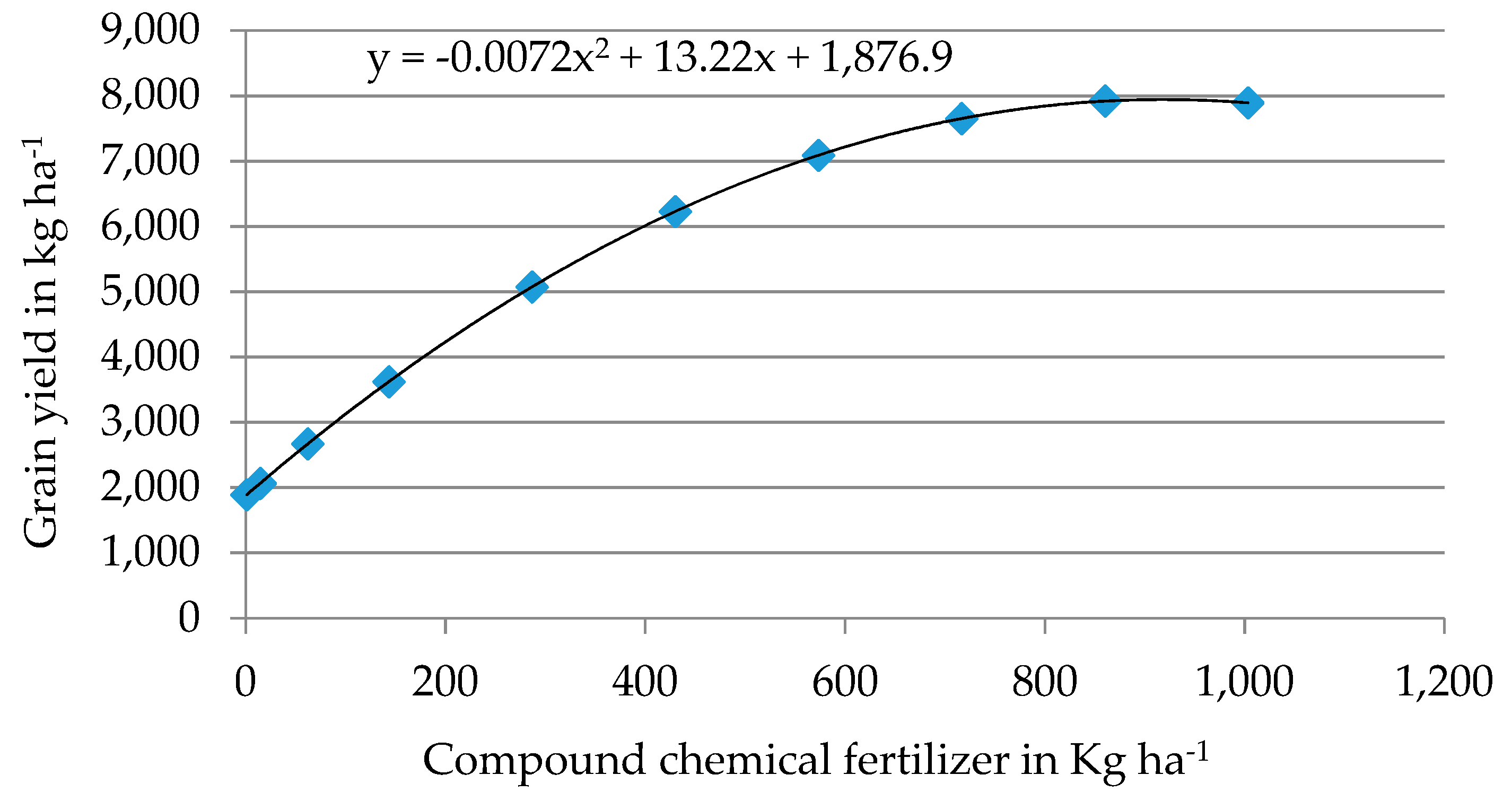
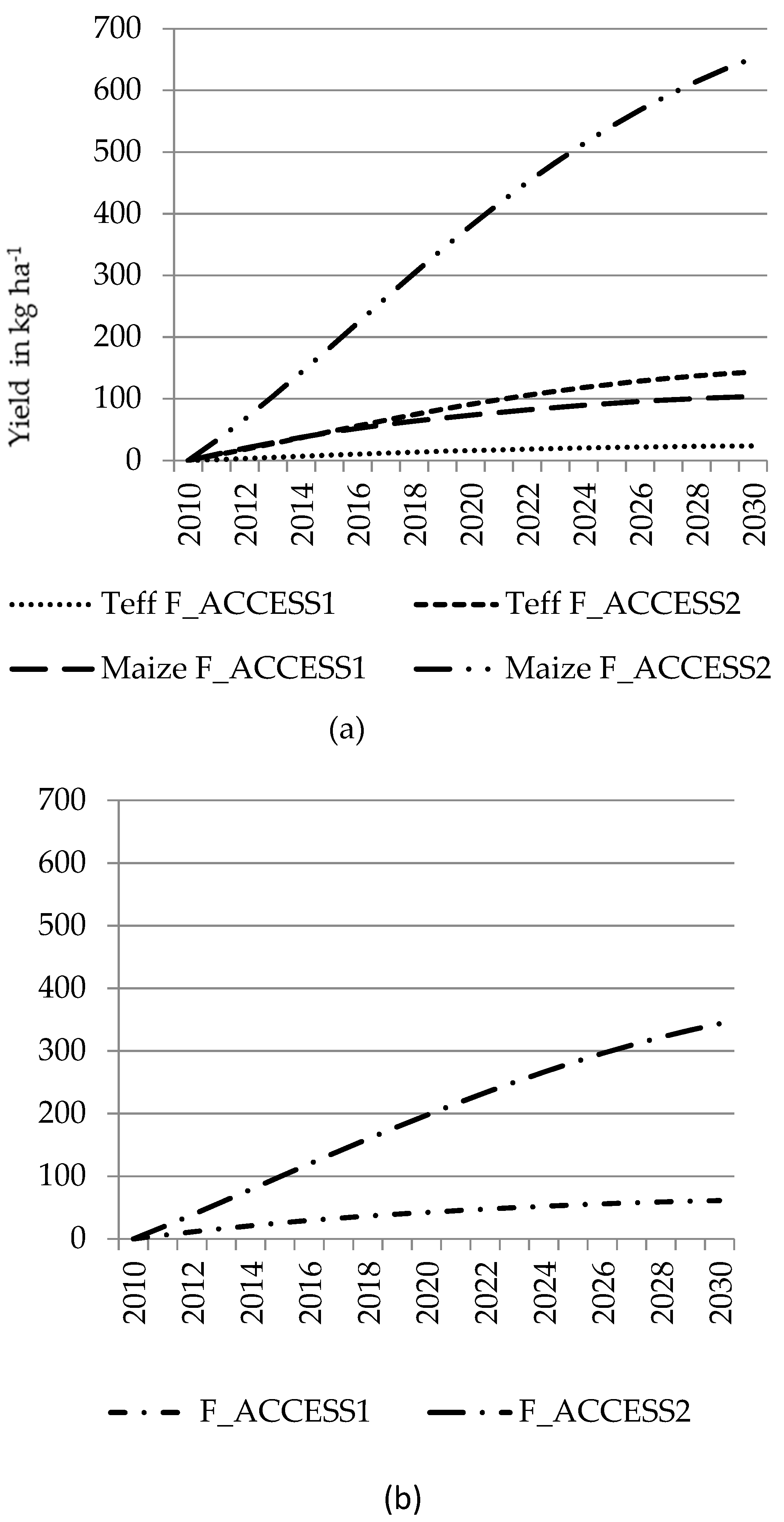
Results show a strong effect of the application rate of mineral fertilizer on maize yield and stover biomass across the AEZs. The national average of maize grain yield under different application rates of the mentioned mix of fertilizers (DAP and urea in a 1:0.9 ratio) is illustrated by
Figure 2. The data points allow for a quadratic approximation which is differentiable with respect to fertilizer use and can thus be used to derive economically optimal fertilizer use rates under alternative input and output price constellations. This yields a fertilizer yield response function for maize. (
Table A5 displays parameters and results of the quadratic approximation function that is integrated into the CGE model)
The results show that the maximum yield level to be obtained in Ethiopia is far above the current maize yield, which is due to low fertilizer use. At given price levels for fertilizer and maize, the profit function that can be obtained from the yield response function has its optimal fertilizer use level per hectare far above the observed levels. The reason might be unobserved costs in fertilizer use in Ethiopia. Thus, to use this yield function in an economic model, the first order condition (FOC) of the profit function has to be calibrated to current use levels, which is explained in
Section 3.3.2.
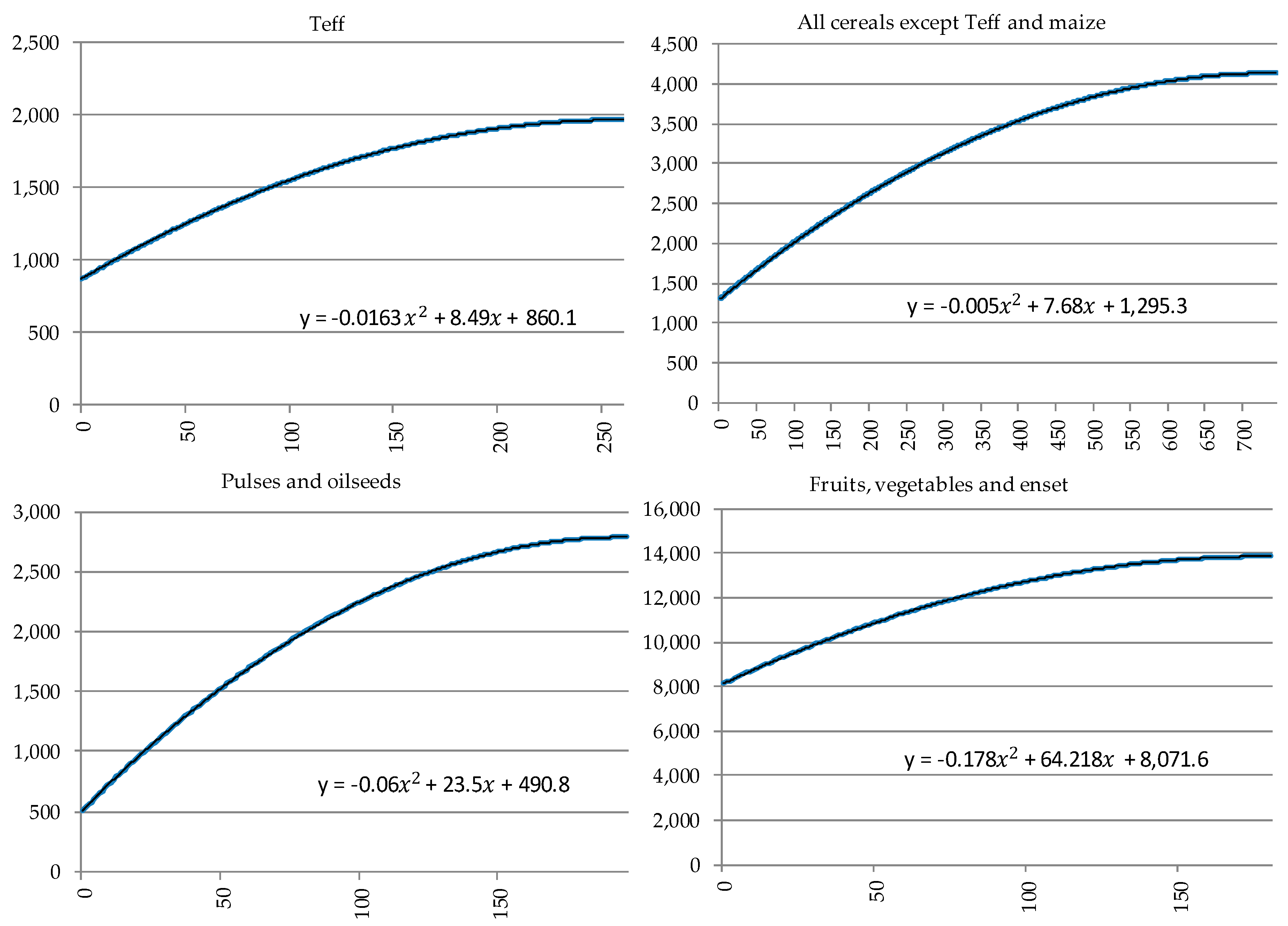
Though we have a crop model only for maize, the other crops in the SAM are considered as well in order to not have maize as the only crop where flexible fertilizer use is linked to productivity. Unlike the estimation strategy applied for maize, actual survey data is used to econometrically estimate fertilizer yield response function for the other crops in the SAM (teff, wheat, barley (
Hordeum vulgare), sorghum, pulses, oilseeds, vegetable and fruits, ‘enset’ (false banana), and cash crops like coffee, chat, flower and sugar). We obtain the required data from three rounds (2009/10, 2010/11 and 2011/12) AgSS dataset. Obviously, fertilizer use efficiency of field experiments and actual farmers’ practices cannot be comparable. In order to narrow the gap, we only use farmers that are relatively best in terms of modern agronomic practices – that are under extension coverage and use improved seeds in addition to chemical fertilizer. The fertilizer-yield response function that we estimated for the other crops (i.e., except maize) is displayed in
Figure A1. As explained above for maize, at given price levels for the crops and fertilizer, the profit functions that can be obtained from the yield response functions have their optimal fertilizer use levels per hectare far above the observed average levels. These differences exhibit the level of unobserved costs in fertilizer use of the average farmers as compared to the best ones.
3.3.2. Integrating Yield Response into the CGE Model
The principal approach to incorporate a fertilizer yield response function to the CGE model is to create a ‘fertilizer module’, i.e., a set of equations that a) calculates yields, b) identifies optimal fertilizer use levels per hectare based on a profit function approach, and c) finally ensures that changes in nominal quantities and prices obtained in this module are translated into equivalent changes in quantities and prices in the CGE model. Moreover, minor changes to a very limited number of equations of the original CGE model have to be made.
First, the yield (
Qyperhaa,c) is defined as a function of fertilizer per hectare by a quadratic model:
Where: a stands for set of activities with fertilizer-yield function and c for set of commodities
is the quadratic parameter in the yield response function
Qabsferta,c is the quantity of fertilizer input per hectare
is the linear parameter in the yield response function
is the constant term in the yield response function
The parameters of the above quadratic function (
fertqa,c, fertlina,c, and
fertconsta,c) are shown in
Figure 2 and
Figure A1. Now it has to be ensured that changes in output (
QAa) per unit of land use (
QFf,a) in the CGE model compared to its base value are equal to changes of simulated yields per hectare (
Qyperhaa,c) relative to its base level (
Qyperha0a,c):
Where: f stands for set of factors but now specifically represents factor land
is a simulated unit of land use
is a unit of land use at the base
The next step is defining a fertilizer demand function that expresses marginal revenues and costs of fertilizer use.
Adding prices for the crops and fertilizer (
Poutputa,c and
Pfertc), the profit per hectare of producing commodity
c from activity
a (π
a,c) can be expressed as:
As yield per hectare (
Qyperhaa,c) is a function of fertilizer input per hectare (
Qabsferta,c), profit per hectare can be re-written by combining Equation 1 and 3. Differentiating it for the decision variable
Qabsferta,c and solving for the fertilizer price (
Pfertc) yields:
The problem is now that if we apply recent average prices (of the crops and fertilizer) in this equation, we would get a much higher fertilizer application rate as observed for Ethiopia. That means there must be unobserved cost elements of fertilizer that were not accounted for, and which we have to add to
Pfertc in order to arrive at observed fertilizer application levels. This fixed calibration factor is thus calculated as the difference between marginal profitability of fertilizer application and marginal fertilizer price. Thus the complete fertilizer demand function is now given as:
Fertcaliba,c can be interpreted as an indicator for unobserved costs in fertilizer marketing and use, and could thus be varied in policy simulations or long-term scenarios of better marketing and use efficiency.
We have created a new equation with the first order condition (FOC) above, and we have created two new variables contained in it, the absolute prices for the crop outputs (
Poutputc) and fertilizer (
Pfertc) that have to be defined in related equations. In these, changes in absolute prices are determined by changes in relative prices in the CGE part of the model where markets determine price changes for the crops and fertilizer:
Where: is the simulated commodity price in the CGE model
is the commodity price in the CGE model at the base
The next step is to enable the CGE model to change its fertilizer input use in accordance with the fertilizer module. By default, single intermediate inputs in the CGE model are a fixed share (icac,a) of total intermediate inputs per activity, i.e., a Leontief demand function.
For variable fertilizer use, this restrictive function has to be relaxed and also altered to better reflect crop production processes. First, the icac,a input-output coefficients for fertilizer input use are made variable for crops with yield functions while leaving the other inputs’ shares in these crops fixed. Generally, input use in such crops is no longer related to the total quantity of inputs (QINTAa in the CGE model), but rather to land use, which is the standard way to describe a production technology in agronomy, meaning that
Where: c stands for fertilizer, a for crop activities with fertilizer-yield function, and f for factor land
For these same cropping activities, total input use (QINTAa) is not a fixed proportion of output anymore but simply the sum of all inputs used (QINTa,c).
QINTAa then enters the equation defining total output as a function of factor use (value added) and input use. With a subset of
icac,a being variable, changes of fertilizer use per unit of land use in the physical fertilizer module can now be translated into input use per unit of land in the CGE model:
The last necessary step is to relax the fixed ‘yield parameter’ fprdf,a that is part of the CGE model equation defining value-added creation through factor use. This parameter serves as an equivalent to the yield per hectare from the fertilizer module and therefore has to be made variable for those activity-commodity pairs for which fertilizer yield response function is available. Counterfactual changes in fprdf,a are then equivalent to changes in crop yields from the yield response functions.