1. Introduction
The recent financial crises have imparted a number of negative consequences on the real economy in the US and the world as a whole. Specifically, the effects of the 2007–2008 global financial crisis and the 2011 European sovereign debt crisis on the global economy resulted in a large number of bank failures. The economic recession that followed the crises alerted that systemic bank failures could have devastating impacts on economic and social stability. Due to this series of events, the systemic risk of the banking sector began to draw the attention of academics as well as policy makers.
The systemic risk of the banking sector generally refers to the potential risk of system breakdown due to the interconnection among financial institutions. Specifically, Engle et al. [
1] defined systemic risk as the propensity of an individual financial institution to be under-capitalized when the financial structure as a whole is under-capitalized. The authors also reported that, in Europe, a traditionally bank-based economy, banks account for nearly 80% of the total systemic risk. Our study investigates whether the systemic risk of the banking sector can be reduced if the financial structure becomes more market-based, relying less on traditional bank financing. Financial structure can be classified as bank-based or market-based, and the literature is inconclusive with regard to the relative advantages of each system. This study contributes to the debate on bank-based versus market-based structure from the perspective of the relative systemic risk of the banking sector.
One stream of the literature has highlighted the merits of a bank-based financial structure. For example, banks can finance industrial expansion more effectively than markets in emerging economies, and state-owned banks can overcome market failures and funnel domestic savings to strategically important projects [
2]. A bank-based structure is more effective for new innovative activities because banks can credibly supply additional funds during projects [
3]. However, the opposite view focuses on the inefficient allocation of capital in a bank-based financial structure. Banks have an inherent bias toward conservative investments; thus, they are likely to avoid funding innovative projects [
4], and powerful banks frequently impede innovation by extracting informational rent and protecting established firms [
5,
6]. State-owned banks are more inclined to supply credit to labor-intensive industries rather than strategic industries, where possible innovation and opportunities exist for growth [
7]. In addition, market-based economies have shown significantly stronger recovery than bank-based economies following a crisis [
8]. An expansion of banking system relative to markets is linked to higher systemic risk and slower economic growth [
9], and the service provided by banking sector becomes relatively less important than those provided by markets as economies grow [
10]. Finally, some literature has documented that banks and markets are irrelevant and complementary to each other for economic growth [
11,
12]. Thus, the overall development of the financial structure, through developing several financing channels, is more important for enhancing capital allocation [
13,
14,
15,
16]. In this perspective, reduction in information asymmetry and/or transaction costs and an improvement in the legal efficiency are the primary issues; thus, whether the financial structure is bank-based or market-based would not matter [
13,
17].
To the best of our knowledge, this study is one of the early papers to directly examine the relationship between the financial structure of an economy and the systemic risk of the banking sector. In this work, we attempt to answer the following questions: (1) Did a shift from bank-based financial structure to market-based financial structure in the Chinese economy reduce the systemic risk of the banking sector? (2) If so, what are the transmission channels?
To answer these questions, this study employs two important approaches that are distinct from those used in previous studies. First, our study uses data from the Chinese banking sector. The Chinese government led the rapid shift in its financial structure, which had been dominated by the banking sector [
18], towards a market-based structure. In 2004, the government proposed, for the first time, that China should vigorously develop security markets and increase the proportion of market-based financing in the economy. The 11th five-year plan, proclaimed at the People’s Congress in 2006, required an increase in the proportion of market financing and placed an emphasis on developing security markets. The third Plenary Session of the 18th Central Committee of the Communist Party of China in 2013 further emphasized the need to increase the proportion of security markets in the financial structure. In 2014, the government again accentuated the healthy development of equity and bond markets. Meanwhile, the Chinese banking sector is considered to have potential risk even without any bank default. The Chinese government provided several aid packages to banks to reduce the potential risk. For instant, Industrial and Commercial Bank of China (ICBC) received capital of 15 billion USD in April 2005, and capital of 19 billion USD was given to Agricultural Bank of China (ABC) in November 2008. Four state-owned asset management companies were established in 1999 to take over the non-performing loans (NPLs) worth 1.4 trillion RMB from the Big Four banks—Bank of China (BoC), China Construction Bank (CCB), ICBC and ABC—at their face value. Thus, the Chinese banking sector provides a noble experimental setting to examine the association between changes in the financial structure and the systemic risk of the banking sector.
Second, we use a market-based approach to measure the systemic risk of the banking sector due to the limitations associated with the traditional accounting measures that are widely used in the literature. Accounting measures of the systemic risk of the banking sector heavily rely on the financial statements of banks, such as the NPL ratio, earnings, profitability, and asset liquidity. Because accounting statements are reported with a delay and only measured quarterly, accounting measures of the systemic risk do not include real-time or short-term risk measurement [
19,
20,
21]. Furthermore, accounting-based measures are exposed to the manipulation and amendment of accounting principles. The unique definition of NPLs in China is another reason why market-based measures are used. The Chinese definition of NPLs excludes low-quality loans transferred to state-owned asset management companies; thus, NPLs of Chinese banks are underestimated [
18]. In addition, market-based risk measures could reflect the risk of the fast-growing shadow banking industry in China, while accounting-based measures cannot, due to the off-balance sheet nature of the business [
22]. The size of China’s shadow banking system was estimated as ranging from 13.7 trillion RMB to 30 trillion RMB during 2012–2013. This is about 14–31% of the aggregate assets of Chinese banks and approximately 26–57% of the GDP in 2012 [
22]. Assessing the systemic risk of the banking sector based on accounting measures would result in an underestimation of the true insolvency risk of the banking sector.
The market-based systemic risk has been widely employed in academic research, because market information can capture the inter-connections between banks that are not shown in banks’ financial statements [
23]. For instance, equity return data were used to calculate the systemic risk, defined as the probability of a given number of simultaneous bank defaults [
24]. The
Nth-to-default probability, which indicates the probability of observing an
Nth default among different financial institutions, used credit default swaps to measure the systemic risk, because price changes reflect the anticipation of future price movement [
19,
20]. Specifically, Merton’s approach has been widely applied for the evaluation of an individual bank’s risk, assessment of credit risk, and pricing deposit insurance [
25,
26,
27]. Merton’s Value at Risk (VaR) framework was utilized to examine the relationship between systemic risk, GDP growth, the bank equity index and inflation rate [
28], and the interactions between default, credit growth, and asset prices in the banking sector of 17 countries [
29].
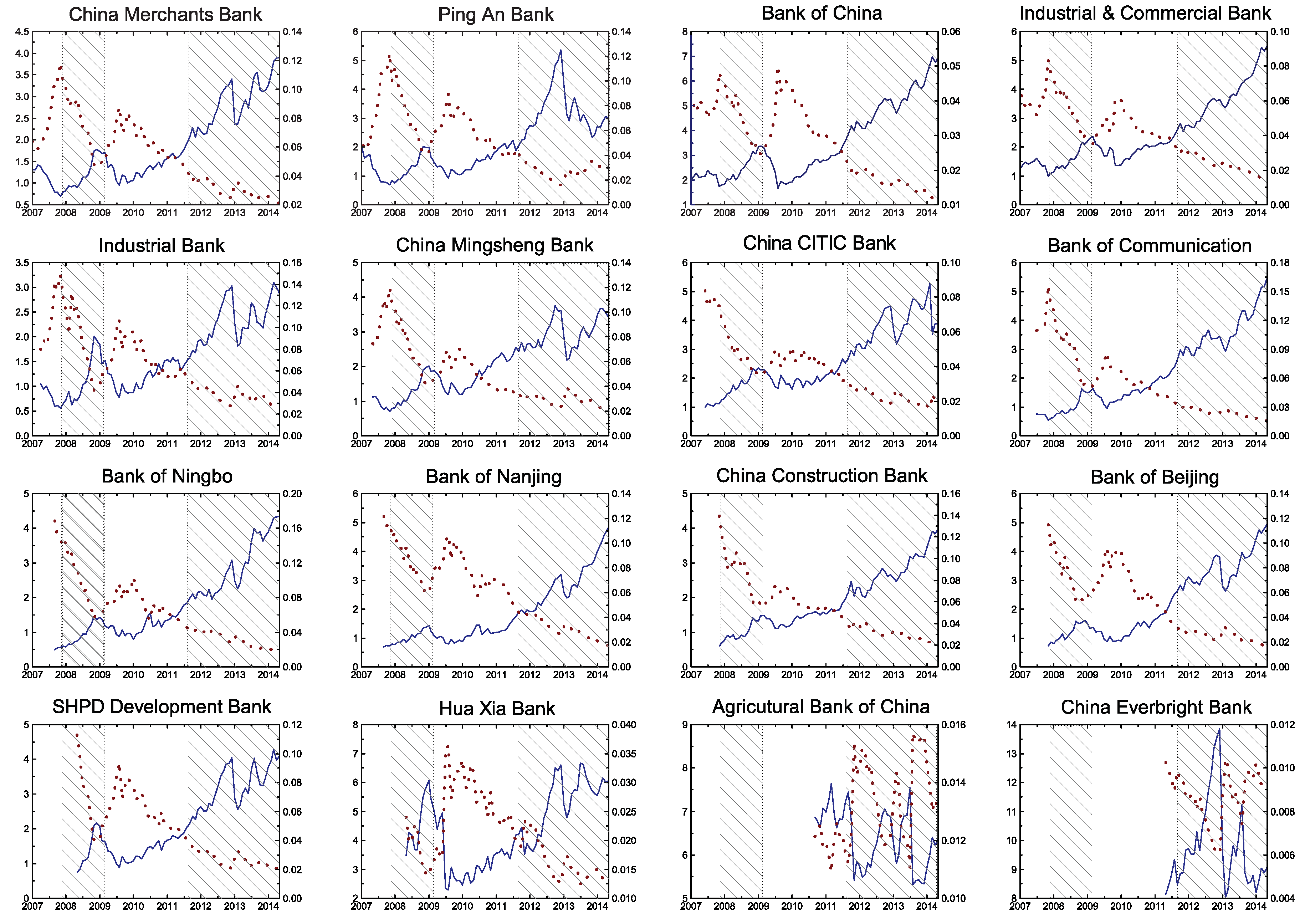
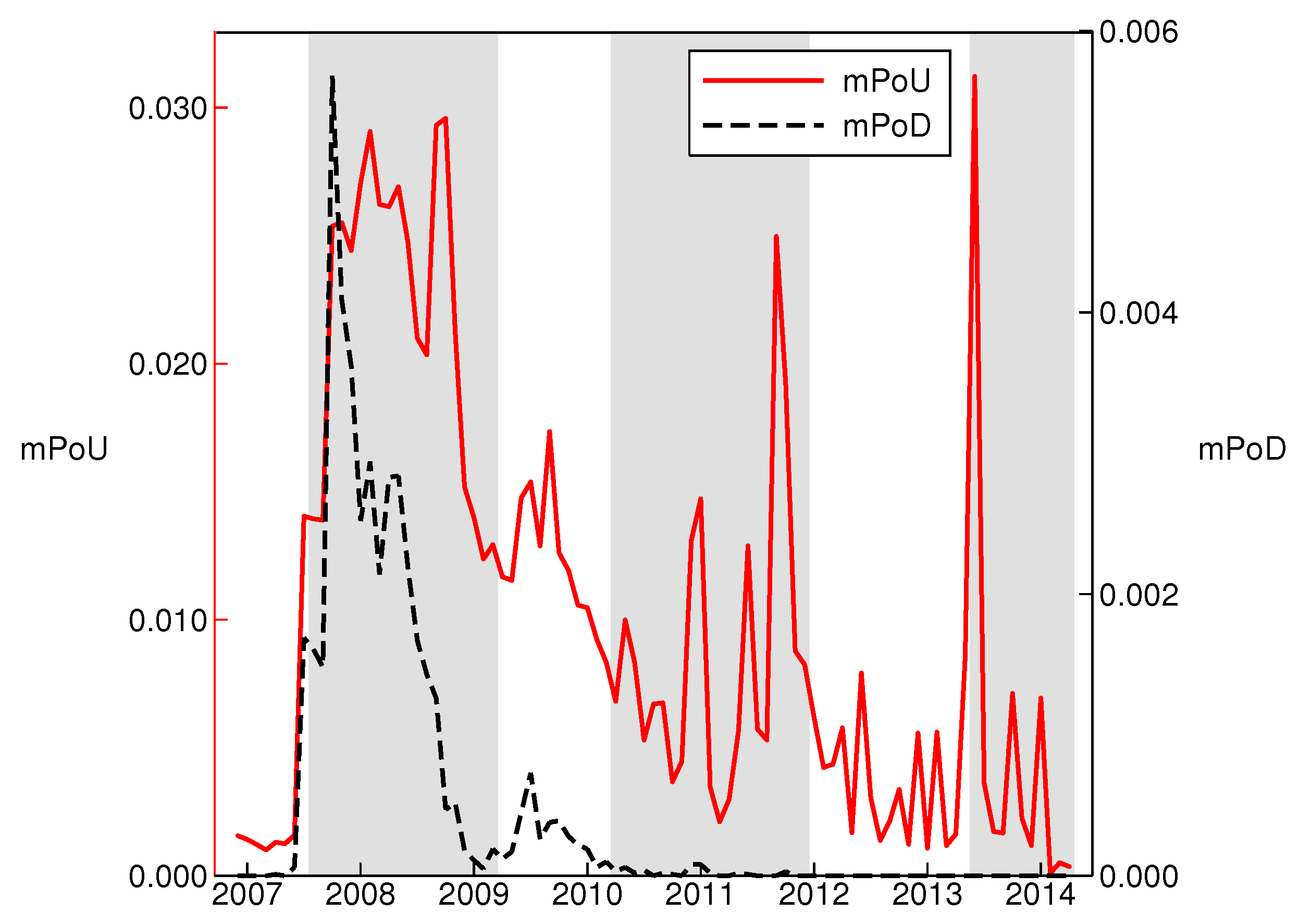
We adopt multiple probability of under-capitalization (mPoU), the aggregation of an individual bank’s probability of under-capitalization (PoU), as the measure of the systemic risk of the banking sector. PoU is conceptually similar to the better-known probability of default (PoD), but with several advantages. Banks are subject to maintain a certain capital adequacy ratio (CAR); thus, under-capitalization is a more imminent threat to banks than default. PoU includes the minimum capital reserve in its calculation, but PoD does not. Furthermore, mPoU takes financial contagion into account through asset correlation in the banking sector. It is essential to do this when measuring the systemic risk of the banking sector because a small shock of an individual bank, originally affecting only a few financial institutions, can easily spread to other banks and put the whole banking system at risk [
30,
31].
Our empirical study first shows that the market-based measure of the systemic risk of the banking sector in China is lower when the financial structure becomes more market-based. This perhaps indicates the effort of the Chinese government to promote a more market-based financial structure paid off by lowering the systemic risk of the banking sector. Although two exogenous changes in banking regulation during the sample period also contribute to the reduction in the systemic risk of the banking sector, we show that the shift to a market-based financial structure further reduces the systemic risk of the banking sector.
Next, we test two transmission channels through which the financial structure can influence the systemic risk of the banking sector. The development of a market-based financial structure and thus higher liquidity in the stock market can have a positive influence on firm performance [
32,
33,
34,
35,
36]. Better firm performance can enhance the debt capacity of a firm, in terms of both short-term and long-term debt, thus decreasing the systemic risk of the banking sector. In addition, the development of a market-based financial structure can slow down the growth of banks’ credit, leading to intensified monitoring efforts of borrowers and new loan applications. Thanks to the enhanced monitoring efforts on credits, individual bank’s credit risk is reduced, thus the systemic risk of the banking sector decreases.
This paper contributes to the literature by providing the link between the financial structure and the systemic risk of the banking sector. The finance sector, including the banking sector, in the 21st century is highly interconnected both domestically and globally. Recent financial crises illustrated how vulnerable the global finance sector is to local bank failure. Our results suggest that reshaping a financial structure towards a more market-based structure could lower the systemic risk of the banking sector in economies dominated by a bank-based financial structure. Our findings imply that the shift of a financial structure from a bank-based to a market-based structure not only leads to the development of financial markets, but also may help to support the stability and sustainability of an economy. In this research, the sustainability of an economy specifically indicates an economy’s ability to maintain long-term growth through the reduction in the systemic risk of the banking sector.
We further add to the literature by suggesting that the financial structure of an economy is another factor that influences the systemic risk of the banking sector. The literature has documented that bank size, leverage, liquidity, non-interest income, and banks’ sovereign debt holdings are the key factors which govern the systemic risk of the banking sector [
37,
38,
39]. In addition, it has been stated that banks with more traditional lending business models and more liquid assets are likely to have a lower systemic risk. However, bank profitability and the market-to-book ratio have been shown to have no significant impact on the systemic risk [
40].
The remainder of this paper is organized as follows.
Section 2 describes the data and methodology used in this study.
Section 3 presents the relationship between financial structure and the systemic risk of the banking sector, and the two transmission channels.
Section 4 provides the conclusion.