The Scale-Dependent Behaviour of Cities: A Cross-Cities Multiscale Driver Analysis of Urban Energy Use
Abstract
1. Introduction
Aim
- To investigate whether power-laws for energy use intensity can be found between urban energy flows—(residential) electricity and natural gas—and urban features associated with urban energy consumption—population, population density, income. This is done by using larger dataset than in previous studies, which includes megacities as well as smaller cities.
- To examine if such power laws could be extended to scales smaller than city scale (municipalities, ZIP codes, etc.), or in other words to investigate the scale (in-)dependency of urban energy power laws. This is done by reviewing relations across 10 cities with data both at the micro-territorial scale (MTU) and at the city scale.
- To investigate if each city of the case study, when looked at infra-urban level, exhibits uniform power laws—thus entailing shared internal processes between cities—regarding energy use intensity and if these provide better information and prediction power than city-scale power-laws.
2. Materials and Methods
2.1. Presentation of the Case Studies and Data
2.1.1. Macroscale Data
2.1.2. Microscale Data
2.2. Method
3. Results
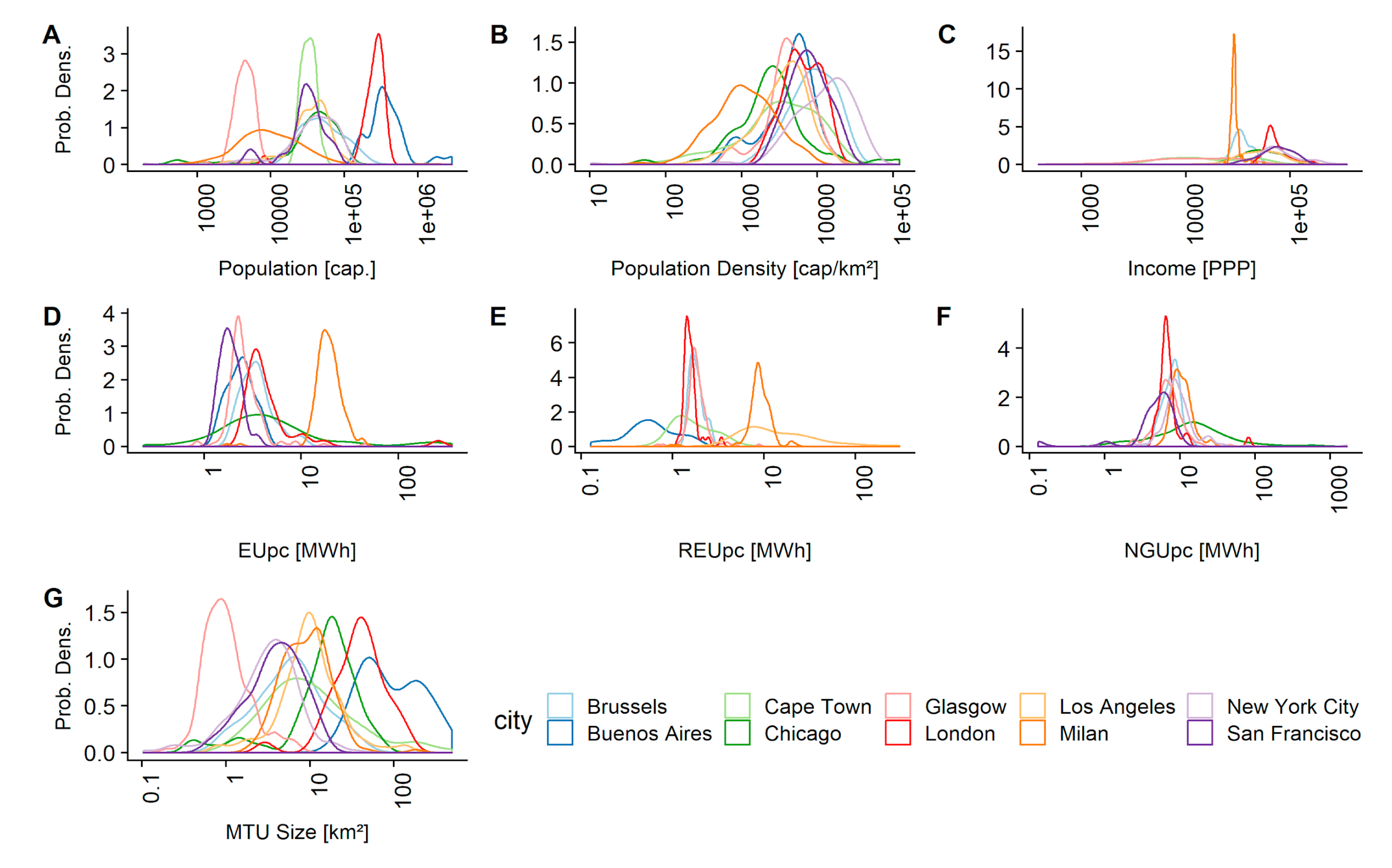
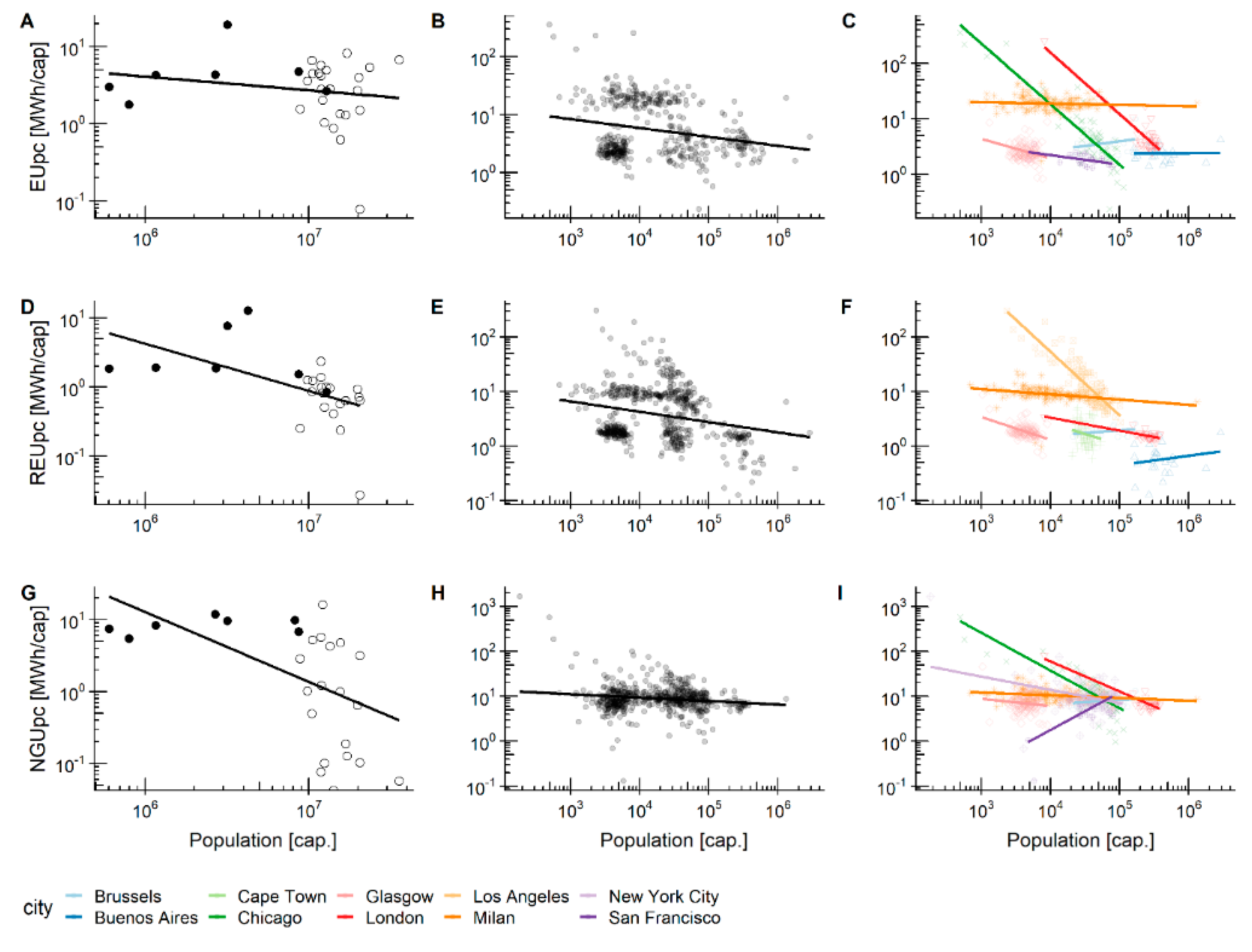
3.1. Energy Use and Population Size
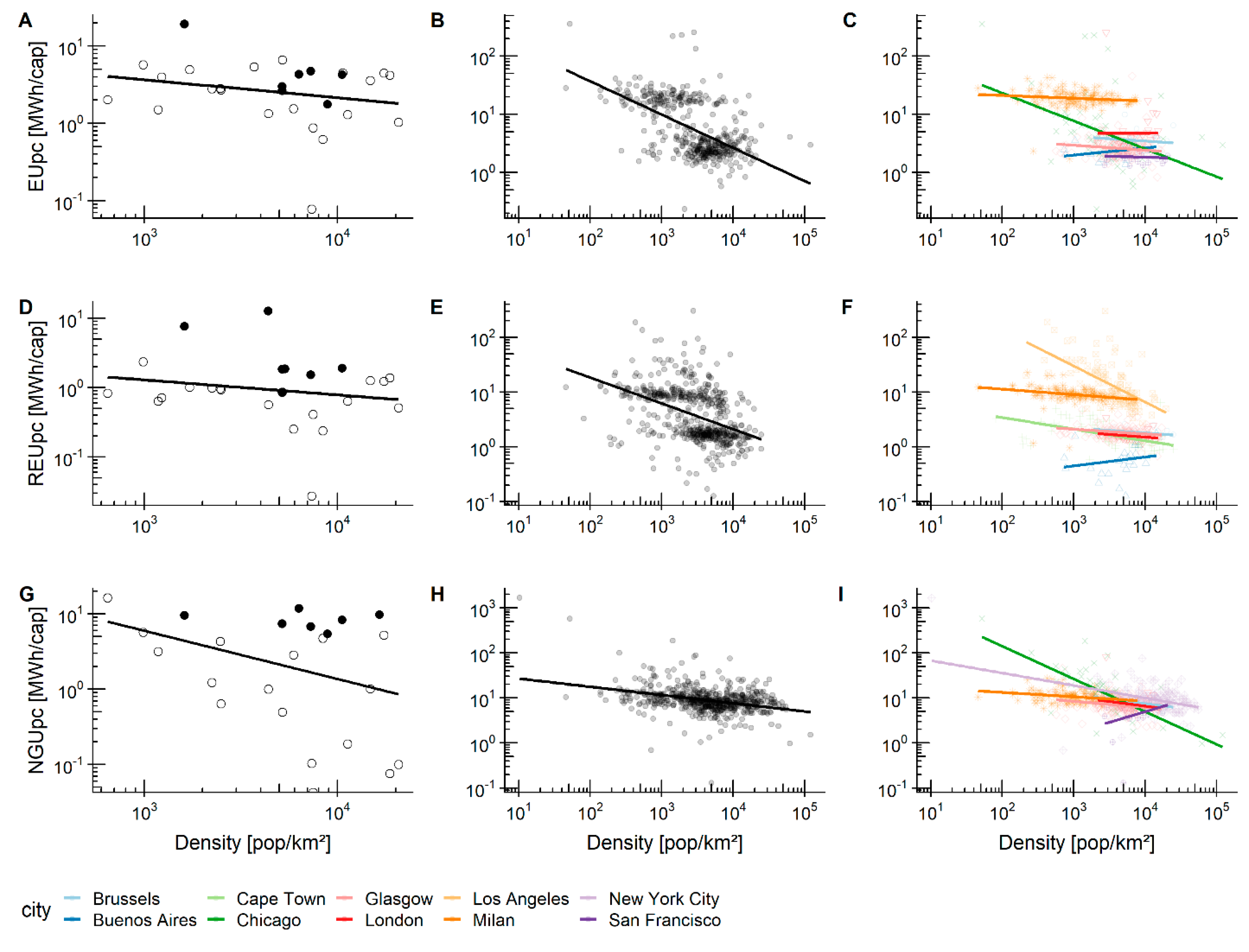
3.2. Energy Use and Population Density
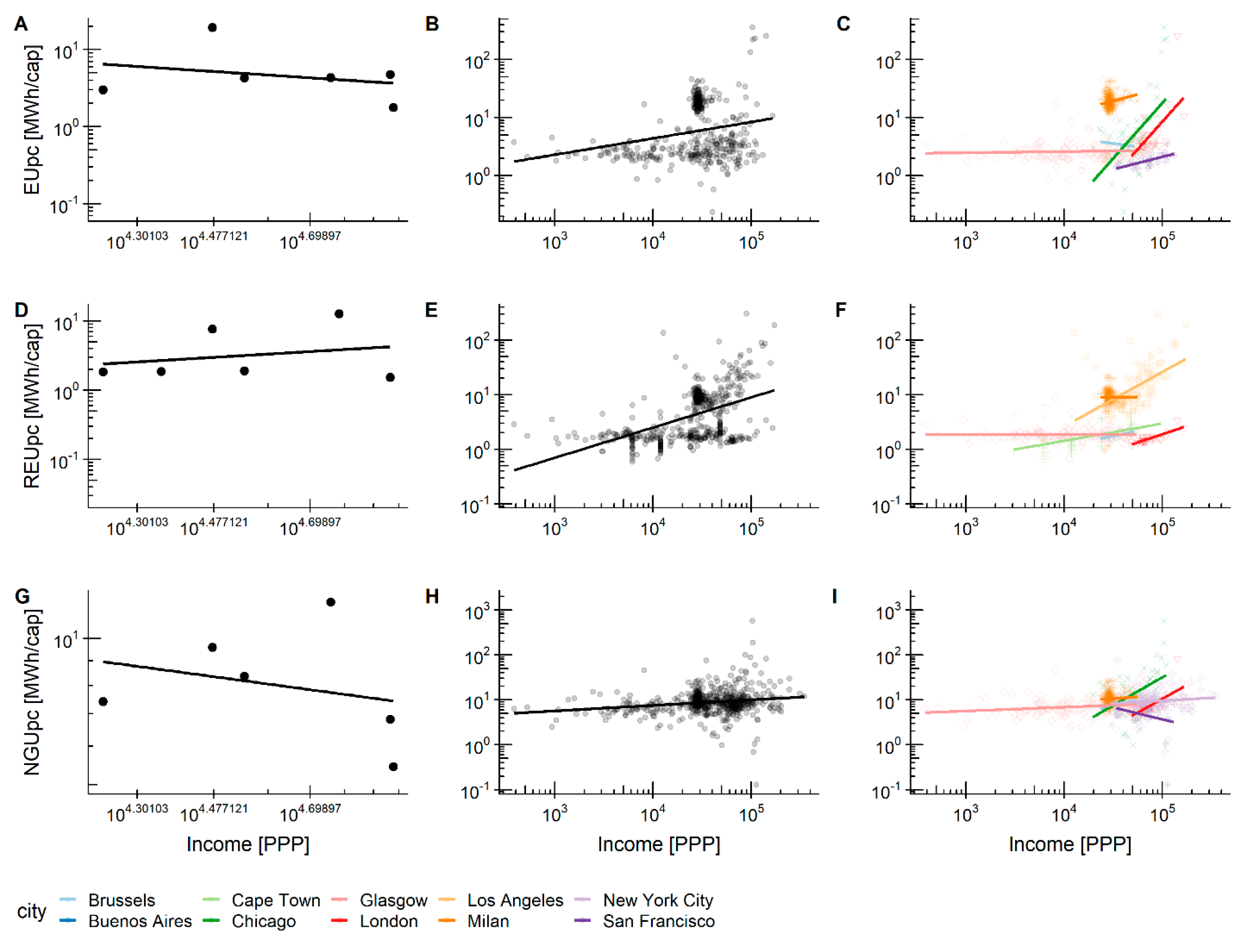
3.3. Energy Use and Median Income (PPP)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seto, K.C.; Dhakal, S.; Bigio, A.; Blanco, H.; Delgado, G.C.; Dewar, D.; Huang, L.; Inaba, A.; Kansal, A.; Lwasa, S.; et al. Human Settlements, Infrastructure and Spatial Planning. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- ICLEI; UNEP; UN-Habitat. Sustainable Urban Energy Planning. A Handbook for Cities and Towns in Developing Countries; UN-Habitat: Nairobi, Kenya, 2009. [Google Scholar]
- UN DESA. World Urbanization Prospects: The 2014 Revision, Highlights; United Nations Department of Economic and Social Affairs Population Division: New York, NY, USA, 2014. [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Bertoldi, P.; Piers de Raveschoot, R.; Paina, F.; Melica, G.; Gabrielaitiene, I.; Janssens-Maenhout, G.; Meijide Orive, A.; Iancu, A. How to Develop a Sustainable Energy Action Plan (SEAP) in the Eastern Partnership and Central Asian Cities; Scientific and Technical Research Reports: Luxembourg, 2014; ISBN 1831-9424. [Google Scholar]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S., III; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Grubler, A.; Bai, X.; Buettner, T.; Dhakal, S.; Fisk, D.J.; Ichinose, T.; Keirstead, J.E.; Sammer, G.; Satterthwaite, D.; Schulz, N.B.; et al. Urban Energy Systems. In Global Energy Assessment—Toward a Sustainable Future; Cambridge University Press: Cambridge, UK; New York, NY, USA; The International Institute for Applied Systems Analysis: Laxenburg, Austria, 2012; Chapter 18; pp. 1307–1400. [Google Scholar]
- Creutzig, F.; Baiocchi, G.; Bierkandt, R.; Pichler, P.P.; Seto, K.C. Global typology of urban energy use and potentials for an urbanization mitigation wedge. Proc. Natl. Acad. Sci. USA 2015, 112, 6283–6288. [Google Scholar] [CrossRef] [PubMed]
- Štreimikienė, D. Residential energy consumption trends, main drivers and policies in Lithuania. Renew. Sustain. Energy Rev. 2014, 35, 285–293. [Google Scholar] [CrossRef]
- Zachariadis, T.; Taibi, E. Exploring drivers of energy demand in Cyprus–Scenarios and policy options. Energy Policy 2015, 86, 166–175. [Google Scholar] [CrossRef]
- Warren-Rhodes, K.; Koenig, A. Escalating Trends in the Urban Metabolism of Hong Kong: 1971–1997. AMBIO J. Hum. Environ. 2001, 30, 429–438. [Google Scholar] [CrossRef] [PubMed]
- Newcombe, K. Energy use in Hong Kong: Part II, sector end-use analysis. Urban Ecol. 1975, 1, 285–309. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Stewart, I.; Facchini, A.; Cersosimo, I.; Mele, R.; Chen, B.; Uda, M.; Kansal, A.; Chiu, A.; Kim, K.G.; et al. Energy and material flows of megacities. Proc. Natl. Acad. Sci. USA 2015, 112, 5985–5990. [Google Scholar] [CrossRef] [PubMed]
- Facchini, A.; Kennedy, C.; Stewart, I.; Mele, R. The energy metabolism of megacities. Appl. Energy 2017, 186, 86–95. [Google Scholar] [CrossRef]
- Athanassiadis, A.; Bouillard, P. Contextualizing the Urban Metabolism of Brussels: Correlation of resource use with local factors. In Proceedings of the CISBAT 2013, International Conference, Cleantech for Smart Cities & Building from Nano to Urban Scale, EPFL-Lausanne, Lausanne, Switzerland, 4–6 September 2013. [Google Scholar]
- Athanassiadis, A.; Christis, M.; Bouillard, P.; Vercalsteren, A.; Crawford, R.H.; Khan, A.Z. Comparing a territorial-based and a consumption-based approach to assess the local and global environmental performance of cities. J. Clean. Prod. 2016, 173, 112–123. [Google Scholar] [CrossRef]
- Lenzen, M.; Dey, C.; Foran, B. Energy requirements of Sydney households. Ecol. Econ. 2004, 49, 375–399. [Google Scholar] [CrossRef]
- Wiedenhofer, D.; Lenzen, M.; Steinberger, J.K. Energy requirements of consumption: Urban form, climatic and socio-economic factors, rebounds and their policy implications. Energy Policy 2013, 63, 696–707. [Google Scholar] [CrossRef]
- Duvigneaud, P.; Denayer-De Smet, S. L’écosystème URBS: L’écosystème urbain bruxellois. In Productivité Biologique en Belgique; Duculot, É., Ed.; Éditions Duculot: Paris, France, 1977. [Google Scholar]
- Wang, Q.; Li, R. Drivers for energy consumption: A comparative analysis of China and India. Renew. Sustain. Energy Rev. 2016, 62, 954–962. [Google Scholar] [CrossRef]
- Shammin, M.R.; Herendeen, R.A.; Hanson, M.J.; Wilson, E.J.H. A multivariate analysis of the energy intensity of sprawl versus compact living in the U.S. for 2003. Ecol. Econ. 2010, 69, 2363–2373. [Google Scholar] [CrossRef]
- Howard, B.; Parshall, L.; Thompson, J.; Hammer, S.; Dickinson, J.; Modi, V. Spatial distribution of urban building energy consumption by end use. Energy Build. 2012, 45, 141–151. [Google Scholar] [CrossRef]
- Baynes, T.; Lenzen, M.; Steinberger, J.K.; Bai, X. Comparison of household consumption and regional production approaches to assess urban energy use and implications for policy. Energy Policy 2011, 39, 7298–7309. [Google Scholar] [CrossRef]
- Pincetl, S.; Newell, J.P. Why data for a political-industrial ecology of cities? Geoforum 2017, 85, 381–391. [Google Scholar] [CrossRef]
- Batty, M. Building a science of cities. Cities 2012, 29, S9–S16. [Google Scholar] [CrossRef]
- McPhearson, T.; Pickett, S.T.A.; Grimm, N.B.; Niemelä, J.; Alberti, M.; Elmqvist, T.; Weber, C.; Haase, D.; Breuste, J.; Qureshi, S. Advancing Urban Ecology toward a Science of Cities. BioScience 2016, 66, 198–212. [Google Scholar] [CrossRef]
- Youn, H.; Bettencourt, L.M.; Lobo, J.; Strumsky, D.; Samaniego, H.; West, G.B. Scaling and universality in urban economic diversification. J. R. Soc. Interface 2016, 13, 20150937. [Google Scholar] [CrossRef]
- Yakubo, K.; Saijo, Y.; Korosak, D. Superlinear and sublinear urban scaling in geographical networks modeling cities. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 022803. [Google Scholar] [CrossRef] [PubMed]
- Um, J.; Son, S.-W.; Lee, S.-I.; Jeong, H.; Kimd, B.J. Scaling laws between population and facility densities. Proc. Natl. Acad. Sci. USA 2009, 106, 14236–14240. [Google Scholar] [CrossRef] [PubMed]
- Samaniego, H.; Moses, M.E. Cities as organisms: Allometric scaling of urban road networks. J. Transp. Land Use 2008, 1, 21–39. [Google Scholar] [CrossRef]
- Pan, W.; Ghoshal, G.; Krumme, C.; Cebrian, M.; Pentland, A. Urban characteristics attributable to density-driven tie formation. Nat. Commun. 2013, 4, 1961. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, E.A.; Andrade, J.S., Jr.; Makse, H.A. Large cities are less green. Sci. Rep. 2014, 4, 4235. [Google Scholar] [CrossRef] [PubMed]
- Nomaler, O.; Frenken, K.; Heimeriks, G. On Scaling of Scientific Knowledge Production in U.S. Metropolitan Areas. PLoS ONE 2014, 9, e110805. [Google Scholar] [CrossRef] [PubMed]
- Lemoy, R.; Caruso, G. Scaling evidence of the homothetic nature of cities. arXiv 2017, arXiv:1102.4101. [Google Scholar]
- Gomez-Lievano, A.; Youn, H.; Bettencourt, L.M. The statistics of urban scaling and their connection to Zipf’s law. PLoS ONE 2012, 7, e40393. [Google Scholar] [CrossRef]
- Gomez-Lievano, A.; Patterson-Lomba, O.; Hausmann, R. Explaining the prevalence, scaling and variance of urban phenomena. Nat. Hum. Behav. 2016, 1, 0012. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Lobo, J.; Youn, H. The hypothesis of urban scaling: Formalization, implications and challenges. arXiv 2013, arXiv:1301.5919. [Google Scholar]
- Bettencourt, L.M.; Lobo, J.; Strumsky, D.; West, G.B. Urban scaling and its deviations: Revealing the structure of wealth, innovation and crime across cities. PLoS ONE 2010, 5, e13541. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kuhnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.; Lobo, J. Urban scaling in Europe. J. R. Soc. Interface 2016, 13, 20160005. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M. The origins of scaling in cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef] [PubMed]
- Batty, M. The New Science of Cities; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Batty, M. The Size, Scale, and Shape of Cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Arbesman, S.; Christakis, N.A. Scaling of Prosocial Behavior in Cities. Physica A 2011, 390, 2155–2159. [Google Scholar] [CrossRef]
- Alves, L.G.; Ribeiro, H.V.; Lenzi, E.K.; Mendes, R.S. Distance to the scaling law: A useful approach for unveiling relationships between crime and urban metrics. PLoS ONE 2013, 8, e69580. [Google Scholar] [CrossRef]
- Pincetl, S.; Bunje, P.; Holmes, T. An expanded urban metabolism method: Toward a systems approach for assessing urban energy processes and causes. Landsc. Urban Plan. 2012, 107, 193–202. [Google Scholar] [CrossRef]
- Batty, M. Urban Modeling. International Encyclopedia of Human Geography; Kitchin, R., Thrift, N., Eds.; Elsevier: Oxford, UK, 2009; pp. 51–58. [Google Scholar]
- Bai, X.; McAllister, R.R.J.; Beaty, R.M.; Taylor, B. Urban policy and governance in a global environment: Complex systems, scale mismatches and public participation. Curr. Opin. Environ. Sustain. 2010, 2, 129–135. [Google Scholar] [CrossRef]
- Bai, X.; Surveyer, A.; Elmqvist, T.; Gatzweiler, F.W.; Güneralp, B.; Parnell, S.; Prieur-Richard, A.-H.; Shrivastava, P.; Siri, J.G.; Stafford-Smith, M.; et al. Defining and advancing a systems approach for sustainable cities. Curr. Opin. Environ. Sustain. 2016, 23, 69–78. [Google Scholar] [CrossRef]
- Bowden, N.; Payne, J.E. The causal relationship between U.S. energy consumption and real output: A disaggregated analysis. J. Policy Model. 2009, 31, 180–188. [Google Scholar] [CrossRef]
- Gross, C. Explaining the (non-) causality between energy and economic growth in the U.S.—A multivariate sectoral analysis. Energy Econ. 2012, 34, 489–499. [Google Scholar] [CrossRef]
- Hoch, I. Income and City Size. Urban Stud. 1972, 9, 299–328. [Google Scholar] [CrossRef]
- Mansfield, E. City Size and Income. In National Bureau of Economic Research. Regional Income; Wealth, R.I., Ed.; NBER: New York, NY, USA, 1949; pp. 271–318. [Google Scholar]
- Brelsford, C.; Lobo, J.; Hand, J.; Bettencourt, L.M.A. Heterogeneity and scale of sustainable development in cities. Proc. Natl. Acad. Sci. USA 2017, 114, 8963–8968. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Phibbs, P.; Simpson, R.; Wasnik, S. The scaling of income distribution in Australia: Possible relationships between urban allometry, city size, and economic inequality. Environ. Plan. B Urban Anal. City Sci. 2016, 45, 603–622. [Google Scholar] [CrossRef]
- Asafu-Adjaye, J. The relationship between energy consumption, energy prices and economic growth: Time series evidence from Asian developing countries. Energy Econ. 2000, 22, 615–625. [Google Scholar] [CrossRef]
- Halicioglu, F. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef]
- Masih, A.M.M.; Masih, R. Energy consumption, real income and temporal causality: Results from a multi-country study based on cointegration and error-correction modelling techniques. Energy Econ. 1996, 18, 165–183. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R.; Ewing, B.T. Energy consumption, income, and carbon emissions in the United States. Ecol. Econ. 2007, 62, 482–489. [Google Scholar] [CrossRef]
- Mindali, O.; Raveh, A.; Salomon, I. Urban density and energy consumption: A new look at old statistics. Transp. Res. Part A Policy Pract. 2004, 38, 143–162. [Google Scholar] [CrossRef]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Pincetl, S.; Graham, R.; Murphy, S.; Sivaraman, D. Analysis of High-Resolution Utility Data for Understanding Energy Use in Urban Systems: The Case of Los Angeles, California. J. Ind. Ecol. 2016, 20, 166–178. [Google Scholar] [CrossRef]
- Newman, P.W.G.; Kenworthy, J.R. Gasoline Consumption and Cities. J. Am. Plan. Assoc. 1989, 55, 24–37. [Google Scholar] [CrossRef]
- Kennedy, C.; Steinberger, J.; Gasson, B.; Hansen, Y.; Hillman, T.; Havránek, M.; Pataki, D.; Phdungsilp, A.; Ramaswami, A.; Mendez, G.V. Greenhouse Gas Emissions from Global Cities. Environ. Sci. Technol. 2011, 45, 3816–3817. [Google Scholar] [CrossRef]
- Athanassiadis, A.; Crawford, R.H.; Bouillard, P. Exploring the Relationship Between Melbourne’s Water Metabolism and Urban Characteristics. In Proceedings of the State of Australian Cities 2015, Gold Coast, Austrila, 9–11 December 2015. [Google Scholar]
- Porse, E.; Derenski, J.; Gustafson, H.; Elizabeth, Z.; Pincetl, S. Structural, geographic, and social factors in urban building energy use: Analysis of aggregated account-level consumption data in a megacity. Energy Policy 2016, 96, 179–192. [Google Scholar] [CrossRef]
- Huebner, G.M.; Shipworth, D. All about size?—The potential of downsizing in reducing energy demand. Appl. Energy 2017, 186, 226–233. [Google Scholar] [CrossRef]
- Shalizi, C.R. Scaling and hierarchy in urban economies. arXiv 2011, arXiv:1102.4101. [Google Scholar]
- Sarkar, S.; Phibbs, P.; Simpson, R.; Wasnik, S.N. The scaling of income inequality in cities. arXiv 2015, arXiv:1509.00959v1. [Google Scholar]
- Sullivan, G.M.; Feinn, R. Using Effect Size-or Why the P Value Is Not Enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef]
- Blyth, C.R. On Simpson’s Paradox and the Sure-Thing Principle. J. Am. Stat. Assoc. 1972, 67, 364–366. [Google Scholar] [CrossRef]
- Rickwood, P.; Glazebrook, G.; Searle, G. Urban Structure and Energy—A Review. Urban Policy Res. 2008, 26, 57–81. [Google Scholar] [CrossRef]
- Echenique, M.H.; Hargreaves, A.J.; Mitchell, G.; Namdeo, A. Growing Cities Sustainably. J. Am. Plan. Assoc. 2012, 78, 121–137. [Google Scholar] [CrossRef]
| Indicators | Europe | North Am. | Africa | South Am. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Milan | London | Brussels | Glasgow | N.-Y.C. | L.A. | San Francisco | Chicago | Cape Town | Buenos Aires | |
| Macroscale | ||||||||||
| Population [Millions cap.] | 3.18 | 8.66 | 1.16 | 0.60 | 8.23 | 4.56 | 0.81 | 3.08 | 3.74 | 12.81 |
| Area [km2] | 1574 | 1572 | 161 | 172 | 775 | 1835 | 121 | 1477 | 2461 | 3209 |
| HDD (15.5/15.5) | 1840 | 1781 | 2080 | 2410 | 1958 | 306 | 754 | 2785 | 458 | 740 |
| CDD (15.5/15.5) | 918 | 349 | 362 | 105 | 1145 | 1413 | 439 | 986 | 1090 | 1423 |
| Average income per household (PPP) [USD] | 29,782 | 76,399 | 35,277 | 16,667 | N/A | 58,820 | 75,813 | 55,437 | 18,461 | N/A |
| EU - Electricity use [GWh] | 61,247 | 40,957 | 5004 | 1279 | N/A | N/A | 1412 | 11,610 | N/A | 34,170 |
| EUpc - Electricity per capita [MWh/cap] | 19.28 | 4.73 | 4.30 | 2.13 | N/A | N/A | 1.75 | 3.77 | N/A | 2.67 |
| REU - Residential electricity use [GWh] | 24,292 | 13,204 | 2226 | 1113 | N/A | 60,662 | N/A | N/A | 5060 | 10,921 |
| REUpc - Resid. Elec. use per cap. [MWh/cap] | 7.65 | 1.52 | 1.91 | 1.85 | N/A | 13.30 | N/A | N/A | 1.35 | 0.85 |
| NGU- Natural gas use [GWh] | N/A | 59,102 | 9732 | 1807 | 81,002 | N/A | 4355 | 31,792 | N/A | N/A |
| NGUpc - Natural gas per capita [MWh/cap] | N/A | 6.82 | 8.36 | 3.00 | 9.84 | N/A | 5.41 | 10.32 | N/A | N/A |
| Microscale | ||||||||||
| MTU boundaries | Munici-palities | Boroughs | Munici-palities | Interme-diate zones | Zip codes | Zip codes | Zip codes | Zip codes | Wards | Partidos |
| Number of MTUs | 134 | 33 | 19 | 133 | 236 | 123 | 27 | 68 | 82 | 25 |
| Average size of MTUs [km2] | 12 | 48 | 8 | 1 | 3 | 15 | 4 | 22 | 30 | 128 |
| EUpc vs. Pop. | REUpc vs. Pop. | NGUpc vs. Pop. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | slope (β) | r2 | n | slope (β) | r2 | n | slope (β) | r2 | |
| City-scale | 30 | −0.09 | 0.02 | 26 | −0.35 | 0.3 ** | 26 | −0.53 | 0.33 ** |
| MTU aggreg. | 425 | −0.14 | 0.05 *** | 535 | −0.13 | 0.04 *** | 580 | −0.08 | 0.03 *** |
| Brussels | 19 | 0.14 | 0.07 | 19 | 0.07 | 0.14 | 19 | 0.09 | 0.06 |
| Milan | 134 | −0.02 | 0.01 | 134 | −0.09 | 0.09 *** | 134 | −0.06 | 0.04 * |
| Cape Town | NA | NA | 82 | −0.24 | 0.02 | NA | NA | ||
| Buenos Aires | 25 | 0.01 | 0 | 25 | 0.07 | 0.03 | NA | NA | |
| Chicago | 58 | −0.97 | 0.85 *** | NA | NA | 58 | −0.79 | 0.71 *** | |
| London | 33 | −1.04 | 0.76 *** | 33 | −0.16 | 0.64 *** | 33 | −0.63 | 0.8 *** |
| San Francisco | 23 | −0.12 | 0.24 * | NA | NA | 23 | 0.43 | 0.34 ** | |
| Los Angeles | NA | NA | 109 | −1.1 | 0.78 *** | NA | NA | ||
| Glasgow | 133 | −0.27 | 0.06 ** | 133 | −0.29 | 0.23 *** | 133 | −0.15 | 0.02 |
| New York City | NA | NA | NA | NA | 180 | −0.3 | 0.18 *** | ||
| EUpc vs. Density | REUpc vs. Density | NGUpc vs. Density | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | slope (β) | r2 | n | slope (β) | r2 | n | slope (β) | r2 | |
| City-scale | 28 | −0.15 | 0.06 | 26 | −0.09 | 0.03 | 24 | −0.31 | 0.11 |
| MTU aggreg. | 425 | −0.49 | 0.33 *** | 535 | −0.37 | 0.2 *** | 580 | −0.17 | 0.13 *** |
| Brussels | 19 | −0.06 | 0.02 | 19 | −0.06 | 0.13 | 19 | −0.18 | 0.3 |
| Milan | 134 | −0.05 | 0.02 | 134 | −0.1 | 0.09 *** | 134 | −0.09 | 0.09 *** |
| Cape Town | NA | NA | 82 | −0.13 | 0.23 *** | NA | NA | ||
| Buenos Aires | 25 | 0.09 | 0.09 | 25 | 0.06 | 0.04 | NA | NA | |
| Chicago | 58 | −0.42 | 0.17 *** | NA | NA | 58 | −0.65 | 0.52 *** | |
| London | 33 | −0.03 | 0 | 33 | −0.06 | 0.07 | 33 | −0.19 | 0.05 |
| San Francisco | 23 | −0.02 | 0.01 | NA | NA | 23 | 0.29 | 0.12 | |
| Los Angeles | NA | NA | 109 | −0.61 | 0.35 *** | NA | NA | ||
| Glasgow | 133 | −0.06 | 0.01 | 133 | −0.06 | 0.04 * | 133 | −0.12 | 0.05 * |
| New York City | NA | NA | NA | NA | 180 | −0.27 | 0.21 *** | ||
| EUpc vs. Income | REUpc vs. Income | NGUpc vs. Income | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | slope (β) | r2 | n | slope (β) | r2 | n | slope (β) | r2 | |
| City-scale | 6 | −0.31 | 0.08 | 6 | 0.33 | 0.07 | 6 | −0.1 | 0.07 |
| MTU aggreg. | 400 | 0.25 | 0.06 *** | 510 | 0.45 | 0.23 *** | 579 | 0.12 | 0.04 *** |
| Brussels | 19 | −0.21 | 0.02 | 19 | 0.23 | 0.17 | 19 | 0.46 | 0.17 |
| Milan | 134 | 0.4 | 0.02 | 134 | −0.02 | 0 | 134 | 0.14 | 0 |
| Cape Town | NA | NA | 82 | 0.19 | 0.26 *** | NA | NA | ||
| Buenos Aires | NA | NA | NA | NA | NA | NA | |||
| Chicago | 58 | 1.67 | 0.34 *** | NA | NA | 58 | 1.18 | 0.22 *** | |
| London | 33 | 1.72 | 0.38 *** | 33 | 0.39 | 0.69 *** | 33 | 1.12 | 0.47 *** |
| San Francisco | 23 | 0.28 | 0.42 *** | NA | NA | 23 | −0.2 | 0.02 | |
| Los Angeles | NA | NA | 109 | 0.93 | 0.27 *** | NA | NA | ||
| Glasgow | 133 | 0.02 | 0 | 133 | 0 | 0 | 133 | 0.07 | 0.04 * |
| New York City | NA | NA | NA | NA | 180 | 0.12 | 0.01 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bettignies, Y.; Meirelles, J.; Fernandez, G.; Meinherz, F.; Hoekman, P.; Bouillard, P.; Athanassiadis, A. The Scale-Dependent Behaviour of Cities: A Cross-Cities Multiscale Driver Analysis of Urban Energy Use. Sustainability 2019, 11, 3246. https://doi.org/10.3390/su11123246
Bettignies Y, Meirelles J, Fernandez G, Meinherz F, Hoekman P, Bouillard P, Athanassiadis A. The Scale-Dependent Behaviour of Cities: A Cross-Cities Multiscale Driver Analysis of Urban Energy Use. Sustainability. 2019; 11(12):3246. https://doi.org/10.3390/su11123246
Chicago/Turabian StyleBettignies, Yves, Joao Meirelles, Gabriela Fernandez, Franziska Meinherz, Paul Hoekman, Philippe Bouillard, and Aristide Athanassiadis. 2019. "The Scale-Dependent Behaviour of Cities: A Cross-Cities Multiscale Driver Analysis of Urban Energy Use" Sustainability 11, no. 12: 3246. https://doi.org/10.3390/su11123246
APA StyleBettignies, Y., Meirelles, J., Fernandez, G., Meinherz, F., Hoekman, P., Bouillard, P., & Athanassiadis, A. (2019). The Scale-Dependent Behaviour of Cities: A Cross-Cities Multiscale Driver Analysis of Urban Energy Use. Sustainability, 11(12), 3246. https://doi.org/10.3390/su11123246






