An Efficient Burst Detection and Isolation Monitoring System for Water Distribution Networks Using Multivariate Statistical Techniques
Abstract
1. Introduction
2. Materials and Methods
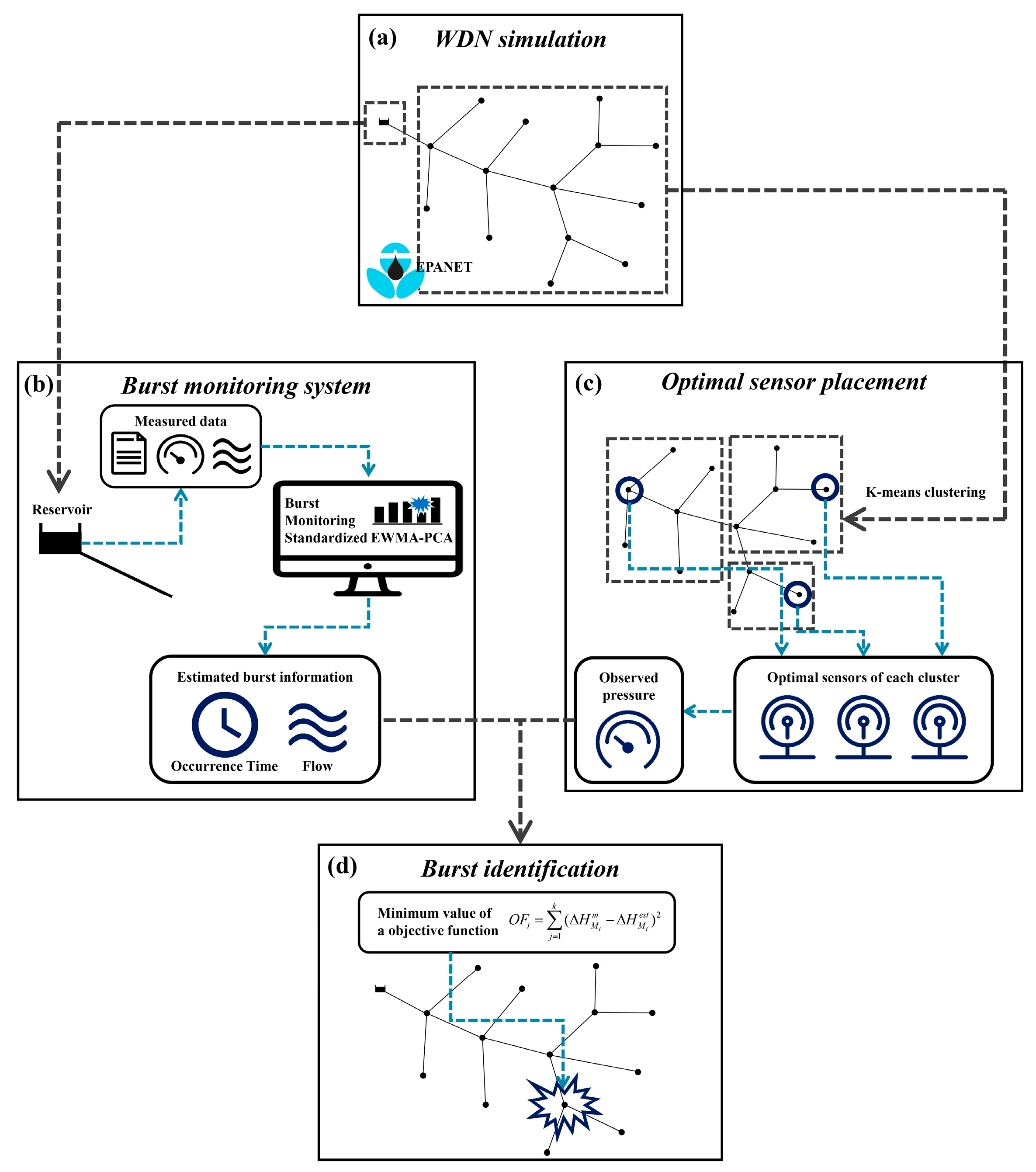
2.1. Research Framework
2.2. Burst Monitoring System
2.2.1. Standardized Exponential Weighted Moving Average (Standardized EWMA)
2.2.2. Principal Component Analysis
2.3. Optimal Pressure Sensor Placement
2.3.1. K-Means Clustering Approach
2.3.2. Sensitivity Analysis
2.4. Burst Identification
3. Results and discussion
3.1. Simulation of a Water Distribution Network
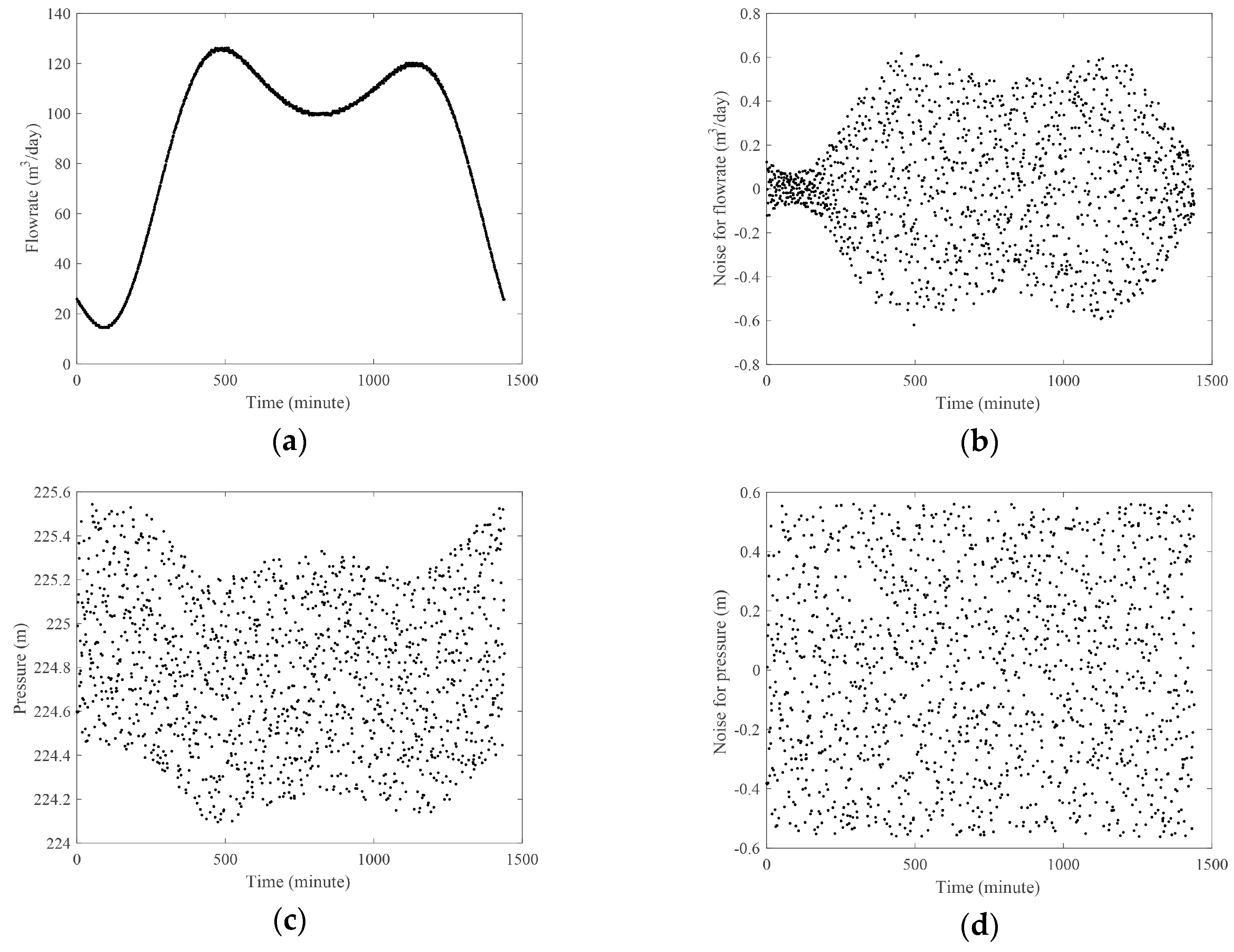
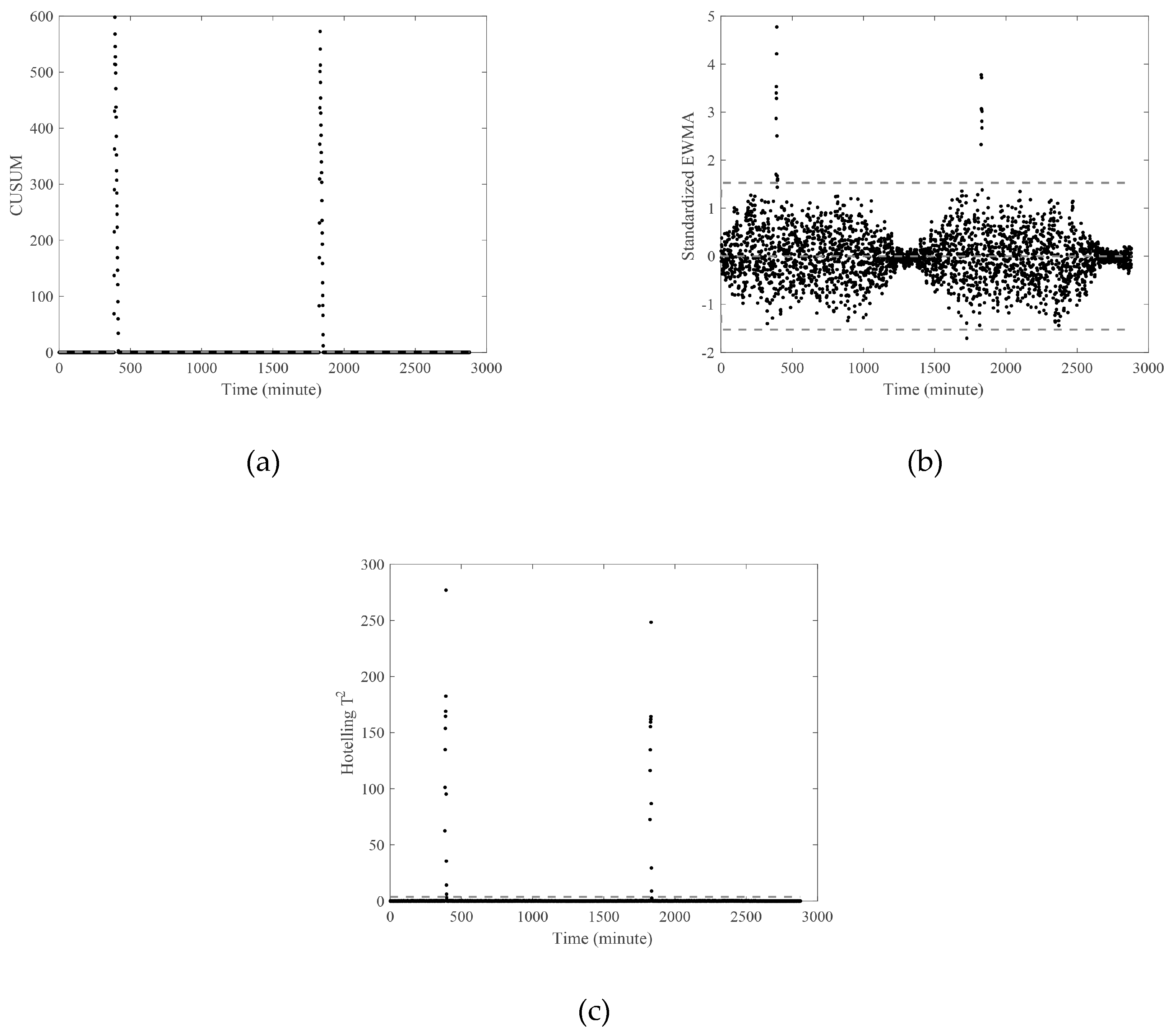
3.2. Monitoring of Burst Occurrence in the WDN
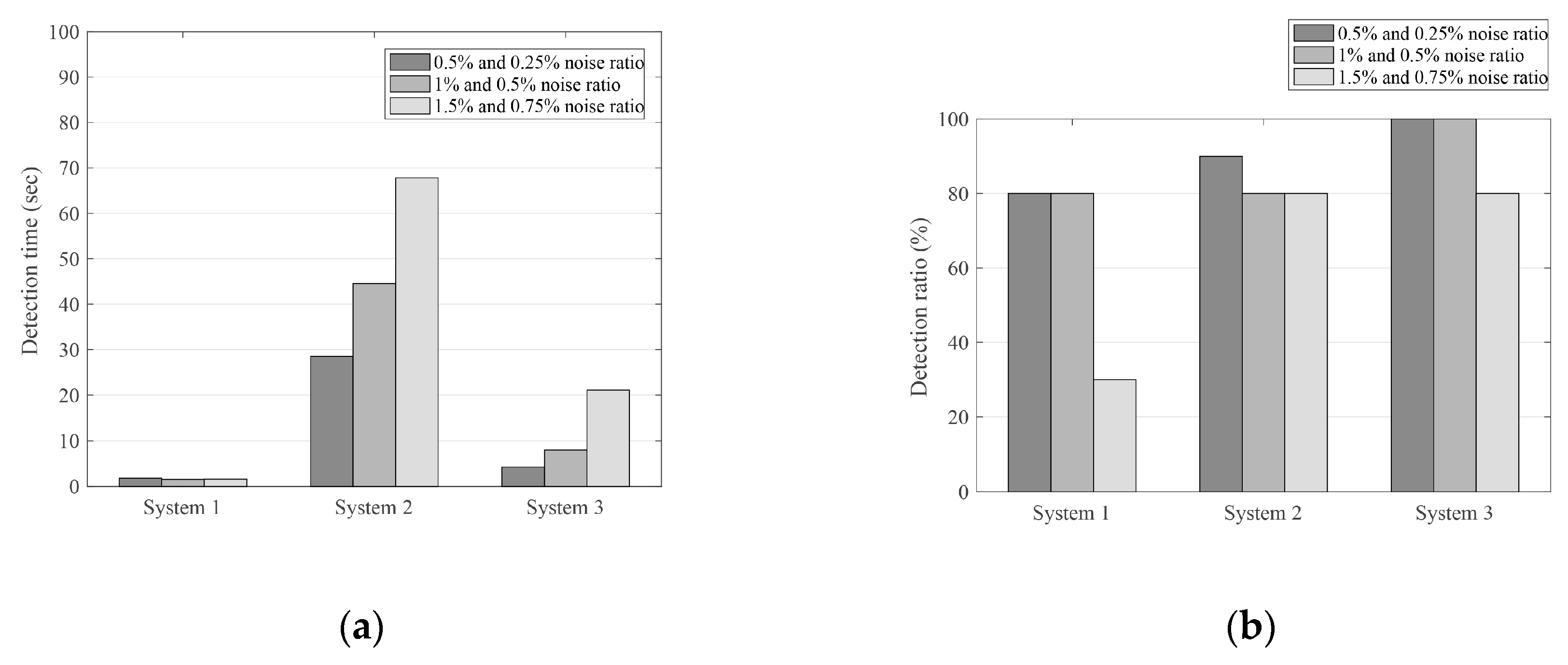
3.3. Robustness of the Three Monitoring Systems
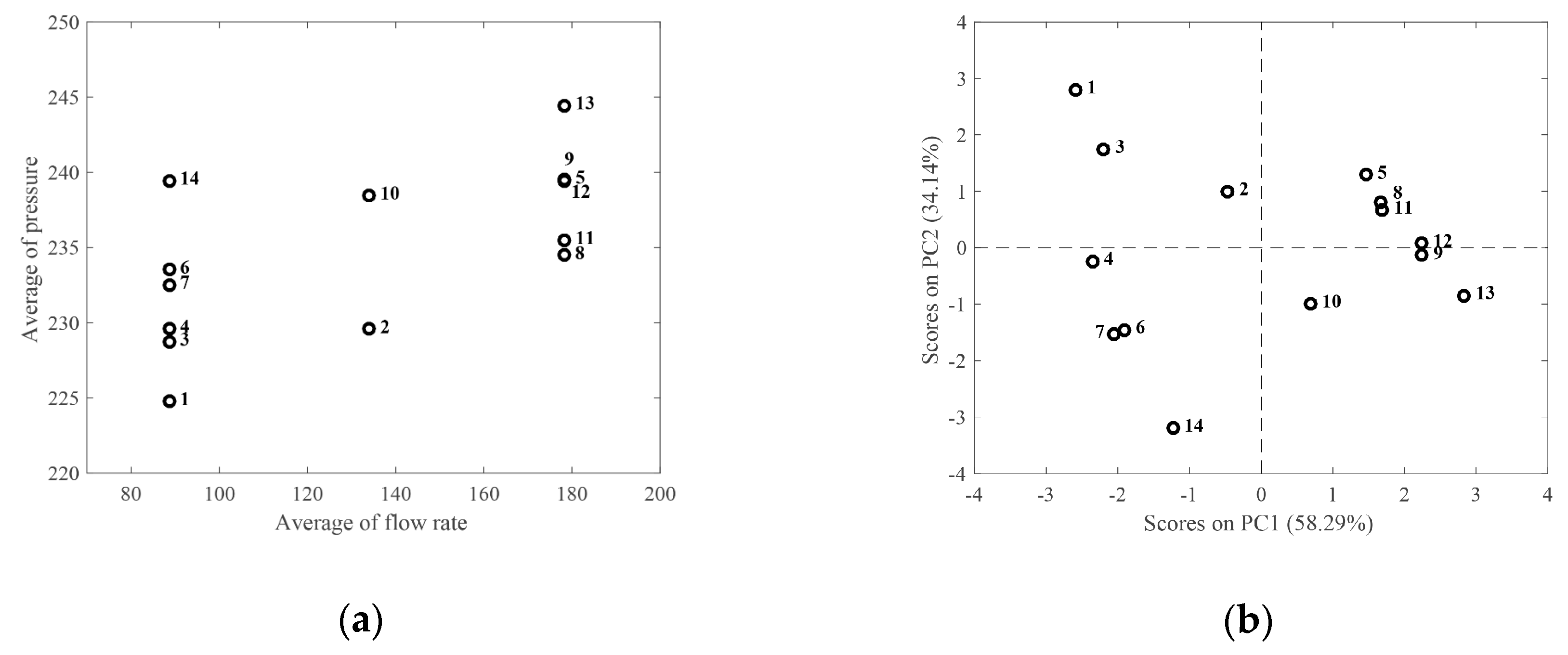
3.4. Optimal Sensor Placement
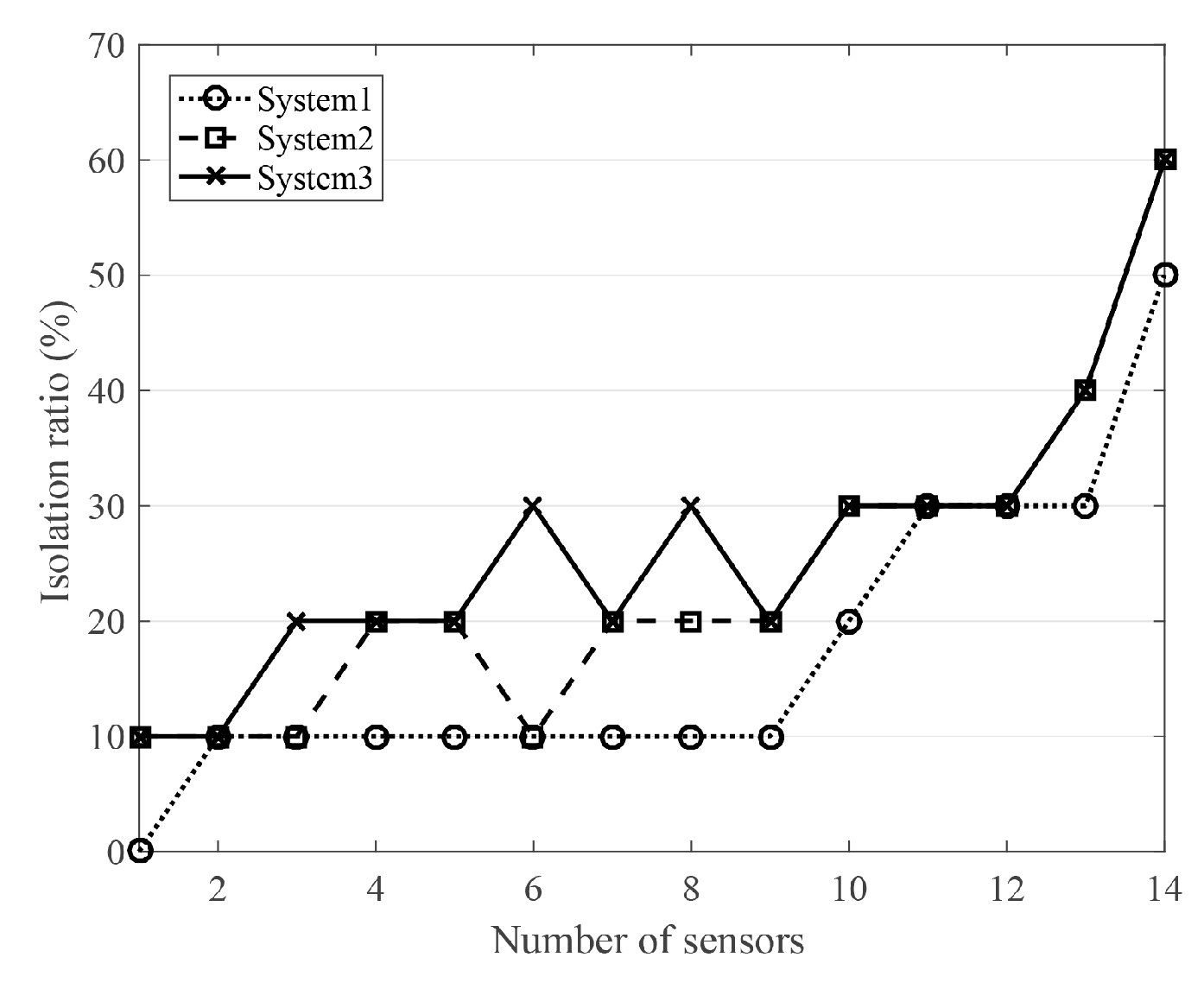
3.5. Burst Isolation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jang, D.; Park, H.; Choi, G. Estimation of leakage ratio using principal component analysis and artificial neural network in water distribution systems. Sustainability 2018, 10, 750. [Google Scholar] [CrossRef]
- Choi, D.Y.; Kim, S.-W.; Choi, M.-A.; Geem, Z.W. Adaptive Kalman filter based on adjustable sampling interval in burst detection for water distribution system. Water 2016, 8, 142. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y.; Yu, X. Performance Evaluation of Water Distribution Systems and Asset Management; American Society of Civil Engineers: Reston, VA, USA, 2018. [Google Scholar]
- Choi, G.B.; Kim, J.W.; Suh, J.C.; Jang, K.H.; Lee, J.M. A prioritization method for replacement of water mains using rank aggregation. Korean J. Chem. Eng. 2017, 34, 2584–2590. [Google Scholar] [CrossRef]
- Jung, S.; Vanli, O.A.; Kwon, S.D. Wind energy potential assessment considering the uncertainties due to limited data. Appl. Energy 2013, 102, 1492–1503. [Google Scholar] [CrossRef]
- Farmani, R.; Kakoudakis, K.; Behzadian, K.; Butler, D. Pipe Failure Prediction in Water Distribution Systems Considering Static and Dynamic Factors. Procedia Eng. 2017, 186, 117–126. [Google Scholar] [CrossRef]
- Rojek, I.; Studzinski, J. Detection and Localization of Water Leaks in Water Nets Supported by an ICT System with Artificial Intelligence Methods as a Way Forward for Smart Cities. Sustainability 2019, 11, 518. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, G.; Suh, J.C.; Lee, J.M. Online burst detection and location of water distribution systems and its practical applications. J. Water Resour. Plan. Manag. 2015, 142, 04015033. [Google Scholar] [CrossRef]
- Wang, B.; Yan, X.; Jin, Y. Fault detection based on polygon area statistics of transformation matrix identified from combined moving window data. Korean J. Chem. Eng. 2017, 34, 275–286. [Google Scholar] [CrossRef]
- Misiunas, D.; Vítkovský, J.; Olsson, G.; Lambert, M.; Simpson, A. Failure monitoring in water distribution networks. Water Sci. Technol. 2006, 53, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Palau, C.; Arregui, F.; Carlos, M. Burst detection in water networks using principal component analysis. J. Water Resour. Plan. Manag. 2011, 138, 47–54. [Google Scholar] [CrossRef]
- Loureiro, D.; Amado, C.; Martins, A.; Vitorino, D.; Mamade, A.; Coelho, S.T. Water distribution systems flow monitoring and anomalous event detection: A practical approach. Urban Water J. 2016, 13, 242–252. [Google Scholar] [CrossRef]
- Hutton, C.; Kapelan, Z. Real-time Burst Detection in Water Distribution Systems Using a Bayesian Demand Forecasting Methodology. Procedia Eng. 2015, 119, 13–18. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A practical multi-objective optimization sectorization method for water distribution network. Sci. Total Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef] [PubMed]
- Romano, M.; Woodward, K.; Kapelan, Z. Statistical Process Control Based System for Approximate Location of Pipe Bursts and Leaks in Water Distribution Systems. Procedia Eng. 2017, 186, 236–243. [Google Scholar] [CrossRef]
- Saccenti, E.; Hoefsloot, H.C.; Smilde, A.K.; Westerhuis, J.A.; Hendriks, M.M. Reflections on univariate and multivariate analysis of metabolomics data. Metabolomics 2014, 10, 361–374. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. A review of data-driven approaches for burst detection in water distribution systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Diao, K.; Rauch, W. Controllability analysis as a pre-selection method for sensor placement in water distribution systems. Water Res. 2013, 47, 6097–6108. [Google Scholar] [CrossRef] [PubMed]
- Farley, B.; Mounce, S.; Boxall, J. Field testing of an optimal sensor placement methodology for event detection in an urban water distribution network. Urban Water J. 2010, 7, 345–356. [Google Scholar] [CrossRef]
- Romero-Tapia, G.; Fuente, M.J.; Puig, V. Leak Localization in Water Distribution Networks using Fisher Discriminant Analysis. IFAC-PapersOnLine 2018, 51, 929–934. [Google Scholar] [CrossRef]
- Sarrate, R.; Blesa, J.; Nejjari, F.; Quevedo, J. Sensor placement for leak detection and location in water distribution networks. Water Sci. Technol. Water Supply 2014, 14, 795–803. [Google Scholar] [CrossRef]
- Costanzo, F.; Morosini, A.F.; Veltri, P.; Savić, D. Model calibration as a tool for leakage identification in WDS: A real case study. Procedia Eng. 2014, 89, 672–678. [Google Scholar] [CrossRef][Green Version]
- Sayyed, M.A.; Gupta, R.; Tanyimboh, T. Modelling pressure deficient water distribution networks in EPANET. Procedia Eng. 2014, 89, 626–631. [Google Scholar] [CrossRef][Green Version]
- Constantin, A.; Niţescu, C.S. Water Distribution Network Design Based on Numerical Simulation in EPANET. In Proceedings of the International Scientific Conference People, Buildings and Environment, Brno, Czech Republic, 17–19 October 2018. [Google Scholar]
- Haq, A.; Khoo, M.B.C. An adaptive multivariate EWMA chart. Comput. Ind. Eng. 2019, 127, 549–557. [Google Scholar] [CrossRef]
- Nam, K.; Kim, M.; Lee, S.; Hwangbo, S.; Yoo, C. Interpretation and diagnosis of fouling progress in membrane bioreactor plants using a periodic pattern recognition method. Korean J. Chem. Eng. 2017, 34, 2966–2977. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ifaei, P.; Karbassi, A.; Lee, S.; Yoo, C. A renewable energies-assisted sustainable development plan for Iran using techno-econo-socio-environmental multivariate analysis and big data. Energy Convers. Manag. 2017, 153, 257–277. [Google Scholar] [CrossRef]
- Yao, J.; Pan, Y.; Yang, S.; Chen, Y.; Li, Y. Detecting Fraudulent Financial Statements for the Sustainable Development of the Socio-Economy in China: A Multi-Analytic Approach. Sustainability 2019, 11, 1579. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modelling of chemical oxygen demand by using ANNs, ANFIS and k-means clustering techniques. J. Hydrol. 2014, 511, 279–289. [Google Scholar] [CrossRef]
- Hatamlou, A.; Abdullah, S.; Nezamabadi-Pour, H. A combined approach for clustering based on K-means and gravitational search algorithms. Swarm Evol. Comput. 2012, 6, 47–52. [Google Scholar] [CrossRef]
- Ifaei, P.; Karbassi, A.; Jacome, G.; Yoo, C. A systematic approach of bottom-up assessment methodology for an optimal design of hybrid solar/wind energy resources—Case study at middle east region. Energy Convers. Manag. 2017, 145, 138–157. [Google Scholar] [CrossRef]
- Ifaei, P.; Farid, A.; Yoo, C. An optimal renewable energy management strategy with and without hydropower using a factor weighted multi-criteria decision making analysis and nation-wide big data—Case study in Iran. Energy 2018, 158, 357–372. [Google Scholar] [CrossRef]
- Liu, L.; Peng, Z.; Wu, H.; Jiao, H.; Yu, Y.; Zhao, J. Fast identification of urban sprawl based on K-means clustering with population density and local spatial entropy. Sustainability 2018, 10, 2683. [Google Scholar] [CrossRef]
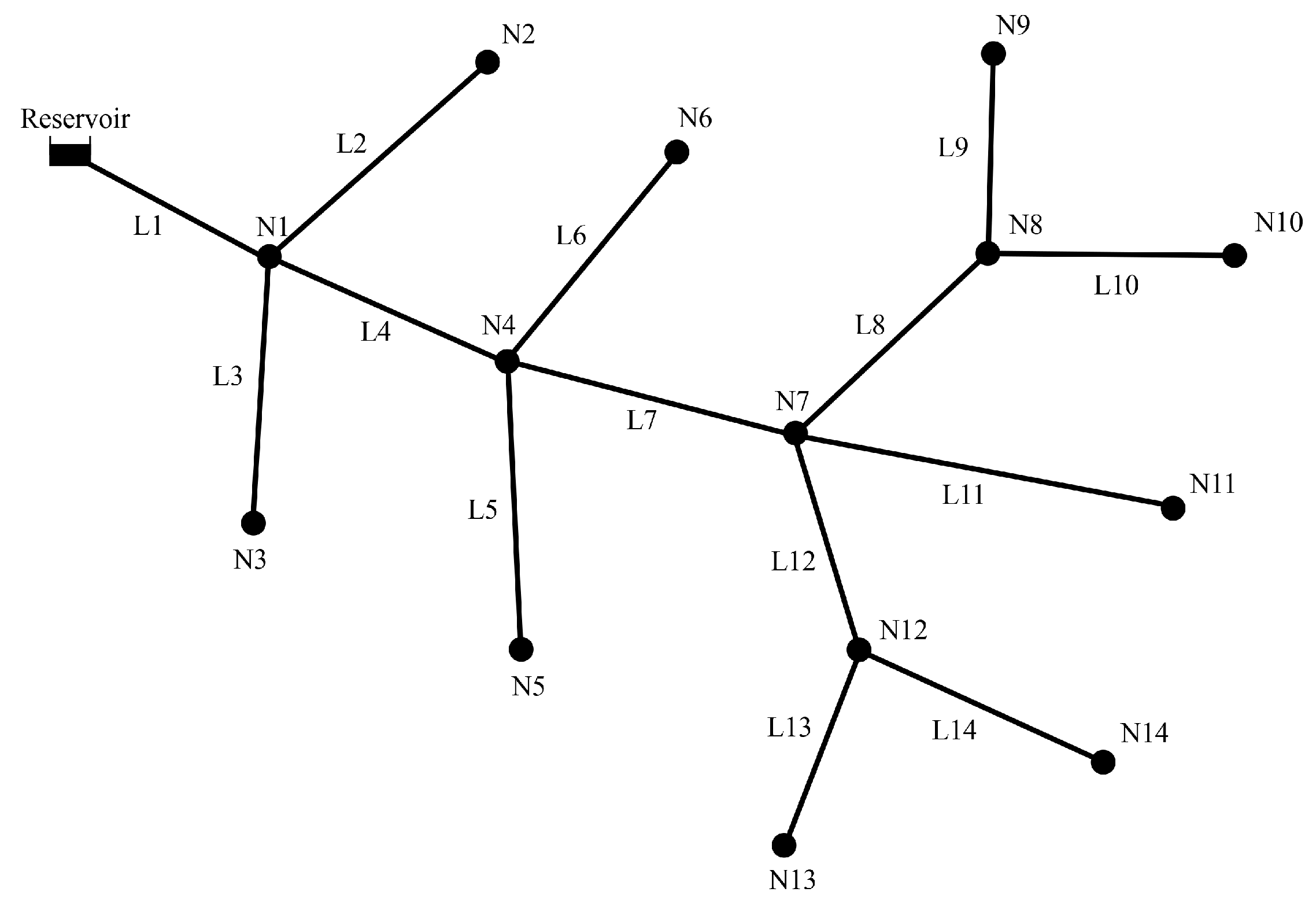

| Node Number | Elevation (m) | Demand (m3/day) | Link | Length (m) | Diameter (mm) |
|---|---|---|---|---|---|
| N1 | 125 | 86 | L1 | 1200 | 400 |
| N2 | 120 | 130 | L2 | 1400 | 150 |
| N3 | 121 | 86 | L3 | 500 | 150 |
| N4 | 120 | 86 | L4 | 700 | 350 |
| N5 | 110 | 173 | L5 | 400 | 150 |
| N6 | 116 | 86 | L6 | 400 | 125 |
| N7 | 117 | 86 | L7 | 600 | 350 |
| N8 | 115 | 173 | L8 | 300 | 250 |
| N9 | 110 | 173 | L9 | 400 | 200 |
| N10 | 111 | 130 | L10 | 500 | 200 |
| N11 | 114 | 173 | L11 | 400 | 200 |
| N12 | 110 | 173 | L12 | 400 | 250 |
| N13 | 105 | 173 | L13 | 350 | 200 |
| N14 | 110 | 86 | L14 | 500 | 150 |
| Scenario | Burst Flowrate (m3/day) | Burst Location | Occurrence Time (min) | Duration (min) |
|---|---|---|---|---|
| S1 | 10 | N14 | 902 | 2 |
| S2 | 20 | N6 | 685 | 5 |
| S3 | 30 | N7 | 551 | 7 |
| S4 | 40 | N10 | 62 | 8 |
| S5 | 50 | N2 | 589 | 7 |
| S6 | 60 | N4 | 384 | 4 |
| S7 | 70 | N7 | 348 | 3 |
| S8 | 70 | N14 | 540 | 7 |
| S9 | 80 | N1 | 744 | 4 |
| S10 | 100 | N7 | 980 | 5 |
| System | Burst Monitoring Method | Sensor Placement Approach | Reference |
|---|---|---|---|
| System 1 | CUSUM chart | Sensitivity analysis | [9] |
| System 2 | Standardized EWMA chart | k-means clustering and sensitivity analysis | This study |
| System 3 | Standardized EWMA and PCA | PCA, k-means clustering, and sensitivity analysis | This study |
| Scenario | CUSUM (system 1) | Standardized EWMA (system 2) | Standardized EWAM-PCA (system 3) |
|---|---|---|---|
| S1 | - | - | 0.88 s |
| S2 | - | 47.72 s | 1.63 s |
| S3 | 4.11 s | 30.27 s | 6.04 s |
| S4 | 3.32 s | 35.52 s | 12.98 s |
| S5 | 1.83 s | 20.87 s | 4.62 s |
| S6 | 1.15 s | 27.51 s | 2.59 s |
| S7 | 1.01 s | 25.99 s | 1.56 s |
| S8 | 0.95 s | 25.36 s | 5.33 s |
| S9 | 1.09 s | 17.41 s | 2.84 s |
| S10 | 0.83 s | 25.84 s | 4.10 s |
| Average | 1.79 s | 28.50 s | 4.26 s |
| Node | N1 | N2 | N3 | N4 | N5 | N6 | N7 |
| Cumulative sensitivity () | |||||||
| Node | N8 | N9 | N10 | N11 | N12 | N13 | N14 |
| Cumulative sensitivity () |
| Node | Parameters of Regression Model | Flow Rate | Pressure | ||||
|---|---|---|---|---|---|---|---|
| p1 | p2 | p3 | Mean | Standard Deviation | Mean | Standard Deviation | |
| N1 | −1.94∙10−5 | −3.46∙10−4 | 225 | 88.6 | 35.34 | 224.79 | 0.11 |
| N2 | −1.70∙10−5 | −5.73∙10−4 | 230 | 134.0 | 53.43 | 229.58 | 0.23 |
| N3 | −2.26∙10−5 | −4.51∙10−4 | 229 | 88.6 | 35.34 | 228.75 | 0.13 |
| N4 | −3.36∙10−5 | −8.12∙10−4 | 230 | 88.6 | 35.34 | 229.63 | 0.20 |
| N5 | −1.09∙10−5 | −4.52∙10−4 | 225 | 178.3 | 71.10 | 239.52 | 0.26 |
| N6 | −4.05∙10−5 | −8.83∙10−4 | 234 | 88.6 | 35.34 | 233.56 | 0.24 |
| N7 | −4.21∙10−5 | −9.16∙10−4 | 233 | 88.6 | 35.34 | 232.54 | 0.25 |
| N8 | −1.16∙10−5 | −4.45∙10−4 | 235 | 178.2 | 71.10 | 234.50 | 0.27 |
| N9 | −1.20∙10−5 | −5.10∙10−4 | 240 | 178.3 | 71.10 | 239.47 | 0.28 |
| N10 | −2.09∙10−5 | −6.85∙10−4 | 239 | 134.0 | 53.43 | 238.48 | 0.28 |
| N11 | −1.10∙10−5 | −4.80∙10−4 | 236 | 178.3 | 71.10 | 235.51 | 0.26 |
| N12 | −1.16∙10−5 | −4.67∙10−4 | 240 | 178.3 | 71.10 | 239.49 | 0.27 |
| N13 | −1.20∙10−5 | −5.26∙10−4 | 245 | 178.3 | 71.10 | 244.47 | 0.28 |
| N14 | −5.06∙10−5 | −9.67∙10−4 | 240 | 88.6 | 35.34 | 239.46 | 0.29 |
| Number of Sensors | Number of Probable Configurations | Selected Measurement Points |
|---|---|---|
| 1 | 14 | 2 |
| 2 | 91 | 2, 10 |
| 3 | 364 | 2, 10, 14 |
| 4 | 1001 | 2, 6, 10, 14 |
| 5 | 2002 | 2, 3, 6, 10, 14 |
| 6 | 3003 | 2, 3, 6, 9, 11, 14 |
| 7 | 3432 | 2, 3, 4, 9, 10, 11, 14 |
| 8 | 3003 | 2, 3, 4, 6, 9, 10, 11, 14 |
| 9 | 2002 | 2, 3, 4, 9, 10, 11, 12, 13, 14 |
| 10 | 1001 | 2, 3, 4, 5, 6, 9, 10, 11, 13, 14 |
| 11 | 364 | 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 14 |
| 12 | 91 | 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14 |
| 13 | 14 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14 |
| 14 | 1 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, K.; Ifaei, P.; Heo, S.; Rhee, G.; Lee, S.; Yoo, C. An Efficient Burst Detection and Isolation Monitoring System for Water Distribution Networks Using Multivariate Statistical Techniques. Sustainability 2019, 11, 2970. https://doi.org/10.3390/su11102970
Nam K, Ifaei P, Heo S, Rhee G, Lee S, Yoo C. An Efficient Burst Detection and Isolation Monitoring System for Water Distribution Networks Using Multivariate Statistical Techniques. Sustainability. 2019; 11(10):2970. https://doi.org/10.3390/su11102970
Chicago/Turabian StyleNam, KiJeon, Pouya Ifaei, Sungku Heo, Gahee Rhee, Seungchul Lee, and ChangKyoo Yoo. 2019. "An Efficient Burst Detection and Isolation Monitoring System for Water Distribution Networks Using Multivariate Statistical Techniques" Sustainability 11, no. 10: 2970. https://doi.org/10.3390/su11102970
APA StyleNam, K., Ifaei, P., Heo, S., Rhee, G., Lee, S., & Yoo, C. (2019). An Efficient Burst Detection and Isolation Monitoring System for Water Distribution Networks Using Multivariate Statistical Techniques. Sustainability, 11(10), 2970. https://doi.org/10.3390/su11102970








