Optimization of Decision Making in the Supply of Medicinal Gases Used in Health Care
Abstract
1. Introduction
- (1)
- Modelling supply systems for medicinal gases with continuous-time Markov chains, looking at different improvement alternatives over the original design of the systems.
- (2)
- Optimizing consumption of resources via objective decision making, which can be opened to public opinion. The result of this optimization is to guarantee clinical sustainability and avoid some consumption of hospital resources and of staff, both medical and nonmedical, patients, and visitors.
- (3)
- Developing multicriteria models using the MACBETH approach and FAHP to optimize the supply systems for medicinal gases.
- (4)
- Comparing the results obtained via the MACBETH approach and FAHP to assess the capacity of MACBETH to handle ambiguous, imprecise, or inadequate information, or the impossibility of giving precise values.
- (5)
- Considering the Buckley method as a means of applying FAHP to guarantee the accuracy of the priorities obtained and to avoid losing information in the results. This avoids certain problems arising from the use of Chang’s extent analysis method.
- (6)
- Applying the multicriteria models, specifically for intake and supply systems, for medicinal gases in health care organizations. These systems have high criticality as many other hospital systems and medical devices rely on them in order to operate. Furthermore, these dependent systems interact directly with patients and can, therefore, affect proper care and treatment.
- (7)
- Analysing the implications for quality of care of maintaining the original design and of introducing the alternative suggested by the multicriteria models.
- (8)
- Applying a model using real systems and data in a Spanish hospital.
2. Multicriteria Technique Methodologies
2.1. The Measuring Attractiveness by a Categorical-Based Evaluation Technique (MACBETH) Approach
- Neutral level (N): an impact level that the decision maker considers neither to be attractive nor unattractive and is assigned the arbitrary score 0.
- Good level (G): the decision maker considers this impact level attractive, and MACBETH assigns it the arbitrary score 100.
- : is more attractive than }. This relation is asymmetric.
- : is not more attractive than and is not more attractive than }. This relation is reflexive and symmetric.
- has better performance than
- has similar performance as
- where the variation in performance between and is negligible or very weak} (encoded as VW in the pairwise judgement matrices included in Section 4).
- where the variation in performance between and is weak} (in the pairwise judgement matrices this judgement is encoded as W).
- where the variation in performance between and is moderate} (encoded as M when this judgement appears in the pairwise matrices).
- when the variation in performance between and is strong} (encoded as S in the pairwise judgement matrices included in Section 4).
- where the variation in performance between and is very strong} (encoded as VS).
- where the variation in performance between and is extreme} (encoded as E).
- (1)
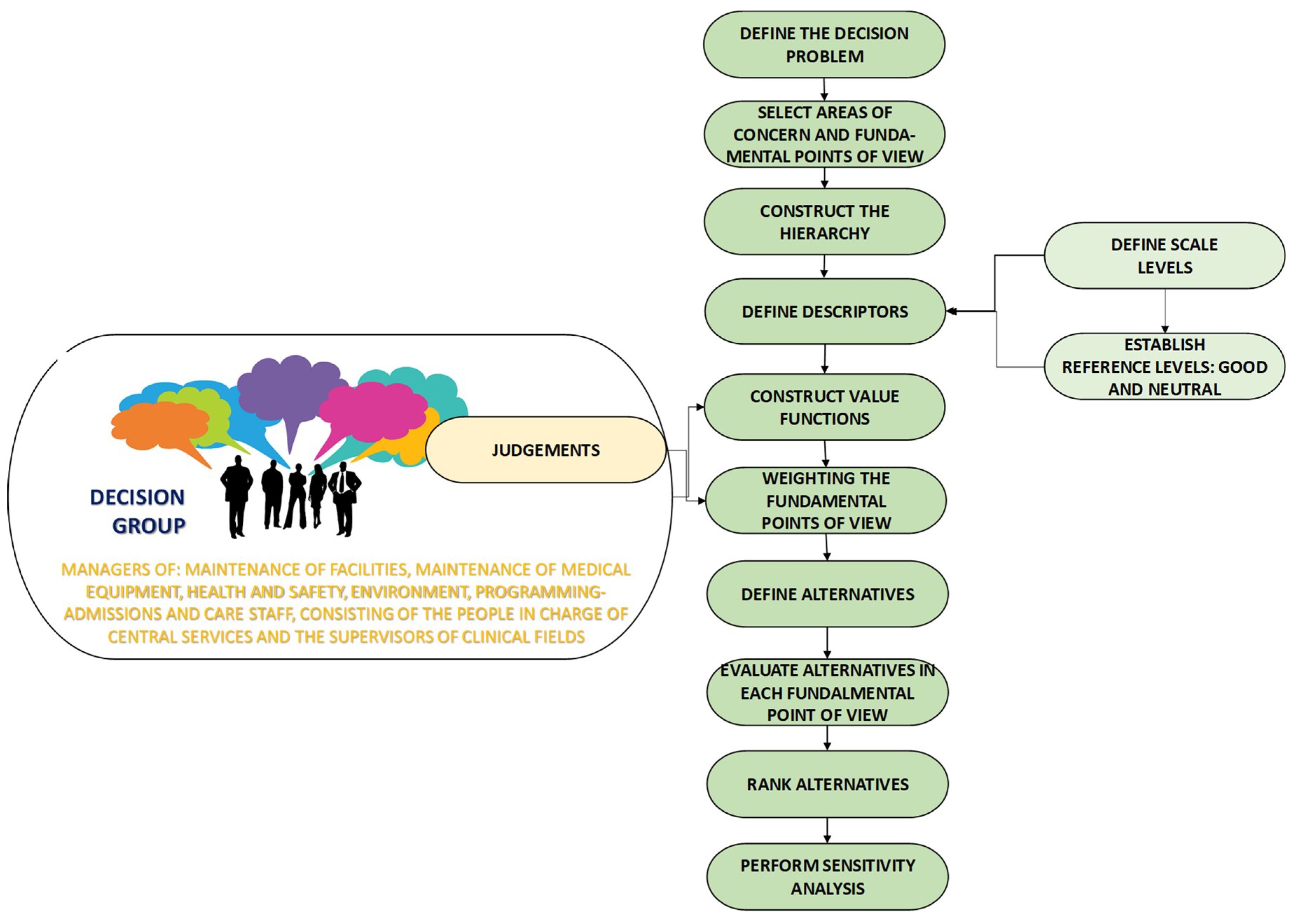
- Define the decision problem. The background of the problem must be analyzed, including the assumptions and the perspective under which the decisions are taken. Different scenarios or stakeholder groups might be necessary to analyze the problem thoroughly.
- (2)
- Select areas of concern and FPV. Each criterion or FPV is some characteristic or property in a specific context that the decision maker or group considers relevant to provide a solution to the problem [50]. The FPVs must have the following characteristics: coherent with the decision, represented on the same scale, measurable, independent of each other, and not unrelated to the alternatives.
- (3)
- Construct the hierarchy. To structure the problem, a value tree must be created, including a goal at the higher level, which gives rise to criteria or areas of concern, attributes or FPVs, and the lower level of the hierarchy incorporates the alternatives [51]. The structuring process starts with the identification of a set of areas of concern, and each comprises one or more FPV’s, which are attributes that allow the alternatives to be assessed.
- (4)
- Define descriptors. For each FPV, a descriptor must be defined and is made up of a performance scale in which the reference levels of neutral and good must be identified. This avoids the problem that, on assessing the FPV in the alternatives, results will not be imprecisely or ambiguously interpreted. The descriptors can measure (qualitatively, quantitatively, or a mix of the two) the degree of performance of an alternative with respect to each FPV. Different types of descriptors are possible: one-dimensional qualitative scales, pictorial descriptors, and multidimensional descriptors.
- (5)
- Construct value functions. Ordinal scales must be transformed into cardinal scales or value functions. A value function is representative of the decision maker’s judgement [52] and are calculated by M-MACBETH applying linear programming [53].The decision maker or group must give judgements using one of the MACBETH semantic categories: N, VW, V, M, S, VS, and E. When there is uncertainty or disagreement within the decision group about assigning a value, MACBETH allows a range of two or more consecutive semantic categories to be included. The category positive (P) can be used when the information available on comparing two scale levels is very limited. M-MACBETH assigns scores of 0 and 100 in the value function to the scale levels of the descriptors identified as neutral and good, respectively.M-MACBETH assesses the consistency of the pairwise judgement matrix every time a judgement is added, generating a value function only if all the judgements given in the matrix are consistent. If the judgement matrix is inconsistent, M-MACBETH suggests revising the inconsistent judgements [54].
- (6)
- Weighting the FPVs. A new alternative is defined with all the FPVs at the neutral level. The decision group uses the MACBETH semantic categories to give judgements about the rise in overall performance, provided by a swing from the neutral level to the good level, in each of the FPVs. This allows the final column of the MACBETH judgement matrix to be completed, and the FPVs end up ordered from greater to lesser attractiveness. A judgement is then given, again through the MACBETH semantic categories, about how much better the change is from a neutral to a good level in the most important FPV compared with the second-placed FPV in the matrix. The process goes on to compare the change from the first FPV, with respect to the third-placed FPV, and then the fourth, the fifth, etc.
- (7)
- Define alternatives. This consists of defining, as accurately as possible, the solutions to a problem. The proposed alternatives should be: available, comparable, real (not ideal), and practical or feasible.
- (8)
- Evaluate alternatives in each FPV. The values that each alternative would have for each criterion or subcriterion should be specified by choosing one of the scale levels of the descriptor.
- (9)
- Rank alternatives. MACBETH uses an additive aggregation method (see Equation (1)) to assess each alternative.where is the alternative assessed; is the global value of alternative calculated from the summation of the FPVs included in the model; (x) is the value of the impact of alternative on FPV i, considering (most desirable impact level on i) = 100, and (most undesirable impact level on i) = 0; and is the weight of FPV i.
- (10)
- Sensitivity analysis. The sensitivity analysis assesses the stability of the model, by making logical changes in the weighting of an FPV while keeping the proportionality of the weightings of the other FPVs, to analyze the resulting changes in the ranking of alternatives. M-MACBETH has graphing tools to perform sensitivity and robustness analyses [53].
2.2. Fuzzy Analytic Hierarchy Process Methodology
- (1)
- Select the expert or group of experts who will provide the information and judgements necessary for the decision-making process.
- (2)
- Construct the hierarchy. Criteria and FPVs relevant to the problem are selected and structured into a hierarchy. The objective is placed at the upper level of the hierarchal structure, the criteria and subcriteria are placed at the intermediate levels, and the alternatives are at the lower level.
- (3)
- Select the fuzzy scale. Saaty’s original scale, made up of the association of a judgement with an integer from one to nine and its inverses, does not permit working with uncertainty, vagueness, or ambiguous situations [65]; however, these characteristics are found in real decision problems. In addition, the decision centres generally feel more confident giving their judgements in the form of intervals rather than as a crisp number [66]. A variety of fuzzy scales are described in the literature [66,67,68,69,70].
- (4)
- Obtain fuzzy judgements between criteria or FPVs and between the levels of scale of each descriptor. Elements of the MACBETH pairwise comparison matrix (see Equation (3)) are the fuzzy values , which express the decision centre’s judgement about the relative importance of element i over element j at the same level of hierarchy.with for and .
- (5)
- (6)
- (7)
- Evaluate the consistency of the judgements. To quantify the consistency of the judgements given, Saaty [74] defined the consistency ratio (CR) as shown Equation (7).where CI is a consistency index calculated from Equation (8), and ICR is a random consistency index obtained from the simulation with random matrices with dimensions equal to those assessed.
3. Markov Chains in Medicinal Gas Supply Systems
3.1. Methodology
- (1)
- Investigate the device. This includes the process characteristics, resources required, technical parameters, maintenance policies applied, etc.
- (2)
- Identify the failure modes of the device. This requires analysis of each element of the device, its working and failure modes, and their possible consequences.
- (3)
- Define the possible solutions of the problem. The possible alternatives to be applied to the system analyzed should be defined, and it should be possible to include redundancies or improvements in the design.
- (4)
- Determine the failure and repair rates. This is commonly done using the records of failures and repairs for the system analyzed. The failure rate of each fault is generally referred to as , while the repair rate for each failure is called .
- (5)
- Establish the Markov graph. The Markov model assesses the probability of passing from one state to another and then returning through failures and repairs. A Markov graph is held to have n + 1 possible states, such that each state represents breakage of components or a level of wear. If k is the maximum number of failed states permitted such that the system can keep working, each level of wear can be identified by the number of failed elements. The following states can be defined [78]:
- State 0. The device is in the perfect state.
- State 1. One of the elements of the device is broken, or the system is in the first possible state of wear.
- State 2. Two subsystems or elements of the device are not functioning, or the device is at the second possible state of wear.
- State n − 1. n − 1 components or subsystems are broken, or the device is at level n − 1 of wear.
- State n. Each element of the system is broken, or the device is in catastrophic breakdown.
- (6)
- Compute the transition matrix. To construct the transition matrix (see Equation (9)) it is first necessary to design the Markov graph. In each row i, corresponding to the columns j, the corresponding rates are placed for the links which leave state i for each of the states j in the graph. To calculate the main diagonal, each row i contains the sum, with the sign changed, of the transition rates for each row. The last column of the matrix is included to guarantee that summing all the probabilities gives the value 1.
- (7)
- Resolve the system of equations. The mathematical process followed to obtain the final system of equations (see Equation (10)) to resolve into continuous Markov chains for repairable systems can be seen in Kaufman [79], Hillier and Lieberman [80], and Haigh [81].with the vector of probabilities in the stationary state [82].Equation (10) can be reformulated in matrix form as follows:Thus, the vector can be calculated from Equation (12).
- (8)
- Calculate the availability of the device. Solving Equation (12) gives the mean availability , but Equation (13) will be applied if the device has a Markov graph with stable working states.where is the coefficient obtained from solving the above system of equations.
3.2. Markov Chain for the Medicinal Gas Supply Systems
- Retaining the original conditions designed for the hospital (Alternative A (ALT A)) with a single external supply.
- Duplicating the external supply (Alternative B (ALT B)). This would involve producing twice the amount of the original hospital design. Although the process took place in the hospital, it was carried out by an authorized company with its own production process.
- Increasing storage of gas to provide a higher level of autonomous operation than the maximum shortage of supply (Alternative C (ALT C)).
4. Multicriteria Model for Optimization of Decision Making in Medicinal Gas Supply Systems
- If the decision group had any doubt or uncertainty when giving judgements, they may assign a range of MACBETH semantic categories.
- M-MACBETH was a helpful software since it facilitated the construction of value functions and the validation of the results obtained. Also, every time a judgement was included in a judgement matrix, its consistency was checked. Additionally, it allowed sensitivity and robustness analyses to be carried out.
- Validation of the results was an important aspect of the MACBETH approach and ensured a greater reliability of the results.
- The use of the reference levels in each descriptor minimized inconsistency and produced more reliable, accurate, and objective results.
- MACBETH was a complete methodology with a complete definition of each step that ensured objective decision making. Other MCDM methods lacked exhaustive and detailed procedures.
4.1. Structuring
- Cost. This included all annual costs, whether direct or indirect, produced by each alternative. It included both operating costs and investment costs:
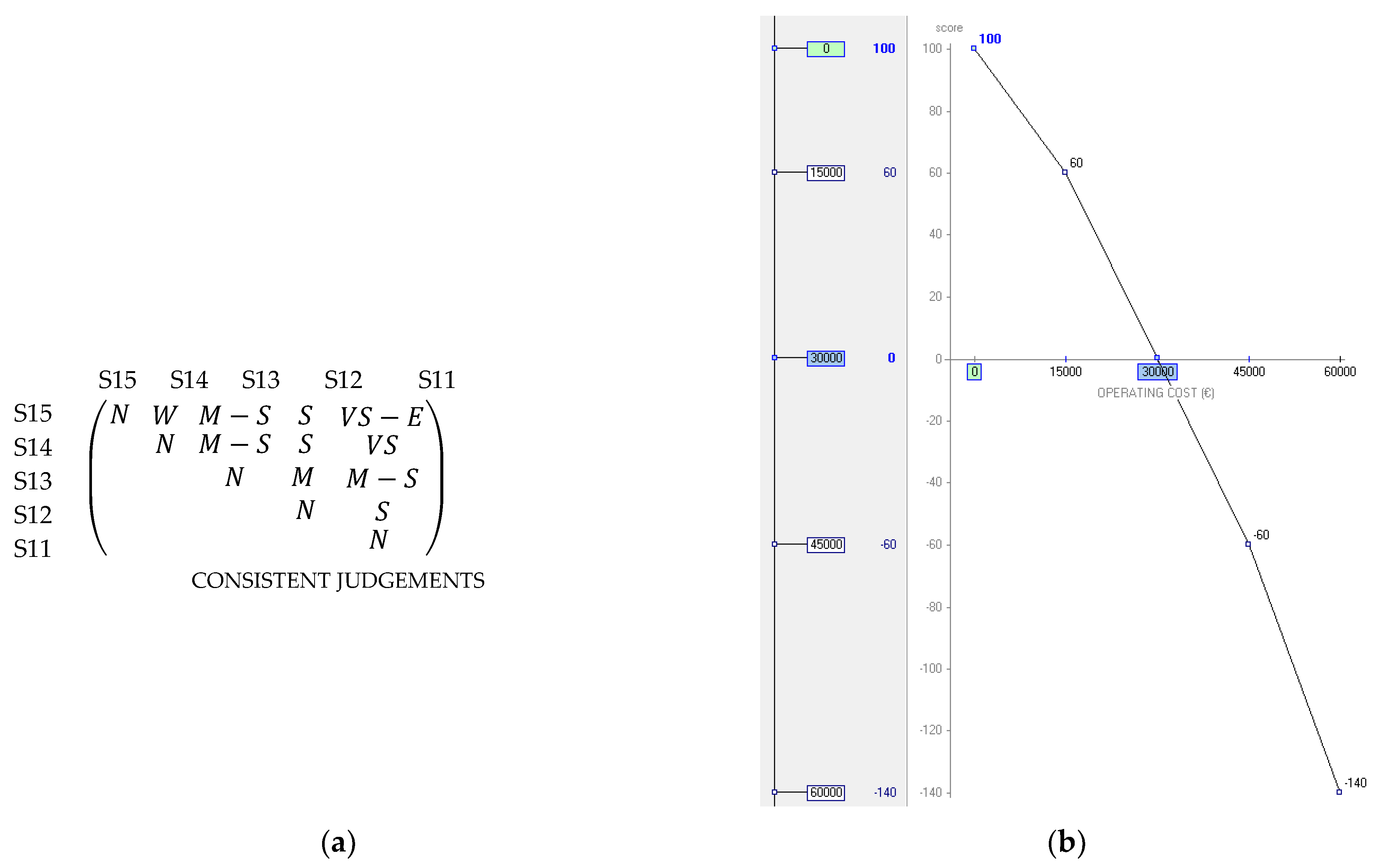
- Operating costs (OPC). This criterion considered the extra annual human resource costs corresponding to the technical maintenance staff. The following scale levels were defined for each descriptor, from lowest to highest level of achievement:
- -
- S11. Up to €60,000.
- -
- S12. Up to €45,000.
- -
- S13. (Neutral) Up to €30,000.
- -
- S14. Up to €15,000.
- -
- S15. (Good) €0.
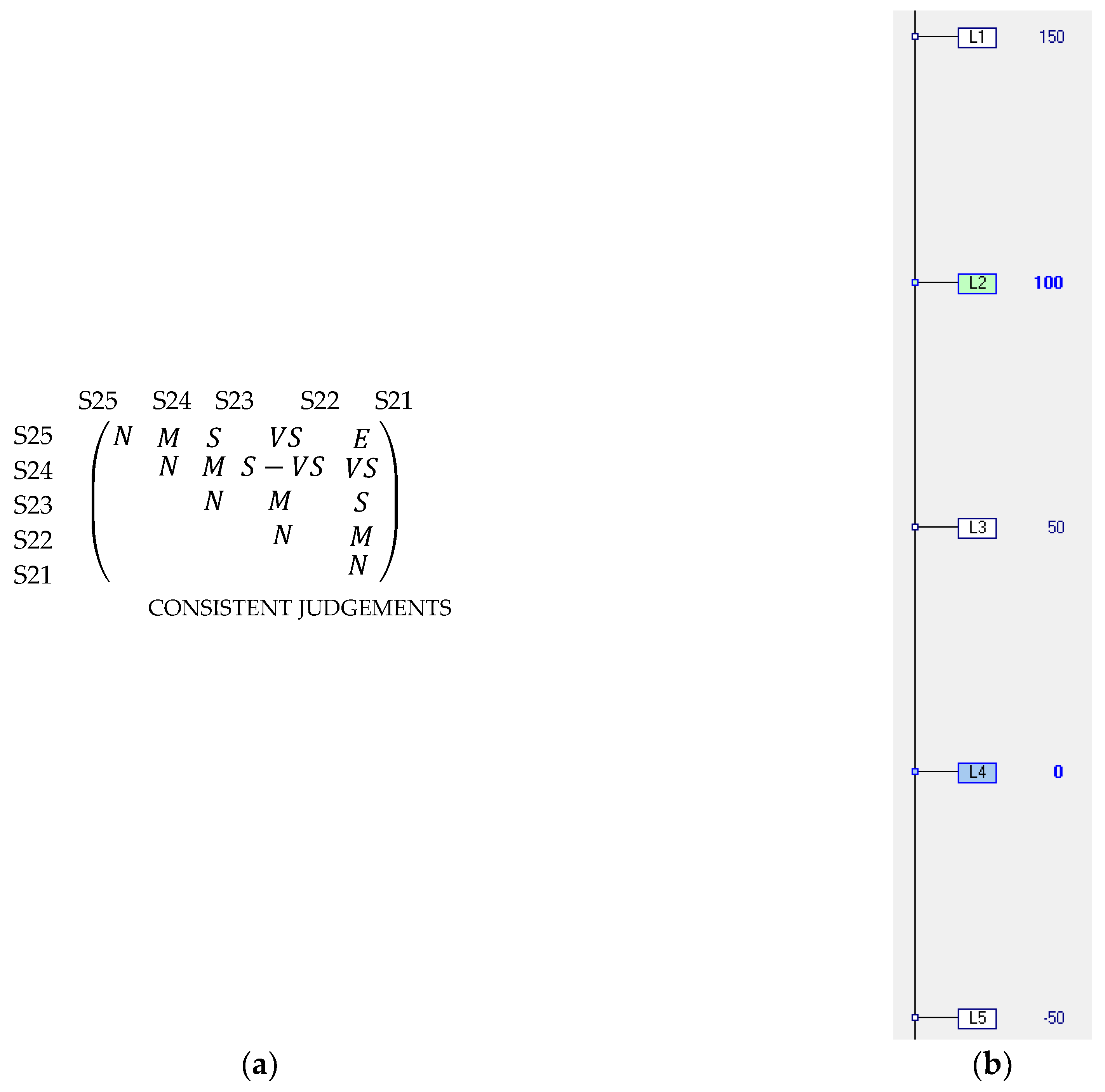
- Investment costs (INC). This included all costs, both of setting up and starting the operation, produced by each action. The estimated value was considered as a percentage of the cost of the existing facilities. The scale levels are shown below, in order of greater to lesser attractiveness:
- -
- S21. Increase greater than 100% over the estimated value of the original facility.
- -
- S22. (Neutral) Increase between 75% and 100% over the estimated value of the original facility.
- -
- S23. Increase between 50% and 75% over the estimated value of the original facility.
- -
- S24. (Good) Increase between 25% and 50% over the estimated value of the original facility.
- -
- S25. Increase of up to 25% over the estimated value of the original facility.
- Risk to workers (RIWs). This FPV assessed the risk to which maintenance workers, and any other hospital or outside workers who interacted with the system, were exposed. The descriptor defined was the existence of a level of risk and the need to take safety precautions. The scale levels of this descriptor in increasing order of relative achievement are:
- -
- S31. There was a definite risk, requiring basic, specific, and emergency precautions to carry out the operational or maintenance activities on the system.
- -
- S32. There was a definite risk, requiring basic precautions plus some specific precautions to carry out activity on the system.
- -
- S33. (Neutral) There was a definite risk, leading to the need to take basic precautions to carry out activity on the system.
- -
- S34. There was a specific potential risk, leading to the need to take certain basic precautions when carrying out activity on the system.
- -
- S35. (Good) No risk to workers was identified at any time, and there was no need to take any safety precautions.
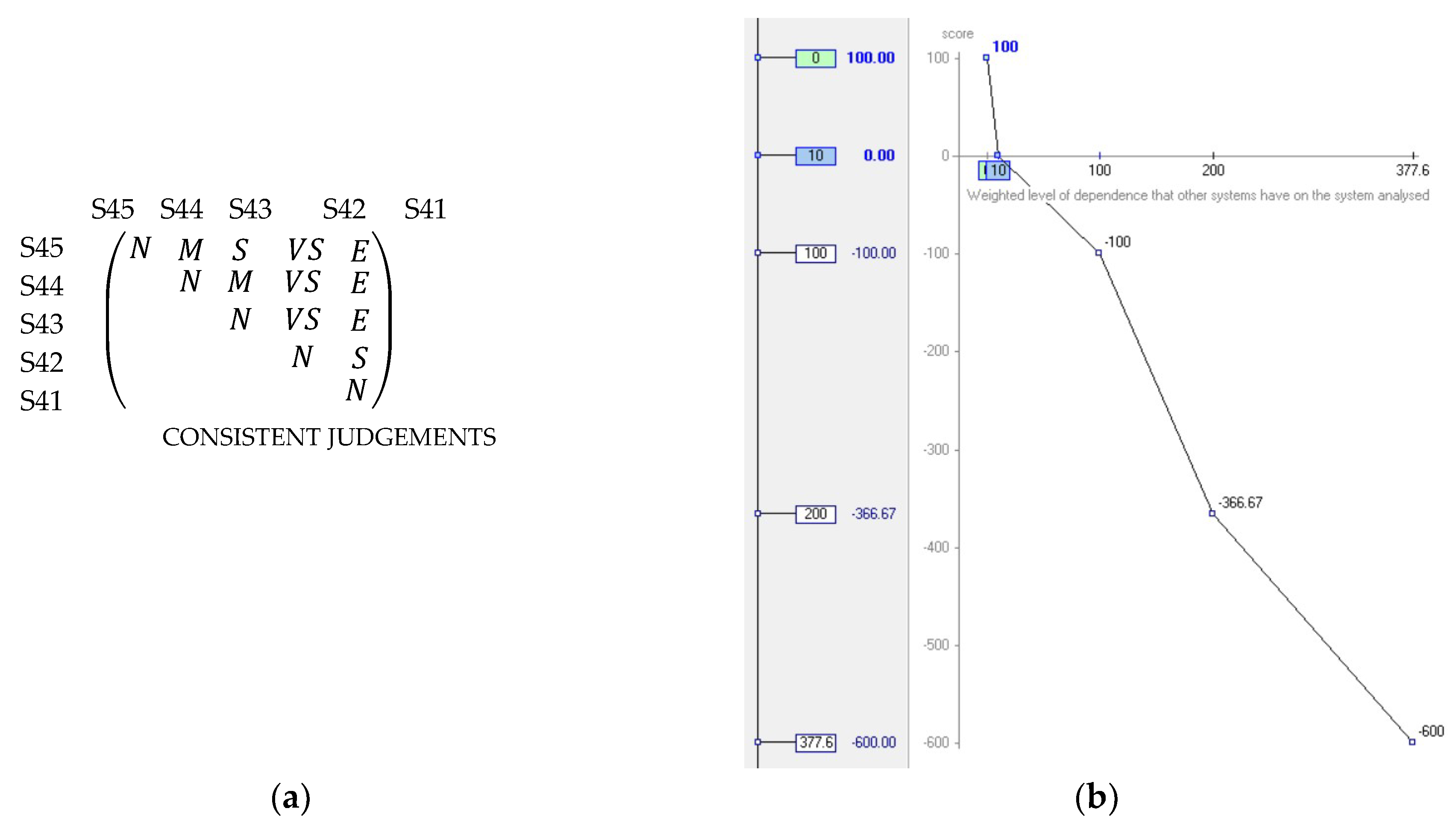
- Impact of unavailability of the supply devices of medicinal gases on hospital activity (IUA). This measured the effect that unavailability of an intake system and supply of medicinal gases would have on dependent systems. The descriptor associated with this criterion is defined in Equation (19).where is the number of critical systems which depend on the gas supply system studied, is the number of important systems, and is the number of dependent systems considered to be of normal criticality. These parameters were multiplied by four, two, or one depending on whether the dependent system was critical, important, or normal, respectively. (1 − ) was the mean unavailability of the system assessed. The scale levels of this descriptor were established as the upper and lower bounds, which were derived from a prior study on the 522 systems that carried out technical activity in the hospital. The most unfavourable scale level was found in the water-cooling system, which comprised four cooling towers. It had 15 critical dependent systems, nine important, and one with normal criticality. Furthermore, it had a mean unavailability of 0.0320. The most unfavourable resulting value was, therefore, 377.60. The most favourable value appeared when there were no dependent systems or the mean unavailability was 0; in both cases, the resulting value was 0. The scale levels of the descriptor Weighted level of dependence of other systems, from lowest to highest level of achievement, were
- -
- S41. (200, 377.60].
- -
- S42. (100, 200].
- -
- S43. (10, 100].
- -
- S44. (Neutral). (0, 10].
- -
- S45. (Good). 0.
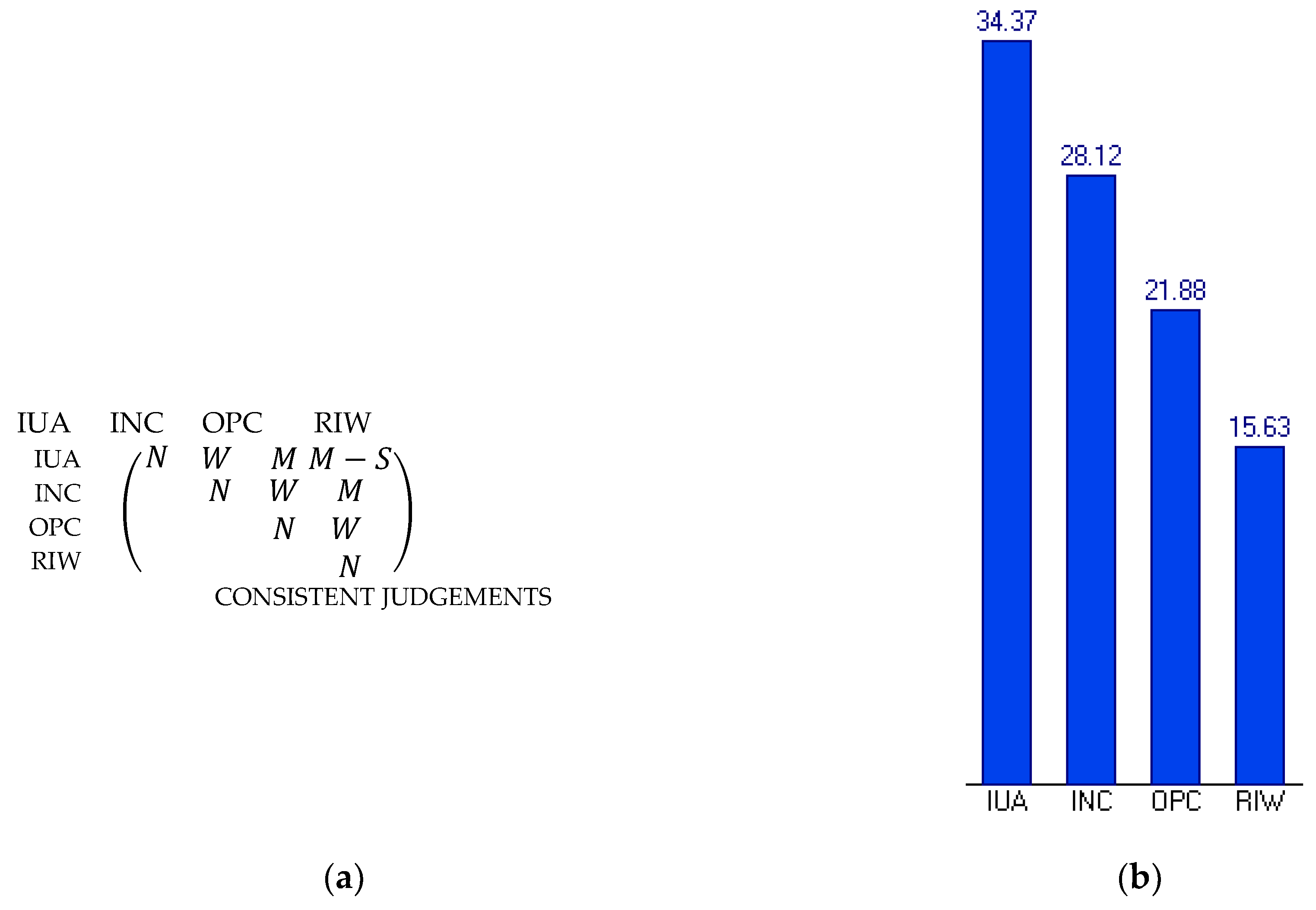
4.2. The MACBETH Approach Model
4.3. The Fuzzy Analytic Hierarchy Process Model
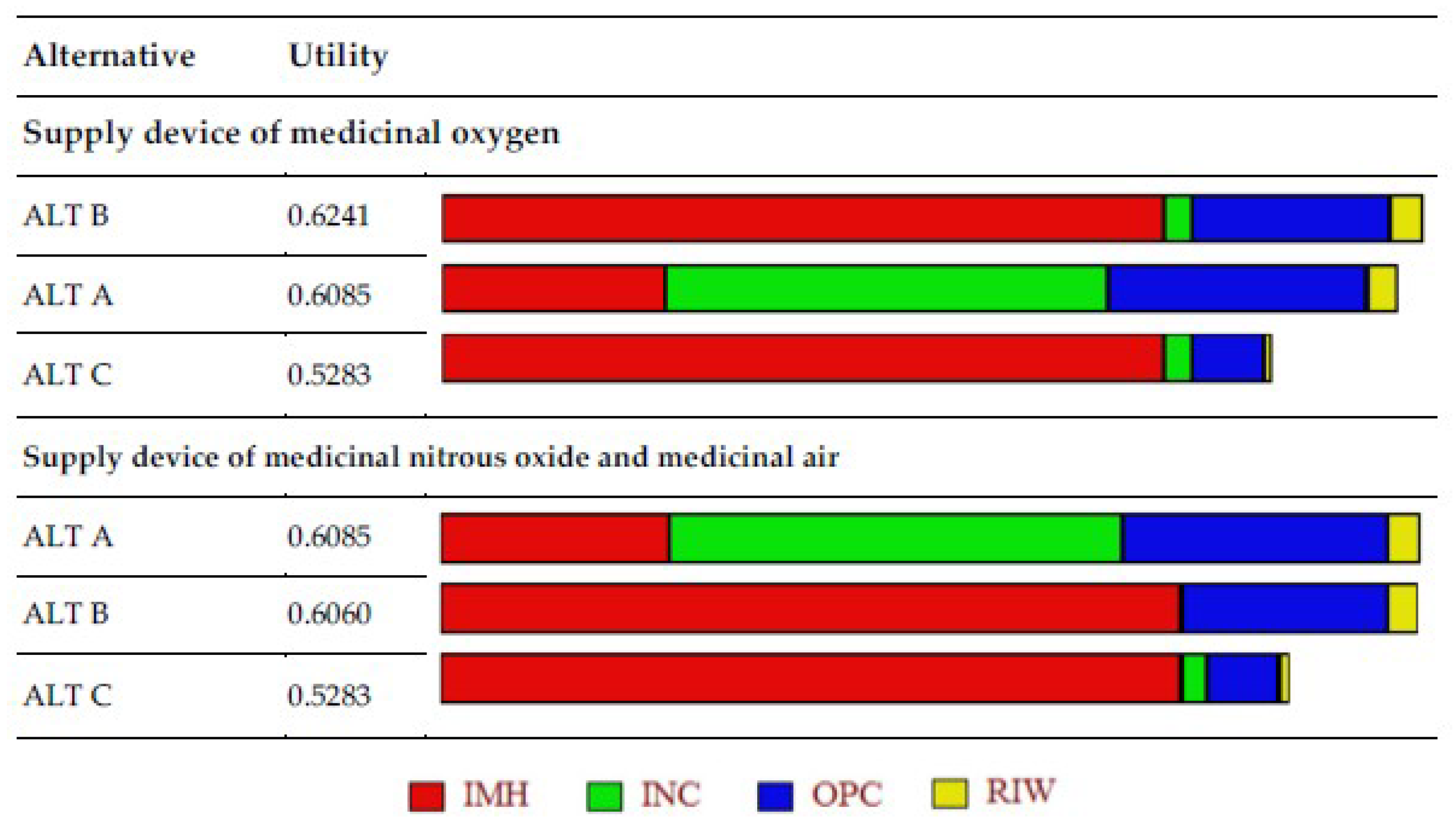
5. Results and Discussion
5.1. Global Scores
5.2. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Domínguez-Gil, A. Gases medicinales, nuevos medicamentos. Farm. Hosp. 2005, 29, 300–302. [Google Scholar] [CrossRef]
- Alonso, F. NTP 630: Riesgo de incendio y explosión en atmósferas sobreoxigenadas; Instituto nacional de Seguridad e Higiene en el Trabajo: Madrid, Spain, 2003. [Google Scholar]
- Linde. Available online: https://www.linde-healthcare.es/es/products_and_services/products_and_services_by_category/medical_gases (accessed on 9 April 2019).
- Asociación Ingeniería Hospitalaria (AIEH); Sociedad Farmacia Hospitalaria (SEFH); Asociación Fabricantes Gases Medicinales (AFGM). Procedimiento de gestión de gases medicinales Estándares de calidad de gases medicinales en el ámbito hospitalario, 2nd ed.; Farmacia Hospitalaria, Fabricantes de Gases Medicinales, Ingeniería Hospitalaria: Madrid, Spain, 2018. [Google Scholar]
- Hayashi, K. Multicriteria analysis for agricultural resource management: A critical survey and future perspectives. Eur. J. Oper. Res. 2000, 122, 486–500. [Google Scholar] [CrossRef]
- Gregory, R.; Failing, L.; Harstone, M.; Long, G.; McDaniels, T.; Ohlson, D. Structured Decision Making: A Practical Guide to Environmental Management Choices. John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Diaby, V.; Campbell, K.; Goeree, R. Multi-criteria decision analysis (MCDA) in health care: A bibliometric analysis. Oper. Res. Health Care 2013, 2, 20–24. [Google Scholar] [CrossRef]
- Thokala, P.; Devlin, N.; Marsh, K.; Baltussen, R.; Boysen, M.; Kalo, Z.; Longrenn, T.; Mussen, F.; Peacock, S.; Watkins, J.; et al. Multiple criteria decision analysis for health care decision making & An Introduction: Report 1 of the ISPOR MCDA emerging Good Practices task force. Value Health 2014, 19, 1–13. [Google Scholar]
- Majumder, M. Impact of Urbanization on Water Shortage in Face of Climatic Aberrations; Springer: New York, NY, USA, 2015. [Google Scholar]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Gómez, A.; Carnero, M.C. Decision Support System for maintenance policy optimization in medicinal gases subsystems. Ifac-Pap. 2016, 49, 268–273. [Google Scholar]
- Bevilacqua, M.; Braglia, M. The analytic hierarchy process applied to maintenance strategy selection. Reliab. Eng. Syst. Safe 2000, 70, 71–83. [Google Scholar] [CrossRef]
- Emblemsvag, J.; Tonning, L. Decision support in selecting maintenance organization. J. Qual. Maint. Eng. 2003, 9, 11–24. [Google Scholar] [CrossRef]
- Bertolini, M.; Bevilacqua, M. A combined goal programming-AHP approach to maintenance selection problem. Reliab. Eng. Syst. Safe 2006, 91, 839–848. [Google Scholar] [CrossRef]
- Shyjith, K.; Ilangkumaran, M.; Kumanan, S. Multi-criteria decision-making approach to evaluate optimum maintenance strategy in textile industry. J. Qual. Maint. Eng. 2008, 14, 375–386. [Google Scholar] [CrossRef]
- Ahmadi, A.; Gupta, S.; Karim, R.; Kumar, U. Selection of maintenance strategy for aircraft systems using multi-criteria decision making methodologies. Int. J. Reliab. Qual. Saf. Eng. 2010, 17, 223–243. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nemery, P. Assigning machines to incomparable maintenance strategies with ELECTRE-SORT. Omega-Int. J. Manag. 2014, 47, 45–59. [Google Scholar] [CrossRef]
- Goossens, A.J.M.; Basten, R.J.I. Exploring maintenance policy selection using the Analytic Hierarchy Process; An application for naval ships. Reliab. Eng. Syst. Safe 2015, 142, 31–41. [Google Scholar] [CrossRef]
- Shafiee, M. Maintenance strategy selection problem: An MCDM overview. J. Qual. Maint. Eng. 2015, 21, 378–402. [Google Scholar] [CrossRef]
- Parmar, M.; Soni, M.; Patidar, S. Selection of Plant Maintenance Strategy and Performance Enhancement of a Wire Manufacturing Industry using AHP. Int. J. Res. Aeronaut. Mech. Eng. 2016, 4, 81–85. [Google Scholar]
- Al-Najjar, B.; Alsyouf, I. Selecting the most efficient maintenance approach using fuzzy multiple criteria decision making. Int. J. Prod. Econ. 2003, 84, 85–100. [Google Scholar] [CrossRef]
- Ghosh, D.; Roy, S. A decision-making framework for process plant maintenance. Eur. J. Ind. Eng. 2010, 4, 78–98. [Google Scholar] [CrossRef]
- Ilangkumaran, M.; Kumanan, S. Selection of maintenance policy for textile industry using hybrid multi-criteria decision making approach. J. Manuf. Technol. Manag. 2009, 20, 1009–1022. [Google Scholar] [CrossRef]
- Aslam-Zainudeen, N.; Labib, A. Practical application of the Decision Making Grid (DMG). J. Qual. Maint. Eng. 2011, 17, 138–149. [Google Scholar] [CrossRef]
- Chan, F.T.S.; Prakash, A. Maintenance policy selection in manufacturing firms using the fuzzy MCDM approach. Int. J. Prod. Res. 2012, 50, 7044–7056. [Google Scholar] [CrossRef]
- Fouladgar, M.M.; Yazdani-Chamzini, A.; Lashgari, A.; Zavadskas, E.K.; Turskis, Z. Maintenance strategy selection using AHP and COPRAS under fuzzy environment. Int. J. Strateg. Prop. Manag. 2012, 16, 85–104. [Google Scholar] [CrossRef]
- Sadeghi, A.; Manesh, R.A. The Application of Fuzzy Group Analytic Network Process to Selection of Best Maintenance Strategy—A Case Study in Mobarakeh Steel Company, Iran. Procedia Soc. Behav. Sci. 2012, 62, 1378–1383. [Google Scholar] [CrossRef][Green Version]
- Kirubakaran, B.; Ilangkumaran, M. Selection of optimum maintenance strategy based on FAHP integrated with GRA–TOPSIS. Ann. Oper. Res. 2016, 245, 285–313. [Google Scholar] [CrossRef]
- Azadeh, A.; Abdolhossein, S. An integrated fuzzy analytic hierarchy process and fuzzy multiple-criteria decision-making simulation approach for maintenance policy selection. Simulation 2016, 92, 3–18. [Google Scholar] [CrossRef]
- Tajadod, M. A Comparison of Multi-Criteria Decision Making Approaches for Maintenance Strategy Selection (A Case Study). Int. J. Strateg. Decis. Sci. 2016, 7, 51–69. [Google Scholar] [CrossRef]
- Danner, M.; Hummel, J.M.; Volz, F.; van Manen, J.G.; Wiegard, B.; Dintsios, C.M.; Bastian, H.; Gerber, A.; IJzerman, M.J. Integrating patients’ views into health technology assessment: Analytic hierarchy process (AHP) as a method to elicit patient preferences. Int. J. Technol. Assess. Health Care 2011, 27, 369–375. [Google Scholar] [CrossRef]
- Radaelli, G.; Lettieri, E.; Masella, C.; Merlino, L.; Strada, A.; Tringali, M. Implementation of EUnetHTA core models in Lombardia: The VTS framework. Int. J. Technol. Assess. Health Care 2014, 30, 105–112. [Google Scholar] [CrossRef]
- Taghipour, S.; Banjevic, D.; Jardine, A.K.S. Prioritization of medical equipment for maintenance decisions. J. Oper. Res. Soc. 2011, 62, 1666–1687. [Google Scholar] [CrossRef]
- Carnero, M.C.; Gómez, A. A multicriteria decision making approach applied to improving maintenance policies in healthcare organizations. Bmc Med. Inf. Decis. Mak. 2016. [Google Scholar] [CrossRef]
- Marciano, F.; Rossi, D.; Cabassa, P.; Cocca, P. Analytic Hierarchy Process to support ergonomic evaluation of ultrasound devices. Ifac-Pap. 2018, 51, 328–333. [Google Scholar] [CrossRef]
- Joshi, V.; Lee, K.; Melson, D.; Narra, V.R. Empirical Investigation of Radiologists’ Priorities for PACS Selection: An Analytical Hierarchy Process Approach. J. Digit. Imaging 2011, 24, 700–708. [Google Scholar] [CrossRef]
- Pecchia, L.; Martin, J.L.; Ragozzino, A.; Vanzanella, C.; Scognamiglio, A.; Mirarchi, L.; Morgan, S.P. User needs elicitation via analytic hierarchy process (AHP). A case study on a Computed Tomography (CT) scanner. Bmc Med. Inf. Decis. Mak. 2013, 13, 2. [Google Scholar] [CrossRef]
- Ivlev, I.; Vacek, J.; Kneppo, P. Multi-criteria decision analysis for supporting the selection of medical devices under uncertainty. Eur. J. Oper. Res 2015, 247, 216–228. [Google Scholar] [CrossRef]
- Agapova, M.; Bresnahan, B.W.; Linnau, K.F.; Garrison, L.P.; Higashi, M.; Kessler, L.; Devine, B. Using the Analytic Hierarchy Process for Prioritizing Imaging Tests in Diagnosis of Suspected Appendicitis. Acad. Radiol. 2017, 24, 530–537. [Google Scholar] [CrossRef]
- Lasorsa, I.; Padoano, E.; Marceglia, S.; Accardo, A. Multi-criteria decision analysis for the assessment of non-clinical hospital services: Methodology and case study. Oper. Res. Health Care 2018, in press. [Google Scholar] [CrossRef]
- Houria, B.; Besbes, Z.; Elaoud, M.; Masmoudi, B.; Masmoudi, M.F. Maintenance strategy selection for medical equipments using fuzzy multiple criteria decision making approach. In Proceedings of the 45th International Conference on Computers and Industrial Engineering, Metz, France, 28–30 October 2015. [Google Scholar]
- Öztürk, N.; Tozan, H. A Fuzzy-Based Decision Support Model for Selecting the Best Dialyser Flux in Haemodialysis. J. Healthc. Eng. 2015, 6, 303–324. [Google Scholar] [CrossRef]
- Jamshidi, S.A.; Rahimi, D.; Ait-kadi, A.; Ruiz, A. Comprehensive fuzzy risk-based maintenance framework for prioritization of medical devices. Appl. Soft. Comput. 2015, 32, 322–334. [Google Scholar] [CrossRef]
- Ozsahin, D.U.; Uzun, B.; Musa, M.S.; Şentürk, N.; Nurçin, F.V.; Ozsahin, I. Evaluating nuclear medicine imaging devices using fuzzy PROMETHEE method. Procedia Comput. Sci. 2017, 120, 699–705. [Google Scholar] [CrossRef]
- Cagri, A. Real options valuation of an IoT based healthcare device with interval Type-2 fuzzy numbers. Socio-Econ. Plan. Sci. 2019, in press. [Google Scholar]
- Guenther, R.; Vittori, G. Sustainable Healthcare Architecture, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zamarrón-Mieza, I.; Yepes, V.; Moreno-Jiménez, J.M.A. Systematic review of application of multi-criteria decision analysis for aging-dam management. J. Clean. Prod. 2017, 147, 217–230. [Google Scholar] [CrossRef]
- Huang, I.B.; Keisler, J.; Linkov, I. Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Sci. Total Environ. 2011, 409, 3578–3594. [Google Scholar] [CrossRef]
- Carnero, M.C. MCDA Techniques in Maintenance Policy Selection. In Encyclopedia of Business Analytics and Optimization; Wang, J., Ed.; IGI Gobal: Hershey, PA, USA, 2014; pp. 406–415. [Google Scholar]
- Bana e Costa, C.A.; Vansnick, J.C. Applications of the MACBETH approach in the framework of an additive aggregation model. J. Multi-Criteria Decis. Anal. 1997, 6, 107–114. [Google Scholar] [CrossRef]
- Bana e Costa, C.A.; Ensslin, L.; Correa, E.C.; Vansnick, J.C. Decision Support System in action: Integrated application in a multicriteria decision aid process. Eur. J. Oper. Res. 1999, 113, 315–335. [Google Scholar] [CrossRef]
- Bana e Costa, C.A.; De Corte, J.M.; Vansnick, J.C. MACBETH. Int. J. Inf. Technol. Decis. Mak. 2012, 11, 359–387. [Google Scholar] [CrossRef]
- Bana e Costa, C.A.; De Corte, J.M.; Vansnick, J.C. MACBETH. User’s guide. 2005. Available online: http://m-macbeth.com/wp-content/uploads/2017/10/M-MACBETH-Users-Guide.pdf (accessed on 24 March 2019).
- Bana e Costa, C.A.; Chagas, M.P. A career choice problem: An example of how to use MACBETH to build a quantitative value model based on qualitative value judgments. Eur. J. Oper. Res. 2004, 153, 323–331. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Cebeci, U. Fuzzy AHP-based decision support system for selecting ERP systems in textile industry by using balanced scorecard. Expert Syst. Appl. 2009, 36, 8900–8909. [Google Scholar] [CrossRef]
- Liang, X.; Zhao, X.; Wang, M.; Li, Z. Small and Medium-Sized Enterprises Sustainable Supply Chain Financing Decision Based on Triple Bottom Line Theory. Sustainability 2018, 10, 4242. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S.; Hua, Z.S. A modified fuzzy logarithmic least squares method for fuzzy analytic hierarchy process. Fuzzy Sets Syst. 2006, 15, 055–3071. [Google Scholar] [CrossRef]
- Xu, R. Fuzzy least-squares priority method in the analytic hierarchy process. Fuzzy Sets Syst. 2000, 112, 359–404. [Google Scholar] [CrossRef]
- Csutora, R.; Buckley, J.J. Fuzzy hierarchical analysis: The lambda-max method. Fuzzy Sets Syst. 2001, 120, 181–195. [Google Scholar] [CrossRef]
- Jenatabadi, H.S.; Babashamsi, P.; Yusoff, N.I. The Combination of a Fuzzy Analytical Hierarchy Process and the Taguchi Method to Evaluate the Malaysian Users’ Willingness to Pay for Public Transportation. Symmetry 2016, 8, 90. [Google Scholar] [CrossRef]
- Bozbura, F.T.; Beskese, A.; Kahraman, C. Prioritization of human capital measurement indicators using fuzzy AHP. Expert Syst. Appl. 2007, 32, 1100–1112. [Google Scholar] [CrossRef]
- Isaai, M.T.; Kanani, A.; Tootoonchi, M.; Afzali, H.R. Intelligent timetable evaluation using fuzzy AHP. Expert Syst. Appl. 2011, 38, 3718–3723. [Google Scholar] [CrossRef]
- Cheng, C.H. Evaluating naval tactical missile systems by fuzzy AHP based on the grade value of membership function. Eur. J. Oper. Res. 1996, 96, 343–350. [Google Scholar] [CrossRef]
- Zhu, K.J.; Jing, Y.; Chang, D.Y. A discussion on Extent Analysis Method and applications of fuzzy AHP. Eur. J. Oper. Res. 1999, 116, 450–456. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y.; Hua, Z. On the extent analysis method for fuzzy AHP and its applications. Eur. J. Oper. Res. 2008, 186, 735–747. [Google Scholar] [CrossRef]
- SeongKon, L.; Gento, M.; SangKon, L.; JongWook, K. Prioritizing the weights of hydrogen energy Technologies in the sector of the hydrogen economy by using a fuzzy AHP approach. Int. J. Hydrog. Energy 2011, 36, 1897–1902. [Google Scholar]
- Park, K.S.; Seo, Y.J.; Kim, A.R.; Ha, M.H. Ship Acquisition of Shipping Companies by Sale & Purchase Activities for Sustainable Growth: Exploratory Fuzzy-AHP Application. Sustainability 2018, 10, 1763. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Defuzzification within a multicriteria decision model. Int. J. Uncertain. Fuzziness Knowl. -Based Syst. 2003, 11, 635–652. [Google Scholar] [CrossRef]
- Chang, T.H.; Wang, T.C. Using the fuzzy multi-criteria decision making approach for measuring the possibility of successful knowledge management. Inf. Sci. 2009, 179, 355–370. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Meixner, O. Fuzzy AHP Group Decision Analysis and its Application for the Evaluation of Energy Sources. In Proceedings of the 10th International Symposium on the Analytic Hierarchy/Network Process, Pittsburgh, PA, USA, 29 July–1 August 2009. [Google Scholar]
- CEI IEC 61165:2006. Application of Markov Techniques; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2006. [Google Scholar]
- Creus, A. Fiabilidad y Seguridad, 2nd ed.; Marcombo S.A.: Barcelona, Spain, 2005. [Google Scholar]
- Kaufman, A. Methods and Models of Operations Research; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Hillier, F.; Lieberman, G. Introduction to Operations Research; McGraw-Hill Science: New York, NY, USA, 2002. [Google Scholar]
- Haigh, J. Probability Models; Springer-Verlag Limited: London, UK, 2002. [Google Scholar]
- Rojo, H.; Miranda, M. Investigación Operativa. Cadenas de Markov; Facultad de Ingeniería, Universidad de Buenos Aires: Buenos Aires, Argentina, 2009. [Google Scholar]










| Linguistic Scale | Fuzzy Scale | Fuzzy Reciprocal Scale |
|---|---|---|
| EI: Equally important | (1, 1, 1) | |
| EI-MI: Between equally and moderately more important | (1/3, 1/2, 1) | |
| MI: Moderately more important | (1/4, 1/3, 1/2) | |
| MI-SI: Between moderately and strongly more important | (1/5, 1/4, 1/3) | |
| SI: Strongly more important | (1/6, 1/5, 1/4) | |
| SI-VSI: Between strongly and very strongly more important | (1/7, 1/6, 1/5) | |
| VSI: Very strongly more important | (1/8, 1/7, 1/6) | |
| VSI-EMI: Between very strongly and extremely more important | (1/9, 1/8, 1/7) | |
| EMI: Extremely more important | (1/9, 1/9, 1/8) |
| IUA | INC | OPC | RIW | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IUA | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 3 | 4 | 3 | 4.500 | 6 |
| INC | 0.333 | 0.500 | 1.000 | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 3 | 4 |
| OPC | 0.250 | 0.333 | 0.500 | 0.333 | 0.500 | 1 | 1 | 1 | 1 | 1 | 2 | 3 |
| RIW | 0.167 | 0.222 | 0.333 | 0.250 | 0.333 | 0.500 | 0.333 | 0.500 | 1 | 1 | 1 | 1 |
| S15 | S14 | S13 | S12 | S11 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S15 | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 4 | 6 | 4 | 5 | 6 | 4 | 6.5 | 9 |
| S14 | 0.333 | 0.500 | 1 | 1 | 1 | 1 | 2 | 4 | 4 | 4 | 5 | 6 | 6 | 7 | 8 |
| S13 | 0.167 | 0.250 | 0.500 | 0.167 | 0.250 | 0.500 | 1 | 1 | 1 | 2 | 3 | 4 | 2 | 4 | 6 |
| S12 | 0.167 | 0.200 | 0.250 | 0.167 | 0.200 | 0.250 | 0.250 | 0.333 | 0.500 | 1 | 1 | 1 | 4 | 5 | 6 |
| S11 | 0.111 | 0.154 | 0.250 | 0.125 | 0.143 | 0.167 | 0.167 | 0.250 | 0.500 | 0.167 | 0.200 | 0.250 | 1 | 1 | 1 |
| Criteria | Scale Levels | Weights after Defuzzification and Normalization | Consistency Ratio (CR) | |
|---|---|---|---|---|
| Extra annual human resource costs corresponding to the technical maintenance staff | ||||
| OPC | S15 S14 S13 S12 S11 | 0.091 | ||
| Costs of setting up and starting the operation as a percentage of the cost of the existing facilities | ||||
| INC | S25 S24 S23 S22 S21 | 0.053 | ||
| Existence of a level of risk and the need to take safety precautions | ||||
| RIW | S35 S34 S33 S32 S31 | 0.052 | ||
| Weighted dependence level of other systems on the system analyzed | ||||
| IUA | S45 S44 S43 S42 S41 | 0.097 | ||
| Device | Alternatives | ||
|---|---|---|---|
| ALT A | ALT B | ALT C | |
| MOSS | 0.9966 | 1 | 1 |
| MPNSS | 0.9966 | 1 | 1 |
| MASS | 0.9966 | 1 | 1 |
| Number of Dependent Systems as a Function of the Class of Criticality for the Hospital | MOSS | MPNSS | MASS |
|---|---|---|---|
| Critical systems | 9 | 14 | 14 |
| Important systems | 23 | 0 | 0 |
| Normal systems | 0 | 0 | 0 |
| 82 | 56 | 56 |
| Alternatives | OPC (€) | INC | RIW | IUA |
|---|---|---|---|---|
| Supply device of medicinal oxygen | ||||
| ALT A | 0 | L1 | L3 | 82 × (1 − 0.9966) × 100 = 27.88 |
| ALT B | 10,000 | L4 | L3 | 82 × (1 − 1) × 100 = 0 |
| ALT C | 20,000 | L4 | L4 | 82 × (1 − 1) × 100 = 0 |
| Supply device of medicinal nitrous oxide and medicinal air | ||||
| ALT A | 0 | L1 | L3 | 56 × (1 − 0.9966) × 100 = 19.04 |
| ALT B | 10,000 | L5 | L3 | 56 × (1 − 1) × 100 = 0 |
| ALT C | 20,000 | L4 | L4 | 56 × (1 − 1) × 100 = 0 |
| Device | Alternative | Cost | Consequences for Hospital Activity | Mean Availability | Alternative | Cost | Consequences for Hospital Activity | Mean Availability |
|---|---|---|---|---|---|---|---|---|
| MOSS | ALT A | €0 | May involve severe consequences for the functioning of medical services over an acceptable period of time. Although, there are emergency racks with sufficient autonomy to address the requirements over a certain period of time. | 0.9966 | ALT B | €150,000 | Guarantees the normal working of care services at all times. | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carnero, M.C.; Gómez, A. Optimization of Decision Making in the Supply of Medicinal Gases Used in Health Care. Sustainability 2019, 11, 2952. https://doi.org/10.3390/su11102952
Carnero MC, Gómez A. Optimization of Decision Making in the Supply of Medicinal Gases Used in Health Care. Sustainability. 2019; 11(10):2952. https://doi.org/10.3390/su11102952
Chicago/Turabian StyleCarnero, María Carmen, and Andrés Gómez. 2019. "Optimization of Decision Making in the Supply of Medicinal Gases Used in Health Care" Sustainability 11, no. 10: 2952. https://doi.org/10.3390/su11102952
APA StyleCarnero, M. C., & Gómez, A. (2019). Optimization of Decision Making in the Supply of Medicinal Gases Used in Health Care. Sustainability, 11(10), 2952. https://doi.org/10.3390/su11102952





