1. Introduction
With an accelerated and large-scale urbanisation process, the whole of society has benefited from the construction industry while a great deal of construction and demolition waste (CDW) has been generated. According to statistics, in the European Union, CDW is estimated to be 25%–30% of all generated wastes [
1]. In the USA, about 535 million tons of CDW was produced in 2014 [
2]. In China, approximately 2 to 3 billion tons of CDW is produced every year [
3], accounting for 30%–40% of municipal solid waste. The vast majority of untreated CDW is directly landfilled or illegally dumped, causing serious pollution to the natural environment and greatly affecting the sustainable development of the construction industry.
Dealing with the potential of CDW to threaten the environment in every country has become a critical issue. Among the various solutions to CDW problems, recycling of CDW by enterprises provides a reasonable alternative to the existing unsustainable disposal methods such as landfilling and fly tipping and it also commonly conforms to the principle of circular economy [
4]. How to encourage CDW recycling and prevent the “garbage siege” phenomenon for sustainable development has become an important issue for governments around the world [
5].
The recycling enterprise (hereinafter called “the recycler”) normally plays an important role in the entire CDW recycling process because the recycler receives wasted building materials from contractors and is responsible for the subsequent waste treatment, e.g., processing the waste into renewable products [
4]. However, owing to the long process chain involved in such recycling, the investment is large and the short-term benefits are not obvious; thus, without incentives from governments, recyclers may not be able to survive [
6].
Given that the situation for CDW recyclers is not optimistic, the government has adopted corresponding supporting policies for the recycling of CDW. For example, since the approval of European Framework Directive 2008/98/EC, Member States have enacted legislation establishing incentives for CDW recycling. Despite such policies, the mean recycling rate in the EU-27 is approximately 46% [
7], which is much lower than the 70% target defined for 2020 in the Waste Framework Directive [
8]. In China, the government has successively issued leading policies to provide support for CDW recyclers, such as “Regulations on The Management of Urban Construction Waste,” the “Circular Economy Promotion Law of The People’s Republic of China,” and the “Green Action Plan,” and some regions have even issued specific financial subsidy standards for CDW treatment enterprises [
9]. However, the implementation of these policies has not achieved substantial results, and the recycling rate of CDW is only 5% [
10], which is much lower than the 13% target defined for 2020 [
11].
Several challenges still exist for governments to incentive recyclers to recycle CDW more effectively. The first challenge is information asymmetry. Generally, it is inevitable that recyclers have private information, such as the recycling technology level. Consequently, owing to the potential motivation of profit maximisation, their behaviours may not satisfy the environmental goals of governments. Specifically, governments (principals) often hope to be able to effectively implement CDW recycling, and reduce CDW from directly landfilled or illegally dumped, while recyclers (agents) desire to maximise their economic benefits. Thus, a recycler with opportunistic behaviour may misreport its information to fraudulently obtain government subsidies (adverse selection); after enjoying the preferential policies, it is likely to reduce its investment in recycling for saving costs (moral hazard), not only hindering the development of CDW recycling but also wasting public funds. The second challenge is the ‘‘dynamic nature’’ of the CDW recycling market. Considering CDW recycling is a long-term process, the cooperation mode between governments and recyclers is likely to be dynamic multi-period. In long-term relationships, observations of interim public signals allow governments and recyclers to dynamically learn about the unknown information, and this process of learning potentially affects the contracts and their decisions. For example, on one hand, the government could observe a recycler’s outputs and form posterior assessments of the recycler’s technology level. The reduced posterior uncertainty about technology level could dynamically affect the government’s contracts. On the other hand, when payoffs are indirectly affected by the recycler’s actions, the recycler can use its “misreporting” actions to influence the government’s dynamic process of learning and, in turn, obtain “information rent”. In addition, the recycler may reduce its efforts over the long run, pursuing its interests at the cost of sacrificing government benefits. Indeed, the dual information asymmetry, as well as the ‘‘dynamic nature’’ of the CDW recycling market, results in a number of barriers for the government to promote CDW recycling and achieve sustainable development.
In line with the discussions above, there is an imperative need to ascertain appropriate government incentives that can be used to constrain the behaviour of the recycler and screen the reported information, ensuring the success of CDW recycling and the effective allocation of public resources. Therefore, this study seeks to address the following research questions.
- (1)
How to design effective static/dynamic incentive contracts to make the recycler report its information faithfully under dual information asymmetry?
- (2)
How do the misreporting behaviour or technology types of the recycler affect the optimal contracts of the government, the decisions of the recycler, and the utilities of the parties?
- (3)
Which mode of cooperation is appropriate for the environment and CDW recycling development?
To answer these question, a principal-agent model was employed wherein the government was the principal and the recycler is the agent. To reveal the true technical level and stimulate CDW recycling efforts effectively, the incentive theory was first used to design the static contracts under one-stage cooperation, and then design the dynamic contracts under dynamic two-stage cooperation, with the technical level and efforts of the recycler being the asymmetric information variables under adverse selection and moral hazard.
To the best of our knowledge, this study represents the first attempt to design the optimal static and dynamic incentive contracts for promoting CDW recycling under dual information asymmetry. It is anticipated that our study will contribute to the body of knowledge on CDW recycling and management, and provide valuable insights regarding the incentives offered for CDW recycling operations. By designing the effective incentive mechanism under dual information asymmetry, the CDW recycling will be encouraged and the sustainable development will be achieved. The models and mathematical techniques used in deriving the theoretical results can also be applied to other coupling markets, particularly under asymmetric information.
The remainder of this paper is organised as follows.
Section 2 provides a survey of the related research and
Section 3 describes our model variables and assumptions. In
Section 4, the modelling framework is presented, and a one-period incentive contract model of the government is developed.
Section 5 extends the one-period model to two periods according to long-term cooperation. In
Section 6, the model is analysed, and the one-period (static) and two-period (dynamic) incentive contract models are compared. The final section concludes the paper. All mathematical proofs are provided in the
Appendix A,
Appendix B,
Appendix C,
Appendix D,
Appendix E,
Appendix F,
Appendix G,
Appendix H,
Appendix I,
Appendix J and
Appendix K.
2. Literature Review
This paper draws on three streams of literature: the CDW recycling under government incentives, the mechanism design under asymmetric information and the principal-agent theory.
2.1. CDW Recycling under Government Incentives
In recent years, scholars have increasingly studied how the government promotes CDW recycling. Kim et al. [
12] investigated the influence of a unit pricing system on illegal dumping and showed that providing compensatory incentives for recycling is a better choice in waste management. Huang et al. [
13] reported that at present, the majority of Chinese recycling enterprises are in fiscal deficit, and it is urgent to provide appropriate economic incentives to promote the recycling market, such as financial subsidies for the improvement of recycling technology. Ajay et al. [
14] concluded that legislation on waste management can effectively promote the recycling of CDW and proposed policy measures whereby substantial CDW can be diverted from the landfill. Jia et al. [
15] introduced a subsidy mechanism for cases of low recovery and reuse ratios and found that subsidies can significantly increase the amount of waste recycled and reused. Liu et al. [
16] employed the method of system dynamics to simulate the environmental benefits of CDW recycling and found that the government could improve the environmental benefits of CDW recycling by adjusting the subsidies for recycling enterprises and the distribution of recycling treatment centres. Zhao et al. [
17] analysed the economic feasibility of different types of waste-treatment centres in CDW recycling activities under different policies and economic environments and proposed that to minimise investment risks for investors, economic and political instruments must be established in advance to provide financial support for recycling centres. To foster the recycling industry, the economic feasibility of recycling centres can be improved by government initiatives through direct influence by subsidising recycling centres or recycled secondary raw materials [
18].
Among the previous studies on CDW recycling, significant efforts have been directed towards investigating the importance of government incentives in CDW recycling; analysing the long-term impacts of different types of government incentives on society, the economy, and the environment through system dynamics, game theory, and other methods and made contributions in promoting the development of CDW recycling. Nevertheless, the background of previous studies is complete information. That means the government as the decision maker could totally know all the information in the CDW recycling market. In fact, the government cannot master all the information of the market; thus, the theoretical model differs from the real situation, preventing the government from formulating effective recycling incentive contracts.
2.2. Mechanism Design under Asymmetric Information
The information asymmetry concept is widely diffused throughout management research, and many scholars [
19,
20,
21] have studied information asymmetry from various aspects. The theory of mechanism design provides solutions to contract design problems with asymmetric information and it has been successfully applied in a variety of supply chain management in which the agent possesses private information and the principal attempts to elicit it by offering a menu of contracts. Many scholars [
22,
23] study problems of incentives for agents in which there is only adverse selection or moral hazard. Some recent papers incorporate both adverse selection and moral hazard to study the incentives, which belongs to the research under “dual information asymmetry” [
24]. Peter et al. [
25] analysed the adverse selection and moral hazard (dual information asymmetry) problems of supply-chain members due to the differences in the supply-chain structure and information asymmetry in a two-stage supply chain. Xiao and Huang [
26] performed a comparative study of two situations in which manufacturers can and cannot obtain accurate information regarding the recycling market. Applying the principal-agent theory, they designed the linear contract for the manufacturer to incentivise the third party. Xu et al. [
27] studied a situation where the recycling capacity and the efforts of recyclers could not be observed and considered the investment of recyclers in constructing an incentive mechanism model. Wang et al. [
28] constructed a closed-loop supply-chain incentive contract with dual information asymmetry compared and analysed two scenarios of government intervention and non-intervention.
Considering the ‘‘dynamic nature’’ of the supply chain, Gaudet et al. [
29] and Hung et al. [
30] extended the single-period incentive to a multi-period incentive, studying the multi-period incentive problem under the assumption of inter-period irrelevance of private information parameters and inter-period complete commitment of the principal. Guo et al. [
31] studied multi-stage incentive problems where the cost information of the manufacturer was asymmetric and proposed a dynamic supply-chain incentive contract model considering the cost reputation of the manufacturer. They obtained the reputation compensation and the cost type displayed by the manufacturer and achieved the goal of weakening the ratchet effect. Li et al. [
32] studied the multi-stage dynamic coordination of a two-stage supply chain according to the principal-agent theory framework. Under dual information asymmetry, Wang et al. [
33] designed a dynamic commercial credit incentive contract to motivate the retailer to disclose its true costs, for increasing supply-chain profits.
In contrast to these papers, which operate from an operations perspective and focus on asymmetric information in view of cost, demand, quality or credit default, we investigated the influence of asymmetric recycling technology level and recycling efforts information on the CDW policies from the perspective of the dynamic interaction between the government and the recycler.
2.3. Principal-Agent Theory
The origin of research on incentive contracts is in the principal-agent theory. The principal-agent theory aims to design the most efficient contracts for ubiquitous agency problems, in which the principal entrusts work or decision-making authority to the agent, but faces some problems, such as (1) split incentive problem—the desires or the goals of the principal and agent conflict; (2) asymmetric information—it is difficult or too expensive to verify the agent’s actions [
34]. Basu, Lal, Srinivasan, and Staelin [
35] were the earliest scholars applying the principal-agent theory to supply chain enterprises when they studied the problems of sales staff salary distribution. Both Lal and Staelin [
36] and Lal and Srinivasan [
37] further studied the principal-agent relationship in supply chains with the addition of asymmetric information factors to the principal-agent theory. Meanwhile, Fayez et al. [
38] summarised the application fields, application purposes and application strategies of the principal-agent theory based on previous academic research and analysed how to apply the principal-agent theory to supply chains and how to clarify the relationships and behaviours of each role in the supply chain in detail on the basis of a broad aggregation of the literature. The agency problem between the government and the recycler should be considered when designing incentive contracts for CDW recycling. Accordingly, the principal-agent theory was employed in this study to develop our models.
3. The Model
3.1. Model Depiction
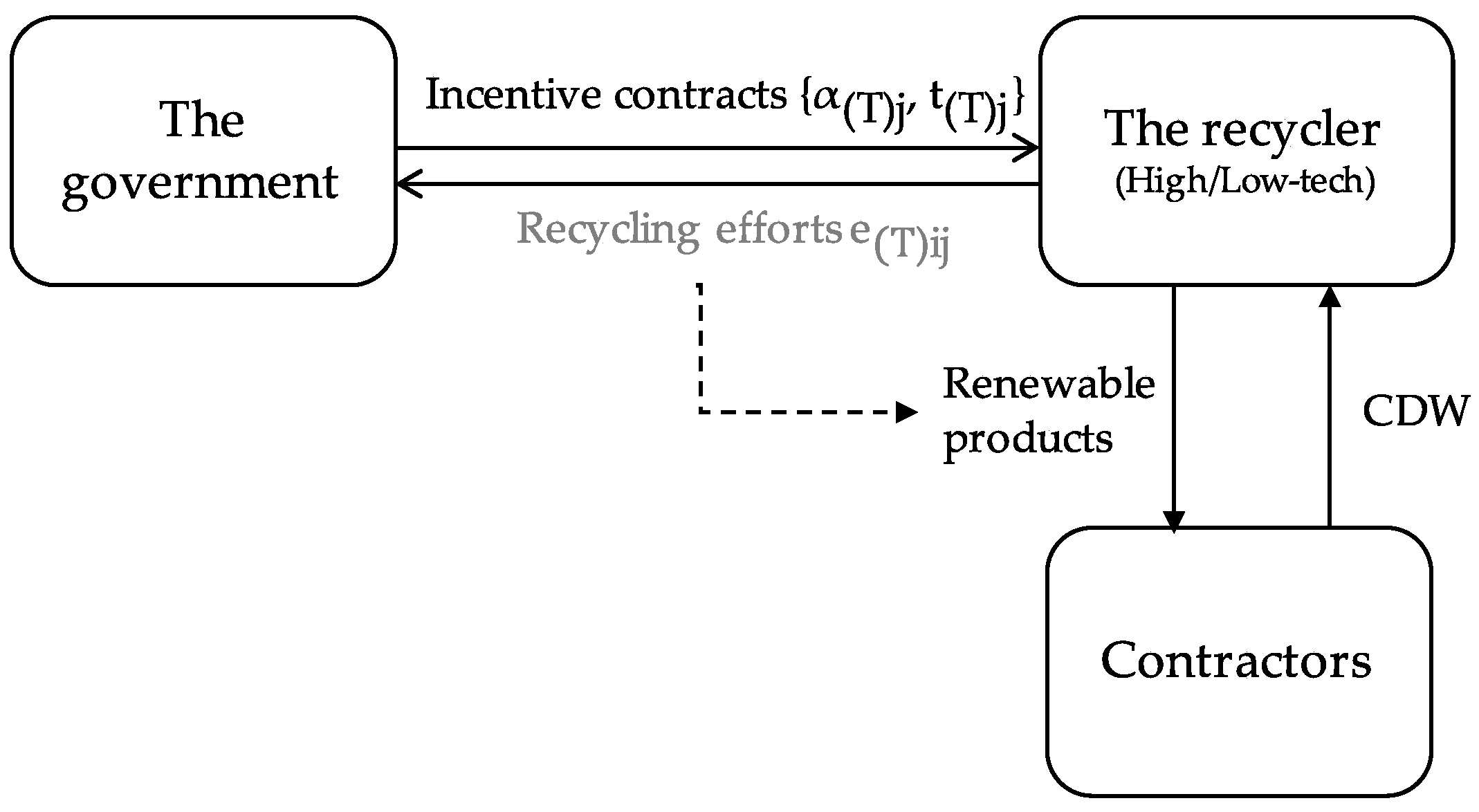
In this article, as shown in
Figure 1, a system consisting of a government and a recycler was considered. As the principal, the government entrusts the recycling of CDW to the recycler. According to assumptions, the recycler possesses high recycling technology level (hereinafter called “technical level”) or low technical level privately, denoted as high-tech recycler or low-tech recycler respectively. For the recycler, the high technical level
in the probability of
, and
in the probability of
, where
>
. As the technical level is known privately to the recycler, the government cannot know it perfectly. As a result, we assume that the government can only know the probability of the recycler being high/low-tech, which means
is common information. Based on the assumptions, the government offers incentive contracts to the recycler for its recycling efforts (hereinafter called “efforts”), which is not directly observable. The recycler makes its efforts by producing renewable products with CDW from contractors. In addition, the recycler sells renewable products back to the contractors. For the government, how to seek the recycler’s private information with the information screening contract is as follows: (1) the government offers two types of contracts; (2) the recycler decides to accept which contract; (3) the government identifies the technical level of the retailer through the contract choice of the recycler.
To provide diverse cooperation mode, we designed two different models, named as a static model (Model S) and a dynamic model (Model D). The pictorial representation of the two models is presented in
Figure 2.
- (1)
In Model S, the government designs static contracts under one-stage cooperation. The government will pay the recycler according to the recycler’s efforts by observing the quantity of renewable product during the whole period. The specific sequence of events is shown in
Figure 3 in
Section 4.
- (2)
In Model D, the government designs dynamic contracts under two-stage cooperation. We divide the cooperation period into two stages, named D1 and D2. The government will pay the recycler at the end of each stage based on the recycler’s efforts. The government determines the recycler’s efforts by the quantity of renewable product during each period, specifically D1 and D2. The specific sequence of events is shown in
Figure 4 in
Section 5.
3.2. Notations
It was assumed that there are only two types of CDW recycling enterprises, with the subscript H representing a high recycling technology level (hereinafter called “high-tech”) and the subscript L representing a low recycling technology level (hereinafter called “low-tech”). The superscript * represents the optimal decision in each scenario, T represents the time period of the dynamic excitation and has no corner mark T in the case of static excitation.
Table 1 presents the notation used in this paper.
3.3. Assumptions
Before building the model, for ease of explanation and analysis, we propose further descriptions and assumptions as follows.
Assumption 1. The government has asymmetric information regarding the behaviour of the recycler. There exists common information between the two parties, but they also have private information throughout the process of CDW recycling. The government cannot completely obtain the valuable information owned by the recycler and can only obtain incomplete information. Consequently, the government designs an incentive contract to constrain the behaviour of the recycler through partial information.
Assumption 2. The government and recycler are both perfectly rational economic entities but have different objectives. The government attempts to maximise social benefits with minimal subsidies while enhancing the CDW recycling market. However, the recycler expects to fulfil its economic interests with the minimal costs to achieve profit maximisation. We assume that the government is risk-neutral and that the enterprise is risk-averse and let , where .
Assumption 3. The recycling rate of CDW is closely related to the technical level and efforts of the recycler. The recycling rate is considered as follows.
Here,
is the basic recycling rate when the recycler does not make any efforts. Therefore, the quantity of renewable products is
, and
is a random factor representing unobservable market fluctuations and follows a normal distribution:
.
Assumption 4. The recycler invests unobservable efforts at a private cost to recycle CDW.
Assumption 5. The technical level of the recycler remains unchanged.
Assumption 6. In each period, the whole of society produces the same amount of CDW.
Assumption 7. Weitzman [
39] proposed and analysed the rationality of linear contracts. Holmstrom and Migrom [
40] proved that linear contracts can achieve optimal results. Therefore, the current design of the incentive system is mostly adopted in the form of a linear contract. The total subsidy that the government offers to the recycler in our paper also adopts the linear incentive contract. Assuming that the government can only observe renewable products quantities
, so the total subsidy function can be expressed as
Here,
is a fixed payment. It cannot influence the degree of effort, but the incentive coefficient (hereinafter called the “subsidy”)
has a great influence on the total subsidies; thus, the level of effort chosen by the recycler is affected. That is, the government selects an appropriate fixed payment and subsidy to design an incentive contract to prompt the recycler to choose the optimal effort and report the true information.
Assumption 8. The government is responsible for the disposal of CDW that has not been recycled, and the unit treatment cost is
. Therefore, the utility of the government consists of environmental-benefit output, subsidy expenditure and CDW treatment cost and is given by
Assumption 9. The market price of renewable products
is relatively stable and is an exogenous variable. The profit of the recycler consists of total subsidy, sales revenue and effort costs and is given by
Thus, according to Assumption 2, the utility function of the risk-averse recycler can be written as
Assumption 10. The discount factor is 1.
4. Static Incentive Model under Dual Information Asymmetry (Model S)
In the static incentive model, we considered a single-stage contract.
Figure 3 shows the static game sequence: the government first designs a set of incentive contracts {
}, {
} for the recycler to choose, and the recycler selects a contract according to its own technical level and pays for the corresponding efforts.
According to a benefit analysis of the gambling relations between the government and the recycler, the objective function of the problem is to maximise the utility of the government. Therefore, the single-period incentive contract model can be expressed as follows:
Equation (6) indicates that the utility of a high-tech recycler choosing the H contract is higher than the utility of the recycler choosing the L contract. Equation (7) indicates that the utility of a low-tech recycler choosing the L contract is significantly higher than the utility of the recycler choosing the H contract. Equations (6) and (7) are both incentive compatibility constraints preventing the recycler from reporting false information, whereby the recycler can maximise its utility. Equations (8) and (9) are participation constraints ensuring that the utility of the recycler is no lower than its conserved utility.
Considering the leader–follower game relationship between the government and the recycler, we next solved the model by using the Lagrange method and backward induction. In this paper, we used propositions to illustrate the optimal strategies of both parties. Based on the propositions, the corollaries further analysed the results to gain management insights.
Proposition 1. The efforts of the recycler depend on its technical level and the government subsidy. A recycler with a higher technical level provides greater efforts. Additionally, a larger subsidy provided by the government yields greater efforts of the recycler.
Proposition 1 indicates that a higher technical level of the recycler yields a higher recycling rate due to its efforts; to obtain a large government subsidy, the recycler is incentivised to invest in recycling efforts. Correspondingly, if the government provides a larger subsidy for renewable products, the recycler is more willing to invest in recycling to produce more renewable products and obtain more subsidies.
Proposition 2. The optimal single-period information-screening contracts set by the government areand.
Here
,
,
The recycler truthfully reports its technical level and makes the best efforts strategy:
The quantities of renewable products are:
Proposition 2 shows that when , the government subsidises the high-tech recycler (); when , the government subsidises the low-tech recycler (). Only when the environmental benefits brought by CDW recycling and the cost of CDW disposal are greater than the risk cost of the recycler will the government offer a CDW recycling incentive.
Corollary 1. In case S:
- (1)
For the high-tech recycler:, , ;
- (2)
For the low-tech recycler:, , ;
- (3)
, , .
As shown in Corollary 1, when the recycler is high-tech, has no influence on the optimal efforts, the number of renewable products, and the optimal government subsidy. However, when the recycler is low-tech, the optimal efforts, the number of renewable products, and the optimal government subsidy decrease monotonously with the increase of . Considering that the high-tech recycler may pretend to be the low-tech recycler, the government will be cautious and limit the subsidy for the low-tech recycler. Therefore, when designing a contract for the low-tech recycler, the government will fully consider the probability distribution of technology types. In addition, the high-tech recycler always receives larger subsidies, makes more efforts to recycle CDW, and produces more renewable products than the low-tech recycler.
Corollary 2. In case S:
- (1)
, , , , , ;
- (2)
, , , , , ;
- (3)
, , , , , .
Corollary 2 shows that the government subsidy increases with the total CDW quantity for the whole society, the environmental-benefit output coefficient, and the CDW treatment cost of the government. When the CDW quantity increases, the social pressure and environmental pressure on the government increase as well; thus, the government is eager for the recycler to deal with more CDW and increases subsidies for encouraging the recycler to make recycling efforts. In the meantime, if recycling unit CDW and converting it into a renewable product can achieve greater environmental benefits or treating unrecycled CDW can lead to higher cost, the government will provide more subsidies for the recycler to improve the environmental benefits or reduce CDW treatment expenses.
Proposition 3. Under the static optimal contract:
- (1)
The optimal utility of the low-tech recycler isand the optimal utility of the high-tech recycler is;
- (2)
The optimal utility of the government is;
- (3)
, .
Proposition 3 shows that the low-tech recycler cannot obtain information rent, owing to its low recycling technology, but can only obtain reservation utility. Due to its information advantages, the high-tech recycler obtains strictly positive information rent, and the information rent decreases with the increase of . The government can identify the technical level of the recycler at the cost of limiting incentives for a low-tech recycler and eliminating some benefits for a high-tech recycler. As increases, the information advantage of the high-tech recycler decreases. The government reduces the information rent to the high-tech recycler, and its own income increases; thus, the government utility increases with .
5. Dynamic Incentive Model Considering Misreporting under Dual Information Asymmetry (Model D)
In dynamic cooperation, the recycler knows its technical level before the government provides incentive options. However, the government only knows the possible types of the technical level of the recycler and the probability of each type. Under the framework of full commitment, the government designs two-stage menus before contracts are executed. Contracts {
}, {
}, {
}, {
} are simultaneously offered to the recycler, and the government has the ability to commit to the implementation of the subsequent phase of the contract, thereby motivating the recycler with information advantages to disclose the true information. The dynamic game timing is shown in
Figure 4.
In contrast to the single-stage game, in the two-stage game, the government makes full use of the information disclosed by the recycler in the first stage for designing the optimal incentive contract. In the first stage of the game, the government has a prior probability to the recycler: and . In the previous section, it was revealed that only a high-tech recycler has a misreporting motive; a low-tech recycler reports its own technical level truthfully, and so . As mentioned previously, it is assumed that the probability of the high-tech recycler misreporting that it is low-tech in each stage is ; thus, and .
According to Bayes’ theorem, the posterior probability of a high-tech recycler is
5.1. Information Screening Model in Second Stage (Model D2)
At the end of the second phase, the government-enterprise cooperation ends, because there are no follow-up factors affecting the decision making of the participants. In the second phase, both parties only need to consider the utility maximisation. The second phase of the incentive mechanism is designed as follows:
Equations (13) and (14) are both incentive compatibility constraints preventing the recycler from reporting false information, whereby the recycler can maximise its utility. Equations (15) and (16) are participation constraints ensuring that the utility of the recycler is no lower than its conserved utility.
By using the Lagrange method and backward induction, we can obtain Proposition 4.
Proposition 4. In the second phase of dynamic cooperation, the optimal information-screening contracts set by the government areand.
Here
,
,
The recycler truthfully reports its technical level and makes the best efforts strategy:
The quantities of renewable products are:
The optimal utility of the low-tech recycler is and the optimal utility of the high-tech recycler is .
Proposition 4 shows that in the second phase, the low-tech recycler can only obtain retained utility, while the high-tech recycler can obtain strictly positive information rent. The incentive provided by the government to the high-tech recycler is not distorted and is the same as the subsidy provided in the single-phase situation. However, the subsidy provided to the low-tech recycler is related to the probability of the high-tech recycler misreporting. The misreporting behaviour of the high-tech recycler in the first stage affects the judgment of the government regarding the posterior probability, indirectly affecting the second-stage decision making of the government, as well as the efforts and utility of the recycler.
Corollary 3. In case D2:
- (1)
For the high-tech recycler:, , , , , ;
- (2)
For the low-tech recycler:, , , , , ;
- (3)
, , .
As shown in Corollary 3, in the second stage, when the recycler is high-tech, and have no influence on the optimal efforts, the quantity of renewable products, and the optimal government subsidy. However, when the recycler is low-tech, the optimal efforts, the quantity of renewable products, and the optimal government subsidy decrease monotonously with the increase of . Obviously, the high-tech recycler always receives a larger subsidy, makes more efforts towards recycling, and produces more renewable products than the low-tech recycler.
5.2. Information Screening Model in First Stage (Model D1)
In the first stage, to obtain greater income, the recycler may choose to misreport its private information; thus, the direct display mechanism fails in the first stage. The government must dynamically consider the total income of the two stages of the recycler when designing contracts in the initial stage. The designed incentive contract must be able to compensate for the information rent lost in the second stage after the recycler discloses the true information in the first stage. The incentive mechanism is designed as follows:
Here, represents the utility of the recycler in the second stage, and is the posterior probability that the government considers the recycler to be -type, with and . Proposition 5 is obtained using the Lagrange method and backward induction.
Proposition 5. In the first phase of dynamic cooperation, the optimal information-screening contracts set by the government areand.
Here , , , .
The recycler truthfully reports its technical level and makes the best efforts strategy:
The quantities of renewable products are:
The optimal utility of the low-tech recycler is and the optimal utility of the high-tech recycler is .
Proposition 5 shows that the low-tech recycler only obtains retained utility, while the high-tech recycler obtains strictly positive information rent. In the first stage, the incentives provided by the government to the high-tech recycler are not distorted and are equal to the subsidy provided in the single-period case.
Corollary 4. In case D1:
- (1)
For the high-tech recycler:, , ;
- (2)
For the low-tech recycler:, , .
In the first stage, when the recycler is high-tech, has no influence on the optimal efforts, the quantity of renewable products, and the optimal government subsidy. However, when the recycler is low-tech, the optimal efforts, the quantity of renewable products, and the optimal government subsidy increase monotonously with the increase of .
Corollary 5. Comparing cases S and D:
- (1)
The government’s optimal subsidy:, , ;
- (2)
For the high-tech recycler:, , , ;
- (3)
For the low-tech recycler:, , , , .
According to Corollary 5, it is clear that the subsidy provided by the government to the high-tech recycler is not affected by whether the contracts are single-period or two-period; thus, the subsidy for the high-tech recycler remains unchanged. This ensures that the high-tech recycler is fully motivated, makes the same efforts, and produces the same quantity of renewable products at all stages, although the utility of the high-tech recycler in dynamic cooperation is greater than that in static cooperation. The subsidy obtained by the low-tech recycler in each stage of dynamic cooperation is higher than that in the case of static cooperation. Thus, the low-tech recycler makes more recycling efforts and produces more renewable products in dynamic cooperation but only obtains reserved utility in each stage.
6. Numerical Analysis
In this section, a numerical study was conducted to analyse the influence of the misreporting probability and the proportion of recycler technology types on the optimal contract of the government, the efforts of the recycler, and the utility of the government and the recycler under different circumstances. According to Yuan and Wang [
41] and Wang [
42], if the density of the generated waste is 1.5 t/m
3, the quantity of CDW in Chengdu in 2017 would be approximately 100 M t, so we set
. Given the fact that the unit profit of renewable products is small [
13], the CDW recycling technology is not mature and the recycling investment is high [
43,
44], the recycler has relatively high risk aversion (i.e.,
,
and
is relatively large), while the contribution of efforts for recycling is relatively small (i.e.,
is relatively small) [
45], we set
and
[
46].
6.1. Comparison between Cases D1 and D2
Figure 5 and
Figure 6 show the fixed payment and subsidy, respectively, provided by the government in each stage of the dynamic incentive. The fixed payment provided by the government to the recycler in the two stages decreases with the increase of the probability of the recycler being high-tech (
). As the probability of misreporting (
) increases, the fixed payment of the government increases in the first stage and decreases in the second stage. The subsidy provided by the government to the high-tech recycler remains unchanged, and the incentives are not distorted. To encourage the high-tech recycler to report true information, the fixed payment provided in the first stage is always greater than that in the second stage, compensating for the loss of information rent for the recycler incurred by telling the truth. Moreover, when
is small, the fixed payment and subsidy provided by the government to the low-tech recycler in the first stage are smaller than those in the second stage. In contrast, when
is relatively large, the government provides a larger fixed payment and subsidy in the first stage.
Figure 7 and
Figure 8 illustrate the recycling efforts and the utility obtained by the recycler at each stage in the dynamic incentive. At all stages, the high-tech recycler is fully motivated, and its efforts remain unchanged. In comparison, the low-tech recycler always makes less effort than the high-tech recycler, owing to the smaller subsidy. Despite that, the efforts of the recycler are closely related to its technical level and the subsidy provided by the government, the efforts of the low-tech recycler in the two stages vary with respect to the government subsidy. Furthermore, the low-tech recycler can only obtain reservation utility in both phases, owing to its low technical level, whereas the high-tech recycler can obtain information rent in both stages because of its information advantages, and the information rent in the first stage is always greater than that in the second stage.
Figure 9 shows the utility of the government at various stages in the dynamic incentive. In the two stages, the utility of the government increases with
. We observed that if the possibility of the recycler being high-tech increases, the government gains more environmental benefits. Additionally, the treatment fee for CDW decreases; thus, the total revenue of the government increases. Moreover, when
is low, the government gains more in the first stage than in the second stage, whereas when
is high, the government gains more in the second stage. The yellow
represents the government CDW treatment fee when the government does not offer a recycling incentive. Clearly, the utility obtained when the government encourages CDW recycling is always greater than that when the government does not.
6.2. Comparison between Cases S and D
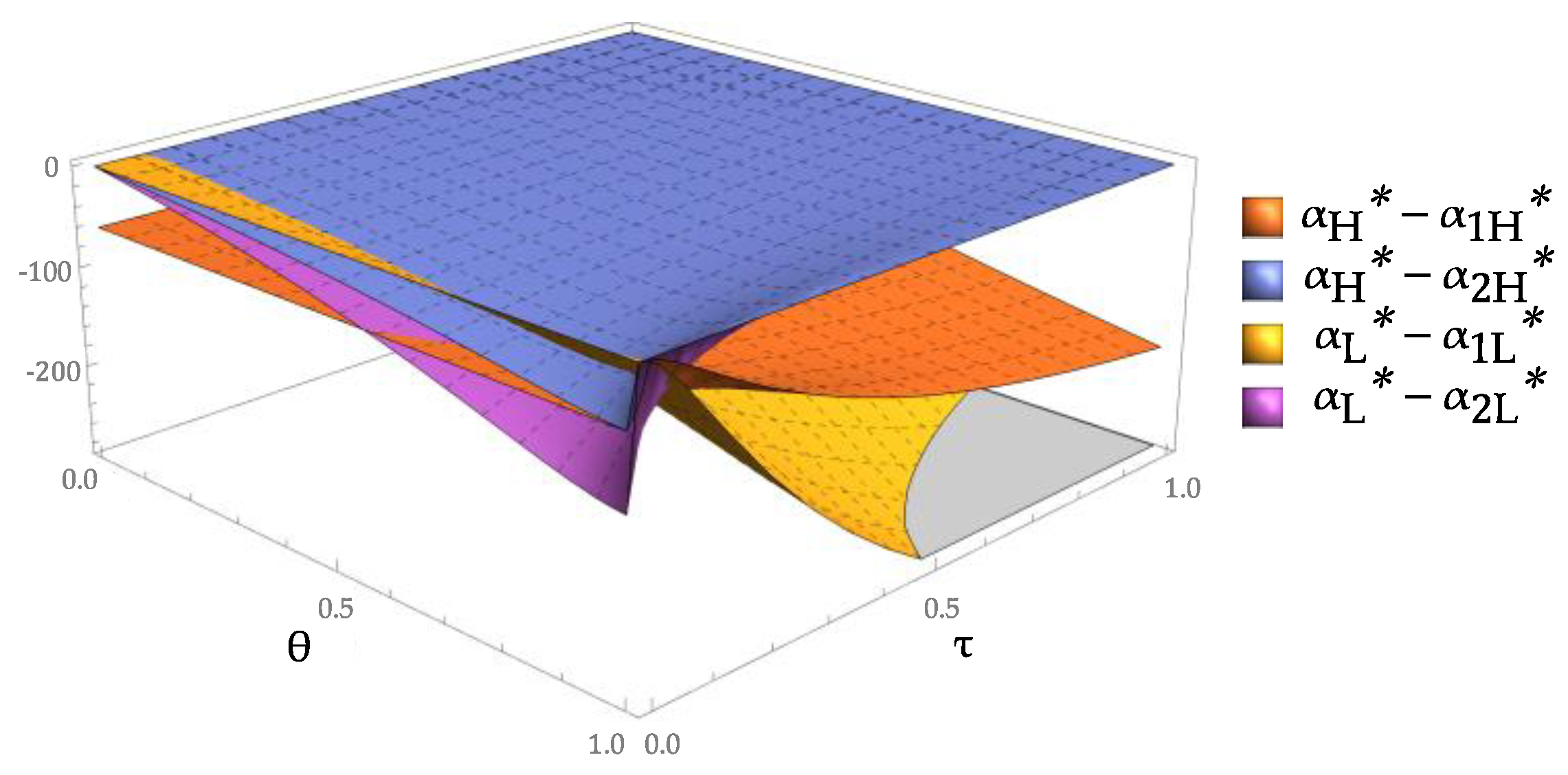
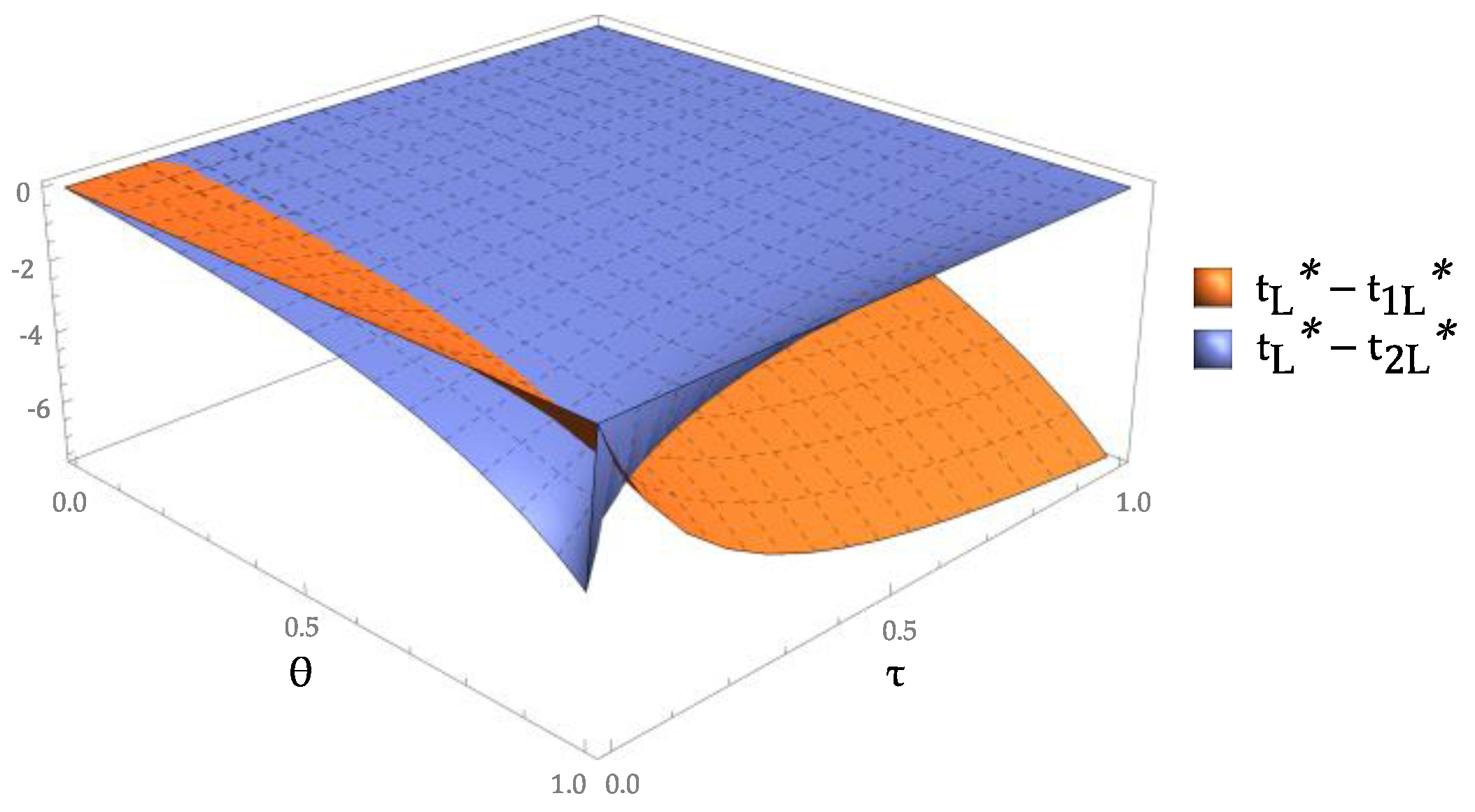
Figure 10 shows the difference between the fixed payments provided by the government in the cases of the static and dynamic incentives (S and D, respectively), and
Figure 11 shows the difference between the government subsidies for the low-tech recycler in the cases of S and D. The fixed payment of the government and the subsidy for the low-tech recycler in the case of the static incentive are smaller than those in the case of the dynamic incentive. Compared with single-stage cooperation, in two-stage cooperation, the government is more likely to believe that the recycler is telling the truth; thus, it is willing to provide a larger subsidy to promote CDW recycling. As the probability of misreporting increases, the difference between the fixed payment and the subsidy provided in S-D1 increases, and the difference between the fixed payment and the subsidy provided in S-D2 decreases.
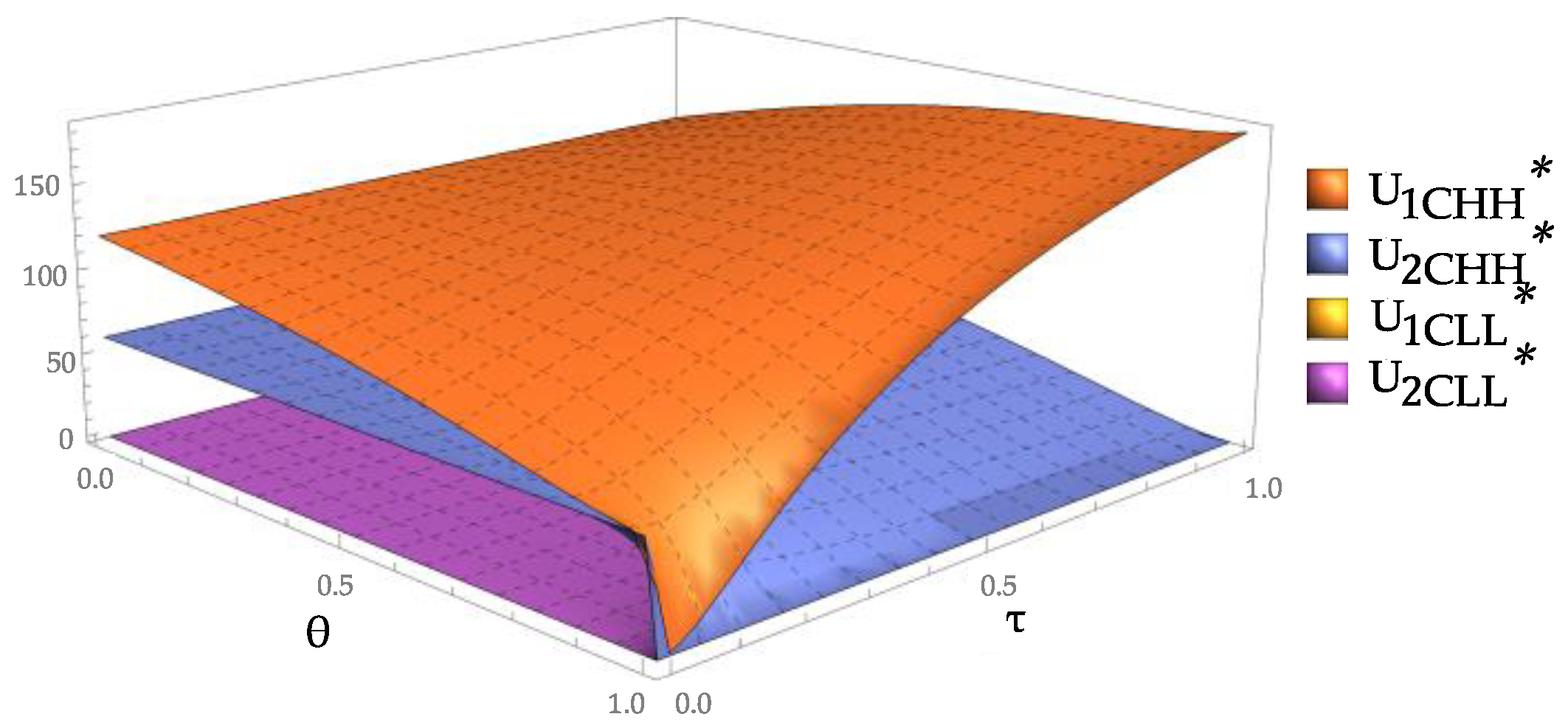
Figure 12 shows the difference in the utilities of the high-tech recycler between the cases of S and D. As
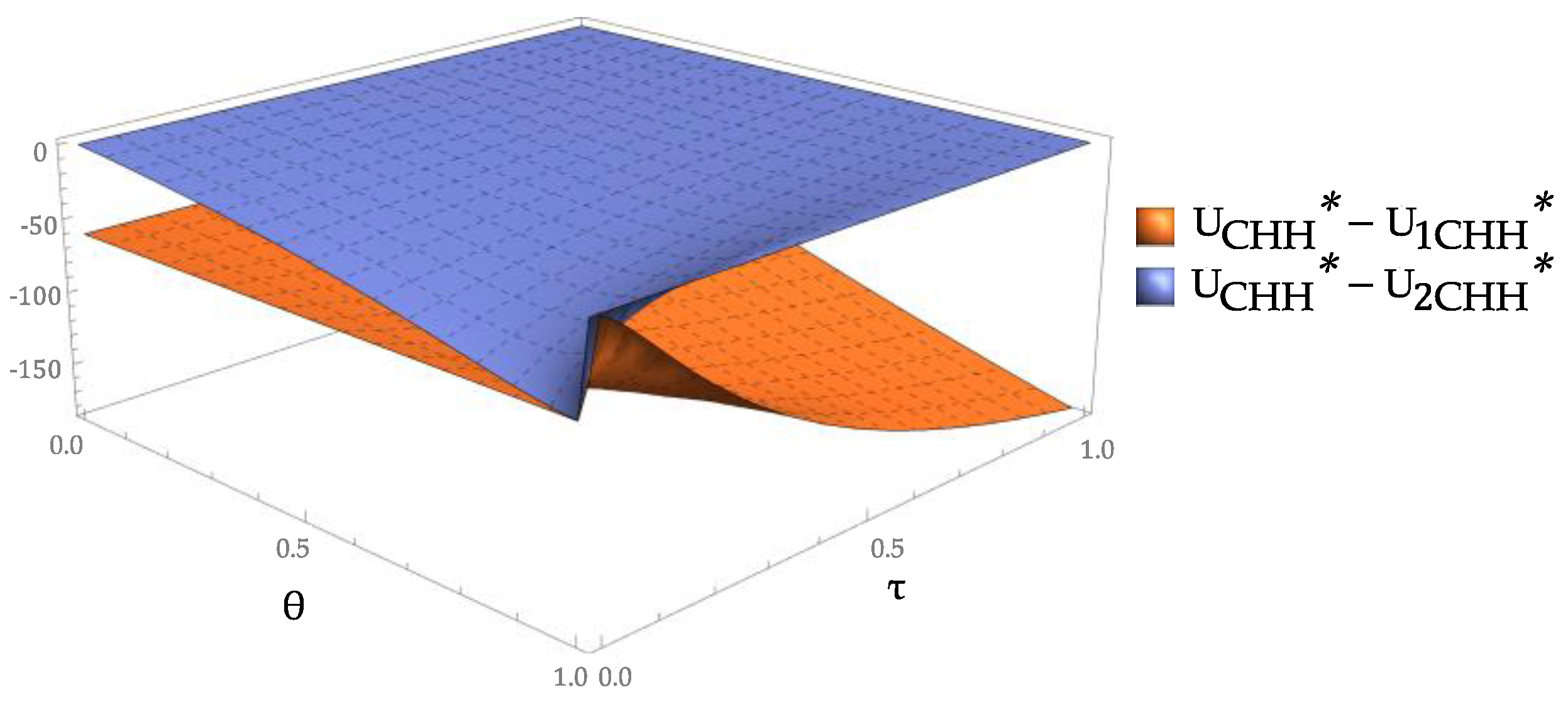
increases, the utility difference between the static case and the first stage of the dynamic case increases, while the utility difference between the static case and the second stage of the dynamic case decreases. The CDW recycler prefers the dynamic incentive contract for long-term cooperation because the utility obtained by the high-tech recycler with the dynamic incentive is greater than that with the static incentive. Thus, we can obtain an important management insight, that is, when profit-oriented, the recycler should choose the long-term cooperation with the government.
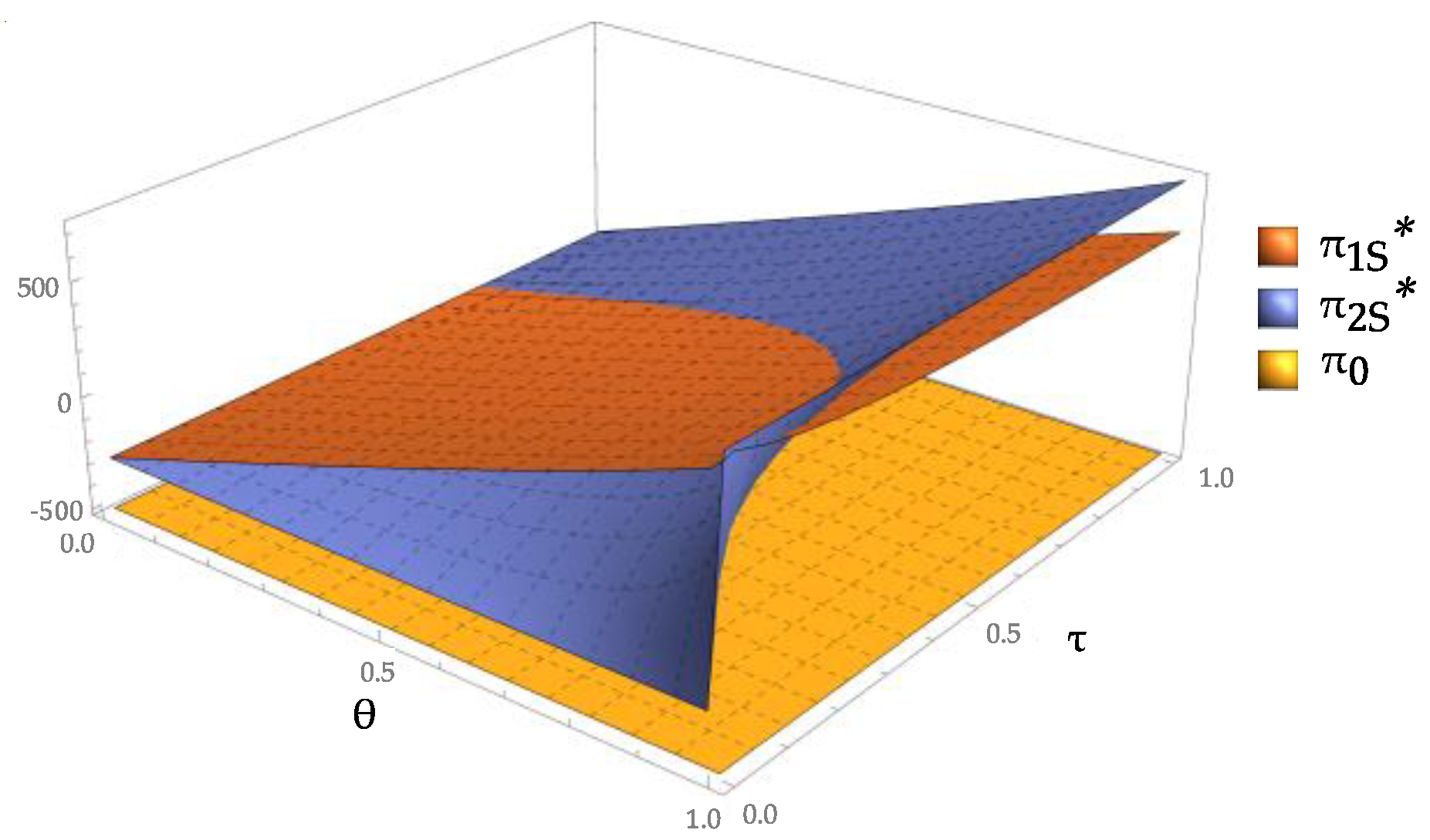
Figure 13 shows the difference in the government utility between the cases of S and D. Compared with single-stage cooperation, the government is willing to provide a larger subsidy in the two-stage cooperation regardless of the changes in
and
, resulting in increased government expenditure and reduced total revenue. However, as shown in
Figure 14, compared with the static incentive, the quantity of renewable products in each stage of the dynamic incentive is larger, and the government obtains greater environmental benefits. Combined with the discussion above, we obtained an important management insight, that is, when profit-oriented, the government should choose the short-term cooperation, and when environment-oriented, the government should choose the long-term cooperation. Therefore, from the viewpoint of sustainability, the government is willing to offer dynamic contracts and undergo long-term cooperation with the recycler. This agrees with the conclusion of Gao etc. [
47] that although the economic benefits brought by CDW recycling activities are not satisfactory, the government should still release system dividends to develop the recycling industry, such as subsidies and incentives for recyclers, because the hidden economic benefits of CDW recycling are greater than the explicit economic benefits.
7. Conclusions
CDW recycling has been commonly regarded as an effective method for minimising CDW disposal and achieving sustainable development. It is clear that the government plays a crucial role in promoting the CDW recycling market. However, asymmetric information is key for regulators to make appropriate environmental policy, which they are struggling for. Thus, in this study, the CDW recycling incentive problems were analysed based on incentive theory from the perspective of the government. To reveal the technical level of the recycler and to incentivise the recycler to make CDW recycling efforts, we first designed static incentive contracts under one-stage cooperation, and further dynamic contracts under two-stage dynamic cooperation, considering the recycling technology level and recycling efforts of the CDW recycler are private information. Subsequently, we have compared the optimal decisions for these contracts. There are some important findings based on the analytical results of our framework.
For the government, the optimal incentive contracts can enable the government to determine the true technical level of the recycler and achieve the objective of information screening. The technology types and misreporting behaviour of the recycler need to be taken into full account when creating incentive contracts. On one hand, technology types and misreporting behaviour will not affect the subsidy for the high-tech recycler; on the other hand, it will affect the subsidy for the low-tech recycler because the government will fully consider technology types and misreporting behaviour when formulating the subsidy. Specifically, with the increase of the probability of the recycler being high-tech, the government will decrease the subsidy. If the probability of the recycler’s misreporting increases, the government will consider to raise the subsidy in the first phase of dynamic cooperation and lower it in the second. Moreover, compared with static cooperation, the government will provide the low-tech recycler with a larger subsidy in dynamic cooperation, which also obtains greater environmental benefits. Therefore, the government should promote long-term cooperation in the future.
For the recycler, the optimal recycling efforts can be chosen based on incentives provided by the government. The efforts of the high-tech recycler remain unchanged while the efforts of the low-tech recycler vary with respect to the proportion of technology types and the probability of misreporting. In addition, the efforts of the low-tech recycler are always smaller than those of the high-tech recycler. Because of the information advantage, the high-tech recycler can obtain the information rent, while the low-tech recycler can only obtain the retention utility. Moreover, the recycler obtains more profits under dynamic incentives. Therefore, the recycler should choose long-term cooperation with the government.
This work provides interesting insights and observations, shedding new light on better understanding and design of future CDW recycling policies. The theoretical method used in our paper can be applied to other coupling markets like electricity market, particularly under asymmetric information. According to the research background and findings of this study, directions are suggested for further research. We can classify the recycling technical level types of recyclers in a more detailed way (not only two kinds of technical levels, but also multiple kinds of levels) and develop more specific subsidy policies. Meanwhile, social factors such as Corporate Social Responsibility (CSR) can be incorporated into our model in more varied situations. Additionally, using the subsidy data obtained from recyclers of other countries, the effectiveness of the subsidy policies can be evaluated according to the research framework.