Green Supplier Selection Based on Consensus Process and Integrating Prioritized Operator and Choquet Integral
Abstract
1. Introduction
2. State-of-the-Art Review
2.1. Methods for Green Supplier Selection
2.2. Consensus Reaching Process
2.3. Application of Prioritized Operator
2.4. Application of Choquet Integral
3. Preliminary
3.1. Hesitant Fuzzy Linguistic Term Set
3.2. The 2-Tuple Linguistic Variable
3.3. The Hesitant 2-Tuple Linguistic Term Set
- (1)
- If , then is superior , denoted by ;
- (2)
- If , then
- a.
- if , then is superior to , denoted by ;
- b.
- if , then is equal to , denoted by .
3.4. Consensus Measure
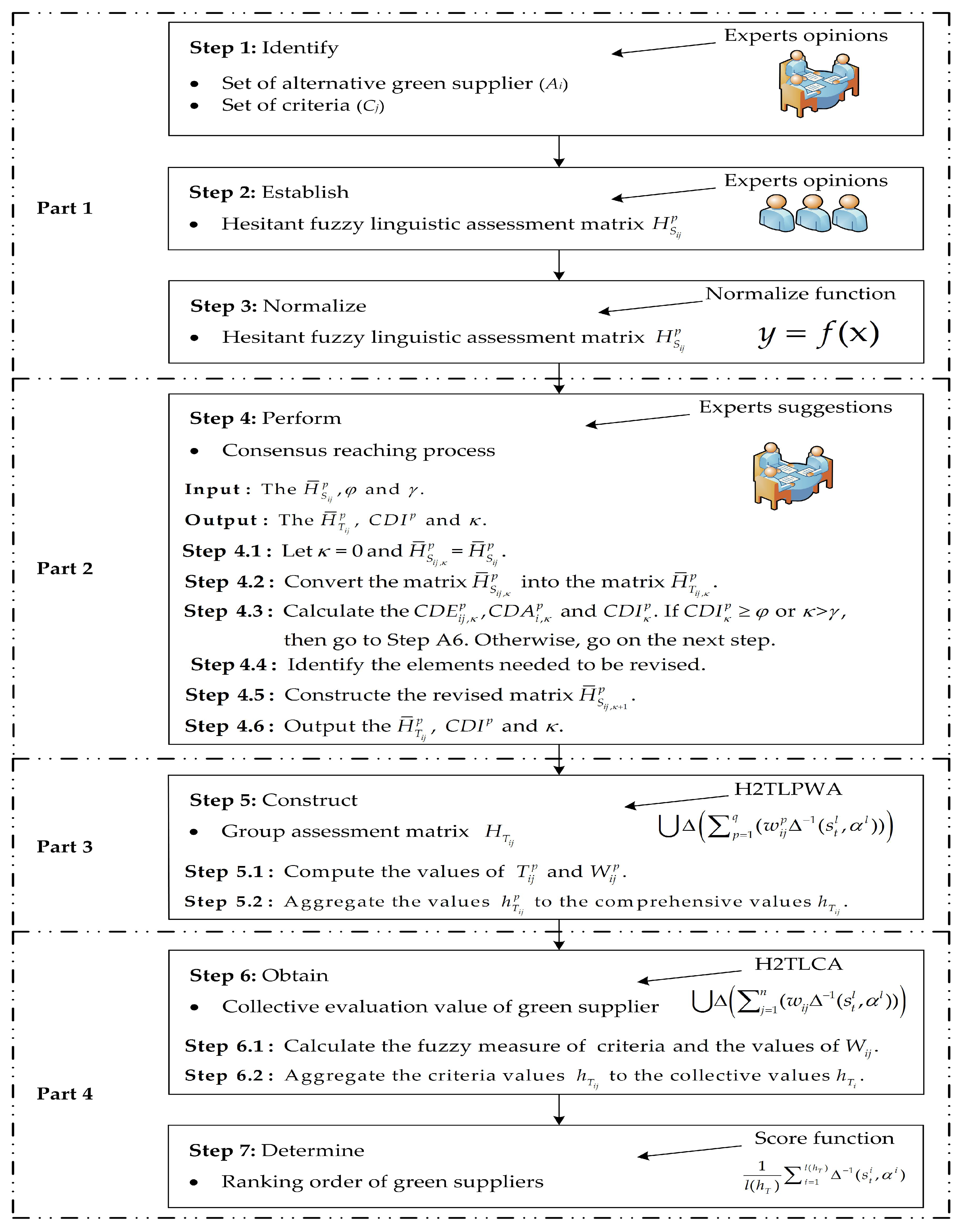
4. The Presented Green Supplier Selection Framework
5. An Illustrative Example
5.1. Comparative Analysis
5.1.1. Solve the Example Using the HFL-TOPSIS Method
5.1.2. Solve the Example Using the HFL-VIKOR Method
5.2. Result Discussion
- In the proposed framework, hesitant fuzzy linguistic information is transformed into hesitant 2-tuple linguistic information to avoid the loss of information, which makes the ranking result more accurate and reasonable.
- The presented method can improve the consensus level among experts by introducing the consensus reaching process into the green supplier selection problem. Therefore, the decision results obtained by this method can be well accepted by the organization or company.
- The priority order relationship between experts can be considered by using the H2TLPWA operator to construct the group decision matrix, which increases the application capacity of the presented method.
- By employing the H2TLCA operator to aggregate the criteria values of each green supplier, the interdependency of criteria are reflected, which makes this method closer to the real situation.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HFLE | Hesitant Fuzzy Linguistic Element |
| HFLTS | Hesitant Fuzzy Linguistic Term Set |
| HFL-TOPSIS | Hesitant Fuzzy Linguistic TOPSIS |
| HFL-VIKOR | Hesitant Fuzzy Linguistic VIKOR |
| H2TLE | Hesitant 2-Tuple Linguistic Element |
| H2TLCA | Hesitant Fuzzy Linguistic Choquet Averaging |
| H2TLPWA | Hesitant Fuzzy Linguistic Prioritized Weighted Averaging |
| GRA | Grey Relational Analysis |
| GSCM | Green Supply Chain Management |
| MABAC | Multi-Attributive Border Approximation area Comparison |
| MCDM | Multi-Criteria Decision Making |
| MCGDM | Multi-Criteria Group Decision-Making |
| MOOR | Multi-Objective Optimization by Ratio Analysis |
| MULTIMOORA | MOORA plus Full Multipliative |
| OWA | Order Weighted Averaging |
| PA | Prioritized Averaging |
| PROMETHEE | Preference Ranking Organization METHod for Enrichment Evaluation |
| QUALIFLEX | Qualitative Flexible multiple criteria method |
| TODIM | an acronym in Portuguese of interactive and multiple attribute decision-making |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| WASPAS | Weighted Aggregated Sum Product ASsessment |
| VIKORA | VIsekriterijumska Optimizacija I Kopromisno Resenje |
Appendix A
| Expert | Alternatives | ||||
|---|---|---|---|---|---|
| Expert | Alternatives | ||||
|---|---|---|---|---|---|
Appendix B
Appendix C
References
- Vachon, S. Green supply chain practices and the selection of environmental technologies. Int. J. Prod. Res. 2007, 45, 4357–4379. [Google Scholar] [CrossRef]
- Beamon, B.M. Designing the green supply chain. Logist. Inf. Manag. 1999, 12, 332–342. [Google Scholar] [CrossRef]
- Wang, K.Q.; Liu, H.C.; Liu, L.; Huang, J. Green supplier evaluation and selection using cloud model theory and the QUALIFLEX method. Sustainability 2017, 9, 688. [Google Scholar] [CrossRef]
- Blome, C.; Hollos, D.; Paulraj, A. Green procurement and green supplier development: Antecedents and effects on supplier performance. Int. J. Prod. Res. 2014, 52, 32–49. [Google Scholar] [CrossRef]
- Boran, F.E.; Genc, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Chang, B.; Chang, C.W.; Wu, C.H. Fuzzy DEMATEL method for developing supplier selection criteria. Expert Syst. Appl. 2011, 38, 1850–1858. [Google Scholar] [CrossRef]
- Büyüközkan, G. An integrated fuzzy multi-criteria group decision-making approach for green supplier evaluation. Int. J. Prod. Res. 2012, 50, 2892–2909. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Karimi, A.; Tavana, M. An integrated green supplier selection approach with analytic network process and improved Grey relational analysis. Int. J. Prod. Econ. 2015, 159, 178–191. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Sari, K. A novel multi-criteria decision framework for evaluating green supply chain management practices. Comput. Ind. Eng. 2017, 105, 338–347. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Liao, H.; Wu, D.; Huang, Y.; Ren, P.; Xu, Z.; Verma, M. Green logistic provider selection with a hesitant fuzzy linguistic thermodynamic method integrating cumulative prospect theory and PROMETHEE. Sustainability 2018, 10, 1291. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Moreno, J.M.; Pérez, I.J.; Herrera-Viedma, E. Analyzing consensus approaches in fuzzy group decision making: Advantages and drawbacks. Soft Comput. 2010, 14, 451–463. [Google Scholar] [CrossRef]
- Xu, X.; Zhong, X.; Chen, X.; Zhou, Y. A dynamical consensus method based on exit–delegation mechanism for large group emergency decision making. Knowl. Based Syst. 2015, 86, 237–249. [Google Scholar] [CrossRef]
- Xu, Y.; Cabrerizo, F.J.; Herrera-Viedma, E. A consensus model for hesitant fuzzy preference relations and its application in water allocation management. Appl. Soft Comput. 2017, 58, 265–284. [Google Scholar] [CrossRef]
- Ciasullo, M.V.; Fenza, G.; Loia, V.; Orciuoli, F.; Troisi, O.; Herrera-Viedma, E. Business process outsourcing enhanced by fuzzy linguistic consensus model. Appl. Soft Comput. 2018, 64, 436–444. [Google Scholar] [CrossRef]
- Xu, Y.; Wen, X.; Zhang, W. A two-stage consensus method for large-scale multi-attribute group decision making with an application to earthquake shelter selection. Comput. Ind. Eng. 2018, 116, 113–129. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, R.; Li, Y. Failure mode and effects analysis considering consensus and preferences interdependence. Algorithm 2018, 11, 34. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Cifci, G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers. Expert Syst. Appl. 2012, 39, 3000–3011. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Yu, D. Prioritized information fusion method for triangular intuitionistic fuzzy set and its application to teaching quality evaluation. Int. J. Intell. Syst. 2013, 28, 411–435. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Y.; Merigó, J.M. Prioritized aggregation for non-homogeneous group decision making in water resource management. Econ. Comput. Econ. Cybern. Stud. Res. 2014, 48, 247–258. [Google Scholar]
- Ma, Y.X.; Wang, J.Q.; Wang, J.; Wu, X.H. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2017, 28, 2745–2765. [Google Scholar] [CrossRef]
- Avilés-Ochoa, E.; León-Castro, E.; Perez-Arellano, L.A.; Merigó, J.M. Government transparency measurement through prioritized distance operators. J. Intell. Fuzzy Syst. 2018, 34, 2783–2794. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets. Knowl. Based Syst. 2015, 76, 127–138. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z. Consistency measures for hesitant fuzzy linguistic preference relations. IEEE Trans. Fuzzy Syst. 2014, 22, 35–45. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. A linguistic 2-tuple multicriteria decision making model dealing with hesitant linguistic information. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems, Istanbul, Turkey, 2–5 August 2015; pp. 1–7. [Google Scholar]
- Wei, C.; Ren, Z.; Rodriguez, R.M. A hesitant fuzzy linguistic TODIM method based on a score function. Int. J. Comput. Int. Syst. 2015, 8, 701–712. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Y. Hesitant fuzzy linguistic aggregation operators based on the Hamacher t-norm and t-conorm. Symmetry 2018, 10, 189. [Google Scholar] [CrossRef]
- Feyzioğlu, O.; Büyüközkan, G. Evaluation of green suppliers considering decision criteria dependencies. In Multple Criteria Decision Making for Sustianable Energy and Transporation System; Springer: Berlin/Heidelberg, Germany, 2010; pp. 145–154. [Google Scholar]
- Nia, A.S.; Olfat, L.; Esaeili, A.; Rostamzadeh, R.; Antuchevičienė, J. Using fuzzy Choquet Integral operator for supplier selection with environmental considerations. J. Bus. Econ. Manag. 2016, 17, 503–526. [Google Scholar]
- Ng, T.F.; Pham, T.D.; Jia, X. Feature interaction in subspace clustering using the Choquet integral. Patern Recognit. 2012, 45, 2645–2660. [Google Scholar] [CrossRef]
- Kaczmarek, P.; Kiersztyn, A.; Pedrycz, W. Generalized Choquet integral for face recognition. Int. J. Fuzzy Syst. 2018, 20, 1047–1055. [Google Scholar] [CrossRef]
- Pacheco, A.G.C.; Krohling, R.A. Aggregation of neural classifiers using Choquet integral with respect to a fuzzy measure. Neurocomputing 2018, 292, 151–164. [Google Scholar] [CrossRef]
- Demirel, D.; Demirel, N.C.; Kahraman, C. Multi-criteria warehouse location selection using Choquet integral. Expert Syst. Appl. 2010, 37, 3943–3952. [Google Scholar] [CrossRef]
- Wen, X.; Yan, M.; Xian, J.; Yue, R.; Peng, A. Supplier selection in supplier chain management using Choquet integral-based linguistic operators under fuzzy heterogeneous environment. Fuzzy Optim. Decis. Mak. 2016, 15, 307–330. [Google Scholar] [CrossRef]
- Demirel, N.C.; Demirel, T.; Deveci, M.; Vardar, G. Location selection for underground natural gas storage using Choquet integral. J. Nat. Sci. Eng. 2017, 45, 368–379. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Göçer, F. Selection of sustainable urban transportation alternatives using an integrated intuitionistic fuzzy Choquet integral approach. Transp. Res. D 2018, 58, 186–207. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Da, R. Choquet integral based aggregation approach to software development risk assessment. Inf. Sci. 2010, 180, 441–451. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, R.; Li, G.; Li, Y. Failure risk assessment of subway vehicle door system considering expert preference correlation and psychological behavior. Comput. Integr. Manuf. Syst. 2018, 24, 689–702. (In Chinese) [Google Scholar]
- Handfield, R.; Waltonb, S.V.; Melnyk, S.A. Applying environmental criteria to supplier assessment: A study in the application of the Analytical Hierarchy Process. Eur. J. Oper. Res. 2002, 16, 70–87. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Zolfani, S.H. Integrated QFD-MCDM framework for green supplier selection. J. Clean. Prod. 2017, 142, 3728–3740. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.E. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Videma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessment. Fuzzy Set Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z. A discrete consensus support model for multiple attribute group decision making. Knowl. Based Syst. 2011, 24, 1196–1202. [Google Scholar] [CrossRef]
- Fu, C.; Yang, S. An evidential reasoning based consensus model for multiple attribute group decision analysis problems with interval-valued group consensus requirements. Eur. J. Oper. Res. 2012, 223, 167–176. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Herrera-Viedma, E. Integrating experts’ weights generated dynamically into the consensus reaching process and its applications in managing non-cooperative behaviors. Decis. Support Syst. 2016, 84, 1–15. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F.; Fujita, H.; Herrea-Viedma, E. A visual interaction consensus model for social network group decision making with trust propagation. Knowl. Based Syst. 2017, 122, 39–50. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, N.; Li, K.W.; Martínez, L.; Zhao, W. Consensus decision models for preferential voting with abstentions. Comput. Ind. Eng. 2018, 115, 670–682. [Google Scholar] [CrossRef]
- Yager, R.R. Modeling prioritized multicriteria decision making. IEEE Trans. Syst. Man Cybern. B 2004, 34, 2396–2404. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Z. Prioritized intuitionistic fuzzy aggregation operators. Inf. Fusion 2013, 14, 108–116. [Google Scholar] [CrossRef]
- Wei, G. Hesitant fuzzy prioritized operators and their application to multiple attribute decision making. Knowl. Based Syst. 2012, 31, 176–182. [Google Scholar] [CrossRef]
- Wu, X.H.; Wang, J.Q.; Peng, J.J.; Chen, X.H. Cross-Entropy and prioritized aggregation operator with simplified neutrosophic sets and their application in multi-criteria decision-making problems. Int. J. Fuzzy Syst. 2016, 18, 1104–1116. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H.Y. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2016, 20, 1–15. [Google Scholar] [CrossRef]
- Yu, S.M.; Wang, J.; Wang, J.Q.; Li, L. A multi-criteria decision-making model for hotel selection with linguistic distribution assessments. Appl. Soft Comput. 2018, 67, 741–755. [Google Scholar] [CrossRef]
- Choquet, G. Theory of capacities. Ann. Inst. Fourier 1953, 5, 131–295. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. An interpretation of fuzzy measures and the Choquet integral as an integral with respect to a fuzzy measure. Fuzzy Set Syst. 1989, 29, 201–227. [Google Scholar] [CrossRef]
- Grabisch, M. Fuzzy integral in multicriteria decision making. Fuzzy Set Syst. 1995, 69, 279–298. [Google Scholar] [CrossRef]
- Tan, C.; Chen, X. Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst. Appl. 2010, 37, 149–157. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Zhou, W. Multi-criteria decision making aased on Choquet integral under hesitant fuzzy environment. J. Comput. Inf. Syst. 2011, 7, 4506–4513. [Google Scholar]
- Peng, X.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Z. New aggregation operators based on the Choquet integral and 2-tuple linguistic information. Expert Syst. Appl. 2012, 39, 2662–2668. [Google Scholar] [CrossRef]
- Sun, H.X.; Yang, H.X.; Wu, J.Z.; Ouyang, Y. Interval neutrosophic numbers Choquet integral operator for multi-criteria decision making. J. Intell. Fuzzy Syst. 2015, 28, 2443–2455. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Liu, X. Prioritized aggregation operators and correlated aggregation operators for hesitant 2-tuple linguistic variables. Symmetry 2018, 10, 39. [Google Scholar] [CrossRef]
- Wang, P.; Shen, J.; Zhan, B. A new method for two-sided matching decision making of PPP projects based on intuitionistic fuzzy choquet integral. J. Intell. Fuzzy Syst. 2016, 31, 2221–2230. [Google Scholar] [CrossRef]
- Wu, Y.; Geng, S.; Zhang, H.; Gao, M. Decision framework of solar thermal power plant site selection based on linguistic Choquet operator. Appl. Energy 2014, 136, 303–311. [Google Scholar] [CrossRef]
- Moradi, M.; Delavar, M.R.; Moshiri, B. A GIS-based multi-criteria analysis model for earthquake vulnerability assessment using Choquet integral and game theory. Nat. Hazards 2017, 87, 1–13. [Google Scholar] [CrossRef]
- Ferreira, J.J.M.; Jalali, M.S.; Ferreira, F.A.F. Enhancing the decision-making virtuous cycle of ethical banking practices using the Choquet integral. J. Bus. Res. 2018, 88, 492–497. [Google Scholar] [CrossRef]
- Wei, C.; Liao, H. A multigranularity linguistic group decision-making method based on hesitant 2-tuple sets. Int. J. Intell. Syst. 2016, 31, 612–634. [Google Scholar] [CrossRef]
- Sugeno, M. Theory of Fuzzy Integrals and Its Applications. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 1974. [Google Scholar]
- Beg, I.; Rashid, T. TOPSIS for Hesitant Fuzzy Linguistic Term Sets. Int. J. Intell. Syst. 2013, 28, 1162–1171. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1343–1355. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multicriteri decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
| Variables | Meanings |
|---|---|
| A set of alternative green suppliers | |
| A set of evaluation criteria | |
| A set of experts | |
| A linguistic term set | |
| The weight vector of experts | |
| The weight vector of criteria | |
| and | Benefit criteria and cost criteria |
| Hesitant fuzzy linguistic evaluation matrix provided by | |
| Normalized hesitant fuzzy linguistic evaluation matrix | |
| Hesitant 2-tuple linguistic evaluation matrix provided by | |
| Hesitant 2-tuple linguistic comprehensive evaluation matrix | |
| A fuzzy measure of criterion |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Li, Y. Green Supplier Selection Based on Consensus Process and Integrating Prioritized Operator and Choquet Integral. Sustainability 2018, 10, 2744. https://doi.org/10.3390/su10082744
Zhu J, Li Y. Green Supplier Selection Based on Consensus Process and Integrating Prioritized Operator and Choquet Integral. Sustainability. 2018; 10(8):2744. https://doi.org/10.3390/su10082744
Chicago/Turabian StyleZhu, Jianghong, and Yanlai Li. 2018. "Green Supplier Selection Based on Consensus Process and Integrating Prioritized Operator and Choquet Integral" Sustainability 10, no. 8: 2744. https://doi.org/10.3390/su10082744
APA StyleZhu, J., & Li, Y. (2018). Green Supplier Selection Based on Consensus Process and Integrating Prioritized Operator and Choquet Integral. Sustainability, 10(8), 2744. https://doi.org/10.3390/su10082744




