Optimizing the Design of a Vertical Ground Heat Exchanger: Measurement of the Thermal Properties of Bentonite-Based Grout and Numerical Analysis
Abstract
1. Introduction
2. Materials and Methods
3. Experimental Results and Discussion
4. Numerical Analysis
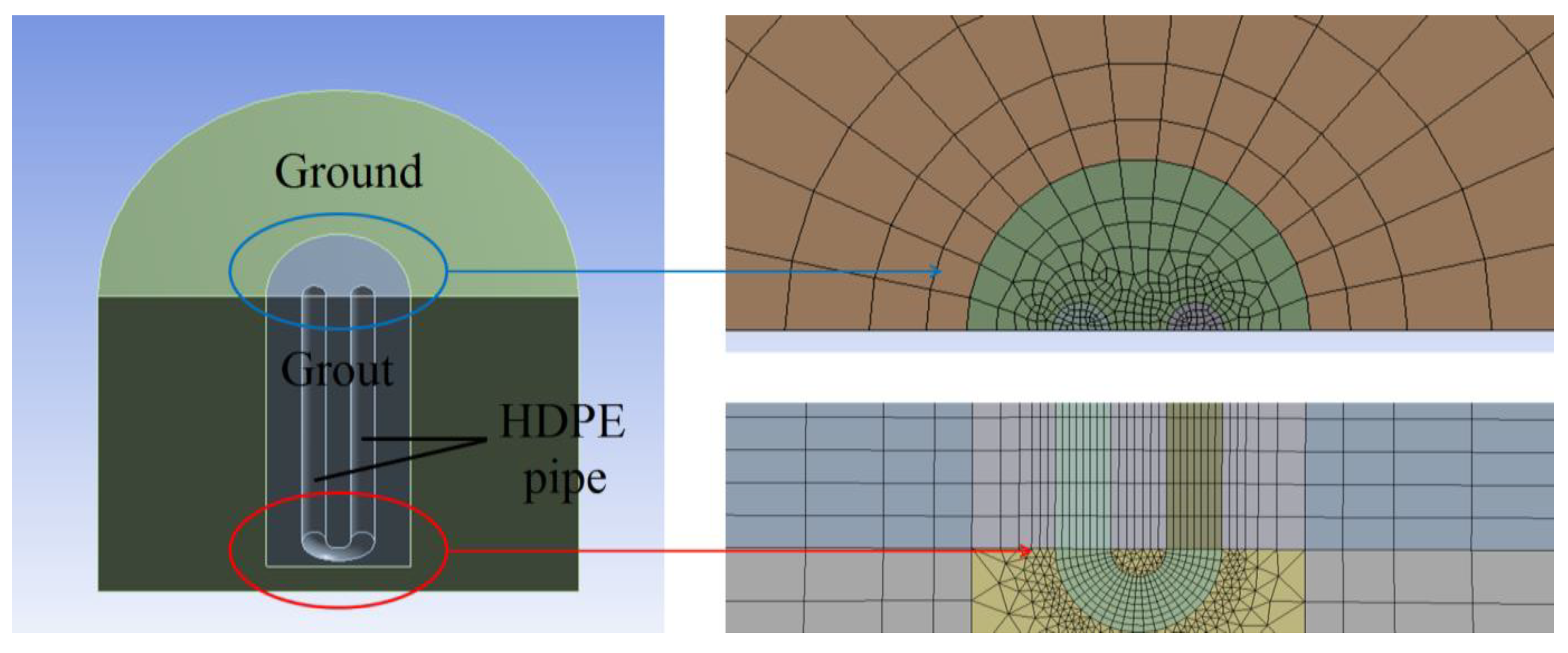
4.1. Numerical Method
- -
- To investigate the effects of the SHC of bentonite-based grouts, HDPE pipe length, and working fluid velocity, the model simulated the cooling mode during intermittent operation (3 h operation time and 3 h off-time) and during continuous 24-h operation.
- -
- To investigate the effects of the operation time and off-time on vertical GHE, the model simulated the cooling mode during intermittent operation (3 h operation time and 3 h off-time) over three days.
- -
- To simulate the intermittent operation mode, user-defined operation times and off-times were modeled.
- -
- When exploring the effects of HDPE pipe length and working fluid velocity, and operation time and off-time, numerical simulations were performed using the thermal properties of the most diverse grout specimens (i.e., BS20-0, which has the lowest TC and the highest SHC, and BS30-30, which has the highest TC and the lowest SHC).
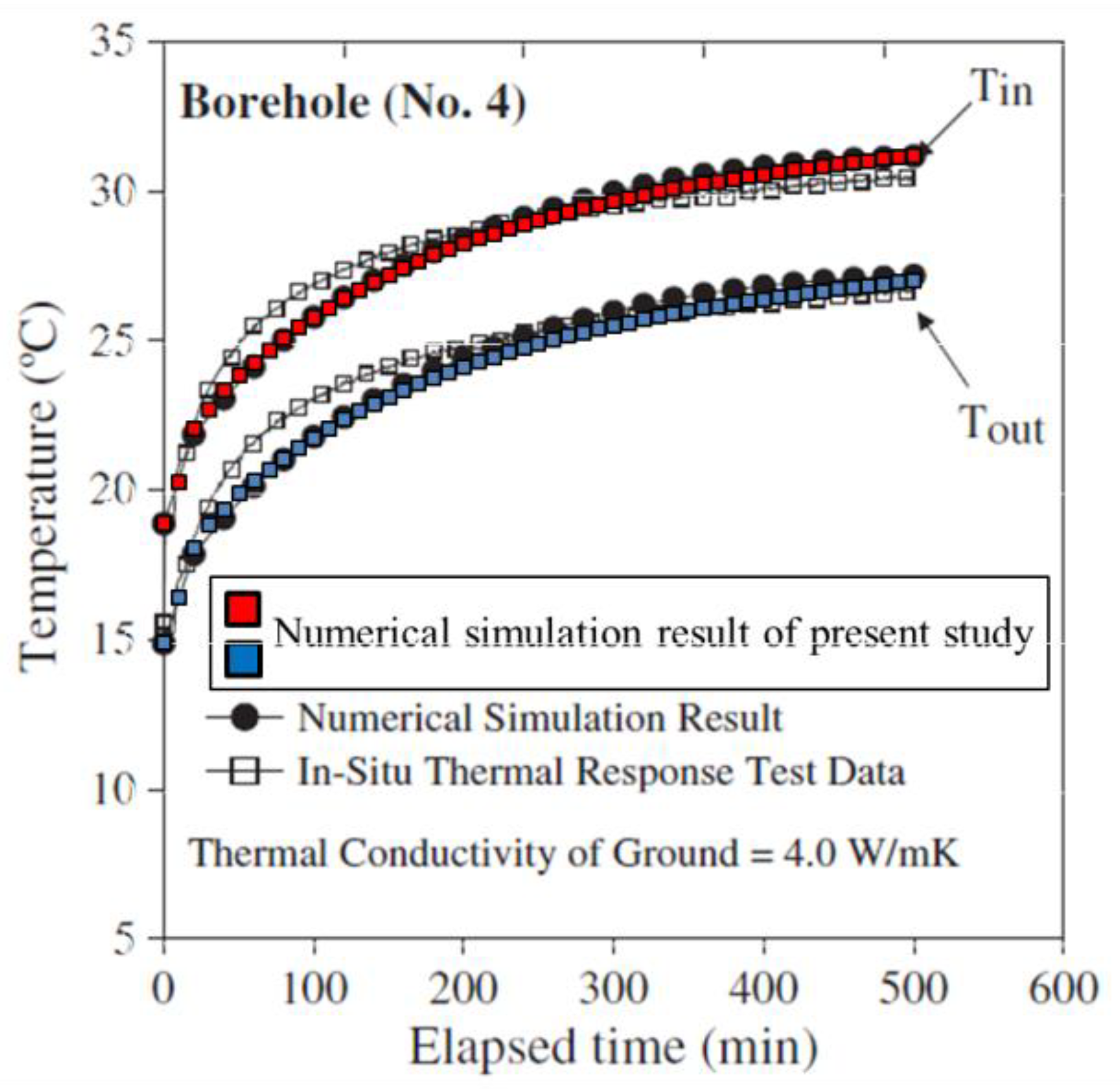
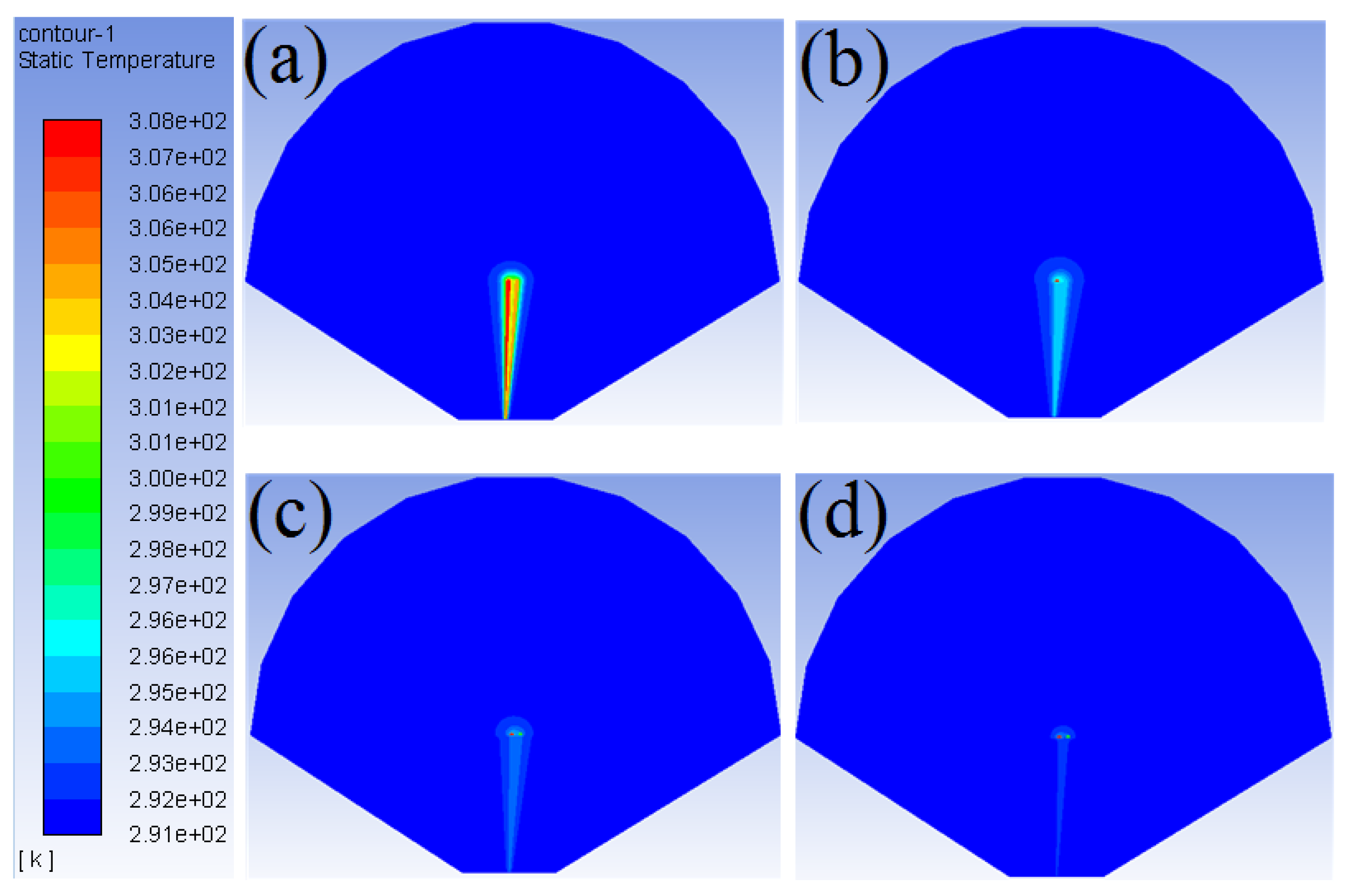
4.2. Validation
4.3. Numerical Results and Discussion
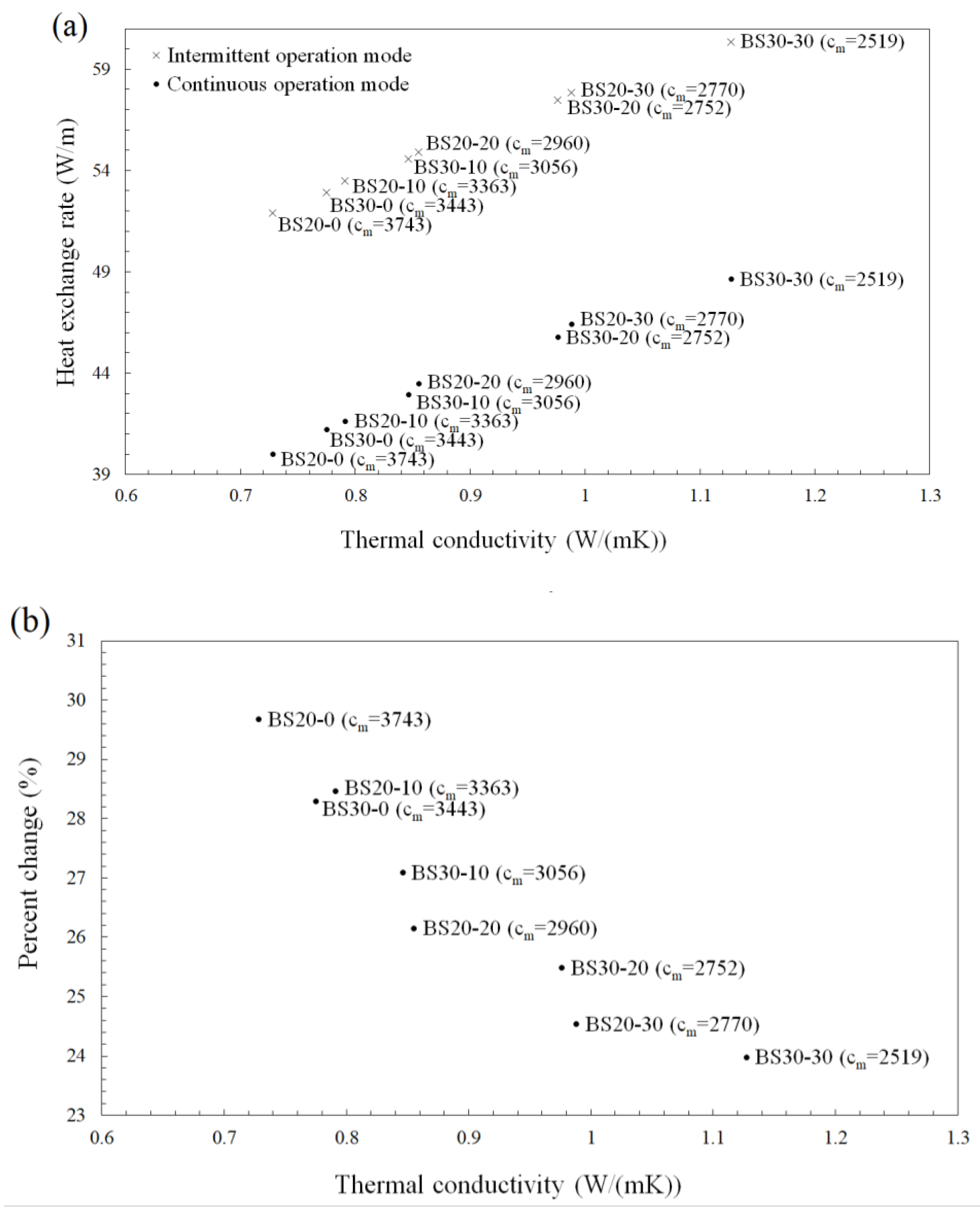
4.3.1. Effects of the Specific Heat Capacity of Bentonite-Based Grouts
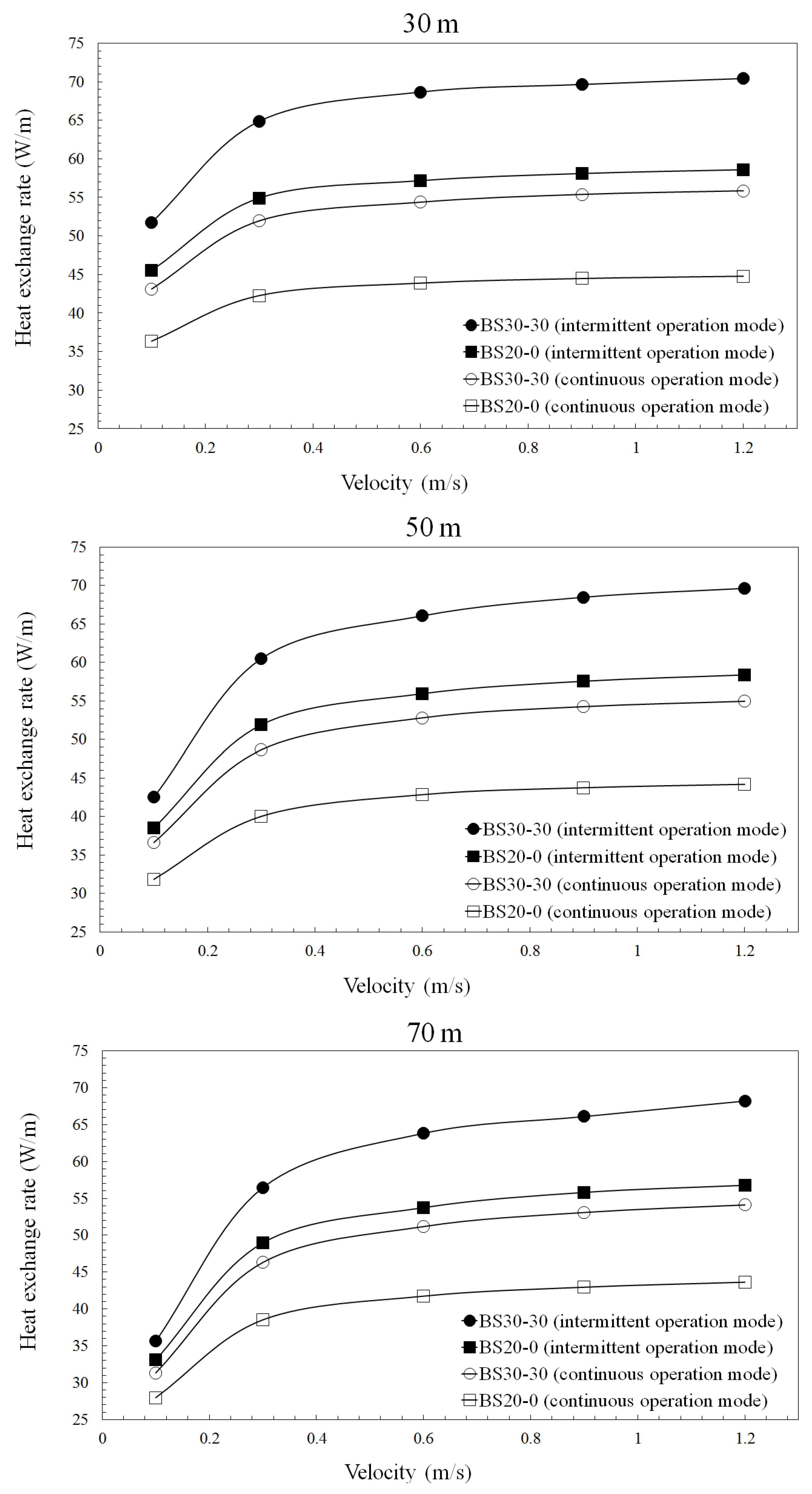
4.3.2. Effects of Working Fluid Velocity and HDPE Pipe Length
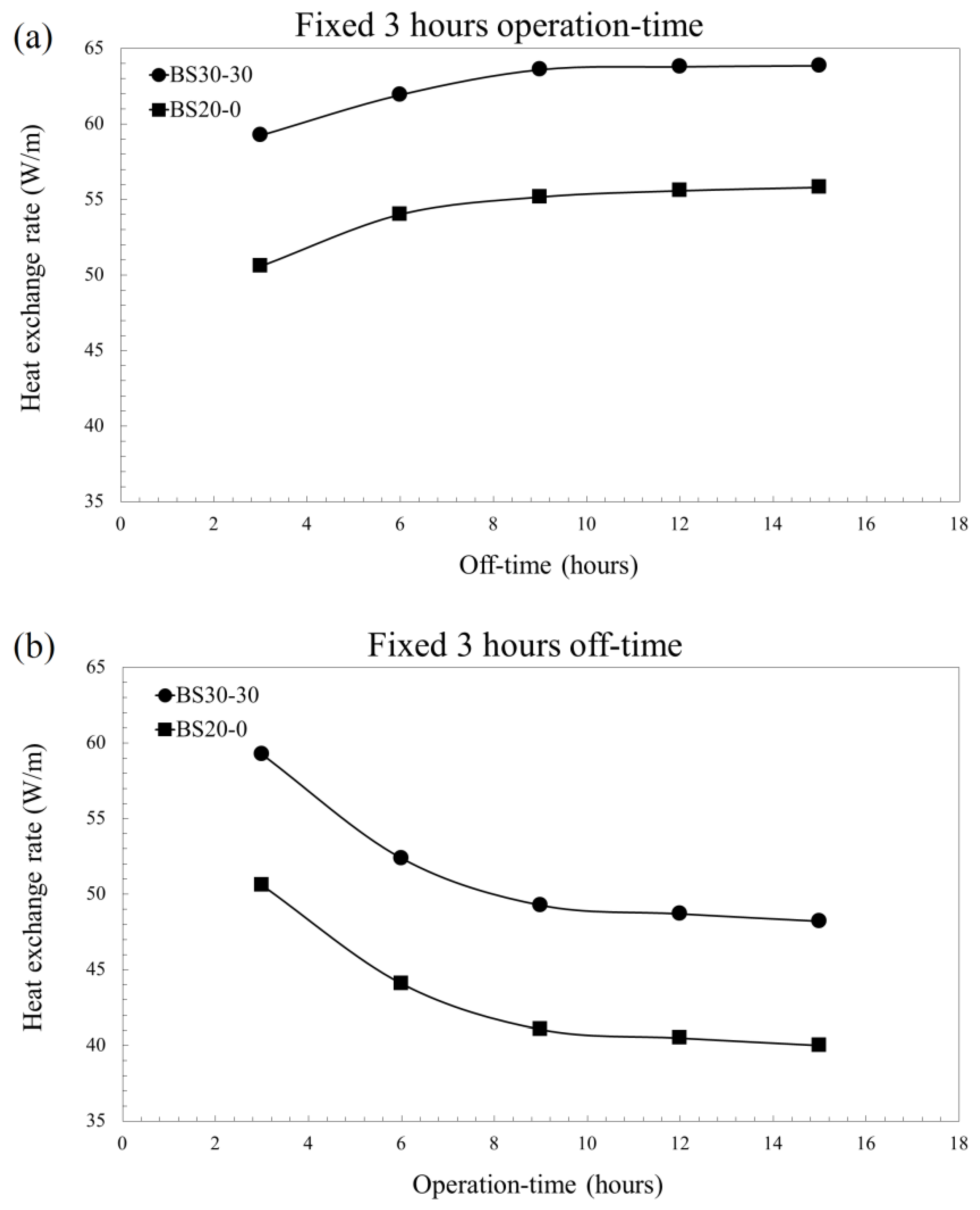
4.3.3. Effects of Various Operation Times and Off-Times during Intermittent Operation
5. Conclusions
- (1)
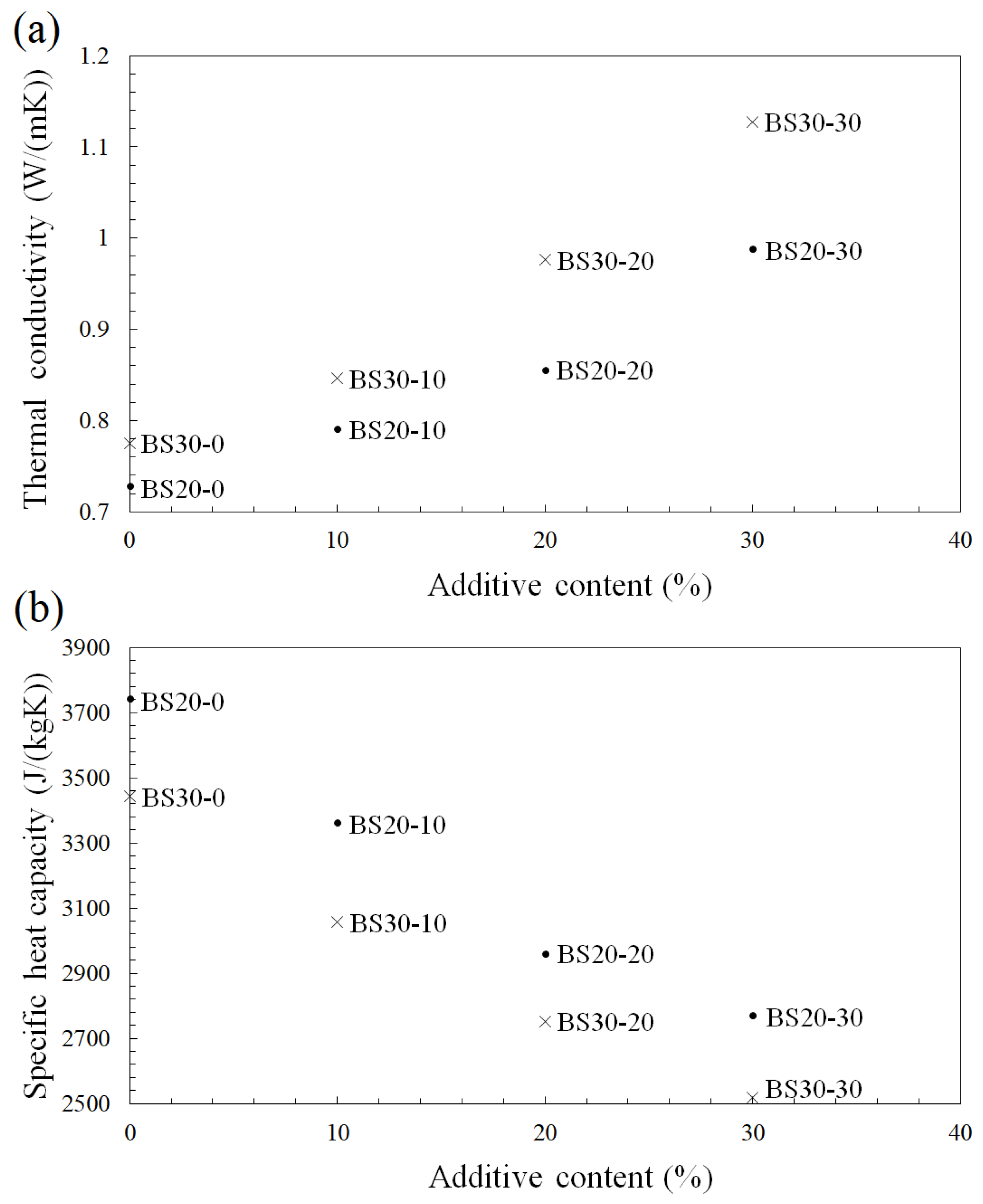
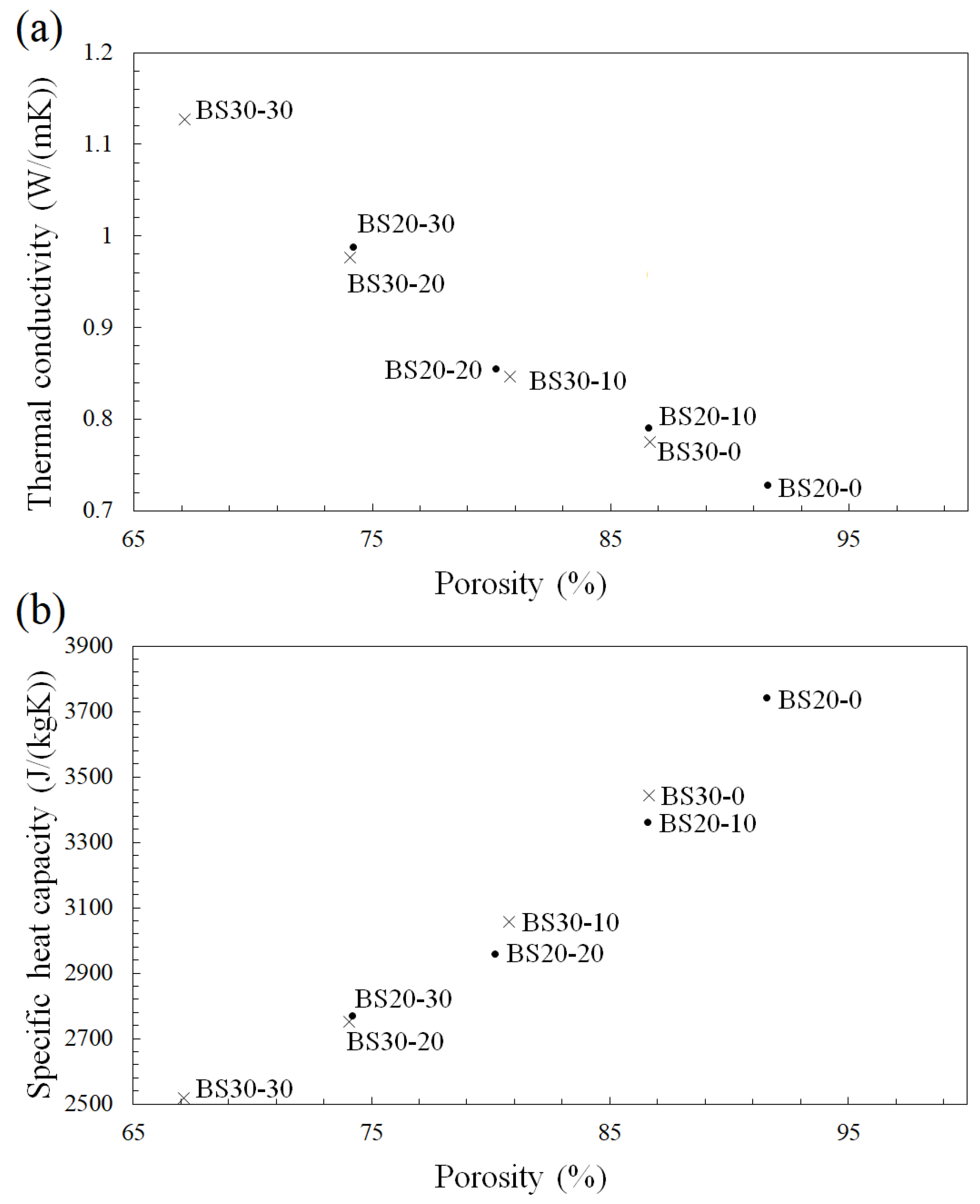
- Under saturated conditions, the TC and SHC of bentonite-based grouts ranged from 0.728–1.127 W/(mK) and 2519–3743 J/(kgK), respectively. As the proportion of silica sand increased, the TC of the bentonite-based grouts increased, but the SHC decreased. The thermal properties of bentonite-based grouts were affected principally by composition and porosity.
- (2)
- For bentonite-based grouts, the mean HER was 27% higher during intermittent operation than during continuous operation. Also, during intermittent operation, grout with high TC and high SHC improved GHE performance. Because the SHC of bentonite-based grout is higher than that of cement-based grout, the effect of bentonite-based grout was more significant.
- (3)
- During both continuous and intermittent operation, GHE performance improved as the working fluid velocity increased. However, there was a critical working fluid velocity that greatly affected the performance of the vertical GHE, regardless of the operation mode, HDPE pipe length, or grout thermal properties; this value was 0.3 m/s. Therefore, it is recommended to set the velocity for operation of the vertical GHE to 0.3 m/s or higher.
- (4)
- During intermittent operation, depending on the operation time and off-time, we found critical time intervals at which the ground temperature was almost completely restored, or any benefit of intermittent operation almost disappeared. Moreover, the method to estimate the critical time intervals for optimizing intermittent operation was proposed. Our results can be used as input data for analyses of the thermal behavior of vertical GHEs to improve GHE performance and operation.
Author Contributions
Funding
Conflicts of Interest
References
- Blazquez, C.S.; Martin, A.F.; Nieto, I.M.; Garcia, P.C.; Sanchez Perez, L.S.; Gonzalez-Aguilera, D. Analysis and study of different grouting materials in vertical geothermal closed-loop systems. Renew. Energy 2017, 114, 1189–1200. [Google Scholar] [CrossRef]
- Wang, H.; Lu, J.; Qi, C. Thermal conductivity of sand bentonite mixtures as a backfill material of geothermal boreholes. GRC Trans. 2011, 35, 1135–1138. [Google Scholar]
- Indacoechea-Vega, I.; Pascual-Muñoz, P.; Castro-Fresno, D.; Calzada-Pérez, M.A. Experimental characterization and performance evaluation of geothermal grouting materials subjected to heating-cooling cycles. Constr. Build. Mater. 2015, 98, 583–592. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Yang, H.; Cui, P.; Fang, Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Cui, P.; Yang, H.; Fang, Z. Numerical analysis and experimental validation of heat transfer in ground heat exchangers in alternative operation modes. Energy Build. 2008, 40, 1060–1066. [Google Scholar] [CrossRef]
- Lee, J.Y. Current status of ground source heat pumps in Korea. Renew. Sustain. Energy Rev. 2009, 13, 1560–1568. [Google Scholar] [CrossRef]
- Hu, J. An improved analytical model for vertical borehole ground heat exchanger with multiple-layer substrates and groundwater flow. Appl. Energy 2017, 202, 537–549. [Google Scholar]
- Chong, C.S.A.; Gan, G.; Verhoef, A.; Garcia, R.G. Comparing the thermal performance of horizontal slinky-loop and vertical slinky-loop heat exchangers. Int. J. Low-Carbon Technol. 2014, 9, 250–255. [Google Scholar] [CrossRef]
- Choi, W.; Ooka, R. Effect of natural convection on thermal response test conducted in saturated porous formation: Comparison of gravel-backfilled and cement-grouted borehole heat exchangers. Renew. Energy 2016, 96, 891–903. [Google Scholar] [CrossRef]
- Desmedt, J.; Van Bael, J.; Hoes, H.; Robeyn, N. Experimental performance of borehole heat exchangers and grouting materials for ground source heat pumps. Int. J. Energy Res. 2012, 36, 1238–1246. [Google Scholar] [CrossRef]
- Remund, C.P.; Lund, J.T. Thermal Enhancement of Bentonite Grouts for Vertical GSHP Systems in Heat Pump and Refrigeration Systems; Den Braven, K.R., Mei, V., Eds.; American Society of Mechanical Engineers: New York, NY, USA, 1993; Volume 29, pp. 95–106. [Google Scholar]
- Lee, C.H.; Lee, K.J.; Choi, H.S.; Choi, H.P. Characteristics of thermally-enhanced bentonite grouts for geothermal heat exchanger in South Korea. China Technol. Sci. 2011, 53, 123–128. [Google Scholar] [CrossRef]
- Allan, M.L.; Philippacopoulos, A.J. Properties and Performance of Thermally Conductive Cement-Based Grouts for Geothermal Heat Pumps; Department of Applied Science, Brookhaven National Laboratory: New York, NY, USA, 1999. [Google Scholar]
- Lee, C.H.; Park, M.S.; Nguyen, T.B.; Sohn, B.H.; Choi, H.S. Performance evaluation of closed-loop vertical ground heat exchangers by conducting in-situ thermal response tests. Renew. Energy 2012, 42, 77–83. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Esen, Y. Temperature distributions in boreholes of a vertical ground-coupled heat pump system. Renew. Energy 2009, 34, 2672–2679. [Google Scholar] [CrossRef]
- Lee, C.; Park, M.; Park, S.; Won, J.; Choi, H. Back-analyses of in-situ thermal response test (TRT) for evaluating ground thermal conductivity. Int. J. Energy Res. 2013, 37, 1397–1404. [Google Scholar] [CrossRef]
- Jalaluddin; Miyara, A. Thermal performance investigation of several types of vertical ground heat exchangers with different operation mode. Appl. Therm. Eng. 2012, 33, 167–174. [Google Scholar] [CrossRef]
- Choi, J.C.; Lee, S.R.; Lee, D.S. Numerical simulation of vertical ground heat exchangers: Intermittent operation in unsaturated soil conditions. Comput. Geotech. 2011, 38, 949–958. [Google Scholar] [CrossRef]
- Li, Y.; An, Q.S.; Liu, L.X.; Zhao, J. Thermal performance investigation of borehole heat exchanger with different U-tube diameter and borehole parameters. Energy Procedia 2014, 61, 2690–2694. [Google Scholar] [CrossRef]
- Bidarmaghz, A.; Narsilio, G.A.; Johnston, I.W.; Colls, S. The importance of surface air temperature fluctuations on long-term performance of vertical ground heat exchangers. Geomech. Energy Environ. 2016, 6, 35–44. [Google Scholar] [CrossRef]
- Congedo, P.M.; Colangelo, G.; Starace, G. CFD simulations of horizontal ground heat exchangers: A comparison among different configurations. Appl. Therm. Eng. 2012, 33–34, 24–32. [Google Scholar] [CrossRef]
- Kim, D.; Kim, G.; Kim, D.; Baek, H. Experimental and numerical investigation of thermal properties of cement-based grouts used for vertical ground heat exchanger. Renew. Energy 2017, 112, 260–267. [Google Scholar] [CrossRef]
- Pu, L.; Qi, D.; Li, K.; Tan, H.; Li, Y. Simulation study on the thermal performance of vertical U-tube heat exchangers for ground source heat pump system. Appl. Therm. Eng. 2015, 79, 202–213. [Google Scholar] [CrossRef]
- Chen, S.; Mao, J.; Han, X.; Li, C.; Liu, L. Numerical analysis of the factors influencing a vertical u-tube ground heat exchanger. Sustainability 2016, 8, 882. [Google Scholar] [CrossRef]
- Chen, J.; Xia, L.; Li, B.; Mmereki, D. Simulation and experimental analysis of optimal buried depth of the vertical U-tube ground heat exchanger for a ground-coupled heat pump system. Renew. Energy 2015, 73, 46–54. [Google Scholar] [CrossRef]
- Jin, G.; Zhang, X.; Guo, S.; Wu, X.; Bi, W. Evaluation and analysis of thermal short-circuiting in borehole heat exchangers. In Proceedings of the 8th International Conference on Applied Energy (ICAE2016), Beijing, China, 8–11 October 2016; pp. 1677–1682. [Google Scholar]
- Welch, S.M.; Kluitenberg, G.J.; Bristow, K.L. Rapid numerical estimation of soil thermal properties for a broad class of heat-pulse emitter geometries. Meas. Sci. Technol. 1996, 7, 932–938. [Google Scholar]
- Bristow, K.L. Measurement of thermal properties and water content of unsaturated sandy soil using dual-probe heat-pulse probes. Agric. Forest Meteorol. 1998, 89, 75–84. [Google Scholar] [CrossRef]
- KD2 Pro Manual. Available online: http://manuals.decagon.com/Manuals/13351_KD2%20Pro_Web.pdf (accessed on 20 July 2018).
- Cengel, Y.A. Heat and Mass Transfer: A Practical Approach; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Hens, H. Applied Building Physics: Boundary Conditions, Building Performance and Material Properties; Wiley: Berlin, Germany, 2010. [Google Scholar]
- Engineeringtoolbox. Available online: http://www.engineeringtoolbox.com/specific-heat-capacity-d_391.html (accessed on 20 July 2018).
- Fluent 6.3 User’s Guide. Available online: https://www.sharcnet.ca/Software/Fluent6/html/ug/main_pre.htm (accessed on 20 July 2018).
- Gao, J.; Zhang, X.; Liu, J.; Li, K.S.; Yang, J. Numerical and experimental assessment of thermal performance of vertical energy piles: An application. Appl. Energy 2008, 85, 901–910. [Google Scholar] [CrossRef]
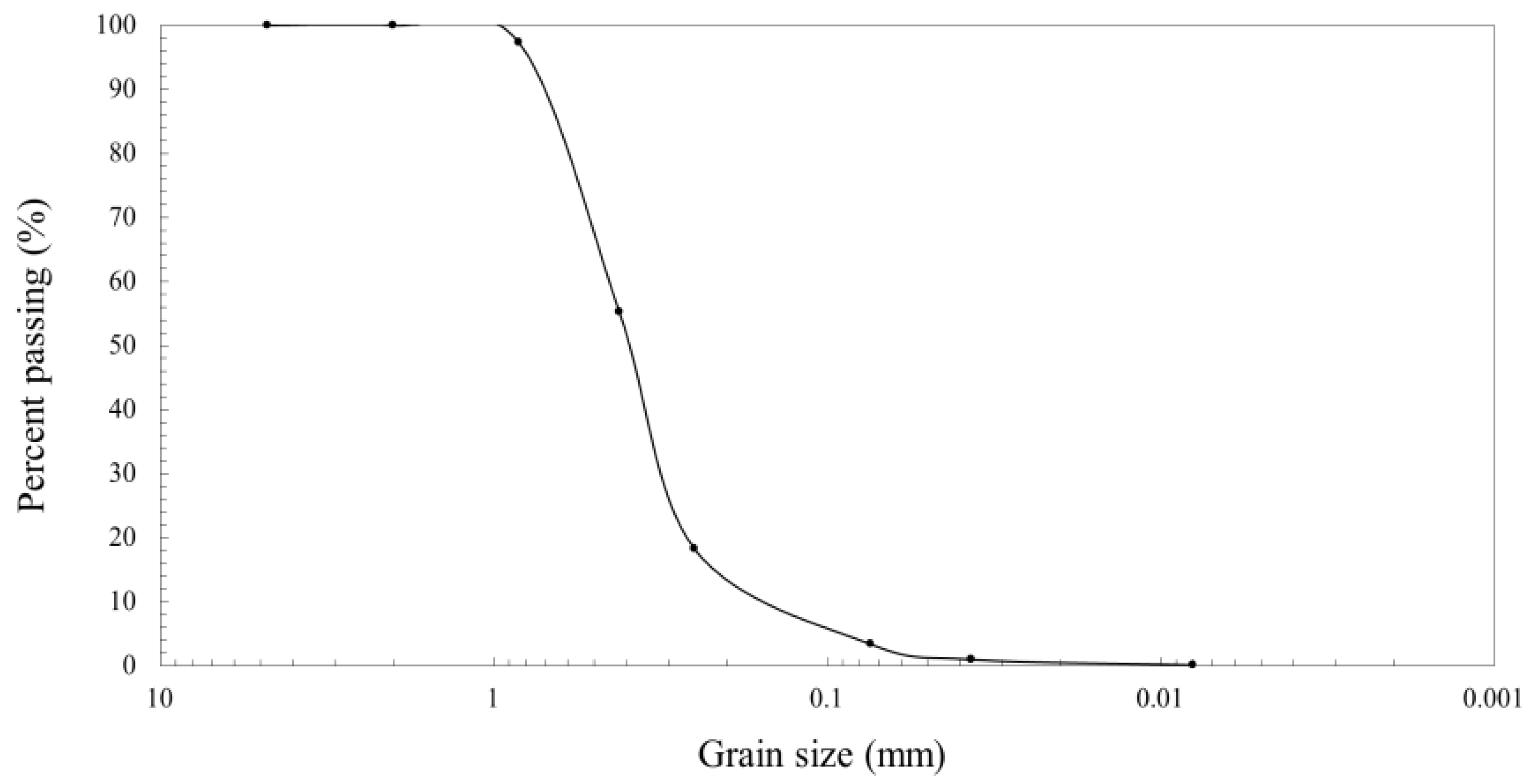
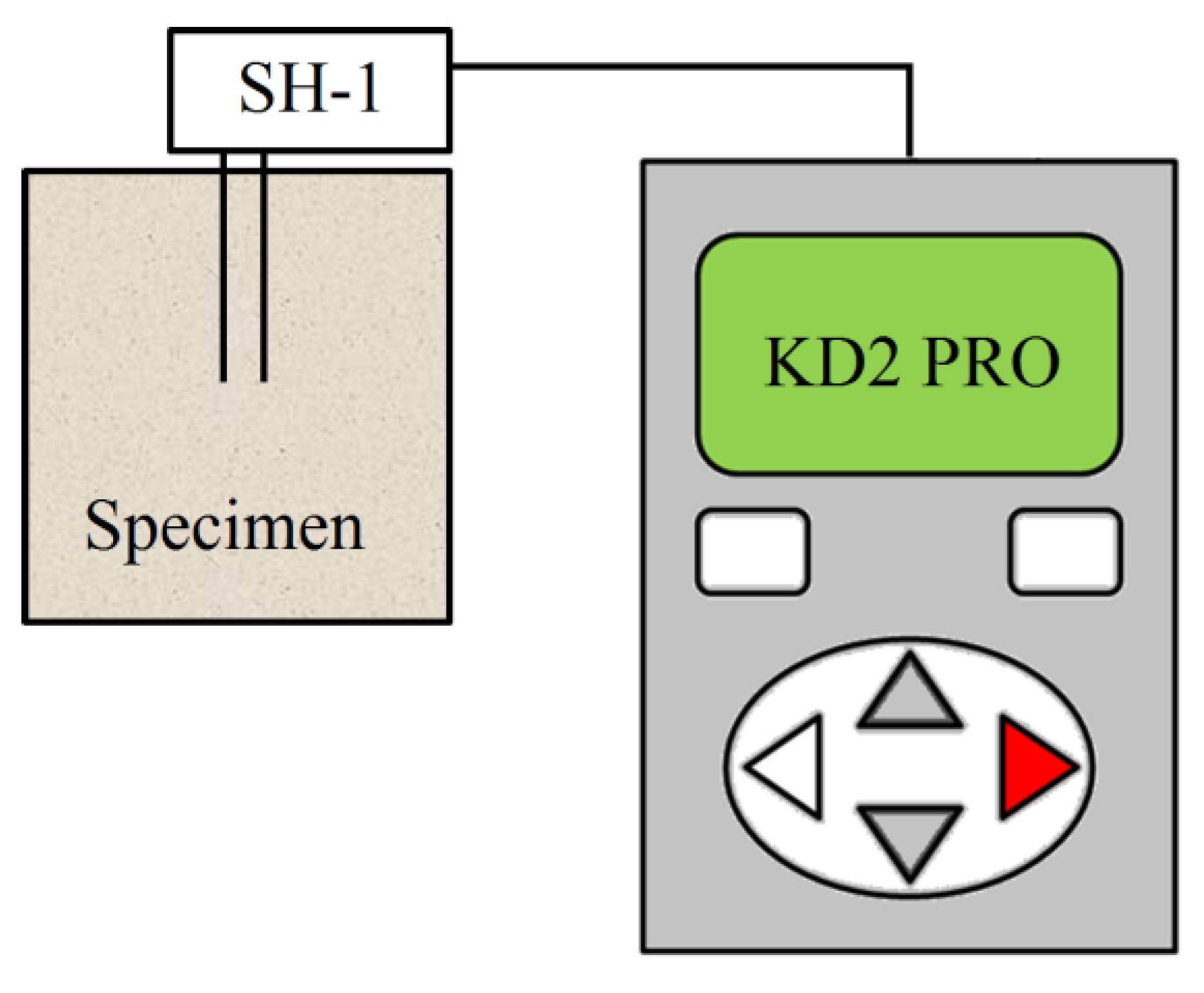
| Permeability (cm/s) | Swelling Potential | Montmorillonite Content (%) | Thermal Conductivity (W/(mK)) | Specific Gravity |
|---|---|---|---|---|
| ≤1 × 10−7 | 25 mL/2.0 g | ≤90 | 0.74 | 2.60 |
| Specimen No. | Bentonite (wt %) | Silica Sand (wt %) | Water (wt %) |
|---|---|---|---|
| BS20-0 | 20 | 0 | 80 |
| BS20-10 | 10 | 70 | |
| BS20-20 | 20 | 60 | |
| BS20-30 | 30 | 50 | |
| BS30-0 | 30 | 0 | 70 |
| BS30-10 | 10 | 60 | |
| BS30-20 | 20 | 50 | |
| BS30-30 | 30 | 40 |
| Specimen No. | Saturated Bulk Density (kg/m3) | Porosity (%) | Thermal Conductivity (W/(mK)) | Specific Heat Capacity (J/(kgK)) |
|---|---|---|---|---|
| BS20-0 | 1096 | 91.57 | 0.728 | 3743 |
| BS20-10 | 1170 | 86.56 | 0.791 | 3363 |
| BS20-20 | 1298 | 80.17 | 0.855 | 2960 |
| BS20-30 | 1354 | 74.19 | 0.988 | 2770 |
| BS30-0 | 1158 | 86.64 | 0.775 | 3443 |
| BS30-10 | 1256 | 80.78 | 0.846 | 3056 |
| BS30-20 | 1359 | 74.06 | 0.976 | 2752 |
| BS30-30 | 1439 | 67.11 | 1.127 | 2519 |
| Item | Description | |||
|---|---|---|---|---|
| Inlet water velocity | 0.3 m/s | |||
| Inlet water temperature | 35 °C (308.15 K) | |||
| Turbulence intensity | 5% | |||
| Initial ground temperature | 18.2 °C (291.35 K) | |||
| Physical Parameters | Density (kg/m3) | Thermal Conductivity (W/(mK)) | Specific Heat Capacity (J/(kgK)) | Viscosity (kg/(ms)) |
| Working fluid | 998.2 | 0.6 | 4182 | 0.001003 |
| HDPE pipe | 955 | 0.4 | 525 | |
| Ground | 2600 | 4.0 | 790 | |
| Continuity equation | ||
| Momentum equation | ||
| Energy equation | ||
| Turbulence equations | Turbulent energy equation | |
| Turbulence dissipation rate equation | ||
| : 1.44, : 1.92 | : turbulent dissipation rate (m2/s2) | |
| , : turbulence kinetic energies (m2/s2) | : viscosity ((Ns)/m2) | |
| : enthalpy of the fluid (J) | : effective viscosity ((Ns)/m2) | |
| : turbulence kinetic energy (m2/s2) | : turbulence viscosity ((Ns)/m2) | |
| : pressure (Pa) | : velocity (m/s) | |
| : source term | : density (kg/m3) | |
| : volumetric heat source (kJ/(m3s)) | : 1.2, , : constant | |
| : time (h) | ||
| : Temperature (°C) | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Oh, S. Optimizing the Design of a Vertical Ground Heat Exchanger: Measurement of the Thermal Properties of Bentonite-Based Grout and Numerical Analysis. Sustainability 2018, 10, 2664. https://doi.org/10.3390/su10082664
Kim D, Oh S. Optimizing the Design of a Vertical Ground Heat Exchanger: Measurement of the Thermal Properties of Bentonite-Based Grout and Numerical Analysis. Sustainability. 2018; 10(8):2664. https://doi.org/10.3390/su10082664
Chicago/Turabian StyleKim, Daehoon, and Seokhoon Oh. 2018. "Optimizing the Design of a Vertical Ground Heat Exchanger: Measurement of the Thermal Properties of Bentonite-Based Grout and Numerical Analysis" Sustainability 10, no. 8: 2664. https://doi.org/10.3390/su10082664
APA StyleKim, D., & Oh, S. (2018). Optimizing the Design of a Vertical Ground Heat Exchanger: Measurement of the Thermal Properties of Bentonite-Based Grout and Numerical Analysis. Sustainability, 10(8), 2664. https://doi.org/10.3390/su10082664




