1. Introduction
The world’s population is growing, and meeting the increasing energy demands while managing environmental, social, and economic issues is one of the greatest challenges of our time. Due to the rapid development of human civilization and the world’s economies, fossil fuel energy is going to be exhausted. On the one hand, increasing demand for energy is partly to blame for the relentless decline of limited fossil energy reserves. On the other hand, the greenhouse effect produced by the use of fossil energy has caused several environmental problems such as global warming. The problems arising from the use of fossil energy have led to widespread considerations of the types and structure of future social energy utilization. In this context, the transformation of alternative energy is thriving. The world’s energy structure is shifting from high-emissions fossil energy to renewable energy and clean energy, such as solar energy, wind energy, and hydropower. Economies of scale and technological advances have seen production costs of renewable energy decline dramatically. This global shift in the energy landscape means generating more renewable energy from sources like solar power which are delivering more clean energy.
According to national policies and practical energy demand, China has increased the contribution of renewable share to its total energy consumption. Solar energy has generally been recognized as a clean form of energy usage; its huge development potential has attracted a lot of attention. In recent years, with more policy support from the Chinese government, the photovoltaic (PV) industry has been experiencing a larger-scale development to replace traditional energy. With the stimulation of relevant national policies, the PV industry in China represents an opportunity for high growth. However, compared with the enormous potential of solar power, the level of its utilization is low at present. Thus, further development of PV power has significant impetus for the in-depth development of energy conservation and emission reduction and the optimization of energy structure adjustment in China.
Our study takes initiative effort in the following two aspects. First, the heterogeneity of our dataset enables us to undertake the DEA method for the first time to compare environmental efficiency of PV plants in China. Second, it is the first time to compare the environmental efficiency of PV power plants based on economic zones and types of plants. The purpose of this study is to examine whether economic zones and PV types are sufficient factors in determining the environmental efficiency of PV power plants in China, and we find high dispersions of efficiency across economic zones and types of PV plants.
2. Literature Review
A large amount of literature has been devoted to the assessment of PV performance from different aspects. This section reviews the most time-sensitive academic paper of PV performance assessment based on four broad streams of literature, which include (a) the efficiency analysis of PV plants at the international level based on DEA; (b) the efficiency analysis of PV plants in China based on DEA; (c) influential factors of PV plants’ performance; (d) environmental efficiency analysis.
In recent years, several methods of estimating PV energy performance have been proposed, which include process-chain analysis, standard parameters, system dynamics model, Balance Scorecard, spatial planning, and performance simulation [
1,
2,
3,
4,
5,
6]. These methods consider different PV technological features together with the actual characteristics of the operating settings. However, the most popular method for benchmarking the performance of PV solar energy is the DEA method. There are a few studies that include PV power plants into the DEA framework at the international level. Jayanthi et al. [
7] applied DEA for the 22 U.S. PV projects in the various stages of the industry value chain to find out the potential of innovations for the policy maker. Sueyoshi et al. [
8] compared generation performance of PV power plants in Germany and the U.S. based on input-oriented DEA with the insolation, number of PV modules, land area, and average annual sunshine as inputs and installed capacity and annual generation as outputs. Their conclusion was that land use and solar irradiation are not essential influence factors on the PV power plants’ efficiency. Wang and Sueyoshi [
9] adopted the similar input and output variables to assess the large commercial rooftop PV system installations in California.
With the rapid development of the PV industry in China, the research on the Chinese PV industry has made great progress. Zhang and Yang [
10] built a comprehensive evaluation index system for Chinese renewable energy technology based on data envelopment analysis (DEA); the result shows that solar PV has the highest technical benefits. Li et al. [
11] formulated an input-orientated dynamic SBM model to measure the operational efficiency of Chinese PV producers and further explore the impact of business models as well as listing markets on the performance of PV companies. Zhao et al. [
12] calculated the total factor productivity growth of 17 Chinese PV cells enterprise from 2008 to 2014, and found that the growth of the PV industry mainly relies on technological progress. Zhang et al. [
13] evaluated the operating performance of 58 Chinese PV listed enterprises, the results indicated that the overall operating performance of the PV industry in China suffers from weak profits due to low technical efficiency. It is noteworthy that these studies focus on management and operation of PV producers and there is hardly any attention on PV power plants in China.
Prior literature has indicated that some specific factors can influence the performance evaluation of solar PV plants [
14]. The following studies present the most important factors that affect performance of PV plants. From the perspective of insolation, the research of Garcia-Domeno et al. [
15] depicted the main effect of insolation on the performance of PV modules. The reductions of output efficiency at relatively lower or higher solar densities were much more severe under indoor and real outdoor conditions [
16,
17]. Apart from the impacts of total solar insolation, sunshine duration is one of the most important factors that affect PV efficiency. The PV plants located in low-latitude regions usually have noticeable changes in power generation due to higher levels of sunshine, while there are no significant changes in power generation for high-latitude PV plants with shorter sunshine duration [
18]. The annual average electricity outputs were found to be better with longer sunshine hours [
19]. Besides, other variables including wind speed, soiling, and clouds can also be the primary factors that influence PV power generation efficiency [
20,
21,
22,
23].
Environmental efficiency begins with the problem of the limitation of energy and the carbon dioxide emissions caused in the process of energy production. However, in the literature, there are only limited studies focusing on emissions reduction and environmental protection of the PV industry. Wang et al. [
24] employed a meta-frontier DEA approach to evaluate carbon reduction efficiency of technologies; the result showed that although solar power has been exploited in power generation for a long time, the sample consists of several groups of projects such as nuclear energy, hydro-electric energy, wind energy, solar energy, and biomass energy in power plants. Li et al. [
25] proposed a sustainability assessment method with the northeast region of England chosen as a case study. However, there were not enough samples to examine the environmental performance in previous studies.
The review of previous literature shows that very few researches intend to take environmental benefits into account and find out the environmental efficiency of PV power plants. Furthermore, there is a lack of comparison studies on the environmental efficiency of PV power plants in China.
This paper tries to find out and compare the environmental efficiency of PV power plants in China. Of which, the environmental efficiency measures each PV plant’s environmental performance of the power-generation process. To achieve this purpose, this study extends the previous two works. The first point is initiating efforts to quantitatively evaluate the environmental efficiencies of PV plants in China. DEA models are implemented to pre-determine three input and four output variables to measure and compare the environmental efficiencies of 118 PV plants. This paper applies output-oriented DEA models to investigate the effects of the variables from the aspects of electricity generation and environmental protection. The second point is comparing environmental efficiency based on economic zones and the types of PV plants. This type of comparison has never been found in the previous studies in PV efficiency analysis.
3. Methodology and Variables
3.1. Data Envelopment Analysis Method
Energy efficiency is an important index for measuring economic benefits in the Electric Power Industry; accordingly, the electrical generation sector tends to be especially dedicated to improving energy efficiency. A variety of research methods are established to estimate the efficiency of power technologies, which are mainly assigned into the parametric method and nonparametric method. Specifically, parametric method (such as Stochastic Frontier Analysis) is built on the basis of cost functions; while cost and production function can be avoided using the nonparametric method (such as Data Envelopment Analysis). The main function of the DEA method is efficiency evaluation [
26], which is especially suitable for evaluating relative advantages and disadvantages between two or more comparative subjects. The DEA method has been widely used to assess the efficiency of the same input and output indicators.
Data Envelopment Analysis (DEA) was first proposed by Charnes, Cooper, and Rhodes in 1978 [
27], which is a performance evaluation method based on the data of peer entities. DEA is a methodology for mathematical modeling operational processes, and its empirical orientation and minimization of prior assumptions have made it possible to use in a number of studies involving efficient frontier estimation in the nonprofit sector, the regulated sector, and the private sector. In DEA, the organizations under study are called Decision Making Units (DMUs). The definition of DMU is regarded as the entity responsible for converting inputs into outputs and whose performances are to be evaluated. The DEA method fully considers the optimal input–output scheme for the DMUs, and compares the degree to which each DMU deviates from the efficiency frontier to ideally reflect the relative effectiveness of each DMU. Specifically, if the DMU falls into a relatively effective production frontier, it can be considered as having an efficient input–output combination with an efficiency value of 1; those who fail to fall into the production frontier can be considered inefficient.
The following sections use some abbreviations, these abbreviations and their explanations are shown in
Table 1.
3.1.1. The CCR Model
The CCR model is the most basic DEA model, which was initially proposed by Charnes et al. [
27] in 1978. From a production function perspective, CCR is an effective approach to measure technical efficiency of the production sector with multiple input and output variables under the constant returns to scale (CRS) assumption. If the value of TE is closer to 1, the technical performance of the production sector is quite better.
The input-oriented and output-oriented CCR models are presented in the following context.
The CCR model has the following input-oriented structure to measure an efficiency score
θ:
As a methodological alternative of the input-oriented model, the CCR has the following output-oriented model to measure the efficiency score η:
θ and η are the total efficiency indexes of DMUs, λ represents a weighting, s− and s+ indicate redundant and insufficient output respectively, xij denotes the amount of the ith input of the jth DMU, yrj denotes the amount of the rth output of the jth DMU. The DMU is CCR efficient if the efficiency index reaches 1, otherwise, the DMU is CCR inefficient.
The input-oriented CCR efficiency explores efficiency from the perspective of input and compares the usage of resources under the current output level. The output-oriented CCR efficiency explores efficiency from the perspective of output and compares the achievement of output under the same level of input. For guiding practical production, improving environmental achievements is more meaningful for the PV industry, so we adopted the output-oriented CCR model in this paper.
3.1.2. The BCC Model
The input-oriented BCC model proposed by Banker et al. [
28] evaluates the efficiency of DMUs by relaxing the assumption of ‘constant returns to scale’ and associating the constraint of
. In the BCC model, the total efficiency (TE) can be decomposed into pure technical efficiency (PTE) and scale efficiency (SE) under the assumption of ‘variable returns to scale’, the results calculated by the BCC model are PTE. The BCC models are shown in the following.
The BCC model has the following input-oriented structure to measure an efficiency score θ:
As a methodological alternative of the input-oriented model, the BCC has the following output-oriented model to measure the efficiency score η:
θ and η are the pure technical efficiency indexes of DMUs, which represents PTE score. λ represents a weighting parameter for each DMU, s− and s+ are slack variables, xij denotes the amount of the ith input of the jth DMU, yrj denotes the amount of the rth output of the jth DMU. Compared with the CCR model, the BCC model has one more constraint to construct to a new envelope surface. Similarly, the DMU is BCC efficient if the efficiency index reach 1, otherwise, the DMU is BCC inefficient.
TE is formulated by taking into account the technical factors and scale factors, which is a result of multiplying PTE and SE together, and indicates the overall operating performance, which can be expressed as follows:
This decomposition allows an insight into the source of inefficiencies. TE is related to the productivity of inputs [
29], which reflects the overall resource allocation and utilization efficiency of a DMU. The PTE is a measure of TE without SE and reflects the managerial performance to organize the inputs during the production process. The SE measure has been used as an index to capture optimum scale of production resources. Besides improper allocation of inputs and outputs, the inefficiency of TE may also be attributed to scale factors. Therefore, input–output configuration and scale factor need to be considered simultaneously for improving the efficiency of the DMU.
The input-oriented BCC model measures the degree to which each input should be reduced to achieve Pure Technical Efficiency without reducing output. Reducing input serves as the main way to increase efficiency for inefficient DMUs. The output-oriented BCC model measures the degree to which each output should be increased to achieve Pure Technical Efficiency without increasing input. Increasing output serves as the main way to increase efficiency for inefficient DMUs. Compared with controlling input variables, increasing outputs has more practical implications for power utility and environmental protection, so we adopted the output-oriented BCC model in this paper.
3.2. Combined Margin Emissions Factor
Due to geographical differences, the intensity of carbon dioxide emitted from different regions is different. In other words, the amount of carbon dioxide emitted per kilowatt hour is generally lower in those areas where there is advanced technology and a higher proportion of renewable energy. Presently, the most common method is adopting the combined margin emissions factor.
The combined margin emissions factors can be affected by changes in the annual emissions and power generation data. The combined margin emissions factor is calculated as follows:
In this formula, EF represents the Combined Emissions Factor; OM represents Operating Margin, which refers to the group of existing power plants whose current electricity generation would be affected by the proposed Clean Development Mechanism project activity; BM represents Build Margin, which refers to the group of prospective power plants whose construction and future operation would be affected by the proposed Clean Development Mechanism project activity;
represents the weighting of operating margin emissions factor (%);
represents the weighting of build margin emissions factor (%) [
30]. In China, the
and
of the solar power generation project activities are assigned to the value of 75% and 25%.
The combined margin emissions factor can be used to calculate CO
2 emission reductions of the PV power plants by the following formula:
3.3. Variables
This study compares PV power plants in China to examine which economic zones and which types of plant are more efficient in their usages and mitigation actions. A total of 118 PV power plants are used for the comparison. In this paper, we introduce three inputs and four outputs to capture the most remarkable characteristics of the environmental protection performance. The input and output route is delineated in
Figure 1.
3.3.1. Input Variables
In this model, we use the insolation, annual sunshine duration, and covering area for the inputs:
Insolation: Solar insolation measured at a given location on Earth with a surface element perpendicular to the Sun’s rays, excluding diffuse insolation (the solar radiation that is scattered or reflected by atmospheric components in the sky). The research of García-Domingo et al. [
15] suggested that direct normal insolation has a major role in affecting the performance of a concentrated PV module. The larger the amount of solar insolation, the greater the amount of power generated. The insolation is directly related to the intensity of sunlight, season, and geographical location.
In this paper, average insolation is measured in terms of peak direct insolation as MJ/m². The insolation parameter data for this study was derived from the average annual insolation that was collected by local environmental protection agencies for each given location. In most cases, the lower the latitude, the greater the solar incident angle, the less sunshine the location has, so that it receives a lower insolation. Accordingly, the western region of China has a significant advantage in both insolation and sunshine over central and eastern regions.
Annual sunshine duration: Sunshine duration is a significant climatological indicator, measuring duration of sunshine in a given period (in this paper, it is measured by one year) for a given location on Earth, typically expressed as an averaged value over several years. It is a general indicator of the cloudiness of a location, and thus differs from insolation, which measures the total energy delivered by sunlight over a given period. Sunshine duration can be influenced by seasonal change; it also depends on the weather conditions, altitude, and geographical location of the observation point. The extension of sunshine duration will increase the economic efficiency of PV power plants [
31].
According to the annual average total sunshine hours disclosed by the China Climate Bulletin, the distribution of the average annual sunshine duration in China has an increasing tendency from the southeast region to the northwest region.
Covering area: Large-scale PV power plants generally need to occupy vast expanses of land. Theoretically, there is a large amount of land in China which can be used for the construction of a PV project, but in actual operation, land issues have become a struggle for the PV project development. In this paper, we adopted the Total Covering Area as an input indicator, which refers to the overall land demand of a PV power plant. We note that land area is also used as input in previous research [
8]. More precisely, total covering area includes both utilized land and idle land within the boundaries of the site. Idle land refers to land that has been approved for use by administrative departments but has not broken ground yet.
3.3.2. Output Variables
We adopted installed capacity and annual electricity generation to measure the operational performance of PV plants in China. Since China is a major carbon dioxide and other greenhouse gas emissions producer, China’s environmental policy could greatly affect the balance of the global climate. To realize sustainable emission reduction and energy saving goals, we also adopted CO2 emission reduction and coal savings to measure the environmental performance. Thus, the following four output variables contribute to the environmental effects of PV plants in China.
Installed Capacity: The total installed capacity of a PV power system refers to the sum of rated effective power of the PV generator sets actually installed in the system. The most common installed capacity unit in China is MW. We note that installed capacity is also used as a desirable output in prior literature. The use of capacity of power generation facilities as output with electricity generation in DEA is a well-documented procedure [
8,
9,
32].
Annual Electricity Generation: Annual power generation is the sum of the electrical energy actually emitted by all generators sets in the system during the whole year, which can be a significant measurement for the performance of any power plant. This data was collected from environmental impact assessment reports prepared by electric companies involved in the operation of PV power plants.
Coal Saving: Electricity in China’s electrical power system is mainly thermal power generation, which is the main consumer of coal, petroleum, and other special fuel. The fuel combustion and standard coal equivalent would be reduced by promoting the use of solar energy. Due to the differences in the capacity and efficiency of thermal power plants across China, the amount of standard coal consumed for each degree of power generation is different, so the saving of coal for PV power plants built in the different regions is also different. This paper regards standard coal saving as a desirable output.
CO2 emission reduction: PV products are highly environmentally friendly, and the utilization of high-efficiency solar energy can reduce large amounts of CO2 emissions and thus achieve environmental sustainability.
According to the coverage of the power grid, China can be divided into six regions. Within each region, an emission reduction factor is calculated based on total emissions (coal, oil, gas) and total power generation (thermal power, hydropower, and other renewable energy sources). Moreover, the emission reduction factors are affected by changes in the annual emissions and power generation data.
According to the annual emission reduction data released by the Climate Division of the National Development and Reform Commission, the following emission reduction factors have been calculated by models (6), and the results are shown in
Table 2. It needs to be mentioned that the PV power plants in this paper were established during years 2012–2016, so we only calculated the CO
2 emission reduction factor from 2012 to 2016.
It can be observed that the CO2 Emission Reduction Factors in most of regions go down with time, while there is no decreasing trend of CO2 Emission Reduction Factors in North China. On the one hand, in the case of the same amount of power generation, more CO2 emissions are produced in northern China. On the other hand, the utilization of PV power can provide a wider influence for CO2 emission to replace carbon-intensive traditional energy in northern China, and even in the whole country. The CO2 emission reduction of each PV power plant is calculated according to Model (7) based on the CO2 Emission Reduction Factors of different region in which it is located and its annual electricity generation.
4. Comparison on PV Power Plants
4.1. General Efficiency Analysis
Table 3 summarizes descriptive statistics for the variables above of PV power plants in China. These data sets include average values, maximum, and minimum values as well as standard deviations, which are helpful for overviewing the variables.
We solve models (2) and (4) with the variables described in
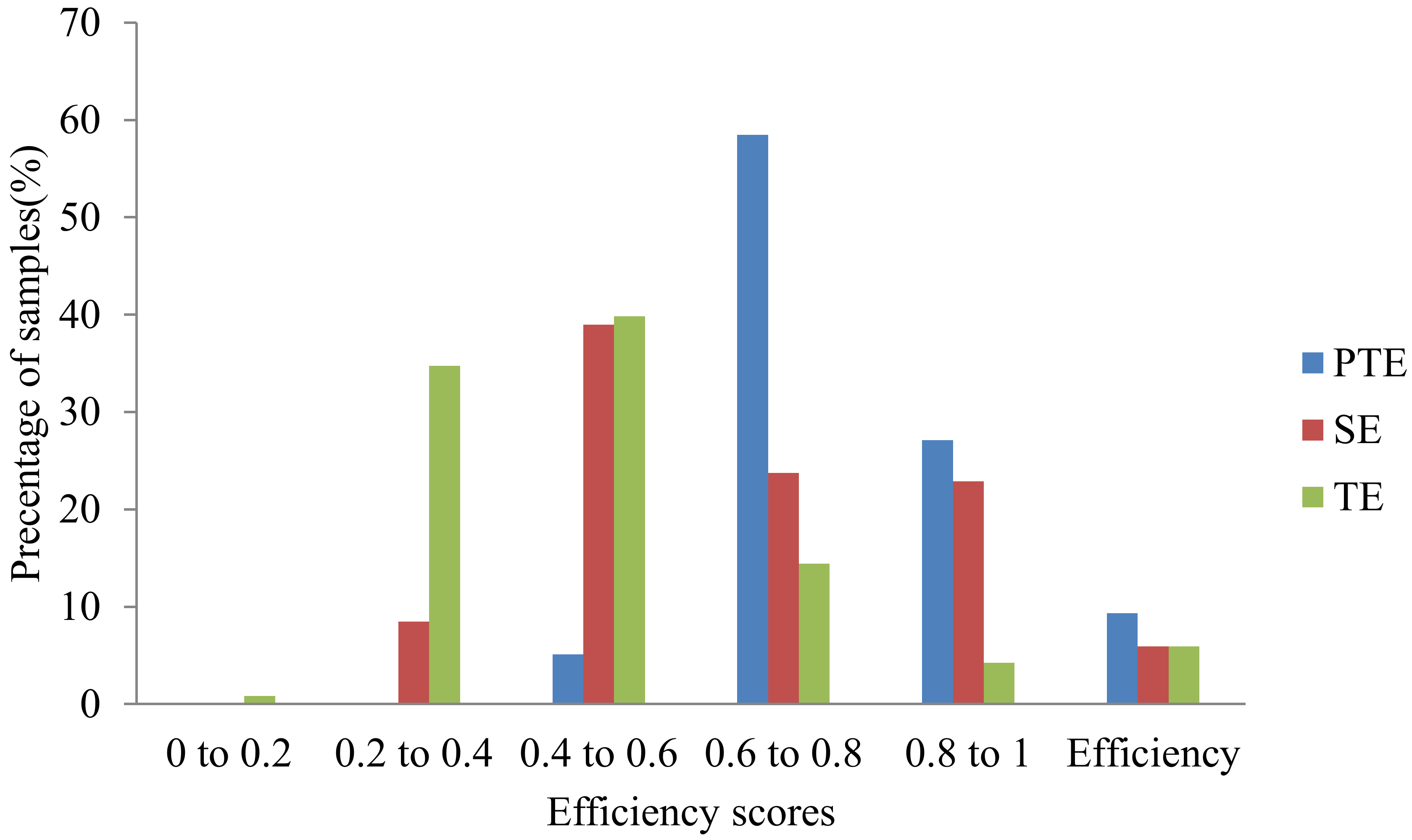
Section 3.3. The calculated efficiency scores are summarized and divided into six intervals, the distribution of efficiency scores from the DEA model is presented in
Figure 2. For both SE and TE, the highest concentration of PV efficiency scores is in the range between 0.4 and 0.6, and approximately 5% can reach SE and TE efficiency. For PTE, we can find almost 90% of the PV power plants in the range between 0.4 and 1, only 10% can achieve PTE efficiency. The wide spread inefficient units indicate that most plants have used specific resources to produce a lower-than-expected level of output, indicating that the allocations of input–output and scales are relatively illogical.
TE can be used to estimate whether the performance is comprehensively efficient, to the extent that each input variable exerts the utility for a power plant’s performance. The average TE value of the 118 PV power plants in China is just 0.5091. The mean shows that the overall efficiency scores of those sample PV plants are at a low level due to 111 PV plants’ TE being lower than 1, the general inefficient situation implies adjustable vacancy is still exists.
Only 7 PV plants reach 1 TE, which can be attributed to their reasonable and practical operating concepts. These PV power plants know how to maximize the role of technical and scale elements in their operation management. However, 111 PV plants are left in inefficient states, the lagging behind of the whole management level might be caused by some deviations in resource allocation, and also a possible contribution coming from the lack of sufficiency of scale advantage for production. The vast majority of PV power plants need to find the problems and the cause, to produce a better environmental performance by technique optimization, management improvement, and input adjustment.
PTE measures the effect of technical factors such as high technology and management leadership on the performance. The results show that the average value of PTE is 0.7688, indicating that the PTE of PV plants are generally preferable. SE measures whether the scale of investment is appropriate or not. The reasonable scale can allow the outputs to respond to the changes of inputs proportionally. The average SE of the 118 sample plants is 0.6559, while the average PTE reaches 0.7688. The results also show that the rankings of TE and SE are similar. Thus, the general inefficiency of PV plants tends to be more affected by scale factors, and accordingly we should attach great emphasis on scale to analyze the inefficiency. At the same time, 7 PV power plants are effective in scale and technique, which only accounts for 5.93%. The minimum SE is 02394 and the maximum SE is 1, indicating that there is a big difference in the scale efficiency among the power plants.
4.2. Economic Zones Efficiency Analysis
We now turn to examine whether the economic zones of PV power plants are related to their performance. To carry out the analysis, we group the PV power plants at the economic zone levels shown in
Table 4. The 118 PV power plants include 36 in Eastern China, 32 in Central China, and 50 in Western China. We do not categorize the power plants by provinces because a province is too small to host enough available power plants for comparison.
Table 5 summarizes descriptive statistics for the variables above of PV power plants in China. In general, the western economic zone has the highest level of natural resources, while the eastern economic zone has the lowest level of natural resources.
Table 6 shows the average efficiency scores of different economic zones. The efficiency distribution of three economic zones in China has an apparent trend, the PTE, SE, and TE in the western region are better than those in the central region, and those in central region are also better than the eastern region.
According to the results shown in
Figure 3, over 70% of TEs in the eastern economic zone are below 0.6; nearly 40% of TEs in the central economic zone are between 0.6 and 0.8, but there is still 30% below 0.6, with 15% having reached 1; from the perspective of low efficiency, the TEs distribution in the western economic zone is slightly better than that in the central economic zone, about 30% of TEs in the western area are between 0.6 and 0.8, and about 20% below 0.6. The PTEs in all three economic zones are distributed over 0.6. Eighty percent of the PTEs in the east had a distribution between 0.6 and 1, with the remaining 20% reaching 1. The situation in the central region is better, and about 80% of PTEs are over 0.8. More than 40% have reached 1; while in the western region, 2/3 PTEs range from 0.8 to 1, and about 21% has reached 1. Eighty percent of the SEs in the Eastern Economic Zone are below 0.8; while the SE in the Central and West is mainly concentrated between 0.6 and 1, however, 20% of the SE in the West is below 0.6.
Several factors may contribute to the differences of efficiency in the different economic zones. The most believable cause rests on the ‘aerosol pollution’ in eastern China. This aerosol pollution in China greatly reduces surface solar PV resources. Especially high aerosol impacts exist over eastern China, where air pollution is severe and electricity demand is greatest [
33]. The aerosol pollution would reduce insolation and annual sunshine duration of PV modules, which influence the environmental efficiency of PV plants in Eastern China negatively.
Also, the high urbanization rate of eastern China could reduce the total efficiency of PV power generation. On the one hand, the rising urbanization rate could lead to a significant increase in energy consumption [
34]. According to the relevant calculation data of the Development Research Center of the State Council, the 1% increase in the urbanization rate would lead to the increase of 60 million tons in standard coal consumption. However, due to the short-term coal-dominated energy pattern it is difficult to fundamentally change, and new energy is hard to grow into the main force of energy consumption. The situation of “high carbon lock” faced by urbanization is hard to crack, resulting in difficulty for PV power generation efficiency. On the other hand, as the urbanization rate increases, a large number of urban construction lands would erode the landscape of PV power generation. The energy storage technology for power generation has not yet been broken, and the increase in the urbanization rate will likely hinder the efficiency of PV power plant in the short term.
4.3. PV Plant Types Efficiency Analysis
According to the four major PV plant types listed in
Table 7, we also group the results by plant types. Those PV plants can be classified into four types: 38 mountain PV plants, 37 desert PV plants, 15 rooftop PV plants, as well as 28 complementary PV plants.
Table 8 summarizes descriptive statistics for the variables above of PV power plants in China. The rooftop plant and complementary plant are two typical distributed plants, while the mountain plant and desert plant are ground-based PV plants, which usually have greater investment and scale.
The average efficiency scores of different PV plant types are shown in
Table 9. The four types of PV power plants have similar PTEs, although the complementary power plants are slightly lower than the other three types; the rooftop power plant has the highest SE, and the SE of the complementary power plant is significantly lower than the other three types; accordingly, the rooftop power plant has the highest TE, while the complementary power plant has the lowest TE.
The specific results are shown in
Figure 4, 40% TEs of Mountain plants are range from 0.6 to 0.8, 50% TEs of desert plants are above 0.8, while 50% of the rooftop’s TEs are 0.6–0.8, and 50% TEs of the complementary power plants are lower than 0.6. The PTEs of the majority PV plants are higher than 0.8, and it is worth mentioning that this proportion of mountain plants and desert plants both reached 95%. Seventy percent of SEs of mountain plants and 60% of SEs of desert plants have a range between 0.6 and 1, while the proportion of desert plants which are in the stages of scale efficiency is slightly higher than mountain plants. Rooftop plants performed best in SE among the four types, 30% SEs achieve scale efficiency, while for the worst performer, complementary plants, about 50% are lower than 0.6, which contributed to its lowest TE.
There are several factors that may lead to differences in the efficiency of different types of plants. Rooftop PV power plants not only can increase the amount of power generation, but also effectively solves the problem of power loss during booster step and long-distance transportation, which improve the efficiencies of rooftop PV plants. Complementary PV plants have several advantages, which can save the land resources and satisfy different crop demands of lighting by different light transmittance of panels. However, this type of PV plant has the lowest efficiency of PTE, SE, and TE. Inevitably, there are often high temperatures caused by thermal dissipation and heat preservation during the power-generation process of the complementary PV plants [
35]. Both the electrical efficiency and the power output of a PV module will decrease with the increase in the operating temperature [
36,
37].
It is beyond the scope of this paper to clarify the impact of these factors on the performance of environmental protection. In general, DEA-based economic zones and types analysis can help solar installers and decision makers to determine the best locations and appropriate types.
5. Discussions and Conclusions
In this research, we applied the traditional nonparametric DEA method to study the performance of 118 PV power plants in China. This approach provides us with a measure of environmental performance of PV plants by modeling these plants as a multi-input multi-output process. The DEA method overcomes some of the limitations and inconsistencies of PV power plants distributed in different economic regions and types. In the implementation process, the model takes one discretionary input to capture the design of power plants, and two non-discretionary inputs to capture the climatic factors. Two of these outputs are capacity and electricity generation, which are two major achievements of PV power plants. The other two outputs are the environmental protection achievements of emission reduction and resource conservation, representing the ecological benefits of PV power plants.
The results manifest widespread inefficient environmental performance of approximately 94% of PV plants in China. There are huge gaps between the actual outputs and the optimal outputs for representative PV plants. This implies that PV plants should try to come up with a better design of the PV system to increase environmental benefits. However, the current DEA cannot determine the fundamental cause of universal inefficiency; more accurate methods need to be utilized to scrutinize the PV plants.
The relationship between combined performance and economic zones, and the relationship between combined performance and the types of plants are also examined in this paper. The performance of economic zones and types of PV plants are quite different. We find those PV plants in western China are the best performers among the three economic zones, while the samples of eastern China are unsatisfied performers. The dispersion of performance is most likely caused by serious aerosol pollution and a high urbanization rate in eastern China. We also find rooftop PV plants have the highest efficiencies among the four types of PV plants due to very little power loss, whereas complementary PV plants have the lowest efficiencies because of high operating temperatures during the process of power generation.
Since the data of many PV power plants in China cannot be obtained directly, the amount of data in this study is limited. Therefore, the results of this study only provides the performance evaluation for the selected samples, and currently cannot represent the overall efficiency level of PV power generation projects in China. For future research, further improvement of the data is needed to get more sophisticated evaluation results.
Traditional DEA models have some drawbacks. At first, the classical DEA models treat each DMU as a “black box” and the internal interactions are disregarded. On the contrary, the internal interactions of a PV power plant should be regarded. Besides, traditional DEA models make an attempt to optimize DMUs efficiency in a single-period condition. However, in the present problem, some inputs and outputs such as insolation and sunshine duration are time-dependent factors. Future study can extend to longer period.
Author Contributions
H.Y. conceived the main method, designed the main stages in the research and wrote the paper. H.F. conducted the empirical analysis and supervised the whole process. X.W. revised the paper. And S.F. collected and sorted the data. All authors read and approved the final manuscript.
Funding
This research was funded by the Consultation Project of the Chinese Academy of Engineering, No. 2017-RC-05; National Natural Science Foundation of China, No. 71273022, 71773006; Research Project on Major Issues in the Philosophy and Social Science Research of the Ministry of Education, No. 17JZD023; Beijing Education Science Planning Project, No. AAA12007.
Acknowledgments
Thanks to the Chinese Academy of Engineering, the National Natural Science Foundation of China, the Philosophy and Social Science Research of the Ministry of Education and Beijing Education Science Planning Project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hafeznia, H.; Yousefi, H.; Astaraei, F.R. A novel framework for the potential assessment of utility-scale photovoltaic solar energy, application to eastern Iran. Energy Convers. Manag. 2017, 151, 240–258. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. Performance assessment and degradation analysis of solar photovoltaic technologies: A review. Renew. Sustain. Energy Rev. 2017, 78, 554–587. [Google Scholar] [CrossRef]
- De Azevedo Dias, C.L.; Branco, D.A.; Arouca, M.C.; Legey, L.F. Performance Estimation of Photovoltaic Technologies in Brazil. Renew. Energy 2017, 114, 367–375. [Google Scholar] [CrossRef]
- Voorspools, K.R.; Brouwers, E.A.; D’Haeseleer, W.D. Energy content and indirect greenhouse gas emissions embedded in ‘emission-free’ power plants: Results for the Low Countries. Appl. Energy 2000, 67, 307–330. [Google Scholar] [CrossRef]
- Liu, J.P.; Long, Y.; Song, X.H. A Study on the Conduction Mechanism and Evaluation of the Comprehensive Efficiency of Photovoltaic Power Generation in China. Energies 2017, 10, 723. [Google Scholar]
- Mostafaeipour, A.; Qolipour, M.; Mohammadi, K. Evaluation of installing photovoltaic plants using a hybrid approach for Khuzestan province, Iran. Renew. Sustain. Energy Rev. 2016, 60, 60–74. [Google Scholar] [CrossRef]
- Jayanthi, S.; Witt, E.C.; Singh, V. Evaluation of Potential of Innovations: A DEA-Based Application to U.S. Photovoltaic Industry. IEEE Trans. Eng. Manag. 2009, 56, 478–493. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. Photovoltaic power stations in Germany and the United States: A comparative study by data envelopment analysis. Energy Econ. 2014, 42, 271–288. [Google Scholar] [CrossRef]
- Wang, D.D.; Sueyoshi, T. Assessment of large commercial rooftop photovoltaic system installations: Evidence from California. Appl. Energy 2017, 188, 45–55. [Google Scholar] [CrossRef]
- Zhang, L.B.; Yang, T. The Evaluation and Selection of Renewable Energy Technologies in China. Energy Procedia 2014, 61, 2554–2557. [Google Scholar]
- Li, N.; Liu, C.; Zha, D. Performance evaluation of Chinese photovoltaic companies with the input-oriented dynamic SBM model. Renew. Energy 2016, 89, 489–497. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y. Technological progress and industrial performance: A case study of solar photovoltaic industry. Renew. Sustain. Energy Rev. 2018, 81, 929–936. [Google Scholar]
- Zhang, L.; Wang, J.; Wen, H.; Fu, Z.; Li, X. Operating performance, industry agglomeration and its spatial characteristics of Chinese photovoltaic industry. Renew. Sustain. Energy Rev. 2016, 65, 373–386. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, K.; Huang, Z. Environment-adjusted operational performance evaluation of solar photovoltaic power plants: A three stage efficiency analysis. CEEP-BIT Work. Pap. 2017, 76, 1153–1162. [Google Scholar] [CrossRef]
- García-Domingo, B.; Aguilera, J.; Casa, J.D.L.; Fuentes, M. Modelling the influence of atmospheric conditions on the outdoor real performance of a CPV (Concentrated Photovoltaic) module. Energy 2014, 70, 239–250. [Google Scholar] [CrossRef]
- Gaglia, A.G.; Lykoudis, S.; Argiriou, A.A.; Balaras, C.A.; Dialynas, E. Energy efficiency of PV panels under real outdoor conditions–An experimental assessment in Athens, Greece. Renew. Energy 2017, 101, 236–243. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, L.; Sun, K. Experimental investigation of the impact of airborne dust deposition on the performance of solar photovoltaic (PV) modules. Atmos. Environ. 2011, 45, 4299–4304. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.H. Shadow analysis of photovoltaic plants at different latitudes. Sol. Energy 2015, 3, 28–31. (In Chinese) [Google Scholar]
- Nayak, S.; Tiwari, G.N. Energy metrics of photovoltaic/thermal and earth air heat exchanger integrated greenhouse for different climatic conditions of India. Appl. Energy 2010, 87, 2984–2993. [Google Scholar] [CrossRef]
- Tiba, C.; Ricardo, E.D.A. Siting PV plant focusing on the effect of local climate variables on electric energy production—Case study for Araripina and Recife. Renew. Energy 2012, 48, 309–317. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2008, 34, 23–29. [Google Scholar] [CrossRef]
- Chen, C.S.; Duan, S.X.; Cai, T.; Liu, B.Y. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.Q. Forecasting Power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2015, 48, 1064–1069. [Google Scholar] [CrossRef]
- Wang, N.; Chen, J.; Yao, S.; Chang, Y.C. A meta-frontier DEA approach to efficiency comparison of carbon reduction technologies on project level. Renew. Sustain. Energy Rev. 2018, 82, 2606–2612. [Google Scholar] [CrossRef]
- Li, T.; Roskilly, T.; Wang, Y. A Regional Life Cycle Sustainability Assessment Approach and its Application on Solar Photovoltaic. Energy Procedia 2017, 105, 3320–3325. [Google Scholar] [CrossRef]
- Picazo-Tadeo, A.J.; Gómez-Limón, J.A.; Reig-Martínez, E. Assessing farming eco-efficiency: A data envelopment analysis approach. Work. Pap. 2011, 92, 1154–1164. [Google Scholar] [CrossRef] [PubMed]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Sathye, M. X-e fficiency in Australian banking: An empirical investigation. J. Bank. Financ. 2001, 25, 613–630. [Google Scholar] [CrossRef]
- Hou, P.; Wang, H.T.; Zhang, H.; Fan, C.D.; Huang, N. Greenhouse Gas Emission Factors of Chinese Power Grids for Organization and Product Footprint. China Environ. Sci. 2012, 32, 961–967. (In Chinese) [Google Scholar]
- Chen, X.; Wang, Y.H. Analysis of Shadow of PV Power Station Based on Operating Data. Yunnan Electr. Power 2015, 43, 1–2. (In Chinese) [Google Scholar]
- Jha, D.K.; Shrestha, R. Measuring Efficiency of Hydropower Plants in Nepal Using Data Envelopment Analysis. IEEE Trans. Power Syst. 2006, 21, 1502–1511. [Google Scholar] [CrossRef]
- Li, X.; Wagner, F.; Peng, W.; Yang, J.; Mauzerall, D.L. Reduction of solar photovoltaic resources due to air pollution in China. Proc. Natl. Acad. Sci. USA 2017, 114, 11867–11872. [Google Scholar] [CrossRef] [PubMed]
- Li, S.L. Research on calculation of new energy’s power generation efficiency and analysis on its driving factors. Resour. Sci. 2016, 33, 321–332. (In Chinese) [Google Scholar]
- Nishioka, K.; Hatayama, T.; Uraoka, Y.; Fuyuki, T.; Hagihara, R.; Watanabe, M. Field-test analysis of PV system output characteristics focusing on module temperature. Sol. Energy Mater. Sol. Cells 2003, 75, 665–671. [Google Scholar] [CrossRef]
- Dincer, F.; Meral, M.E. Critical factors that affecting efficiency of solar cells. Smart Grid Renew. Energy 2010, 1, 47–50. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, J.N.; Seshadri, B. Temperature Dependent Photovoltaic (PV) Efficiency and Its Effect on PV Production in the World—A Review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).