Risk Transfer among Housing Markets in Major Cities in China
Abstract
1. Introduction
2. Literature Review
2.1. Housing Market Risk
2.2. The Estimation of Housing Market Risk
3. Empirical Model
3.1. Model for the Estimation of Housing Market Risk
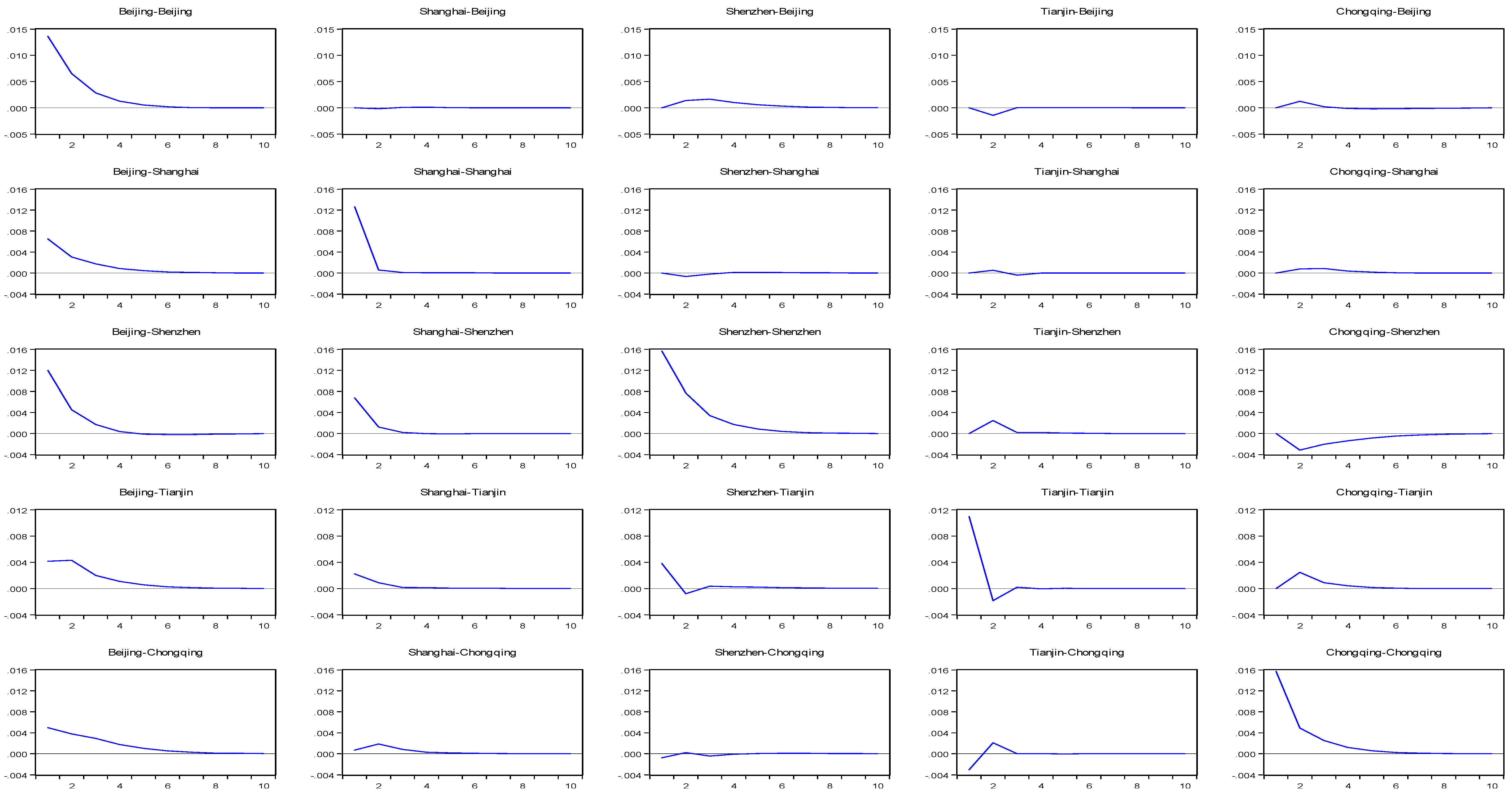
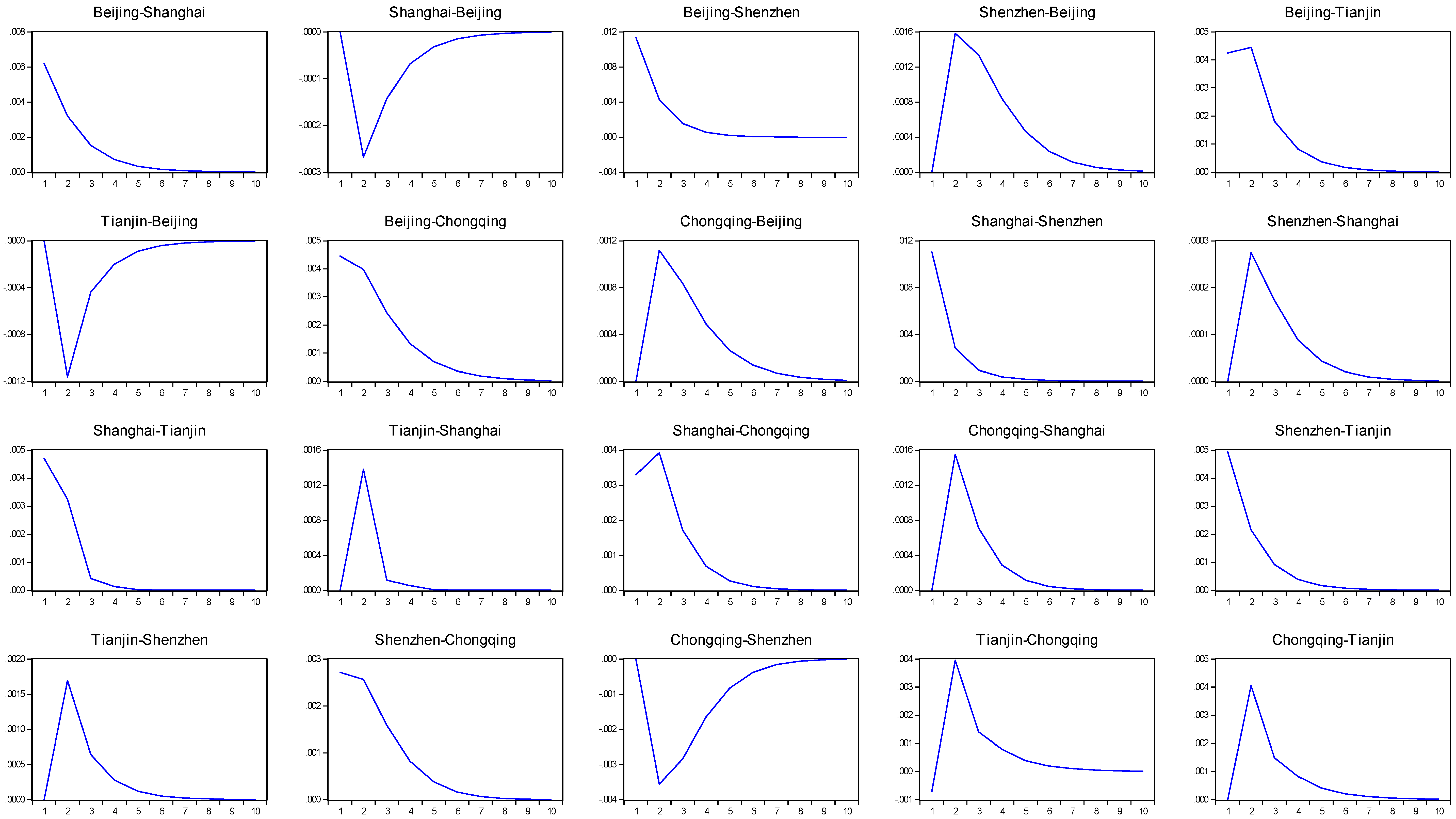
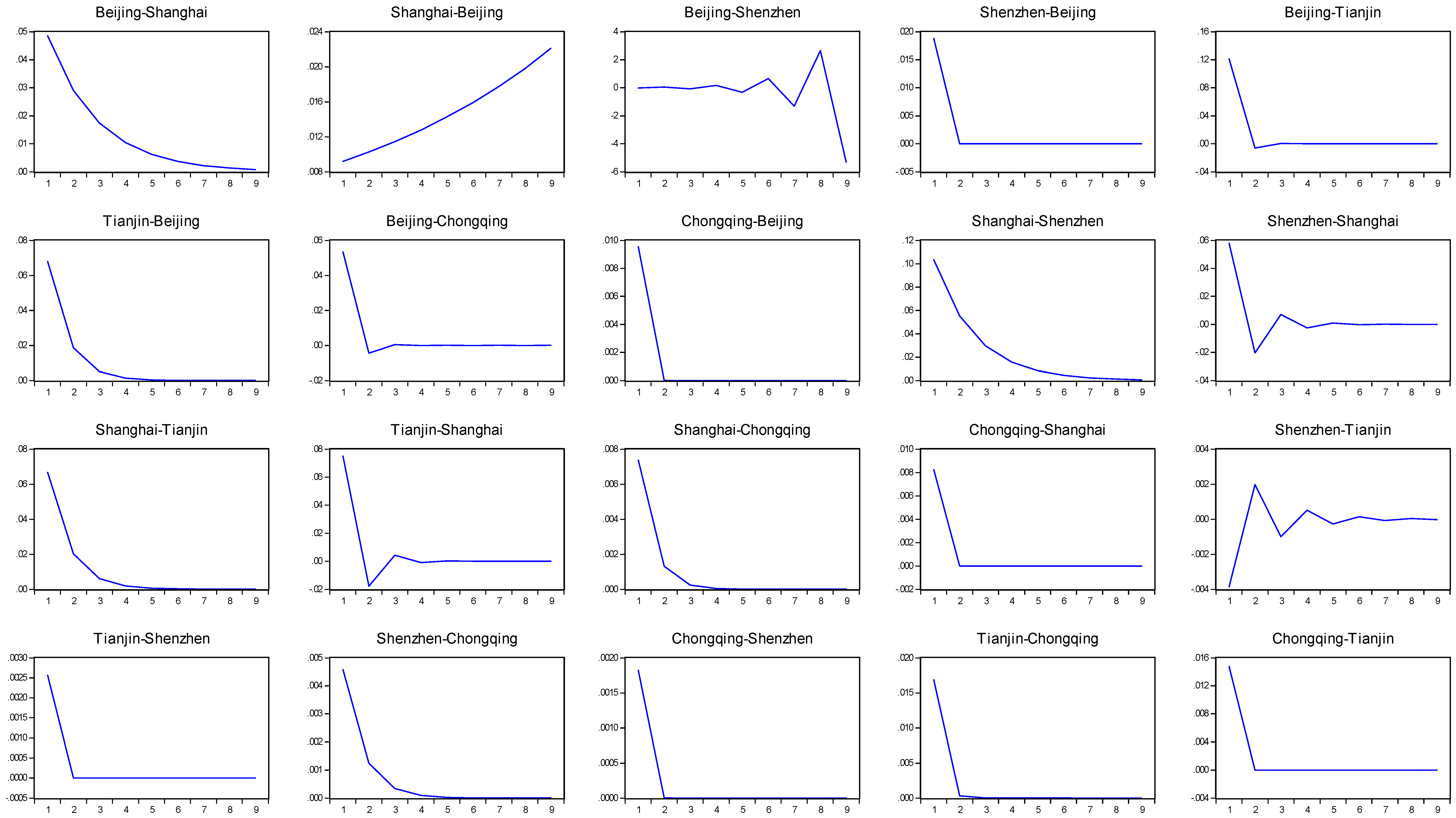
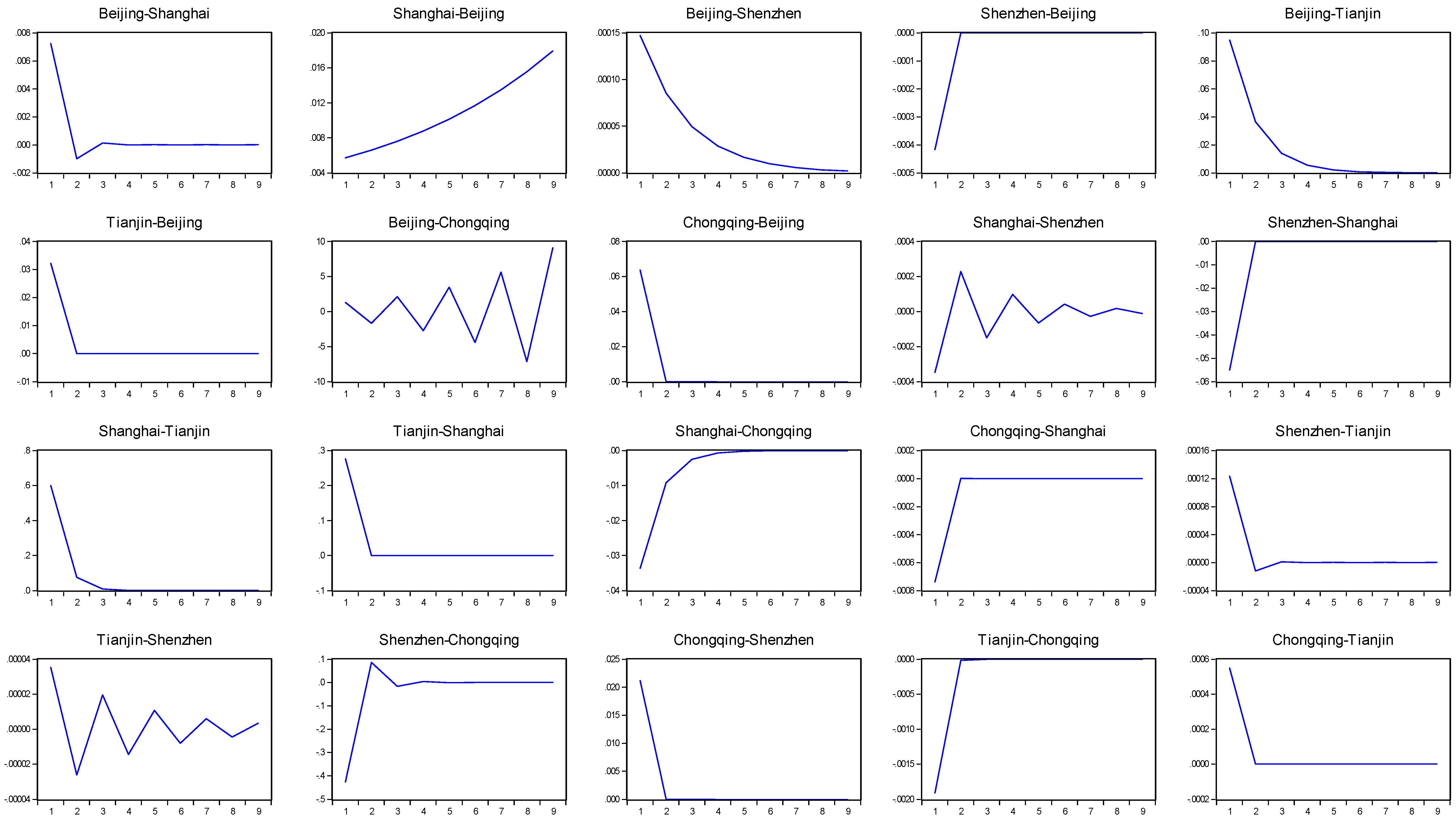
3.2. The Estimation for VIRF
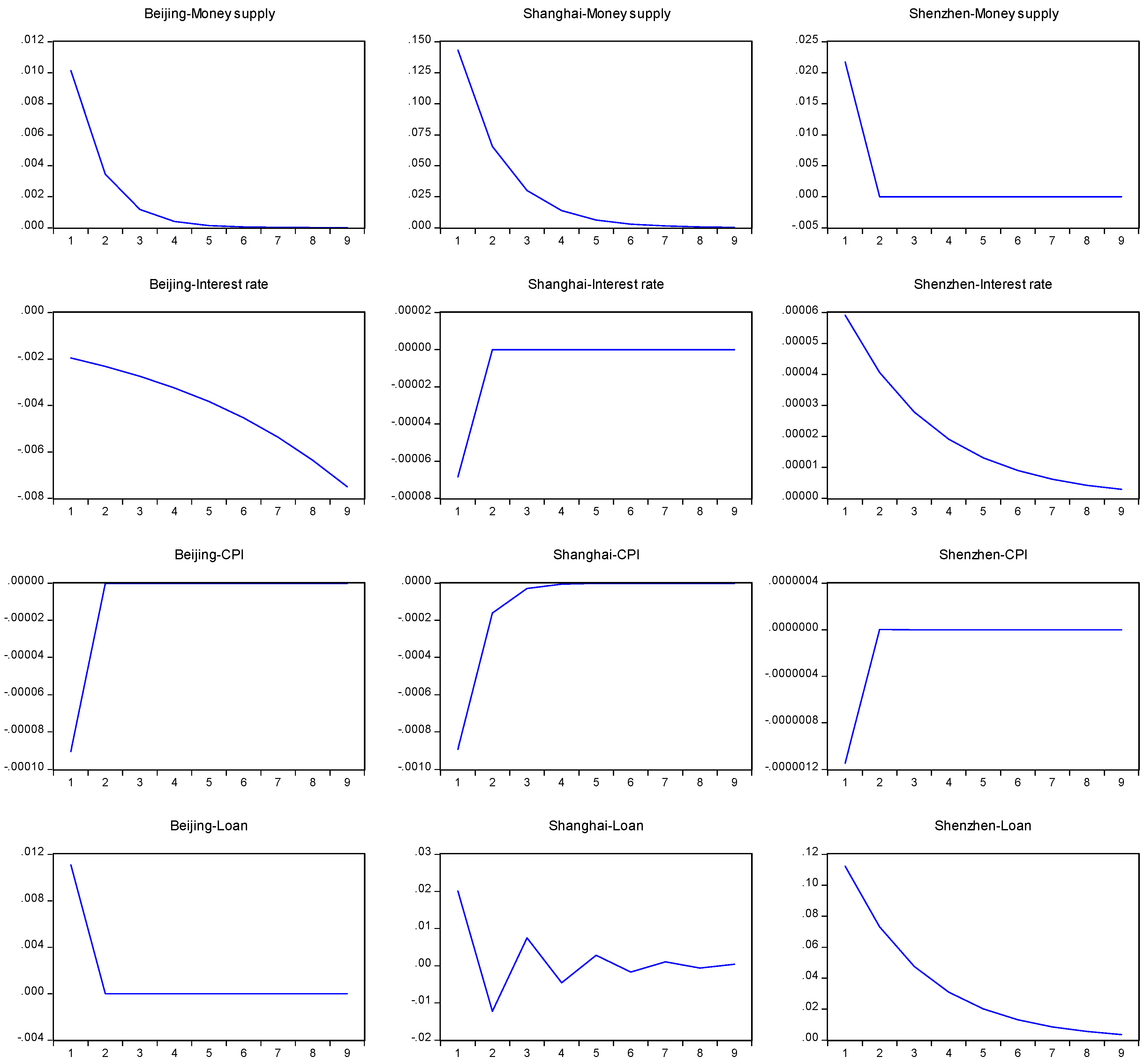
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahuja, A.; Cheung, L.; Han, G.; Porter, N.; Zhang, W. Are House Prices Rising too Fast in China? IMF Working Paper No. 10/274; International Monetary Fund: Washington, DC, USA, 2011. [Google Scholar]
- Shi, G.; Liu, X.; Zhang, X. Time-varying causality between stock and housing markets in China. Financ. Res. Lett. 2017, 22, 227–232. [Google Scholar] [CrossRef]
- Banks, J.; Blundell, R.; Oldfield, Z.; Smith, J.P. Housing Price Volatility and Housing Ownership over the Lifecycle; Discussion Papers in Economics 04-09; University College London: London, UK, 2004. [Google Scholar]
- Chandler, D.; Disney, R. The housing market in the United Kingdom: Effects of house price volatility on households. Fisc. Stud. 2014, 35, 371–394. [Google Scholar] [CrossRef]
- Liu, H.; Park, Y.W.; Zheng, S. The interaction between housing investment and economic growth in China. Int. Real Estate Rev. 2002, 5, 40–60. [Google Scholar]
- Deng, Y.; Girardin, E.; Joyeux, R.; Shi, S. Did bubbles migrate from the stock to the housing market in China between 2005 and 2010? Pac. Econ. Rev. 2017, 22, 276–292. [Google Scholar] [CrossRef]
- Ren, Y.; Xiong, C.; Yuan, Y. House price bubbles in China. China Econ. Rev. 2012, 23, 786–800. [Google Scholar] [CrossRef]
- Shen, L. Are house prices too high in China? China Econ. Rev. 2012, 23, 1206–1210. [Google Scholar] [CrossRef]
- Feng, Q.; Wu, G.L. Bubble or riddle? An asset-pricing approach evaluation on China’s housing market. Econ. Model. 2015, 46, 376–383. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Yue, S. Housing price bubbles in Hong Kong, Beijing and Shanghai: A comparative study. J. Real Estate Financ. Econ. 2006, 33, 299–327. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Gu, Q. Study of Guangzhou house price bubble based on state-space model. Int. J. Strateg. Prop. Manag. 2009, 13, 287–298. [Google Scholar]
- Hou, Y. Housing price bubbles in Beijing and Shanghai? A multi-indicator analysis. Int. J. Hous. Mark. Anal. 2010, 3, 17–37. [Google Scholar] [CrossRef]
- Guo, S.; Li, C. Excess liquidity, housing price booms and policy challenges in China. China World Econ. 2011, 19, 76–91. [Google Scholar] [CrossRef]
- Yu, H. Size and characteristic of housing bubbles in China’s major cities: 1999–2010. China World Econ. 2011, 19, 56–75. [Google Scholar] [CrossRef]
- Dreger, C.; Zhang, Y. Is there a bubble in the Chinese housing market? Urban Policy Res. 2013, 31, 27–39. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q. Fundamental factors in the housing markets of China. J. Hous. Econ. 2014, 25, 53–61. [Google Scholar] [CrossRef]
- Shih, Y.-N.; Li, H.-C.; Qin, B. Housing price bubbles and inter-provincial spillover: Evidence from China. Habitat Int. 2014, 43, 142–151. [Google Scholar] [CrossRef]
- Liu, R.; Hui, E.C.M.; Lv, J.; Chen, Y. What drives housing markets: Fundamentals or bubbles? J. Real Estate Financ. Econ. 2017, 55, 395–415. [Google Scholar] [CrossRef]
- Zhao, S.X.B.; Zhan, H.; Jiang, Y.; Pan, W. How big is China’s real estate bubble and why hasn’t it burst yet? Land Use Policy 2017, 64, 153–162. [Google Scholar] [CrossRef]
- Wu, J.; Gyourko, J.; Deng, Y. Evaluating the risk of Chinese housing markets: What we know and what we need to know. China Econ. Rev. 2016, 39, 91–114. [Google Scholar] [CrossRef]
- Chowdhury, R.A.; Maclennan, D. Regional house price cycles in the UK, 1978–2012: A Markov switching VAR. J. Eur. Real Estate Res. 2014, 7, 345–366. [Google Scholar] [CrossRef]
- Lee, C.L.; Reed, R. Volatility decomposition of Australian housing prices. J. Hous. Res. 2013, 23, 21–43. [Google Scholar]
- Karolyi, G.A. A Multivariate GARCH Model of international transmissions of stock returns and volatility: The case of the United States and Canada. J. Bus. Econ. Stat. 1995, 13, 11–25. [Google Scholar]
- Bekiros, S.D. Exchange rates and fundamentals: Co-movement, long-run relationships and short-run dynamics. J. Bank. Financ. 2014, 39, 117–134. [Google Scholar] [CrossRef]
- Sogiakas, V.; Karathanassis, G. Informational efficiency and spurious spillover effects between spot and derivatives markets. Glob. Financ. J. 2015, 27, 46–72. [Google Scholar] [CrossRef]
- Jiang, J.; Thomas, T.L.; Tozer, P.R. Policy induced price volatility transmission: Linking the U.S. crude oil, corn and plastics markets. Energy Econ. 2015, 52, 217–227. [Google Scholar] [CrossRef]
- Andreasson, P.; Bekiros, S.; Nguyen, D.K.; Uddin, G.S. Impact of speculation and economic uncertainty on commodity markets. Int. Rev. Financ. Anal. 2016, 43, 115–127. [Google Scholar] [CrossRef]
- Elder, J. An impulse-response function for a vector autoregression with multivariate GARCH-in-mean. Econ. Lett. 2003, 79, 21–26. [Google Scholar] [CrossRef]
- Conrad, C.; Karanasos, M. The impulse response function of the long memory GARCH process. Econ. Lett. 2006, 90, 34–41. [Google Scholar] [CrossRef]
- Hafner, C.M.; Herwartz, H. Volatility impulse responses for multivariate GARCH models: An exchange rate illustration. J. Int. Money Financ. 2006, 25, 719–740. [Google Scholar] [CrossRef]
- Le Pen, Y.; Sévi, B. Volatility transmission and volatility impulse response functions in European electricity forward markets. Energy Econ. 2010, 32, 758–770. [Google Scholar] [CrossRef]
- Tian, Y.; Gallagher, K.P. Housing Price Volatility and the Capital Account in China; GEGI Working Paper; Global Economic Governance Initiative: Boston, MA, USA, 2015. [Google Scholar]
- Weng, Y.; Gong, P. On price co-movement and volatility spillover effects in China’s housing markets. Int. J. Strateg. Prop. Manag. 2017, 21, 240–255. [Google Scholar] [CrossRef]
- Shiller, R.J. Understanding Recent Trends in House Prices and Homeownership. In Housing, Housing Finance and Monetary Policy; Jackson Hole Conference Series; Federal Reserve Bank of Kansas: Kansas City, MO, USA, 2008; pp. 85–123. [Google Scholar]
- McDonald, J.F.; Stokes, H.H. Monetary policy and the housing bubble. J. Real Estate Financ. Econ. 2013, 46, 437–451. [Google Scholar] [CrossRef]
- Liang, Q.; Cao, H. Property prices and bank lending in China. J. Asian Econ. 2007, 18, 63–75. [Google Scholar] [CrossRef]
- Tsai, I.-C. Monetary liquidity and the bubbles in the U.S. housing market. Int. J. Strateg. Prop. Manag. 2015, 19, 1–12. [Google Scholar] [CrossRef]

| Growth Rate | Beijing | Shanghai | Shenzhen | Tianjin | Chongqing | M2 | SR | CPI | Loan |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.0076 | 0.0071 | 0.0074 | 0.0049 | 0.0041 | 0.0126 | −0.0015 | 0.0000 | 0.0138 |
| S.D. | 0.0155 | 0.0145 | 0.0233 | 0.0137 | 0.0184 | 0.0106 | 0.0219 | 0.0061 | 0.0186 |
| Skewness | −1.0443 | −1.1856 | −1.6859 | 0.2647 | −0.0521 | 0.8063 | −3.3386 | −0.4035 | −0.0560 |
| Kurtosis | 14.2592 | 19.9408 | 34.5483 | 9.5731 | 7.4609 | 5.1182 | 26.1266 | 4.7960 | 11.7206 |
| J-B | 1081.8350 | 2414.0530 | 8304.9580 | 358.7539 | 164.2613 | 58.4693 | 4780.2530 | 31.9846 | 627.5103 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| PP | −8.8642 | −12.4901 | −8.9398 | −14.5283 | −9.9034 | −15.5449 | −10.3162 | −13.6745 | −7.4736 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| LB Q(5) | 108.38 | 23.286 | 51.976 | 36.310 | 50.838 | 35.029 | 47.552 | 10.542 | 300.980 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| LB Q(10) | 121.22 | 24.723 | 56.150 | 50.750 | 54.141 | 62.489 | 51.853 | 21.869 | 535.450 |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) | (0.0000) |
| Cites | Beijing | Shanghai | Shenzhen | Tianjin | Chongqing |
|---|---|---|---|---|---|
| 0.4081 *** (4.7301) | 0.2046 ** (2.2789) | 0.0395 (0.2988) | 0.2652 *** (3.3372) | 0.0637 (0.6000) | |
| −0.0646 (−0.7881) | 0.0612 (0.7173) | −0.1590 (−1.2647) | 0.0915 (1.2125) | 0.1028 (1.0189) | |
| 0.1204 (2.2450) | −0.0534 (−0.9561) | 0.4425 *** (5.3802) | −0.0133 (−0.2685) | −0.0383 (−0.5795) | |
| −0.1103 (−1.3492) | 0.0615 (0.7219) | 0.1686 (1.3447) | −0.1263 (−1.6760) | 0.2783 *** (2.7648) | |
| 0.0775 (1.3521) | 0.0499 (0.8366) | −0.2006 ** (−2.2816) | 0.1566 *** (2.9638) | 0.3127 *** (4.4297) | |
| 0.0043 *** (3.8265) | 0.0049 *** (4.2222) | 0.0050 ** (2.9158) | 0.0023 (2.2216) | 0.0005 (0.3531) | |
| Log likelihood | 2852.157 | ||||
| Akaike information criterion | −28.6513 | ||||
| Schwarz criterion | −28.1514 | ||||
| Variable: Variable: | Beijing-Shanghai | Beijing-Shenzhen | Beijing-Tianjin | Beijing-Chongqing | Shanghai-Shenzhen | Shanghai-Tianjin | Shanghai-Chongqing | Shenzhen-Tianjin | Shenzhen-Chongqing | Tianjin-Chongqing |
|---|---|---|---|---|---|---|---|---|---|---|
| Dependent Variable: | ||||||||||
| 0.4800 *** (6.6076) | 0.3956 *** (5.1972) | 0.5082 *** (7.2067) | 0.4412 *** (6.5213) | 0.1512 (1.8604) | 0.1249 (1.6467) | 0.1340 (1.8443) | 0.3956 *** (5.6230) | 0.4487 *** (6.9676) | 0.0239 (0.3518) | |
| −0.0211 (−0.2721) | 0.0881 (1.7419) | −0.0961 (−1.2050) | 0.0680 (1.1931) | 0.0153 (0.3022) | 0.1100 (1.3694) | 0.0927 (1.6190) | 0.1336 (1.1161) | −0.2097 *** (−2.5706) | 0.2426 *** (4.7880) | |
| 0.0041 *** (3.6396) | 0.0039 *** (3.6289) | 0.0042 *** (3.8323) | 0.0040 *** (3.6450) | 0.0058 *** (5.0923) | 0.0056 *** (4.8504) | 0.0057 *** (4.9963) | 0.0039 *** (2.3877) | 0.0050 *** (3.1589) | 0.0038 *** (3.7649) | |
| Dependent Variable: | ||||||||||
| 0.2080 *** (2.7904) | −0.0571 (−0.4837) | 0.3645 *** (5.5396) | 0.1906 ** (2.2685) | −0.1716 (−1.4403) | 0.2393 *** (3.3779) | 0.1991 ** (2.3024) | 0.1055 *** (2.3345) | 0.0772 (1.4574) | 0.3214 *** (3.6851) | |
| 0.0546 (0.6851) | 0.4479 *** (5.7044) | −0.1305 (−1.7537) | 0.3065 *** (4.3332) | 0.4789 *** (6.4629) | −0.0404 (−0.5386) | 0.3252 *** (4.7738) | −0.0174 (−0.2266) | 0.3511 *** (5.2316) | 0.3428 *** (5.2818) | |
| 0.0051 *** (4.3663) | 0.0046 *** (2.7227) | 0.0028 *** (2.6783) | 0.0014 (1.0035) | 0.0051 *** (3.0593) | 0.0034 *** (3.1386) | 0.0013 (0.9738) | 0.0042 *** (3.9959) | 0.0021 (1.5733) | 0.0011 (0.8420) | |
| Log likelihood | 1148.071 | 1081.584 | 1158.687 | 1097.818 | 1070.519 | 1142.639 | 1086.401 | 1064.098 | 1009.242 | 1105.320 |
| A. I. C. | −11.5946 | −10.9196 | −11.7024 | −11.0845 | −10.8073 | −11.5395 | −10.9685 | −10.7421 | −10.1852 | −11.1606 |
| S. C. | −11.4946 | −10.8196 | −11.6024 | −10.9844 | −10.7073 | −11.4395 | −10.8686 | −10.6421 | −10.0852 | −11.0606 |
| : : | Beijing-Shanghai | Beijing-Shenzhen | Beijing-Tianjin | Beijing-Chongqing | Shanghai-Shenzhen |
|---|---|---|---|---|---|
| Mean model: | |||||
| 0.3088 *** | 0.5207 *** | 0.6504 *** | 0.5267 *** | 0.4577 *** | |
| 0.2154 *** | 0.2066 ** | −0.0285 | 0.0897 | −0.0037 | |
| 0.0110 | 0.0835 | 0.2417 ** | 0.3049 *** | 0.2121 *** | |
| Mean model: | |||||
| 0.0663 | −0.0864 | 0.2709 *** | 0.1344 ** | −0.0342 | |
| 0.2737 *** | 0.5731 *** | 0.1911 ** | 0.4838 *** | 0.5195 *** | |
| 0.5066 *** | 0.2799 *** | 0.1159 | 0.0589 | 0.2406 *** | |
| 1.5777 *** | −0.9708 *** | 0.3064 *** | 0.2105 | 0.8481 *** | |
| 0.5988 *** | −2.0079 *** | −0.0505 | −0.0839 | 0.5352 *** | |
| −0.6423 *** | 0.9186 *** | 0.1241 | 0.1497 | 0.5491 *** | |
| −0.6418 *** | 1.6348 *** | 0.5332 *** | 0.5469 *** | 2.0986 *** | |
| −0.2520 *** | −0.4064 *** | 0.0753 | 0.1829 | 0.7394 *** | |
| 0.0790 | −0.2831 ** | −0.3175 | −0.3744 *** | −0.2217 | |
| −0.1327 | 0.0138 | −0.2113 | −0.0704 | −0.3071 *** | |
| −0.1861 | 0.2959 *** | 0.7664 *** | 0.8486 *** | 0.0843 | |
| 0.3356 ** | 0.6891 *** | 1.2492 *** | 1.2649 *** | 0.4490 ** | |
| 0.3277 | −0.4475 *** | 0.5343 *** | 0.4463 *** | 0.4556 ** | |
| 1.1160 *** | 0.0000 | 0.2745 *** | 0.0000 | −0.3513 | |
| Log Likelihood | −635.5467 | −672.5319 | −613.9682 | −655.0680 | −680.1842 |
| Beijing- | Beijing- | Beijing- | Beijing- | |
|---|---|---|---|---|
| Mean model: | ||||
| 0.6025 *** | 0.5677 *** | 0.5490 *** | 0.4538 *** | |
| 0.0774 | 0.0279 | 0.3804 ** | 0.0348 | |
| 0.1408 | 0.2797 ** | 0.2001 *** | 0.3159 *** | |
| Mean model: | ||||
| −0.0475 | 0.2127 ** | 0.0666 ** | −0.0020 | |
| −0.1707 ** | 0.2779 | 0.1051 | 0.7813 *** | |
| 1.5084 *** | −0.2055 | −0.1265 *** | 0.2437 *** | |
| 0.2776 *** | 0.2920 ** | 0.6404 *** | −0.2470 ** | |
| −0.0849 | 0.1232 | 0.0400 | 0.0178 | |
| 0.0381 | 0.0020 | 1.5065 *** | 0.0419 | |
| 0.4402 *** | 0.6955 *** | 0.0941 | 1.0802 *** | |
| 0.1959 | −0.1339 | −0.0515 | 0.3615 | |
| 0.2463 | −0.3369 | 0.0475 | 0.5652 *** | |
| 0.1161 | −0.0187 | 0.8198 *** | −0.0093 | |
| 0.7587 *** | 0.4822 *** | −0.7586 *** | 0.0092 | |
| 1.2640 *** | 1.2899 *** | 0.6123 *** | 1.2394 *** | |
| −0.1328 | 0.0683 | 0.392 *** | −0.1307 | |
| 0.3407 | 1.1827 *** | 0.0001 | 0.0000 | |
| Log Likelihood | −617.6144 | −727.1466 | −499.0443 | −649.6231 |
| Shanghai- | Shanghai- | Shanghai- | Shanghai- | |
|---|---|---|---|---|
| Mean model: | ||||
| 0.5452 *** | 0.1592 *** | 0.2993 *** | 0.1406 ** | |
| 0.0206 | −0.0106 | −0.206 | 0.1079 | |
| 0.3963 *** | 0.7144 *** | 0.4520 *** | 0.5166 *** | |
| Mean model: | ||||
| −0.0052 | 0.0808 | 0.0642 ** | −0.0339 | |
| −0.1585 ** | 0.6596 *** | 0.0069 | 0.8278 *** | |
| 1.4253 *** | −0.0864 | −0.0377 | 0.2090 *** | |
| 1.1006 *** | 0.1275 | 0.3607 *** | −0.0507 | |
| −0.0698 | −1.0544 *** | 0.0472 | −0.4245 *** | |
| 0.2225 ** | 0.1065 | −2.0562 *** | −0.0572 | |
| 0.4075 *** | 1.1876 *** | 0.1462 | 1.1490 *** | |
| 0.1017 | −0.5294 ** | −0.2327 | 0.0039 | |
| −0.0572 | −0.0295 | −0.0991 | −0.0338 | |
| 0.071 | 0.0538 | −0.3916 | 0.0773 | |
| −0.8048 *** | 0.3836 *** | 0.7371 *** | 0.0170 | |
| 0.8696 *** | 1.1839 *** | 0.5833 *** | 1.4092 *** | |
| −0.0455 | 0.0369 | 0.3355 | 0.1372 | |
| 0.4573 *** | 0 | 0.1791 | −0.6115 *** | |
| Log Likelihood | −610.0859 | −688.4462 | −487.3369 | −646.4284 |
| Shenzhen- | Shenzhen- | Shenzhen- | Shenzhen- | |
|---|---|---|---|---|
| Mean model: | ||||
| 0.4951 *** | 0.6939 *** | 0.4958 *** | 0.2986 *** | |
| −0.1392 *** | −0.0067 | −0.2706 ** | −0.2638 *** | |
| 0.4096 *** | 0.2479 *** | 0.2420 *** | 0.9387 *** | |
| Mean model: | ||||
| 0.0315 | 0.0650 | 0.0371 ** | 0.0278 | |
| −0.1063 | 0.2469 *** | 0.0428 | 0.6578 *** | |
| 1.3513 *** | 0.0038 | −0.0221 | 0.2702 *** | |
| 2.2748 *** | 2.2638 *** | 1.3586 *** | 1.6001 *** | |
| −0.0886 | 0.0997 | 0.0827 ** | −0.2190 *** | |
| −0.2766 *** | 0.1116 ** | −1.6219 *** | −0.3830 *** | |
| 0.1819 ** | 0.7157 *** | 0.0602 | 1.1610 *** | |
| −0.0050 | 0.0911 | −0.0175 | −0.1515 | |
| 0.0346 | −0.3333 *** | −0.0589 ** | −0.1825 *** | |
| −0.1453 | 0.0520 | 0.3036 | 0.0338 | |
| 0.9353 *** | 0.6368 *** | 0.9571 *** | −0.2530 | |
| 0.4986 *** | 0.6926 *** | 0.6556 *** | 1.0392 *** | |
| 0.3073 ** | 0.1434 | −0.1454 | 0.2695 ** | |
| 0.0000 | 0.6859 *** | 0.0000 | 0.6501 *** | |
| Log Likelihood | −663.0777 | −768.3753 | −526.4602 | −702.1470 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, I.-C.; Chiang, S.-H. Risk Transfer among Housing Markets in Major Cities in China. Sustainability 2018, 10, 2386. https://doi.org/10.3390/su10072386
Tsai I-C, Chiang S-H. Risk Transfer among Housing Markets in Major Cities in China. Sustainability. 2018; 10(7):2386. https://doi.org/10.3390/su10072386
Chicago/Turabian StyleTsai, I-Chun, and Shu-Hen Chiang. 2018. "Risk Transfer among Housing Markets in Major Cities in China" Sustainability 10, no. 7: 2386. https://doi.org/10.3390/su10072386
APA StyleTsai, I.-C., & Chiang, S.-H. (2018). Risk Transfer among Housing Markets in Major Cities in China. Sustainability, 10(7), 2386. https://doi.org/10.3390/su10072386





