1. Introduction
Modern agriculture has given priority to chemical inputs in pest control and soil fertility management. However, particularly in monocultures and in landscapes with limited shares of natural vegetation, farmers still have problems with pest control and frequently report/observe declining soil fertility, as well as increasing pest problems. Since pests and declining fertility (i.e., annihilation of soil structures and micro-biological activities) can strongly decrease yields, nature-based methods have regained some attraction (at least in academics: Sandu et al. [
1]). For practical farming, increasing unit costs of production will most likely prevail in the future (see the danger of myopic behaviour: Pemsl, et al. [
2]) if ecosystem services diminish. Many public players, as sustainability advocates, request the implementation of ecologically-sound land use practices [
3]. Problems with sustainable agriculture haven been discussed thoroughly in the past [
4] and crop rotation is one important element. In fact, problems have emerged in agriculture in the context of soil fertility going beyond minerals or chemical pest control and resistance of species to pesticides, for example, black grass. Additionally, the concern for decreasing biodiversity and conservation is now a request for measures directed at the reduction of negative externalities. However, these problems are not solely limited to farming; ecologically-oriented researchers and the society, itself, see major problems of biodiversity loss from converting traditional cultural landscapes into production steppes [
5,
6]. Some authors (Fiedler et al. [
7] and Lindborg et al. [
8]) think that if the demand for nature conservation in cultural landscapes is not given priority (which is actually an environmental service, ecosystem service, of multi-functional agriculture for the society) problems of sustainability in the landscape will persist. This seems to be exogenous to the farming sector. However, again, the sector itself faces frequent problems of fertility [
9,
10]. Thus, we have an endogeneity problem. To a growing extent, farmers face problems with diminishing ecosystem services (fertility) even as a private good (natural resources and input) which reduces individual revenues, (i.e., yields, outputs, etc.) increases costs (inputs, labour, etc.), and reduces income [
11].
In this context two strains of thought emerge: (1) What are the real costs of alternatives (natural pest control, rotation, mixed farming, etc.), i.e., vs. chemical control (more external input, more labour and machinery, etc.)? For example, what is the scope of fertility control by rotation and, hence, caring for nature? This issue is exaggerated by increasing prices for chemicals. In Germany, for instance, for 30 years (until 2009) the costs of combating pests and maintaining soil fertility with chemical substances were relatively stable, but then (since 2010) it seems that costs are picking up [
12]. This is a trend and, as part of global energy price increases in the last decade (peaking in 2008 and, again, in 2018), we will most likely foresee a new situation of high input costs again. Then, (2) due to processes like the appearance of resistance against chemicals, the effectiveness of chemical substances seems to decline [
13] and costs increase, as more substances are needed. This trend will change the competitiveness of chemical vs. natural methods. Real costs are changing absolutely and relatively and ecosystem services and their returns may even become a vision for farmers. A crucial thing is also labour cost. Since external costs are important, a question is to what extend do ecosystem services change labour requirements? For such questions we need to address rotations.
However, directed towards monocultures and uniform landscapes, those appearances are driven by economies of scale and concerns for large farms. At least currently, specialization drive and use of chemicals (as strategy) are pertinent. This is grounded in the farmers’ knowledge system (as an example see typical reports like those of USDA: [
14]); farmers seemed to work with a perfect chemical system. As a majority, they are no longer willing to maintain land productivity through “natural” measures, such as rotations. They, rather, applied more and more pesticides, artificial fertilizer, and other technical measures to keep their land “fertile”. Though some scientists (Regev et al. [
15]) spoke very early of problems, including the public good character of pest problems, as well as the consequences of myopic behaviour, not much work is done concerning the long-term cost comparison between traditional and modern modes of farming. Additionally, is there really an alternative? As suggested by Schönhard et al. [
16] one way to maintain fertility and combat pests is to deal with crop rotation extensively from the point of view of agronomy and economy. They showed how representative farms can make choices on existing and recommended patterns for different rotations. Note that choices on rotation types were normally embedded in cultural traditions and not real choices, as there was an understanding in agronomy of typical (standardized) locally-confined rotations, though these rotations followed well-explained procedures [
17,
18,
19]. Rotation choices were part of farm routines followed as collective knowledge and action. They were even partly enforced by local authorities. However, due to modern inputs, complex rotations seem to become obsolete because rationality changed. In particular, as a result of needs to economize on profitable crops, less profitable crops were dropped in rotations and fields increased in size because of limited recognition of essentials in rotations (ecosystem services from a mosaic of small fields; see below). Nowadays large machinery drives choices, farms are maximizing gross margins with a preference for high-yielding crops, well-priced crops, etc. In contrast, from an ecological point, it seems necessary and sound to integrate as many crops in rotations as feasible and follow a landscape-oriented analysis [
20] for the benefits from rotation (see below).
However, today farmers will tell ecologists they make less money with ecologically-sound rotations. There is a tendency to reduce the complexity of rotations and even to introduce mono-cropping from a very narrow economic point of view of survival. Though it is argued by simulations that farmers could do better by including diversity through rotations and mixed cropping, they refuse. This clash of “culture” has strong implications on ecology and also the appearance of landscapes which could provide ecosystem services. Landscapes become uniform and there is a vicious cycle. In fertile areas, for example, pasture/meadow land has been strongly reduced, though it was part of traditional rotations. As a consequence, some organisms (including. micro-organisms in the soils) are no longer present/abundant and farmers voice that they cannot rely on ecosystem services. In summary, modern farms are composed of large fields and use few, highly profitable crops (wheat, rape seed, etc.) and seemingly do not care for rotation, unless it is incentivised externally (for example, payments for “greening”, like in the EU).
Currently, for most farmers it does not seem to pay off to care for long-lasting soil fertility and natural pest control through crop rotation and landscape management. Thus, why do they act in the current way? Knowing that crop rotation and conservation have a considerable impact on soil and yields [
21], there might be a (“wrong”) reasoning for saying that planning and simulation have not yet reached farmers. Rather, due to the overwhelming pressure of economies of scale and short-term thinking, they prefer to strongly discount benefits of rotation. The (ir)-rationality of such behaviour seems to be evident, perhaps from the perspective of ecologists. However, farmers also expect that the pesticide industry offers new substances to deal with pests occurring as a consequence of mono-cropping. They also seem to have lost experiences and knowledge on the positive impacts of diversified crop rotations. At the same time farmers face growing problems with resistances, new pests, and declining ecosystem services, like reduced pollination, ground water formation, natural soil fertility, etc. Note that these services are traditionally based on landscape functions (foremost, diversity). A major problem in this respect is that the modelling and programming of rotations is quite complex and the seemingly very profound academic programming tools are not adapted. It is here where we suggest endeavouring into new approaches.
We will start by showing the potential for the application of the state-and-transition concept and corresponding transition matrix to rotation modelling at the farm level and then make some remarks for landscape inclusion and extension. It is the objective of this paper to show how it may be possible to increase the appreciation of advantages of long-term rotations through changed modelling and programming tools. By suggesting advanced modelling concepts of rotations which are in line with the capacity to handle them at the farm level, we think one can increase awareness of long-term effects of declining natural fertility and conduct better cost-benefit analyses for long-term commitments to rotations. These have to be locally appropriate and adapted and should not reduce income significantly. An essential question is how a potential drop in fertility can be linked to economic planning of crops, space, and rotation? For a researcher in agronomy the interesting issue is: how do deficits in farm planning methods (programming) determine behaviour? Then, how can things change? Is there scope for counselling on methods and recommendations, etc? We will show that there are deficits in the current planning methods and suggest a new concept (method) for temporal optimization of land use at the farm and landscape levels. This concept includes a transition matrix depicting degradation (or upgrading) of land. It is based on pre-fabricated rotations as references, but offers deliberate choices at the individual and landscape level.
In this context our paper will address the question of how modelling as an instrument can be used in the assessment of long-term effects of rotations (soil fertility and ecosystem services). The aim is that concepts become more appropriate for programming and portraying short- and long-term effects of crop use. However, it is not the aim to solve the “fundamental” conflict between the goals of ecology and economy; rather, a conceptual framework within the farming sphere is presented which could make farming more ecologically oriented. A mathematical tool is presented which helps to include thresholds, dynamics, and spatial aspects fundamental for rotation design. Assessments should work in a time frame of dynamic programming which is pre-defined. Hereby we want to address sustainability, spatial appearance, and ecosystem services from the farmers’ perspective, but also the landscape view. A further aim is to present a dynamic optimization approach, including rotation and spatial design of landscapes which is specifically oriented towards field sizes, field edges, and needs to accommodate low-yielding crops. The paper is organized along a problem statement, a review on the state of the art, methodological problems and solutions, and it gives an outline of work to be done.
2. State of the Art
The issue of programming optimal land use as an instrument for crop rotation modelling, specifically designed for farmers or, by extension, working with farmers, has not been very intensively studied over the last decades. Yet El-Nazer and McCarl [
22] worked with yield regressions which were implemented in linear programming LPs. Detlefsen [
23] suggests working with network analysis and Klein et al. [
24] studied crop successions as constraints. However, their approach is already very complex. They used an algorithm which, due to its complexity, its data requirement, and software problems, will most likely not be used by farmers. Recently, other complex models have been developed in operation research by Alfandari [
25], but rotations are only shallowly tackled.
For example, rotation options are given in decision trees (on the one hand) which looks simple, but becomes very complex (on the other hand) because we deal with many years of foresight. Additionally, in contrast to theoretical insight, empirical research seems to confirm that narrow rotations suit current aims of maximizing profits best; even though no long-term concerns exist. Mostly, guided by the programming of activities with purchased inputs, farmers believe that new pesticide types will help to combat pests in the future. By chemical inputs, zero tillage, etc., benefits of rotations are qualified as marginal and should be simply based on empirical findings [
26]. Thus, it is plausible that, in practice, farmers have departed from complex rotations.
As another method, threshold analysis was used by Lundkvist [
27] as a rule of thumb. Weed control should no longer be based on successions of crops, but on the observation of thresholds. In line with this thinking, some decision support models are based on the economics of weed depression [
28] through short-term reaction and not rotation. No wonder that rotation is outdated; yet, in this research, ecosystem service functions may not be really reflected, appreciated, and integrated. However, the economics of a full integration of weed depression is limited. It has created a need to model long-term effects using bio-economic approaches.
Another integration of crop models and economic models in a bio-economic approach for practical applications has recently been worked out by Cong et al. [
29]. It works on soil organic matter as natural capital. In a further recent article an agricultural economist used programming [
30] as a tool for dynamic optimization of crop mixes by indexed soil fertility. Again, in a simplified dynamic on the basis of the dynamics of a single variable to describe ecological effects [
31], we get a future positive response to diverse rotations. Ecological (soil fertility) effects are mostly working on carbon in soil. However, there is more behind rotation: ecosystem health. The issue is: is this farm or landscape related?
In order to address the higher degree of complexity in dynamic optimization models in a frame of landscape and ecosystem services, the many needed aspects have been included by Cong et al. [
32]. The bottleneck is again that “too” many differential equations are needed. Further note that researchers who have worked on an overview and review of existing models [
33] showed deficits in capacity and practical reasoning to apply rotation. However, this has increased the esteem for methodological requests and farmers (as applicants) rarely will be capable of understanding and using the complex models. There is a need for compromise in modelling which enables more practical application and which, by providing a comprehensive outline on ecological processes, is capable to valuing the long-term benefits of rotation.
4. Transition Matrices in Eco-System Dynamics and Links to Farm Productivity
We suggest a new measure to detect a potential decline in soil fertility due to “too” narrow crop rotations (in extreme mono-cropping) based on a transition matrix approach [
34]. The aim of this paper is to show how the transition matrix (approach) can be used in a modelling of rotation choice. Achievable results shall then fit into a dialogue with practical applications. Yet it is not the intention to substitute crop science-based decisions; rather, the emphasis is on modelling and the depiction of economic consequences of different rotations with regards to long-term effects. The transition matrix approach can be embedded in a conceptual framework which has been worked out by ecologists under the topic “state-and-transition” (for recent applications: Van Dyke [
35,
36]). A transition matrix enables research to include processes and thresholds. For example, an agronomist can set up a temporal link between yield potentials of today and yields in the future (it is an extension of forecasting bringing in ecological knowledge: see Christensen et al. [
37]). It should be extended towards many potential crops (crop mix and rotation, as ordered mix over time) and can be based on a joint ecological and agronomical assessment of the fertility of land. It applies discrete states on the quality of the ecosystem (see below) and the process of transgression is at the level of probability. The potential cropping pattern of each period (and as an anticipated process for future yields) is dependent on an endogenous cropping pattern decision (built on an algorithm) that is implemented as a recursive planning tool. States are not used as in an aggregate single variable version but, rather, a Markov type of approach [
38] is postulated. Then, using a transition matrix, we can establish a dynamic programming approach in bio-economic modelling being closely linked to ecological arguing and modelling of system change. It is a type of recursive modelling and planning [
39] which uses forecasting and decisions in models simultaneously.
Note that Markov chains are categorical; for instance we can take the states. Then, by using probabilities to switch the states in the model between categories, the Markov chain provides a structural change outline or filter. Here, for example, the ecosystem states and fertility are discrete. States are frequently used, for instance, in sector analysis; they are dynamic units. Recently, the analysis has been extended to filtering methods which enable learning while time passes (see by Dean et al. [
40]).
To explain further why “Markov” is suggested, why this needs attention, and why it fits into a conceptual framework of transition-and-state which gives more room to ecologically-oriented thinking in agricultural economics, we refer to work on state-and-transition modelling, for example, in pasture management [
41]. For instance, if the rotation choice puts too much emphasis on single crops, there is a problem already in the depiction of the potential decline in yields of other crops for the next years. Rooted in the interaction of crops, soil, micro-organism, etc., soil and ecosystems, in general, are entities which can best be explained by thresholds, multiple interactions, etc. (see also the chapter on empirical foundations below).
Thus, what is the response in agricultural economics? We think “degradation” has an overall effect for many other crops which can be depicted by a system approach referring to a transition matrix. In ecological economics this is the “capture by a state” description. In our case we refer to a measurement of degradation vs. fertility as a share of land in different states. Then, for practical reasons, the inclusion of the matrix enables the delineation of negative externalities (degradation) in programming techniques using software like GAMS (General Algrebraic Modelling System, GAMS Corporation, Washington, USA; for detail see Domptail et al. [
41].) GAMS enables dynamic modelling by taking discrete, annual steps and transferring results from one period to the next as an element of endogenous optimization.
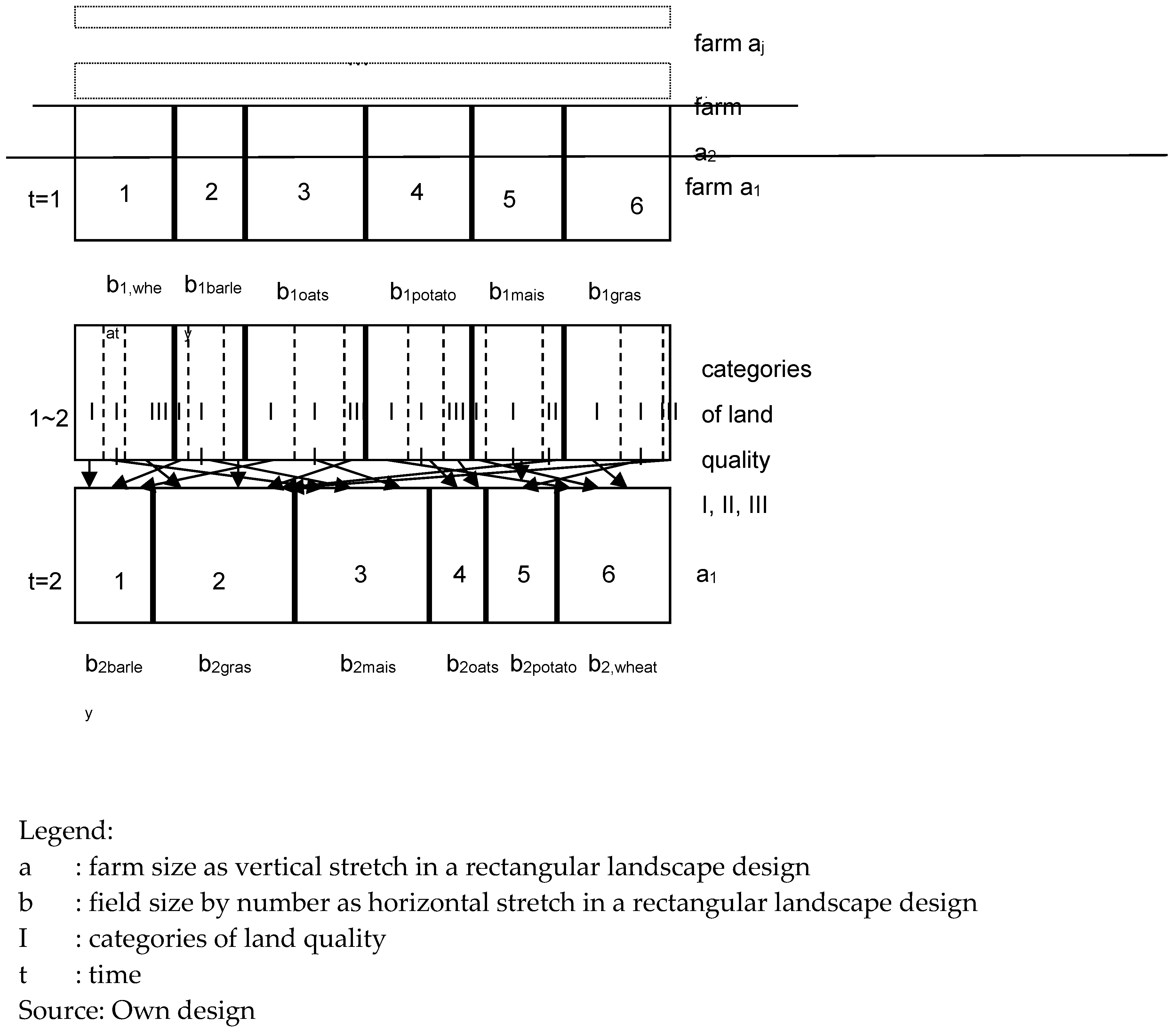
In
Figure 1 the main principle is outlined. The modelling works with “planned” areas for crops at time t which are given as a percentage of farm area (spatial aspects will be tackled soon) and the impact on states at t + 1. Hereby categories of land quality are distinguished and they deliver constraints to farming in future periods. This means that land for farming is split into different fertility categories appreciable jointly by farmers and ecologists. Farmers face quality “states” of their land (as a mix) being the consequence of farming in the past and future relies on the past. They can “plan” the future of their land through programming within the computer model. “States” are characterized by discrete fertility categories, for instance “very fertile, …, fertile, poor, …, very poor”. In each category yields are different and the assumption is that farmers’ knowledge is based on assigning quality categories by referring to potential yields. These yields should reflect the natural fertility and not that which is coming from artificial fertilizer. By assigning the land quality categories one can simplify matters. Then, the focus is on land-related activities changing land composition and quality. In
Figure 1 we depict a situation in which past land use activities, given as a percentage of land use, can create improved or degraded options in the future. Planned areas in period t + 1 must fit into the inheritance categories of land quality.
On the left-hand side we have land in different quality categories which are the result of cropping patterns in the previous period. Yields and gross margins of land quality categories are varying systematically. This does not mean that the observed yields are declining if monocultures prevail, only natural fertility (yields) diminishes. The analysis is on the potential natural fertility (yields); this means that, eventually, more fertilizer is used and the underlying natural fertility declines. Alternative management options can be assigned through programming; in this case as discrete choices with separate gross margins (such as wheat, for example with 30, 40, or 50 dt/ha, etc.). If, for example, more and more land is in a low-quality category, farmers face limited choices in the natural fertility of land for the future and have to use more chemicals to maintain yields. Consequently, increasing unit costs prevail, or yields may even decline, reducing revenue, which finally results in a decrease of gross margins.
A corresponding choice for production alternatives is given in
Figure 2 for clarification. In this structure the highest yields are only reached from land in category 1. In category 2 we see lower “natural” yields (meaning more inputs are needed) and choices for crops within this category are limited. Technically, in GAMS the choices in period t are converted into constraints in t + 1. Note, on the right side, choice potentials are collected from different crops and represent the fertility composition at farm and landscape level. A necessity is to change practices (conceptually, rotations), eventually also for advancements of better quality in the future. For farmers, if they want less land in poor categories and are willing to transfer land in the category “best”, this is only feasible if “good” rotation choice is practiced. Rotation choice is part of a set assignment in GAMS. It makes “good” land available. Apparently, the analysis can be made more complex if we include a possibility to substitute natural fertility and the use of chemicals. Hence, rotation choices are imbedded in farm practice and activities (see programming in computers of linear systems: LP). Farmers are offered alternatives which fit into their management, also including, for example, the use of pesticides.
The matrix depiction in
Figure 1 and
Figure 2 is a substitute for differential equations in dynamic resource economics. It works with land classification (discrete one) which is perceivable by farmers and enables communication on states. The matrix anticipates local knowledge on transitions or, alternatively, it can be derived from ecological-economic modelling [
41]. In a similar context of pasture management [
41] work showed that, applying an ecological modelling to derive a transition matrix, is a step to formulate a holistic rangeland transition dependent on farming intensity, choice of activities, and response to degradation. In fact a similarity is given of arable farming and finding the matrix is also feasible. Using minimal maths and simple calculi, or working with tables, the matrix approach for management of degradation can be transferred to mixed farming on arable land and inclusion of pasture land.
As a follow up, states can be differentiated along productivity, and productivity of states give options for different cropping activities, apparently with different yields in the future! We must formulate land use in different categories being suitable for different crops. For example, if a farm is almost completely degraded, i.e., land is in the worst category (perhaps V), on this land a farmer could only produce rye, yet at a reasonable gross margin. Imagine, rye will still offer a reasonable yield, even if land is “exhausted”; i.e., wheat will yield comparatively poorly (soil fertility and pest pressure can be linked if yields are given in a category to measure discrete states of natural yields). Then the farmer has the choice of rotation to upgrade. Usually it is fallowing, or clover, grassland, etc., which may contribute to an upgrading and reaching of yield goals in grade IV. Apparently it can last several years to get back to good yields, so probabilities are consecutive. Vice versa, if there is a threat of dropping down in yields (actual yield category), for example, after several years of wheat mono-cropping, only the adoption of a “better” rotation helps. The information on the switches is displayed in the transition matrix linking states and land occupation. The information comes from agro-ecology and experts, or also from models [
41]. However, that would merely be a description of an eventual causal (though quantifiable) process of degradation. To use the state-and transition concept and the look at the scope for improvements, as well as to see programming of rotation as an aim, the causal analysis has to be transferred into a normative approach.
Figure 2 expresses the second feature of a transition matrix in terms of specifying the land classification categories, as well as formulating when a “constraint” is to be met. In terms of an endogenous, recursive optimization for period t + 1 the land shares in the given categories form the scope of using different crops most productively.
The tool is the transition matrix T with probabilities π and the request of the vector q for land quality; q is then the result of a combination of activities c and quality achievements are built at the level of probabilities: T c ≤ q. Now, in
Figure 2, as compared to
Figure 1, we differentiated the land categories along the potential to grow crops with different yields.
Crops with different yields, as suggested in
Figure 2 are the basic categories in land use and, hence, also for programming production activities we can use these categories. Though, now T is a tool to achieve a combination of crops which is conducive for maintaining the quality of land, in the context of consecutive and recursive modelling it makes the choice of one endogenous period to the next. Imagine that programming starts from the end and runs backward. This apparently implies that the final state (perhaps after 60 years of simulation) has to be given. Again this is normative and there must be reasoning for a mix of states.
5. Field Location and Allocation in Dynamic Programming of Rotations
As a next step in modelling a cluster of fields with different states of fertility must be outlined. In
Figure 3 the computerized choice for land use is depicted. Fields are farm and landscape structures conducive to rotations. Farm land is always spatial. For modelling we have to stylize/simplify the reality. In modelling a crucial aspect is to initialize the current fields, but also to give flexibility. A compromise is stylization (example: a polder). We assume a rectangular form of fields and size: a
i∙b
j (
Figure 3). Under such conditions land area and size are portrayed by b
j (fields and note: a
i is fixed). Fields are programmed by the distance of b
j as stretch (a
i is constant).
The figure depicts two time periods, t = 1 and t = 2, of optimized land use out of a range of several periods (dynamic optimization. The interim period 1–2 is artificial and the computer uses it for a calculation of a consolidated plan in t = 2. It is composed of several options in quality categories (for illustration: I, II, and III) which give the final status after the weighted average calculation. Weights are given by the size of I, II, and III, which is the forwarded “prediction” in the computer program. A farm is composed of fields and their size or can be expressed as a cluster of fields. A field has a certain total length Σ b
j = B. In this distance we have to fit parcels (plots, fields) as activities in rotation, which means a constraint in programming prevails for land. The consecutive step is assigning activities in land use (cropping pattern) for the future. A way of doing so is introducing different categories of crops, yields, and types of crop-yield combinations as part of a rotation (see above). In
Figure 3 we illustrate three different quality categories (I, II, III), but it can be more.
Additionally, in the figure we illustrate that the allocation can change from period t to t + 1. As preferred crops, like wheat, generally require “best” land, the program would sequentially allocate land to, for example, wheat (land in “I”: best) first. The program will do this through the optimization of gross margins. Here, on paper, it is for demonstration purposes only. However, area is numerically given by the size of the field. After the transition between periods, then, programming will reproduce a distribution of land quality as a constraint. In the program, model activities (as the allocation of land to crops) for each year are chosen according to long-term profits (discounted profits). We work with dynamic programming and discounted flows of gross margins are the objective. Additionally investments in machines and economies of scale can be tested. Prevailing, for instance, over a horizon of 30 years or more, the land allocation in each year is optimized recursively.
In the just-given conceptual outline to formulate a programming model, we have to categorize bj further as bj,q,t (crop, quality, and time). As an augmented choice on crops, quality categories, “q”, become involved, which represent different classes of “natural” productivity of the land in time t and t + 1; hence, natural yield effects are captured. Note: high natural yields being ecosystem services save costs. For example, wheat yields can be as said: “best, good, medium, poor, and low”. In terms of activities wheat production is categorized in fixed yields and the underlying practices are discretely formulated. The advantage is that farm planning can be associated with categories and gross margins simultaneously, requiring minimal knowledge on system development and degradation. Furthermore, categories which require different technologies to answer degradation must be separated, which is regularly done in programming. With deteriorated yields farmers have to use more inputs (combatting pests and recovering soil nutrients).
The above type of modelling can now be combined with different technology coefficients in programming to depict the quality category change in terms of new options. Quality categories become temporal constraints (see above). Categories are plannable and foreseeable for farmers; at least in the computerized forecast future categorical states of fertility provide information on scopes to conserve fertility. As a consequence the availability of land in different quality categories changes (as planned) over time. Vice versa, by actions in the past, farmers can improve land through rotation choice. Temporal constraints show the availability of good land in t+… and in different productivity categories as subject to the choice of a specific rotation (see below). Nevertheless, in between the whole period there is an option to also change the “pre-fabricated” rotation. The model is flexible in regards to strategies. Note, categories (sizes in b) indicate different declines in productivity, need of inputs, and come up with different gross margins. For instance, eventually in category III wheat will require a great deal of inputs. Without inputs it would perform worse than rye. As mentioned above, being in category V, wheat would not perform in terms of yields at all and rye would be the “only” choice if previous degradation has resulted in poor land quality. Thus, it was a matter of “choice” (see below for the “choice of rotation” and depiction of alternatives at the meta-level).
6. Anticipation of Results in Rotation as a Design Problem for Agronomists
To be able to introduce knowledge on potential rotations into the previously-explained modelling concept of applying a transition matrix (soil quality, spatial, time, etc.; i.e., to specify alternatives in rotation) a foundation of alternatives as discrete choices is required. Two aspects prevail: (1) agronomists’ concepts on “designing” rotation alternatives; and (2) the programming techniques (modes). As (1) crops can be distinguished according to their stand in a rotation (in
Figure 4 a complex rotation is given first, a simplex, second, and, finally, a complex rotation of, eventually, 12 years). A rotation might start with wheat after wheat “WW” or wheat after rape “RW”. Technically, it would mean adding a fourth dimension “r” in b
c,j,q,r,t, to land use activities which characterizes the type of rotation that is an upper layer choice beyond the crop. Sequences in rotations are fixed by experts (knowledge of scientists). Theoretically, the production for crop c, at a plot j (“size of b”), with the quality of land q and rotation r can now be identified by the five dimensions: crop, location (field), quality, rotation and time (eventually as the farm number may add, see below for landscape). Normally, linear programming has no spatially-oriented algorithm to assign crops to fields, but by numbering fields we can construct a substitute for field j. As a ranking, like in time and in space, in GAMS, a ranked numbering of fields is possible. In programming by a selection process for the most profitable alternatives we use all the dimensions (technically in GAMS). We will find numerical solutions and this means that many b’s become zeros, though they are possible (note: unused alternatives are automatically set to zero by the computer and program choices are limited). A selection of b means that only one quality, rotation, and location opportunity becomes selected, for instance, by an if-else statement. This is possible through deliberate programming and reflects actual choices of farms.
Our compromise is that information from crop science is further used to specify typical rotation choices (alternatives for pre-selection) and the computer looks at the sequential cost-benefits for the “package”. A package requests a full run of years at maximum given by the longest rotation. For short rotations they are a repeated set; thus, choices on rotation have a long-term commitment. However, it does not exclude if the farmer switching after the maximal year (for example, 12 consecutive years of fulfilling a rotation) is transgressed. At least, by the length of the dynamic modelling (the number of years and investigations), several full runs can be depicted. In general, we make some suggestions and clarifications on how issues arising from the modelling of fixed rotation and choices on switches can be put into programming.
In
Figure 4 the second line after the first line (the sequence of crops in field 1) is lacking, i.e., field 2 lacks one period behind field 1. Further, as can be seen from the diagonal from wheat, for instance, wheat moves from field i in t to field I + 1 in t + 1, yet it is a “normed crop rotation”. At the rights side in the figure, a simple version of three crops and two years of wheat is presented for comparison. Wheat dominates and rye and rape are paying off; secondly, apparently some rotation, though minor, is practiced; yet economically pre-stated, the farm has a preference for high gross margins. For a reference of a similar approach in the whole area (admittedly, an easier case of pasture management [
41]) we refer to the programming techniques which are optional given in GAMS, for example as “if-else” statements. What follows is an outline of adapting rotation to programming techniques. For the programming as given in
Figure 4, sequences are to be conducted at fields.
The practicability of farm management may impose additional constraints, such as labour constraints for certain crops and machinery. A first step is that information on practical crop rotations is depicted as crop sequencing. For example, in
Figure 5 such an “ideal rotation” is given by 12 years. This implies that, for example, plot “1” has to follow a sequence: wheat, barley, potato, rye, cow peas, maize, oats, alfalfa, livestock with legumes, rape seed, fallow, and carrots (w-b-p-r-c-m-o-a-l-s-f-a); i.e., if this rotation is chosen it binds the farmer to finish the rotation. After finishing, however, he has a choice. For the digital modelling, such conditionality can be programmed. Indeed this applies only to plot 1. Then plot “2” follows with one year lacking and plot “3” with two years, etc., (i.e., steps of rotation are spatially transferred: see
Figure 4). Under this condition the spatiality of the farm is recognized and designed rotations are implemented along a necessary number of plots. As indicated by the number of steps in a rotation, plots are potentially given for the choice algorithm. Thus, we most likely get small fields. For the GAMS program outline potential numbers, and not actual fulfilments, count. Further, technically, by summation of the rotation options we guarantee that no other system or sequence is selected. Flexibility lies in the size of the plots.
However, other sequences (rotations with lower consecutive numbers: for example, w-p-r) are potentially possible. Rotations, which are eventually prescribed by a consortium of experts, are optional and the programming shall select the “best” rotation. However, the rotation systems can be changed if it is opportune, as said after the years to complete. Simulations must be longer than just one sequence (we suggest four times; then, with 12 years, 48 years are optimized). The rotation systems depend on the recommendation of agronomists and are given for one run or sequence; for example, for 12 years at a maximum it is reasonable to say that back-and-forth is feasible for “neighbouring” rotations. Nevertheless, they can be swapped more frequently if we extend the time frame and look for several episodes of replications (even more than 60 years, which means five sequences). Note that usually in dynamic programming the lifespan of a decision can be extended, which is a technicality of programming. Then, in
Figure 5, we see alternatives on plot “1” (1a–h). The flexibility, built in, comes with the choice of alternatives at the plot level; though choices are discretionary, they can be anticipative.
The needed different modes in rotation for soil fertility management can increase the complexity of rotations and can open the way for longer rotations. Pest pressure, seasonality, increased labour at smaller plots, etc., are elements constituting the different options and choices on rotation. Additionally, special crops in the particular rotation system, as well as eventual modern technologies to offset disadvantages from narrow rotation, can be explicitly recognized and modelled. However, the alternatives must be discrete. For instance, pesticides and mineral fertilizer are complementary inputs in narrow rotations and they substitute natural fertility accomplished through commitments to ecologically-sound rotations. Though, in the activity spectrum, more chemical inputs may appear for narrow rotations, which may not pay off. The programs’ logic (being similar to the farmers’ goal of maximizing long-term gains) will decide rotation A B C; which means we name them and they are “sets” in GAMS. Even maize in a mono-culture can be an alternative (1h).
It is exactly here where the dispute between proponents of modernization and proponents of sustainable agriculture lay, and people clash in grey zones of not testing alternatives. The modelling can do the testing and give answers. Again, for our purpose of obtaining a spatial representation it is sufficient to have benchmark rotations. To get simple and treatable structures we propose using a “block” combined of 12 years as the “offer” and elements of the “most suitable” crop rotation. Within this framework of potential rotations and plot outlets the “design” of the field composition must include a type of “supply” flexibility between rotations, i.e., superficial activities in programming activities are to be created equally. What suits the special type of rotations in a discrete order is endogenous.
Next, as optimization is based on five distinct dimensions, for practicability reasons the results must be aggregated to given fields. This is done at the level of priority. As an example, in period 3, plot (field) 2 shall be mainly under livestock in rotation 1; for logical reasons it must take over all corresponding activities given at this time.Additionally the dominant land quality category obtained in the area under livestock is of category 5. The dominant category is the one that is conducted. Different results are summarized in crop categories for a given slot following the choice of the relevant rotation as a priority. The consequence is a reasonable flexibility, though still the choices of the “rotation system” are along the dominant category and, temporarily, the dominant one is the fixed one. For the moment it looks that such a practical procedure and the flexibility in dimensions are enough and they can open an outline in which they fit with farmers’ choices. Apparently this is based on knowledge of alternatives. Making things sufficiently flexible requires a relaxation in the fixed rotation sequence. A compromise would be allowing a split into a restrictive and a less restrictive treatment of combinations, or traditional versus modern rotations.
For an explanation of
Figure 5: In field 1 (see first two columns of
Figure 5) we contrast the options 1a and 1b (but we can go up to 1h of the pre-designed rotations). The computer chooses the best sequence “a, b …or h” and crops “i” for b
ki. For example, 2h means that the monoculture M (maize) rotation has been chosen on plot 2. 1g would have meant that two years of wheat are followed by two years of barley, etc.; however, after choice 2h the combinations are exclusively M in that field. This means that in programming, firstly, a choice between types of rotations (a–h) has to be made, and then field sizes are determined secondarily. Determining the size of the plot is the actual optimization program, but choice and optimization can be programmed simultaneously, because one can use if-else statements in GAMS.
(1) The consecutive choice in time is a mixture of rotations. For instance, after 12 years as the threshold period, a new rotation is chosen because yields are good. This is projected using the transition matrix running parallel to the issue of land quality. The alternative is a split in the plot size between rotations. In practical terms this is normally impossible. It would imply a fragmentation of fields. Since a split (fragmentation) is unattractive due to economies of scale, we aggregate and the dominant crop wins the field occupation. To solve this problem with the logic applied in programming, the application of an “if-else” function is a possibility, i.e., if field 1a is larger than 1b, the computer takes the option (1a) for the whole plot size. (i.e., the if-else in the GAMS code assures that the winner takes all). This is relevant because, in our modelling approach, an inter-temporal implication is envisaged based on the land use in period t which is transferred in period t + 1 via transition-and-state via the transition matrix changes occurring in land quality from this year to next year’s crop based on the probabilities modelled in the transition-and-state concept. Note the predecessor crop in the rotation mode determines yield potentials and crop choices for the next period (see above). The transfer between periods matters for future choices (crop choices, i.e., understanding soil mining crops vs. soil recovering crops).
(2) However, we have to not only restrict choices and let conservation prevail. A further issue in programming is that a switch between rotations (towards higher-yielding crops) shall be possible in a more episodically-specified manner. Yet it inherits the risk of being inhibited due to maturing rehabilitation costs in the next periods. Rehabilitation costs reflect rehabilitation activities as shadow prices. However, the objective within the algorithm (discounted future profits) assures that only profitable regimes are presented as regards to the total profitability (discounted), and such activities are only chosen, as if no final capital restrictions exist.
(3) The implementation of the outlined procedure in software programs is of major relevance. For example, in programming, as mentioned above, the exclusion of an activity by the disposal of another can be achieved through assignments. In GAMS we can specify it as an “if-else” statement on the basis of “greater (less) equal”, and then let the model solve the problem of which rotation is optimal. This can be extended to several transition matrices and their dynamic constraints. Specifically, in GAMS there is the option to create “if-else” statements for choice sets in which dynamic equations and constraints (matrices) prevail. In terms of the transition matrix, itself, we configure them dependent of activities. This means we can use thresholds and can then switch the relevant transition matrices and corresponding rotation on or off. Rotation choices are represented by transition matrices. This refers to modelling farmers’ decisions, investments in soil fertility, pesticides, or modern technology change constraints, etc., as if choice sets are used. Passing thresholds opens options for less restrictive rotations in the future, and vice versa. Investments are separate activities. To adapt a new constraint function (for instance, a narrow rotation instead of an old complex), investments are to be made to climb over an edge (threshold). The effects can be tested in computer simulations. The consequence will be an outcompeting of old by new rotation systems; done potentially, but not necessarily, the farmer will come back to which rotation suits him, i.e., if investments are cheap, farmers prefer narrow rotations; if not, they opt for complex ones. Since we model a dynamic (constraint) system, a switch in the strategy of farmers should be possible, but it has temporal effects. The matter of an underlying strategy can help to understand the importance of rotation choices three-fold: (1) what matters is the state of soil fertility and ecosystem health; (2) as rotation planning, it is embedded in dynamic programming (i.e., conditions to obtain good yields or gross margins) to minimize costs of pesticide matters. Then applications of the model control land use pattern. The pattern, however, can change in time; and (3) investments through spraying or decontamination are decision variables which could make a modern rotation (i.e., a simple one) still preferable.
For dynamic optimization, the start and end conditions further play a major role. Hence, we may start with a situation of depleted stocks of soil fertility. The consequence is a need to restore fertility by crop rotation. In this context we can use an index of soil fertility “I”. It can be used to specify conditions under which a switch in rotations is relevant. Apparently, the size of the criteria index I > s (threshold) is a matter of open debate and subject to agronomist knowledge. In programming, at least for the final period, the threshold is exogenous. i.e., before the threshold is transgressed we may suggest a fixing of the index as a sustainability criterion. Technically, the criterion of the threshold or the index that needs to be passed in order to pursue a simple rotation instead of a complex one is normally given exogenously. Why do we have to do so? Simple rotations give higher gross margins, because low-yielding crops, pertinent for traditional crop rotations, are excluded. This should only be possible if the state of nature is good and no threat of future decline appears.
On the other hand the threshold constitutes the ecosystem behaviour as a response to mono-cropping. Thus, the threshold is a critical value and it serves as an interface between the ecological and economic aspects of a farming system. We need joint knowledge. The issue is that, today, farmers should already anticipate deteriorations in crop rotations according to the transition matrix, knowing the ecology of the system [
42]. This means, in the given framework, according to a threshold, either the traditional or modern rotation is applicable. This is the output of the software/program. Yes, this is normative, but it is given by a farmer’s ecosystem service request. In principle, for decision support and sensitivity analyses communications with farmers are necessary. The question is whether the threshold is exogenous or endogenous to knowledge, i.e., are we facing the problem of whether the norm or threshold is up to decision-making? From the point of view of endogenous decision-making, exogeneity is questionable if the health of ecosystems does not matter. Vice versa, ecologist will say ecosystem health is a norm which cannot be compromised. Accordingly, periodic decisions which follow should be known. At the moment envisaged decision-making rests on the periodicity of rotations and norms; thus, sizes of land chosen for crops will change.
7. Empirical Foundation, Eco-System Services, and Landscape
In the case of small farms, the issue of crop rotation must be extended to landscapes, if ecosystem services are to be more prominently addressed. Yet landscapes are a public good. To address landscape issues, we need a deeper thought on ecosystem health and landscape design [
43]. For the ranking of land quality categories we could employ states of the ecosystem at the hamlet or parish level, which are jointly farmed. We suggest a modelling of yields grounded in an ecological framework or modelling functions and species [
44]. Categorizing productivity of land-based ecosystem states in landscapes, yet by expert opinion, modelling, forecast, etc., can be a method that is highly successful if it works in the same framework and with the categories outlined above. However, reducing complexity in ecosystem analysis remains an issue [
45]. Farmers and researchers can build assessments of rotation problems on the landscape analysis level only if there is cooperation. The assessments should include a common understanding of classes, or “states”, of nature, which are associated with soil fertility, resistance decline, prevalent pests, etc., and threats of further pest problems, etc., For this we need a common box of relevance: ecosystem conservation. The use of the service is not a goal, per se, but secondary and a mean. It could also include diminishing water and moisture problems, which go beyond the farm level and is watershed-oriented. If performed decently and anticipated correctly, states contain quantitative and qualitative information on system health at the larger scale. Underlying service provisions, for instance, of pollination and water retention, are always beyond the farm level. The transition matrix must be extended to the landscape level. Hereby it changes its character from farm to system knowledge.
From the farmers’ point of view, reckoning the ecosystem service (system) underlying farming systems, the decision on rotations contains a double hurdle: a control of negative effects on the farm (1) and on the landscape (2) levels. At the landscape level dynamics and equilibria between prey and predatory species in nature through designing rotations and landscapes must be understood. This seems to be a high aspiration. However, to support agronomists and farmers in designing rotations landscape analysis can help to employ ecological modelling, in particular by finding transition matrices with a ubiquity claim. Though ecological modelling is frequently detailed and very complex, the advantage is that it can integrate landscape interactions and elements at a larger scale. Another advantage is that it can establish classifications for states characterising ecosystem health (also for farming purposes) at the system level. Traditional and local knowledge helps in conceptualizing states. This hopefully enables projections of ecosystem trajectories in order to fully explore rotation effects. A technique of receiving information might be a straightforward ecological modelling of rotation systems based on events and triggers which are containing stochastic elements and fuzziness. This can help to accommodate disturbances created by farming and the effects can be demonstrated by simulating ecological consequences by spatial ecological models [
46]. Rotations and their consequences for ecosystems can stabilize farming systems.
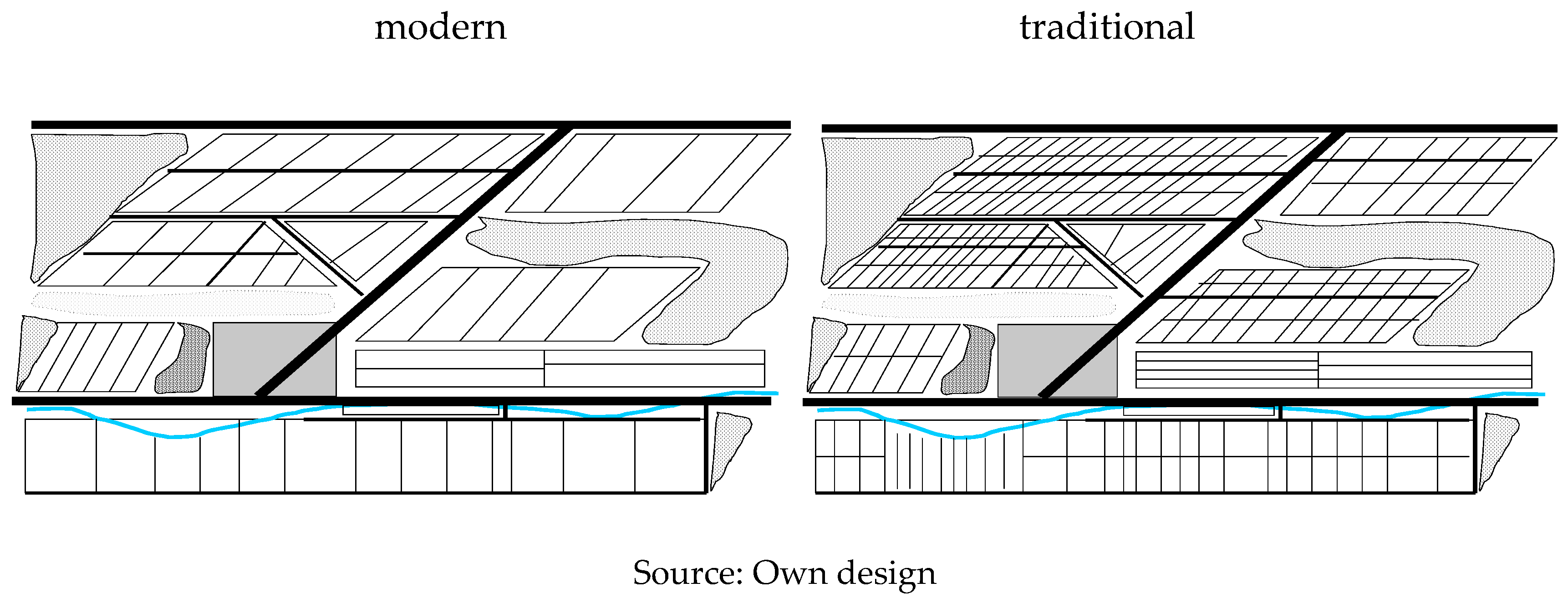
However, what landscape and what farming style are we heading for?
Figure 4 gives a comparison between traditional and modern landscapes. We can mediate between these two systems by creating a “surrogate” of diversity over time by rotations and deliver services. Rotation also has an impact on field sizes; not necessarily, but the logic tells us more crops need more fields and fields become smaller. An ecosystem is more than rotation at the farm level. Rotation experiments at the farm level have to be embedded into landscape designs. Then we can really observe what happens, if (neighbourhood) effects between farms exist. Research shows that ecosystem services depend on landscape diversity. We have to extend farm analysis to simulations with several farms also at the spatial level to fully explore rotation benefits. In
Figure 6 the landscape effects of rotations are depicted. It shows, in a stylized version, the effects of modern vs. traditional choices of rotation and field size combinations on landscape appearance.
In principle we should become capable of transferring cropping patterns of a current period given a number of farms at a collective level into an availability of land fertility classes in the following period. Note that this implies a new matrix outline of cross effects and we should necessarily implement productivity improvements at the farming system level dependent on landscape elements, such as hedges, buffer strips, etc., Rotations become interconnected to landscape elements. Further improvements, for instance, by fallowing, clover, and legume inclusion, etc., in the rotation can be implemented as an augmenting function of good land quality for the community. The management is land allocation at different quality levels and beyond farms.
8. Discussion on Management Units
As a deduction, we have to think about decision-making on soil fertility and thresholds in a broader sense. Hereby appears the question about the unit of decision-making: who makes decisions on rotation? If we proceed with methodological individualism, representative farmers optimize their discounted income flow, but does it also work at the community level? It is possible to minimize the costs of food production at the community level and farmers are modelled as participating in actions (rotation). However, deliberations on rotation choice may be a joint exercise between landscape ecologist, agronomists, and farmers. Deliberations may start with results of individual rotation optimization, assuming an average farm in terms of size, labour, etc., Adjustments can be expected in the case of labour input and machinery, as the size of the operation is concerned. As there is flexibility in the input choice, a pre-determined product mix must be anticipated with different technologies. The input choice is given based on average results from the rotation optimization. This choice should be expressed in an “economies of scale” section of the model, because this will especially determine the size of the farm.
However, we then have to expand beyond the farm level to obtain “rotation” as a prescription. The farm size is correlated with technology choice, rotation, and landscape needs for ecosystem services: is this a dilemma? If the approach stops at the farm level, we would not correctly address the farm and landscape connectivity and potentials. Thus, we have to extend the approach to the landscape level and calculate the implication from rotation decisions of several individual farmers on landscape appearance. For this, a planner is necessary. The task is manifold grouped in three steps: (1) it has to be explained how individual and collective decisions are compatible; (2) the issue of retrieving a quality index for the landscape must be discussed at the landscape level; (3) a recursive implementation of the quality index as a measure to guide rotation decisions must be outlined; and (4) to address questions of landscape organization and ecology, an explicit spatial programming of fields, farm size, and rotation strategies (that goes beyond individual farms) is necessary. It aims at synthesising several farms in one larger approach. This, again, is complex; it normally goes beyond a simple programming model. A compromise is to stylize the spatial organization of farming at the landscape level (
Figure 6) and iterates farm behaviour with more complex rotation interactions. To emphasize: at the centre of this analysis stands the newly-suggested transformation matrix for the landscape which shall translate a certain choice of cropping patterns in period t into ecological effects of a consecutive period t + 1 in a landscape. The ecological effects are decoded as a certain value of on-farm productivity change. The empirical foundation of the analysis can be provided by a productivity ranking, as well as by the determination of the pest danger in the predominant farming system of the landscape. The ranking is implemented by different states of the ecosystem that are jointly elaborated.
Farmers and researchers can then base their management propositions jointly on a modelled assessment of the crop rotation problem as a landscape problem. This is depicted by eventual planning of a “central unit”. Assessment is based on common (community) understanding of classes, or “states”, of the ecology in the whole landscape. We must assume that farmers, agronomists, and scientists have a reasonable understanding of the outlined problem (i.e., traditional and local knowledge, conceptualized capacities to project ecosystem trajectories, information on mechanisms in ecology, etc.). To achieve such understanding “states” can be used and the aim should be that community plans reflect the “state” achievements in the future. For instance, if soil fertility in the landscape declines, the model must be capable to project different states at the landscape level (note, it must not be equal to the farms’ assessments), as well as show diminishing moisture and pest problems (from very good to very poor). From a point of view of the landscape, a custodian for farmers has to be installed as an agent. However, as a consequence, stylized rotation plans at the community level should follow underlying simple ecosystem detections. We hope that farmers’ views of possible alternatives (in farming and categories at the farm level) change practice. For this intention a characterization and valuation of a defined “best” rotation in a participatory way is important. Yet it goes beyond rotation as a technical concept; rotation can become a bit ecologically-oriented; however, we cannot solve the conflict by modelling, but give hints. The reason is that some beneficial organisms eventually only occur (and with them positive externalities) if we introduce community-oriented landscape elements (notability as elements of rotation: meadows). Finally, ecological equilibria can be regulated by designing landscapes and rotations simultaneously based on fields, farm size, fallow, etc., Notice, though, the intention can be to recognize the scope for interaction of ecological and economic knowledge in rotation design; admittedly, rotation remains a farming tool. Not to raise too great an aspiration, rotation is a tool in the farmers’ rationale of long-term profit.