Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River
Abstract
1. Introduction
2. Materials and Methods
2.1. The Distributed Crop Water Consumption Model
- (a)
- Calculation of for Each Weather Station
- (b)
- Interpolation of and Meteorological Variables in the Entire Heihe River Basin
- (c)
- Screening of the Main Influencing Factors of Crop Water Consumption
- (d)
- Obtention of the Distributed Crop Water Consumption Model over Time
- (e)
- Consideration of Water Deficit in Distributed Crop Water Consumption Model
2.2. The Crop Suitability
2.3. The Optimization Model
2.4. Study Area and Data
3. Results and Discussions
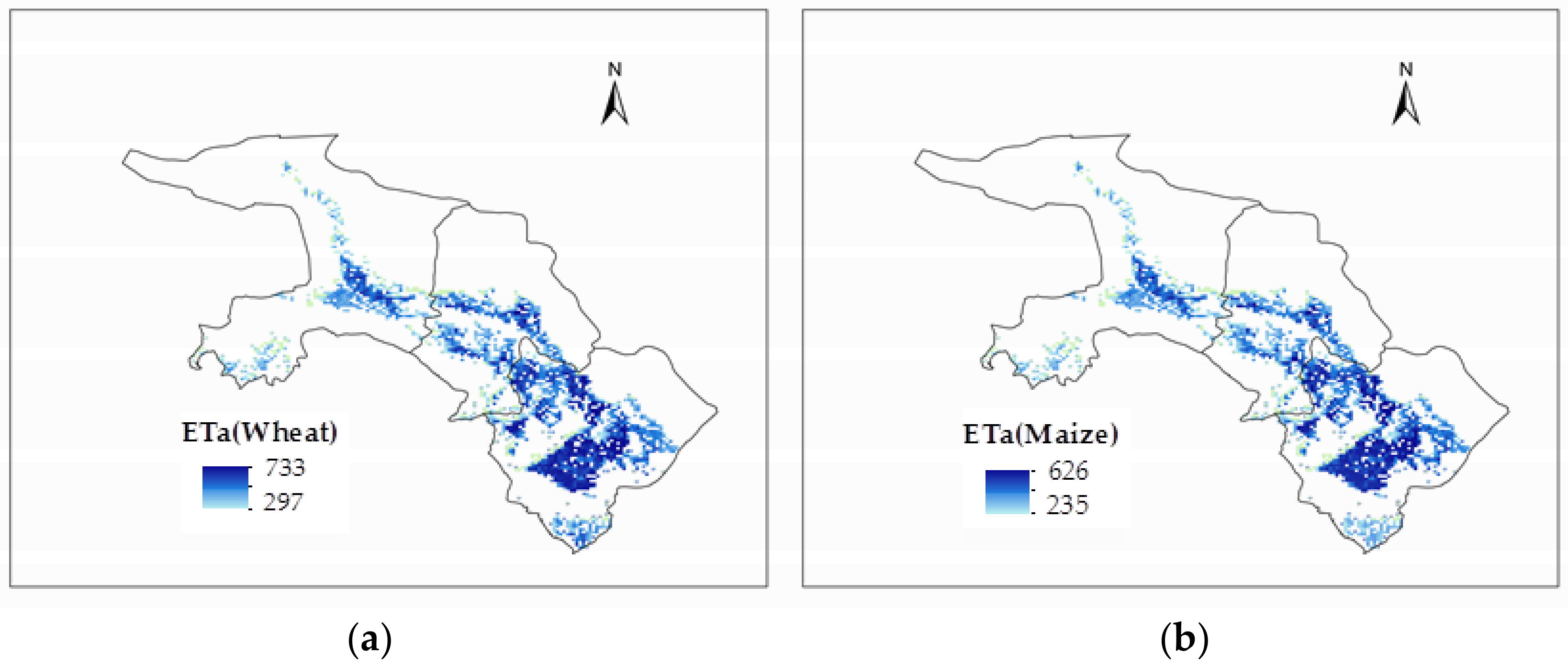
3.1. Distributed Crop Water Consumption Model
3.2. Crop Suitability
3.3. Optimization of Planting Pattern in Different Hydrological Years
3.4. Comparative Advantages
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- The United Nations World Water Development Report 2015-Water for Sustainable World (WWDR 2015). Available online: http://www.unesco.org/new/en/natural-sciences/environment/water/wwap/wwdr/2015-water-for-a-sustainable-world/ (accessed on 18 August 2017).
- Zou, M.Z.; Niu, J.; Kang, S.Z.; Li, X.L.; Lu, H.N. The contribution of human agricultural activities to increasing evapotranspiration is significantly greater than climate change effect over Heihe agricultural region. Sci. Rep. 2017, 7, 8805. [Google Scholar] [CrossRef] [PubMed]
- The Ministry of Water Resources of the People’s Republic of China. Available online: http://www.mwr.gov.cn/sj/tjgb/szygb/201707/t20170711_955305.html/ (accessed on 15 August 2017).
- Wagener, T.; Sivapalan, M.; Troch, P.A.; McGlynn, B.L.; Harman, C.J.; Gupta, H.V.; Kumar, P.; Rao, P.S.; Basu, N.B.; Wilson, J.S. The future of hydrology: An evolving science for a changing world. Water Resour. Res. 2010, 46, 1369–1377. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S.N. Development and application of an optimization model for the maximization of net agricultural return. Agric. Water Manag. 2012, 115, 267–275. [Google Scholar] [CrossRef]
- Singh, A. Irrigation planning and management through optimization modeling. Water Resour. Manag. 2014, 28, 1–14. [Google Scholar] [CrossRef]
- An, P.L.; Ren, W.; Liu, X.L.; Song, M.M.; Li, X.M. Adjustment and Optimization of the Cropping Systems under Water Constraint. Sustainability 2016, 8, 1207. [Google Scholar] [CrossRef]
- Noory, H.; Liaghat, A.M.; Parsinejad, M.; Haddad, O.B. Optimizing irrigation water allocation and multicrop planning using discrete PSO algorithm. J. Irrig. Drain. Eng. 2016, 138, 437–444. [Google Scholar] [CrossRef]
- Otieno, F.A.O.; Adeyemo, J.A. Strategies of differential evolution for optimum cropping pattern. Trends Appl. Sci. Res. 2010, 5, 1–15. [Google Scholar] [CrossRef]
- Karamouz, M.; Zahraie, B.; Kerachian, R.; Eslami, A. Crop pattern and conjunctive use management: A case study. Irrig. Drain. 2008, 59, 161–173. [Google Scholar] [CrossRef]
- Zhang, L.J.; Yin, X.A.; Xu, Z.H.; Zhi, Y.; Yang, Z.F. Crop planting pattern optimization for water scarcity alleviation in China. J. Ind. Ecol. 2016, 20, 435–445. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P. An efficient irrigation water allocation model under uncertainty. Agric. Syst. 2016, 144, 46–57. [Google Scholar] [CrossRef]
- Singh, A. An overview of the optimization modelling applications. J. Hydrol. 2012, 466–467, 167–182. [Google Scholar] [CrossRef]
- Cui, L.; Li, Y.P.; Huang, G.H. Planning an Agricultural Water Resources Management System: A Two-Stage Stochastic Fractional Programming Model. Sustainability 2015, 7, 9846–9863. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.P.; Chen, X.; Ma, Y.G. Optimization of the irrigation water resources for agricultural sustainability in Tarim River Basin, China. Agric. Water Manag. 2012, 107, 74–85. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties. Appl. Math. Model. 2014, 38, 4897–4911. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A coupled random fuzzy two-stage programming model for crop area optimization—A case study of the middle Heihe River basin, China. Agric. Water Manag. 2015, 155, 53–66. [Google Scholar] [CrossRef]
- Garg, N.K.; Dadhich, S.M. Integrated non-linear model for optimal cropping pattern and irrigation scheduling under deficit irrigation. Agric. Water Manag. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Zhao, C.S.; Xia, J.; Li, Z.L.; Liu, Y.; Tang, B.H.; Tang, R.L.; Yan, Z.Q.; Ouyang, X.Y. Using high-temporal geostationary satellite data to analysis temporal and spatial pattern of regional water consumption—A case study of the agricultural district upstream the Bengbu Sluice in the Huaihe River Basin in spring drought season. J. Nat. Resour. 2008, 6, 1055–1067. [Google Scholar] [CrossRef]
- Cai, J.L.; Varis, O.; Yin, H. China’s water resources vulnerability: A spatio-temporal analysis during 2003–2013. J. Clean. Prod. 2017, 142, 2901–2910. [Google Scholar] [CrossRef]
- He, R.Y.; Jin, Y.F.; Kandelous, M.M.; Zaccaria, D.; Sanden, B.L.; Snyder, R.L.; Jiang, J.B.; Hopmans, J.W. Evapotranspiration estimate over an almond orchard using Landsat satellite observations. Remote Sens. 2017, 9, 436. [Google Scholar] [CrossRef]
- Multsch, S.; Grabowski, D.; Lüdering, J.; Alquwaizany, A.S.; Lehnert, K.; Frede, H.-G.; Winker, P.; Breuer, L. A practical planning software program for desalination in agriculture–SPARE: WATERopt. Desalination 2017, 404, 121–131. [Google Scholar] [CrossRef]
- Sethi, L.N.; Panda, S.N.; Nayak, M.K. Optimal crop planning and water resources allocation in a coastal groundwater basin, Orissa, India. Agric. Water Manag. 2006, 83, 209–220. [Google Scholar] [CrossRef]
- Brown, P.D.; Cochrane, T.A.; Krom, T.D. Optimal on-farm irrigation scheduling with a seasonal water limit using simulated annealing. Agric. Water Manag. 2010, 97, 892–900. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wang, Y.F.; Niu, H.S. Spatio-temporal variations in the areas suitable for the cultivation of rice and maize in China under future climate scenarios. Sci. Total Environ. 2017, 601–602, 518–531. [Google Scholar] [CrossRef] [PubMed]
- Pietrucha-Urbanik, K. Multidimensional comparative analysis of water infrastructures differentiation. In Proceedings of the Conference on Environmental Engineering IV, Lublin, Poland, 03–05 September 2012; pp. 29–34. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K. Assessing the Costs of Losses Incurred as a Result of Failure. In Proceedings of the 11th International Conference on Dependability and Complex Systems (DepCoS-RELCOMEX), Brunow, Poland, 27 June–01 July 2016; pp. 355–362. [Google Scholar] [CrossRef]
- Tchorzewska-Cieslak, B.; Rak, J. Method of identification of operational states of water supply system. In Proceedings of the 3rd Congress of Environmental Engineering, Lublin, Poland, 13–16 September 2019; pp. 521–526. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Tchorzewska-Cieslak, B. Water Supply System operation regarding consumer safety using Kohonen neural network. In Proceedings of the 22nd Annual Conference on European Safety and Reliability (ESREL), Amsterdam, Netherlands, 29 September–2 October 2013; pp. 1115–1120. [Google Scholar]
- Abah, R.C.; Petja, B.M. Crop suitability mapping for rice, Cassava, and Yam in North Central Nigeria. J. Agric. Sci. 2017, 9, 96–108. [Google Scholar] [CrossRef]
- Piikki, K.; Winowiecki, L.; Vågen, T.G.; Ramirez-Villegas, J.; Söderström, M. Improvement of spatial modelling of crop suitability using a new digital soil map of Tanzania. S. Afr. J. Plant Soil 2017, 34, 243–254. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring Soil Water Potential for Water Management in Agriculture: A Review. Sustainability 2010, 2, 1226–1251. [Google Scholar] [CrossRef]
- Li, J.; Zhu, T.; Mao, X.M.; Adeloye, A.J. Modeling crop water consumption and water productivity in the middle reaches of Heihe River Basin. Comput. Electron. Agr. 2016, 123, 242–255. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evaporation: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Lei, N.; Xie, Z.K.; Ma, Z.M. The research on water requirement of spring wheat and corn in Heihe Areas. In The Study on Crop Water Requirement and Water Saving Irrigation in Arid Areas; Li, S.Q., Lan, N.J., Eds.; Gansu Science and Technology Press: Lanzhou, China, 1992; pp. 25–34, (In Chinese). ISBN 7-5424-0428-8. [Google Scholar]
- Chen, T.; Ren, L.L.; Yuan, F.; Yang, X.L.; Jiang, S.H.; Tang, T.T.; Liu, Y.; Zhao, C.X.; Zhang, L.M. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in Hydrological Modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Fang, S.B.; Jia, R.F.; Tu, W.R.; Sun, Z.L. Assessing factors driving the change of irrigation water-use efficiency in China based on geographical features. Water 2017, 9, 759. [Google Scholar] [CrossRef]
- Zhong, B.; Yang, A.X.; Wu, S.L.; Li, J.; Zeng, Y.L.; Liu, Q.H.; Zhao, J.; Xu, B.D. HiWATER: 1km/5day compositing Vegetation Index (NDVI/EVI) product of Heihe River Basin. Cold and Arid Regions Science Data Center at Lanzhou. 2014. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Wang, W.Z.; Hu, X.L.; Xu, Z.W.; Wen, J.G.; et al. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Z.Y.; Weisman, J.; Wang, R.S. Ecological niche suitability model with an application in Taojiang land use planning. J. Environ. Sci. 1994, 6, 449–456. [Google Scholar]
- Singh, R.B.; Chauhan, C.P.S.; Minhas, P.S. Water production functions of wheat (Triticum aestivum L.) irrigated with saline and alkali waters using double-line source sprinkler system. Agric. Water Manag. 2009, 96, 736–744. [Google Scholar] [CrossRef]
- Liu, W.Z.; Hunsaker, D.J.; Li, Y.S.; Xie, X.Q.; Wall, G.W. Interrelations of yield, evapotranspiration, and water use efficiency from marginal analysis of water production functions. Agric. Water Manag. 2002, 56, 143–151. [Google Scholar] [CrossRef]
- Jiang, P.H.; Zhao, R.F.; Zhao, H.L.; Fan, J.P.; Wang, J.Z.; Liu, C. Spatial-Temporal Evolution of Land Use/Cover Change in Middle Section of Heihe Basin since 1975. J. Ecol. Rural Environ. 2012, 28, 473–479, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Li, Q.S.; Zhao, W.Z. Effect of Water Allocation of the Heihe River on Plan Structure and Stable Development of the Ecosystem in the Linze Oasis, Gansu—A Case Study in the Pingchuan Irrigation District in Linze County at the middle reaches of the Heihe River. J. Glaciol. Geocryol. 2004, 3, 333–343, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Tan, M.H.; Zheng, L.Q. Different irrigation water requirements of seed corn and filed corn in the Heihe River Basin. Water 2017, 9, 66. [Google Scholar] [CrossRef]
- Tu, J.J.; Hua, J. An evaluation on farmland eco-economical suitability in mountain area based on niche fitness model and GIS technology. Chinese High Technology Letters. 2013, 4, 436–441, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Mao, L.X.; Zhao, J.F.; Xu, L.L.; Yan, H.; Li, S.; Li, Y.F. Climatic suitability of spring maize planted in the “sickle bend” area of China and regulation suggestion. Chin. J. Appl. Ecol. 2016, 27, 3935–3943. [Google Scholar] [CrossRef]





| March | April | May | June | July | August | September | |
|---|---|---|---|---|---|---|---|
| Wheat | 0.594 | 0.812 | 1.336 | 1.665 | 1.739 | / | / |
| Maize | / | 0.418 | 0.483 | 0.723 | 1.211 | 1.377 | 1.562 |
| Item | Yield (y) (kg/ha) | Cost Price (c) ($/ha) | Market Price (v) ($/kg) | ) (104 ha) | Irrigation Water Use Efficiency (λ) |
|---|---|---|---|---|---|
| Wheat | 6373.5 | 888.46 | 0.38 | 1.2 | 0.53 |
| Maize | 8196 | 888.46 | 0.33 | 1.0 | |
| Seed Corn | 8196 | 1776.92 | 0.62 | 6.4 |
| Item | Dry Year | Normal Year | Wet Year |
|---|---|---|---|
| Agricultural available water (108 m3) | 9.39 | 9.92 | 10.45 |
| Effective rainfall in wheat growth period (mm) | 40.0 | 64.3 | 80.1 |
| Effective rainfall in maize growth period (mm) | 82.6 | 102.8 | 125.5 |
| Index | Crops | Dry Year | Normal Year | % | Wet Year | % |
|---|---|---|---|---|---|---|
| Area (104 ha) | Wheat | 1.20 | 1.20 | - | 1.20 | - |
| Maize | 1.00 | 1.00 | - | 1.00 | - | |
| Seed Corn | 12.54 | 13.21 | 5.34 | 13.84 | 10.37 | |
| Total | 14.74 | 15.41 | 4.54 | 16.04 | 8.82 | |
| Net Income (104 $) | Wheat | 373.43 | 368.22 | −1.40 | 366.99 | −1.73 |
| Maize | 691.03 | 691.03 | 0 | 691.03 | 0 | |
| Seed Corn | 45,805.25 | 48,107.89 | 5.03 | 50,363.88 | 9.95 | |
| Total | 46,869.70 | 49,167.14 | 4.90 | 51,421.90 | 9.71 | |
| Total water consumption (108 m3) | 6.57 | 6.64 | 1.07 | 7.27 | 10.65 | |
| Net income per unit area ($/ha) | 3179.76 | 3190.60 | 0.34 | 3205.85 | 0.82 | |
| Unilateral water benefits ($/m3) | 0.71 | 0.74 | 3.66 | 0.71 | −0.86 | |
| Index | Crops | Present | Strategy I | % | Strategy II | % |
|---|---|---|---|---|---|---|
| Area (104 ha) | Wheat | 1.29 | 1.29 | - | 1.20 | −6.97 |
| Maize | 1.20 | 1.20 | - | 1.00 | −16.67 | |
| Seed Corn | 6.40 | 6.40 | - | 6.69 | 4.53 | |
| Total | 8.89 | 8.89 | - | 8.89 | - | |
| Net Income (104 $) | Wheat | 1947.83 | 2100.85 | 7.86 | 1941.71 | −0.31 |
| Maize | 2187.03 | 2269.75 | 3.78 | 1855.96 | −15.14 | |
| Seed Corn | 20,907.32 | 28,423.71 | 35.95 | 29,498.38 | 41.09 | |
| Total | 25,042.18 | 32,794.31 | 30.96 | 33,296.05 | 32.96 | |
| Total water consumption (108 m3) | 4.30 | 4.63 | 7.67 | 4.61 | 7.21 | |
| Net income per unit area ($/ha) | 2816.89 | 3688.90 | 30.96 | 3745.34 | 32.96 | |
| Unilateral water benefits ($/m3) | 0.58 | 0.71 | 21.37 | 0.72 | 23.75 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Wang, S.; Peng, C.; Tan, Q. Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River. Sustainability 2018, 10, 2119. https://doi.org/10.3390/su10072119
He L, Wang S, Peng C, Tan Q. Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River. Sustainability. 2018; 10(7):2119. https://doi.org/10.3390/su10072119
Chicago/Turabian StyleHe, Liuyue, Sufen Wang, Congcong Peng, and Qian Tan. 2018. "Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River" Sustainability 10, no. 7: 2119. https://doi.org/10.3390/su10072119
APA StyleHe, L., Wang, S., Peng, C., & Tan, Q. (2018). Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River. Sustainability, 10(7), 2119. https://doi.org/10.3390/su10072119




