An Improvement of Gain-Loss Price Bounds on Options Based on Binomial Tree and Market-Implied Risk-Neutral Distribution
Abstract
1. Introduction
2. Methodology: Gain-Loss Pricing Bounds
2.1. The Properties of Gain–Loss Ratio
2.2. The Implied Risk-Neutral Probability and IBT Model
2.3. Our Methodology: Implied Gain-Loss Option Pricing Bounds
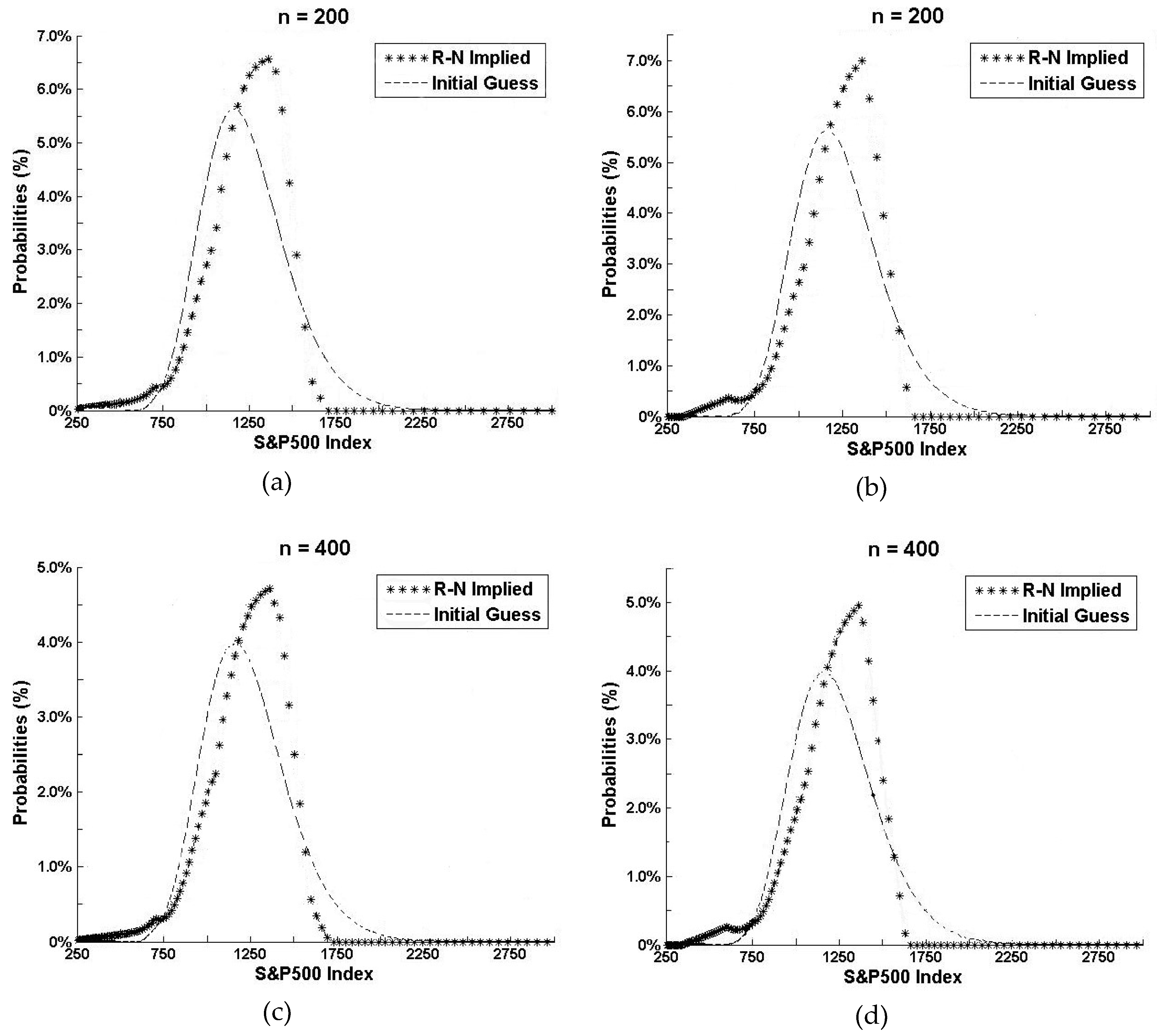
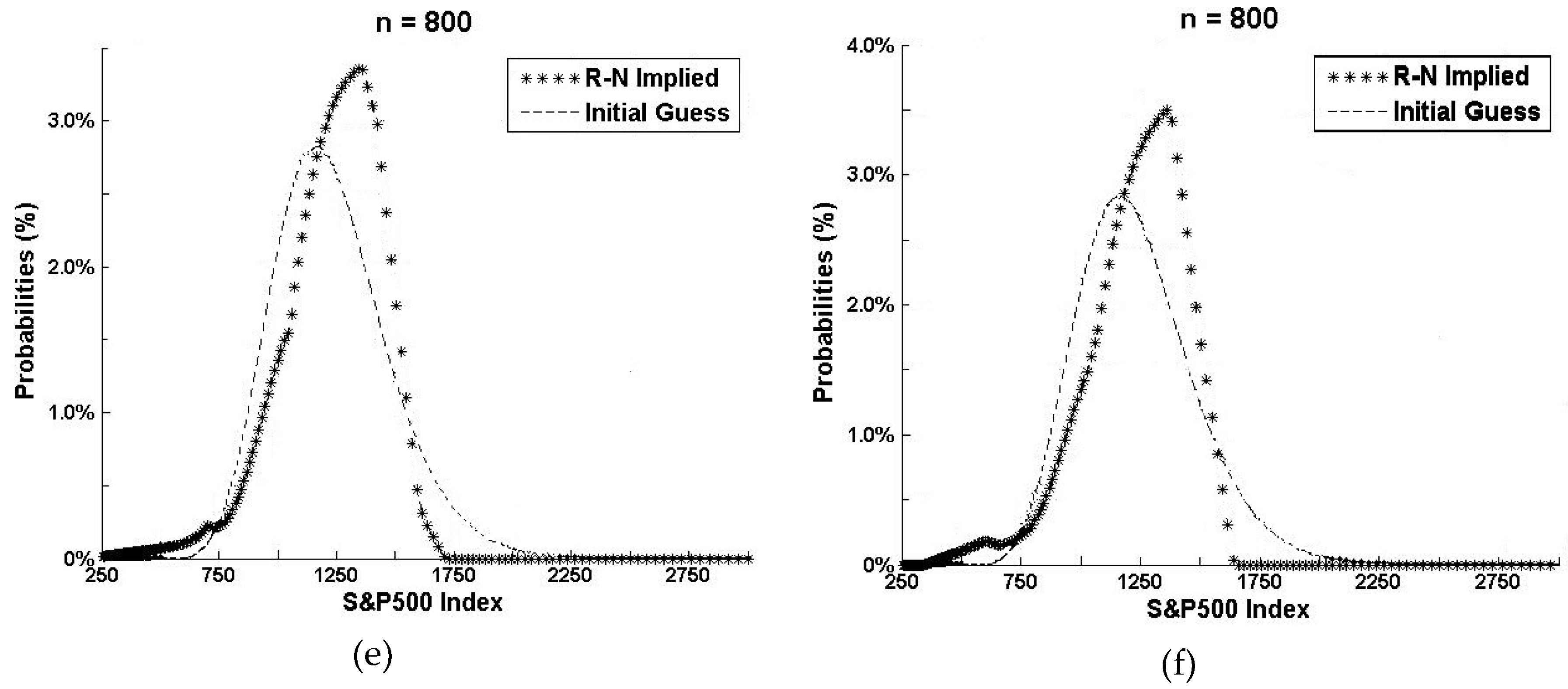
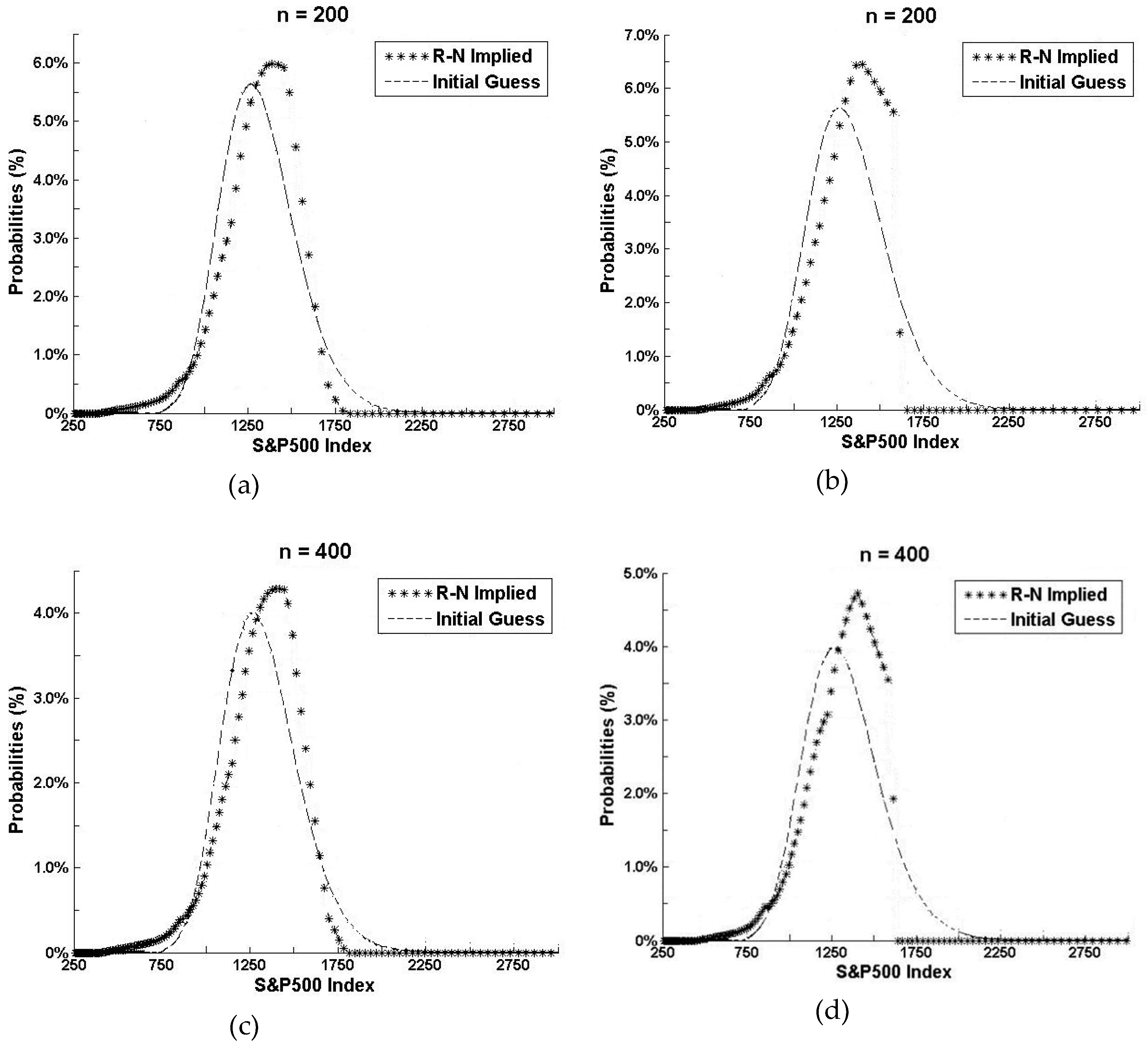
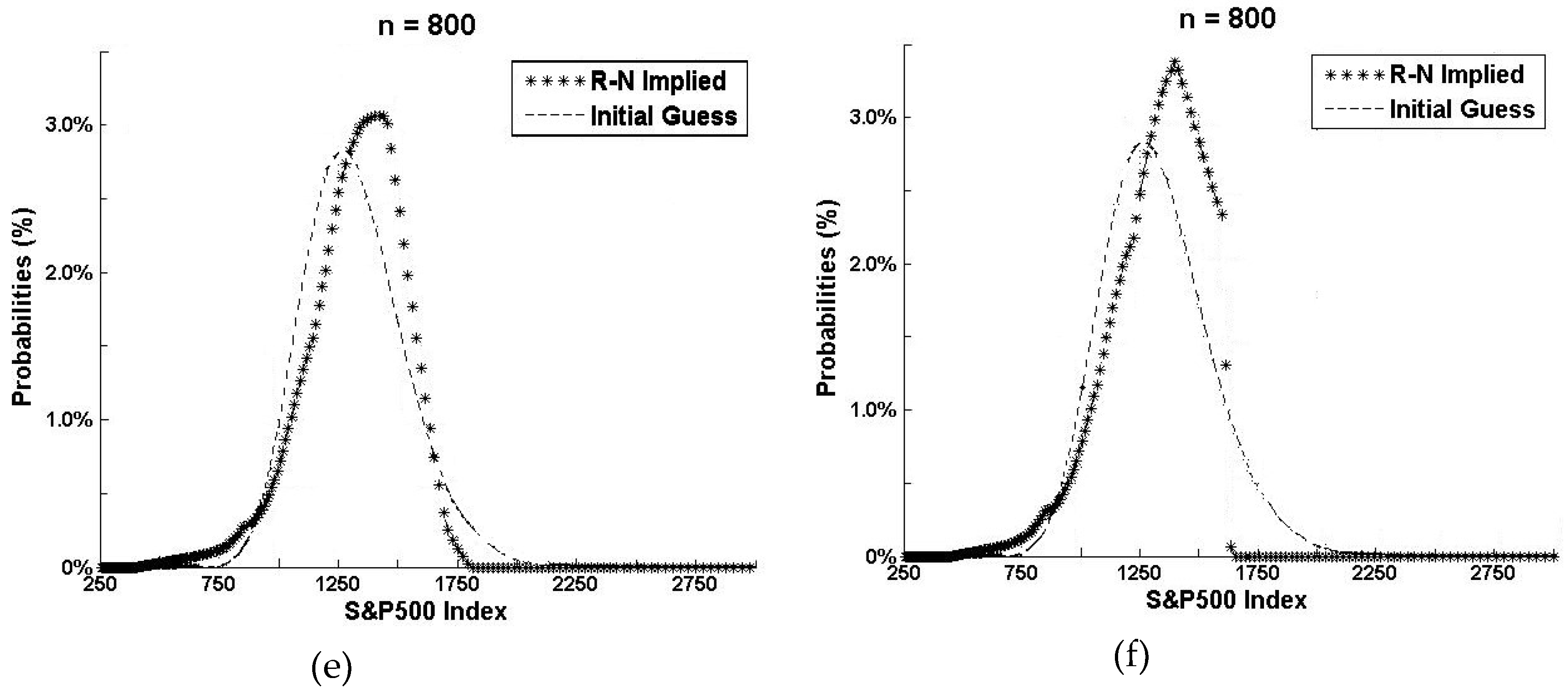
3. Data and Estimated Risk-Neutral Distribution
3.1. Market-Implied Distributions
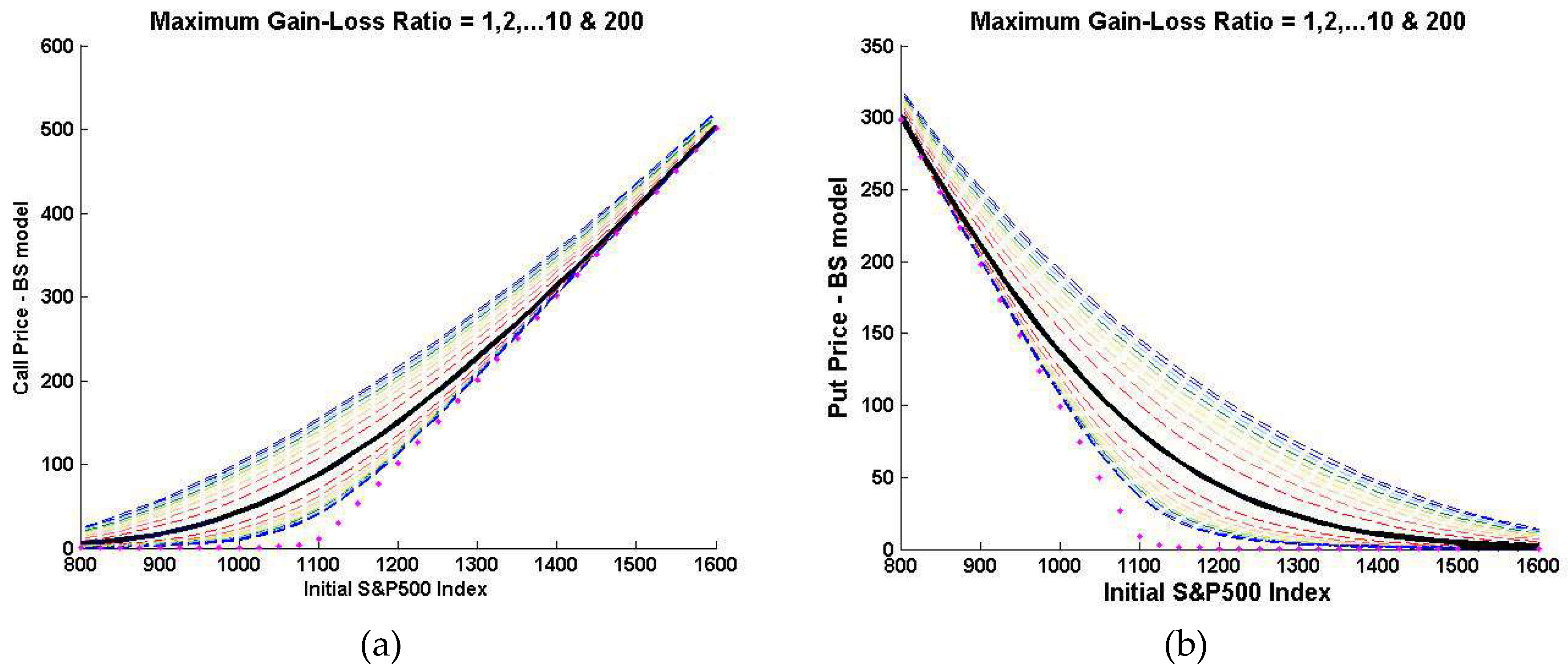
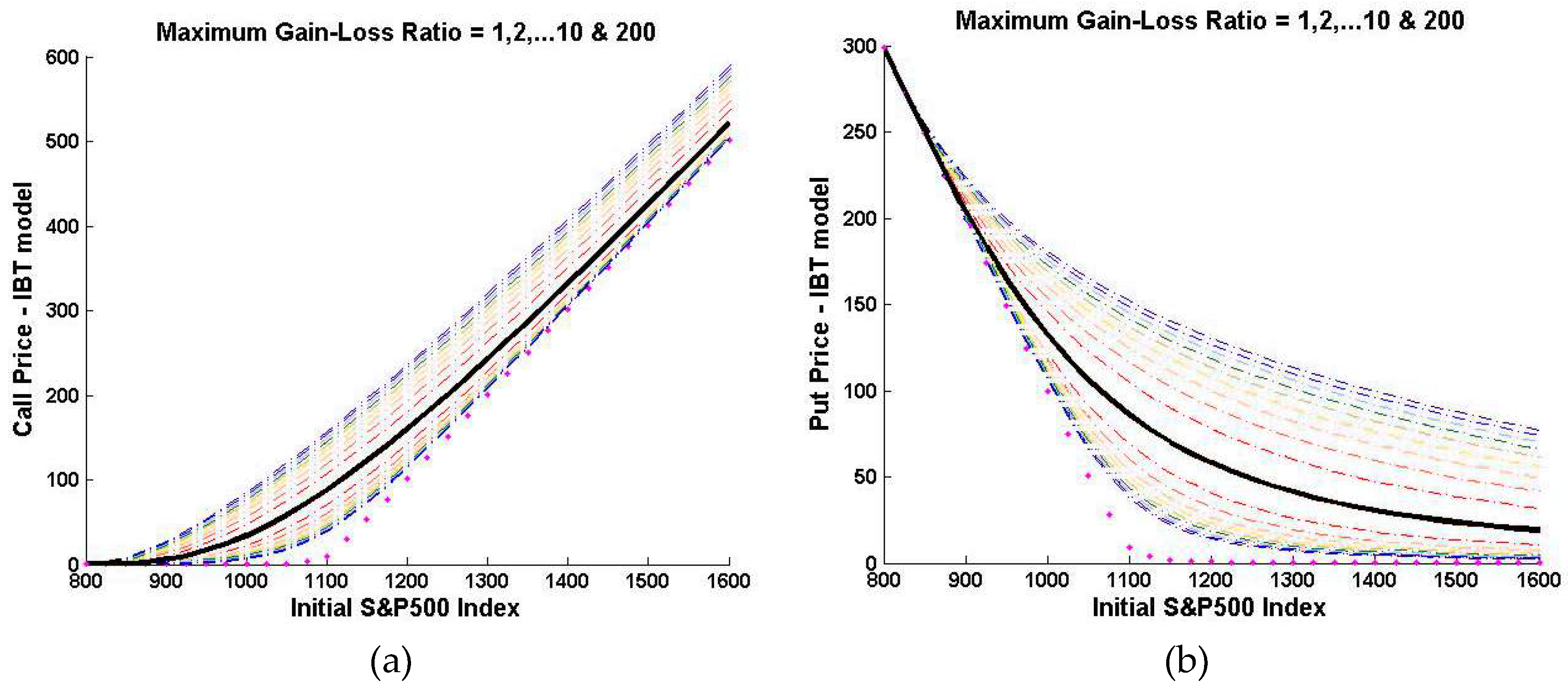
3.2. Market-Implied Option Pricing Bounds
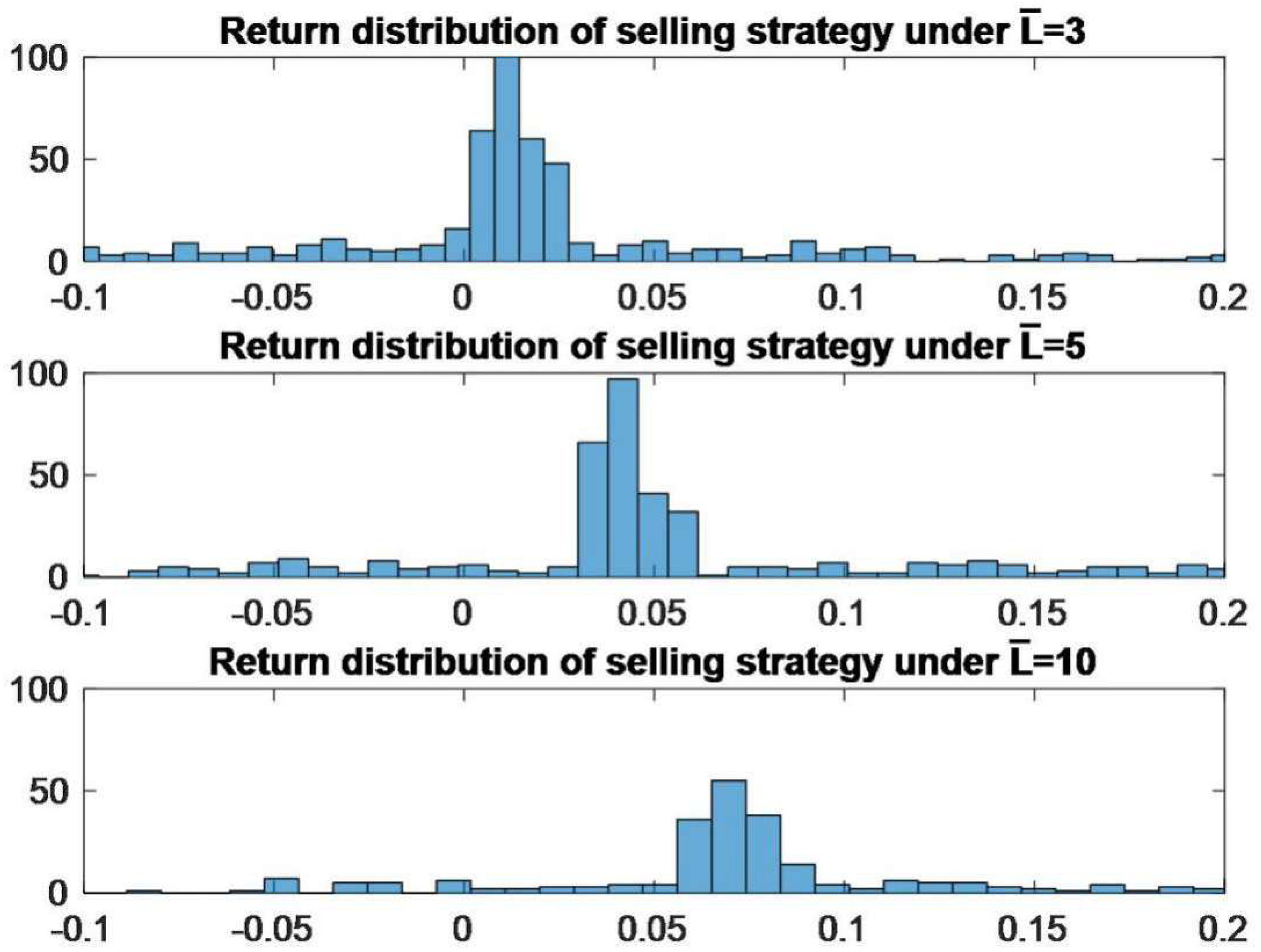
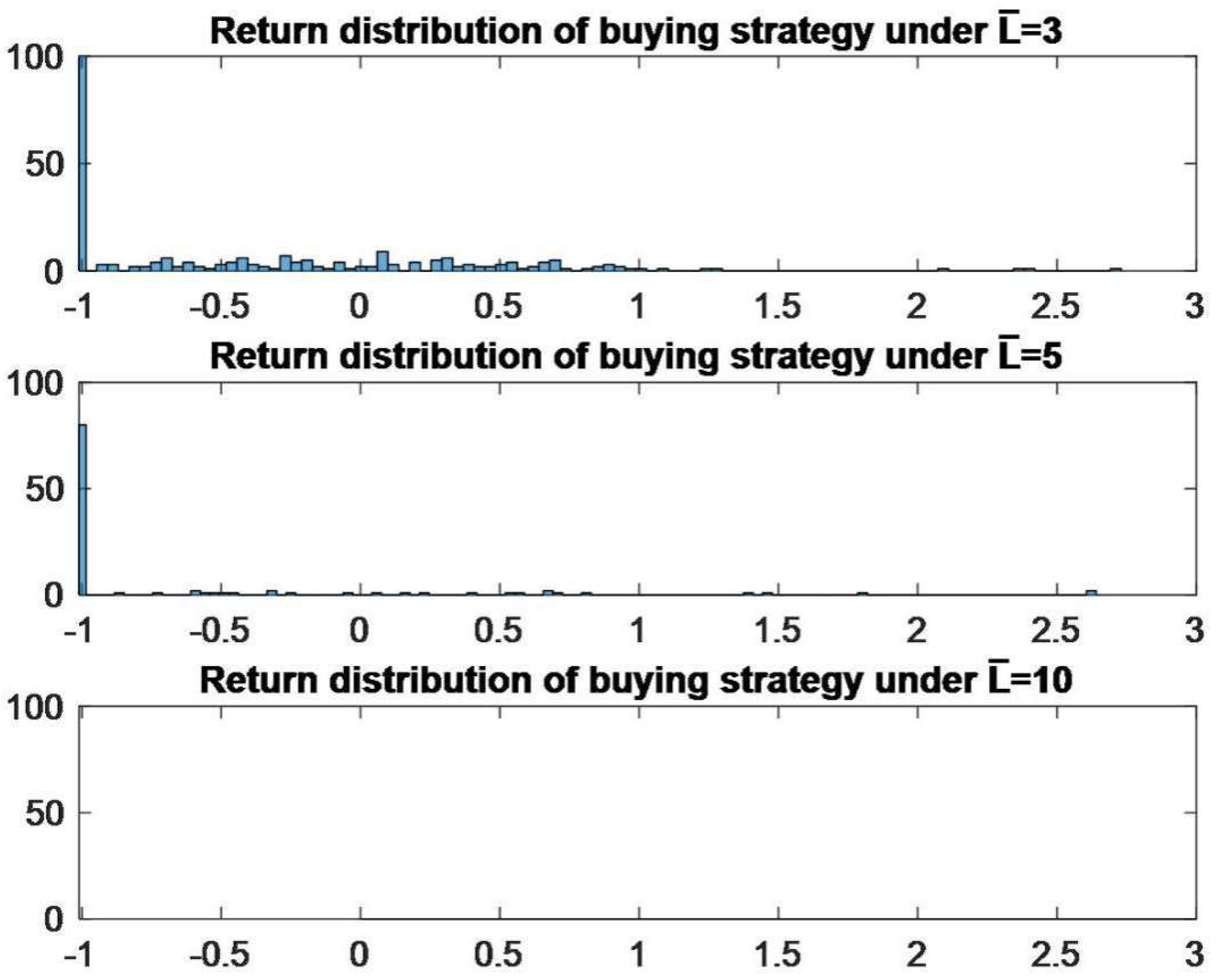
3.3. The Good Deal Trading Strategy
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| S0 | Upper Bound | |||||||||||||||||
| 800 | 825 | 850 | 875 | 900 | 925 | 950 | 975 | 1000 | 1025 | 1050 | 1075 | 1100 | 1125 | 1150 | 1175 | 1200 | ||
| 1 | 4.37 | 6.42 | 9.12 | 12.43 | 16.51 | 21.50 | 27.52 | 34.66 | 42.93 | 52.40 | 63.09 | 74.96 | 87.93 | 102.00 | 117.13 | 133.25 | 150.36 | |
| 2 | 7.92 | 11.25 | 15.46 | 20.47 | 26.29 | 33.04 | 40.75 | 49.46 | 59.14 | 69.80 | 81.41 | 93.93 | 107.28 | 121.46 | 136.43 | 152.16 | 168.65 | |
| 3 | 10.91 | 15.15 | 20.32 | 26.36 | 33.27 | 41.00 | 49.62 | 59.13 | 69.49 | 80.70 | 92.74 | 105.55 | 119.08 | 133.31 | 148.22 | 163.78 | 180.00 | |
| 8 | 21.38 | 28.06 | 35.59 | 43.89 | 52.95 | 62.75 | 73.25 | 84.41 | 96.18 | 108.54 | 121.45 | 134.90 | 148.84 | 163.26 | 178.15 | 193.50 | 209.31 | |
| 9 | 22.94 | 29.92 | 37.72 | 46.28 | 55.54 | 65.54 | 76.22 | 87.53 | 99.44 | 111.90 | 124.92 | 138.44 | 152.42 | 166.88 | 181.79 | 197.13 | 212.92 | |
| 10 | 24.39 | 31.62 | 39.68 | 48.45 | 57.92 | 68.08 | 78.90 | 90.35 | 102.36 | 114.93 | 128.02 | 141.60 | 155.64 | 170.12 | 185.05 | 200.39 | 216.17 | |
| 200 | 81.97 | 94.18 | 106.82 | 119.75 | 132.98 | 146.53 | 160.39 | 174.53 | 188.96 | 203.64 | 218.57 | 233.74 | 249.13 | 264.74 | 280.56 | 296.58 | 312.80 | |
| Inf | 800.00 | 825.00 | 850.00 | 875.00 | 900.00 | 925.00 | 950.00 | 975.00 | 1000.00 | 1025.00 | 1050.00 | 1075.00 | 1100.00 | 1125.00 | 1150.00 | 1175.00 | 1200.00 | |
| S0 | S0 | |||||||||||||||||
| 825 | 850 | 875 | 900 | 925 | 950 | 975 | 1000 | 1025 | 1050 | 1075 | 1100 | 1125 | 1150 | 1175 | 1200 | |||
| 1 | 4.37 | 6.42 | 9.12 | 12.43 | 16.51 | 21.50 | 27.52 | 34.66 | 42.93 | 52.40 | 63.09 | 74.96 | 87.93 | 102.00 | 117.13 | 133.25 | 150.36 | |
| 2 | 2.32 | 3.49 | 5.07 | 7.08 | 9.70 | 13.07 | 17.39 | 22.84 | 29.52 | 37.61 | 47.21 | 58.36 | 70.99 | 85.11 | 100.66 | 117.49 | 135.58 | |
| 3 | 1.58 | 2.40 | 3.51 | 4.96 | 6.90 | 9.45 | 12.85 | 17.29 | 22.94 | 30.08 | 38.92 | 49.54 | 61.92 | 76.09 | 91.95 | 109.31 | 128.07 | |
| 8 | 0.61 | 0.94 | 1.39 | 1.99 | 2.84 | 4.00 | 5.67 | 8.02 | 11.30 | 16.01 | 22.62 | 31.62 | 43.29 | 57.77 | 74.81 | 93.87 | 114.54 | |
| 9 | 0.54 | 0.84 | 1.24 | 1.78 | 2.54 | 3.58 | 5.11 | 7.25 | 10.29 | 14.71 | 21.03 | 29.80 | 41.37 | 55.91 | 73.13 | 92.42 | 113.35 | |
| 10 | 0.49 | 0.75 | 1.12 | 1.61 | 2.30 | 3.25 | 4.64 | 6.62 | 9.45 | 13.62 | 19.68 | 28.23 | 39.71 | 54.31 | 71.70 | 91.20 | 112.35 | |
| 200 | 0.02 | 0.04 | 0.06 | 0.08 | 0.12 | 0.17 | 0.26 | 0.38 | 0.58 | 0.95 | 1.71 | 3.63 | 10.90 | 29.28 | 52.60 | 76.85 | 101.49 | |
| -Inf | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.75 | 25.75 | 50.75 | 75.75 | 100.75 | |
| S0 | Upper Bound | |||||||||||||||||
| 1225 | 1250 | 1275 | 1300 | 1325 | 1350 | 1375 | 1400 | 1425 | 1450 | 1475 | 1500 | 1525 | 1550 | 1575 | 1600 | |||
| 1 | 168.37 | 187.22 | 206.80 | 227.06 | 247.90 | 269.26 | 291.15 | 313.49 | 336.25 | 359.35 | 382.77 | 406.45 | 430.34 | 454.40 | 478.64 | 503.01 | ||
| 2 | 185.85 | 203.74 | 222.26 | 241.38 | 261.05 | 281.23 | 301.96 | 323.18 | 344.87 | 366.99 | 389.51 | 412.38 | 435.54 | 458.96 | 482.65 | 506.56 | ||
| 3 | 196.84 | 214.28 | 232.28 | 250.83 | 269.88 | 289.42 | 309.48 | 330.03 | 351.07 | 372.55 | 394.46 | 416.73 | 439.34 | 462.28 | 485.54 | 509.07 | ||
| 8 | 225.57 | 242.27 | 259.39 | 276.95 | 294.90 | 313.25 | 332.03 | 351.23 | 370.80 | 390.77 | 411.16 | 431.98 | 453.19 | 474.78 | 496.75 | 519.08 | ||
| 9 | 229.14 | 245.80 | 262.87 | 280.34 | 298.19 | 316.44 | 335.10 | 354.14 | 373.56 | 393.38 | 413.62 | 434.28 | 455.33 | 476.76 | 498.57 | 520.72 | ||
| 10 | 232.37 | 248.99 | 266.00 | 283.40 | 301.19 | 319.34 | 337.89 | 356.79 | 376.09 | 395.78 | 415.90 | 436.42 | 457.33 | 478.62 | 500.28 | 522.27 | ||
| 200 | 329.21 | 345.83 | 362.62 | 379.59 | 396.73 | 414.04 | 431.55 | 449.21 | 467.00 | 484.96 | 503.08 | 521.35 | 539.78 | 558.32 | 577.02 | 595.99 | ||
| Inf | 1225.00 | 1250.00 | 1275.00 | 1300.00 | 1325.00 | 1350.00 | 1375.00 | 1400.00 | 1425.00 | 1450.00 | 1475.00 | 1500.00 | 1525.00 | 1550.00 | 1575.00 | 1600.00 | ||
| S0 | Lower Bound | |||||||||||||||||
| 1225 | 1250 | 1275 | 1300 | 1325 | 1350 | 1375 | 1400 | 1425 | 1450 | 1475 | 1500 | 1525 | 1550 | 1575 | 1600 | |||
| 1 | 168.37 | 187.22 | 206.80 | 227.06 | 247.90 | 269.26 | 291.15 | 313.49 | 336.25 | 359.35 | 382.77 | 406.45 | 430.34 | 454.40 | 478.64 | 503.01 | ||
| 2 | 154.74 | 174.85 | 195.73 | 217.30 | 239.42 | 261.96 | 284.95 | 308.29 | 331.93 | 355.81 | 379.90 | 404.16 | 428.56 | 453.06 | 477.65 | 502.32 | ||
| 3 | 147.98 | 168.89 | 190.51 | 212.80 | 235.59 | 258.72 | 282.22 | 306.00 | 330.02 | 354.23 | 378.59 | 403.07 | 427.66 | 452.31 | 477.03 | 501.81 | ||
| 8 | 136.35 | 159.04 | 182.27 | 205.91 | 229.88 | 254.03 | 278.36 | 302.84 | 327.43 | 352.11 | 376.85 | 401.64 | 426.48 | 451.34 | 476.23 | 501.15 | ||
| 9 | 135.37 | 158.23 | 181.62 | 205.38 | 229.45 | 253.68 | 278.08 | 302.62 | 327.25 | 351.96 | 376.73 | 401.54 | 426.40 | 451.28 | 476.18 | 501.10 | ||
| 10 | 134.55 | 157.57 | 181.09 | 204.95 | 229.10 | 253.40 | 277.86 | 302.44 | 327.10 | 351.84 | 376.63 | 401.47 | 426.33 | 451.22 | 476.14 | 501.07 | ||
| 200 | 126.27 | 151.13 | 176.04 | 200.97 | 225.92 | 250.88 | 275.86 | 300.83 | 325.81 | 350.80 | 375.79 | 400.78 | 425.78 | 450.77 | 475.76 | 500.76 | ||
| -Inf | 125.75 | 150.75 | 175.75 | 200.75 | 225.75 | 250.75 | 275.75 | 300.75 | 325.75 | 350.75 | 375.75 | 400.75 | 425.75 | 450.75 | 475.75 | 500.75 | ||
| S0 | Upper Bound | |||||||||||||||||
| 800 | 825 | 850 | 875 | 900 | 925 | 950 | 975 | 1000 | 1025 | 1050 | 1075 | 1100 | 1125 | 1150 | 1175 | 1200 | ||
| 1 | 0.15 | 0.44 | 1.20 | 2.84 | 5.74 | 10.21 | 16.43 | 24.41 | 34.09 | 45.35 | 58.20 | 72.38 | 87.78 | 104.43 | 122.03 | 140.60 | 159.92 | |
| 2 | 0.30 | 0.86 | 2.29 | 5.20 | 9.96 | 16.68 | 25.33 | 35.74 | 47.58 | 60.80 | 75.23 | 90.68 | 107.06 | 124.40 | 142.46 | 161.25 | 180.63 | |
| 3 | 0.45 | 1.26 | 3.29 | 7.18 | 13.33 | 21.55 | 31.64 | 43.30 | 56.41 | 70.64 | 85.92 | 102.09 | 119.07 | 136.86 | 155.28 | 174.33 | 193.90 | |
| 8 | 1.15 | 3.09 | 7.23 | 14.48 | 24.19 | 35.88 | 49.25 | 63.87 | 79.62 | 96.10 | 113.33 | 131.20 | 149.64 | 168.65 | 188.09 | 207.98 | 228.19 | |
| 9 | 1.29 | 3.42 | 7.90 | 15.56 | 25.70 | 37.72 | 51.60 | 66.40 | 82.44 | 99.25 | 116.75 | 134.83 | 153.44 | 172.59 | 192.16 | 212.14 | 232.46 | |
| 10 | 1.42 | 3.74 | 8.56 | 16.54 | 27.05 | 39.52 | 53.66 | 68.83 | 84.93 | 101.99 | 119.72 | 138.00 | 156.77 | 176.05 | 195.71 | 215.77 | 236.14 | |
| 200 | 16.08 | 26.26 | 40.19 | 56.78 | 74.11 | 93.21 | 112.69 | 132.54 | 153.10 | 174.27 | 195.70 | 217.33 | 239.13 | 261.11 | 283.23 | 305.48 | 327.84 | |
| Inf | 800.00 | 825.00 | 850.00 | 875.00 | 900.00 | 925.00 | 950.00 | 975.00 | 1000.00 | 1025.00 | 1050.00 | 1075.00 | 1100.00 | 1125.00 | 1150.00 | 1175.00 | 1200.00 | |
| S0 | Lower Bound | |||||||||||||||||
| 800 | 825 | 850 | 875 | 900 | 925 | 950 | 975 | 1000 | 1025 | 1050 | 1075 | 1100 | 1125 | 1150 | 1175 | 1200 | ||
| 1 | 0.15 | 0.44 | 1.20 | 2.84 | 5.74 | 10.21 | 16.43 | 24.41 | 34.09 | 45.35 | 58.20 | 72.38 | 87.78 | 104.43 | 122.03 | 140.60 | 159.92 | |
| 2 | 0.08 | 0.22 | 0.61 | 1.49 | 3.13 | 5.86 | 9.90 | 15.56 | 22.92 | 32.06 | 43.16 | 56.00 | 70.44 | 86.59 | 104.02 | 122.70 | 142.35 | |
| 3 | 0.05 | 0.15 | 0.41 | 1.01 | 2.15 | 4.11 | 7.16 | 11.60 | 17.60 | 25.46 | 35.38 | 47.38 | 61.29 | 77.21 | 94.66 | 113.59 | 133.61 | |
| 8 | 0.02 | 0.06 | 0.16 | 0.39 | 0.84 | 1.65 | 3.03 | 5.20 | 8.41 | 13.12 | 20.21 | 29.90 | 42.54 | 58.22 | 76.23 | 96.26 | 117.55 | |
| 9 | 0.02 | 0.05 | 0.14 | 0.34 | 0.75 | 1.47 | 2.71 | 4.70 | 7.61 | 12.00 | 18.71 | 28.22 | 40.56 | 56.36 | 74.42 | 94.64 | 116.11 | |
| 10 | 0.02 | 0.04 | 0.12 | 0.31 | 0.67 | 1.33 | 2.45 | 4.30 | 6.96 | 11.07 | 17.46 | 26.67 | 38.90 | 54.67 | 72.91 | 93.31 | 114.93 | |
| 200 | 0.00 | 0.00 | 0.01 | 0.02 | 0.03 | 0.07 | 0.13 | 0.24 | 0.43 | 0.68 | 1.40 | 3.61 | 10.10 | 29.62 | 52.58 | 77.08 | 101.64 | |
| -Inf | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.75 | 25.75 | 50.75 | 75.75 | 100.75 | |
| S0 | Upper Bound | |||||||||||||||||
| 1225 | 1250 | 1275 | 1300 | 1325 | 1350 | 1375 | 1400 | 1425 | 1450 | 1475 | 1500 | 1525 | 1550 | 1575 | 1600 | |||
| 1 | 179.95 | 200.52 | 221.61 | 243.11 | 265.02 | 287.28 | 309.84 | 332.68 | 355.78 | 379.07 | 402.53 | 426.14 | 449.89 | 473.74 | 497.69 | 521.72 | ||
| 2 | 200.56 | 220.95 | 241.78 | 262.97 | 284.50 | 306.36 | 328.49 | 350.89 | 373.53 | 396.36 | 419.35 | 442.50 | 465.80 | 489.21 | 512.72 | 536.31 | ||
| 3 | 213.93 | 234.35 | 255.16 | 276.30 | 297.76 | 319.51 | 341.50 | 363.71 | 386.14 | 408.75 | 431.53 | 454.45 | 477.51 | 500.69 | 523.94 | 547.28 | ||
| 8 | 248.81 | 269.64 | 290.73 | 312.00 | 333.50 | 355.20 | 377.04 | 399.14 | 421.39 | 443.78 | 466.30 | 488.93 | 511.65 | 534.45 | 557.35 | 580.32 | ||
| 9 | 253.08 | 273.93 | 295.04 | 316.36 | 337.90 | 359.64 | 381.57 | 403.67 | 425.94 | 448.33 | 470.83 | 493.40 | 516.12 | 538.90 | 561.78 | 584.73 | ||
| 10 | 256.81 | 277.73 | 298.90 | 320.28 | 341.88 | 363.67 | 385.64 | 407.77 | 430.04 | 452.40 | 474.87 | 497.46 | 520.15 | 542.93 | 565.80 | 588.74 | ||
| 200 | 350.31 | 372.84 | 395.46 | 418.13 | 440.86 | 463.64 | 486.46 | 509.33 | 532.23 | 555.16 | 578.12 | 601.11 | 624.14 | 647.19 | 670.27 | 693.37 | ||
| Inf | 1225.00 | 1250.00 | 1275.00 | 1300.00 | 1325.00 | 1350.00 | 1375.00 | 1400.00 | 1425.00 | 1450.00 | 1475.00 | 1500.00 | 1525.00 | 1550.00 | 1575.00 | 1600.00 | ||
| S0 | Lower Bound | |||||||||||||||||
| 1225 | 1250 | 1275 | 1300 | 1325 | 1350 | 1375 | 1400 | 1425 | 1450 | 1475 | 1500 | 1525 | 1550 | 1575 | 1600 | |||
| 1 | 179.95 | 200.52 | 221.61 | 243.11 | 265.02 | 287.28 | 309.84 | 332.68 | 355.78 | 379.07 | 402.53 | 426.14 | 449.89 | 473.74 | 497.69 | 521.72 | ||
| 2 | 162.86 | 183.98 | 205.69 | 227.81 | 250.35 | 273.24 | 296.40 | 319.82 | 343.46 | 367.26 | 391.21 | 415.28 | 439.47 | 463.74 | 488.08 | 512.48 | ||
| 3 | 154.55 | 176.14 | 198.31 | 220.88 | 243.85 | 267.14 | 290.66 | 314.41 | 338.36 | 362.44 | 386.64 | 410.94 | 435.34 | 459.81 | 484.32 | 508.89 | ||
| 8 | 139.86 | 162.74 | 186.13 | 209.75 | 233.66 | 257.78 | 282.05 | 306.46 | 330.96 | 355.53 | 380.16 | 404.85 | 429.59 | 454.36 | 479.16 | 503.97 | ||
| 9 | 138.58 | 161.60 | 185.12 | 208.87 | 232.87 | 257.07 | 281.39 | 305.86 | 330.42 | 355.03 | 379.69 | 404.41 | 429.18 | 453.97 | 478.79 | 503.62 | ||
| 10 | 137.53 | 160.67 | 184.28 | 208.14 | 232.22 | 256.48 | 280.86 | 305.37 | 329.98 | 354.62 | 379.31 | 404.05 | 428.85 | 453.66 | 478.50 | 503.35 | ||
| 200 | 126.48 | 151.31 | 176.23 | 201.17 | 226.10 | 251.06 | 276.02 | 300.99 | 325.97 | 350.95 | 375.93 | 400.92 | 425.90 | 450.90 | 475.89 | 500.88 | ||
| -Inf | 125.75 | 150.75 | 175.75 | 200.75 | 225.75 | 250.75 | 275.75 | 300.75 | 325.75 | 350.75 | 375.75 | 400.75 | 425.75 | 450.75 | 475.75 | 500.75 | ||
References
- Rubinstein, M. The valuation of uncertain income streams and the pricing of options. Bell J. Econ. 1976, 7, 407–425. [Google Scholar] [CrossRef]
- Brennan, M.J. The pricing of contingent claims in discrete time models. J. Financ. 1979, 34, 53–68. [Google Scholar] [CrossRef]
- Ross, S. Mutual fund separation in financial theory: The separation distributions. J. Econ. Theory 1978, 17, 254–286. [Google Scholar] [CrossRef]
- Cochrane, J. Asset Pricing: Revised Edition; Princeton University Press: Princeton, NJ, USA, 2005; ISBN 9780691121376. [Google Scholar]
- Lehar, A.; Scheicher, M.; Schittenkopf, C. GARCH vs. stochastic volatility: Option pricing and risk management. J. Bank Financ. 2002, 26, 323–345. [Google Scholar] [CrossRef]
- Cochrane, J.; Saa-Requejo, J. Beyond arbitrage: Good-deal asset price bounds in incomplete markets. J. Polit. Econ. 2000, 108, 79–119. [Google Scholar] [CrossRef]
- Bernardo, A.; Ledoit, O. Gain, loss and asset pricing. J. Polit. Econ. 2000, 108, 173–206. [Google Scholar] [CrossRef]
- Corrado, C.; Su, T. Implied volatility skews and stock index skewness and kurtosis implied by S&P 500 index option prices. J. Deriv. 1997, 4, 8–19. [Google Scholar]
- Jackwerth, J.C.; Rubinstein, M. Recovering probability distributions from contemporary security prices. J. Financ. 1996, 51, 1611–1631. [Google Scholar] [CrossRef]
- Breeden, D.; Litzenberger, R. Prices of state-contingent claims implicit in options prices. J. Bus. 1978, 51, 621–651. [Google Scholar] [CrossRef]
- Rubinstein, M. Implied binomial trees. J. Financ. 1994, 49, 771–818. [Google Scholar] [CrossRef]
- Aїt-Sahalia, Y.; Lo, A. Nonparametric estimation of state-price densities implicit in financial asset prices. J. Financ. 1998, 53, 499–548. [Google Scholar] [CrossRef]
- Aїt-Sahalia, Y.; Lo, A. Nonparametric risk management and implied risk aversion. J. Econom. 2000, 94, 9–51. [Google Scholar] [CrossRef]
- Jackwerth, J.C. Recovering risk aversion from option prices and realized returns. Rev. Financ. Stud. 2000, 13, 433–451. [Google Scholar] [CrossRef]
- Longstaff, F. Option pricing and the martingale restriction. Rev. Financ. Stud. 1995, 8, 1091–1124. [Google Scholar] [CrossRef]
- Aparicio, S.; Hodges, S. Implied risk-neutral distribution: A comparison of estimation methods. In FORC Preprint; Working Paper; Warwick University: Coventry, UK, 1998. [Google Scholar]
- Corrado, C. Option pricing based on the generalized lambda distribution. J. Futures Mark. 2001, 21, 213–236. [Google Scholar] [CrossRef]
- De Jong, C.; Huisman, R. From Skews to a Skewed-t: Modelling Option-Implied Returns by a Skewed Student-t. In Proceedings of the IEEE/IAFE/INFORMS 2000 Conference on Computational Intelligence for Financial Engineering, New York, NY, USA, 28 March 2000. [Google Scholar]
- Ritchey, R. Call option valuation for discrete normal mixtures. J. Financ. Res. 1990, 13, 285–295. [Google Scholar] [CrossRef]
- Melick, W.; Thomas, C. Recovering an asset’s implied PDF from option prices: An application to crude oil during the Gulf crisis. J. Financ. Quant. Anal. 1997, 32, 91–115. [Google Scholar] [CrossRef]
- Buchen, P.; Kelly, M. The maximum entropy distribution of an asset inferred from option prices. J. Financ. Quant. Anal. 1996, 31, 143–159. [Google Scholar] [CrossRef]
- Rockinger, M.; Jondeau, E. Entropy densities with an application to autoregressive conditional skewness and kurtosis. J. Econom. 2002, 106, 119–142. [Google Scholar] [CrossRef]
- Härdle, W.; Yatchew, A. Dynamic nonparametric state price density estimation using constrained least squares and the bootstrap. In Working Paper; Humboldt University Berlin: Berlin, Germany, 2002. [Google Scholar]
- Mayhew, S. On estimating the risk-neutral probability distribution implied by option prices. In Working Paper; Purdue University: West Lafayette, IN, USA, 1995. [Google Scholar]
- Andersen, A.; Wagener, T. Extracting risk neutral probability densities by fitting implied volatility smiles: Some methodological points and an application to the 3M EURIBOR futures option prices. In Working Paper; European Central Bank: Frankfurt, Germany, 2002. [Google Scholar]
- Rosenberg, J. Nonparametric pricing of multivariate contingent claims. J. Deriv. 2003, 10, 9–26. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, M.; Han, Y.; Zhou, J. A fuzzy expression way for air quality index with more comprehensive information. Sustainability 2017, 9. [Google Scholar] [CrossRef]
- Wan, H. Pricing American-style basket options by implied binomial tree. In Working Paper; Haas School of Business: Berkeley, CA, USA, 2002. [Google Scholar]
- Cox, J.; Ross, S.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Longarela, I. Gain, loss, and asset pricing: It is much easier. A note. In Working Paper; Stockholm School of Economics: Stockholm, Sweden, 2008. [Google Scholar]
- Stephan, J.; Whaley, R. Intraday price change and trading volume relations in the stock and stock option markets. J. Financ. 1990, 45, 191–220. [Google Scholar] [CrossRef]
- Bergsma, K.; Fodor, A.; Singal, V.; Tayal, J. Intraday option to stock volume ratios and stock return predictability. Social Science Electronic Publishing. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3095239 (accessed on 16 May 2018).
- Birru, J.; Figlewski, S. Anatomy of meltdown: The risk neutral density for the S&P 500 in the fall of 2008. J. Financ. Mark. 2012, 15, 151–180. [Google Scholar] [CrossRef]
- Stoll, H.; Whaley, R. Programme trading and expiration-day effects. Financ. Anal. J. 1987, 43, 16–28. [Google Scholar] [CrossRef]
- Longarela, I. A Simple linear programming approach to gain, loss and asset pricing. Top. Theor. Econ. 2015, 2, 1064. [Google Scholar] [CrossRef]
- Pinar, M. Gain-loss pricing under ambiguity of measure. ESAIM Control Optim. Calc. Var. 2010, 16, 132–147. [Google Scholar] [CrossRef]
- Voelzke, J.; Mentemeier, S. Computing the substantial-gain-loss-ratio. In CQE Working Papers; Center for Quantitative Economics: Münster, Germany, 2017. [Google Scholar]
- Mugwagwa, T.; Ramiah, V.; Moosa, I. The profitability of option-based contrarian strategies: An empirical analysis. Int. Rev. Financ. 2015, 15, 1–26. [Google Scholar] [CrossRef]
| Annual Return under BS Bounds | Annual Return under IBT Bounds | |||||
|---|---|---|---|---|---|---|
| Year | = 3 | = 5 | = 10 | = 3 | = 5 | = 10 |
| 2008 | 3.41% | 4.52% | 7.61% | 10.06% | 13.21% | 14.88% |
| 2009 | 1.45% | 1.54% | 1.68% | 4.50% | 4.75% | 5.63% |
| 2010 | 0.55% | 1.35% | 1.52% | 2.66% | 3.15% | 4.27% |
| 2011 | 3.75% | 4.51% | 6.69% | 6.99% | 6.77% | 7.64% |
| 2012 | 2.75% | 3.95% | 5.07% | 6.71% | 5.28% | 10.58% |
| 2013 | 0.19% | 0.44% | 0.67% | 0.71% | 0.97% | 2.89% |
| 2014 | 1.41% | 2.08% | 3.21% | 1.71% | 3.09% | 4.34% |
| Cumulative returns | 14.25% | 19.81% | 29.38% | 38.08% | 43.12% | 61.68% |
| Annual Return under BS Bounds | Annual Return under IBT Bounds | |||
|---|---|---|---|---|
| Year | = 3 | = 5 | = 3 | = 5 |
| 2008 | 91.19% | 51.86% | 182.42% | 196.10% |
| 2009 | −7.09% | - | 0.58% | - |
| 2010 | −59.88% | - | −40.64% | - |
| 2011 | −44.23% | - | −23.62% | - |
| 2012 | −73.01% | - | −51.93% | - |
| 2013 | −62.72% | −65.38% | −55.48% | −39.39% |
| 2014 | −0.85% | - | −2.62% | - |
| Cumulative returns | −96.03% | −47.43% | −73.16% | 79.47% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.-j.; Lei, M.; Chung, C.-H. An Improvement of Gain-Loss Price Bounds on Options Based on Binomial Tree and Market-Implied Risk-Neutral Distribution. Sustainability 2018, 10, 1942. https://doi.org/10.3390/su10061942
Jiang S-j, Lei M, Chung C-H. An Improvement of Gain-Loss Price Bounds on Options Based on Binomial Tree and Market-Implied Risk-Neutral Distribution. Sustainability. 2018; 10(6):1942. https://doi.org/10.3390/su10061942
Chicago/Turabian StyleJiang, Shi-jie, Mujun Lei, and Cheng-Huang Chung. 2018. "An Improvement of Gain-Loss Price Bounds on Options Based on Binomial Tree and Market-Implied Risk-Neutral Distribution" Sustainability 10, no. 6: 1942. https://doi.org/10.3390/su10061942
APA StyleJiang, S.-j., Lei, M., & Chung, C.-H. (2018). An Improvement of Gain-Loss Price Bounds on Options Based on Binomial Tree and Market-Implied Risk-Neutral Distribution. Sustainability, 10(6), 1942. https://doi.org/10.3390/su10061942




