1. Introduction
Cartels cause tremendous damage to perfect competition markets and consumers by effectually applying upward pressure on prices and downward pressure on quality; moreover, cartels are difficult to detect because of their tacit nature. In this way, cartels mitigate against perfect competition under which consumers are offered the best goods and services at the lowest possible prices. Antitrust authorities have continuously sought to maintain a free-market system against cartels, but with only partial and limited success.
In previous research, the probability of cartel detection was a key indicator for measuring the effectiveness of antitrust policies. Detection is the state in which unobserved cartels are caught by the antitrust authority. After introducing a leniency program as a new antitrust policy, both the number of cartel investigations and the probability of cartel detection increase. The higher the probability of cartel detection, the greater the expected penalties, and therefore, the likelihood of cartel formation will decrease. On this principle, it is possible to measure the deterrence effect according to the change in antitrust policy. This study uses the probability of cartel penalization as a key indicator.
The Markov transition process and the birth and death process model were widely used. Bryant and Eckard [
1] constructed the birth and death process model to empirically analyze cartel data provided by the United States (US) Department of Justice, and estimated the probability of cartel detection in the US in 1961–1988 as between 13–17%. Using the same method, Combe et al. [
2] estimated European Commission (EC) cartel detection probabilities of 12.9–13.2% for 1969–2007. When the birth and death model has two states of competition and collusion, the lifetimes and inter-arrival times between the births of cartels were independent and had exponential distributions with means of
and
. The number of cartels at a particular time
tfollows a Poisson distribution with a mean of
. Both Bryant and Eckard [
1] and Combe et al. [
2] assumed that every cartel would eventually be caught and prosecuted. However, this assumption is not realistic, because some cases are not penalized, despite having been detected.
Further, Bryant and Eckard [
1] and Combe et al. [
2] do not take account of the unobservable cartel population. J. E. Harrington and Chang [
3] sought to estimate the unobservable population by developing the birth and death model from that noted above. They concluded that cartel duration could be a good indicator of whether new competition law had a significant cartel-dissolution effect. Using Harrington and Chang [
3]’s model, Zhou [
4] analyzed the EC cartel data for 1985–2012, and concluded that the EU’s new leniency program in 2002 had the effect of deterring cartels.
In the research of Bryant and Eckard [
1], Combe et al. [
2], Harrington and Chang [
3], and Zhou [
4], the probability of cartel detection—as derived from cartel duration—entailed the determination of the time-average probability from continuous variables. On the other hand, there is research indicating that the probability of cartel detection represents the ensemble-average probability obtained from discrete variables such as caseloads. The time-average probability is the average of a stochastic process that is obtained by selecting a sample path randomly, and taking the average of a period in a particular state on that sample path over the observation period. The ensemble-average probability is that mean of a quantity at time
that is estimated by the average of the ensemble of possible states of total sample paths in stochastic process theory [
5,
6].
Miller [
7] formulated a cartel behavior model using the Markov process, and used the number of cartel cases as discrete variables. The model assumed that the cartel transition process is in a non-absorbing and first-order Markov chain in contrast with previous Markov models, and showed the change of the number of cartel detections before and after a leniency program. He concluded that the introduction of this leniency program in 1993 increased the detection and deterrence capabilities of competition enforcement. The previous research above [
1,
2,
3,
4,
7] used Markov process models; this research had two notable points.
First, the duration of cartels and inter-arrival times between cartels follow exponential distributions. Verifying this assumption requires a hypothesis testing of the null hypothesis that “the distribution is exponential”. The cumulative distribution function
of durations and inter-arrival times is given by:
Under the exponential distribution,
should be approximately linear in
x. The result of these previous works indicates that the cartels’ duration and inter-arrival times between cartels follow the exponential distribution; therefore, models can be applied to the Markov process [
7].
Second, this research assumed that the cartel process was stationary for adopting the Markov process, and that the values could be analyzed when the cartel process attained a steady state; this is also unrealistic. In the research of Bryant and Eckard [
1] and Combe et al. [
2], the probability is the resultant value when it reaches a steady state. This kind of probability is called a time-independent probability. Otherwise, the form of estimators needs to be a time-dependent rather than time-independent, because the purpose of estimating the probability of cartel detection is evaluating the effects of various competition policies [
8]. Thus, Hinloopen [
8]’s research was an theoretical literature review for analyzing a subgame of collusion.
A new mathematical methodology has emerged recently in the form of a non-Markov process. Ormosi [
9] estimated the annual probability of cartel detection by employing capture–recapture methods based on EC information in the period between 1981–2001. The methods of Ormosi [
9], which are frequently used in ecology, reflect that transition parameters are not steady state, and that detection and survival rates are time-independent. However, there are two unreasonable assumptions. First, capture–recapture methods assume that temporary migrations between the two states (compete–collude) do not exist; thus, they are regarded as robust design methods. The antitrust policy tends to vary broadly according to governmental power or social issues. Second, Ormosi [
9] deduced a result from moving average methods, specifically in the moving average of three or five years. If the probability is used on the basis of a single year, the accuracy of the probability may decrease due to data insufficiency. The industry reacts immediately to changes in competition law; therefore, the probability needs to be estimated for the smallest unit of time.
This paper seeks to estimate the probability of cartel penalization using a Bayesian approach and evaluate the impact of the leniency program as an antitrust policy. This study uses the conjugate family of the beta-binomial in that the cartel occurs in binomial events. The posterior mean of the beta distribution is the probability of cartel penalization in a year. This shows the trend of the probability of cartel penalization, and can then improve the antitrust policy using the measured impact of the leniency program. In this light, the present research makes three contributions.
First, this paper estimates the probability of cartel penalization for analyzing cartels in contrast to the probability of cartel detection as treated in previous research. The probability of cartel detection means the probability that unobserved cartels will be investigated, prosecuted, and penalized. However, the probability of cartel penalization means the penalized likelihood of investigated cartels through sufficient investigation. This is used as an indicator with which to evaluate the impact of the leniency program and the capability of antitrust authorities.
Second, the methodology of this paper makes up for the weak points of previous probability estimation methods. Previous methods have many unrealistic assumptions such as the analyzed cases being eventually caught/detected cases, the time-average probability, etc. We can improve on these assumptions by estimating the time-dependent ensemble-average probability based on the discrete data of caseloads, which is more practical than the time-average probability for the sensitive estimation of probability.
Third, this study shows that the Bayesian approach could play a practical role in modeling and analyzing the cartel situation. Although the Markov process model, which was commonly used in previous research, is an essential consideration “in steady-state probability”, it is difficult to assume “in steady-state probability”, because cartel cases continuously vary over time. The probability of cartel penalization estimated using the Bayesian approach does not need to consider “steady-state probability”. The Bayesian approach for estimating probability can contain significant uncertainty, but has good predictive performance in itself [
10]. The bias between the estimation probability and the actual value could be solved from the update procedure of the Bayesian approach. Therefore, we present reliable results using the non-informative prior and conjugate prior distribution when prior information is insufficient.
The paper is organized as follows:
Section 2 defines the penalization probability and Bayesian probabilistic model;
Section 3 presents an empirical study based on US cartel data; and
Section 4 draws conclusions.
2. Bayesian Probabilistic Model
When faced with suspected cartel cases, a competition authority carries out an initial investigation to determine whether there are sufficient grounds to prosecute. Prosecuted cartels are penalized in the form of fines through a trial. Eventually, the three states of cartel cases are investigation, prosecution, and penalization [
11]. The estimated probability of this study is based on investigation and penalization states. The probability of cartel penalization (
ρt) is described as the proportion of the numbers of penalized cases to investigated cases for year
t (
).
The estimation of the penalization probability using the Bayesian approach involves two assumptions. First, the unit of case is an industry. Accordingly, the research of Bryant and Eckard [
1] and Miller [
7] is based on the analysis unit of the industry. Bos and Harrington [
12] argued that firm-based analysis is more realistic; nonetheless, this study was analyzed based on the analysis unit of industry for easy analysis. In practice, cartels can participate in all firms of an industry. Second, a cartel only arises as one event during a year. Every cartel is transferred to the competition as a result of punishment by the authorities. This is called the “Grim trigger strategy” [
13,
14]. Thereafter, if some player deviates from the cartel, the game cannot be colluded indefinitely.
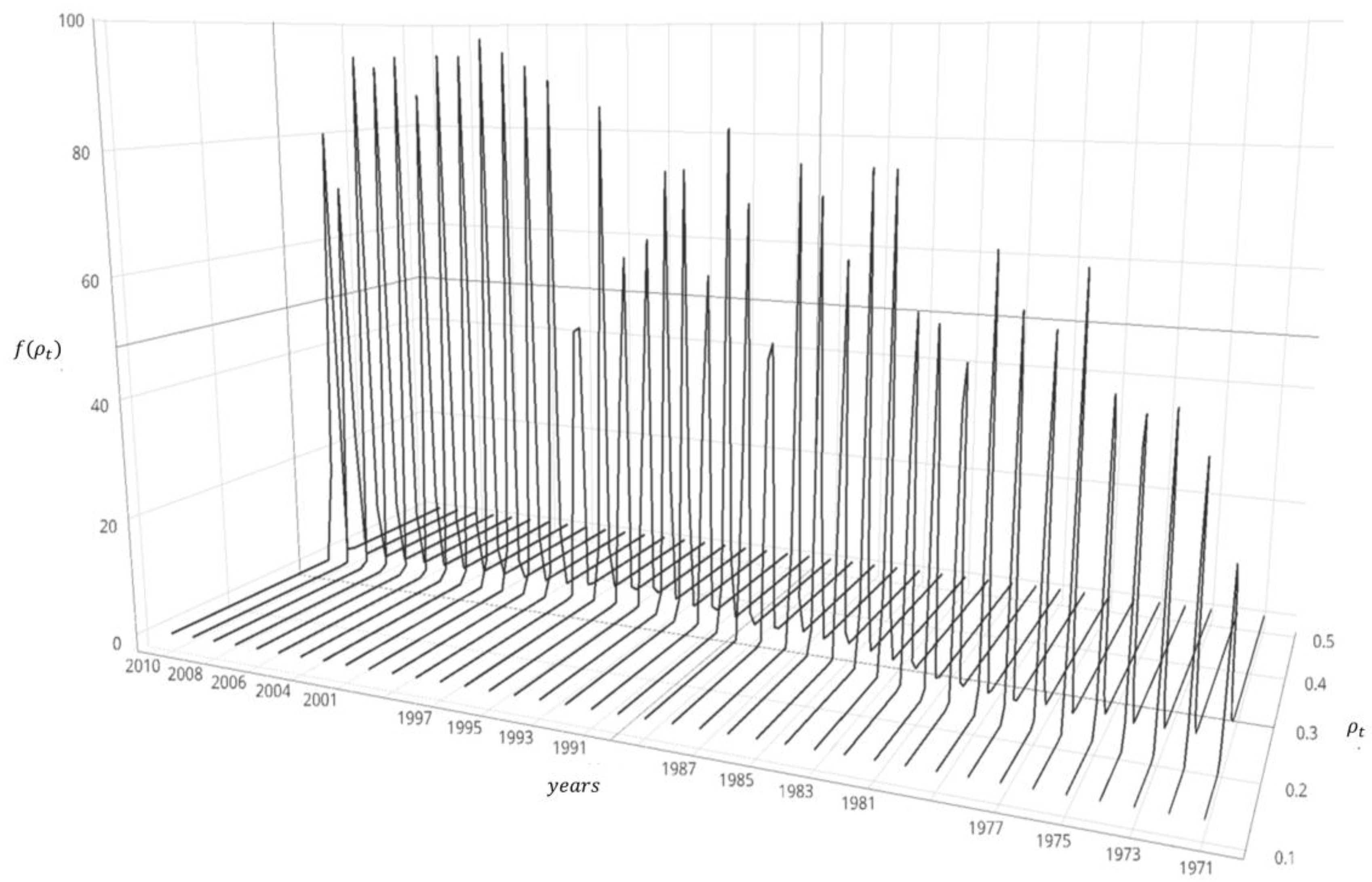
This study constructed a Bayesian probabilistic model to estimate the probability of cartel penalization. The probability of cartel penalization is the posterior mean calculated from the posterior distribution. Inferring a posterior distribution requires determining the proper prior distribution. A Bayesian probabilistic model is comprised of a prior distribution to induce a posterior distribution, hyperparameters, and a likelihood function. A Bayesian sequential analysis of the dynamic Bayesian model can be used to reflect the latest trends of time-series data [
15,
16].
Two things should be considered to induce a posterior distribution from a prior distribution: the likelihood function and the parameters in the prior distribution, which are known as hyperparameters [
17]. The natural conjugate priors are generally recommended in the Bayesian approach, because its functional form is similar to the likelihood distribution [
18,
19]. Therefore, we have to obtain the appropriate likelihood function to adopt the notion of natural conjugacy. Consider the following notations for the Bayesian probabilistic model.
ρt: The probability of cartel penalization cases in year t
nt: The number of cartel investigation cases by the competition authority in year t
kt: The number of cartel penalization cases by the competition authority in year t
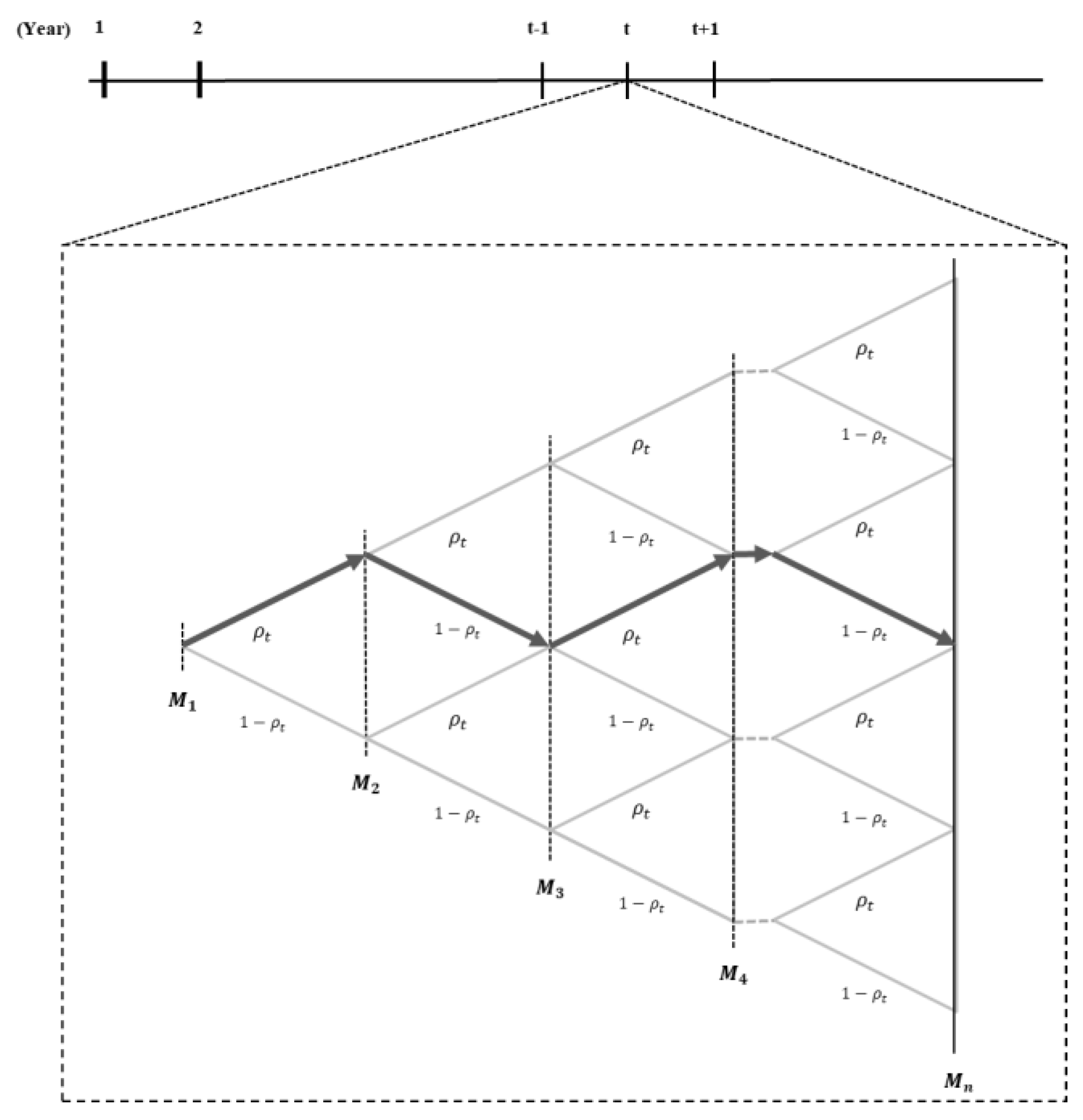
When the investigated industry participating in a cartel is
n,
Figure 1 shows a binomial tree to demonstrate the process of cartel formation and demise in year
t.
In
Figure 1,
is the industry of investigated cartels in year
t. Arrows in the path show whether the investigated cartels were finally penalized. When a route contains an arrow pointing to the right, this cartel will be finally penalized; otherwise, it is not penalized. For example, the industry
is in the left direction; this means that industry
will be not finally penalized as the probability
ρt. This study wants to infer the probability of industry
n + 1 penalization in path G; this probability is estimating the likelihood function based on the data from industry 1 to
n, and the prior distribution while inferring a posterior distribution from the Bayesian approach [
13]. The expectation of a posterior distribution indicates the probability of cartel penalization.
2.1. Likelihood Function and Prior Distribution
The variable
nt is the number of cartel cases investigated in year
t, and each case follows the Bernoulli process with an independent and identical distribution. Therefore, the Bernoulli random variable
with one case shown is given by:
where
i is the number of cartel firm (
) and
. The probability mass function of the random variable, which is known as the Bernoulli probability, is given by:
Once the number of cases
nt is investigated, and
kt is penalized in year
t, the joint probability mass function of cartel cases is given by:
The probability of cartel penalization has a value between 0 and 1. In Equation (2),
is a binomial form as the prior distribution, because there are only two final states of a cartel: whether it has been penalized or not. Thus, we use the beta distribution as a prior distribution based on the natural conjugacy [
17,
20]. The prior distribution
is the beta distribution with hyperparameters
α and
β; thus, the probability density function is given by:
where
and
are the hyperparameters. The function
is a gamma function, which is defined as:
Note that when α is a positive integer, .
2.2. Bayesian Estimation
In the Bayesian approach, the posterior distribution is given by:
The joint probability distribution
in Equation (5), which reflects the multiplicative laws of probability in Equations (2) and (3), is:
The marginal probability distribution
, which is calculated by the law of total probability, is given by:
where
.
Suppose that the initial probability (
ρt) is 0.5 meaning whether the investigated or the non- investigated case for eliminating the dependence on the prior information. The hyperparameters
α and
β are 1 as a non-informative prior. Therefore, the posterior distribution is a beta distribution with the parameters
and
. The posterior distribution of Equation (5) is represented by:
The posterior mean
from Equation (8) is:
4. Conclusions
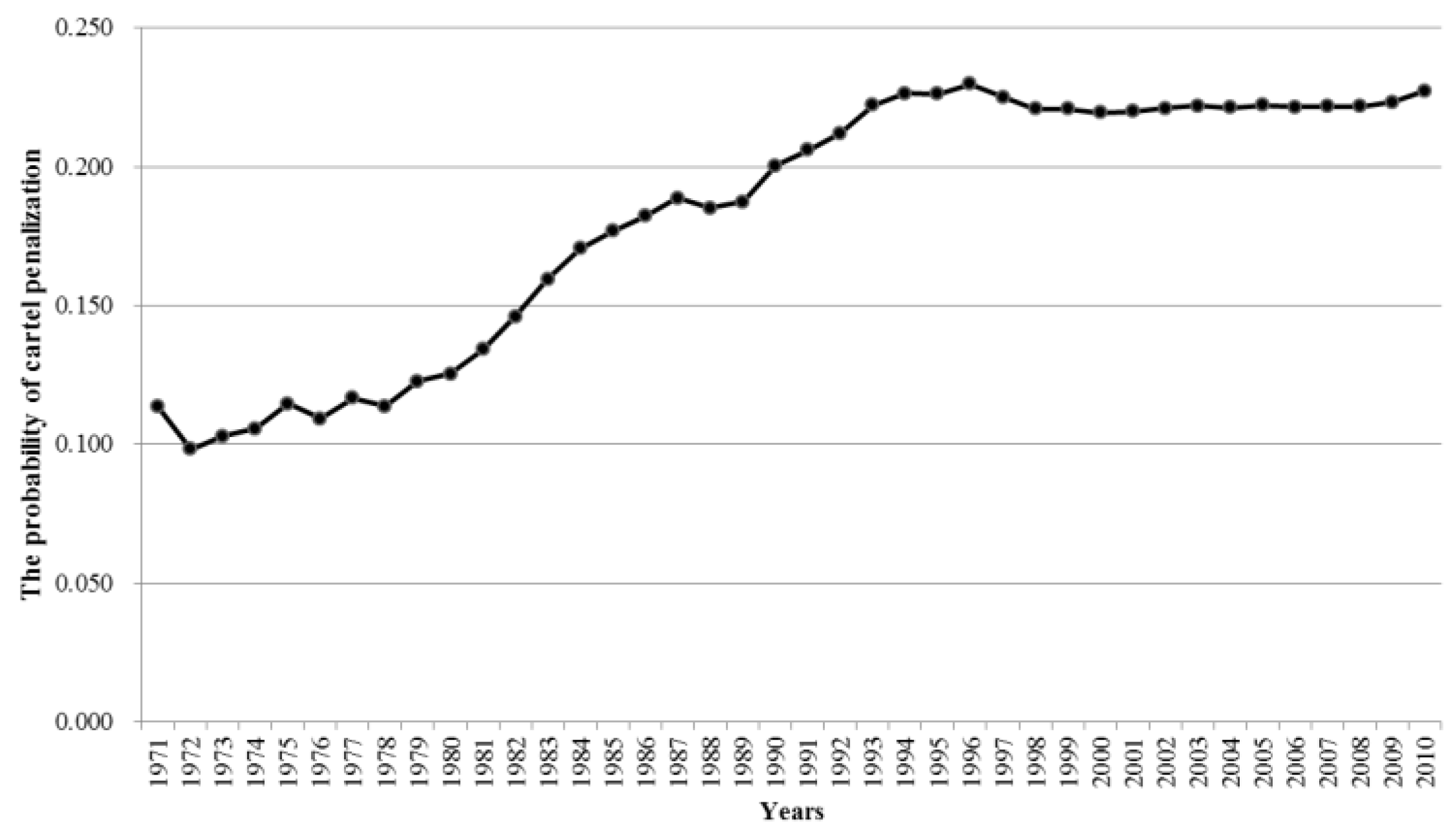
This study attempted to estimate the probability of cartel penalization using a Bayesian approach. Bryant and Eckard [
1], Combe et al. [
2], Harrington and Chang [
3], and Zhou [
4] estimated the probability of cartel detection in the form of the time-average probability from continuous data. However, the probability of cartel penalization of this study was estimated in the form of the ensemble-average probability from Workload statistics. Bryant and Eckard [
1], Combe et al. [
2], Harrington and Chang [
3], Zhou [
4], and Miller [
7] all assumed that the duration of cartels and the inter-arrival times between cartels follow exponential distributions, and that the stochastic process for cartel cases is stationary. However, we built a Bayesian probabilistic model, as it did not need to consider a stationary process. This study made two assumptions: an industry-based analysis, and the grim trigger strategy. On the basis of the 1970–2009 Workload statistics from the US Department of Justice, the determined probability of cartel penalization reflected a sensitive response according to the change of antitrust policy. The result of the policy simulation of the impact of the leniency program was about 65%. The results are similar with the results of Chang and Harrington [
24] and Miller [
7], and similar to that of Bryant and Eckard [
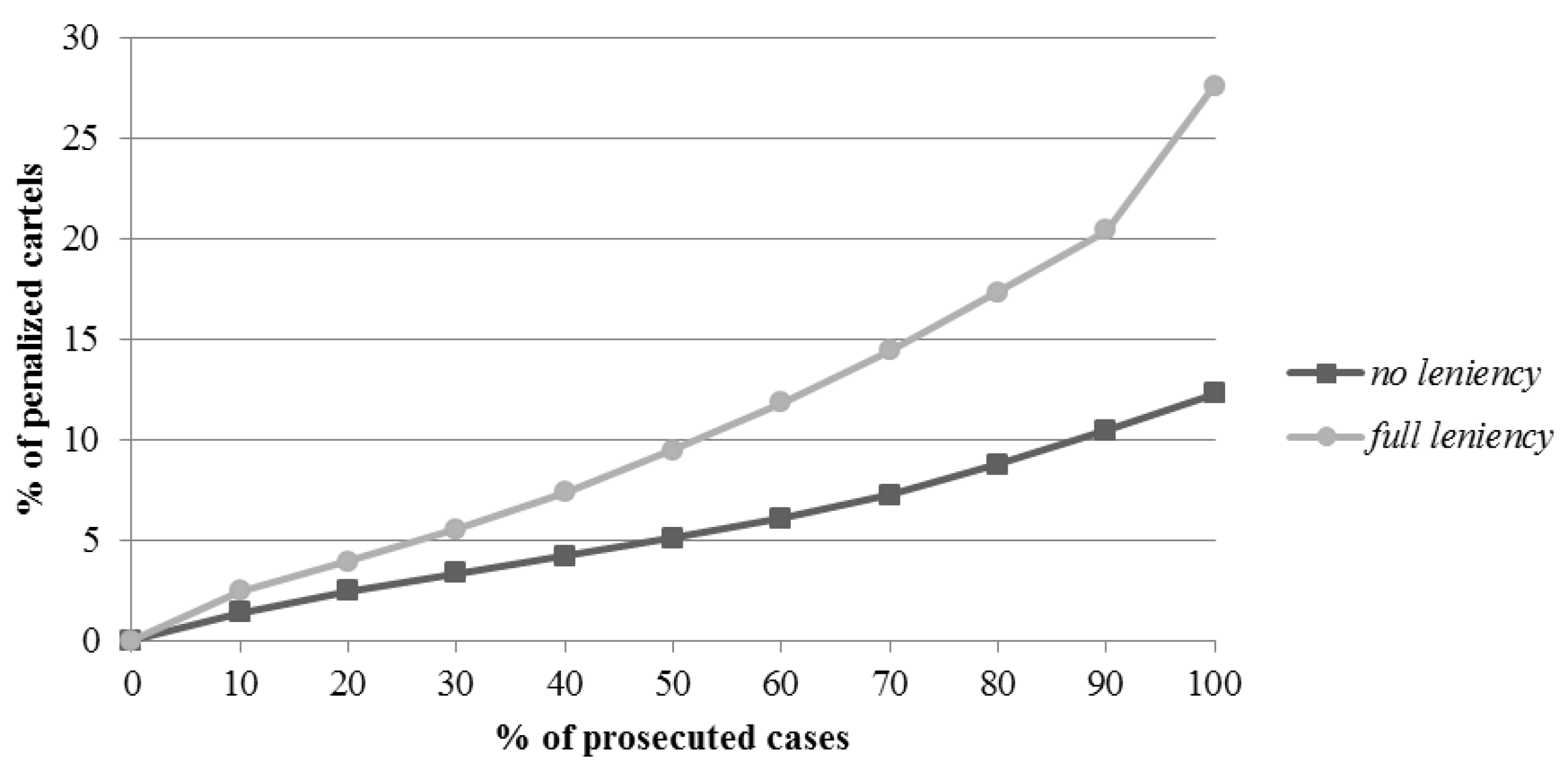
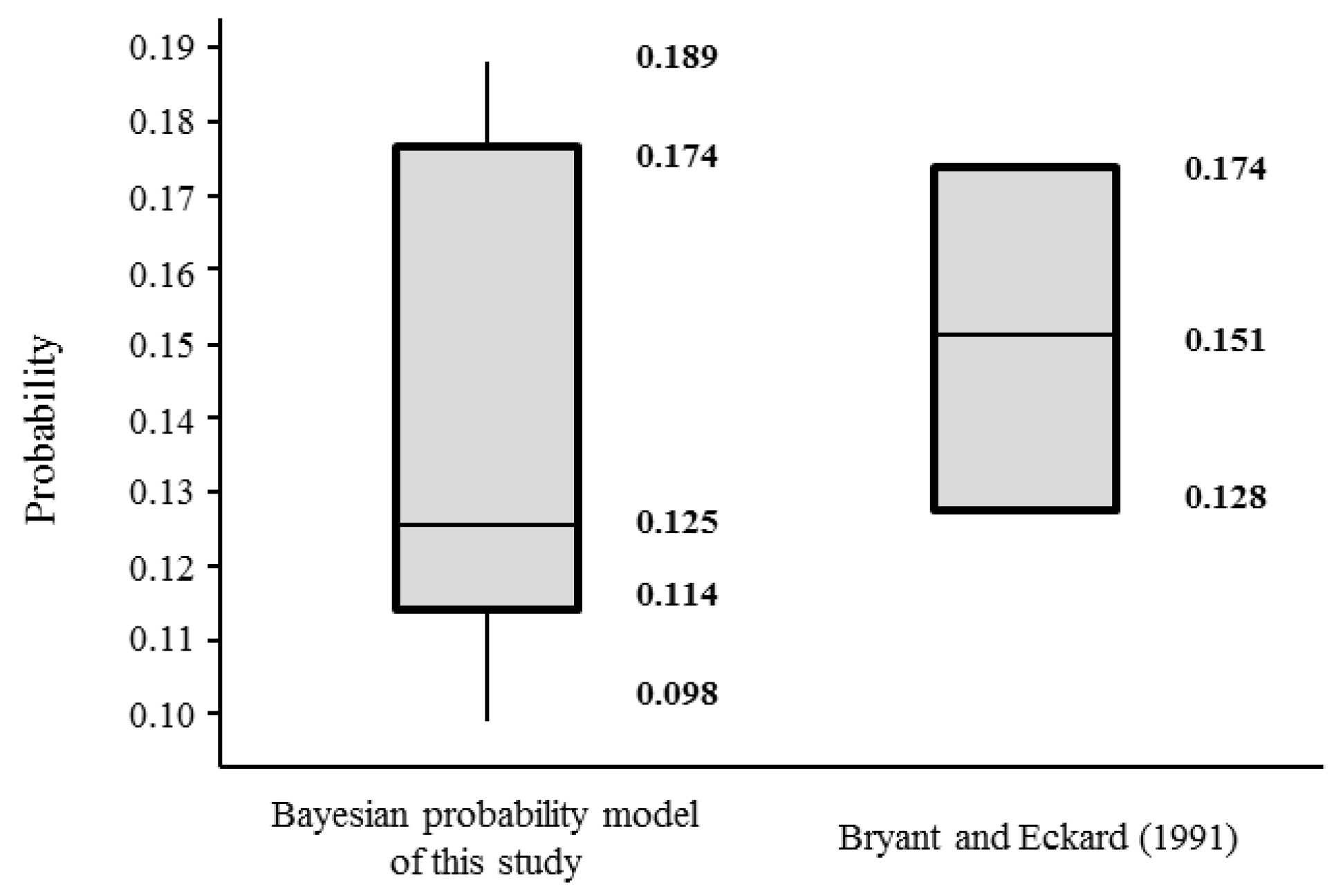
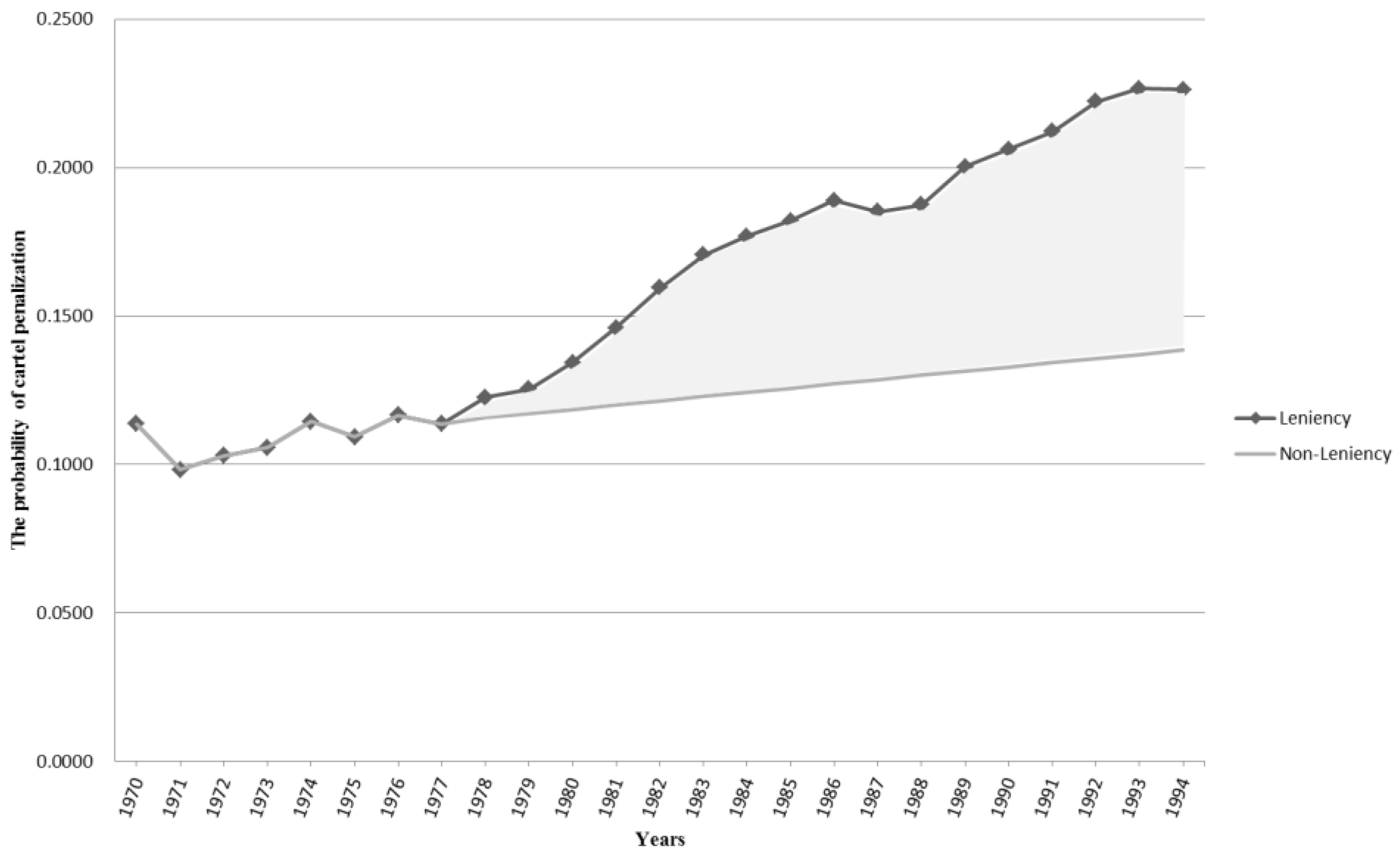
1]; indeed, the common finding among all of the studies, including the current study, was that the leniency program is a very effective policy.
This study evaluated the impact of antitrust policy and, therefrom estimated the probability of cartel penalization. From the antitrust authority standpoint, it provides an improved optimal policy, and from the corporate standpoint, it provides more effective decision-making. Certainly, the present paper has several limitations. First, further studies on realistic situations in specific countries and industries are needed. New antitrust policies recently have been introduced, such as for example, Amnesty Plus, punitive damage, class action, and consent order. These were also considered in further study.