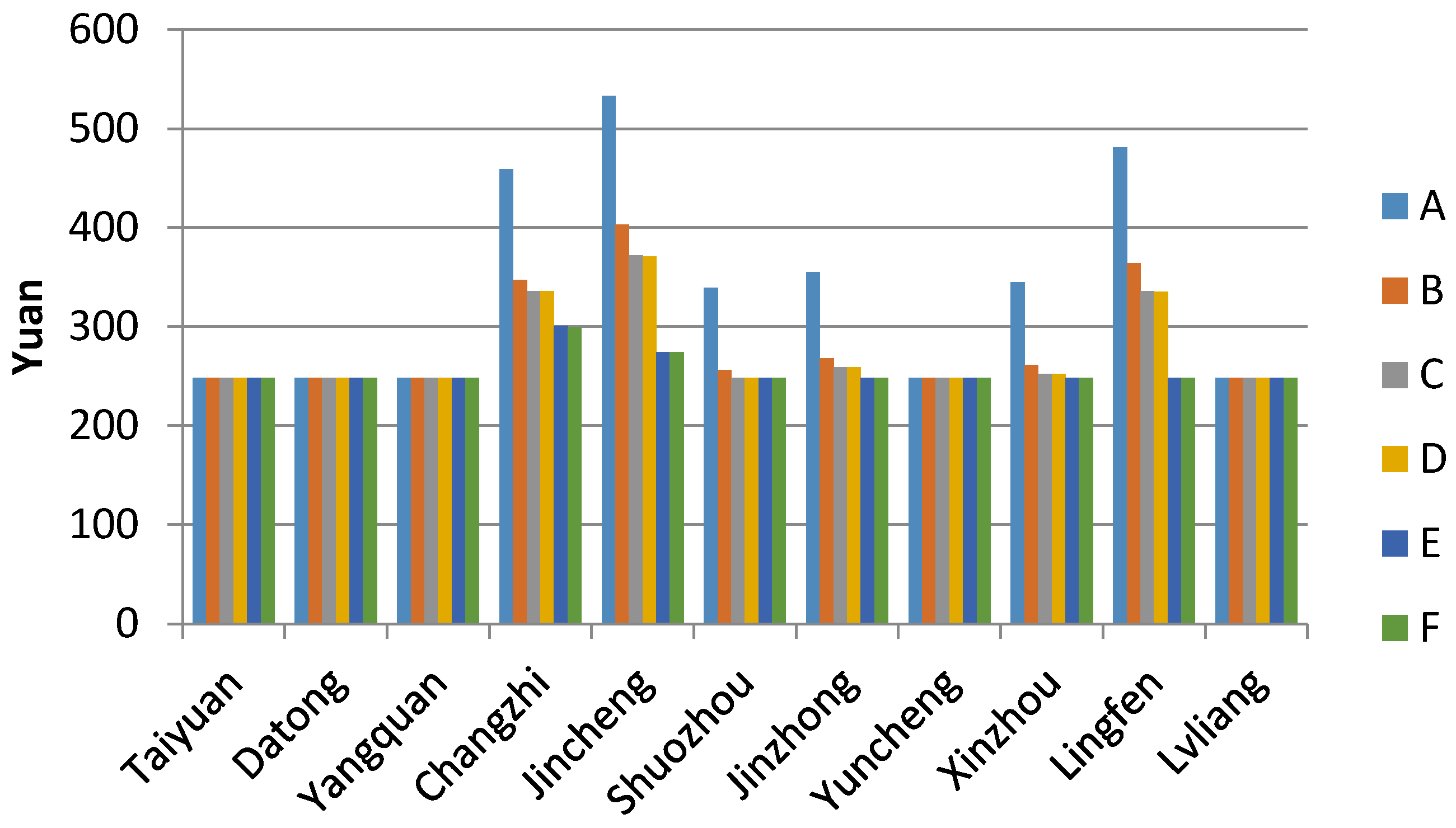1. Introduction
Recently, it has been widely recognized that ‘smart’ policies accounting for the interconnectedness between water, food, and energy should be able to offer solutions that are more favorable to sustainability than those made in ‘silos’ [
1,
2,
3,
4,
5,
6,
7,
8,
9]. Such ’nexus’ solutions will be more efficient across sectors and regions and will thus enable an optimal use of limited resources, which is especially important because of the growing population and increasing demand.
In the literature, different situations entailing interconnected water, food, and energy resources are considered and referred to as the water–food–energy (WFE) nexus. Perhaps most commonly, this term is used to emphasize the interconnection between agro-energy generation and agriculture on common land [
10,
11,
12,
13]. This situation is typical in many regions of the world, for example, in Brazil and the United States. Another widespread manifestation of the WFE nexus is the interconnection between hydropower generation and agriculture [
11,
12,
13,
14]. A number of approaches for dealing with the complexity of the WFE nexus-related issues have been proposed in the literature, including soft model linkage (e.g., CLEW [
15]), scenario analysis (e.g., WEAP-LEAP [
16]), and metabolism-based analysis (MuSIASEM [
11,
12]).
In this paper, we consider yet another example of the WFE nexus, as observed in northwest China, where agriculture and coal production compete for limited water and land. China is the largest producer and consumer of coal in the world and the largest user of coal-derived electricity. The coal industry, from coal mining to coal processing and coal conversion, is a very water-intensive industry, consuming 11–20% of water in China [
17]. Yet, most of the coal reserves are located in water-scarce areas. Moreover, in China, more than 40% of the agricultural land overlaps with the coal-mining territory [
18] and agriculture is the largest consumer of water in the country, consuming 64% of water in China [
19]. Land subsidence caused by coal mining is also a threat for agriculture. In addition to the water and land availability issue, coal production also generates a significant negative environmental impact, including air pollution and greenhouse gas emissions [
20,
21,
22,
23,
24]. It is imperative for the sustainable development of China in the next 10 years to resolve the conflict between agriculture and the coal industry over access to the limited water and land while also ensuring that environmental quality is at an acceptable level.
Traditionally, policies on coal and agricultural production have been developed independently from one another, and different regions have often been considered separately. Models used to support such policies also operate at different scales. Some models focus only on the local aspects of resource management, while others provide aggregated development scenarios [
25,
26]. As a result, decisions made to improve the functionality of one sector or region are often suboptimal for other sectors and regions [
27]. While some descriptive research on land and water as constraints to the coal and agricultural industry in China is available [
18,
19,
28,
29], to the best of our knowledge, there has been no study with an integrated analysis of coal and agriculture development paths that includes an account of the interdependencies among water, food, and energy, together with environmental impacts.
In this study, we develop an integrated cost-minimizing model to support decision making on the production allocation and investment in water-saving technologies under given resource availability (land and water) and environmental constraints. The model derives an optimal solution that meets the specified food and energy demands. Investment in water-saving technologies allows production to be increased, while the allocation of the production, aligned with the spatial heterogeneity in sub-regions, enables cost-savings due to the various advantages provided not only by local hydrological, glaciological, climatological, and geographical conditions, but also by the complex relationships among the WEF components.
2. Methodology
2.1. Model
A rather general cost-minimizing and spatially detailed modeling framework was previously formulated in [
30].
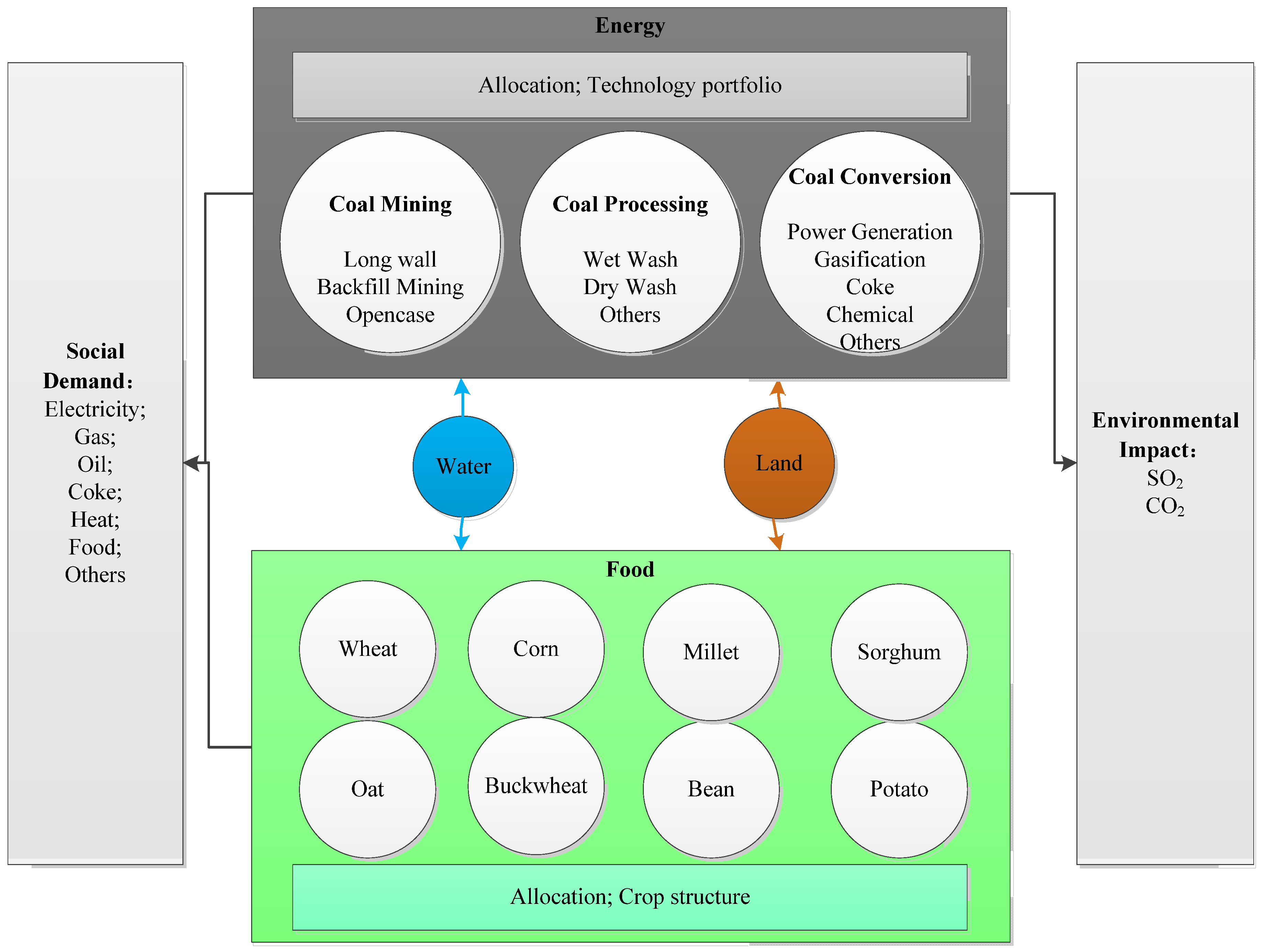
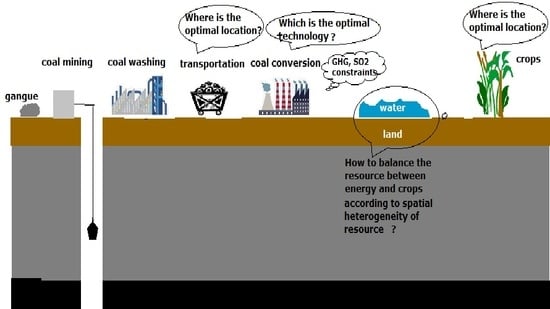
Figure 1 delineates the interconnections between the water, food, and energy in the model, along with the socioeconomic and environmental constraints. It is assumed that the region under consideration is split into sub-regions. Given the constraints, the model chooses the coal and agriculture production locations, together with technologies used in coal mining, processing, and conversion, as well as the crops to be grown. The coal-related technologies considered in this model version have different efficiencies and water intensities. Details of those technologies are available in
Table S1 in the Supplementary Material. We have not included agriculture-related technologies here, for example, those that improve irrigation efficiency. This and other simplifying assumptions that we make in this model version are dictated mainly by the availability of data from the case study. The general modeling framework is very flexible to include decision variables and constraints relevant to a specific research question in the context of the regional WEF.
The decision variables of this model version include (1) the amount of coal mined by each technology in each sub-region, (2) the amount of coal processed by each technology in each sub-region, (3) the amount of coal conversion product resulting from each technology in each sub-region, and (4) the amount of each crop produced in each sub-region.
The model constraints include the limitations on the total use of water and land resources; the supply of energy and food products should meet the demand, given exogenously, and the environmental impact should not exceed a pre-defined level.
The model finds the values of the decision variables selected to minimize the total cost, including the cost of coal mining, processing, and coal conversion, the cost of crop production, and the transportation costs. Its complete mathematical description can be found in the
Supplementary Material.
2.2. Case Study: Shanxi Province, China
Accounting for a quarter of the national coal reserve, Shanxi is one of the 14 energy bases proposed in the 12th Energy Plan by China’s National Energy Agency. As a water-intensive industry, coal production is facing water-shortage challenges—water is scarce in Shanxi, with per capita water use being only 1/25th of the average value in the world [
31,
32]. That is why competition for water between coal mining and agriculture is increasing.
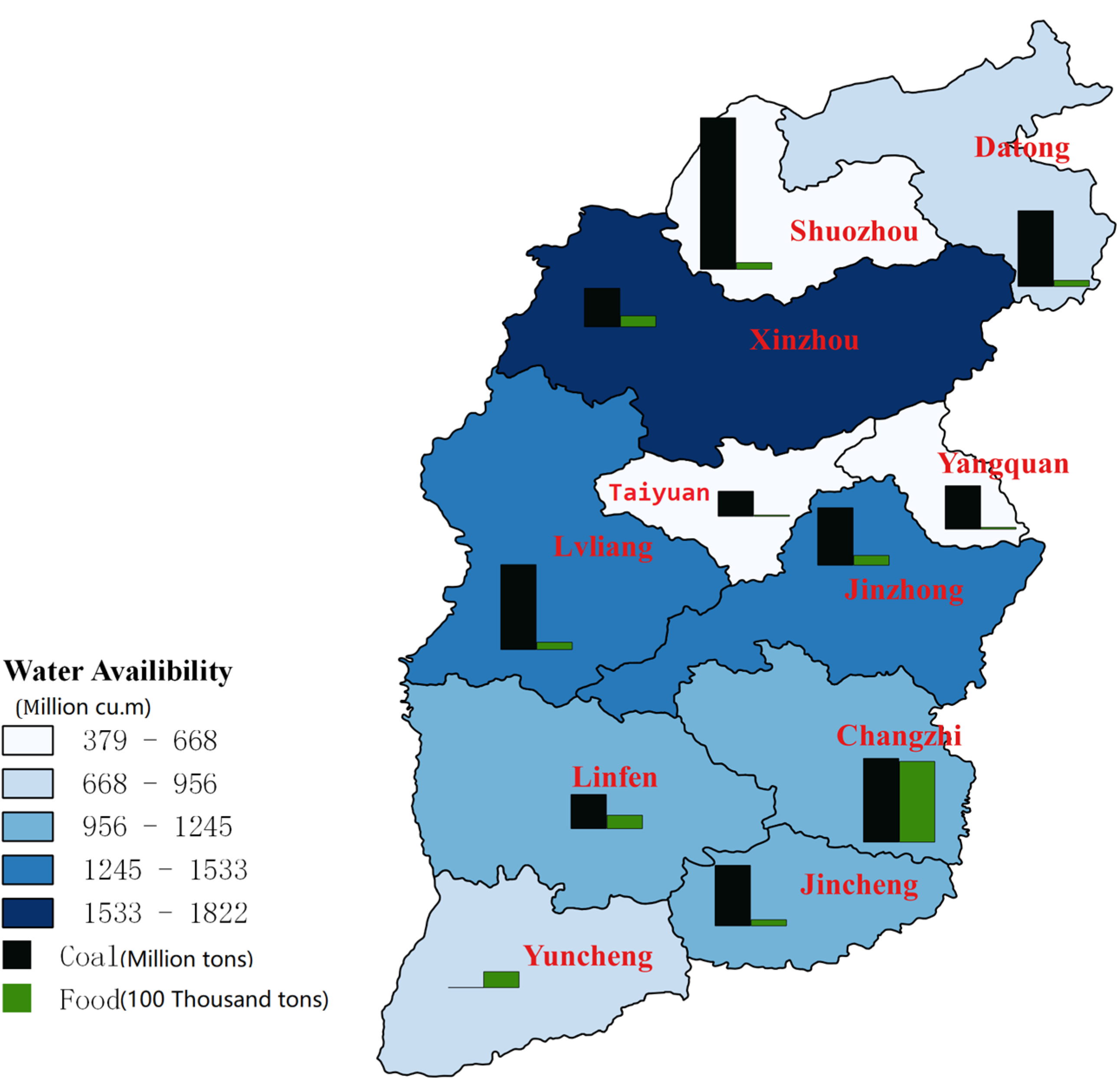
Figure 2 illustrates the mismatch between the available water, the coal productive capacity, and food production in 2012 in eleven prefectures of Shanxi province. For instance, in Shouzhou, Changzhi, Datong, and Yangquan, where water is particularly scarce, coal and crop production are both very high. In Xinzhou, the situation is the opposite. Due to the spatial heterogeneity of the water availability in Shanxi, a reallocation of coal and crop production could be a way of alleviating the water shortage problem in some prefectures.
Land is also a limiting factor in Shanxi, mainly for agriculture, but also for coal production. The coal industry occupies 40% of arable land [
33] and because of land subsidence, agriculture, and coal mining are also competing for land.
2.3. Design of Simulations
We designed the model-based numerical experiments with two purposes in mind. First, we aim to demonstrate how the optimized production allocation, technologies, and crops can indeed take advantage of spatial heterogeneity across sub-regions (prefectures), and hence how the total demand for energy and food can be satisfied without stressing the natural resources of land and water beyond their capacity—also keeping the environmental impact within a pre-defined limit. Second, we investigate how the most feasible resource-efficient combination of coal and crop production—the so-called production-possibility frontier—can be affected by the availability of natural resources (land and water). The latter would be very useful for policymakers who need to set long-term production targets in China. If a combination of production types is infeasible, even with the optimized allocations and best technologies, the target would turn into an unattainable goal.
To address the first purpose, we apply the data from the year 2012 in Shanxi. The crop and coal demands are defined at the level of the entire Shanxi province, so that a decision-maker could reallocate production across the province and among the 11 sub-regions (prefectures) to optimize resource use. The resource constraints are set in sub-regions according to site-specific characteristics. Extra constraints come from Chinese legislation. For example, according to 2012 legislation, at least 60% of the coal across the whole province should be washed. The full list of constraints can be found in
Table S16 Supplementary Material. We discuss the main model simplifications and limitations in the Discussion section.
To address the second purpose, we first observe that water availability has more pronounced annual fluctuations than land availability and that the land subsidence caused by coal mining can recover at some level after reclamation. We thus conclude that competition for land is less severe than for water, especially in the long term. Hence, we here focus on the sensitivity of optimal solutions to the varying water availability. We define water availability scenarios for 11 sub-regions (prefectures) based on the historical data. We considered four scenarios:
Business-As-Usual Water Availability (BAUWA): The water availability in prefectures is set to be equal to the actual water consumption by the coal industry and agriculture in 2012, which amounts to 107% of the average amount over the time period 1994–2012;
High Water Availability (HWA): The water availability in prefectures is set to be equal to the highest actual water consumption by the coal industry and agriculture in each prefecture during the time period 1994–2012, which is 116% of the average amount over the time period 1994–2012;
Low Water Availability (LWA): The water availability in prefectures is set to be equal to the lowest actual water consumption by the coal industry and agriculture in each prefecture during the time period 1994–2012, which is 60% of the average amount over the time period 1994–2012;
Average Water Availability (AWA): The water availability in prefectures is set to be equal to the average actual water consumption by the coal industry and agriculture in each prefecture during the time period 1994–2012.
In all scenarios, we assume that the percentage of the total available water used by the two sectors combined remains the same as in 2012. Chart S1 in the
Supplementary Material presents the spatial and temporal variations of water that was available across Shanxi Province during 1994–2012; these variations were quite significant between prefectures and between dry and wet years.
To show the production-possibility frontier under different water scenarios, we combine the above four water availability scenarios with different plausible levels of coal and crop demand. In the numerical experiments, according to the real productions, we assume that there are 10 plausible coal-production levels varying from 773.75 to 1001.00 million tons and 100 plausible crop-production levels varying from 6.17 to 20.17 million tons of grains. Hence, in total, we have 1000 coal-crop production combinations. We obtain the production-possibility frontier by investigating the feasibility of these combinations under four water scenarios specified above. On this basis, we also obtain the sensitivity of the production-possibility frontier with respect to the varying water availability.
3. Results
3.1. Allocation of Coal and Crop Production
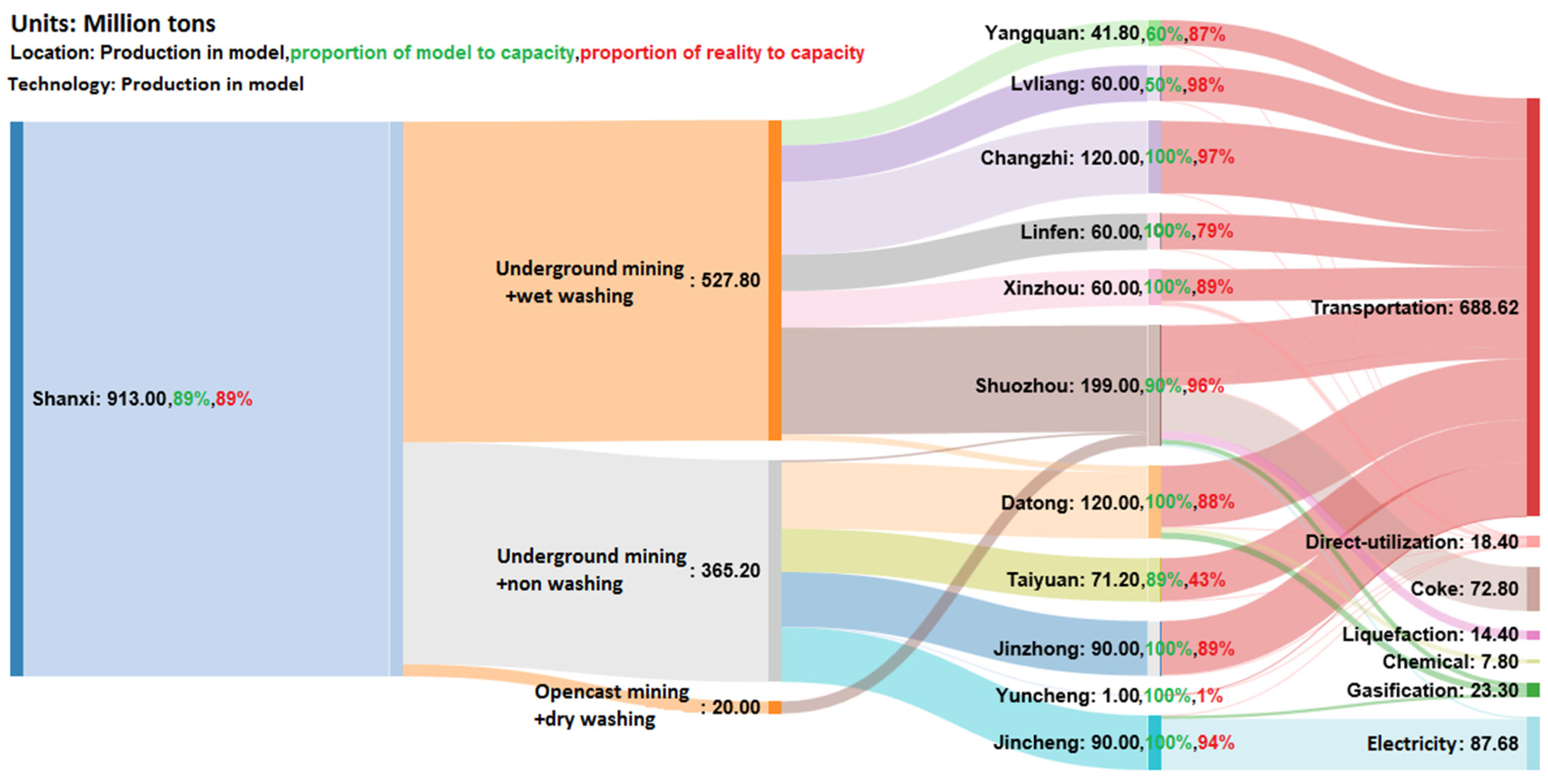
Figure 3 presents the optimal distribution of coal production and compares it with historical data. In 2012, 913 million tons of coal, constituting 89% of the total production capacity, were produced across all prefectures and by different technologies.
Notably, without the water-availability constraint, coal transportation among prefectures would have been unnecessary. Under the water constraint, however, the model recommends that coal and crop production should be redistributed among the prefectures for an optimal solution to be achieved. According to the model, the production of 913 million tons of coal under the water constraint could be distributed across 11 prefectures within minimal costs, if 8 of them (Changzhi, Linfen, Xinzhou, Datong, Taiyuan, Jinzhong, Yuncheng, and Jincheng) were to produce more coal (namely, 612 million tons, which is 17% more than they actually produced) and the remaining three (Yangquan, Lüliang, and Shuozhou) were to produce less coal (namely, 301 million tons, which is 23% less than they actually produced).
In reality, none of the prefectures utilized their full production capacity, while the model recommends that seven of the eight that could increase their production should do so up to their maximum limit. However, as the model assumes the same marginal costs of a technology in all prefectures and does not account for the size of individual producers, some effects of the economy of scale and spatial heterogeneity are not included. This might explain the difference between the historical data and the optimal solution.
In water-scarce prefectures, the model balances the costs of the introduction of the water-saving technologies and the transportation costs from a more efficient distribution of production. For example, the model recommends that in Datong, which is a very water-scarce prefecture, more than 90% of coal produced should be exported to other provinces without washing and conversion.
Figure 4 illustrates the optimal mix of crops across the eleven prefectures. Due to the high water requirement of crops, the available water resources play an important role in how crop production should be distributed among prefectures. The water requirements of different crops also vary across prefectures, depending on the climate and irrigation infrastructure (
Table S7), with irrigation being the dominant factor. In Taiyuan, for example, the water needs of all crops is less than the average [
34], which can be explained by the efficient irrigation infrastructure. The model consequently recommends that crop production should be increased in Taiyuan. In Xinzhou, corn requires less water than corn in other prefectures, while other crops, such as wheat, require more water than in other prefectures. Because of these differences, the model recommends that crop production should be distributed among prefectures for the most efficient use of water.
3.2. Production-Possibility Frontier under Different Water Scenarios
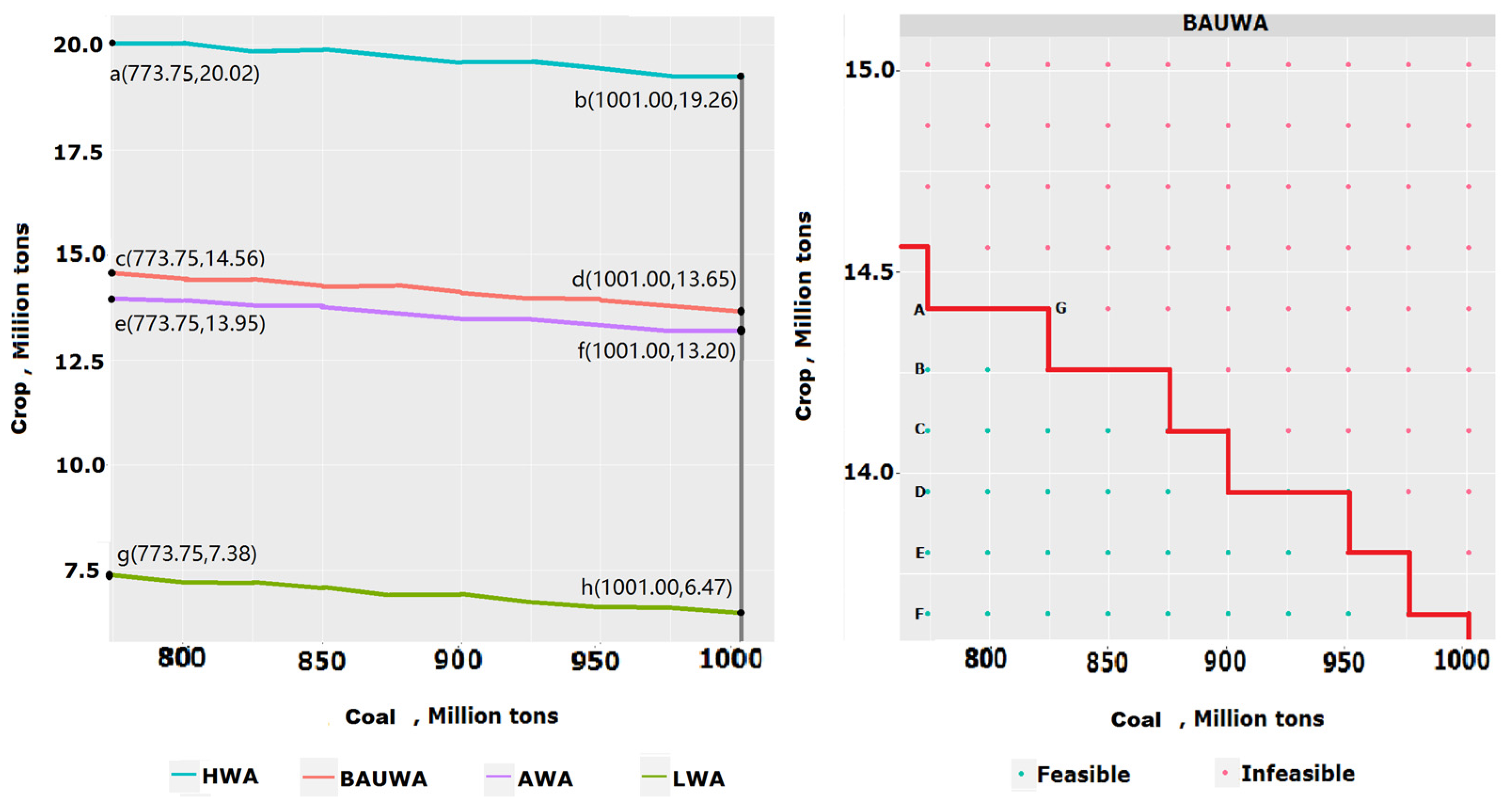
The left-hand panel in
Figure 5 displays the feasible sets of coal and crop production under four water scenarios. Each curve illustrates the production-possibility frontier and the quantified tradeoff between the coal and crop production as computed by the model that we developed. In each water-availability scenario, a regional planner finds an optimal balance between coal and crop production.
As agricultural activities are highly water-intensive, in each water-availability scenario, the ranges of feasible crop production differ, while the range of feasible coal production remains the same. In the AWA scenario, the identified feasible crop production ranges from 13.20 to 13.95 million tons, while in the BAUWA scenario, it ranges from 13.65 to 14.56 million tons. In the LWA scenario, when water is very scarce, the feasible crop production varies from 6.47 to 7.38 million tons, which is about half of what could be produced under the BAUWA scenario. Conversely, in the HWA scenario, when water is relatively abundant, feasible crop production varies from 19.29 to 20.02 million tons, which is approximately 40% more crop production than under the BAUWA scenario.
The feasible combination and allocation of coal and agricultural production is highly water-dependent. Notably, the 2012 level of crop production would not have been feasible if there had been a drought (e.g., the LWA scenario). This suggests that if droughts become more frequent, the planned expansion of coal production could jeopardize regional agriculture. By pursuing even a modest energy-security target of 774 million tons, which is 15% less than the 2012 level, agricultural production could reach only approximately 7.4 million tons of crops, which is 42% less than in 2012. Such a dramatic decrease in production capacity would greatly threaten regional food security.
The plot on the right-hand panel in
Figure 5 presents the production feasibility frontier for the BAUWA scenario. The graph depicts the tradeoff between coal mining and agricultural production. On average, the opportunity cost is approximately 4.4 thousand tons of crops for 1 million tons of coal. It is notable that the tradeoff curves in the right-hand panel are piece-wise constant containing flat segments. The flat segments reflect that by keeping crop production at the same level, coal production could expand under limited water resources, with the use of water-saving technologies. Consider, for example, the segment from A to G. Here, increasing coal production does not affect the level of crop production because the coal industry can utilize more water-saving technologies, although at a higher cost. Water-saving technologies, such as dry washing and air cooling, play an essential role in the LWA scenario. More details on the choices of the technologies under different scenarios are available in
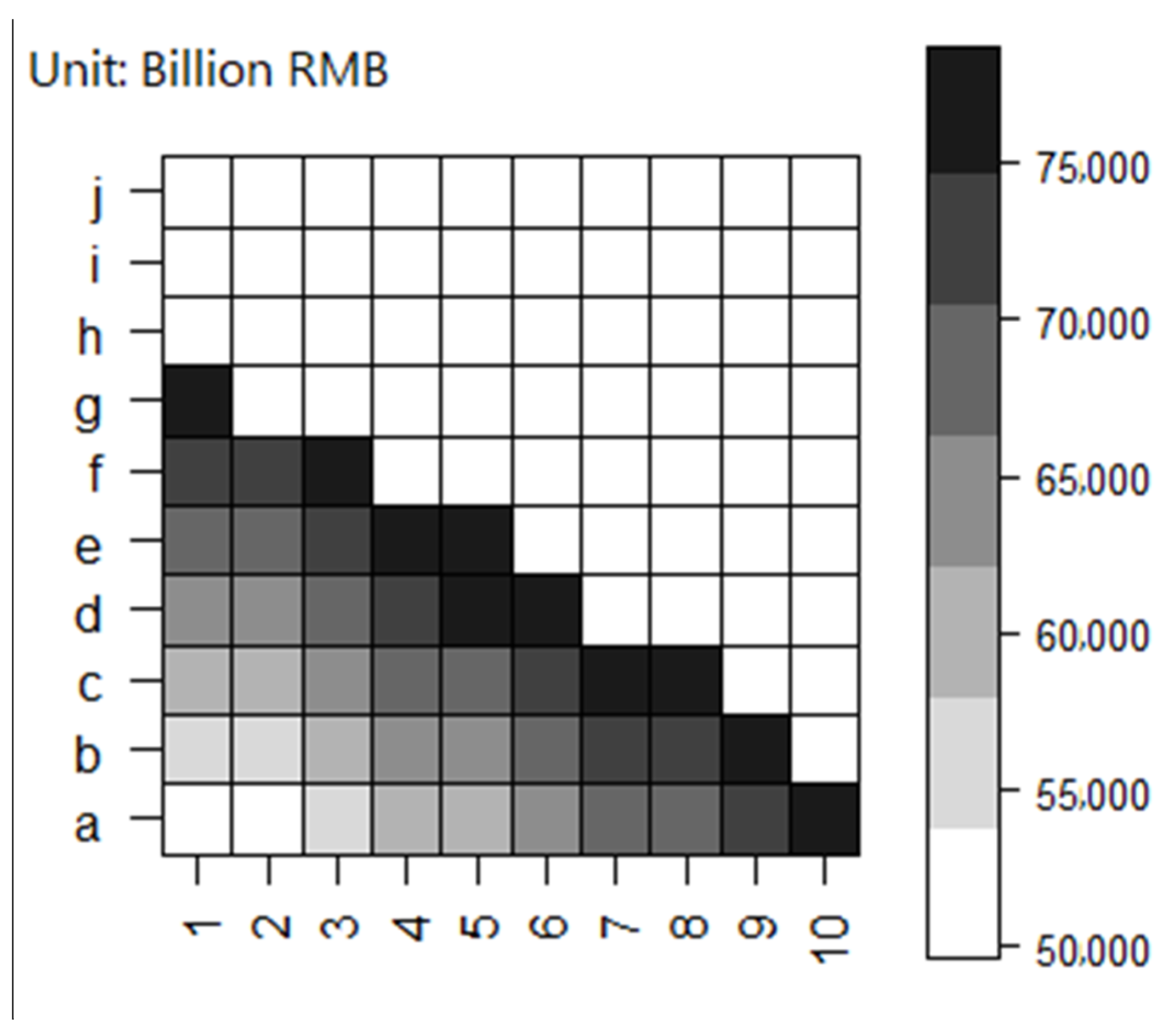
Table S1 in the Supplementary Material. Introduction of these technologies into optimal technological portfolios explains the high sensitivity of water consumption. We could also see the effect of the water shortage from the cost, taking point “g” in the left-hand panel which is feasible in all water scenarios; in the left-hand panel of
Figure 5, for example, the total cost in the LWA scenario is 77,088 billion RMB, higher than the cost in the other three scenarios which have the same cost of 23,030 billion RMB. This shows that water in other scenarios is sufficient without the need for water-saving technologies and reallocation.
Figure 6 delineates the landscape of the costs of all feasible combinations in the BAUWA scenario. The cost at the margin of the feasible set is much larger than the one inside, which shows how water constraints force water-saving technologies to be implemented, as production expands.
3.3. Water Scarcity, Shadow Price, and Water Pricing
In the northwest of China, due to the water shortage, a market for trading water rights, including in the industry and agriculture sectors, has been developing for several years. Water can be allocated efficiently if the water-pricing mechanism is properly set. One way to set reasonable prices for water is to use the water shadow prices from a production-optimizing model as a benchmark. Meanwhile, a high water shadow price is also a warning sign of severe water over-consumption and scarcity in a prefecture.
To show how the water shadow price changes with the water consumption change in prefectures, we selected six different coal–crop demand combinations (see right-hand panel of
Figure 5 and points A[773.75,14.56], B[773.75,14.41], C[773.75,14.26], D[773.75,14.11], E[773.75, 13.95], and F[773.75,13.80]), where crop production gradually decreases from 14.56 to 13.80 million tons. The points are within the production frontier under the BAUWA scenario.
Figure 7 displays the water shadow prices of A to F for 11 locations. In some locations, there is a decrease in the water price due to a reduction in water consumption by agriculture.
A ranking of the locations according to the water shadow prices provides policymakers with useful information about which locations to prioritize to enhance energy and crop production; namely, a higher water shadow price indicates a higher level of water scarcity.
4. Discussion
The aim of this study was to develop an integrated spatially detailed cost-minimizing model to support water–food–energy nexus management by distributing energy and agriculture production geographically within a region. Specifically, we explored the potential for the introduction of proper water-saving technologies aligned with the heterogeneity of the resource abundance in different sub-regions of a region, especially where production and resources are mismatched. The model, with its capability of capturing spatial characteristics of sub-regions, permits the derivation of cost-effective spatially detailed production and investment strategies. Notably, similar models available in the literature, of which we are aware, ignore the spatial dimension [
35,
36]. In our model, we make a disaggregation of a region into sub-regions where climate, landscape, and other conditions are different and, hence, the model is able to find an optimal use of those.
For illustrative purposes, the model was applied to Shanxi province in China. We derived an optimal allocation of production of coal and agriculture across 11 prefectures of Shanxi and compared it with the factual one in 2012. We also explored how the production-possibility frontier would be affected by the resource level and found it to be very sensitive to water availability. Finally, we computed the water shadow prices and argued that they could be used as a market mechanism to incentivize decision makers to locate production sites and choose technologies and crops, according to the optimal solution recommended by the model.
In this model version, we had to make a number of simplifying assumptions, mostly dictated by data availability. For example, in the model, we did not include technologies that enhance irrigation efficiency—for example, drip and sprinkler methods—as we were not able to find data on their costs and efficiency. Given that the agriculture sector is very water-intense, irrigation efficiency improvement is of exceptional importance for WFE security, as it helps expand the feasibility set. However, as these technologies are costly, our cost-minimizing model would deploy them only if demands are too high to be satisfied without them. Exploring the sensitivity of solutions to various demand levels is an interesting research question for investigation in future research. Another major simplification of this model version is that we did not include any pollution issues, in particular, GHG emissions from transportation caused by reallocation, and we set no constraints on those. While the general modeling framework easily allows for that, there are no sectoral emission quotas in China; hence, to disaggregate the total emission constraint on the entire regional economy into sectors is a separate problem which is beyond the scope of this study. Essentially, one has to anticipate the emergence of yet another tradeoff in this context between water consumption and environmental quality, which has important policy implications for long-term planning.
Spatial and temporal patterns are two dimensions, from which strategies consistent across sectors in the long term can be derived. So far, our model only accounts for the spatial aspect, while the temporal aspect requires a substantial model extension. Its importance becomes even larger if the variation of some input variables changes over time. These and many other aspects missing in this model version are the subjects of future work.
When we applied the scenarios analysis to deal with the uncertainty in the water supply, the model suggested that the optimal solution can be very different in different scenarios. If a policymaker would, for instance, choose such a scenario-dependent solution, irreversible costs could be incurred if a different scenario is actually realized. As water availability uncertainty is strongly affected by climate change, robust solutions that are ‘optimal’ over all or most potential water availability scenarios need to be derived for the long term. Hence, the research presented in our paper sets the stage for such modeling—a stochastic version will be required that allows for the explicit treatment of uncertainties, variability, and robust solutions.
5. Conclusions
In the northwest of China, the competition for water and land between the agriculture and energy sectors is increasing. In this paper, we developed an integrated spatially detailed cost-minimizing model under constraints on land and water availability to support sustainable management in a region. We applied the model to the case study of Shanxi province, China. We presented the production-possibility frontier, represented by feasible combinations of coal and crop production under the resource constraints, in which water and land are used most efficiently. This production-possibility frontier can be seen as a quantitative characteristic of the water–food–energy nexus. It gives regional decision makers an idea of the tradeoffs in which they need to strike a balance. Taking maximum advantage of the spatial heterogeneity in resource abundance helps decision makers to alleviate the conflicts around the water–food–energy (WFE) nexus. We next demonstrated that in water-scarce regions, like Shanxi, the production capacity and corresponding production solutions are highly sensitive to the water constraint; hence, to avoid high adaptation costs, robust solutions need to be developed for long-term planning. Finally, we estimated water shadow prices using the model and proposed that these could be the basis for intelligent differentiated water permit pricing. This will enable decentralized decision-making, leading to globally optimal outcomes in terms of resource allocation between agriculture and the coal industry—and also across regions to achieve cost-effective WFE management. The case study presented in this paper is an illustration of how a policy optimization model can be used to inform decisions on WFE management in a regional context.
Supplementary Materials
The following are available online at
https://www.mdpi.com/2071-1050/10/6/1689/s1, Figure S1: The minimum, maximum, the 2012 year, and the average water availability by regions, Shanxi, from 1994 to 2012; Table S1: Coal technologies in Shuozhou under four water scenarios, Detailed mathematical description of the model; Table S2: Sown area of major farm crops in Shanxi (2012); Table S3: Output of major farm crops in Shanxi (2012); Table S4: Water availability in each city from 1994 to 2012; Table S5: Proportion of water withdrawals by industry and agriculture sectors over the total water availability in 2012; Table S6: Coal productive capacity in Shanxi (2012); Table S7: Area of coal field in Shanxi; Table S8: Water withdrawals (water needed for production of a unit of coal) by technology; Table S9. Water withdrawals (water needed for production of a unit of crops) by crops in Shanxi; Table S10: Distance between major cities in Shanxi; Table S11: Efficiency of conversion technologies; Table S12: Demand for coal end-use products energy; Table S13. Demand for crops; Table S14: Water constraints and consumption data; Table S15: The land requirement for each crop in sub-regions; Table S16: List of the constraints and data in the case study.
Author Contributions
J.G. developed the computer code, assembled all the data, analyzed the results, and contributed to the paper text; X.X. initiated the research and contributed to the paper text; G.C. discussed and revised the manuscript; Y.M.E. and T.Y.E. designed the model; T.Y.E. advised on the implementation of the model into computer code and discussed the results and contributed to the paper text; E.A.R. designed the research questions, discussed the results, and contributed to the paper text; All authors read and approved the final manuscript.
Funding
The study is supported by the Fundamental Research Funds for the Central Universities, Grant Number: 2018QG01.
Acknowledgments
The first author gratefully acknowledges the financial support from the China Scholarship Council. We very much appreciate the insightful comments and suggestions from the editors and anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kurian, M. The water-energy-food nexus: Trade-offs, thresholds and transdisciplinary approaches to sustainable development. Environ. Sci. Policy 2017, 68, 97–106. [Google Scholar] [CrossRef]
- Gulati, M.; Jacobs, I.; Jooste, A.; Naidoo, D.; Fakir, S. The water–energy–food security nexus: Challenges and opportunities for food security in South Africa. Aquat. Proc. 2013, 1, 150–164. [Google Scholar] [CrossRef]
- Kaddoura, S.; El Khatib, S. Review of water-energy-food Nexus tools to improve the Nexus modelling approach for integrated policy making. Environ. Sci. Policy 2017, 77, 114–121. [Google Scholar] [CrossRef]
- Keskinen, M.; Guillaume, J.H.; Kattelus, M.; Porkka, M.; Räsänen, T.A.; Varis, O. The water-energy-food nexus and the transboundary context: Insights from large Asian rivers. Water 2016, 8, 193. [Google Scholar] [CrossRef]
- Wichelns, D. The water-energy-food nexus: Is the increasing attention warranted, from either a research or policy perspective? Environ. Sci. Policy 2017, 69, 113–123. [Google Scholar] [CrossRef]
- Giupponi, C.; Gain, A.K. Integrated spatial assessment of the water, energy and food dimensions of the sustainable development goals. Reg. Environ. Chang. 2017, 17, 1881–1893. [Google Scholar] [CrossRef]
- Chang, Y.; Li, G.; Yao, Y.; Zhang, L.; Yu, C. Quantifying the water-energy-food nexus: Current status and trends. Energies 2016, 9, 65. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Ruddell, B.L.; Reed, P.M.; Hook, R.I.; Zheng, C.; Tidwell, V.C.; Siebert, S. The food-energy-water nexus: Transforming science for society. Water Resour. Res. 2017, 53, 3550–3556. [Google Scholar] [CrossRef]
- Taniguchi, M.; Masuhara, N.; Burnett, K. Water, energy, and food security in the Asia Pacific region. J. Hydrol. Reg. Stud. 2017, 11, 9–19. [Google Scholar] [CrossRef]
- Rathmann, R.; Szklo, A.; Schaeffer, R. Land use competition for production of food and liquid biofuels: An analysis of the arguments in the current debate. Renew. Energy 2010, 35, 14–22. [Google Scholar] [CrossRef]
- Giampietro, M.; Richard, J.; Aspinall, R.; Bukkens, S.G.F.; Benalcazar, J.C.; Diaz-Maurin, F.; Flammini, A.; Gomiero, T.; Kovacic, Z.; Madrid, C.; et al. An Innovative Accounting Framework for the Food-Energy-Water Nexus: Application of the MuSIASEM Approach to Three Case Studies; Environment and Natural Resources Working Paper No. 56; FAO: Rome, Italy, 2013; ISBN 9789251079645. [Google Scholar]
- Giampietro, M.; Aspinall, R.J.; Ramos-Martin, J.; Bukkens, S.G.F. (Eds.) Resource Accounting for Sustainability Assessment: The Nexus between Energy, Food, Water and Land Use; Routledge: New York, NY, USA, 2014; ISBN 9781317962083. [Google Scholar]
- Flammini, A.; Puri, M.; Pluschke, L.; Dubois, O. Walking the Nexus Talk: Assessing the Water-Energy-Food Nexus in the Context of the Sustainable Energy for All Initiative; Environment and Natural Resources Working Paper No. 58; FAO: Rome, Italy, 2014; ISBN 9789251084878. [Google Scholar]
- Salmaso, F.; Crosa, G.; Espa, P.; Gentili, G.; Quadroni, S.; Zaccara, S. Benthic macroinvertebrates response to water management in a lowland river: Effects of hydro-power vs. irrigation off-stream diversions. Environ. Monit. Assess. 2018, 190, 33. [Google Scholar] [CrossRef] [PubMed]
- Howells, M.; Hermann, S.; Welsch, M.; Bazilian, M.; Segerström, R.; Alfstad, T.; Ramma, I. Integrated analysis of climate change, land-use, energy and water strategies. Nat. Clim. Chang. 2013, 3, 621–626. [Google Scholar] [CrossRef]
- Dale, L.L.; Karali, N.; Millstein, D.; Carnall, M.; Vicuña, S.; Borchers, N.; Bustos, E.; O’Hagan, J.; Purkey, D.; Heaps, C.; et al. An integrated assessment of water-energy and climate change in Sacramento, California: How strong is the nexus? Clim. Chang. 2015, 132, 223–235. [Google Scholar] [CrossRef]
- Pan, L.; Liu, P.; Ma, L.; Li, Z. A supply chain based assessment of water issues in the coal industry in China. Energy Policy 2012, 48, 93–102. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, G.; Xiao, W.; Li, J.; Yang, Y.; Yu, Y. Farmland damage and its impact on the overlapped areas of cropland and coal resources in the eastern plains of China. Resour. Conserv. Recycl. 2014, 86, 1–8. [Google Scholar] [CrossRef]
- Zhuo, L.; Mekonnen, M.M.; Hoekstra, A.Y. Consumptive water footprint and virtual water trade scenarios for China—With a focus on crop production, consumption and trade. Environ. Int. 2016, 94, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Finkelman, R.B.; Tian, L. The health impacts of coal use in China. Int. Geol. Rev. 2017, 60, 579–589. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Q.; Tong, D.; Zheng, B.; Li, M.; Huo, H.; He, K.B. High-resolution inventory of technologies, activities, and emissions of coal-fired power plants in China from 1990 to 2010. Atmos. Chem. Phys. Discuss. 2015, 15, 13299–13317. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, C.; Feng, Y.; Zhi, G.; Li, J.; Zhang, G. Measurements of emission factors of PM2. 5, OC, EC, and BC for household stoves of coal combustion in China. Atmos. Environ. 2015, 109, 190–196. [Google Scholar] [CrossRef]
- Xue, Y.; Tian, H.; Yan, J.; Zhou, Z.; Wang, J.; Nie, L.; Wu, X. Temporal trends and spatial variation characteristics of primary air pollutants emissions from coal-fired industrial boilers in Beijing, China. Environ. Pollut. 2016, 213, 717–726. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Hu, J.; Ying, Q.; Hao, H.; Wang, D.; Zhang, H. Current and future emissions of primary pollutants from coal-fired power plants in Shaanxi, China. Sci. Total Environ. 2017, 595, 505–514. [Google Scholar] [CrossRef] [PubMed]
- Fricko, O.; Parkinson, S.C.; Johnson, N.; Strubegger, M.; Vliet, M.T.V.; Riahi, K. Energy sector water use implications of a 2 °C climate policy. Environ. Res. Lett. 2016, 11, 03401. [Google Scholar] [CrossRef]
- Havlík, P.; Schneider, U.A.; Schmid, E.; Böttcher, H.; Fritz, S.; Skalský, R.; Leduc, S. Global land-use implications of first and second generation biofuel targets. Energy Policy 2011, 39, 5690–5702. [Google Scholar] [CrossRef]
- Barnett, J.; Rogers, S.; Webber, M.; Finlayson, B.; Wang, M. Sustainability: Transfer project cannot meet China’s water needs. Nature 2015, 527, 295–297. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Wu, Q.; Dong, D.; Jiao, J. Avoiding coal–water conflicts during the development of China’s large coal-producing regions. Mine Water Environ. 2012, 31, 74–78. [Google Scholar] [CrossRef]
- Huang, W.; Ma, D.; Chen, W. Connecting water and energy: Assessing the impacts of carbon and water constraints on China’s power sector. Appl. Energy 2017, 185, 1497–1505. [Google Scholar] [CrossRef]
- Xu, X.; Gao, J.; Cao, G.Y.; Ermoliev, Y.M.; Ermolieva, T.Y.; Kryazhimskii, A.V.; Rovenskaya, E.A. Systems analysis of coal production and energy-water-food security in China. Cybern. Syst. Anal. 2015, 51, 370–377. [Google Scholar] [CrossRef]
- Dang, X.; Webber, M.; Chen, D.; Wang, M.Y. Evolution of water management in Shanxi and Shaanxi provinces since the Ming and Qing dynasties of China. Water 2013, 5, 643–658. [Google Scholar] [CrossRef]
- Shanxi Statistical Yearbook 2013. Available online: http://www.stats-sx.gov.cn/tjsj/tjnj/nj2013/html/njcx.htm (accessed on 30 January 2017).
- Qiao, Z. The impact on the water and land from the coal mining in Shanxi. Soil Water Conserv. Sci. Technol. 2007, 4, 1–5. [Google Scholar]
- Qu, X. The research on the countermeasure and current situation of the irrigation in Shanxi. Water Resour. Dev. Res. 2011, 11, 21–27. [Google Scholar]
- Lotfi, M.M.; Ghaderi, S.F. Possibilistic programming approach for mid-term electric power planning in deregulated markets. Int. J. Electr. Power 2012, 34, 161–170. [Google Scholar] [CrossRef]
- Zhang, X.; Vesselinov, V.V. Integrated modeling approach for optimal management of water, energy and food security nexus. Adv. Water Resour. 2017, 101, 1–10. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).