Computation Offloading Algorithm for Arbitrarily Divisible Applications in Mobile Edge Computing Environments: An OCR Case
Abstract
:1. Introduction
- We propose a theoretical model for offloading arbitrarily divisible applications in mobile edge computing environments;
- We derive closed-form expressions for the sizes of segments and the minimum makespan of the entire application;
- Based on the closed-form expressions, a heuristic is proposed for partitioning and distributing arbitrarily divisible applications in mobile edge computing environments.
- One method is proposed to estimate these decision parameters in real environments.
2. Related Work
3. Model and Algorithm for Offloading Arbitrarily Divisible Applications
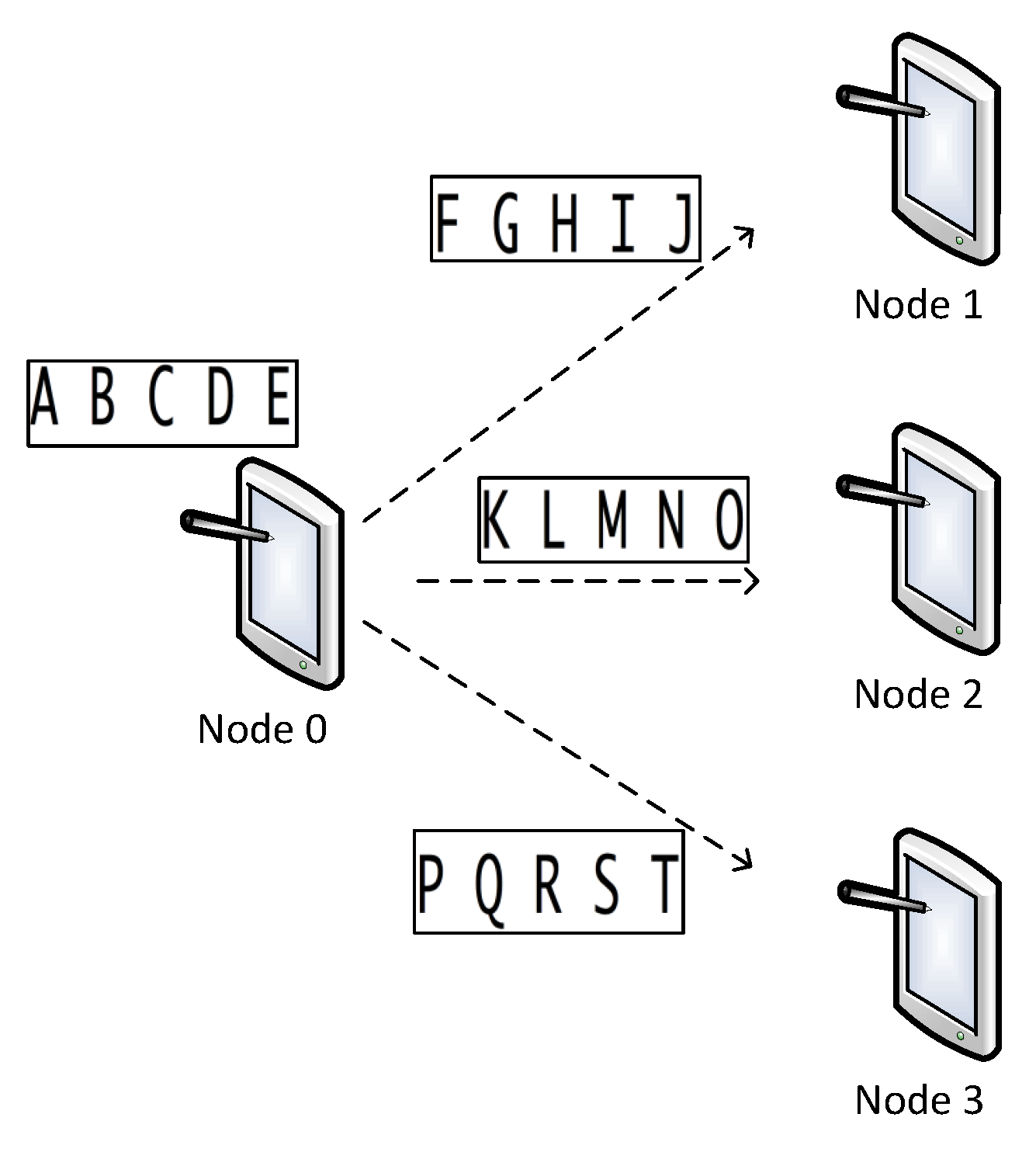
3.1. Optical Character Recognition: A Typical Arbitrarily Divisible Application
3.2. Model and Algorithm for Offloading OCR-Like Applications
- (1)
- The client node sends the OCR segment to the surrogate node;
- (2)
- After receiving the entire OCR segment, the surrogate node start processing the segment;
- (3)
- The surrogate node returns the result to the client node.
| Algorithm 1: Algorithm for adaptively partitioning and allocating a divisible OCR application. |
| input: Application Info: Resource Info: output: Offloading decision, and makespan (1) Find out the number k of available resources and their parameters ; (2) Calculate and partition the task for the client node based on Formula (5); (3) Calculate and partition the task for each surrogate based on Formula (4); (4) Calculate the makespan based on Formula (6). |
4. Experiments and Results
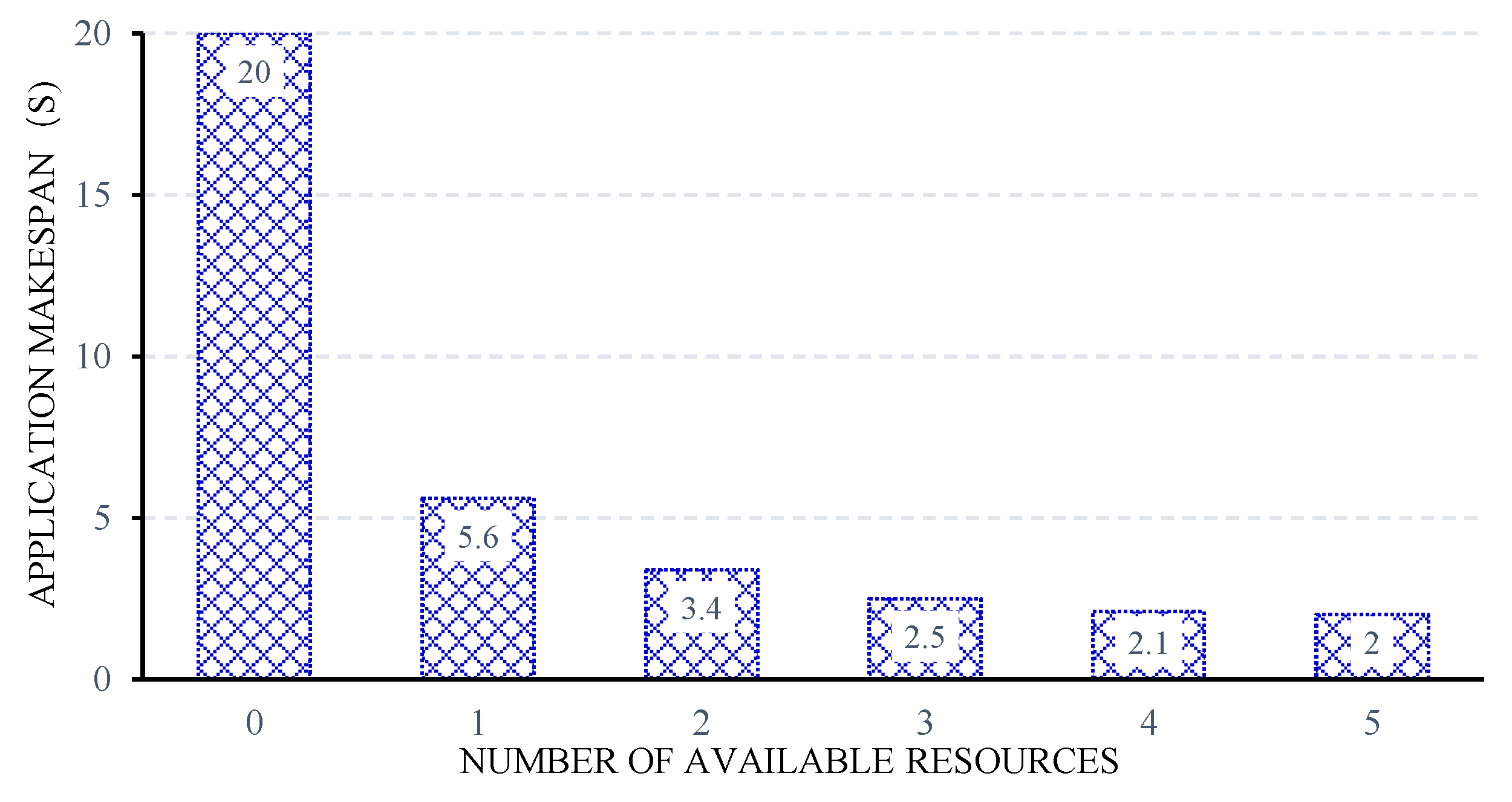
4.1. Simulation Environments
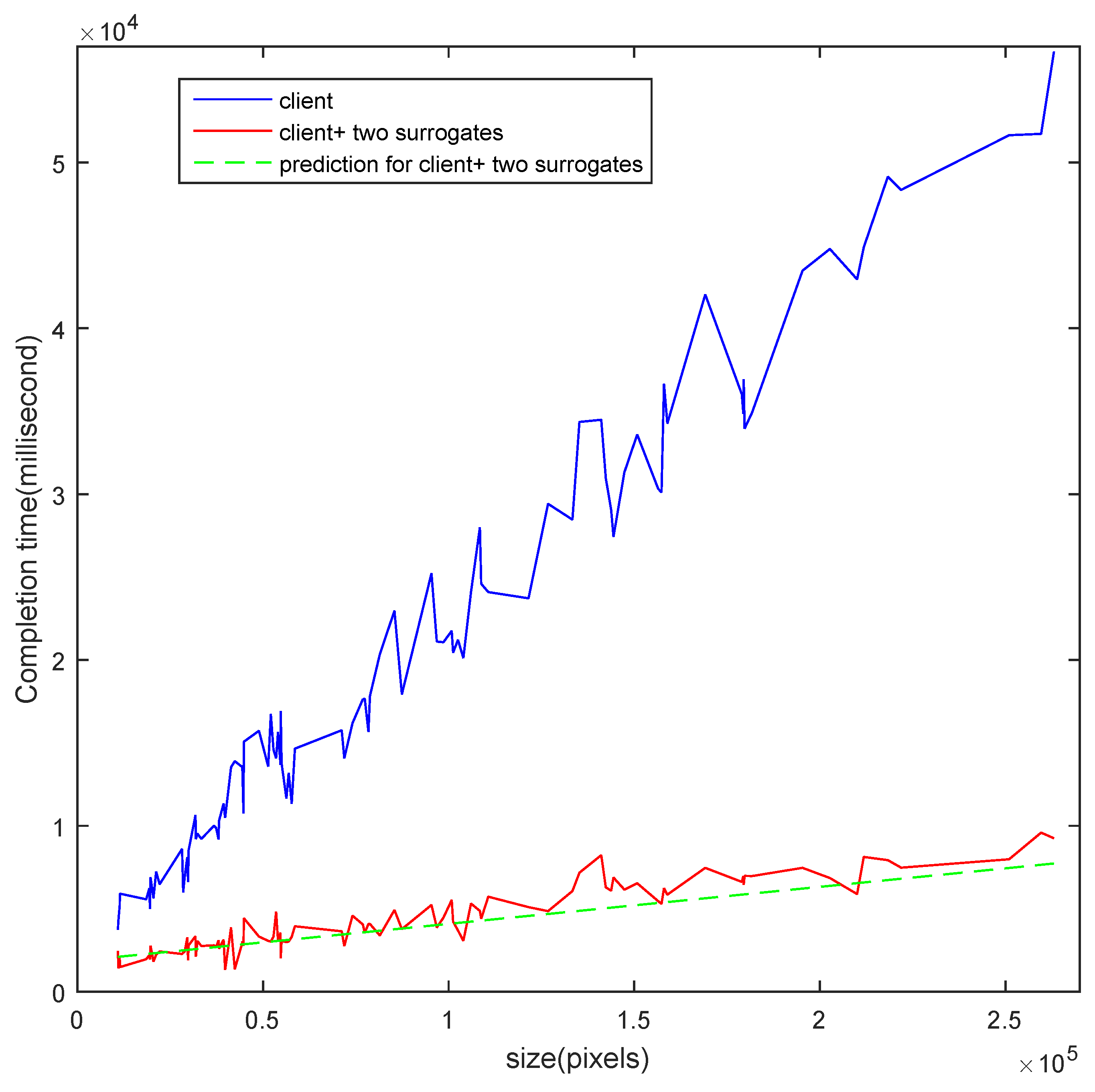
4.2. Real Experiments
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| MEC | Mobile Edge Computing |
| OCR | Optical Character Recognition |
| IoT | the Internet of Things |
References
- Balan, R.; Flinn, J.; Satyanarayanan, M.; Sinnamohideen, S.; Yang, H.I. The case for cyber foraging. In Proceedings of the 10th Workshop on ACM SIGOPS European Workshop, Saint-Emilion, France, 1 July 2002; ACM: New York, NY, USA, 2002; pp. 87–92. [Google Scholar]
- Li, B.; Pei, Y.; Wu, H.; Shen, B. Heuristics to allocate high-performance cloudlets for computation offloading in mobile ad hoc clouds. J. Supercomput. 2015, 79, 3009–3036. [Google Scholar] [CrossRef]
- Abolfazli, S.; Sanaei, Z.; Ahmed, E.; Gani, A.; Buyya, R. Cloud-based augmentation for mobile devices: Motivation, taxonomies, and open challenges. IEEE Commun. Surv. Tutor. 2014, 16, 337–368. [Google Scholar] [CrossRef]
- Lee, B.D.; Lim, K.H.; Choi, Y.H.; Kim, N. An adaptive computation offloading decision for energy-efficient execution of mobile applications in clouds. IEICE Trans. Inf. Syst. 2014, 97, 1804–1811. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef]
- Chen, M.; Hao, Y. Task Offloading for Mobile Edge Computing in Software Defined Ultra-dense Network. IEEE J. Sel. Areas Commun. 2018. [Google Scholar] [CrossRef]
- Lewis, G.A.; Echeverria, S.; Simanta, S.; Bradshaw, B.; Root, J. Cloudlet-based cyber-foraging for mobile systems in resource-constrained edge environments. In Proceedings of the ICSE Companion 2014 Companion Proceedings of the 36th International Conference on Software Engineering, Hyderabad, India, 31 May–7 June 2014; pp. 412–415. [Google Scholar]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog Computing and Its Role in the Internet of Things. In Proceedings of the First Edition of the MCC Workshop on Mobile Cloud Computing (MCC ’12), Helsinki, Finland, 17 August 2012; ACM: New York, NY, USA, 2012; pp. 13–16. [Google Scholar] [CrossRef]
- Neto, J.; Yu, S.; Macedo, D.; Nogueira, J.; Langar, R.; Secci, S. ULOOF: A User Level Online Offloading Framework for Mobile Edge Computing. IEEE Trans. Mob. Comput. 2018. [Google Scholar] [CrossRef]
- Giatsoglou, N.; Ntontin, K.; Kartsakli, E.; Antonopoulos, A.; Verikoukis, C. D2D-Aware Device Caching in mmWave-Cellular Networks. IEEE J. Sel. Areas Commun. 2017, 35, 2025–2037. [Google Scholar] [CrossRef]
- Datsika, E.; Antonopoulos, A.; Zorba, N.; Verikoukis, C. Software Defined Network Service Chaining for OTT Service Providers in 5G Networks. IEEE Commun. Mag. 2017, 55, 124–131. [Google Scholar] [CrossRef]
- Antonopoulos, A.; Kartsakli, E.; Perillo, C.; Verikoukis, C. Shedding Light on the Internet: Stakeholders and Network Neutrality. IEEE Commun. Mag. 2017, 55, 216–223. [Google Scholar] [CrossRef]
- Liu, J.; Ahmed, E.; Shiraz, M.; Gani, A.; Buyya, R.; Qureshi, A. Application partitioning algorithms in mobile cloud computing: Taxonomy, review and future directions. J. Netw. Comput. Appl. 2015, 48, 99–117. [Google Scholar] [CrossRef]
- Liu, L.; Chang, Z.; Guo, X.; Mao, S.; Ristaniemi, T. Multiobjective Optimization for Computation Offloading in Fog Computing. IEEE Internet Things J. 2018, 5, 283–294. [Google Scholar] [CrossRef]
- Wu, H. Multi-Objective Decision-Making for Mobile Cloud Offloading: A Survey. IEEE Access 2018, 6, 3962–3976. [Google Scholar] [CrossRef]
- Huang, C.M.; Chiang, M.S.; Dao, D.T.; Su, W.L.; Xu, S.; Zhou, H. V2V Data Offloading for Cellular Network Based on the Software Defined Network (SDN) Inside Mobile Edge Computing (MEC) Architecture. IEEE Access 2018, 6, 17741–17755. [Google Scholar] [CrossRef]
- Camp, T.; Boleng, J.; Davies, V. A survey of mobility models for ad hoc network research. Wirel. Commun. Mob. Comput. 2002, 2, 483–502. [Google Scholar] [CrossRef]
- Suresh, S.; Kim, H.; Run, C.; Robertazzi, T.G. Scheduling nonlinear divisible loads in a single level tree network. J. Supercomput. 2012, 61, 1068–1088. [Google Scholar] [CrossRef]
- Wang, K.; Robertazzi, T.G. Scheduling divisible loads with nonlinear communication time. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2479–2485. [Google Scholar] [CrossRef]
- Bharadwaj, V.; Ghose, D.; Robertazzi, T. Divisible load theory: A new paradigm for load scheduling in distributed systems. Clust. Comput. 2003, 6, 7–17. [Google Scholar] [CrossRef]
- Suresh, S.; Omkar, S.N.; Mani, V. Parallel implementation of back-propagation algorithm in networks of workstations. IEEE Trans. Parallel Distrib. Syst. 2005, 16, 24–34. [Google Scholar] [CrossRef]
- Othman, S.G.M. Comprehensive Review on Divisible Load Theory: Concepts, Strategies, and Approaches. Math. Probl. Eng. 2014, 2014, 460354. [Google Scholar]
- Beaumont, O.; Casanova, H.; Legrand, A.; Robert, Y.; Yang, Y. Scheduling divisible loads on star and tree networks: Results and open problems. IEEE Trans. Parallel Distrib. Syst. 2005, 16, 207–218. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Kang, H. Sensing workload scheduling in sensor networks using divisible load theory. In Proceedings of the IEEE GLOBECOM 2007, Washington, DC, USA, 26–30 November 2007; pp. 785–789. [Google Scholar]
- Redondi, A.; Cesana, M.; Tagliasacchi, M.; Filippini, I.; Dán, G.; Fodor, V. Cooperative image analysis in visual sensor networks. Ad Hoc Netw. 2015, 28, 38–51. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, Y.; Yang, G. Scheduling divisible loads in the dynamic heterogeneous grid environment. In Proceedings of the 1st International Conference on Scalable Information Systems, Hong Kong, China, 1 June 2006; Volume 152, p. 8. [Google Scholar]
- Hu, M.; Luo, J.; Veeravalli, B. Optimal provisioning for scheduling divisible loads with reserved cloud resources. In Proceedings of the 2012 18th IEEE International Conference on Networks, Singapore, 12–14 December 2012; pp. 204–209. [Google Scholar]
- Lin, W.; Liang, C.; Wang, J.Z.; Buyya, R. Bandwidth-aware divisible task scheduling for cloud computing. Softw. Pract. Exp. 2014, 44, 163–174. [Google Scholar] [CrossRef]
- Khan, L.I.L. Implementation and performance evaluation of a scheduling algorithm for divisible load parallel applications in a cloud computing environment. Softw. Pract. Exp. 2015, 45, 765–781. [Google Scholar]
- Abdullah, M.; Othman, M. Cost-based multi-QoS job scheduling using divisible load theory in cloud computing. Procedia Comput. Sci. 2013, 18, 928–935. [Google Scholar] [CrossRef]
- Veeravalli, B.; Viswanadham, N. Suboptimal solutions using integer approximation techniques for scheduling divisible loads on distributed bus networks. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 2000, 30, 680–691. [Google Scholar] [CrossRef]
- Li, X.; Bharadwaj, V.; Ko, C. Divisible load scheduling on single-level tree networks with buffer constraints. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1298–1308. [Google Scholar]
- Veeravalli, B.; Li, X.; Ko, C.C. On the influence of start-up costs in scheduling divisible loads on bus networks. IEEE Trans. Parallel Distrib. Syst. 2000, 11, 1288–1305. [Google Scholar] [CrossRef]
- Li, X.; Veeravalli, B. PPDD: Scheduling multi-site divisible loads in single-level tree networks. Clust. Comput. 2010, 13, 31–46. [Google Scholar] [CrossRef]
- Abdullah, M.; Othman, M. Scheduling Divisible Jobs to Optimize the Computation and Energy Costs. Int. J. Eng. Sci. Invent. 2015, 4, 27–33. [Google Scholar]
- Yang, K.; Ou, S.; Chen, H.H. On effective offloading services for resource-constrained mobile devices running heavier mobile Internet applications. IEEE Commun. Mag. 2008, 46, 56–63. [Google Scholar] [CrossRef]

| References | The Model Considered in the Reference(s) | The Model Considered in This Paper |
|---|---|---|
| [28] | (1) Workload can be divided into M equal-sized independent tasks. | (1) Workload can be divided arbitrarily. |
| (2) When calculating the cost of processing, network latency and start-up time of virtual machines were not considered. | ||
| [18] | The computation time function for any given processor is a polynomial equation in load fraction size. | The computation time function for divisible application is linearly proportional to the load fraction size. |
| [25] | Network latency and start-up time were NOT considered. | Network latency and start-up time of virtual machines were taken into account in the mathematical model. |
| [29,32] | A divisible application is scheduled to N available computing workers in a sequence fashion. | A divisible application is scheduled to N available computing workers in parallel. |
| [33] | Load fractions are transmitted from the control unit to available processors one by one. | Load fractions are transmitted from the client node to available surrogates in parallel by using the collective communication model. |
| [30,34] | Focus on static scheduling of a group of applications at the same time. | Focus on dynamic scheduling of one single divisible application. |
| [35] | (1) Both computation and energy cost were considered. | (1) Only computation cost is considered. |
| (2) Communication cost was not taken into account. | (2) Communication cost-related parameters (bandwidth and latency) were taken into account. |
| Notation | Definition |
|---|---|
| C (MI) | the total computation amount of the divisible application |
| (MI) | the computation amount allocated for node |
| the ratio of the computation amount and the size of data | |
| k | the number of surrogate nodes available |
| (MIPS) | the computation capability of node |
| (MB/s) | the bandwidth of the link between nodes i and node 0, |
| (s) | the start-up cost in communication time of node |
| (s) | the round-trip network latency of the link between nodes 0 and |
| Parameter | Description | Values |
|---|---|---|
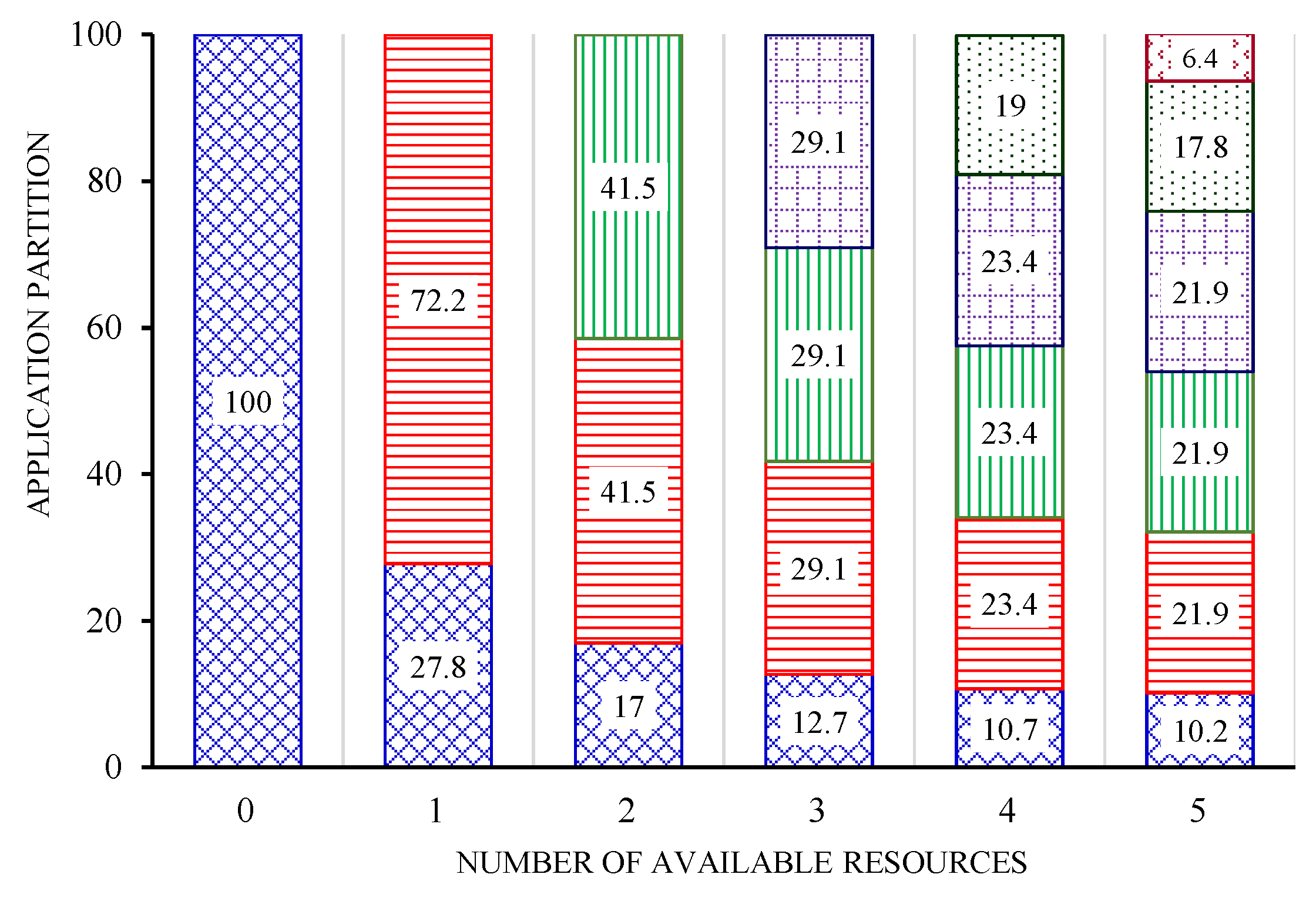
| C | the total computation amount of the divisible application | 100 MI |
| the ratio of the computation amount and the size of data | 0.2 | |
| k | the number of surrogate nodes available | 0 to 5 |
| The computation capacity of the client node | 5 MIPS | |
| the computation capability of node i | MIPS | |
| the bandwidth of the link between nodes i and 0 | data units per second MB/s | |
| the round-trip latency between nodes 0 and i | second |
| Device | Model | CPU | RAM | OS |
|---|---|---|---|---|
| client node | Huawei H30 | Kirin910 1.6 GHz | 1 GB | Android 4.0 |
| surrogate node 1 | Lenovo M40 | I3-4030U 1.9 GHz | 2 GB | Windows 7 |
| surrogate node 2 | Lenovo N50 | I5-5200U 2.2 GHz | 4 GB | Windows 7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; He, M.; Wu, W.; Sangaiah, A.K.; Jeon, G. Computation Offloading Algorithm for Arbitrarily Divisible Applications in Mobile Edge Computing Environments: An OCR Case. Sustainability 2018, 10, 1611. https://doi.org/10.3390/su10051611
Li B, He M, Wu W, Sangaiah AK, Jeon G. Computation Offloading Algorithm for Arbitrarily Divisible Applications in Mobile Edge Computing Environments: An OCR Case. Sustainability. 2018; 10(5):1611. https://doi.org/10.3390/su10051611
Chicago/Turabian StyleLi, Bo, Min He, Wei Wu, Arun Kumar Sangaiah, and Gwanggil Jeon. 2018. "Computation Offloading Algorithm for Arbitrarily Divisible Applications in Mobile Edge Computing Environments: An OCR Case" Sustainability 10, no. 5: 1611. https://doi.org/10.3390/su10051611
APA StyleLi, B., He, M., Wu, W., Sangaiah, A. K., & Jeon, G. (2018). Computation Offloading Algorithm for Arbitrarily Divisible Applications in Mobile Edge Computing Environments: An OCR Case. Sustainability, 10(5), 1611. https://doi.org/10.3390/su10051611







