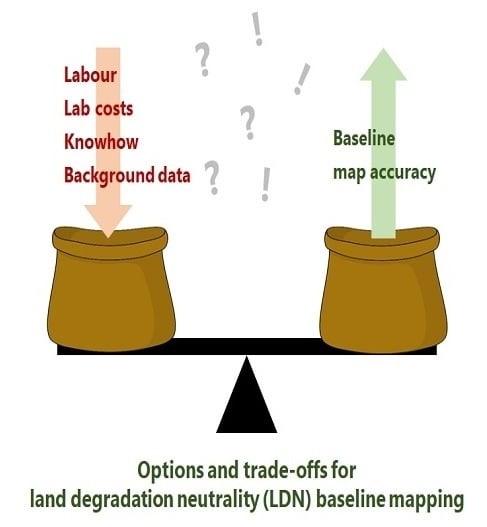
Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia
Abstract
1. Introduction
2. Methods
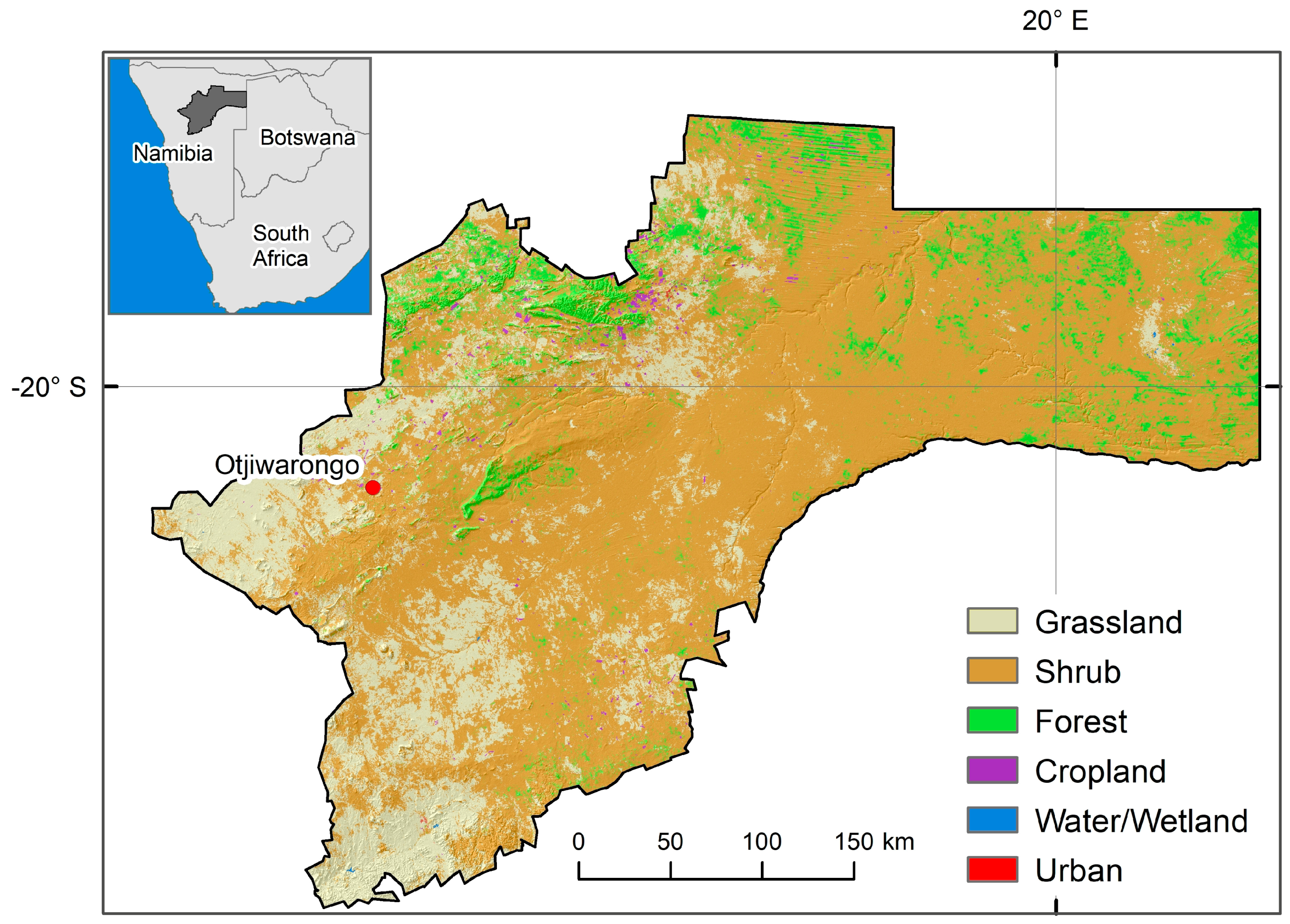
2.1. Area of Interest
2.2. Study Scope and Design
2.3. Soil Sampling and Soil Analyses
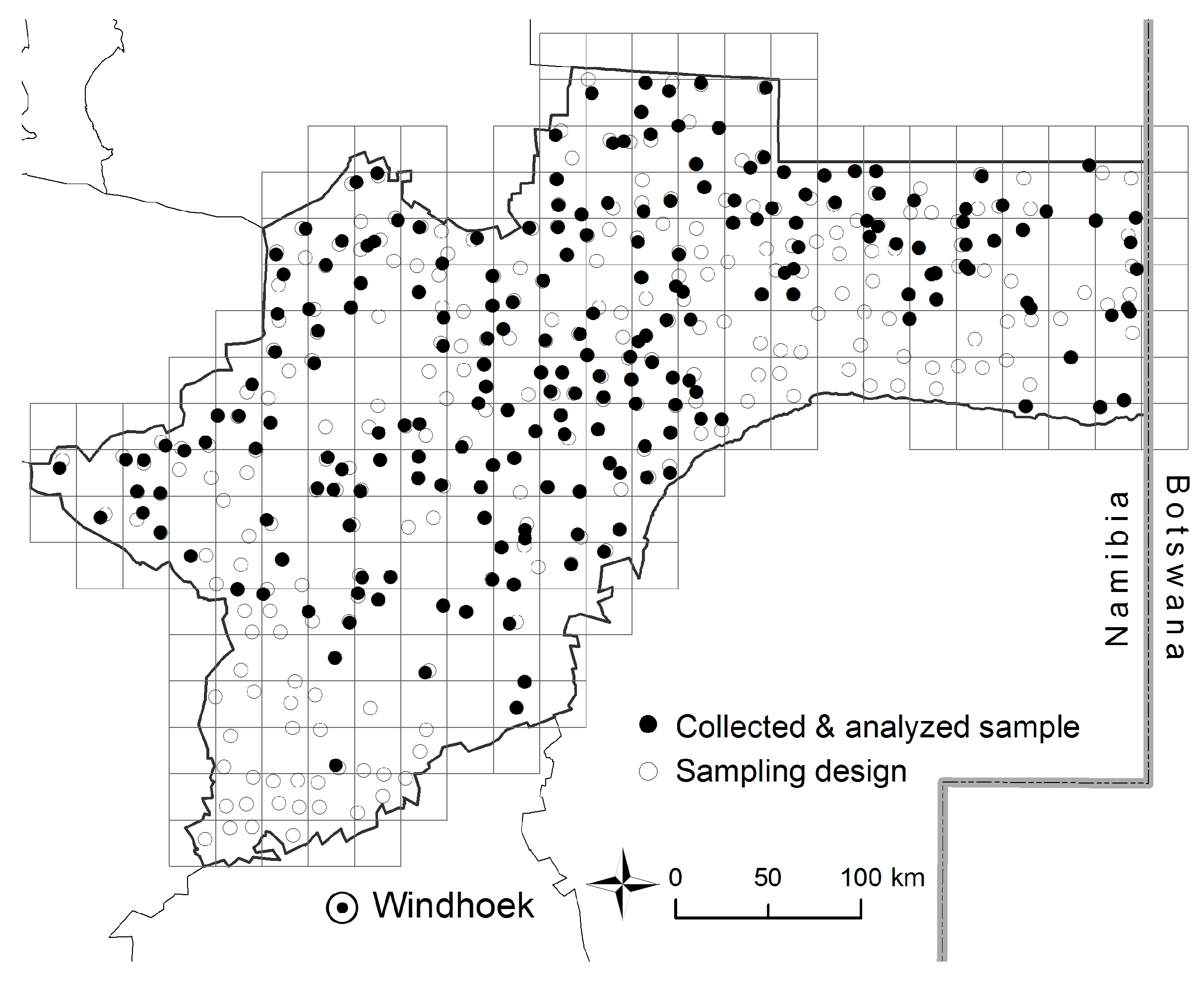
2.3.1. Sampling Design
2.3.2. Soil Sample Collection and Laboratory Analyses
- Extract soil from the center of each of the four sub-plots to a depth of 30 cm using a soil auger. Record the exact auger depth at each sub-plot.
- Bulk samples from each subplot together in a bucket and mix the soil thoroughly.
- Take a representative 1 kg sub-sample from the bucket and place it in a paper bag. Place the paper bag in a clear plastic bag (double bag) and place a paper label inside the outer one with details seen from outside. Air-dry the sample.
2.4. Mapping Methods
- SOC stock derived from the Soilgrids250m dataset (SG) (Tier 1);
- Ordinary kriging of the collected field data (OK) (Tier 3);
- Regression kriging of the collected field data using SG as a single covariate (RK) (Tier 4); and
- Random Forest kriging of the collected field data with a large stack (n = 222) of (freely available) environmental covariates in addition to SG (RFK) (Tier 4).
2.4.1. Soilgrids250m
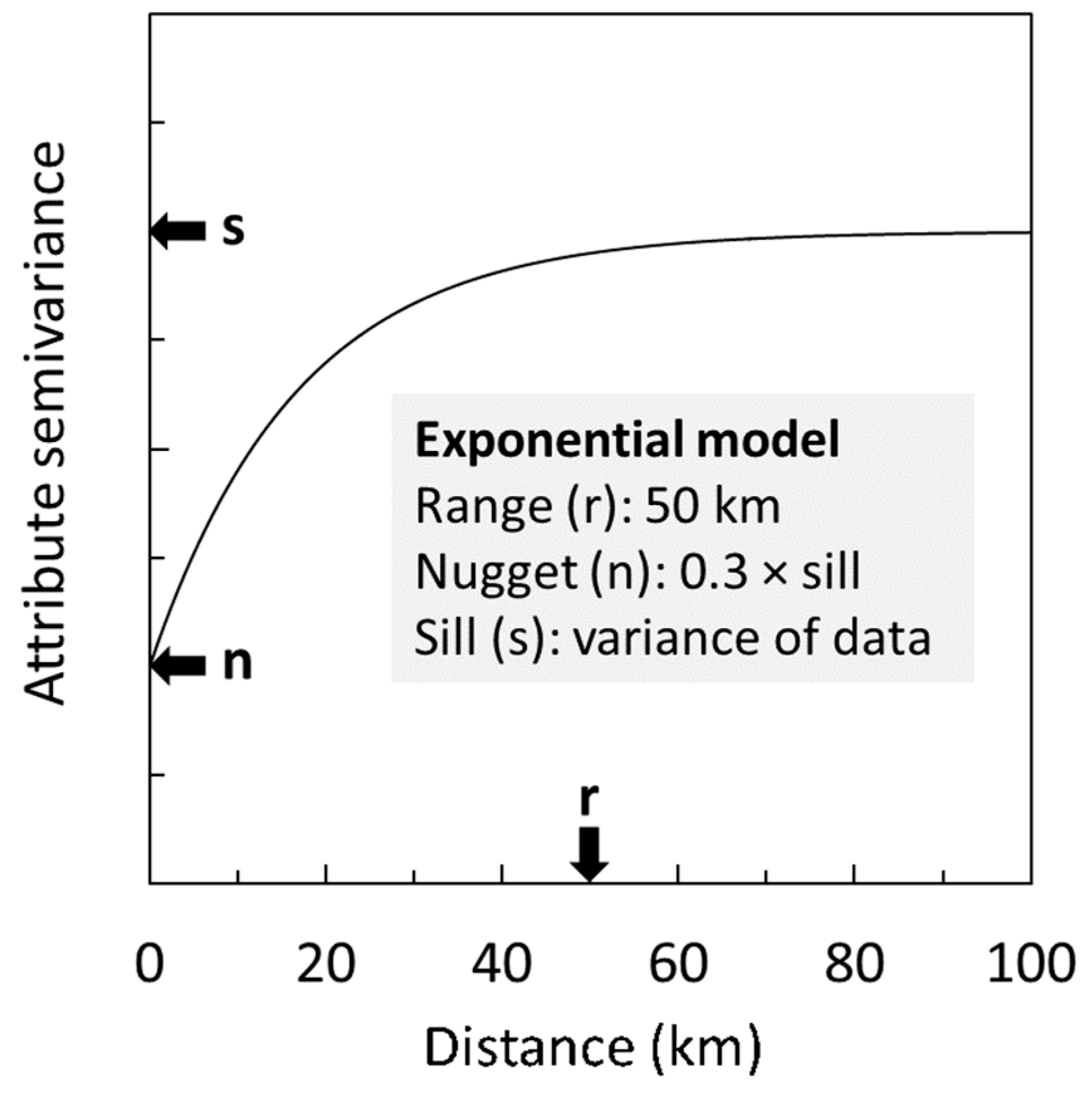
2.4.2. Ordinary Kriging
2.4.3. Regression Kriging
2.4.4. Random Forest Kriging (RFK)
- Select m covariates at random from the full set of p covariates, where m is often taken as the square root of p or p/3.
- Select the best covariate/split-point among the m. This is the covariate/split-point that results in the largest reduction in error.
- Split the node into two daughter nodes.
2.4.5. Applying the Mapping Methods
2.5. Evaluation of the Mapping Approaches
2.6. Method Complexity and Cost Estimation
2.7. Software
3. Results
3.1. Soil Sampling
3.2. Descriptive Statistics
3.3. Method Complexity and Cost Estimation
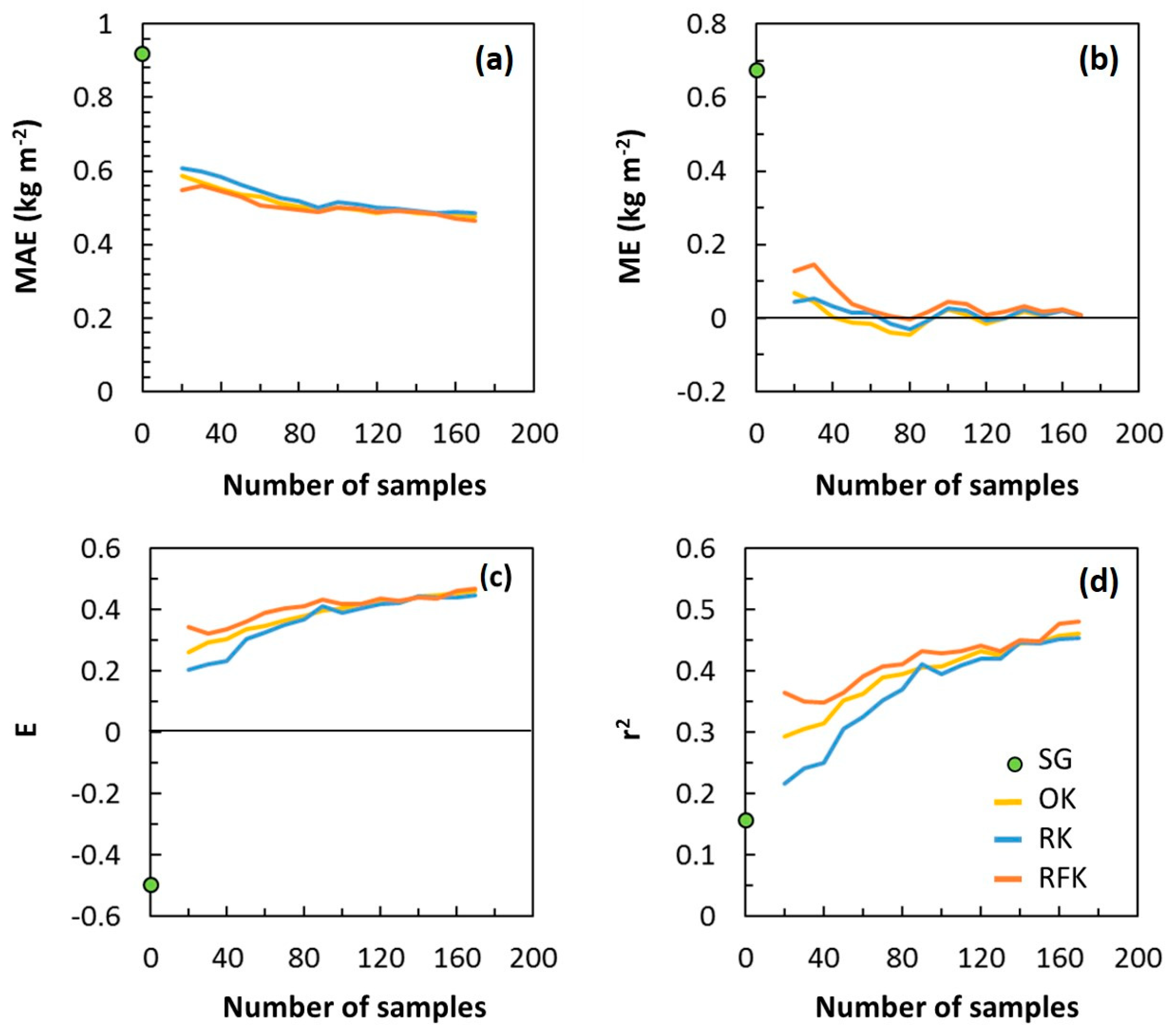
3.4. Map Accuracy versus Sampling Density
3.5. Maps
4. Discussion
4.1. Map Accuracy vs. Cost Considerations
4.2. Local Adaptation of Large-Extent Maps
4.3. Model Complexity and Costs
4.4. Recommendations
4.5. General Validity of the Results
5. Conclusions
- (i)
- taking a few local soil samples (e.g., 20) is necessary to assess the local accuracy of the large-scale map. The soil samples can also be used to alleviate local bias of the large scale map;
- (ii)
- taking more local samples further improves the map accuracy. The improvement will generally be smaller for each additional sample taken;
- (iii)
- using relevant environmental covariates will most likely improve the baseline SOC stock map. A relatively larger improvement in accuracy can be expected when soil sampling densities are used; and
- (iv)
- taking accessibility into account when designing the sampling can considerably save costs and labor in some areas.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization (FAO). The State of the World’s Land and Water Resources for Food and Agriculture (SOLAW)—Managing Systems at Risk; Food and Agriculture Organization of the United Nations: Rome, Italy; Earthscan: London, UK, 2011; ISBN 978-1-84971-326-9. [Google Scholar]
- Lal, R.; Safriel, U.; Boer, B. Zero Net Land Degradation: A New Sustainable Development Goal for Rio+20; United Nations Convention to Combat Desertification (UNCCD): Paris, France, 2012. [Google Scholar]
- United Nations Convention to Combat Desertification (UNCCD). Report of the Conference of the Parties on Its 12th Session, Ankara, 12–23 October 2015. Available online: https://www2.unccd.int/official-documents/cop-12-ankara-2015 (accessed on 24 April 2018).
- ELD Initiative. The Value of Land: Prosperous Lands and Positive Rewards through Sustainable Land Management. 2015. Available online: https://reliefweb.int/report/world/value-land-prosperous-lands-and-positive-rewards-through-sustainable-land-management (accessed on 24 April 2018).
- Vlek, P.L.G.; Khamzina, A.; Tamene, L. Land Degradation and the Sustainable Development Goals: Threats and Potential Remedies. 2017. Available online: http://hdl.handle.net/10568/81313 (accessed on 24 April 2018).
- The Montpellier Panel. No Ordinary Matter: Conserving, Restoring and Enhancing Africa’s Soils. 2014. Available online: https://ag4impact.org/wp-content/uploads/2014/12/MP_0106_Soil_Report_LR1.pdf (accessed on 23 March 2018).
- United Nations Convention to Combat Desertification (UNCCD). Submission by the United Nations Convention to Combat Desertification on Decision 6/CP.17. 2011. Available online: http://unfccc.int/resource/docs/2012/smsn/igo/99.pdf (accessed on 23 March 2018).
- Kust, G.; Andreeva, O.; Cowie, A. Land Degradation Neutrality: Concept development, practical applications and assessment. J. Environ. Manag. 2017, 195, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Grainger, A. Is Land Degradation Neutrality feasible in dry areas? J. Arid Environ. 2015, 112, 14–24. [Google Scholar] [CrossRef]
- Stavi, I.; Lal, R. Achieving Zero Net Land Degradation: Challenges and opportunities. J. Arid Environ. 2015, 112, 44–51. [Google Scholar] [CrossRef]
- Orr, B.J.; Cowie, A.L.; Castillo Sanchez, V.M.; Chasek, P.; Crossman, N.D.; Erlewein, A.; Louwagie, G.; Maron, M.; Metternicht, G.I.; Minelli, S.; et al. Scientific Conceptual Framework for Land Degradation Neutrality. A Report of the Science-Policy Interface. United Nations Convention to Combat Desertification (UNCCD), 2017. Available online: https://www2.unccd.int/publications/scientific-conceptual-framework-land-degradation-neutrality-report-science-policy (accessed on 24 April 2018).
- Cowie, A.; Orr, B.; Castillo Sanchez, V.M.; Chasek, P.; Crossman, N.D.; Erlewein, A.; Louwagie, G.; Maron, M.; Metternicht, G.I.; Minelli, S.; et al. Land in balance: The scientific conceptual framework for Land Degradation Neutrality. Environ. Sci. Policy 2018, 79, 25–35. [Google Scholar] [CrossRef]
- Chasek, P.; Safriel, U.; Shikongo, S.; Fuhrman, V.F. Operationalizing Zero Net Land Degradation: The next stage in international efforts to combat desertification? J. Arid Environ. 2015, 112, 5–13. [Google Scholar] [CrossRef]
- Akhtar-Schuster, M.; Stringer, L.C.; Erlewein, A.; Metternicht, G.; Minelli, S.; Safriel, U.; Sommer, S. Unpacking the concept of land degradation neutrality and addressing its operation through the Rio Conventions. J. Environ. Manag. 2017, 195, 4–15. [Google Scholar] [CrossRef] [PubMed]
- United Nations Convention to Combat Desertification (UNCCD). Land Degradation Neutrality Target Setting—A Technical Guide. 2016. Available online: http://www2.unccd.int/ldn-target-setting-technical-guide (accessed on 23 March 2018).
- Smith, J. Towards Achieving Land Degradation Neutrality: Turning the Concept into Practice Project Evaluation: Final Report. UNCCD, Global Mechanism, 2015. Available online: http://www2.unccd.int/sites/default/files/relevant-links/2017-01/LDN%20project%20evaluation%20formatted%20report_0.pdf (accessed on 23 March 2018).
- Aynekulu, E.; Lohbeck, M.; Nijbroek, R.; Ordóñez, J.C.; Turner, K.G.; Vågen, T.; Winowiecki, L. Review of Methodologies for Land Degradation Neutrality Baselines: Sub-National Case Studies from Costa Rica and Namibia. 2017. Available online: http://hdl.handle.net/10568/80563 (accessed on 23 March 2018).
- Namibia Statistics Agency. Namibia 2011 Population and Housing Census Main Report. 2011. Available online: https://cms.my.na/assets/documents/p19dmn58guram30ttun89rdrp1.pdf (accessed on 25 April 2018).
- Ministry of Environment and Tourism, Republic of Namibia. Namibia—Land Degradation Neutrality National Report 2015. 2015. Available online: https://knowledge.unccd.int/sites/default/files/inline-files/namibia-ldn-country-report-updated-version2.pdf (accessed on 24 April 2018).
- Gilolmo, P.; Lobo, A. On the Relationship between Land Tenure and Land Degradation. A Case Study in the Otjozondjupa Region (Namibia) Based on Satellite Data. 2016. Available online: https://www.iss.nl/sites/corporate/files/43-ICAS_CP_Gilolm_and_Lobo.pdf (accessed on 23 March 2018).
- Zeidler, J.; Kandjinga, L.; David, A. Study on the Effects of Climate Change in the Cuvelai Etosha Basin and Possible Adaptation Measures; Integrated Environmental Consultants of Namibia (IECN): Windhoek, Namibia; Integrated Environmental Consultants Namibia: Windhoek, Namibia, 2010; Available online: http://www.the-eis.com/data/literature/Climate%20Change%20in%20Cuvelai%20Etosha%20Basin%202010.pdf (accessed on 24 April 2018).
- Global Mechanism of the UNCCD. Methodological Note to Set National Voluntary Land Degradation Neutrality (LDN) Targets Using the UNCCD Indicator Framework. 2016. Available online: http://www2.unccd.int/actions/ldn-target-setting-programme/ldn-methodological-note (accessed on 23 March 2018).
- Hengl, T.; Mendes de Jesus, J.S.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Burrough, P.A.; McDonnell, R.A. Principles of GIS; Oxford University Press: London, UK, 1998; ISBN 9780198742845. [Google Scholar]
- Olsson, D.; Söderström, M. An automated method to locate optimal soil sampling sites using ancillary data. In Proceedings of the 4th European Conference on Precision Agriculture, Berlin, Germany, 15–17 June 2003. [Google Scholar]
- Wetterlind, J.; Stenberg, B.; Söderström, M. The use of near infrared (NIR) spectroscopy to improve soil mapping at the farm scale. Precis. Agric. 2008, 9, 57–69. [Google Scholar] [CrossRef]
- Sims, J.R.; Haby, V.A. Simplified colorimetric determination of soil organic matter. Soil Sci. 1971, 112, 137–141. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 131–137. [Google Scholar] [CrossRef]
- Arrouays, D.; McKenzie, N.; Hempel, J.; Richer de Forges, A.C.; McBratney, A.B. GlobalSoilMap: Basis of the Global Spatial Soil Information System; CRC Press/Balkema: London, UK, 2014; ISBN 9781138001190. [Google Scholar]
- De Brogniez, D.; Ballabio, C.; Stevens, A.; Jones, R.J.A.; Montanarella, L.; van Wesemael, B. A map of the topsoil organic carbon content of Europe generated by a generalized additive model. Eur. J. Soil Sci. 2015, 66, 121–134. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Stoorvogel, J.J.; Bakkenes, M.; Temme, A.J.; Batjes, N.H.; Brink, B.J. S-World: A Global Soil Map for Environmental Modelling. Land Degrad. Dev. 2017, 28, 22–33. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists. Statistics in Practice, 2nd ed.; John Wiley & Sons Inc.: Chichester, UK, 2007; ISBN 978-0-470-02858-2. [Google Scholar]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes-heterotopic co-kriging and regression kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Sreenivas, K.; Dadhwal, V.K.; Kumar, S.; Harsha, G.S.; Mitran, T.; Sujatha, G.; Suresh, G.J.R.; Fyzee, M.A.; Ravisankar, T. Digital mapping of soil organic and inorganic carbon status in India. Geoderma 2016, 269, 160–173. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Minasny, B.; Triantafilis, J. Comparing data mining classifiers to predict spatial distribution of USDA-family soil groups in Baneh region, Iran. Geoderma 2015, 253–254, 67–77. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2008; ISBN 978-0-387-84858-7. [Google Scholar]
- Strobl, C.; Malley, J.; Tutz, G. An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of Classification and Regression Trees, Bagging, and Random Forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed]
- Piikki, K.; Söderström, M.; Stadig, H. Local adaptation of a national digital soil map for use in precision agriculture. Adv. Anim. Biosci. 2017, 8, 430–432. [Google Scholar] [CrossRef]
- Janssen, P.H.M.; Heuberger, P.S.C. Calibration of process-oriented models. Ecol. Model. 1995, 831, 55–66. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 103, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Brau, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Pebesma, E. Multivariable geostatistics in S: The gstat package. Comput. Geosci 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. R J. 2016, 8, 204–218. [Google Scholar]
- Wickham, H. The Split-Apply-Combine Strategy for Data Analysis. J. Stat. Softw. 2011, 40, 1–29. [Google Scholar] [CrossRef]
- Hijmans, R. raster: Geographic Data Analysis and Modeling. R Package Version 2.5-8. 2016. Available online: https://CRAN.R-project.org/package=raster (accessed on 24 April 2018).
- Bivand, R.; Keitt, T.; Rowlingson, B. rgdal: Bindings for the Geospatial Data Abstraction Library. R Package Version 1.2-5; 2016; Available online: https://CRAN.R-project.org/package=rgdal (accessed on 23 March 2018).
- Pebesma, E.; Bivand, R. Classes and methods for spatial data in R. R News 2005, 5, 9–13. [Google Scholar]
- Bivand, R.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013; ISBN 9781461476177. [Google Scholar]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R; Chapman and Hall; CRC Press: London, UK, 2015; ISBN 9781482210200. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training. R Package Version 6.0-73. 2016. Available online: https://CRAN.R-project.org/package=caret (accessed on 23 March 2018).
- Hengl, T. GSIF: Global Soil Information Facilities. R Package Version 0.5-3. 2016. Available online: https://CRAN.R-project.org/package=GSIF 01-1315 (accessed on 23 March 2018).
- Nijbroek, R.; Mutua, J.; Söderström, M.; Piikki, K.; Kempen, B.; Hengari, S. Pilot Project Land Degradation Neutrality (LDN), Namibia: Establishment of a Baseline for Land Degradation in the Region of Otjozondjupa. 2017. Available online: https://cgspace.cgiar.org/handle/10568/80090 (accessed on 24 April 2018).
- Malone, B.P.; Styc, Q.; Minasny, B.; McBratney, A.B. Digital soil mapping of soil carbon at the farm scale: A spatial downscaling approach in consideration of measured and uncertain data. Geoderma 2016, 290, 91–99. [Google Scholar] [CrossRef]
- Grundy, M.J.; Rossel, R.A.V.; Searle, R.D.; Wilson, P.L.; Chen, C.; Gregory, L.J. Soil and landscape grid of Australia. Soil Res. 2015, 53, 835–844. [Google Scholar] [CrossRef]
- Malone, B.P.; McBratney, A.B.; Minasny, B.; Wheeler, I. A general method for downscaling earth resource information. Comput. Geosci. 2012, 41, 119–125. [Google Scholar] [CrossRef]
- Roudier, P.; Malone, B.P.; Hedley, C.B.; Minasny, B.; McBratney, A.B. Comparison of regression methods for spatial downscaling of soil organic carbon stocks maps. Comput. Electron. Agric. 2017, 142, 91–100. [Google Scholar] [CrossRef]
- Söderström, M.; Piikki, K.; Cordingley, J. Improved usefulness of continental soil databases for agricultural management through local adaptation. S. Afr. J. Plant. Soil 2017, 34, 35–45. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.; de Jesus, J.M.; Tamene, L.; et al. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Söderström, M.; Sohlenius, G.; Rodhe, L.; Piikki, K. Adaptation of regional digital soil mapping for precision agriculture. Precis. Agric. 2016, 17, 588–607. [Google Scholar] [CrossRef]
- Piikki, K.; Söderström, M. Digital soil mapping of arable land in Sweden–Validation of performance at multiple scales. Geoderma 2017, in press. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B. Near infrared spectroscopy for within field soil characterisation—Small local calibrations compared with national libraries augmented with local samples. Eur. J. Soil Sci. 2010, 61, 823–843. [Google Scholar] [CrossRef]


| Tier (Method) | Data Requirement | Labour Requirements | Software Requirements | Skills Requirements | Budget Requirements | Overall Complexity |
|---|---|---|---|---|---|---|
| 1 (SG) | -Soilgrids250m | -soil sampling (−) -lab analyses (−) -data preparation (+) -data analyses (−) -interpretation (+) -reporting (+) | -GIS | -GIS | -labour (+) -software (+) * | Very low |
| 2 (OK) | -Local soil sample data | -soil sampling (+) -lab analyses (+++) -data preparation (++) -data analyses (++) -interpretation (+) -reporting (+) | -GIS | -Sampling design -Geostatistics -GIS | -labour (++) -lab analyses (+++) -software (+) * | Low |
| 3 (RK) | -Soilgrids250m -Local soil sample data | -soil sampling (+) -lab analyses (+++) -data preparation (+++) -data analyses (+++) -interpretation (+) -reporting (+) | -GIS -Statistical software | -Sampling design -Geostatistics -GIS | -labour (+++) -lab analyses (+++) -software (+) * | Medium |
| 4 (RFK) | -Soilgrids250m -Local soil sample data -Covariate data | -soil sampling (+) -lab analyses (+++) -data preparation (+++++) -data analyses (+++++) -interpretation (+) -reporting (+) | -GIS -Data mining software -Statistical software | -Sampling design -Geostatistics -GIS -Data mining | -labour (+++++) -lab analyses (+++) -covariate data (++) * -software (+) * | High |
| Measure | Abbreviation | Formula | Interpretation | Reference |
|---|---|---|---|---|
| Mean absolute error | MAE | The MAE is the average of the absolute prediction errors. | [43] | |
| Mean error | ME | The ME is a measure of prediction bias. A positive ME indicates an overestimation of the predicted values, while a negative ME indicates an underestimation. Ideally, the ME should be zero, meaning that predictions are unbiased. | [43] | |
| Modelling efficiency | E | The modelling efficiency measures the relative improvement in accuracy over the mean of the calibration dataset. A value of 1 means that all predicted values are equal to the observed values. A value larger than zero means that the model predictions are an improvement over the mean of the calibration dataset, while a value smaller than zero indicates that the calibration dataset mean is more accurate than the predicted values. | [44] | |
| Coefficient of determination of a linear regression model between the predicted and observed values. | r2 | The r2 takes values in the range [0, 1]. A high value indicate a linear relationship between the observed and the predicted values but says nothing about the sign of the relationship or whether there is any displacement of the predictions (m ≠ 0) or if there is an error in scale (k ≠ 1). | [45] |
| Statistic | Soilgrids250m | Soil Samples | ||||
|---|---|---|---|---|---|---|
| SOC (g kg−1) | BD (t m−3) | SOC Stock (kg m−2) | SOC (g kg−1) | BD (t m−3) | SOC Stock (kg m−2) | |
| Min | 3.1 | 1.4 | 1.5 | 0.7 | 0.7 | 0.3 |
| Median | 4.8 | 1.6 | 2.2 | 3.7 | 1.5 | 1.3 |
| Mean | 4.4 | 1.6 | 2.1 | 2.9 | 1.5 | 1.6 |
| Max | 12 | 1.6 | 5.3 | 13.3 | 1.8 | 5.6 |
| Cost | Details | Daily Rate (USD) | SG | OK | RK | RFK |
|---|---|---|---|---|---|---|
| Field work | ||||||
| Soil sampling (4 samples/day) | Technicians (4 people/team) | 200 | 0 | 50 × n | 50 × n | 50 × n |
| Transportation | Four-Wheel-Drive | 80 | 0 | 20 × n | 20 × n | 20 × n |
| Lab work | ||||||
| Lab analyses (USD/sample) | Local lab | n/a | 0 | 20 × n | 20 × n | 20 × n |
| Data analyses | ||||||
| Sampling design | Data analyst | 400 | 0 | 400 | 400 | 400 |
| Data preparation | Data analyst | 400 | 400 | 600 | 800 | 2400 |
| Data analyses | Data analyst | 400 | 400 | 800 | 1200 | 1200 |
| Other | ||||||
| Software | Freeware (R) | 0 | 0 | 0 | 0 | |
| Covariate data | Open data (ISRIC) | 0 | 0 | 0 | 0 | |
| Total cost | 800 | 1800 + 90 × n | 2400 + 90 × n | 4000 + 90 × n |
| Method | N | MAE (kg m−2) | ME (kg m−2) | E | r2 |
|---|---|---|---|---|---|
| SG | 0 | 0.9 | 0.7 | −0.49 | 0.16 |
| OK | 20 | 0.6 | 0.1 | 0.26 | 0.29 |
| RK | 20 | 0.6 | 0.0 | 0.20 | 0.22 |
| RFK | 20 | 0.5 | 0.1 | 0.34 | 0.36 |
| OK | 100 | 0.5 | 0.0 | 0.41 | 0.41 |
| RK | 100 | 0.5 | 0.0 | 0.39 | 0.40 |
| RFK | 100 | 0.5 | 0.0 | 0.42 | 0.43 |
| OK | 170 | 0.5 | 0.0 | 0.46 | 0.46 |
| RK | 170 | 0.5 | 0.0 | 0.45 | 0.46 |
| RFK | 170 | 0.5 | 0.0 | 0.47 | 0.48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nijbroek, R.; Piikki, K.; Söderström, M.; Kempen, B.; Turner, K.G.; Hengari, S.; Mutua, J. Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia. Sustainability 2018, 10, 1610. https://doi.org/10.3390/su10051610
Nijbroek R, Piikki K, Söderström M, Kempen B, Turner KG, Hengari S, Mutua J. Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia. Sustainability. 2018; 10(5):1610. https://doi.org/10.3390/su10051610
Chicago/Turabian StyleNijbroek, Ravic, Kristin Piikki, Mats Söderström, Bas Kempen, Katrine G. Turner, Simeon Hengari, and John Mutua. 2018. "Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia" Sustainability 10, no. 5: 1610. https://doi.org/10.3390/su10051610
APA StyleNijbroek, R., Piikki, K., Söderström, M., Kempen, B., Turner, K. G., Hengari, S., & Mutua, J. (2018). Soil Organic Carbon Baselines for Land Degradation Neutrality: Map Accuracy and Cost Tradeoffs with Respect to Complexity in Otjozondjupa, Namibia. Sustainability, 10(5), 1610. https://doi.org/10.3390/su10051610