1. Introduction
For emerging and promising 5G mobile services, despite their diverse application scenarios, it is widely agreed that they share a common primary requirement: either high data rate or high reliability. To meet such requirement, evolving wireless techniques and novel network infrastructures for 5G are no doubt necessary. However, we believe that the existing Concurrent Multipath Transfer (CMT) [
1] technology could also contribute to the fulfillment of needs of 5G mobile services. CMT can not only improve communication throughput, but also provide communication reliability. CMT in 5G scenarios will pool multiple heterogeneous wireless resources by employing a variety of Radio Access Technologies (RATs) concurrently. Thus, the bandwidth of every RAT will be aggregated [
2], achieving higher throughput. Also, thanks to diversity gain of heterogeneous RATs, the communication reliability can be improved [
3]. Meanwhile, it is potentially more viable to adopt CMT for mobile services in 5G, since 5G is envisioned to consist of various types of RATs (such as millimeter wave communication, LTE-A and Wi-Fi). Meanwhile, more and more mobile devices have been equipped with multiple wireless interfaces [
4].
Multipath techniques that can achieve CMT are still in development, while TCP-based CMT solutions will be in the dominant position. There are many reasons why multipath is not widely used. First, they cannot be widely applied to a variety of network environments. For example, the performance of Multipath TCP (MPTCP) [
5], the most popular multipath protocol working at a transport layer, will be severely degraded in some cases [
6,
7]. Second, the vast majority of operating systems, such as Windows, Linux, and MacOS, do not support multipath protocols well. Since most mobile services will still use TCP for now and for the foreseeable future, feasible CMT solutions for 5G services will be based on TCP. These solutions can be viewed as a middleware between the transport layer and network layer, which is transparent to the existing operating systems. Also, the interoperability between existing TCP based network infrastructure will not be compromised.
However, the performance of TCP flow transferred over multiple heterogeneous wireless networks would be adversely affected by path heterogeneity. This will be a critical feature of the highly integrative 5G system [
8]. Briefly, such performance degradation is due to the packet reordering issue [
9] caused by the different link quality of employed heterogeneous wireless networks. The inherent re-sequencing mechanism of TCP can correct the problem when the packet reordering is no more than two positions [
10]. However, the throughput may drop drastically due to the reduction of the TCP transmission window caused by more serious packet reordering [
4]. Some contributions were proposed to solve the problem. Earliest Delivery Path First (EDPF) [
11] schedules packets over different links based on their estimated delivery time. Delay Aware Packet Scheduling (DAPS) [
12] distributes packets over different links depending on the ratio between slowest and fastest Round-Trip Time (RTT) as well as congestion window. Yet, without the thorough understanding of TCP performance in the given situation, these contributions only provide limited improvement.
If we can analyze how heterogeneous networks affect the performance of TCP flow concurrently transferred over them, more efficient and elegant CMT schemes for 5G mobile services can be developed based on TCP and TCP-like congestion control protocols. Such TCP-based CMT schemes would be more deployable in 5G heterogeneous wireless networks since they are compatible with the current Internet infrastructure.
In this paper, a performance analysis model for TCP over multiple heterogeneous wireless networks is presented. To the best of our knowledge, no similar model has been reported in the literature. The proposed model can provide guidance to the design of novel CMT solutions for 5G mobile services. The main contributions of this paper are as follows:
- (1)
We have taken field investigation on present heterogeneous wireless networks to reveal the severe extent of link quality asymmetry in terms of delay and bandwidth. This proves that the impact of network heterogeneity in future 5G is anything but empty talk.
- (2)
A performance analysis model is derived based on the careful analysis of segments transmission and acknowledgement response over multiple heterogeneous paths. Both bandwidth asymmetry and delay asymmetry are taken into consideration in the proposed model.
- (3)
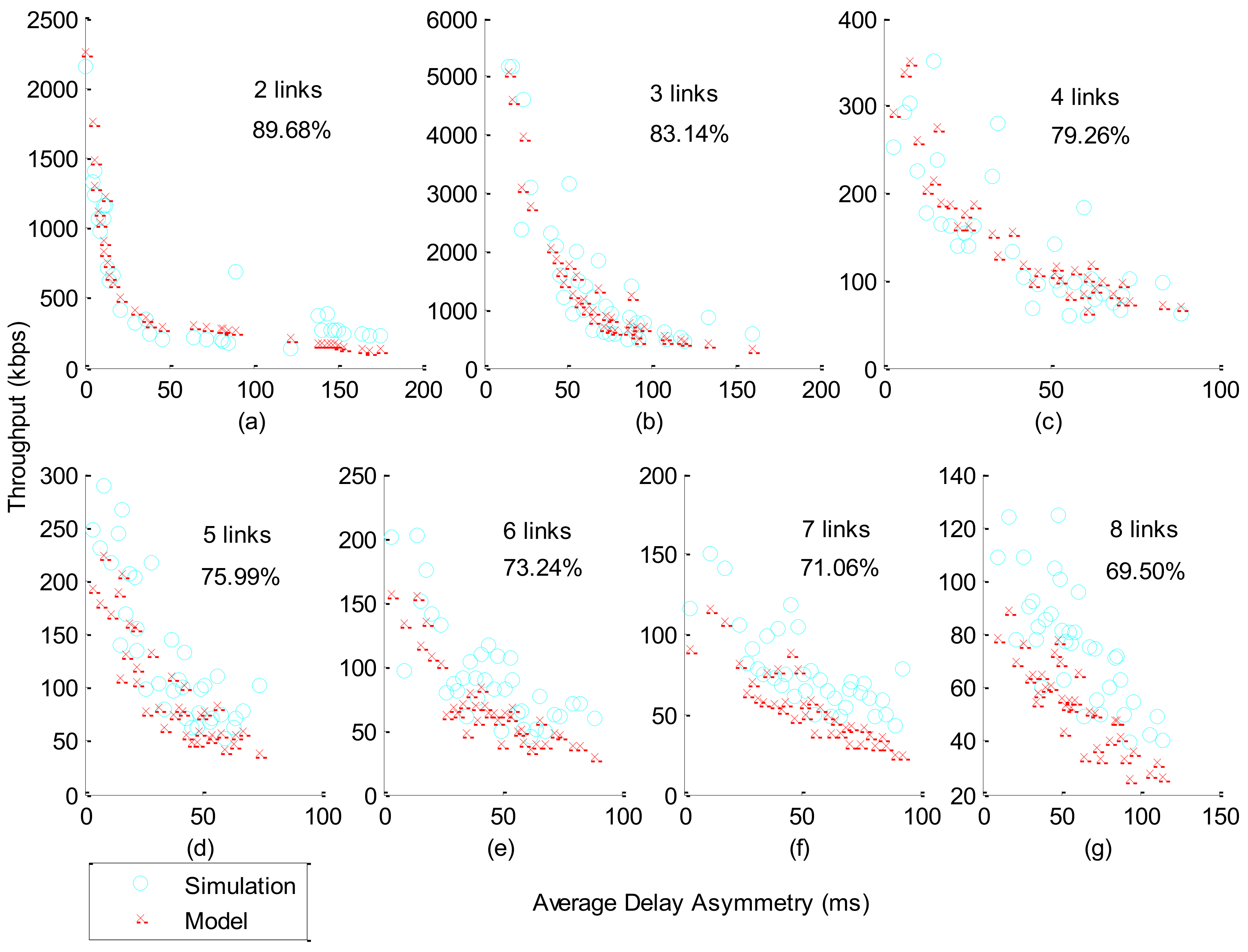
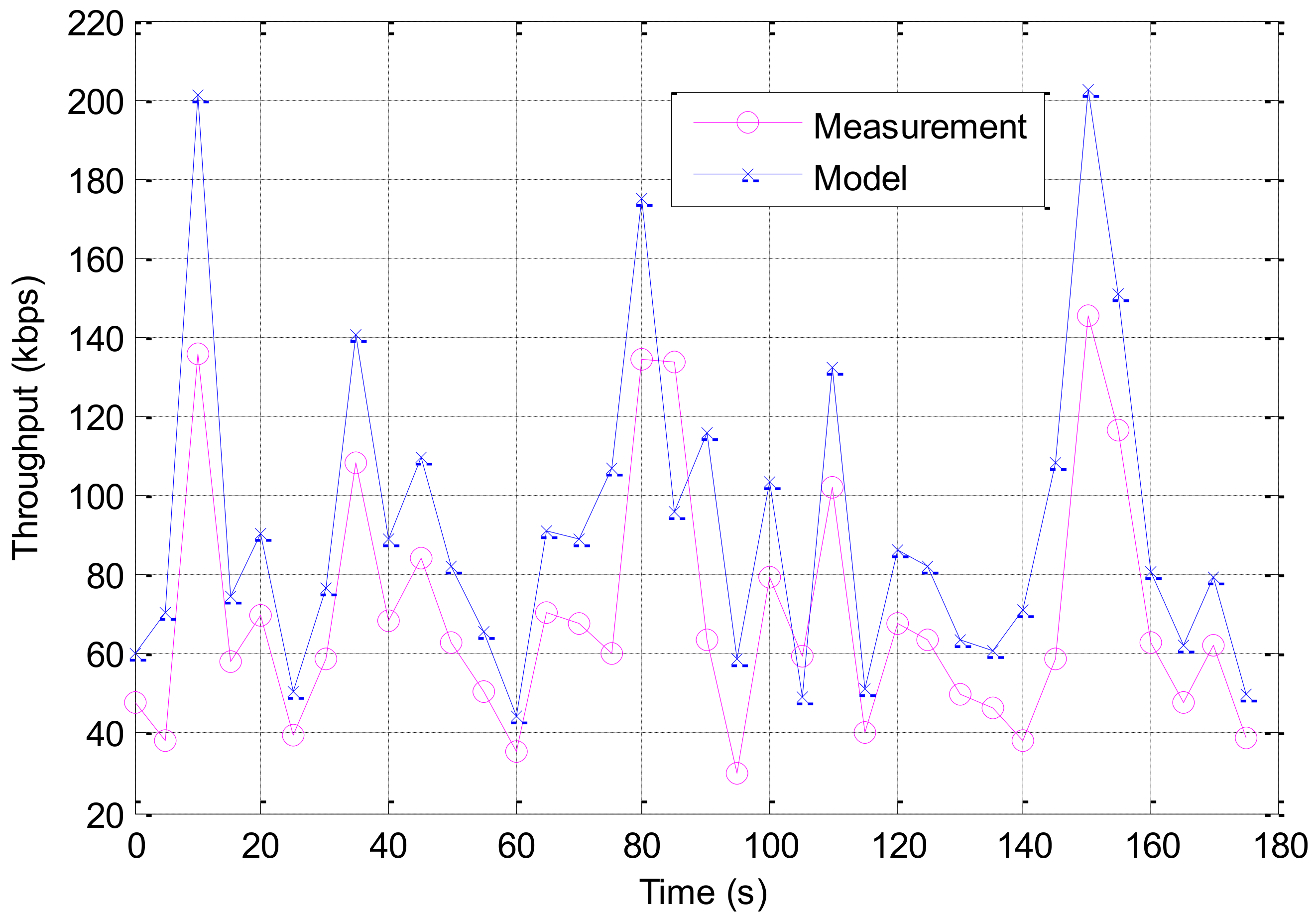
High analytical accuracy is validated by comparison to the simulation study and field experiment. It proves that our model can be applied in practical environments. Simulation of TCP over multiple heterogeneous paths is created in NS3, while the field measurement is performed in a real-world mobile scenario. The predicted throughput using the proposed model can fit the simulation results and the field measurement results with high accuracy.
- (4)
Some interesting inferences are drawn from the proposed model. First, compared to bandwidth asymmetry, delay asymmetry between multiple links is the dominant factor that affects the performance of TCP over heterogeneous paths. Second, the criteria of determining the appropriate number of links to be employed to optimize the TCP multipath performance is discussed.
The remainder of this paper is organized as follows. Some related work is introduced in
Section 2.
Section 3 details the issue of link quality asymmetry based on the results of field investigation. In
Section 4, the performance analysis model for TCP over heterogeneous paths is derived. The accuracy of the proposed model is validated in
Section 5. In
Section 6 we investigate the effect of path heterogeneity based on the proposed model.
Section 7 provides some discussion and design guidance.
Section 8 concludes the paper.
2. Related Work
To meet the requirement for high data rate and reliability, some contributions were proposed to try to achieve stable and high-quality communication based on multipath transmission. Stream Control Transmission Protocol (SCTP) [
13,
14] and its extensions [
15,
16] try to aggregate the bandwidth of multiple paths. MPTCP, a multipath extension to TCP, has also been standardized to transmit data over multiple paths simultaneously to improve reliability and throughput. IETF Multiple Interfaces (MIF) working group is developing the standards [
17] for nodes with multiple interfaces. Recently, the cellular-based multipath solutions are generating more interest with the rapid development of 5G heterogeneous networks. For example, femocells-based schemes [
18,
19] were proposed to support seamless mobility and maximize the network recourse utilization using multiple interfaces. Device to Device (D2D) communication using multiple access technologies were deployed to support massive connectivity [
20,
21].
However, apart from the practical deployment challenges, such as the existence of various types of middle boxes [
6], the main difficulty is that the performance of multipath solutions may decrease significantly under the circumstances of path heterogeneity, especially when there are some bottleneck paths [
7,
22,
23,
24].
Packet reordering is considered the dominant challenge for multipath transmission because it leads to an undesirable reduction in throughput [
1]. RFC5236 [
25] introduces a metric named reorder density to show how far packets are displaced from their original position. Therefore, an efficient multipath solution must reduce the impact of packet reordering to alleviate its effects. Multipath forwarding is the main reason of packet out-of-order [
26]. Different technologies and different paths can lead to significant differences in delay and bandwidth. When packets are forwarded over paths with different characteristics, they are likely to arrive at the receiver out of order.
Some state-of-the-art research [
27,
28] has measured the characteristics of heterogeneous paths in terms of delays. However, their main purpose is to analyze the performance of different scheduling algorithms in heterogeneous networks, rather than theoretically analyze the relationship between path diversity and TCP performance.
The research of TCP performance analysis, especially in terms of throughput, is still making progress, as TCP is one of most widely deployed transport protocols in today’s Internet. The research can be categorized into two kinds: one aims at improving the accuracy of prior model by novel methods [
29,
30,
31], the other focuses on the performance of TCP applied in emerging scenarios [
32,
33]. However, the proposed models in these papers only analyze the situation where single path is used for transmitting TCP segments.
Overall, to the best of our knowledge, no one has given a performance analysis model to analyze TCP performance over multiple paths with different link quality in heterogeneous networks, although there are many schemes [
34] working at different protocol layers that are proposed to try to improve the performance over multiple paths. We believe that this model can help us design more practical multipath schemes in the future wireless networks.
3. Problem Description and Network Model
Network heterogeneity will become a concrete issue in 5G with the popularity of multi-access devices and deployment of emerging heterogeneous RATs. Multi-access devices that can connect to more than one wireless networks are gaining bigger market share, such as smart phones supporting dual-SIM dual stand-by mode. These devices can concurrently use up to three interfaces, including Wi-Fi, for data transmission. For such a device, the connected multiple wireless networks may share heterogeneous access technologies (e.g., WLAN vs. cellular network), heterogeneous standards or heterogeneous service providers [
35]. Even if two interfaces are connected to an identical wireless network, the wireless signals are likely to experience heterogeneous pass loss due to small scale fading. Considering that in 5G more heterogeneous RATs will be deployed and utilized by multi-access devices, the network heterogeneity issue will become more severe than in previous four generations.
Network heterogeneity of multi-access devices is intuitively revealed by the difference in network link quality. For two heterogeneous wireless networks, their network link quality is normally different from each other, to which we refer as network link quality asymmetry. Generally, Data Rate (DR) and RTT are used to describe the network link quality. DR reveals the capacity of a network link, while RTT directly reflects the transmission delay. Accordingly, the network link quality asymmetry can be indicated by DR asymmetry and RTT asymmetry.
Intuitively, the performance of TCP transmission would be prone to network link quality asymmetry, if multiple heterogeneous wireless networks are concurrently employed for delivering segments. Consequently, the performance of TCP-based CMT in 5G will also be degraded by link quality asymmetry. This is because the transmitted segments would suffer different transmission delays due to the dissimilar network link quality of employed wireless networks. This results in segments reaching the receiver out-of-order. This segment reordering issue is widely regarded as the major challenge that undermines the performance of concurrent multipath transmission, as it causes unnecessary retransmission, prevents the congestion window from growing and disrupt
ACK-clocking. The higher network link quality asymmetry becomes, the more negative impact it has on TCP performance. The analytical discussion of the relationship between the performance of TCP over multiple wireless networks and the link quality asymmetry will be detailed in
Section 4.
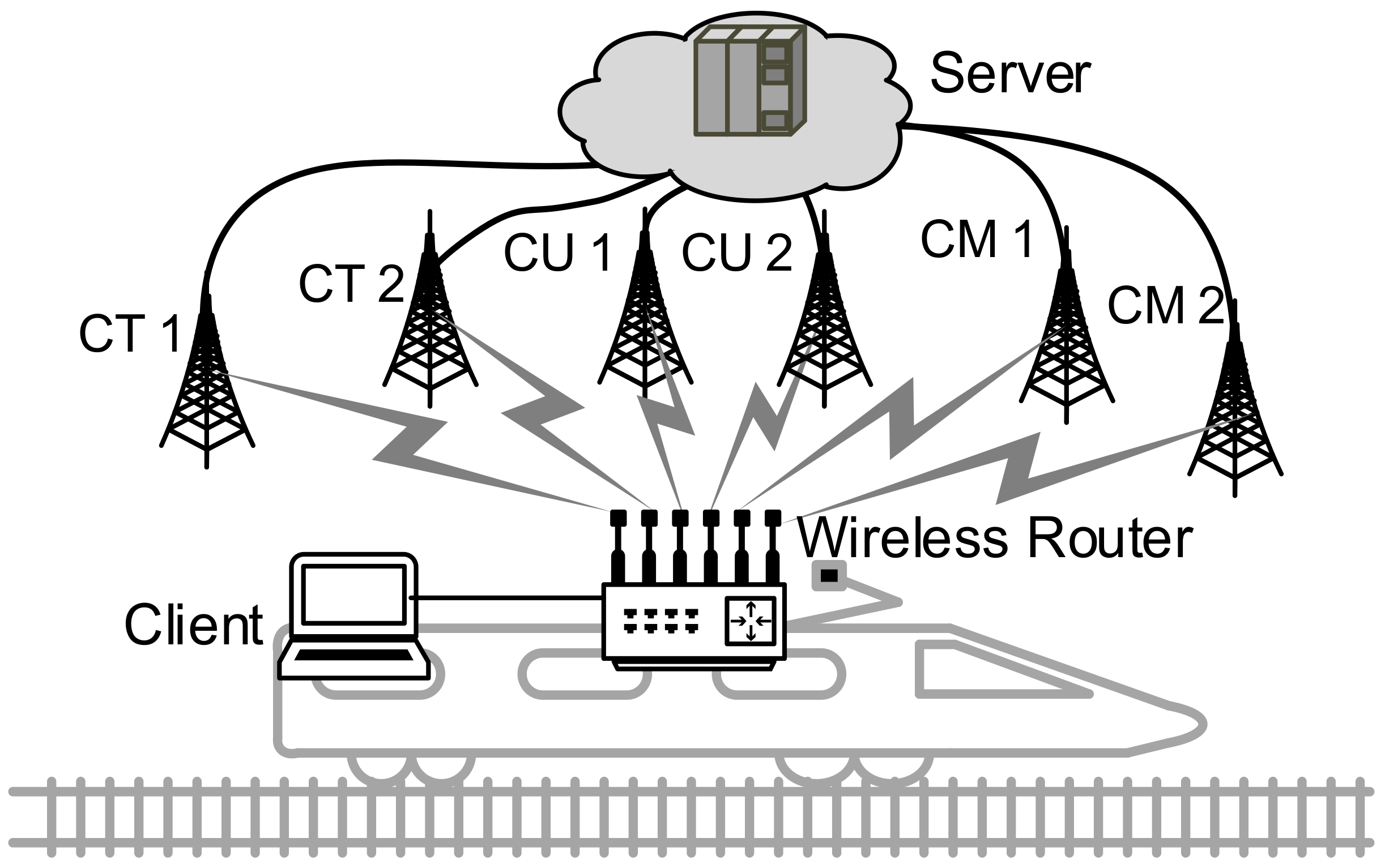
To investigate the extent of network link quality asymmetry in a real-world situation, we have taken a filed measurement on a group of heterogeneous wireless networks, and found that their link quality deviated significantly from each other. The measurement was carried out in a test train running on a newly constructed high-speed railway before its service, where few passengers were on board. Thus the interference from other wireless devices can be eliminated. Inside the test train, a dedicated box PC with our proprietary measuring program was deployed to automatically measure and store the download DR and RTT of a certain wireless network. Incorporating different kinds of wireless modems, this device can simultaneously access multiple heterogeneous mobile networks. In the measurement, up to eight modems were adopted, including three FDD-LTE (Frequency Division Duplexing-Long Term Evolution) modems of China Telecom (CT), three FDD-LTE modems of China Unicom (CU) and two TD-LTE (Time Division-Long Term Evolution) modems of China Mobile (CM). After the measurement, a group of RTT dataset and two download DR values (average and maximum) were collected on each modem. We need to clarify that the modem is a factor that can influence the link quality of wireless networks. Different modems connecting to the same wireless network may also cause link quality asymmetry. To minimize this influence, we used identical modems to access wireless networks with same communication standards.
The statistics from the measurement result is shown in
Figure 1. Regarding RTT, a boxplot diagram is depicted based on collected dataset of each modem. The blue rectangle in a boxplot diagram represents the interquartile ranges (IQR) of the variation, while the band inside the rectangle represents the median. The red crosses depict the outliers. By visually comparing the two boxplot diagrams, statistical inference can be made about the difference of two dataset. If the median of one dataset does not overlap the IQR of the other dataset, it can be inferred that difference exists between two datasets. Further, if two IQRs don’t overlap, the difference is significant. Applying this criterion to
Figure 1, we can infer that the RTT of CT1, CU3, CM1 and CM2 are significantly higher than those of CT2, CU1, CU2. Meanwhile, the RTT of CT1, CU3, CM1 and CM2 are different from the others. These conclusions can reveal the dispersion of RTT among eight modems.
Regarding download DR, the average and maximum values are shown using bar graphs. For maximum download DR, the ratio between the highest (CT1) and the lowest (CU3) is 8.2. As for average download DR, this ratio is even more pronounced, reaching 15.1. This means that notable deviation exists in download DR among eight modems.
To sum up, the field measurement results allow to conclude that the network link quality asymmetry in a real-world situation is truly significant. Besides, it is revealed that the link quality asymmetry not only exists between two heterogeneous networks, but also between two modems using access technology operated by same telecommunication company. According to the above conclusions, we can infer that the network heterogeneity in future 5G will be more severe and become a concrete threat, since the wireless networks in 5G will become more diverse than nowadays with the deployment of emerging RATs.
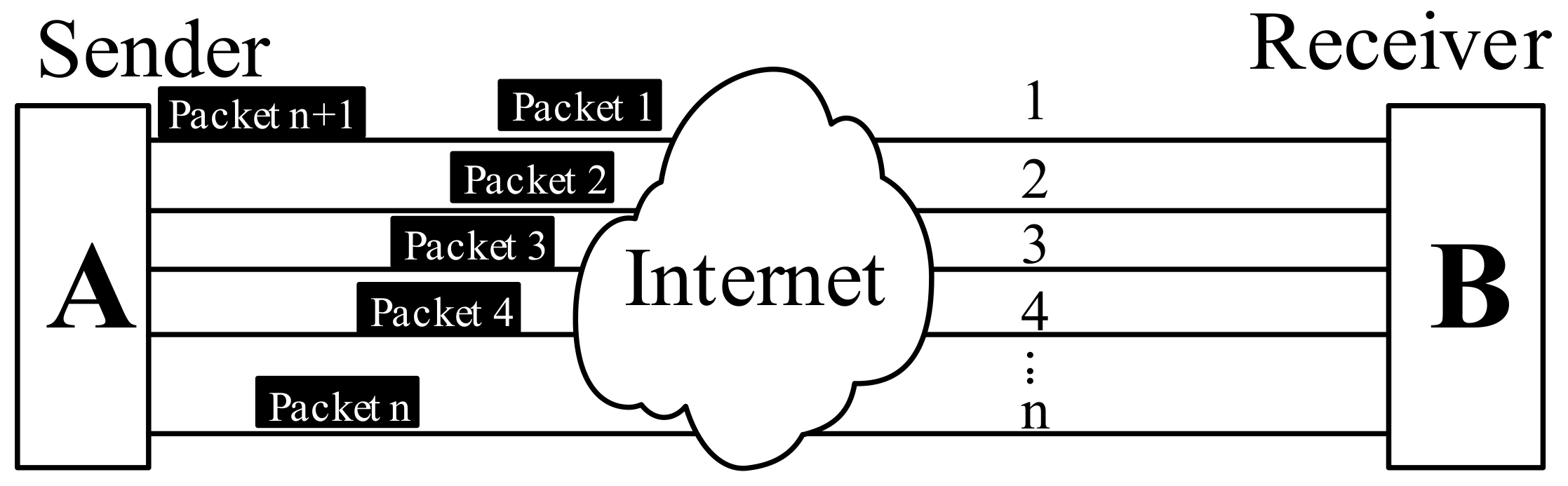
As we have demonstrated, the network heterogeneity will affect the performance of TCP-based CMT solutions for 5G mobile services. Thus, it is very essential to create a quantitative performance analysis model regarding the relationship between the link quality asymmetry and TCP multipath performance. To build such a performance analysis model, we first present the network model of TCP flow transferred over multiple heterogeneous links, as shown in
Figure 2. In this network model, the segments of single TCP connection are concurrently distributed over multiple paths between two endpoints. We use
to denote the set of all available heterogeneous links, the number of elements in
is
. Let
denote the set of round-trip propagation delay, and
denote the set of bandwidth. The number of elements in
and
are both
. The bandwidth and round-trip propagation delay of link
is
and
To simplify the analysis, we assume that the propagation delay from the receiver to sender is zero. Round Robin (RR) is used to dispatch packets in the given network mode, which let multiple paths take turns in transferring data packets in a periodically repeated order. We choose NewReno [
36] as the congestion control algorithm since it is still the widely deployed variant of TCP.
4. Performance Analysis Model
In this section, the performance analysis model of TCP over multiple heterogeneous paths is built by analyzing the average throughput. We divide the TCP flow into consecutive transmission round. The duration time as well as the number of segments transmitted at each round are first analyzed. Then, the average throughput is derived using an iteration model. At last, the effect of link quality asymmetry on average throughput is discussed.
Table 1 summarizes important parameters used in this paper.
4.1. Analysis of i-th Transmission Round
First, we focus on the transmission of segments at sender side. Let denote the number of transmission round from the beginning of the transmission. At -th round, sender transmits a certain number of unsent segments and waits for the acknowledgements. Since in most TCP implementations (such as NS3) only non-duplicate ACK triggers the transmission of previously unsent data, we can conclude that the -th round begins with the arrival of -th non-duplicate ACK.
Let
denote the total number of segments transmitted at
-th round.
equals the free space in the congestion window, which is composed of two parts: the increment in size of congestion window and the decrement in number of outstanding segments. We define
as the size of the congestion window of
-th round, and
as the increment of the congestion window. Let
denote the number of segments newly acknowledged by
-th non-duplicate
ACK, then
can be expressed as:
The
-th segment of
is defined as
. Let
denote the number of the link used to send the
, where
and
. Supposing segments are scheduled over
links in a round-robin manner, and the first one travels over link
. Hence
can expressed as:
The round-trip propagation delay as well as the bandwidth of link are and respectively. Let be the time elapsed between the beginning of -th round and when reaches the receiver, which is the sum of queuing delay and propagation delay experienced by . Thus,
In Equation (3), is the quotient of j and n, while is the average size of segments. The queuing delay is represented by , while represents the propagation delay.
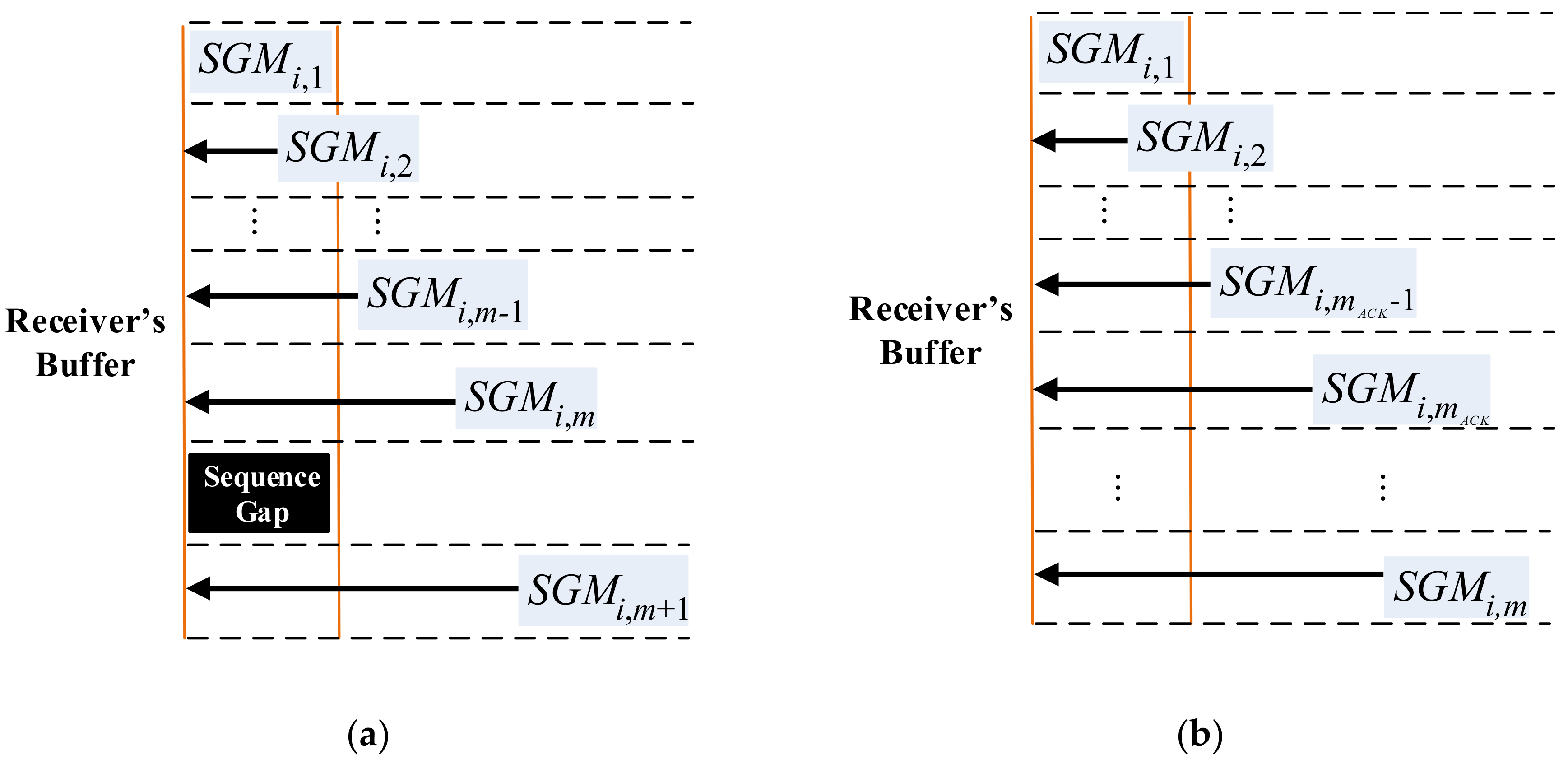
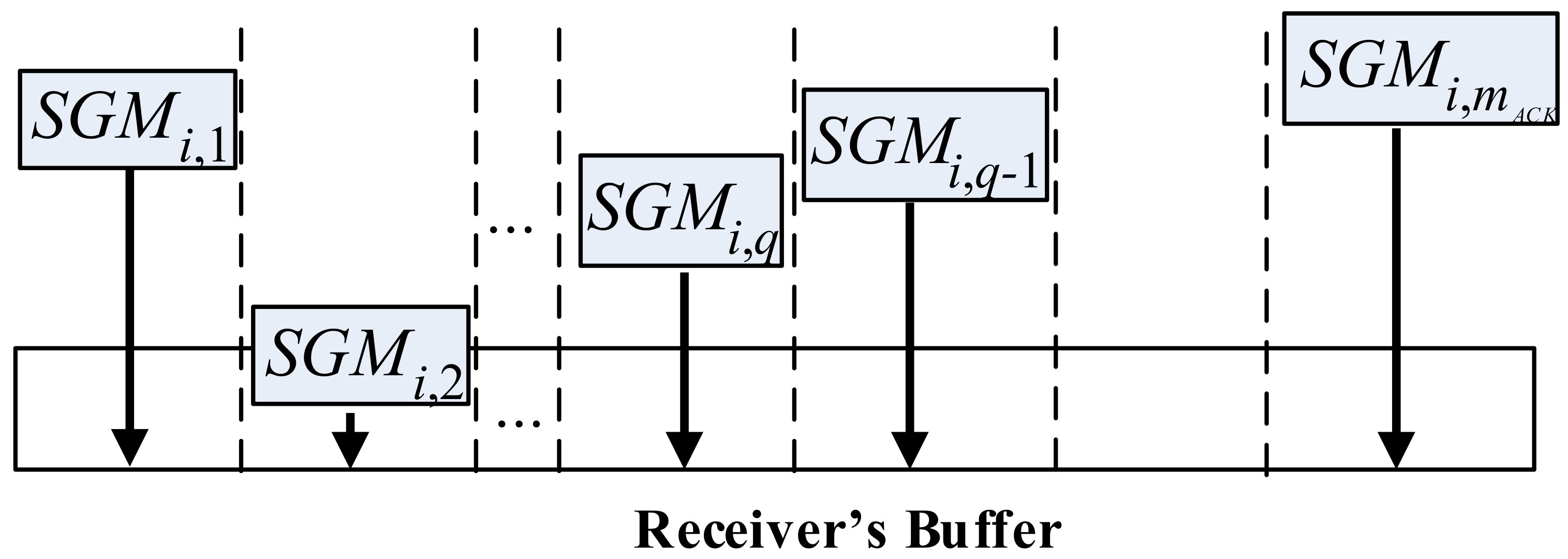
Then we discuss the arrival of segments and the response of ACKs at receiver side. We define as the latency between the beginning of -th round and the time when sender receives the first non-duplicate ACK that starts the -th round from the receiver. The number of segments the first non-duplicate acknowledges is exactly . A non-duplicate ACK will be fired by the receiver only if: (1) an expected number of consecutive segments are received; (2) the first out-of-order segments arrives after some consecutive segments or (3) a segment that fills the gap in the receiver’s buffer arrives. The satisfaction of these criteria highly associates with the arrival order of the first segment transmitted at -th round, which is . Hence, based on whether is the first to reach the receiver, we respectively calculate and .
4.1.1. Case I: is the First to Reach the Receiver
We define
as the probability that
arrives at the receiver first, which can be presented as:
The segments are scheduled over the links in a round-robin manner, thus follows a uniform distribution after a large amount of transmission rounds. Hence approximately equals .
Most TCP implementations (such as NS3) utilize a counter to delay replying cumulative
ACK. Let
denote this counter, after receiving
consecutive segments the receiver will reply an
ACK. In this case, since the receiver receives
first, it will wait for the following
segments before replying an
ACK until the arrival of first out-of-order segment, as shown in
Figure 3. Let
be the number of consecutive segments received before the arrival of first out of order segments. In other words,
to
arrive consecutive and
is out-of-order. Thus, the receiver will reply the first non-duplicate
ACK acknowledging
segments approximately after the arrival of
.
If
is smaller than
, we have
and
where
is the time between the beginning of
-th round and arrival of
. The probability
can be calculated as:
If
is equal to or larger than
,
and
. The corresponding probability
can be calculated as:
Let
and
denote the expected value of
and
under the condition that
is the first to reach the receiver. Based on the probabilities calculated in Equations (5) and (6), and the corresponding
and
,
and
can be derived as:
4.1.2. Case II: is not the First to Reach the Receiver
is defined as the probability of the
, where it is not the first to reach the receiver, which approximately equals
. In this case, the receiver will not reply any non-duplicate
ACK before the arrival of
. Moreover, since the segments transmitted subsequent to
arrives at the receiver earlier than it, there must be gaps in the receiver’s buffer before the arrival of
. As shown in
Figure 4, the receiver will immediately reply a non-duplicate
ACK after receiving
, since the
will fill part of the existing gap. Hence,
equals
.
Let
denote the number of received consecutive segments counting from
before the arrival of
. Hence, the number of segments the non-duplicate
ACK can acknowledge equals
, consequently we have
. The probability of
is derived as follows:
Let
and
denote the expected value of
and
under the condition that
is not the first to reach the receiver, which can be derived as:
Based on case I and case II, we can derive the expected value of
and
as
and
. Given that
and
,
and
can be calculated as follows:
From Equations (8) and (11) we can find that the expected value of depends on , which means is a function of . For simplicity, we define . Since equals the sum of and , the increment of the congestion window needs to be discussed.
In the slow start phase, the congestion window is incremented by one segment for each
ACK, thus
equals 1. Let
denote the slow start threshold of congestion window, and
the initial size of congestion window. Let
be the number of rounds that the slow start phase ends. Since the congestion window is increased by one every round, thus:
In the congestion avoidance phase, the congestion is increased by
on every incoming
ACK that acknowledges new data. Thus, we have
. The congestion window at
-th round can be expressed as:
Based on the above analysis, the relationship between
and
can be derived as Equation (15), where function
is defined in Equation (13):
4.2. Iteration for Average Throughput
According to Equation (16), the number of segments transmitted at next round can be derived based on that at the current round. Thus, the total segments transmitted from the beginning to current round of transmission can be calculated by iteration from the first round. The total time spent on transmitting can also be obtained by summing up the duration time of each transmission round. Consequently, the average throughput can be derived.
Therefore, we formulate the performing process of the model iteration as follows:
- Step 1
Supposing bytes of data are expected to be received by the receiver. At the first round of transmission, segments are sent within seconds, where equals the initial size of the congestion window, which is . can be calculated according to (12).
- Step 2
At -th round (), substituting into (15), we can get .
- Step 3
At -th round (), substituting and into (16), we can get . Further, according to (12), is computed.
- Step 4
Compute total transmitted bytes from beginning to
-th round, which is:
- Step 5
Let
denote total transmission time from beginning to
-th round, which can be computed as:
- Step 6
If total transmitted bytes is smaller than
, which is the number of bytes expected by the receiver, repeat
Steps 2–5. Otherwise, the iteration stops, and the average throughput can be calculated as:
4.3. Discussion of Link Quality Asymmetry
Here we discuss how link quality asymmetry affects the throughput of TCP transferred over multiple heterogeneous links. According to the proposed model, when transmitting a certain number of bytes, the average throughput is inversely proportional to the total transmission time
. Since
is the sum of
defined in Equation (12), the average throughput decreases with increasing
. Substituting
defined in (7) and
defined in (10) into (12),
can be evaluated as:
Apart from parameter
,
is primarily associated with
, where
.
represents the time difference between the arrival of the first transmitted segment
and the
-th transmitted segment
at the receiver side. Longer time difference increments the overall
. Substituting (3),
can be evaluated as:
As demonstrated in Equation (18), is mainly dominated by two elements, and . and are respectively the delay difference and bandwidth difference between two links that transmit and , i.e., and . Increasing and leads to greater , and consequently causes larger , which eventually results in a decrease in average throughput.
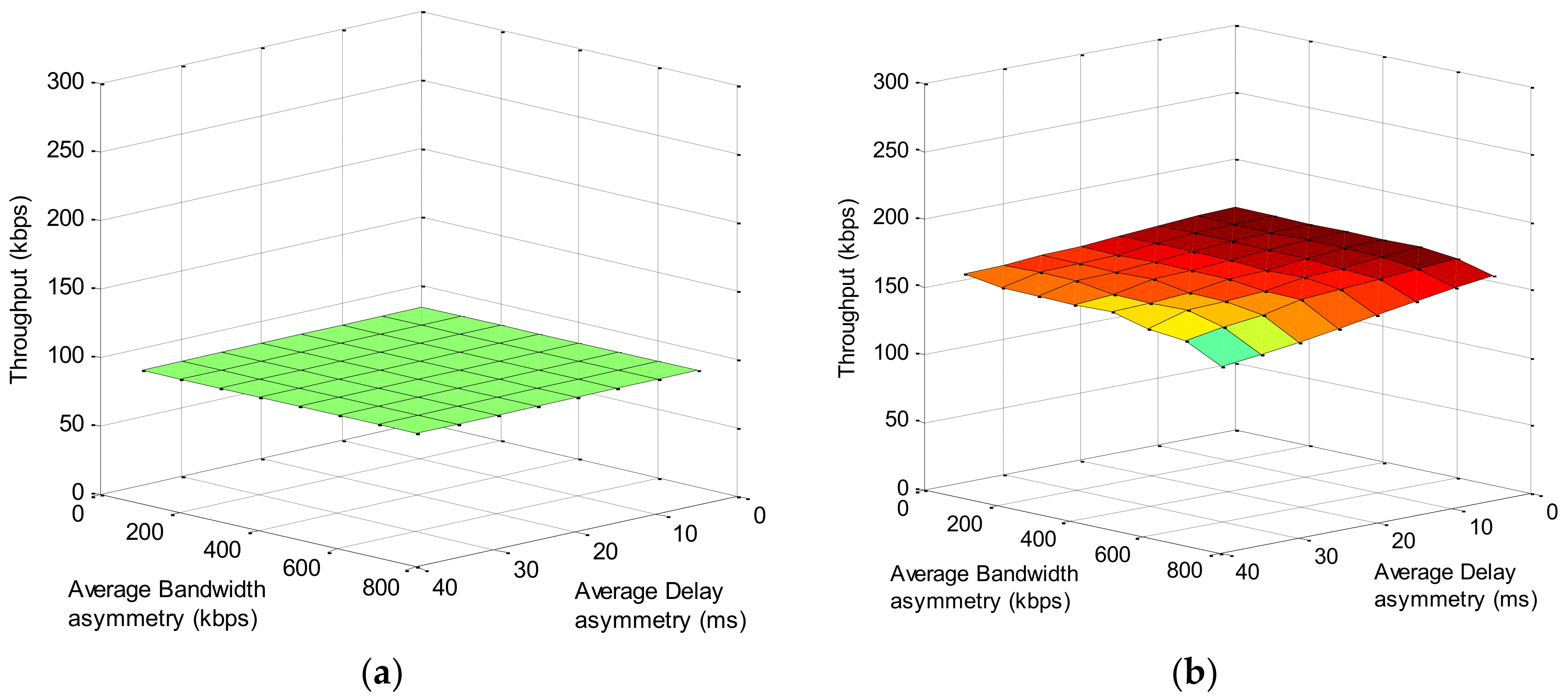
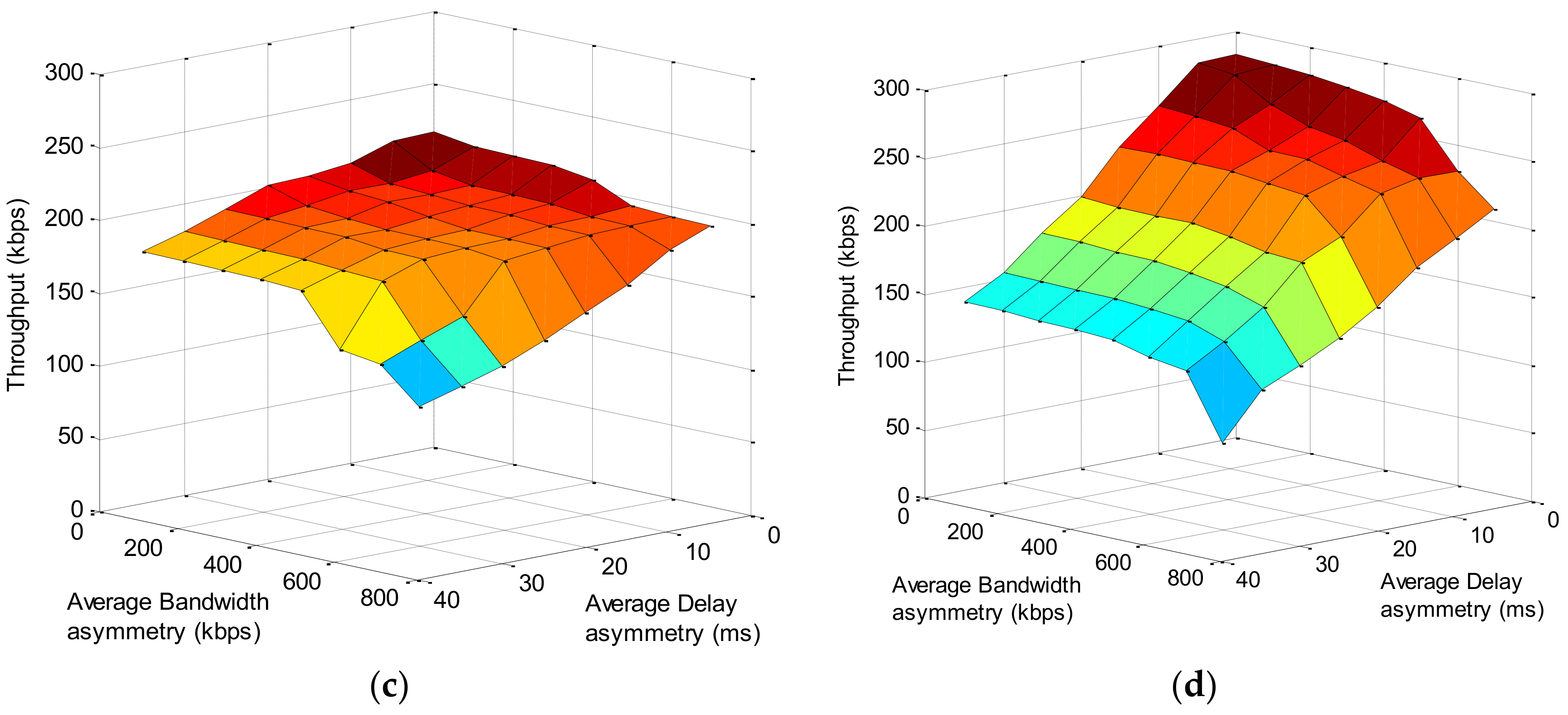
As mentioned earlier, when scheduled in round-robin manner, the possibility of selecting one of available links to transmit a certain segment follows a uniform distribution after a large amount of transmission rounds. Thus, and can represent any two links of set . Note that is not the first link of available links, but the link used to transmit . Equally, and can be the delay difference and bandwidth difference between any two links. From this point of view, and reflect the extent of deviation in link quality of all links. We refer to such delay difference and bandwidth difference between any two links as delay asymmetry and bandwidth asymmetry. Therefore, it can be concluded that the average throughput is subject to delay asymmetry and bandwidth asymmetry. The more significant these two parameters become, the lower average throughput will be.
To quantify delay asymmetry, we introduce Average Delay Asymmetry, which is defined as the average absolute delay difference between any two links of
available links. Average Delay Asymmetry can be calculated as:
Similarly, Average Bandwidth Asymmetry can be defined as:
Average Delay Asymmetry and Average Bandwidth Asymmetry can both affect the performance of TCP transferred over multiple heterogeneous links. Comparison of extent of these two parameters on TCP performance will be presented in
Section 6.