A Sustainable Land Utilization Pattern for Confirming Integrity of Economic and Ecological Objectives under Uncertainties
Abstract
:1. Introduction
2. Application
2.1. Study Area
2.2. Construction of an Integrated Crop–Forest System
2.3. Modeling Formulation
- Reallocated land resource with market approach:In a traditional land utilization plan, the actual land resources can be reallocated to each plant by the proportion based on expected target. The market approach can be introduced to prompt land resources from lower value to higher value by the law of value, which can support land reallocation optimally. Model (2a) shows land resources reallocation based on market approach, where the productivities of land resources can be improved by reallocated actions ( and ) based on total land resources () (ha). is the total land resources in study region (ha).
- Water quantity and water supply capacity for irrigative activities:Model (2b) presents available water for irrigation and forest without market approach, where a land plan associated with water quantity based on regional water resource load can be expressed. If water cannot satisfy the expected land targets, water deficits occur, which are caused by uncertain water availabilities. Water availability equals available water from surface and underground ( and ) minus evaporation (), watercourse loss () and minimum ecological requirement () (m3). is the available water from surface (m3); is the available water from underground (m3); is the total evaporation in study region (m3); is the watercourse loss (m3); is water conservation ability of forest per ha (m3/ha); and is rainfall runoff coefficient (%). In Model (6b), since available water can be deemed as stochastic and random variables impacted by spatio-temporal factors, fuzzy measure Cr can be advocated to express such fuzziness, where is the credibility level through the QSF method (as shown in the Appendix A). Model (2c) shows the water supply capacity for irrigative activities in period t under probability (m3). The model presents that maximum supply capacity (i.e., ) can be restricted by water availability. A market approach can prompt the efficiency of land plan; limited water resources can restrict the development of crop planting and environmental protecting. Thus, Model (2d) presents available water for irrigation and forest protection through a market approach, where water deficits occur when water cannot be delivered to the reallocated land. and are the water shortage area (ha).
- Pollution purification capacity through market approach:
- Total nitrogen allowance:
- Total phosphorus allowance:
- Soil and water conservation capacity:Model (2e) presents that capacity of purification from forest system (through ecological effect) with market approach hinges on the coefficient of purification (i.e., , ) under probability (m3) in period t. and are the actual pollution purification capacities through ecological effect with a market approach (ton). and are the coefficient of purification with consideration of ecological effect, which can be obtained based on previous research works. Models (2f) and (2g) present that pollutant discharges from crop irrigation would impose restrictions on discharge allowance ( and ). and are maximum allowable TN and TP discharges from irrigation in period t (ton), which have been expressed as credibility fuzzy manners. In fact, actual nitrogen and phosphorus discharges would be original discharge from irrigative activities minus the values that being purification through ecological effect [as shown in Models (2f) and (2g)]. Since the capacity of water conservation and soil erosion of forest can relieve the adverse effect from irrigation, Models (2h) and (2i) present that the total capacities of water and soil conservation would be restricted by their maximum capacities ( and ) in study region. and are the coefficients of ecological effect for soil and water conservation from a forest system in period t (%). and are maximum allowances for water and soil erosion in period t (ton).
- Non-negativity:Model (2j) is non-negativity restrictions.
2.4. Data Acquisition
3. Result Analysis
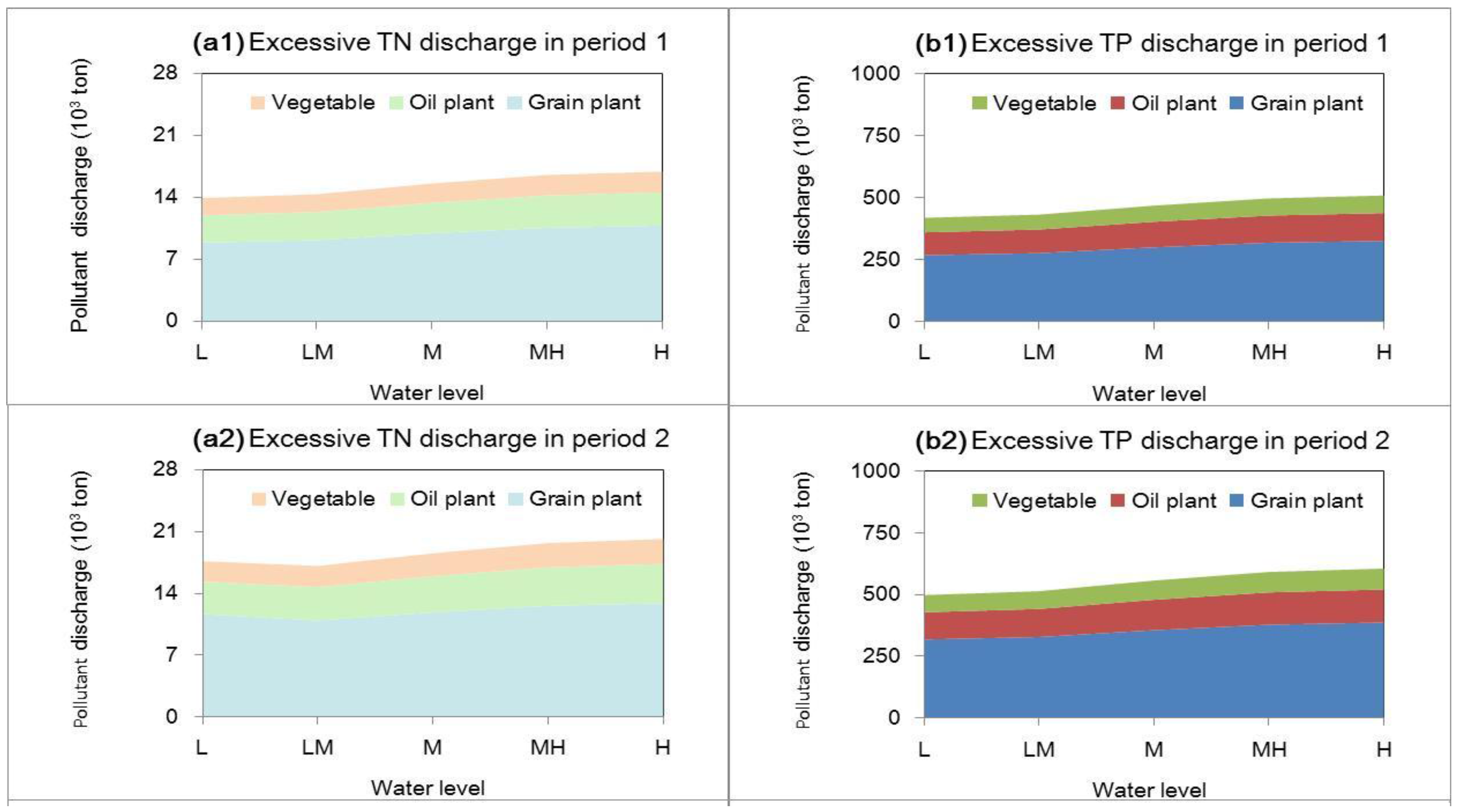
3.1. Adverse Effects from Crop Irrigation without Market Approach
3.2. Land Trade between Forest and Irrigation
3.3. Ecological Effects and Corresponding Benefit from Market Approach
3.4. System Benefit with and without Market Approach
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References and Notes
- Mensing, D.M.; Galatowitsch, S.M.; Tester, J.R. Anthropogenic effects on the biodiversity of riparian forests of a northern temperate landscape. J. Environ. Manag. 1998, 53, 349–377. [Google Scholar] [CrossRef]
- Rai, R.; Zhang, Y.; Paudel, B.; Li, S.; Khanal, N.R. A synthesis of studies on land use and land cover dynamics during 1930–2015 in Bangladesh. Sustainability 2017, 9, 1866. [Google Scholar] [CrossRef]
- Motesharrei, S.; Rivas, J.; Kalnay, E. Human and nature dynamics (HANDY): Modeling inequality and use of resources in the collapse or sustainability of societies. Ecol. Econ. 2014, 101, 90–102. [Google Scholar] [CrossRef]
- Weißhuhn, P.; Reckling, M.; Stachow, U.; Wiggering, H. Supporting agricultural ecosystem services through the integration of perennial polycultures into crop rotations. Sustainability 2017, 9, 2267. [Google Scholar] [CrossRef]
- Calatrava, J.; Garrido, A. Spot water markets and risk in water supply. Agric. Econ. 2005, 33, 131–143. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Xiao, H.N.; Qin, X.S. An inexact two-stage quadratic program for water resources planning. J. Environ. Inform. 2007, 10, 99–105. [Google Scholar]
- Abildtrup, J.; Garcia, S.; Stenger, A. The effect of forest land use on the cost of drinking water supply: A spatial econometric analysis. Ecol. Econ. 2013, 92, 126–136. [Google Scholar] [CrossRef]
- Ondei, S.; Prior, L.D.; Williamson, G.J.; Vigilante, T.; Bowman, D.M. Water, land, fire, and forest: Multi-scale determinants of rainforests in the Australian monsoon tropics. Ecol. Evol. 2017, 7, 1592–1604. [Google Scholar] [CrossRef] [PubMed]
- Samie, A.; Deng, X.; Jia, S.; Chen, D. Scenario-based simulation on dynamics of land-use-land-cover change in Punjab province, Pakistan. Sustainability 2017, 9, 1285. [Google Scholar] [CrossRef]
- Johnson, K.A.; Polasky, S.; Nelson, E.; Pennington, D. Uncertainty in ecosystem services valuation and implications for assessing land use tradeoffs: An agricultural case study in the Minnesota River Basin. Ecol. Econ. 2012, 79, 71–79. [Google Scholar] [CrossRef]
- Zeng, X.T.; Yang, X.L.; Yu, L.Y.; Chen, H.L. A mix inexact-quadratic fuzzy water resources management model of floodplain (IQT-WMMF) for regional sustainable development of Dahuangbaowa, China. Water 2015, 7, 2771–2795. [Google Scholar] [CrossRef]
- Perez-Garcia, J.; Joyce, L.A.; Mcguire, A.D. Temporal uncertainties of integrated ecological/economic assessments at the global and regional scales. For. Ecol. Manag. 2002, 162, 105–115. [Google Scholar] [CrossRef]
- Hauk, S.; Gandorfer, M.; Wittkopf, S.; Müller, U.K.; Knoke, T. Ecological diversification is risk reducing and economically profitable—The case of biomass production with short rotation woody crops in south German land-use portfolios. Biomass Bioenergy 2017, 98, 142–152. [Google Scholar] [CrossRef]
- Zeng, X.T.; Li, Y.P.; Huang, W.; Bao, A.M.; Chen, X. Two-stage credibility-constrained programming with Hurwicz criterion (TCP-CH) for planning water resources management. Eng. Appl. Artif. Intell. 2014, 35, 164–175. [Google Scholar] [CrossRef]
- Whelan, M.J.; Hope, E.G.; Fox, K. Stochastic modelling of phosphorus transfers from agricultural land to aquatic ecosystems. Water Sci. Technol. 2002, 45, 167–175. [Google Scholar] [PubMed]
- Han, Y.; Huang, Y.; Wang, G. Interval-parameter linear optimization model with stochastic vertices for land and water resources allocation under dual uncertainty. Environ. Eng. Sci. 2011, 28, 197–205. [Google Scholar] [CrossRef]
- Djanibekov, U.; Khamzina, A. Stochastic economic assessment of afforestation on marginal land in irrigated farming system. Environ. Resour. Econ. 2016, 63, 95–117. [Google Scholar] [CrossRef]
- Djanibekov, U.; Villamor, G.B. Market-based instruments for risk-averse farmers: Rubber agroforest conservation in Jambi Province, Indonesia. Environ. Dev. Econ. 2016, 22, 133–155. [Google Scholar] [CrossRef]
- Guo, P.; Huang, G.H.; Li, Y.P. Inexact Fuzzy-Stochastic Programming for Water Resources Management Under Multiple Uncertainties. Environ. Model. Assess. 2010, 15, 111–124. [Google Scholar] [CrossRef]
- Zeng, X.T.; Zhao, J.Y.; Yang, X.L.; Wang, X.; Xu, C.W.; Cui, L.; Zhou, Y. A land-indicator-based optimization model with trading mechanism in wetland ecosystem under uncertainties. Ecol. Indic. 2017, 74, 279–299. [Google Scholar] [CrossRef]
- Dunn, S.M.; Brown, I.; Sample, J.; Post, H. Relationships between climate, water resources, land use and diffuse pollution and the significance of uncertainty in climate change. J. Hydrol. 2012, 434–435, 19–35. [Google Scholar] [CrossRef]
- Inuiguchi, M.; Ramík, J. Possibilistic linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst. 2000, 111, 3–28. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Sen, Z. Fuzzy logic model of lake water level fluctuations in Lake Van, Turkey. Theor. Appl. Climatol. 2007, 90, 227–233. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Yeomans, J.S. An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Deng, X.; Xu, Y.; Han, L.; Yu, Z.; Yang, M. Assessment of river health based on an improved entropy-based fuzzy matter-element model in the Taihu Plain, China. Ecol. Indic. 2015, 57, 85–95. [Google Scholar] [CrossRef]
- Chena, M.J.; Huang, G.H. A derivative algorithm for inexact quadratic program-application to environmental decision-making under uncertainty. Eur. J. Oper. Res. 2001, 128, 570–586. [Google Scholar] [CrossRef]
- Huang, G.H.; Loucks, D.P. An inexact two-stage stochastic programming model for water resources management under uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.K. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar]
- Trumbo, C.W.; McComa, K.A. The Function of Credibility in Information Processing for Risk Perception. Risk Anal. 2003, 23, 343–353. [Google Scholar] [CrossRef] [PubMed]
- The statistical yearbook of Henan province (SYH), 2000, China, 2001.
- The statistical yearbook of Henan province (SYH), 2004, China, 2005.
- The statistical yearbook of Henan province (SYH), 2009, China, 2010.
- The statistical yearbook of Henan province (SYH), 2013, China, 2014.








| Sector | Period | |||
|---|---|---|---|---|
| t = 1 | t = 2 | t = 3 | ||
| Net Benefit ($103/ha) | ||||
| Farming corps | Grain | (11.0 ✕ + 210.7) | (8.0 ✕ + 229.0) | (9.0 ✕ + 255.0) |
| Oil plants | (23.0 ✕ + 203.3) | (5.0 ✕ + 257.0) | (7.0 ✕ + 260.7) | |
| Vegetable | (9.0 ✕ + 225.0) | (8.0 ✕ + 237.0) | (9.0 ✕ + 265.0) | |
| Forest system | Economic forest | (5.5 ✕ + 181.6) | (11.5 ✕ + 198.6) | (11.5 ✕ + 254.7) |
| Shelter forest | (75.5 ✕ + 177.0) | (75.5 ✕ + 202.0) | (85.5 ✕ + 237.6) | |
| Forest park | (75.5 ✕ + 184.0) | (145.5 ✕ + 188.6) | (85.5 ✕ + 227.0) | |
| Penalty of Water Deficit ($103/ha) | ||||
| Farming corps | Grain | (6.5 ✕ + 316.67) | (8.0 ✕ + 329.0) | (9.0 ✕ + 355.0) |
| Oil plants | (23.0 ✕ + 303.9) | (5.0 ✕ + 35.07) | (7.0 ✕ + 360.6) | |
| Vegetable | (7.5 ✕ + 336.0) | (7.0 ✕ + 341.3) | (9.0 ✕ + 357.6) | |
| Forest system | Economic forest | (5.5 ✕ + 281.6) | (11.5 ✕ + 298.7) | (11 ✕ + 354.6) |
| Shelter forest | (7.0 ✕ + 277.0) | (7.0 ✕ + 302.0) | (8.5 ✕ + 337.8) | |
| Forest park | (7.0 ✕ + 284.0) | (14.0 ✕ + 288.6) | (8.5 ✕ + 327.0) | |
| Period | ||||
|---|---|---|---|---|
| t = 1 | t = 2 | t = 3 | ||
| Maximum irrigation scale (ha) | Grain plant | 1635 | 1678 | 1724 |
| Oil plant | 165 | 189 | 222 | |
| Vegetable plant | 350 | 388 | 416 | |
| TP discharge rate of crop irrigation (10−3 ton/ha year) | Grain plant | 9.8 | 9.9 | 10 |
| Oil plant | 9.1 | 9.1 | 9.2 | |
| Vegetable plant | 10.2 | 10.3 | 10.2 | |
| TN discharge rate of crop irrigation (10−3 ton/ha year) | Grain plant | 0.43 | 0.45 | 0.46 |
| Oil plant | 0.45 | 0.45 | 0.45 | |
| Vegetable plant | 0.52 | 0.52 | 0.53 | |
| Maximum allowance total TP discharge (103 ton/year) | 2.35 | 2.43 | 2.56 | |
| Maximum allowance total TN discharge (103 ton/year) | 0.33 | 0.36 | 0.39 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Cui, L.; Tan, Q.; Li, Z.; Huang, G. A Sustainable Land Utilization Pattern for Confirming Integrity of Economic and Ecological Objectives under Uncertainties. Sustainability 2018, 10, 1307. https://doi.org/10.3390/su10051307
Zeng X, Cui L, Tan Q, Li Z, Huang G. A Sustainable Land Utilization Pattern for Confirming Integrity of Economic and Ecological Objectives under Uncertainties. Sustainability. 2018; 10(5):1307. https://doi.org/10.3390/su10051307
Chicago/Turabian StyleZeng, Xueting, Liang Cui, Qian Tan, Zhong Li, and Guohe Huang. 2018. "A Sustainable Land Utilization Pattern for Confirming Integrity of Economic and Ecological Objectives under Uncertainties" Sustainability 10, no. 5: 1307. https://doi.org/10.3390/su10051307
APA StyleZeng, X., Cui, L., Tan, Q., Li, Z., & Huang, G. (2018). A Sustainable Land Utilization Pattern for Confirming Integrity of Economic and Ecological Objectives under Uncertainties. Sustainability, 10(5), 1307. https://doi.org/10.3390/su10051307








